Radial stiffness characteristics of the overlap regions of sarcomeres in isolated skeletal myofibrils in pre-force generating state

Abstract

We have studied the stiffness of myofilament lattice in sarcomeres in the pre-force generating state, which was realized by a relaxing reagent, BDM (butane dione monoxime). First, the radial stiffness for the overlap regions of sarcomeres of isolated single myofibrils was estimated from the resulting decreases in diameter by osmotic pressure applied with the addition of Dextran. Then, the radial stiffness was also estimated from force-distance curve measurements with AFM technology. The radial stiffness for the overlap regions thus obtained was composed of a soft and a rigid component. The soft component visco-elastically changed in a characteristic fashion depending on the physiological conditions of myofibrils, suggesting that it comes from cross-bridge structures. BDM treatments significantly affected the soft radial component of contracting myofibrils depending on the approach velocity of cantilever: It was nearly equal to that in the contracting state at high approach velocity, whereas as low as that in the relaxing state at low approach velocity. However, comparable BDM treatments greatly suppressed the force production and the axial stiffness in contracting glycerinated muscle fibers and also the sliding velocity of actin filaments in the in vitro motility assay. Considering that BDM shifts the cross-bridge population from force generating to pre-force generating states in contracting muscle, the obtained results strongly suggest that cross-bridges in the pre-force generating state are visco-elastically attached to the thin filaments in such a binding manner that the axial stiffness is low but the radial stiffness significantly high similar to that in force generating state.

Significance.

The measurements of radial stiffness with AFM of an overlap region in sarcomeres of skeletal myofibrils showed that the cross-bridges in pre-force generating state realized by the addition of BDM (relaxing reagent) are anisotropically and visco-elastically attached to the thin filaments. The radial stiffness in force-generating state with BDM was comparable to that without BDM, whereas the axial stiffness of contracting fibers was substantially reduced with BDM.

Skeletal muscle fiber is a bundle of myofibrils composed of a periodic series of sarcomeres, the contractile unit of muscle fiber [1]. In the sarcomere, actomyosin filaments are arranged in a regular lattice producing the overlap region of the two myofilaments, the thick (myosin) and the thin (actin) filaments. The contractile force is produced by the interaction of cross-bridges protruding from the thick filaments with the thin filaments. The molecular mechanism of the force production has extensively been studied based on the axial mechanical properties of cross-bridges interacting with the thin filaments. However, the analysis of the atomic structures of myosin head and the thin filament [2,3] showed that, associated with the force production or the power stroke, myosin heads interact with the thin filament changing its axial as well as radial configurations relative to the filament axis. Therefore, the radial mechanical properties of cross-bridges interacting with the thin filaments should also be clarified for elucidating the detailed molecular basis for the force production in muscle fiber.

The radial stiffness of skeletal muscle fibers in various physiological states was studied by compressing with the osmotic pressure produced by the addition of high molecular weight polymers like Dextran [4–6]. By the radial compressions, the force production as well as ATP cycling in muscle fibers were suppressed [7–9]. Further it was reported that the radial elasticity of cross-bridges changed depending on the physiological conditions in skinned muscle fibers [10]. By applying AFM technology, similar studies were performed for single myofibrils isolated from skeletal muscle [11–14] which is known to retain the characteristic filament structures and contractility [15,16]. As isolated single myofibrils are devoid of soluble and membranous components present in muscle fibers, the radial stiffness component coming from the actomyosin filament lattice incorporated in sarcomeres was identified based on the radial stiffness measurements for the overlap regions of single myofibrils with AFM [14].

In the present study, we extended these AFM experiments of isolated single skeletal myofibrils and examined the radial stiffness of the pre-force generating cross-bridges in the actomyosin filament lattice. The pre-force generating cross-bridges were realized by the addition of BDM (butane dione monoxime) to contracting myofibrils, the effect of which was to shift the cross-bridge population from the force generating to the pre-force generating state [17–19]. Here the radial stiffness of the overlap regions was estimated by the compressions with Dextran and also with AFM cantilever. In the latter experiments, in order to clarify visco-elastic characteristics due to the attachment and detachment of cross-bridges in the filament lattice, dynamic changes of the radial stiffness of the overlap regions were examined by changing the compression velocity of AFM cantilever, where we also examined the effects of AMPPNP, a non-hydrolysable ATP analogue known to specifically bind to cross-bridges and make them weakly attached to the thin filaments [1,20].

Further, in parallel to the above experiments, we examined the effects of BDM on the force production and axial stiffness of glycerinated muscle fibers and also on the sliding of actomyosin filaments in the in vitro motility assay. And based on the results obtained by the above experiments, we will discuss the stiffness characteristics of the pre-force generating cross-bridges in contracting muscle.

Materials and Methods

Preparations of glycerinated muscle fibers, single myofibrils and muscle proteins

The psoas muscles dissected from white rabbits were used for experiments. The care of animals and the experimental protocols of animal experiments were approved by the Animal Care and Use Committee of Tokyo University of Science. Muscle proteins for the in vitro motility assay were prepared from the back and leg white muscles, and fluorescent actin filaments were prepared by incubating actin in a solution containing rhodamine-phalloidin as previously described [21]. Glycerinated muscle fibers were prepared as previously described [22] by skinning thin muscle bundles split from psoas muscle tissues in a relaxing solution (see the composition of solutions below) containing 1.0% Triton X-100, and stored in a relaxing solution containing 50% glycerol at −20°C. Single muscle fibers for force experiments were dissected from glycerinated muscle fibers as previously described [23]. Single myofibrils for AFM experiments were prepared by mechanically homogenizing glycerinated muscle fibers as previously described [16].

AFM measurements of force-distance curves for isolated single myofibril preparations

AFM measurements were performed as previously with an AFM instrument (NV2500; Olympus, Tokyo, Japan) incorporated in an inverted optical microscope (IX-70; Olympus, Tokyo, Japan) [11]. A modified cantilever, called a bead-tip cantilever (see Fig. 1A), was used [13], which had a glass micro-bead of 2 μm in diameter (Thermo Fisher Scientific, MA, USA) glued via another micro-bead (5 μm in diameter) to the tip of the commercial cantilever having spring constant of 20 pN/nm (OMCL-TR400PSA-HW; Olympus, Tokyo, Japan).

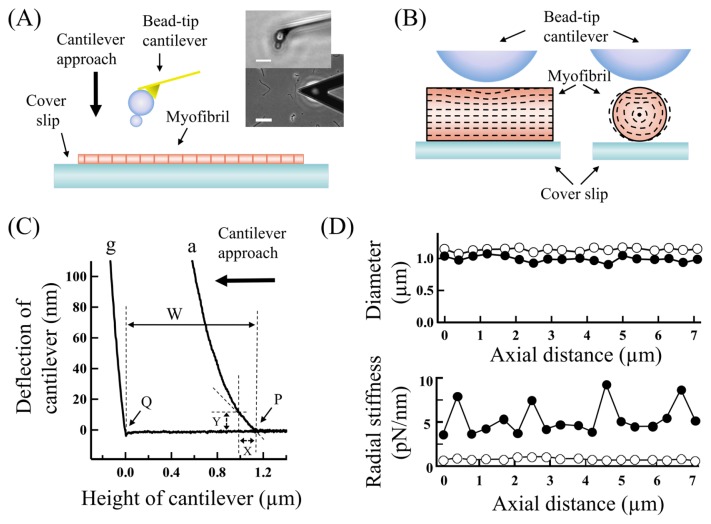
Figure 1.

(A) A schematic side view of the arrangement for AFM measurements of a single myofibril. (Inset) Optical microscopic images of a cantilever positioned over a single skeletal myofibril adsorbed to the surface of cover glass treated with amino-silane (scale, 50 μm) and an enlarged side-view of the bead-tip cantilever (scale, 10 μm). (B) Schematic cross-sectional views of the arrangement of a rigid bead over an elastic cylindrical rod put on a rigid plate, mimicking the AFM experiments of single myofibrils. The dashed images show deformations in the rod compressed with the bead by 10% of its diameter, simulated by the finite element analysis. (C) Typical force-distance curves for the overlap region of a single skeletal myofibril adsorbed to cover glass in rigor state (a) and also for the cover glass (g). The same letter (g) is assigned to force-distance curves for cover glass in the following figures. The thickness of the overlap region, represented by W, is the height of the top surface of the overlap region P from the surface of the cover glass Q. Y represents the deflection of cantilever produced by lowering the cantilever from the top surface of the overlap region by X. And the indentation of the overlap region is X minus Y. (D) Typical distributions of the diameter and radial stiffness along a single myofibril adsorbed to cover glass in (filled circles) rigor and (open circles) relaxed states, which were obtained at the cantilever approach velocity of 0.1 μm/s. The thick vertical and horizontal arrows in (A) and (C), respectively, indicate the direction of cantilever approach relative to the specimen. For more details, see the text.

An experimental chamber for AFM measurements (about 100 μl in volume) was a trough cut in a silicone-rubber sheet and glued on a cover glass (C024601; Matsunami, Osaka, Japan). Before each AFM experiment, the surface of the bottom cover glass of the experimental chamber was cleaned and treated with amino-silane to facilitate the adsorption of myofibrils [24]. After introducing a myofibril suspension into the experimental chamber and making myofibrils adsorbed to its bottom surface, the chamber was installed to the microscope stage of AFM system. The bathing solution in the experimental chamber was manually exchanged by a solution having appropriate compositions. AFM measurements were performed within 5–10 min after the exchange of solutions. Single myofibrils stably adsorbed to the surface of cover glass treated with amino-silane as described above showed no changes in the overall shapes and striation patterns during measurements, even in contracting solutions over one hour. Their sarcomere lengths were 2.0–2.2 μm under the optical microscope, in which the thin and thick filaments were fully overlapped [22]. On the other hand, preparations not stably adsorbed to cover glass were greatly deformed when put into contracting solutions. It is suggested that the adsorption of single myofibrils to cover glass greatly stabilizes their filament lattice structures, although we cannot exclude a possibility that the nanoscopic structure of a myofilament lattice just above the adsorbed cover glass may slightly be distorted.

By positioning the cantilever tip at an appropriate locus under optical microscope within the error of about 0.15 μm, force-distance curves were obtained by approaching the cantilever to specimen basically at a velocity of 0.1 μm/s, named a slowly moving cantilever, and also at faster velocities up to 38 μm/s. Actually, in the present AFM system, the cantilever was fixed at an appropriate position and the experimental chamber was moved via the microscope stage by use of a built-in 3D actuator system having a working distance of about 12 μm with the precision of ±2 nm (P-753.11C/E-501.00; Physik Instrumente, Berlin, Germany) controlled by a computer system (Lab-View; National Instruments, TX, USA). Both the height and the deflection of cantilever were recorded on a digital oscilloscope (Model 20; Nicolet, WI, USA) and analyzed on a computer.

Estimations of the radial stiffness of the overlap region in single myofibril preparations

In this study, we have studied relative difference of the radial stiffness of the overlap regions among myofibrils in various physiological states. The radial stiffness was estimated by two different methods as below, both based on force-distance curves for the overlap regions of single myofibrils adsorbed to a cover glass (see Fig. 1A). The force-distance curves for the overlap region were obtained by positioning the tip of AFM cantilever at the top of and near the center of the overlap region of an appropriate sarcomere of single myofibrils by monitoring the microscopic image of their striation pattern [11]. The parameters used for analyses are depicted in Figure 1C using typical force-distance curves for a rigor myofibril adsorbed to a cover glass and also for the cover glass. To estimate the radial stiffness, we have experimentally determined the values of these parameters except for the area of contact between the tip of cantilever and the surface of myofibrils, which was tentatively estimated as described below.

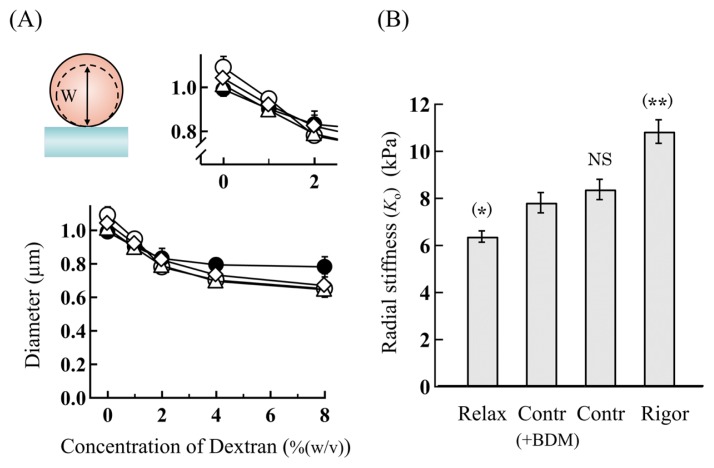
First, the radial stiffness was estimated based on the diameter decrease in the overlap region produced by the osmotic compression with Dextran (Fig. 4A, inset left). Thus the radial stiffness (K_o), expressed in kPa unit, was determined as the increase in the osmotic pressure due to Dextran (π) divided by the fractional diameter decrease of the overlap region (ΔW/W), basically following the method employed by others [5,6]. The diameter of the overlap region (W) was determined from its thickness based on force-distance curves as depicted in Figure 1C, namely as the height of the top surface of an overlap region (P) from the surface of cover glass close to the overlap region (Q), the positions of which were determined by extrapolating the slope of the initial uprising region of force distance curves to the base line by use of the least mean square fitting. The diameter was determined with the error of about 5% due to the positioning error of cantilever (see the cross-sectional view in Fig. 1B). The osmotic pressure due to the addition of Dextran was employed from the values documented in the literatures [25–27].

Figure 4.

(A) Diameter changes of the overlap regions of single skeletal myofibrils in various physiological states as a function of the Dextran concentration. (Inset, top-left) Schematic cross-sectional view of a single myofibril. The dotted image shows that the diameter (W) of a myofibril is compressed with the addition of Dextran. (Inset, top-right) Enlarged around the Dextran concentration of 0–2%(w/v). (filled circles) Rigor, (open triangles) contracting, (open diamonds) contracting(+BDM) and (open circles) relaxed myofibrils. (B) Comparison of the radial stiffness (K_o) of the overlap regions among myofibrils in various physiological states. The statistical difference levels between the radial stiffness (K_o) of myofibrils in various physiological states and that of contracting(+BDM) myofibrils are represented by (*) for p<0.05, (**) for p<0.01, and NS (not significant) for p>0.10 at the top of the pillars. The concentration of BDM: 20 mM. The vertical bars represent the SEM (n=5–7), several of which are omitted for clarity in (A). See the details in the text.

Second, the radial stiffness of the overlap regions was estimated based on the indentation of the surface of overlap regions produced by the cantilever compression. The radial stiffness was expressed by a N/m unit as previously [13,14], namely the elastic constant as the force applied to the cantilever (F) divided by the indentation of overlap regions (D). The force applied to cantilever (F) was determined from the deflection of cantilever considering its spring constant. The indentation of overlap regions (D) was calculated as the distance of the cantilever lowered from the top surface of the overlap region minus the deflection of cantilever (X minus Y in Fig. 1C). In order to compare with the radial stiffness (K_o), the radial stiffness was also expressed by a Pa unit, called the radial stiffness (K_m), as the pressure applied to the cantilever (π) divided by the fractional indentation of the overlap region (D/W); i.e., the radial stiffness (K_m)=π/(D/W). The pressure applied to the overlap region (π) was calculated as the force applied to cantilever (F) divided by the contact area (S) produced between the cantilever tip and the overlap region. The contact area (S) was estimated based on the finite element analysis as below.

The deformations of the overlap regions were simulated for an elastic cylindrical rod placed on a rigid plate and compressed with a rigid bead by use of a computer software for the finite element analysis (MSC Nastran; MacNeal-Schwendler, CA, USA). The rod was assumed to be uniform having the Young’s modulus of 10–90 kPa considering the values measured for the overlap region of skeletal myofibrils [11]. In Figure 1B are shown typical deformed images of the cross-sections of a rod having the Young’s modulus of 10 kPa compressed by 10% of its diameter. It can be seen that the top area of the rod is indented and some other areas expanded, suggesting that the regular filament lattice of overlap regions would be non-uniformly deformed by the cantilever compressions. In the following, to minimize the contributions from non-uniform deformations, the radial stiffness was analyzed based on the slope of the initial uprising region of force-distance curves where the overlap regions were indented up to 100 nm from their surface, about 10% of the diameter. And based on the above simulation, the contact area was assumed to be 0.4 μm² when the overlap regions were indented by 100 nm. The radial stiffness (K_m) introduced in the present study may be comparable to the apparent radial Young’s modulus employed in our previous studies [11,14].

For reference, typical distributions of the diameter and the radial stiffness along a single myofibril adsorbed to cover glass are shown in Figure 1D. The overlap regions of actomyosin filaments in sarcomeres were soft and rigid in relaxing and rigor solutions respectively, and could readily be located in between very rigid Z-discs in rigor solutions. In relaxing solutions, the Z-discs apparently got soft, which may be artifacts due to tilting of the Z-discs by the cantilever compressions [11].

Measurements of the force production and the axial stiffness of glycerinated single muscle fibers

The force production and the axial stiffness of single muscle fibers were measured as previously reported [23]. Single fibers of glycerol-extracted muscle fibers were mounted via thin rods between a force transducer (AE801; SesoNor, Norway) and a servomotor with a driver (VM-500+, MiniSax; General Scanning, Watertown, MA, USA) by gluing the fiber ends to the rods with collodion. The fibers (having the length of 2–3 mm and the diameter of 40–80 μm measured under optical microscope) were put in an experimental chamber and kept at their slack length L₀ (having the average sarcomere length of 2.4 μm measured with optical diffraction of a He-Ne laser light). The Lucite experimental chamber was composed of several compartments (each about 200 μl) filled with appropriate solutions. To exchange the bathing solution, fiber preparations were lifted up from one compartment and quickly dipped into another compartment.

The force production and the axial stiffness of muscle fibers immersed in bathing solutions were continuously measured by applying small sinusoidal length oscillations with the driver (0.2% of the slack length at 2 kHz). The in-phase and 90-degree out-of-phase tension components were separated with a lock-in amplifier (LI5630; NF, Yokohama, Japan), from which the in-phase, quadrature and total stiffness were obtained. The changes in tension and stiffness were recorded on a digital oscilloscope (GL-900; Graphtec, Yokohama, Japan) and analyzed on a computer.

Motility assay

The in vitro motility assay of actin filaments sliding over a myosin-coated glass surface was performed as previously reported [28]. A fresh cover glass was coated with nitrocellulose by dipping it in 0.1% collodion and drying. On the cover glass thus treated, a pair of thin cover glass was placed in parallel with an appropriate space, and a flow cell (having a space of 75 μm thick) was constructed by covering it with another fresh cover glass.

First, the bottom cover glass of the flow cell was coated with myosin filaments by flowing a washing solution containing either 0.05 or 2.0 μM myosin molecules into the flow cell. After a wash with a fresh washing solution, a sliding solution containing 11.1 nM fluorescent actin filaments (labeled with rhodamine-phalloidin) was put into the flow cell to initiate the filament sliding. The fluorescent actin filaments were observed as previously described [22] under an inverted fluorescence microscope (IX-70; Olympus, Tokyo, Japan) equipped with a highly sensitive TV camera (C7190-21; Hamamatsu Photonics, Hamamatsu, Japan) and their images recorded on a video tape-recorder (AG-7355; Panasonic, Osaka, Japan). The velocity of the filament sliding was determined by analyzing recorded images of fluorescent filaments by use of a computer program (NIH Image; NIH, MD, USA).

Solutions and chemicals

The composition of solutions (in mM) was as follows. For AFM experiments; relaxing solution: K⁺-propionate, 133; MgCl₂, 5; EGTA, 10; ATP, 5; PIPES, 20, contracting solution: K⁺-propionate, 155; MgCl₂, 5; CaCl₂, 2.3; EGTA, 2; ATP, 5; PIPES, 20, and +AMPPNP solution: K⁺-propionate, 148; MgCl₂, 5; EGTA, 2; AMPPNP, 2.5; PIPES, 20. For force experiments; relaxing solution: KCl, 125; MgCl₂, 4; EGTA, 4; ATP, 4; PIPES, 20, and contracting solution: KCl, 125; MgCl₂, 4; CaCl₂, 4; EGTA, 4; ATP, 4; PIPES, 20. For motility experiments; washing solution: KCl, 25; MgCl₂, 2; CaCl₂, 0.2; HEPES, 25, and sliding solution: KCl, 25; MgCl₂, 2; CaCl₂, 0.2; ATP, 0.5; HEPES, 25. All solutions for motility experiments contained 4.5 mg/ml glucose, 216 μg/ml glucose oxidase, 36 μg/ml catalase and β-mercaptoethanol 1% (v/v). Solutions containing BDM and/or Dextran were prepared by dissolving appropriate amounts of BDM and/or Dextran in the above solutions. The pH of solutions for AFM and force experiments was adjusted to 7.0, and that for motility experiments to 7.6. The ionic strength and free Ca²⁺ concentration of solutions were calculated as previously described [16]. And the ionic strength of solutions for AFM and force experiments was 0.2 M, and that for motility experiments 0.054 M. The free Ca²⁺ concentration of contracting solutions was pCa 4.0.

ATP, AMPPNP, BDM, rhodamine-phalloidin, glucose oxidase and catalase were purchased from Sigma-Aldrich (MO, USA). Dextran T-500 (MW 500 kD) was purchased from Amersham Pharmacia Biotech AB (Sweden). All other chemicals were of analytical grade and purchased from Wako Chemicals (Osaka, Japan).

All measurements of the force, AFM and motility experiments were performed at room temperature (22±2°C).

Statistics and curve fittings

Data are expressed as the mean±SEM (standard error of the mean) with the number of preparations examined. The statistical differences between the data were analyzed by employing the paired and un-paired Student’s t-tests appropriately. The regression analysis of experimental data was performed by use of Igor Pro software (WaveMetrics, OR, USA) on a computer.

Results

Effects of BDM on the contractility of muscle fibers and on the sliding velocity of the thin filaments in the motility assay

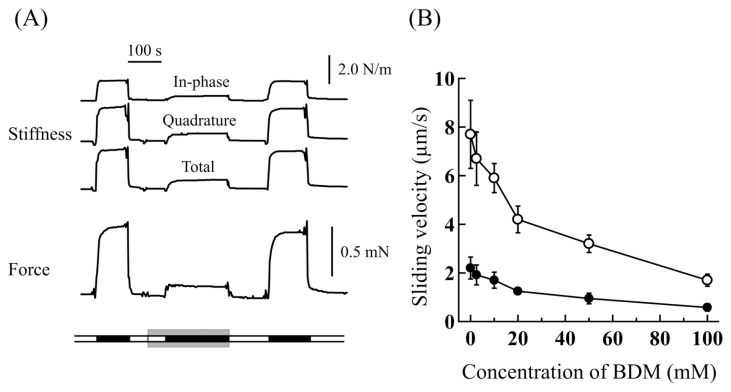
First, the effects of BDM on the contractile properties of glycerinated single muscle fibers were examined. Typical force and axial stiffness traces of a single isometric muscle fiber are shown in Figure 2A. It can be seen that both the force production and the axial stiffness were greatly suppressed by BDM in a reversible fashion, as previously reported [17,29]. The force produced and the total axial stiffness in a contracting solution without BDM was 200±10 kN/m² and 2.61±0.06 N/m (n=12) (mean±SEM) respectively, in which the cross-sectional area of single fibers, tentatively assumed cylindrical, was determined from their diameter measured under optical microscope. And they were decreased to 28.2±3.2 kN/m² and 0.65±0.05 N/m (n=6), respectively, in a contracting solution containing 20 mM BDM. Thus the force production and also the total axial stiffness were suppressed by 85.9±1.6% and by 75.3±1.8%, respectively. In contracting solutions containing 10 mM BDM, they were suppressed by 71.9±4.6% and by 62.8±4.2% respectively. On the other hand, the force production and the axial stiffness were naught in relaxing solutions with and without BDM.

Figure 2.

(A) Typical traces of the force production and axial stiffness (in-phase, quadrature and total) of a glycerinated single muscle fiber showing the effects of BDM. The bathing solutions are indicated on a broad line at the bottom; (open sections) relaxing solution and (filled sections) contracting solution. The bathing solutions in the sections sandwiched between gray bars contained 20 mM BDM. (B) Sliding velocity of fluorescent actin filaments as a function of the BDM concentration in the in vitro motility assay. The flow cell pre-treated with washing solutions containing 2.0 μM (open circles) and 0.05 μM (filled circles) myosin molecules. The vertical bars represent the SEM (n=5–7). See the details in the text.

Secondly, the effects of BDM on the sliding velocity of actin filaments were examined by the in vitro motility assay. Consistent with other study [30], fluorescent actin filaments slid at the velocity of 2–8 μm/s in a sliding solution without BDM, faster for the cover glass more densely coated with myosin molecules. As can be seen in Figure 2B, the sliding velocity of actin filaments was greatly suppressed, by about 40%, in sliding solutions containing 20 mM BDM, almost independent of the density of myosin molecules coated on the cover glass. Compared with the force production and the axial stiffness of glycerinated muscle fibers, the sliding velocity of actin filaments was fairly less suppressed by BDM.

Radial stiffness measurements of the overlap regions of single myofibrils

Force-distance curves for the overlap regions were obtained for single myofibrils firmly adsorbed to the bottom of the AFM experimental chamber and their radial stiffness was determined as detailed in Materials and Methods. Taking the above results into considerations, contracting solutions containing 20 mM BDM, simply called contracting(+BDM) solutions, were employed for the bathing solutions to examine the effects of BDM on the radial stiffness of the overlap regions.

1) Osmotic compressions with Dextran

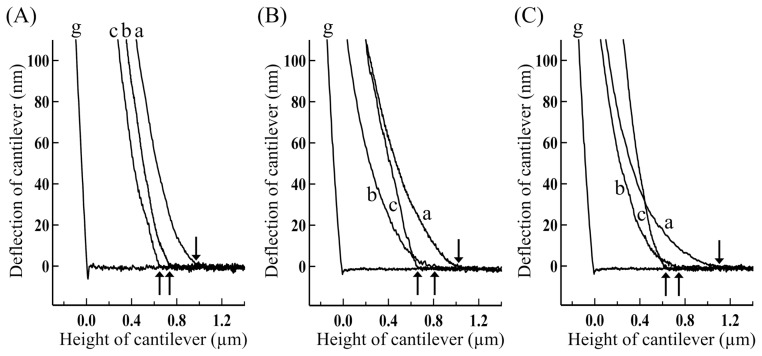
First, the radial stiffness (K_o) of the overlap region of single myofibrils was estimated based on its diameter decrease produced by the Dextran treatment as detailed in Materials and Methods. To determine the quantity of the diameter change (the change in W as shown in the left inset of Fig. 4A), force-distance curves were measured with AFM for single myofibrils put in various bathing solutions containing no Dextran, and then similarly measured by changing the bathing solutions to those containing Dextran. Typical force-distance curves for various myofibrils, simply called a relaxed myofibril, a contracting(+BDM) myofibril and so on, obtained by increasing the Dextran concentration are shown in Figure 3. It can readily be noted that the overlap regions got shrank and more rigid as the Dextran concentration was increased. The diameter of the overlap regions was determined based on the force-distance curves thus obtained as depicted in Figure 1C. To correct for the diameter variation of overlap regions, the diameter of appropriate overlap regions to be examined was firstly determined in a relaxing solution, and it was used for the normalization of diameter differences.

Figure 3.

Force-distance curves for the overlap regions of single skeletal myofibrils in various physiological solutions containing various concentrations of Dextran. (A) Contracting, (B) contracting(+BDM), and (C) relaxed myofibrils. The concentration of Dextran: (a) 0%, (b) 2% and (c) 8% (w/v). The concentration of BDM: 20 mM. The cantilever was approached at 0.1 μm/s and its tip touched the top surface of the overlap regions at small arrows.

In bathing solutions containing no Dextran, the diameter of the overlap region was 1.09±0.05 μm (n=10) in relaxing solution, 1.03±0.04 μm (n=10) in +AMPPNP solution, 1.01±0.05 μm (n=10) in contracting solution, and 0.99±0.03 μm (n=10) in rigor solution. The diameter of relaxed myofibrils was significantly greater than those for other conditions, consistent with previous studies [4,14]. The diameter of the overlap region for contracting(+BDM) myofibrils was 1.04±0.06 μm (n=10), comparable to those for contracting and +AMPPNP myofibrils, and slightly greater than that of rigor myofibrils. By increasing the Dextran concentration in the bathing solutions, the diameter decrease took place via two common phases for single myofibrils in various physiological states as can be seen in Figure 4A. Namely the overlap region was composed of a soft and a rigid component having significantly different stiffness, consistent with the results of our previous studies [14]. In the first phase, the diameter was decreased by 20–25% by increasing the concentration of Dextran up to about 2% (w/v), and in the second phase it was slightly decreased by further increasing the Dextran concentration.

As can be seen in Figure 4A (right inset), the soft component distinctly changed depending on the physiological conditions of myofibrils. As detailed previously [14], we may assume that the soft component comes from cross-bridge structures in the actomyosin filament lattice as (1) the overlap regions of isolated single myofibrils are almost exclusively composed of the actomyosin filament lattice and (2) the change in the size of the soft component is nearly equal to the bending distance of cross-bridges extruded from the thick filaments [that is, (the distance between the thick and the thin filaments, i.e., about 25 nm) × (the proportion of the decrease in the myofibril width, i.e., (20–25)%) is equal to (5–6) nm]. The radial stiffness (K_o) for the soft component was determined from the decrease in diameter vs. the Dextran concentration by assuming the osmotic pressure of 1% (w/v) Dextran to be 1 kPa [25–27]. Related to this, it was reported that Dextrans smaller than 20 kD penetrate into the filament lattice, so that we used Dextran T-500 (MW 500 kD) in the present studies to minimize the unfavorable effects on the osmotic pressure due to penetration of small Dextrans [26]. The radial stiffness (K_o) thus obtained was 6.38±0.24 kPa (n=5) for relaxed myofibrils, 8.38±0.43 kPa (n=5) for contracting myofibrils, and 10.84±0.50 kPa (n=5) for rigor myofibrils. The radial stiffness (K_o) for contracting(+BDM) myofibrils was 7.82±0.44 kPa (n=5). It was significantly great compared with that for relaxed myofibrils, but nearly comparable to that for contracting myofibrils, and significantly small compared with that for rigor myofibrils. These results are summarized in Figure 4B for comparison.

Thus, by the addition of 20 mM BDM, the radial stiffness (K_o) for contracting myofibrils was suppressed by about 7%. Notably the suppressive effect of BDM on the radial stiffness was far less than those on the force production, axial stiffness of contracting muscle fibers and the sliding velocity of actin filaments in the motility assay.

2) Mechanical compressions with cantilever

Second, the radial stiffness (K_m) was estimated from the indentation of the overlap regions produced by approaching the tip of cantilever at 0.1 μm/s, the slowest compression as described in Materials and Methods. Typical force-distance curves for the overlap regions of single myofibrils put in various bathing solutions containing no Dextran are shown in Figure 5A. It can be seen that the radial stiffness of overlap regions was great in the order of relaxed, +AMPPNP, contracting(+BDM), contracting and rigor myofibrils. The radial stiffness (K_m) was determined based on initial rising slopes of force-distance curves in which the overlap regions were indented by 100 nm from their surface. The radial stiffness (K_m) thus obtained was 1.41±0.18 kPa (n=10) for relaxed myofibrils, 1.76±0.18 kPa (n=10) for +AMPPNP myofibrils, 3.20±0.54 kPa (n=10) for contracting myofibrils, and 9.16±0.18 kPa (n=10) for rigor myofibrils. These results are in accord with those of our previous studies [7,10]. The radial stiffness (K_m) for contracting(+BDM) myofibrils was 1.78±0.27 kPa (n=10). It was comparable to those for relaxed and +AMPPNP myofibrils, significantly small compared with that for contracting myofibrils and far small compared with that for rigor myofibrils. These results are summarized in Figure 5B (open pillars) for comparison.

Figure 5.

(A) Typical force-distance curves for the overlap regions of single skeletal myofibrils obtained by approaching the cantilever at 0.1 μm/s. (a) Rigor, (b) contracting, (c) contracting(+BDM), (d) +AMPPNP, and (e) relaxed myofibrils. Traces are vertically shifted appropriately. The tip of cantilever touched the top surface of the overlap regions at small arrows. (B) Comparison between the radial stiffness (K_m) obtained by the cantilever approach at 0.1 μm/s (open pillars) and the radial stiffness (K_mf) obtained by the cantilever approach at 38 μm/s (fillled pillars) for various myofibrils. The concentrations of BDM and AMPPNP: 20 mM and 2.5 mM, respectively. The statistical difference levels between the radial stiffness of various myofibrils and that of contracting(+BDM) myofibrils are represented by (*) for p<0.05, (**) for p<0.01, and NS (not significant) for p>0.10 at the top of the open pillars for the radial stiffness (K_m) and at the top of the filled pillars for the radial stiffness (K_mf), respectively. The vertical bars represent the SEM (n=5–7). See the details in the text.

Thus, by the addition of 20 mM BDM, the radial stiffness (K_m) for contracting myofibrils was suppressed by about 45%. Again the suppressing effects of BDM on the radial stiffness were much less than those on the force production and the axial stiffness of glycerinated muscle fibers. However the radial stiffness (K_m) obtained by the AFM method using a slowly moving tip of cantilever (open pillars in Fig. 5B) was substantially more suppressed by BDM than the radial stiffness (K_o) obtained by the osmotic pressure method (see Fig. 4B).

3) Fast mechanical compressions with cantilever

Some of the apparent discrepancies between the BDM effects based on the radial stiffness (K_o) and those based on the radial stiffness (K_m) obtained above may be attributable to the difference in the pattern of radial compression, i.e., the static compressions with Dextran and the dynamic compressions with the cantilever. Considering that biological specimen is generally visco-elastic [31], the deformations of the filament lattice would depend how quickly the compressions are applied. Therefore, in order to extract the elastic component in the radial stiffness of the overlap regions, we examined the force-distance relationship at larger approach velocities of cantilever.

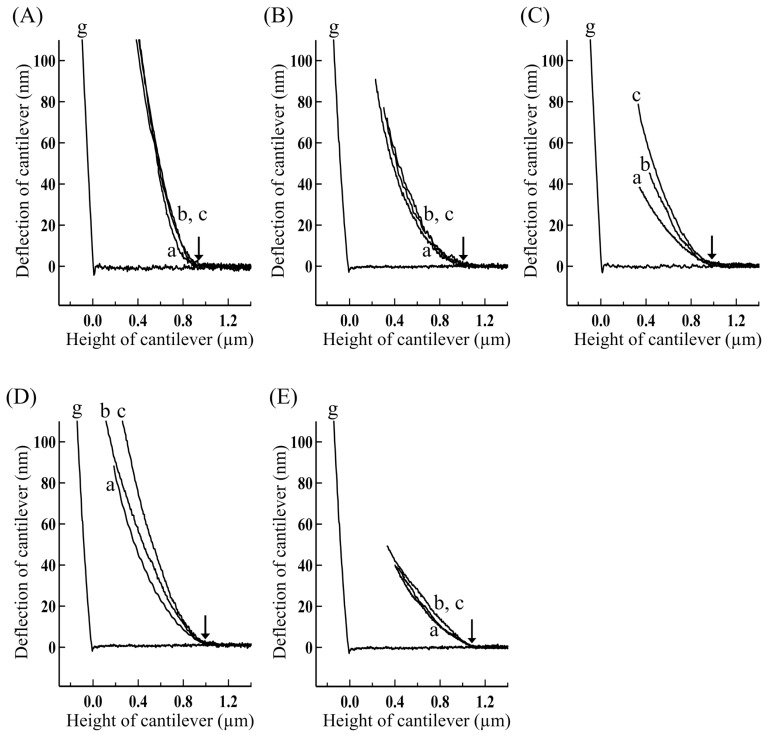
Typical force-distance curves for various myofibrils thus obtained by changing the cantilever approach velocity are shown in Figure 6. It can be seen that the force-distance curves became steeper as the cantilever approach velocity got faster, indicating the presence of visco-elastic components. Measurements similar to those shown in Figure 6 were performed for several other myofibril preparations by approaching the cantilever at various velocities. After determining the radial stiffness (K_m) for force-distance curves thus obtained, the relationship between the radial stiffness (K_m) and the approach velocity of cantilever for various myofibrils are summarized in Figure 7. It can be seen that the contributions of viscous components were decreased relative to the elastic components as the approach velocity of cantilever was increased. Further, the contribution of viscous components characteristically changed depending on the physiological conditions of myofibrils, especially great for contracting (+BDM) and +AMPPNP myofibrils, small for contracting and relaxed myofibrils, and very small for rigor myofibrils. The radial stiffness (K_m) obtained at the fastest compression of 38 μm/s, denoted by the radial stiffness (K_mf), was 2.26±0.32 kPa (n=5) for relaxed myofibrils, 4.88±0.41 kPa (n=5) for contracting myofibrils, 4.20±0.27 kPa (n=5) for contracting(+BDM) myofibrils, 4.20±0.72 kPa (n=5) for +AMPPNP myofibrils and 9.70±0.14 kPa (n=5) for rigor myofibrils. These results are included in Figure 5B (filled pillars) for comparison.

Figure 6.

Force-distance curves for the overlap regions of single skeletal myofibrils in various physiological states obtained by approaching the cantilever at various velocities. (A) Rigor, (B) contracting, (C) contracting(+BDM), (D) +AMPPNP and (E) relaxed myofibrils. The approach velocity of cantilever: (a) 0.1, (b) 18, and (c) 38 μm/s. The tip of cantilever touched the top surface of the overlap regions at small arrows. The concentrations of BDM and AMPPNP: 20 mM and 2.5 mM, respectively.

Figure 7.

Effects of the cantilever approach velocity on the radial stiffness (K_m) for skeletal myofibrils in various physiological states. (filled circles) Rigor, (open triangles) contracting, (open diamonds) contracting(+BDM), (filled triangles) +AMPPNP, and (open circles) relaxed myofibrils. The concentrations of BDM and AMPPNP: 20 mM and 2.5 mM, respectively. The vertical bars represent the SEM (n=5–7), several of which are smaller than the size of symbols.

As can be seen in Figure 5B, the radial stiffness (K_mf) (filled pillars) was greater than the radial stiffness (K_m) obtained by the slow cantilever approach (open pillars) for various myofibrils, especially distinct for contracting(+BDM) myofibrils. And, by the addition of 20 mM BDM, the radial stiffness (K_mf) for contracting myofibrils was suppressed by about 14%, which was much less suppressed than the radial stiffness (K_m) for contracting myofibrils estimated by the slow approach velocity. Thus the suppressing effects of BDM on the radial stiffness (K_mf) for contracting myofibrils was far less than those on the force production, the axial stiffness of contracting muscle fibers and the sliding velocity of actin filaments in the motility assay. Notably, however, the suppressing effects of BDM based on the AFM methods (14–45%) (Fig. 5B) were still significantly greater than that based on the osmotic pressure method (about 7%) (Fig. 4B).

Discussion

In Table 1 are summarized the effects of BDM (20 mM) on the contractility and the stiffness of various actomyosin filament systems clarified in the present studies. It can be seen that BDM distinctly affects the axial and radial mechanical properties of the actomyosin system in contracting state. In comparing these results, it should be kept in mind that there exist differences in the experimental conditions, although we think they will not seriously affect the discussions below.

Table 1.

Comparison of BDM suppressions of the force production and the axial stiffness in contracting muscle fibers, the filament sliding in the motility assay, and the radial stiffness of the overlap regions in contracting skeletal myofibrils

aRelative suppressions by BDM (%)
bForce production	85.9±0.5 (5)
bAxial stiffness	75.3±0.6 (5)
cSliding velocity	40.6±7.2 (10)
dRadial stiffness (Ko)	6.7±6.2 (5)
eRadial stiffness (Kmf)	13.9±6.1 (5)

^aValues for contracting (or sliding) solutions containing 20 mM BDM relative to those containing no BDM. Means±SEM with the number of preparations examined.

^bBased on isometric single glycerinated muscle fibers.

^cBased on purified actomyosin molecules in a flow cell pre-treated with a washing solution containing 2.0 M myosin molecules.

^dBased on the osmotic compression of single skeletal myofibrils with Dextran.

^eBased on the mechanical compression of single skeletal myofibrils with the tip of AFM cantilever at the approach velocity of 38 μm/s.

Axial characteristics of the pre-force generating cross-bridges

Consistent with the results of previous studies [17], BDM greatly suppressed the force production and also the axial stiffness in contracting glycerinated muscle fibers (Fig. 2A). It is generally believed that both the force production and axial stiffness of muscle fibers increase with the number of the force generating cross-bridges strongly attached to the thin filaments [1,32], although their quantitative relationship is known to be complicated [33]. And the above results are explained as BDM shifts the cross-bridge population from the force generating (strongly bound) state to the pre-force generating (weakly bound) state in contracting muscle fibers [17–19], by assuming that the pre-force generating cross-bridges do not produce the active force and hardly contribute to the axial stiffness.

X-ray diffraction studies of BDM-treated muscle fibers showed that the pre-force generating cross-bridges are attached to the thin filaments [34]. In the motility assay shown above (Fig. 2B), the sliding velocity of actin filaments was greatly suppressed by BDM. These results are consistent with the view that the pre-force generating cross-bridges are weakly attached to the thin filaments and produce the drag force against the filament sliding [35].

Radial characteristics of the pre-force generating cross-bridges

The present experiments showed that the estimation of the radial stiffness of the overlap regions greatly depended on the pattern and condition of the radial compressions employed. Namely the actomyosin filament lattice would differently be deformed by the Dextran compressions and the cantilever compressions.

In the case of the cantilever compressions, the filament lattice would dynamically be deformed, locally and non-uniformly as simulated for a uniform cylindrical rod by the finite element analysis (dotted images in Fig. 1B). Therefore visco-elastic deformations would come from time-dependent structural changes of the filament lattice, which depends on how many and how strongly cross-bridges are attached to the thin filaments. If all of the cross-bridges are firmly attached to the thin filaments as in rigor myofibrils [32,36], the configuration of the filament lattice would hardly be deformed and the small deformation would occur independent of the relaxation process due to the attachment-detachment dynamics of cross-bridges. If all cross-bridges are detached from the thin filaments as expected in relaxed myofibrils [1], the configuration of the filament lattice would readily be deformed and the large deformation would occur almost independent of the relaxation process due to the cross-bridge dynamics. On the other hand, if cross-bridges are transiently attached to the thin filaments as in contracting, contracting(+BDM) and +AMPPNP myofibrils, the configuration of the filament lattice would progressively be deformed with some relaxation rate characteristic of each state. This means that the stiffness obtained may depend on the compression velocity: the slower the compression velocity is (especially slower than the characteristic relaxation time), the stiffness obtained may be smaller.

In the present AFM experiments, the overlap region was compressed with the cantilever for 2.6 ms to 1 s (100 nm divided by 0.1 to 38 μm/s). In accord with the above considerations, the radial stiffness (K_m) changed depending on the cantilever compression velocity as shown in Figure 7. Namely the distinct change in the stiffness was not observed for the rigor, which is understandable because the lifetime of rigor actomyosin complex, about 1000 s in the absence of applied load and 1 s even under high load [37], is longer than the compression time with a cantilever. On the other hand, the stiffness in the contracting state changed at the compression velocity of about 10 μm/s or less (corresponding to 10 ms or longer) and saturated at higher than 30 μm/s (i.e., the compression time shorter than about 3 ms), which may reflect the lifetime of force-generating cross-bridges under the isometric condition. And the stiffness in the +AMPPNP and the contracting(+BDM) conditions, respectively, changed at about 20 μm/s (i.e., 5 ms) and 25 μm/s (i.e., 4 ms), which may reflect the life time of weakly attached (non-force generating) cross-bridges. In accord with these assumptions, in the cross-bridge cycle in the contracting state under the isometric condition, strongly attached (force generating) cross-bridges detach from the thin filaments with the rate of an order of 50–1000 s⁻¹ (corresponding relaxation time, 1–20 ms) at 5°C under stretching force [38]. Although it is difficult to quantitatively consider the situations for the +AMPPNP and contracting(+BDM) states because no kinetic data exists on these states. However it is reasonable that the compression velocity dependency would be shifted toward the higher velocity region (corresponding to the shorter relaxation time of cross-bridge attachment-detachment kinetics) for these states.

It is also possible to understand the results shown in Figure 7 based on a visco-elastic three-element model, e.g., Zener model [39]. That is, the proportion of the elastic term and viscous term is different depending on the state of myofibrils. In the rigor state, the elastic term is predominant, whereas, in the contracting, contracting(+BDM) and +AMPPNP states, the contribution of the viscous deformations to the radial stiffness becomes apparent. The reason why the values of the apparent compression velocity at which the radial stiffness changed increased in the order of contracting, +AMPPNP and contracting(+BDM) states is attributable to that the contribution of viscous term relatively increases in this order. In any case the radial stiffness (K_m) determined by the cantilever compression would reflect the visco-elastic characteristics of the cross-bridges in various states, especially apparent for the contracting(+BDM) state.

In the case of the Dextran compressions, the filament lattice would statically and almost uniformly deformed via all radial directions surrounding overlap regions (left inset of Fig. 4A). It is reported that the lattice spacing of the actomyosin filaments uniformly changes by the Dextran treatments of glycerinated muscle fibers under various physiological conditions [26]. It is further reported that the fiber width and the spacing of the actomyosin filament lattice change in parallel by the compression with the osmotic pressure in skinned muscle fibers [40] and in skeletal myofibrils [41]. Based on these results, we may assume that, by the Dextran compressions of isolated single myofibrils, the diameter of the overlap region changes in parallel with the spacing of the actomyosin filament lattice with keeping the regular lattice structure. Thus the radial stiffness (K_o) determined by the Dextran compressions (Fig. 4B) would reflect the radial stiffness of the cross-bridges in various states. Namely the cross-bridges in contracting and contracting (+BDM) states are much rigid than those in relaxed state, and much elastic than those in rigor state. And the radial stiffness of cross-bridges in contracting(+BDM) state is almost comparable in magnitude to that in contracting state. Considering that BDM shifts the cross-bridge population from the force generating to the pre-force generating states in contracting myofibrils [17–19], this strongly suggests that the radial stiffness of pre-force generating cross-bridges is nearly as rigid as that of force generating cross-bridges.

Based on the above considerations, we conclude that the pre-force generating cross-bridges are visco-elastically attached to the thin filaments and contribute to the radial stiffness of the filament lattice with nearly comparable magnitudes to that of force generating cross-bridges.

Anisotropic structures of the pre-force generating cross-bridges

As discussed above, the pre-force generating cross-bridges are attached to the thin filaments, and contribute greatly to the radial stiffness of the filament lattice but hardly to the axial stiffness. This suggests that the pre-force generating cross-bridges are attached to the thin filaments in a mechanically anisotropic fashion in the axial and radial directions. The anisotropic structure of the pre-force generating cross-bridges could be one of the factors causing the difference between the BDM suppression based on the radial stiffness (K_m) at slow cantilever approach and that based on the radial stiffness (K_o) observed above. While the radial stiffness (K_o) is estimated by uniform deformations of the filament lattice along the filament axis (left inset of Fig. 4A), the radial stiffness (K_m) is estimated by non-uniformly deforming the filament lattice (Fig. 1B). Notably, in the latter deformations, the filament lattice would locally be stretched in the axial direction. If BDM transforms the attached (force-generating) cross-bridges to those having anisotropic structures, more elastic along the axial direction than in the radial direction, it may partly be explained why the BDM suppression based on the radial stiffness (K_m) was greater than that based on the radial stiffness (K_o) as observed.

The anisotropy of pre-force generating cross-bridges may be compared with the finding that the force generating cross-bridges are attached to the thin filaments with an anisotropic elasticity relative to the shortening direction in contracting muscle fibers [42]. In this connection, in relaxed state, the axial stiffness of muscle fibers was naught (Fig. 2A), while the radial stiffness (K_o) of the overlap regions of single myofibrils was significantly great (Fig. 4B), suggesting that the sarcomere has anisotropic structures in a relaxed state. If all cross-bridges are detached from the thin filaments in relaxed state as generally believed [1], this may be largely attributable to the anisotropic elasticity of the liquid-crystalline sarcomeric structure composed not only of myofilament lattice but also of other components like the Z-disc, the M-line, and titin interconnecting with thick filaments and Z-disc [1,43,44]. It was reported that the radial stiffness of the overlap regions in rigor state did not significantly change by selective digestions of titin [13] and that cross-bridges made contact with the thin filaments even in relaxed muscle fibers [45,46]. Considering these results, we may assume that some cross-bridges are interacting with the thin filaments in an anisotropic fashion even in relaxed muscle fibers.

Finally, we would like to mention that the present results give experimental basis for the model of SPOC (Spontaneous Oscillatory Contraction, ref. 47) on the contractile system of muscle, in which not only force generating cross-bridges but also non-force (and pre-force) generating cross-bridges, i.e., a total number of cross-bridges, 1) contribute nearly equally to the radial stiffness of myofibrils and 2) contribute to the axial force balance along the long axis of myofibrils as a molecular friction (drag) that is proportional to the sliding velocity [35]. These assumptions were essential for our SPOC model [48–50].

Conclusion

The present studies clarified that the cross-bridges in preforce generating state are anisotropically and visco-elastically attached to the thin filaments, with radial rigidity nearly comparable to that in force generating state. In other words, the lattice structure of the actomyosin filaments is robust against the radial mechanical stress during the cross-bridge cycling, which would facilitate stable force production in contracting muscle fibers.

Abbreviations

AFM

Atomic force microscope

AMPPNP

Adenylyl-imidodiphosphate

BDM

Butane dione monoxime

EGTA

Ethylene glycol tetraacetic acid

PIPES

Piperazine-1,4-bis(2-ethanesulfonic acid)

HEPES

4-(2-hydroxyethyl)piperazine-1-ethanesulfonic acid