Neural scaling laws for an uncertain world

Abstract

Autonomous neural systems must efficiently process information in a wide range of novel environments, which may have very different statistical properties. We consider the problem of how to optimally distribute receptors along a one-dimensional continuum consistent with the following design principles. First, neural representations of the world should obey a neural uncertainty principle—making as few assumptions as possible about the statistical structure of the world. Second, neural representations should convey, as much as possible, equivalent information about environments with different statistics. The results of these arguments resemble the structure of the visual system and provide a natural explanation of the behavioral Weber-Fechner law, a foundational result in psychology. Because the derivation is extremely general, this suggests that similar scaling relationships should be observed not only in sensory continua, but also in neural representations of “cognitive’ one-dimensional quantities such as time or numerosity.

The adapatability of mammals, humans in particular, to many novel environments has been one of the keys to our evolutionary success. This flexibility is made possible, among other things, by the ability of the sensory systems to represent information efficiently in a wide range of circumstances. For instance, consider the differing demands on the visual system in a desert, or a dense forest, or an office environment (Torralba & Oliva, 2003). One evolutionary strategy would be to adapt the properties of the sensors to a particular environment, or a particular stimulus. The “y detectors” in the frog’s brain described by Maturana and colleagues provides an early example of this reasoning (Lettvin, Maturana, McCulloch, & Pitts, 1959; Maturana, Lettvin, McCulloch, & Pitts, 1960). However, if the efficiency of the visual system depended critically on the statistics of a particular visual environment, it would leave the organism at a disadvantage if it moved to a different environment, or if the environment changed. Of course, these considerations do not only apply to vision; analogous arguments can be made for other sensory modalities and even neural representation of more abstract quantities, such as time or numerosity. This suggests a design principle for the brain: the structure of neural representations should make as few assumptions as possible about the statistical structure of the world, which one might call a neural uncertainty principle, and convey, as much as possible equivalent information about environments with different statistics, which one might call a neural equanimity principle.

We will argue in this paper that the Weber-Fechner law (Fechner, 1860/1912), the observation that the change in the perceptual magnitude of many one-dimensional quantities¹ depends on the relative, rather than absolute change in the physical quantity, can be understood as a behavioral manifestation of these design principles. The psychological scales of physical dimensions x obeying the Weber-Fechner law are logarithmic. In the brain some external scalar quantities, such as weight and luminance, may be expressed simply as the intensity of the response of a single receptor. This paper is concerned with variables, such as extrafoveal retinal position, that are expressed by a distributed pattern of firing across a set of receptors (which Stevens, 1957 referred to as metathetic variables). Each receptor is associated with a receptive field, which describes the response of the receptor to a constant stimulus with a particular value x. Each receptor responds to stimuli in a circumscribed range of values of x; the array of all receptors can thus represent functions over x, f(x) (Ma, Beck, Latham, & Pouget, 2006). In this paper we study how to optimally distribute receptors in order to represent arbitrary unknown functions in the world. Before formalizing this problem, we make some simple mathematical observations about logarithmic scaling of receptors and then briefly review the evidence that the visual system does (and does not) utilize this form of neural scaling.

Logarithmic neural scales

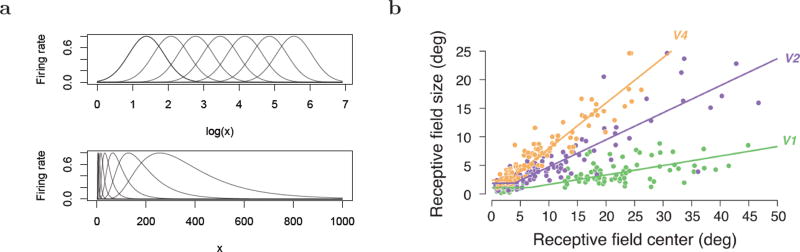
Receptive fields that are evenly-spaced and of equal width on a logarithmic scale (Fig. 1a, top) lead naturally to the Weber-Fechner perceptual law. A logarithmic scale implies several properties of the receptive fields (Fig. 1a bottom). A logarithmic scale implies that there should be fewer receptive fields centered at high values of x, and receptors coding for higher values of x should have wider receptive fields. These qualitative impressions can be refined to several quantitatively precise relationships. If the receptive fields are evenly-spaced on a logarithmic axis then the width of receptive fields centered on a value x should go up proportional to x. More generally, if the ith receptor has a receptive field centered on x_i, then the shape of the receptive field should be constant for all receptors, but the width of the receptive field should scale with the value of x_i. If we denote the center of the ith cells receptive field as x_i and define Δ_i ≡ x_i − x_i−1, then a logarithmic scale implies that the ratio of adjacent receptors, Δ_i+i/Δ_i, is a constant for all values of i.² Finally we note that because log 0 is not finite, a logarithmic scale with a finite number of receptors cannot continue to x = 0. In practice, this means that if the brain makes use of logarithmic scales, there must be some other consideration for values near zero. In fact, as we will see below, the brain appears to solve this problem in the visual system by including a region of approximately constant receptor spacing for small x (note the at region around zero in Fig. 1b).

Figure 1.

a. Weber-Fechner law can be generated from receptive fields that are of equal width and density as a function of log x. This results in receptive fields that increase in width and decrease in density as a function of x. The increase in receptive field width should go up linearly with x; the density should go down like 1/x. The spacing of adjacent receptors should be a constant ratio for all values of x. b. Width of visual receptive fields as a function of eccentricity in three regions of macaque visual cortex. The “fovea” can be seen as a region of constant spacing (at line) near an eccentricity of zero. There is a linear relationship outside of the fovea for all three regions. Figure taken from Freeman & Simoncelli (2011) who performed a metaanalysis on empirical studies cited therein.

Logarithmic neural scales in the mammalian brain

There is strong evidence that the visual system in mammals obeys logarithmic scaling in representing extrafoveal retinal position. In monkeys, both the spacing of receptive fields (the cortical magnification factor) (Daniel & Whitteridge, 1961; Hubel & Wiesel, 1974; Van Essen, Newsome, & Maunsell, 1984; Gattass, Sousa, & Gross, 1988) and the width of receptive fields (Hubel & Wiesel, 1974; Gattass et al., 1988; Schwartz, 1977) obey the quantitative relationships specified by logarithmic scaling to a good degree of approximation outside of the fovea. Figure 1b (reproduced from Freeman & Simoncelli, 2011) shows receptive field width in the macaque across several cortical regions. The fovea is visible as a region of constant receptive field width, followed by a much larger region showing a linear relationship between field width and eccentricity, consistent with logarithmic scaling. If the curves obeyed logarithmic scaling precisely, the lines would continue to the origin rather than flattening out in the fovea. However, because the spacing between receptors would go to zero, this would require an infinite number of receptors.

In the case of vision, logarithmic scaling can ultimately be attributed to the distributions of receptors along the surface of the retina. However, this logarithmic mapping may be more general, extending to other sensory (Merzenich, Knight, & Roth, 1973) and motor maps (Schwartz, 1977). In addition, evidence suggests that logarithmic scaling holds for variables that are not associated with any sensory organ. Neural evidence from monkeys and humans (Nieder & Miller, 2003; Harvey, Klein, Petridou, & Dumoulin, 2013) suggests that neural representations of non-verbal numerosity are arranged on a logarithmic scale, consistent with a broad range of behavioral studies of non-verbal mathematical cognition (Gallistel & Gelman, 1992; Feigenson, Dehaene, & Spelke, 2004). Behavioral and theoretical work (Balsam & Gallistel, 2009; Howard, Shankar, Aue, & Criss, 2015) suggests that a similar form of logarithmic scaling could also apply to representations of time, which is qualitatively consistent with growing body of neurophysiological evidence from “time cells” in the hippocampus, entorhinal cortex, and striatum (Salz et al., 2016; Kraus et al., 2015; Mello, Soares, & Paton, 2015). The neurophysiological evidence that these “cognitive” variables use logarithmic scaling is not nearly as well-quantified as visual receptive fields.

Overview

If a set of receptors was optimized under the expectation of a particular form of statistics in the world, it would be suboptimal, perhaps disastrous, if the organism encountered a state of the world with very different statistics. The next section (“Optimal receptor distribution…”) considers the problem of optimally placing receptors to represent an unknown arbitrary function from a local perspective. The result of this section is that for all receptors to convey the same amount of information as their neighbors, receptor spacings should be in a constant ratio. The following section (“Global function representation”) considers the amount of information conveyed by a set of receptors about a function controlled by some fixed, but unknown, scale. The global organization that leads to equivalent information for a wide range of scales has a region of constant spacing (ratio 1) followed by a region with constant ratio spacing (ratio > 1) which resembles the organization of the visual system with a closely-packed fovea surrounded by a logarithmic scale.

Optimal receptor distribution for representing arbitrary unknown functions

We want to represent a function in the world over some continuous real value x. Receptors sample the function in some neighborhood such that each receptor is “centered” on a particular value of x. The goal is to distribute the receptors to enable them to represent an arbitrary and unknown function f(x). In order for this problem to be meaningful we must assume that there is a finite number of receptors. We assume here that the lower and upper bounds of the scale x are physically constrained. At the lower bound, perhaps there is some minimal degree of resolution that can be achieved with the receptors. In some cases the upper bound may be given by the properties of the world or anatomy. For instance, in vision, ecccentricity cannot possibly be larger than π. Our question, then is how to distribute the location of the receptors within the range of x values to be represented.

Each additional receptor provides an additional benefit to the organism to the extent that it provides additional information about the function. Intuitively, if we clumped all of the receptors close together this would be suboptimal, because the receptors would all be conveying the same information and there would be no receptors to communicate information about other regions of the function. Naively, we might expect that the solution is trivial—perhaps receptors should be evenly-spaced along the x-axis. It will turn out that this is not in general the optimal solution. Rather, the spacing of each pair of receptors should be in a constant ratio to the spacing of the previous pair of receptors. Constant spacing corresponds to a ratio of 1; it will turn out that other ratios are admissable as well.

In order to do the calculation we need to measure the redundancy between a pair of receptors. There are a number of measures of redundancy one might use. For instance, we might measure the mutual information between the output of two receptors after observing the world for some period of time. There are other measures that one might use. All things equal, we would expect the redundancy between two receptors to be higher for receptors that are placed close together rather than receptors that are placed far apart. The development below applies to any measure of redundancy that obeys some basic properties.³ The distribution of receptors is optimal if each receptor is expected to be as redundant with its predecessor as it is with its successor. If that was not the case, then we could move one of the receptors and get more non-redundant information out about the function.

Formulation of the problem

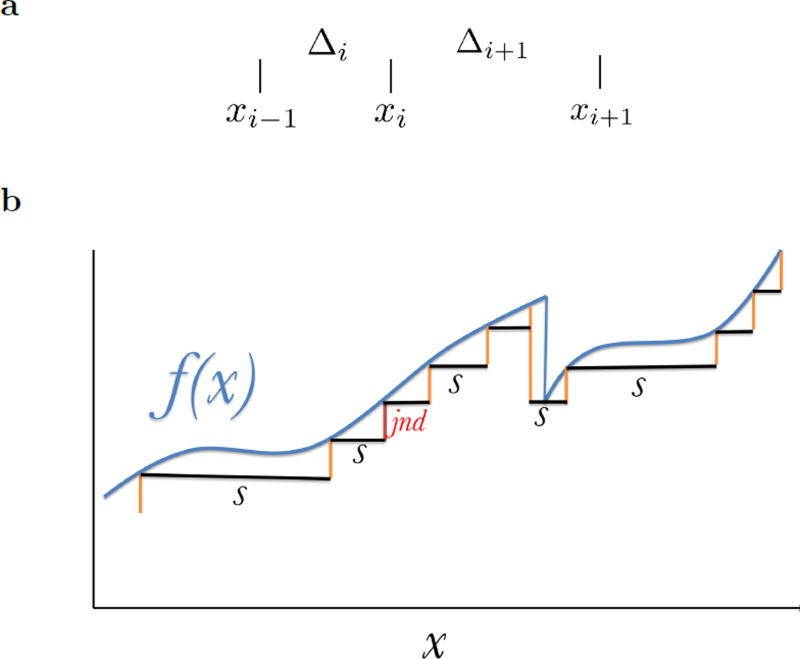
Suppose we have set of receptors with receptive fields centered on positions x₁, x₂, … x_N. As before, let us denote the distance between the locations of receptor x_i−1 and x_i as Δ_i. Constant receptor spacing would imply that Δ_i = Δ_i+1 for all i. It will turn out that this is not the general solution to our problem. Rather, the solution is to space the receptors such that the ratio of adjacent receptor spacings is a constant across the scale. That is, the ratio Δ_i+1/Δ_i takes the same value for all i.

We assume that in the neighborhood of each x_i, the function is controlled by some scale s_xi. To quantify this in an unambiguous way, assume that our receptors can only respond over a finite range with some non-zero resolution. Accordingly, we discretize the function to be represented to some degree of resolution (Figure 2a) so that at each value of x, s_x gives the distance to the next value of x where the discretized function would take a different value than the discretized f(x). That is, for each x, the discretized function f(x) = f(x′) for each x < x′ < x + s_x.

Figure 2.

a. Discretizing the function. After picking some small resolution (“jnd” in the figure), we discretize the signal. This defines a variable s(x) describing the distance (or scale) between x and the next location where the function takes on a different discretized value. b. Schematic for notation. The derivation assumes that there are receptors at x_i−1 and x_i separated by Δ_i. The goal is to choose Δ_i+1 (and thus x_i+1) such that the redundancy between the pairs of receptors is equated.

Note that if we knew the scale s_xi at x_i, it would be straightforward to estimate the redundancy between the receptor at x_i and the receptor at x_i+1. If we knew that the spacing between receptors Δ_i+1 were much smaller than s_xi, the receptors would measure the same value and we would expect the redundancy to be high. In contrast, if we knew that the spacing between the receptors were much smaller than s_xi then the value of the function would have changed at least once between x_i and x_i+1 and we would expect the redundancy to be low. Let us denote the function relating the redundancy we would observe between receptors spaced by a particular value Δ_i if we knew the scale took a particular value s as α(s; Δ_i). We assume α(s; Δ_i) to be a monotonically decreasing function of its argument. Note that we could choose any number of different ways to measure redundancy. For instance, we could treat mutual information as our measure of redundancy and this, coupled with knowledge of the properties of the receptors, would specify a specific form for α(s; Δ_i). But we could just as well measure redundancy in other ways or assume different properties of our receptors, which would result in a different form for α(s; Δ_i). The arguments below about optimal receptor spacing apply to any measure of redundancy that obeys some basic properties described below and does not depend critically on how one chooses to measure redundancy.

Observing the redundancy between the receptors at x_i−1 and x_i spaced by Δ_i allows us to infer the value of the scale at the first receptor s_xi−1. For instance, if the redundancy is maximal, that implies that the function did not change between x_i−1 and x_i. In contrast, if the redundancy between the receptors at x_i−1 and x_i is very small, that implies that the scale of the function at x_i−1, s_xi−1 was smaller than Δ_i. Knowing the scale at x_i−1 places constraints on the value at x_i. For instance, if we knew with certainty that s_xi−1 = Δ_i + C, then we would know with certainty that s_xi = C. So, if we knew the probability of each value of s_xi−1 this constrains the probability distribution for s_xi.

Let us fix the spacing Δ_i between the receptors at x_i−1 and x_i, sample the world for some time (observing many values of the the receptor outputs in response to many samples from the function) and denote the average value of redundancy we observe as α_obs. Denoting the (unknown) probability of observing each possible value of s_xi−1 as p_i−1 (s), then the observed value of redundancy, α_obs, resulted from an integral:

$${\alpha }_{\text{obs}}=\int p_{i-1}(s)\alpha (s;{\mathrm{\Delta }}_i)\mathit{\text{ ds}}$$ (1)

This can be understood as an inference problem; observation of α_obs leads us to some belief about the distribution p_i−1 (s). Informed by this knowledge, we then place the third receptor at a spacing Δ_i+1. If we knew the distribution of scales at x_i, p_i (s), then we would expect to observe a redundancy of

$${\alpha }_{\text{pred}}=\int p_i(s)\alpha (s;{\mathrm{\Delta }}_{i+1})\mathit{\text{ ds}}$$ (2)

between the second pair of receptors. Our problem is to choose Δ_i+1 such that we would expect α_pred = α_obs.

Minimal assumptions about the statistical properties of the world

The actual value of Δ_i+1 that makes α_pred = α_obs of course depends on the detailed properties of the receptors, the function α(s; Δ) and the statistics of the world. We show, however, that for minimal assumptions about the world, this problem results in the solution that, whatever the value of α_obs one finds that for some spacing Δ_i, the choice of Δ_i+1 is such that only Δ_i+1/Δ_i is affected by the observed value α_obs.

First, we make minimal assumptions about the function to be estimated. We assume an uninformative prior for p_i−1 (s). We make the minimal assumptions that successive values of s are independent, and that the value of the function past the s_x is independent of the value at x. That is we assume that f(x) and f(x + s_x) are independent of one another, as are s_x and s_{x + sx}.⁴

Second, we require that the receptors do not introduce a scale via α(s; Δ). In general, the function α(s; Δ) will depend on how we choose to quantify redundancy and the properties of the receptors. However, as long as α(s; Δ) rescales, such that it can be rewritten in a canonical form

$$\alpha (s;\mathrm{\Delta })=\widehat{\alpha }(s/\mathrm{\Delta }),$$ (3)

the conclusions in this section will hold. One can readily imagine idealized settings where Eq. 3 will hold. For instance, we could assume we have perfect receptors that sample the function at only one point and take our measure of redundancy to be one if the receptors observe the same value up to the resolution used to specify s (Fig. 2b) and zero otherwise. More generally, for imperfect receptors that sample a range of values, Eq. 3 requires that the receptive fields scale up with Δ. This assumption is necessary, but not sufficient to equate redundancy between receptors.

Our third requirement is referred to as the Copernican principle. Because it is critical to the argument in this section, we discuss it in some detail in the next subsection.

The Copernican Principle

In addition to minimal assumptions about the statistics of the world and the properties of the receptors, we assume that the world’s choice of s_xi−1 is unaffected by our choice of Δ_i. The belief that there is nothing privileged about one’s point of observation is referred to as the Copernican principle. The Copernican principle was employed by Gott (1993) to estimate a probability distribution for the duration of human civilization. Because this provides a concrete illustration of an important concept, it is worth explaining Gott’s logic in some detail.

Suppose we observe Fenway Park in 2017 and learn it has been standing for 103 years. Knowing nothing about construction techniques or the economics of baseball we want to estimate how much longer Fenway Park will stand. Because there is nothing special about our current viewpoint in 2017, our observation of Fenway should be uniformly distributed across its lifetime. That is, the observation at t_now in 2017 ought to be uniformly distributed between t_start when Fenway Park was constructed (in 1914) and the unknown time of its destruction t_end. Gott argued that we should expect t_now to be uniformly distributed between t_start and t_end, such that we should expect t_end − t_now to be longer than t_now − t_start half the time. This means that the age of the structure (102 years) fixes the units of the distribution of t_end − t_start. If we observed an object that has been existing for 1030 years, or for 103 seconds, then our inference about its expected duration would have the same shape, but only differ in the choice of units.

The Copernican argument also applies to our inference problem. Here the scale at the first receptor s_xi−1 plays a role analogous to the duration of the object t_end − t_start. Suppose that we have a set of receptors with a known function α(s; Δ) that obeys Eq. 3 and we encounter a world with some unknown statistics. In this first world we choose some Δ_i, observe some measure of redundancy α_obs, use some method of inference to estimate p_i−1 (s) and p_i (s) and then select the value of Δ_i+1 to yield the expectation that α_pred = α_obs. Let us refer to the distribution of p_i (s) that we inferred from fixing Δ_i to its particular value and observing α_obs as p_α (s; Δ_i). Now, suppose that we encounter another world with the same receptors. Assume further that we choose a different Δ_i but observe the same value of α_obs. How should our inference about the distribution of s_xi be related to our inference from the first world? If Eq. 3 holds, the Copernican Principle requires that all of the distributions that can be inferred for a particular value of α_obs must be related to one another via a canonical form:

$$p_{\alpha }(s;{\mathrm{\Delta }}_i)=\frac{1}{{\mathrm{\Delta }}_i}{\widehat{p}}_{\alpha }(s/{\mathrm{\Delta }}_i).$$ (4)

If Equation 4 did not hold, it would imply that we can infer something about the world’s choice of s_xi from our choice of Δ_i+1 beyond that communicated by the value of α_obs. As long as the receptors and our measure of redundancy scale with Δ_i as in Eq. 3 then any such effect would imply that the world’s choice of s and our choice of Δ_i are not independent and thus violate the Copernican Principle.

Ratio scaling results from minimal assumptions about the statistics of the world and the Copernican Principle

Equations 3 and 4 imply that redundancy is equated for receptor spacings in some ratio. To see this, let us rewrite Eq. 2 and find

$${\alpha }_{\text{pred}}({\mathrm{\Delta }}_{i+1})=\frac{1}{{\mathrm{\Delta }}_i}{\int }_0^{\infty }{\widehat{p}}_{\alpha }(s/{\mathrm{\Delta }}_i)\widehat{\alpha }({\mathrm{\Delta }}_{i+1}/s)\mathit{\text{ ds}}={\int }_0^{\infty }{\widehat{p}}_{\alpha }(s\prime )\widehat{\alpha }(r/s\prime )\mathit{\text{ ds}}\prime$$ (5)

In the second line s′ ≡ s/Δ_i and we define the ratio r ≡ Δ_i+1/Δ_i. The right hand side of Equation 5 clearly does not depend on Δ_i+1 directly, but only on the ratio.

The finding, then, is that a principle of minimal assumptions about the statistics of the world coupled with the Copernican Principle implies that the optimal distribution of receptor locations is such that the ratio of successive receptor spacings is constant. Logarithmic neural scales also imply that the ratio of successive receptor spacings are constant. In this sense, logarithmic scales can be understood as a response to the demand that the receptor layout are expected to equalize redundancy across receptors in a world with unknown statistics. Because logarithmic scales do not uniquely predict constant ratio spacing this cannot be the entire story. We pursue additional constraints that imply logarithmic scales, with some important exceptions when x approaches zero, in the next section. Before that, for concreteness we include a worked example for a idealized set of receptors and a specific choice for α(s; Δ).

A worked example

The general development above provides a set of conditions that result in a constant ratio of spacing between receptors. In order to make this more concrete, we work out a specific example with specific choices for the properties of the receptors, the measure of redundancy and the method of inference.

This example assumes that the receptors are perfect and the ith receptor samples the function only at the location x_i. For simplicity we define a measure of redundancy that gives α = 1 if the two receptors observe the same value of f and α = 0 otherwise. This lets us write out

$$\alpha (s;{\mathrm{\Delta }}_i)=\{\begin{array}{cc}1,\hfill & \text{if }{\mathrm{\Delta }}_i<s_{x_{i-1}}\hfill \\ 0,\hfill & \text{if }{\mathrm{\Delta }}_i\ge s_{x_{i-1}}\hfill \end{array}$$

The same holds for α(s; Δ_i+1), only comparing Δ_i+1 to s_xi. With our simplified definition of redundancy, any value of α_obs that is not zero or one must have resulted from a mixture of those two cases with probability α_obs and 1 − α_obs respectively. Let us first consider the case where Δ_i < s_xi−1, as it aligns perfectly with the Gott argument.

If s_xi−1 > Δ_i, then s_xi−1 plays the role of the unknown duration of the lifetime of an object such as Fenway Park, t_end − t_start. The difference between the two receptors Δ_i plays the role of the time of the current observation t_now − t_start and the unknown s_xi+1 is analogous to t_end − t_now. Gott’s calculation defines the ratio r = (t_end − t_now) = (t_now − t_start). The Copernican Principle leads to the belief that t_now ought to be uniformly distributed between t_start and t_end. Thus the cumulative distribution of r obeys:

$$P(r>Y)=\frac{1}{1+Y}$$ (6)

Note that the elapsed duration t_now − t_start only enters this expression via the ratio.

Similar arguments apply to the spacing of receptors. If we observe α_obs = 1, then the posterior p_i (s) is controlled by Eq. 6, with Δ_i in place of t_now − t_start and Δ_i+1 in place of t_end − t_now.⁵ In this toy problem, the value of α_pred is given by Eq. 6 if α_obs = 1. If instead of α_obs = 1, we observed α_obs = 0, we would infer a uniform distribution of s(x_i).⁶ If our prior on the distribution of s_xi−1 is uniform, then α_pred will be one for any finite value of Δ_i+1.

After sampling the world for some period of time, if we observe α_obs as a number between zero and one, then our posterior distribution of scales should be a mixture of the inference from the two cases and simplify Eq. 2 as:

$${\alpha }_{\text{pred}}({\mathrm{\Delta }}_{i+1})={\alpha }_{\text{obs}}\frac{1}{1+{\mathrm{\Delta }}_{i+1}/{\mathrm{\Delta }}_i}+(1-{\alpha }_{\text{obs}})$$ (7)

It is clear that the right hand side is only a function of the ratio r ≡ Δ_i+1/Δ_i so that the value of Δ_i+1 that makes α_pred = α_obs depends only on the ratio.⁷ For any value of α_obs, the same value of r satisfies this equation for any choice of Δ_i. In this simple problem we see that the choice of Δ_i can only affect the answer by fixing its units. This naturally results in the ratio of adjacent receptor spacings being constant, as implied by logarithmic receptor scales.

Global function representation

The foregoing analysis conducted at the level of pairs of receptors showed that the optimal spacing in order to represent arbitrary functions places the receptors in constant ratio, but does not specify the value of the ratio. It is convenient to parameterize the ratio between adjacent receptors by a parameter c such that $r\equiv \frac{{\mathrm{\Delta }}_{i+1}}{{\mathrm{\Delta }}_i}=1+c$. If c = 0, receptor spacing is constant; if c > 0 the ratio is constant, as in a logarithmic scale. We consider the global coding properties of these two schemes as well as a hybrid scheme in which the first part of the axis has constant spacing (c = 0) followed by a region with logarithmic spacing (c > 0), analogous to the organization of the visual system, with the region of constant spacing corresponding roughly to the fovea (Fig. 1b).

Formulating the problem

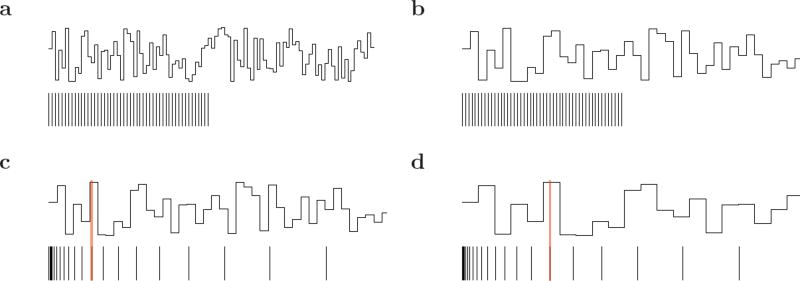
For simplicity, we assume that each receptor perfectly samples the value of a function in the world at a single perfectly-specified location and consider a simple class of functions f_s(x), which consist of independently chosen values over the range 0 to 1 at a spacing of s such that f_s(x) and f_s(x + s) are independent and f_s(x) and f_s(x + s − ε) are identical for ε < s. The information about a function contained in a given range by a particular instantiation of the function is just the number of entries specifying the values of the function over that range. Note that s controls the density of information conveyed by f_s over a given range of x. We assume that f_s(x) is specified over the entire range of x from zero to infinity so that the total amount of information that could be extracted from a function is infinite for every finite scale. Figure 3 shows several functions and choices of receptor scaling in cartoon form.

Figure 3. Cartoon illustrating the interaction of receptor spacing and function scale.

In each panel, the top curve shows a specific function f_s(x); the functions in the four panels differ only in their scale s. On the bottom of each panel, the vertical lines display receptor locations. a–b. Constant spacing. When c = 0, the receptors are evenly-spaced, fixing a scale to the receptors. If the function has the same scale as the receptors, as in a, each receptor captures a different value of the function, the veridical region runs the entire length of the receptor array and the information transmitted is maximal. However, if the scale of the function is larger than the constant spacing, as in b, the array of receptors conveys less information because there is less information in the function over that range. c–d. Ratio spacing. When c > 0, the receptors can extend over a much wider range of x values than with constant spacing. The receptors carry information about the function over a veridical region where Δ_i < s; the border of the veridical regions is shown (in cartoon form) as a vertical red line. As s increases (from c to d), the size of the veridical region in x changes, but as long as the border is covered by the receptors, the amount of nonredundant information in the veridical region is constant as a function of s. This property does not hold if the scale of the function approaches the minimum receptor spacing.

A set of receptors can do a “good” job in representing a function f_s(x) as long as the spacing between the receptors is less than or equal to s. With the simplifying assumptions used here, each of the non-redundant values of the function is captured by at least one receptor allowing reconstruction of the function with error in the x location no worse than s. More generally, even with coarse-graining and noisy receptors it is clear that there is a qualitative difference between the ability of the receptors to measure the function when Δ < s compared to when Δ > s. Let us define the veridical region of the function as the range of x over which Δ_i < s. We also assume there is some minimum possible receptor spacing Δ_min. We measure the amount of veridical information I conveyed by the set of receptors as the number of unique function values that the function has within the veridical region.

Constant receptor spacing, c = 0

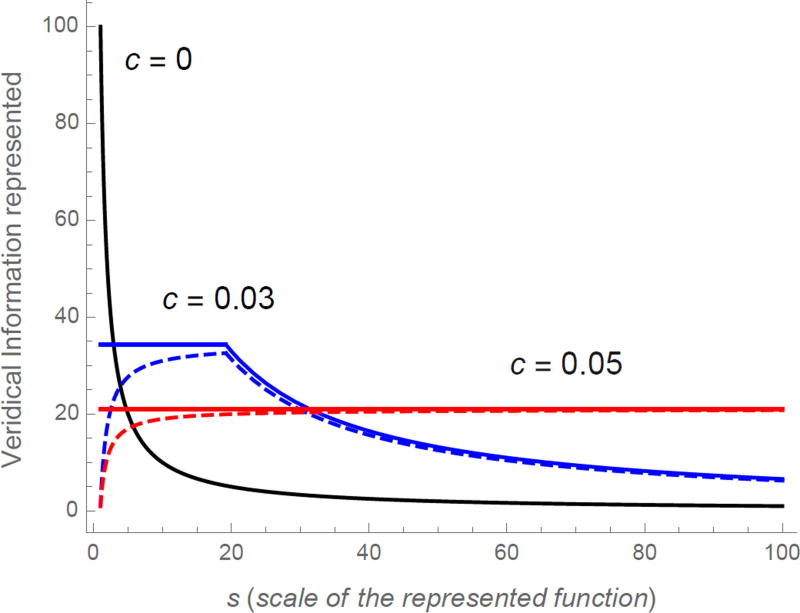
First, consider the implications of constant receptor spacing. If we knew the value of s controlling f_s(x), placing our receptors with constant separation Δ = s would be sufficient to convey all of the information in the function over the entire range of x values covered by the receptors. N receptors would be able to accurately represent the function over a veridical region of width NΔ and the amount of information conveyed about the function in that region is just N. However, our constant choice of spacing would have poor consequences if our choice of Δ did not correspond to the world’s choice of s. If s > Δ, the veridical region is still of length NΔ, but the amount of information contained in that region is only $N\frac{\mathrm{\Delta }}{s}$, decreasing dramatically as s increases (curve labeled c = 0 in Figure 4). With constant spacing, c = 0, the amount of information conveyed by the receptors depends dramatically on s.

Figure 4. Information in the veridical region as a function of scale for three forms of receptor spacing.

The curve labeled c = 0 shows the results for constant spacing. This falls off rapidly for scales larger than the scale set by the receptor spacing. Solid curves show results for ratio spacing (c > 0) with a fovea; dashed curves show results for ratio spacing without a fovea. N = 100 for all curves. See Figure 5a for an intuitive explanation of why the information decreases for small values of s. The fovea has an additional 1/c receptors. Note that there is a region where the amount of information conveyed is approximately constant as a function of scale before falling off as the veridical region exhausts the number of receptors N. For c = .05, this region is off the scale of this figure. Note also the error at small scales for c > 0 without a fovea.

Constant receptor spacing ratio, c > 0

If we set c > 0 such that all receptors are placed in constant ratio the responsiveness to functions of different scales is very different. Let us place the zeroth receptor x₀ at x_f, and the first receptor at x₁ = x_f + Δ_min. Continuing with Δ_i = (1 + c) Δ_i−1, we find that the spacing of the ith receptor is given by

$${\mathrm{\Delta }}_i={\mathrm{\Delta }}_{\text{min}}{(1+c)}^{i-1}$$ (8)

The position of the ith receptor is thus given by the geometric series

$$x_i=x_f+\frac{{\mathrm{\Delta }}_{\text{min}}}{c}[{(1+c)}^i-1]$$ (9)

Equations 8 and 9 show that when c > 0 the range of x values and scales that can be represented with N receptors goes up exponentially like (1 + c)^N. For a function of scale s, the set of ratio-scaled receptors has a veridical region ranging from x_f to

$${\widehat{x}}_s=\{\begin{array}{cc}s\frac{1+c}{c}-\frac{{\mathrm{\Delta }}_{\text{min}}}{c}+x_f\hfill & s\le {\mathrm{\Delta }}_N\hfill \\ x_N\hfill & s>{\mathrm{\Delta }}_N\hfill \end{array}$$ (10)

The amount of information present in the function in the veridical region is just (x̂_s − x_f)/s, which is given by

$$I_{c>0}=\{\begin{array}{cc}\frac{1+c}{c}-\frac{{\mathrm{\Delta }}_{\text{min}}}{\mathit{\text{sc}}}\hfill & s\le {\mathrm{\Delta }}_N\hfill \\ \frac{x_N-x_f}{s}\hfill & s>{\mathrm{\Delta }}_N\hfill \end{array}$$ (11)

The second expression, which happens when s is larger than the largest spacing among the set of receptors, is closely analogous to the case with constant spacing (c = 0), decreasing like s⁻¹. However, the first expression with s ≤ Δ_N includes a term (1 + c)/c which is independent of s. The second term is small when s is large, so that for large values of s the information conveyed is approximately constant. However, when s is small the second term is substantial and constant ratio spacing (c > 0) fails to convey much information about the function in the veridical region. When s = Δ_min the veridical region includes only one value of the function (see Figure 5a). The dashed line in Figure 4 shows the analytic result when c > 0 and is constant across all receptors.

Figure 5. Rationale for inclusion of a fovea.

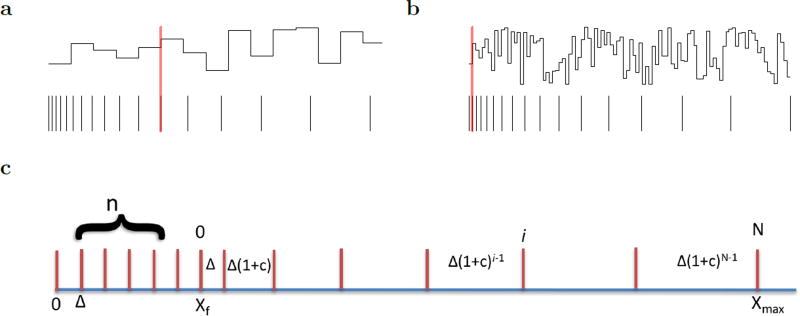
a–b. Functions are shown with different scales, as in Figure 3 for logarithmically-spaced receptor locations. a. With a function scale that is much larger than Δ_min, several values of the function can be represented (here I = 5). b. When the scale goes to Δ_min, then much less total information can be represented. Here only one function value fits into the veridical region. Note that the information conveyed by the same set of receptors decreases as s decreases, as in the dashed lines in Figure 4. c. Schematic for notation for hybrid neural scaling. The first part of the scale, analogous to a fovea, has n evenly spaced receptors from 0 to x_f. The second part of the scale region, from x_f to x_N has N receptors spaced such that the ratio of adjacent differences is 1 + c. The derivation suggests n should be fixed at 1/c, whereas N can in principle grow without bound. If x_f = Δ_min/c, the scale starts precisely at x = 0.

A “fovea” surrounded by a logarithmic scale

Note that if the $\frac{{\mathrm{\Delta }}_{\text{min}}}{\mathit{\text{sc}}}$ term in Eq. 11 were canceled out, the amount of information in the veridical region conveyed by the set of receptors would be precisely invariant with respect to s over the central range. This can be accomplished by preceding the region of ratio spacing (c > 0) with a region of constant spacing (c = 0). In order to equalize the information carried at small scales, the region of constant spacing should have $n=\frac{1}{c}$ receptors each spaced by Δ_min, as in Figure 5b. Adding a set of constantly spaced receptors enables constant information transfer over a range of scales starting exactly at Δ_min (at solid curves in Figure 4). When the region with ratio spacing starts at $x_f=\frac{{\mathrm{\Delta }}_{\text{min}}}{c}$, then the region of constant spacing starts at x = 0. Note that the number of receptors in the fovea is controlled only by c and is independent of the number of receptors in the region with ratio spacing. The ratio of adjacent receptor spacings is constant within each region and only fails to hold exactly at the transition between regions.

Discussion

Current technology is rapidly leading to a situation where we can design intelligent agents. The results in this paper point to a design choice that may have played out on an evolutionary time scale. To the extent neural representations of very different one-dimensional quantities all obey the same scaling laws, it suggests convergent evolution optimizing some design principle. One strategy that could be taken in designing receptor systems is to optimally adapt the organism to the behaviorally-relevant statistics of the environment. Evolution has certainly made this choice in a number of cases—the putative “y detectors" in the frog’s visual system are a famous example of this approach (Lettvin et al., 1959; Maturana et al., 1960, see also Herzog & Barlow, 1992). However, optimizing receptor arrays to a specific configuration of the world comes with a cost in terms of flexibility in responding to changes in the world.

Logarithmic receptor scales and natural statistics

In this paper, we have pursued the implications of a neural uncertainty principle— maintaining maximum ignorance about the statistics of the world—for the design of sensory receptors. Operationally, this means we have made only minimal assumptions about the statistics of the functions to be represented, limiting ourselves to uniform priors and the assumption of independence. Had we assumed a non-uniform distribution for the prior of s, this would have required us to estimate at least one parameter. Similarly, if the successive values of s_x were not independent, we would have to have estimated at least one parameter to characterize the nature of the dependence. It can be shown that the arguments developed in the first section of this paper (“Optimal receptor distribution …”) for uniform priors also generalize to scale-free (power law) priors (see footnote 4). Much empirical work has characterized statistical regularities in the world. For instance, power spectra in natural images tend to be distributed as a power law with exponent near −2 (Field, 1987; Ruderman & Bialek, 1994; Simoncelli & Olshausen, 2001). Similarly, it has been argued that power spectra for auditory stimuli are distributed as a power law with exponent −1 (Voss & Clarke, 1975). Perhaps it would be adaptive to design a set of receptors that is optimized for these naturally occurring statistics (e.g., Wei & Stocker, 2012; Piantadosi, 2016).

Results showing power law spectra with similar exponents for natural images mask variability across orientations and categories of images (Torralba & Oliva, 2003). For instance, the exponent observed, and especially second-order statistics, vary widely across pictures of landscapes vs pictures of office environments or pictures of roads. To the extent these statistics differ, if receptors were optimized for any one of these categories of images, they would be suboptimally configured for other environments (Wei & Stocker, 2012). Moreover, because the eyes are constantly in motion, the statistics of natural images are not necessarily a good proxy for the statistics of light landing on the retina averaged by synaptic time constants. More concretely, the temporal variation due to fixational eye movements has the effect of whitening images with conventional power law spectra (Kuang, Poletti, Victor, & Rucci, 2012; Rucci, 2008). In the time domain, it can be shown that in the presence of long-range correlated signals, logarithmic receptor spacing is optimal for predicting the next stimulus that will be presented (Shankar & Howard, 2013).

A derivation based on a uniform prior is more general than a belief that the statistics of the world should be power law. The former would apply across a range of environments and equally well apply to any world with some unknown statistics. Moreover, the development in the next section (entitled “Global function representation”), which predicts the existence of a fovea under some circumstances, would be quite different if we had a strong prior belief about the probability of observing a particular scale s. If the goal was to maximize the information across states of the world, and if there was a non-uniform prior about the distribution of scales, we would not have obtained asymptotically logarithmic receptor spacing.

Specific predictions deriving from the approach in this paper

There have been a great many other approaches to understanding the ubiquity of logarithmic psychological scales and the more general problem of constructing psychological scales with well-behaved mathematical properties from continua in the world. These are briefly reviewed in the next subsection (entitled “Placing this work in historical context”) with special attention to drawing contrasts with the present paper. However, to our knowledge, the predictions about the scaling of the foveal region are unique to the present approach.

Asymptotically, a logarithmic neural scale enables a set of receptors to provide equivalent information about functions of a wide range of intrinsic scales, implementing the principle of neural equanimity. However, logarithmic neural scales are untenable as Δ goes to zero—the number of receptors necessary tends to infinity and the set of receptors conveys less information about functions with scale near the smallest receptor spacing (corresponding to the maximum resolution). In the absence of a fovea, there is a small-scale correction (dashed lines Fig. 4). A region of constant receptor spacing near zero—a fovea—solves this problem allowing the set of receptors to carry the same amount of non-redundant information about functions with every possible scale ranging from Δ_min to Δ_N.

Equalizing the information across scales results in a fixed number of receptors within the fovea. Critically, the number of receptors along a radius of the fovea, measured in units of Δ_min, depends only on c. The value of c can be estimated from noting the slope of the line relating receptor size to the center of the receptive field, as in Figure 1b.⁸ Note that the value of c is estimated from receptive fields outside of the fovea, whereas Δ_min and the number of receptors along a radius are estimated from information about the fovea. As such, measurement of the two quantities ought to be completely independent. This quantitative relationship constitutes a specific prediction of this approach and can be evaluated across brain regions within the same modality, and even across modalities.

Placing this work in historical context

The present paper provides a rational basis for logarithmic neural scales and the presence of a “fovea” for values of x near zero. It also adds to a long tradition of work in mathematical psychology organized along several themes.

Measurement theory

Researchers in mathematical psychology have long considered the form of psychological spaces. This work has concluded, contra the present approach, that there is not a privileged status for logarithmic psychological scales. Fechner’s (1860/1912) reasoning for logarithmic psychological scales started with the empirical observation of a constant Weber fraction and then made what was apparently a straightforward conclusion: integration of the Weber law results in logarithmic psychological scale. That is, the Weber law states that the change in the psychological discriminability Δp due to a change in the magnitude of a physical stimulus Δx goes like $\mathrm{\Delta }p\propto \frac{{\mathrm{\Delta }}_x}{x}$. Taking the limit as Δx goes to zero and integrating gives a logarithmic scale p = log x + C. On its face this seems reasonable; surely the psychological distance between two stimuli should be the sum of the JNDs along the path between them.

Luce and Edwards (1958) noted that Fechner’s reasoning is not in general sound; the integration procedure is only valid if the empirical Weber fraction result holds. Luce (1959) showed that a logarithmic psychological scale is one of a class of relationships that can map a physical scale with a natural zero (a ratio scale) onto an interval scale that is translation-invariant (Stevens, 1946). Dzhafarov and Colonius (1999,2001) developed a much more general framework for constructing multidimensional psychological spaces from local discriminability functions (see Luce & Suppes, 2002 for an accessible introduction to the history of these questions) that also does not find any privileged status for logarithmic functions. And none of these approaches provides a natural account for the existence of a “fovea"—a region of heightened discriminability near x = 0. To the extent that logarithmic neural scales are a general property of the brain, the neural considerations described in this paper provide a potentially important complement to measurement theory.

Recent approaches to Weber-Fechner scaling

More recently, investigators in mathematical psychology and related fields have also considered the rationale underlying the apparent ubiquity of the Weber-Fechner law. These approaches have in general taken a more restrictive approach than the quite general considerations in this paper. Moreover, they do not lead to the specific predictions regarding the fovea derived here. Some recent approaches have noted that if the psychological scale is designed to minimize a relative error measure (Sun, Wang, Goyal, & Varshney, 2012; Portugal & Svaiter, 2011), logarithmic scales naturally result. For instance, in stimulus quantization, the goal is to choose a discrete quantization of the stimulus space in order to minimize the expected value of some measure of reconstruction error between the true stimulus and the quantized stimulus. If one minimizes mean squared error, the optimal quantization is uniform. However, if one attempts to minimize relative error, and if the quantization is constrained to have a fixed entropy, it can be shown that the optimal quantization is on a logarithmic scale independent of the input stimulus statistics (Sun & Goyal, 2011; Sun et al., 2012). Wilkes (2015) compared the suitability of various relative error measures from an evolutionary perspective. These approaches depend critically on the assumption of relative error measures, without explaining why those might be desirable (other than that they result in Weber-Fechner scales).

Other recent approaches that result in Weber-Fechner spacing make specific assumption about the statistics of the world. For instance Shouval, Agarwal, and Gavornik (2013) described the variability in perception as due to the variability in spike count statistics from a neuron with some I/O function and Poisson variability. They concluded that the Weber law is optimal if the world has power law statistics. Similarly, Piantadosi (2016) derived a Weber-Fechner scale for numerosity under the assumption that the probability that each possible number will be utilized goes down like a power law. This builds on earlier work deriving a rational basis for power law forgetting on the probability of use of a memory a certain time in the past (Anderson & Schooler, 1991). Wei and Stocker (2012) argued that receptor spacings should be constructed so that each receptor carries the same amount of information about the world. This depends on the statistics of the world and a logarithmic neural scale results only if the world has power law statistics with exponent −1. To the extent that the world has different statistics in different modalities and different environments, these approaches are limited in accounting for the ubiquity of Weber-Fechner neural scales. The approach in the present paper is more general in that it does not make any strong prior assumptions about the statistics of the world.

Universal exponential generalization

On its face, logarithmic neural scales seem to be closely related to Shepard’s work on universal exponential generalization (Shepard, 1987). If the mapping between the physical world and the neural scale is logarithmic, one would expect that the mapping between the neural scale and the physical world is exponential. Indeed, the approach in the section “Optimal receptor distribution …” was very much inspired by Shepard’s pioneering approach to the structure of an abstract psychological space (Shepard, 1987). However, the results are actually quite distinct.

Shepard (1987) studied the problem of generalization; if a particular stimulus x leads to some response, what is the optimal way to generalize the response to other stimuli in the neighborhood of x? Shepard’s derivation hypothesizes a consequential region of unknown size. Although the results depend on one’s prior belief about the distribution of sizes, if one uses a Copernican principle like Gott to set the prior, one obtains an exponential generalization gradient. The size of the consequential region in Shepard’s work plays a role analogous to the scale of the function in this paper. And an exponential gradient is analogous to a logarithmic scale.

The value 1 + c serves the role of the base of the logarithm in the scales derived here. This corresponds (roughly) to an exponential generalization gradient that goes like (1 + c)^x. In Shepard’s framework, the “space constant” of the exponential gradient is controlled by the expected size of the consequential region, which functions like a prior choice of scale. Note that the neural scales developed here would not lead to an exponential generalization gradient around any particular point x. The width of receptive fields (which is proportional to Δ) provides a natural lower limit to generalization. We would not expect this generalization gradient to be symmetric in x (see Fig. 1a). Of course psychological generalization need not be solely a function of neural similarity and is more difficult to observe than receptive fields.

Neural scales for cognitive dimensions

The quantitative evidence for spacing of visual receptive fields is quite strong, due to intense empirical study for decades (Daniel & Whitteridge, 1961; Hubel & Wiesel, 1974; Van Essen et al., 1984). The derivation in this paper applies equally well to any one-dimensional quantity over which we want to represent a function. If the neural uncertainty principle is a design goal for the nervous system, it should be possible to observe similar scaling laws for representations of other dimensions. As discussed in the introduction, there is evidence that the brain maintains receptive fields for dimensions that do not correspond to sensory continua. In the visual system, a neuron’s spatial receptive field is the contiguous region over visual space that causes the neuron to be activated. Cognitive continua can also show the same coding scheme. For instance, in a working memory task that required macaques to remember the number of stimuli presented over the delay, neurons in lateral prefrontal cortex responded to a circumscribed set of numbers to be remembered. That is, one neuron might be activated when the number of stimuli to be remembered is 3–5, but another neuron might be activated when the number to be remembered is 4–7.

Time cells fire during a circumscribed period of time within a delay interval. Each time cell can be thought of as having a receptive field over past time. In much the same way that a neuron with a visually-sensitive receptive field fires when a stimulus is in the appropriate part of the visual field, so too the time cell fires when a relevant stimulus, here the beginning of the delay interval, enters its temporal receptive field. Because different time cells have different receptive fields, as the stimulus recedes into the past with the passage of time, a sequence of time cells fire. In this way, receptive fields tile time, a continuous dimension in much the same way that eccentricity or numerosity would be coded.

Time and numerosity do not correspond to sensory receptors in the same way that, say, eccentricity in the visual system does. Nonetheless, the logic of the arguments in this paper apply equally well to time and numerosity. Do these “cognitive” receptive fields show logarithmic spacing? Although this is still an open empirical question, qualitative findings are consistent with logarithmic spacing. Logarithmic spacing would imply that the width of time fields should increase linearly with the time of peak firing within the delay. Although a precisely linear relationship has not been established, it is certain that the width of time fields increases with time of peak firing. This is true in the hippocampus (MacDonald, Lepage, Eden, & Eichenbaum, 2011; Salz et al., 2016), entorhinal cortex (Kraus et al., 2015), striatum (Akhlaghpour et al., 2016; Mello et al., 2015; Jin, Fujii, & Graybiel, 2009), and medial prefrontal cortex (Tiganj, Kim, Jung, & Howard, in press). Similarly, logarithmic spacing implies that the number density of cells with a time field centered on time τ should go down like τ⁻¹. While this quantitative relationship has not been established thus far, it is certain that the number density goes down with τ. This qualitative pattern at least holds in all of the regions where time cells have been identified thus far.

In addition to logarithmic spacing, the logic motivating the existence of a fovea would apply equally well to cognitive dimensions. This does not imply that foveal organization ought to be ubiquitous. We would expect the size of the fovea to be large when c is small. The cost of choosing a small value of c is that the range of scales that can be represented with a fixed N goes down dramatically (Eq. 8). In domains where there is no natural upper limit to x, such as numerosity or (arguably) time, this concern may be quite serious. However, the cost of failing to represent arbitrarily large scales is perhaps not so high in cases where there is a natural upper bound on the function to be represented. In the case of vision, there is a natural upper bound to the value of eccentricity that could be observed. In the case of functions of numerosity, the subitizing range, the finding that small integers are represented with little error, may be analogous to the fovea. In the case of functions of time, the analog of a fovea would correspond to something like traditional notions of short-term memory. In any case, direct measurement of c, which can be estimated from the width of receptive fields as a function of their peak, would provide strong constraints on whether or not there ought to be a “fovea” for numerosity and/or time.

Constructing ratio scales for cognitive dimensions

Ultimately, one can understand the spacing of the retinal coordinate system, or other sensory domains, as the result of a developmental process that aligns receptors along the sensory organ. However, if these arguments apply as well to non-sensory dimensions such as number and time, then this naturally raises the question of how the brain constructs “receptors” for these entities. One recent hypothesis for constructing representations of time, space and number describes time cells—which have receptive fields for particular events in the past—as extracted from exponentially-decaying neurons with long time constants. The requirement for logarithmic neural scales amounts to the requirement that the time constants of exponentially-decaying cells should be organized such that “adjacent” cells, along some gradient, should have time constants in a constant ratio.

There is now good evidence for long time constants in cortex both in vitro (Egorov, Hamam, Fransén, Hasselmo, & Alonso, 2002) and in vivo (Leitner et al., 2016). The long time constants can be implemented at the single cell level using known biophysical properties of cortical neurons (Tiganj, Hasselmo, & Howard, 2015). Noting that a set of exponentially-decaying cells encode the Laplace transform of the history, it has been proposed that time cells result from an approximate inversion of the Laplace transform (Shankar & Howard, 2013). The inversion can be accomplished with, essentially, feedforward on-center/off-surround receptive fields.

The mathematical basis of this approach is extremely powerful. It is straightfoward to show that the computational framework for a representation of time can be generalized to space and number (Howard et al., 2014) or any variable for which the time derivative can be computed. Moreover, access to the Laplace domain means one can implement various computations, for instance implementing translation (Shankar, Singh, & Howard, 2016) or comparison operators (Howard et al., 2015). To the extent that representations from different domains utilize the same scaling relationships, access to a set of canonical computations could lead to a general computational framework for cognition.