Abstract
People’s decisions and judgments are disproportionately swayed by improbable but extreme eventualities, such as terrorism, that come to mind easily. This article explores whether such availability biases can be reconciled with rational information processing by taking into account the fact that decision-makers value their time and have limited cognitive resources. Our analysis suggests that to make optimal use of their finite time decision-makers should over-represent the most important potential consequences relative to less important, put potentially more probable, outcomes. To evaluate this account we derive and test a model we call utility-weighted sampling. Utility-weighted sampling estimates the expected utility of potential actions by simulating their outcomes. Critically, outcomes with more extreme utilities have a higher probability of being simulated. We demonstrate that this model can explain not only people’s availability bias in judging the frequency of extreme events but also a wide range of cognitive biases in decisions from experience, decisions from description, and memory recall.
Keywords: judgment and decision-making, bounded rationality, cognitive biases, heuristics, probabilistic models of cognition
Human judgment and decision making have been found to systematically violate the axioms of logic, probability theory, and expected utility theory (Tversky & Kahneman, 1974). These violations are known as cognitive biases and are assumed to result from people’s use of heuristics – simple and efficient cognitive strategies that work well for certain problems but fail on others. While some have interpreted the abundance of cognitive biases as a sign that people are fundamentally irrational (Ariely, 2009; Marcus, 2009; Sutherland, 1992; McRaney, 2011) others have argued that people appear irrational only because their reasoning has been evaluated against the wrong normative standards (Oaksford & Chater, 2007), that the heuristics giving rise to these biases are rational given the structure of the environment (Simon, 1956; Todd & Gigerenzer, 2012), or that the mind makes rational use of limited cognitive resources (Simon, 1956; Lieder, Griffiths, & Goodman, 2013; Griffiths, Lieder, & Goodman, 2015; Wiederholt, 2010; Dickhaut, Rustichini, & Smith, 2009).
One of the first biases interpreted as evidence against human rationality is the availability bias (Tversky & Kahneman, 1973): people overestimate the probability of events that come to mind easily. This bias violates the axioms of probability theory. It leads people to overestimate the frequency of extreme events (Lichtenstein, Slovic, Fischhoff, Layman, & Combs, 1978) and this in turn contributes to overreactions to the risk of terrorism (Sunstein & Zeckhauser, 2011) and other threats (Lichtenstein et al., 1978; Rothman, Klein, & Weinstein, 1996). Such availability biases result from the fact that not all memories are created equal: while most unremarkable events are quickly forgotten, the strength of a memory increases with the magnitude of its positive or negative emotional valence (Cruciani, Berardi, Cabib, & Conversi, 2011). This may be why memories of extreme events, such as a traumatic car accident (Brown & Kulik, 1977; Christianson & Loftus, 1987) or a big win in the casino, come to mind much more easily (Madan, Ludvig, & Spetch, 2014) and affect people’s decisions more strongly (Ludvig, Madan, & Spetch, 2014) than moderate events, such as the 2476th time you drove home safely and the 1739th time a gambler lost $1 (Thaler & Johnson, 1990).
The availability bias is commonly assumed to be irrational, but here we propose that it might reflect the rational use of finite time and limited cognitive resources (Griffiths et al., 2015). We explore the implications of these bounded resources within a rational modeling framework (Griffiths, Vul, & Sanborn, 2012) that captures the inherent variability of people’s decisions (Vul, Goodman, Griffiths, & Tenenbaum, 2014) and judgments (Griffiths & Tenenbaum, 2006). According to our mathematical analysis, the availability bias could serve to help decision-makers focus their limited resources on the most important eventualities. In other words, we argue that the overweighting of extreme events ensures that the most important possible outcomes (i.e., those with extreme utilities) are always taken into account even when only a tiny fraction of all possible outcomes can be considered. Concretely, we show that maximizing decision quality under time constraints requires biases compatible with those observed in human memory, judgment, and decision-making. Without those biases the decision-maker’s expected utility estimates would be so much more variable that her decisions would be significantly worse. This follows directly from a statistical principle known as the bias-variance tradeoff (Hastie, Tibshirani, & Friedman, 2009).
Starting from this principle, we derive a rational process model of memory encoding, judgment, and decision making that we call utility-weighted learning (UWL). Concretely, we assume that the mind achieves a near-optimal bias-variance tradeoff by approximating the optimal importance sampling algorithm (Hammersley & Handscomb, 1964; Geweke, 1989) from computational statistics. This algorithm estimates the expected value of a function (e.g., a utility function) by a weighted average of its values for a small number of possible outcomes. To ensure that important potential outcomes are taken into account, optimal importance sampling optimally prioritizes outcomes according to their probability and the extremity of their function value. The resulting estimate is biased towards extreme outcomes but its reduced variance makes it more accurate. To develop our model, we apply optimal importance sampling to estimating expected utilities. We find that this enables better decisions under constrained resources. The intuitive reason for this benefit is that overweighting extreme events ensures that the most important possible outcomes (e.g., a catastrophe that has to be avoided or an epic opportunity that should be seized) are always taken into account even when only a tiny fraction of all possible outcomes can be considered.
According to our model, each experience o creates a memory trace whose strength w is proportional to the extremity of the event’s utility u(o) (i.e., where is a reference point established by past experience). This means that when a person experiences an extremely bad event (e.g., a traumatic accident) or an extremely good event (e.g., winning the jackpot) the resulting memory trace will be much stronger than when the utility of the event was close to zero (e.g., lying in bed and looking at the ceiling). Here, we refer to events such as winning the jackpot and traumatic car accidents as ‘extreme’ not because they are rare or because their utility is far from zero but because they engender a large positive or large negative difference in utility between one choice (e.g., to play the slots) versus another (e.g., to leave the casino).
In subsequent decisions (e.g., whether to continue gambling or call it a day), the model probabilistically recalls past outcomes of the considered action (e.g., the amounts won and lost in previous rounds of gambling) according to the strengths of their memory traces. As a result, the frequency with which each outcome is recalled is biased by its utility even though the recall mechanism is oblivious to the content of each memory.
Concretely, the probability that the first recalled outcome is an instance of losing $1 would be proportional to the sum of its memory traces’ strengths. Although this event might have occurred very frequently, each of its memory traces would be very weak. For instance, while there might be 1345 memory traces their strengths would be small (e.g., with close to u(−$1)). Thus, the experience of losing $1 in the gamble would be only moderately available in the gambler’s memory (total memory strength . Therefore, the one time when the gambler won $1000 might have a similarly high probability of coming to mind because its memory trace is significantly stronger (e.g., one memory trace of strength . According to our model, this probabilistic retrieval mechanism will sample a few possible outcomes from memory. These simulated outcomes (e.g., o1 = $1000, o2 = $ − 1, o5 = $1000) are then used to estimate the expected utility of the considered action by a weighted sum of their utilities where the theoretically derived weights partly correct for the utility-weighting of the memory traces (i.e., with . Finally, the considered action is chosen if and only if the resulting estimate of the expected utility gain is positive.
Our model explains why extreme events come to mind more easily, why people overestimate their frequency, and why they are overweighted in decision-making. It captures published findings on biases in memory recall, frequency estimation, and decisions from experience (Ludvig et al., 2014; Madan et al., 2014; Erev et al., 2010) as well as three classic violations of expected utility theory in decisions from description. Our model is competitive with the best existing models of decisions from experience and correctly predicted the previously unobserved correlation between events’ perceived extremity and the overestimation of their frequencies. The empirical evidence that we present strongly supports the model’s assumption that the stronger memory encoding of events with extreme utilities causes biases in memory recall that in turn lead to biases in frequency estimation and decision-making. Concretely, people remember extreme events more frequently than equally frequent events of moderate utility, overestimate their frequency, and overweight them in decision-making (Ludvig et al., 2014). Furthermore, the magnitude of overweighting increases significantly with the magnitude of the memory bias (Madan et al., 2014), and we found that the extent to which people overestimate an event’s frequency correlates significantly with its extremity. The theoretical significance of our analysis is twofold: it provides a unifying mechanistic and teleological explanation for a wide range of seemingly disparate cognitive biases and it suggests that at least some heuristics and biases might reflect the rational use of finite time and limited cognitive resources (Griffiths et al., 2015).
The remainder of this paper proceeds as follows: We start by deriving a novel decision mechanism as the rational use of finite time under reasonable, abstract assumptions about the mind’s computational architecture. We show that the derived mechanism captures people’s availability biases in frequency judgment and memory recall. Next, we demonstrate that the same mechanism can also account for three classic violations of expected utility theory and evaluate it against alternative models of decisions from description. We proceed to show that our model can also capture the heightened availability, overestimation, and overweighting of extreme events in decisions from experience. Finally, we show that utility-weighted sampling can emerge from a biologically-plausible learning mechanism that captures the temporal evolution of people’s risk preferences in decisions from experience and evaluate it against alternative models of decisions from experience. We conclude with implications for the debate on human rationality and directions for future research.
Resource-rational decision-making by utility-weighted sampling
According to expected utility theory (Von Neumann & Morgenstern, 1944), decision-makers should evaluate each potential action a by integrating the probabilities P(o|A = a) of its possible outcomes o with their utilities u(o) into the action’s expected utility . Unlike simple laboratory tasks where each choice can yield only a small number of possible payoffs, many real-life decisions have infinitely many possible outcomes.1 As a consequence, the expected utility of action a becomes an integral:
| (1) |
In the general case, this integral is intractable to compute. Below we investigate how the brain might approximate the solution to this intractable problem.
Sampling as a decision strategy
To explore the implications of resource constraints on decision-making under uncertainty, we model the cognitive resources available for decision-making within a formal computational framework that has been successfully used to develop rational process models of human cognition and can capture the variability of human performance, namely sampling (Griffiths et al., 2012). Sampling methods can provide an efficient approximation to integrals such as the expected utility in Equation 1 (Hammersley & Handscomb, 1964), and mental simulations of a decision’s potential consequences can be thought of as samples. The idea that the mind handles uncertainty by sampling is consistent with neural variability in perception (Fiser, Berkes, Orbán, & Lengyel, 2010) and the variability of people’s judgments (Vul et al., 2014; Denison, Bonawitz, Gopnik, & Griffiths, 2013; Griffiths & Tenenbaum, 2006). For instance, people’s predictions of an uncertain quantity X given partial information y are roughly distributed according to its posterior distribution p(X|y) as if they were sampled from it (Griffiths & Tenenbaum, 2006; Vul et al., 2014). Such variability has also been observed in decision-making: in repeated binary choices from experience animals chose each option stochastically with a frequency roughly proportional to the probability that it will be rewarded (Herrnstein & Loveland, 1975). This pattern of choice variability, called probability matching, is consistent with the hypothesis that animals perform a single simulation and chose the simulated action whenever its simulated outcome is positive. People also exhibit probability matching when the stakes are low, but as the stakes increase their choices transition from probability matching to maximization (Vulkan, 2000). This transition might arise from people gradually increasing the number of samples they generate to maximize the amount of reward they receive per unit time (Vul et al., 2014). Decision mechanisms based on sampling from memory can explain a wide range of phenomena (N. Stewart, Chater, & Brown, 2006). Concordant with recent drift-diffusion models (Shadlen & Shohamy, 2016) and query theory (Johnson, Häubl, & Keinan, 2007; Weber et al., 2007), this approach assumes that preferences are constructed (Payne, Bettman, & Johnson, 1992) through a sequential, memory-based cognitive process.
Assuming that people make decisions by sampling, we can express time and resource-constraints as a limit on the number of samples, where each sample is a simulated outcome: According to our theory, the decision-maker’s primary cognitive resource is a probabilistic simulator of the environment. The decision-maker can use this resource to anticipate some of the many potential futures that could result from taking one action versus another, but each simulation takes a non-negligible amount of time. Since time is valuable and the simulator can perform only one simulation at a time, the cost of using this cognitive resource is thus proportional to the number of simulations (i.e. samples).
If a decision has to be based on only a small number of simulated outcomes, what is the optimal way to generate them? Intuitively, the rational way to decide whether to take action a is to simulate its consequences o according to one’s best knowledge of the probability p that they will occur and average the resulting gain in utility Δu(o) to obtain an estimate of of the expected gain or loss in utility for taking action a over not taking it, that is
| (2) |
This decision strategy, which we call representative sampling (RS), generates an unbiased utility estimate. Yet – surprisingly – representative sampling is insufficient for making good decisions with very few samples. Consider, for instance, the choice between accepting versus declining a game of Russian roulette with the standard issue six-round NGant M1895 revolver. Playing the game will most likely, i.e. with probability , reward you with a thrill and save you some ridicule (Δu(o1) = 1) but kill you otherwise . Ensuring that representative sampling declines a game of Russian roulette at least 99.99% of the time, would require 51 samples – potentially a very time-consuming computation.
Like Russian roulette, many real-life decisions are complicated by an inverse relationship between the magnitude of the outcome and its probability (Pleskac & Hertwig, 2014). Many of these problems are much more challenging than declining a game of Russian roulette, because their probability of disaster is orders of magnitude smaller than and it may or may not be large enough to warrant caution. Examples include risky driving, medical decisions, diplomacy, the stock market, and air travel. For some of these choices (e.g., riding a motor cycle without wearing a helmet) there may be a one in a million chance of disaster while all other outcomes have negligible utilities:
| (3) |
If people decided based on n representative samples, they would completely ignore the potential disaster with probability 1 − (1 − 10−6)n. Thus to have at least a 50% chance of taking the potential disaster into account they would have to generate almost 700000 samples. This is clearly infeasible; thus one would almost always take this risk even though the expected utility gain is about −1000. In conclusion, representative sampling is insufficient for resource-bounded decision-making when some of the outcomes are highly improbable but so extreme that they are nevertheless important. Therefore, the robustness of human decision-making suggests that our brains use a more sophisticated sampling algorithm—such as importance sampling.
Importance sampling is a popular sampling algorithm in computer science and statistics (Hammersley & Handscomb, 1964; Geweke, 1989) with connections to both neural networks (Shi & Griffiths, 2009) and psychological process models (Shi, Griffiths, Feldman, & Sanborn, 2010). It estimates a function’s expected value with respect to a probability distribution p by sampling from an importance distribution q and correcting for the difference between p and q by down-weighting samples that are less likely under p than under q and up-weighting samples that are more likely under p than under q. Concretely, self-normalized importance sampling (Robert & Casella, 2009) draws s samples x1, ⋯, xs from a distribution q, weights the function’s value f (xj) at each point xj by the weight and then normalizes its estimate by the sum of the weights:
| (4) |
| (5) |
With finitely many samples, this estimate is generally biased. Following Zabaras (2010), we approximate its bias and variance by
| (6) |
| (7) |
We hypothesize that the brain uses a strategy similar to importance sampling to approximate the expected utility gain of taking action a and approximate the optimal decision by
| (8) |
| (9) |
Note that importance sampling is a family of algorithms: each importance distribution q yields a different estimator, and two estimators may recommend opposite decisions. This leads us to investigate which distribution q yields the best decisions.
Which distribution should we sample from?
Representative sampling is a special case of importance sampling in which the simulation distribution q is equal to the outcome probabilities p. Representative sampling fails when it neglects crucial eventualities. Neglecting some eventualities is necessary, but particular eventualities are more important than others. Intuitively, the importance of potential outcome oi is determined by |p(oi) · u(oi)| because neglecting oi amounts to dropping the addend p(oi) · u(oi) from the expected-utility integral (Equation 1). Thus, intuitively, the problem of representative sampling can be overcome by considering outcomes whose importance (|p(oi) · u(oi)|) is high and ignoring those whose importance is low.
Formally, the agent’s goal is to maximize the expected utility gain of a decision made from only s samples. The utility foregone by choosing a sub-optimal action can be upper-bounded by the error in a rational agent’s utility estimate. Therefore the agent should minimize the expected squared error of its estimate of the expected utility gain, which is the sum of its squared bias and variance, that is (Hastie et al., 2009). As the number of samples s increases, the estimate’s squared bias decays much faster (O(s−2)) than its variance (O(s−1)); see Equations 6–7. Therefore, as the number of samples s increases, minimizing the estimator’s variance becomes a good approximation to minimizing its expected squared error.
According to variational calculus the importance distribution
| (10) |
minimizes the variance (Equation 7) of the utility estimate in Equation 9 (Geweke, 1998; Zabaras, 2010; see Appendix A). This means that the optimal way to simulate outcomes in the service of estimating an action’s expected utility gain is to over-represent outcomes whose utility is much smaller or much larger than the action’s expected utility gain. Each outcome’s probability is weighted by how disappointing or elating it would be to a decision-maker anticipating to receive the gamble’s expected utility gain . But unlike in disappointment theory (Bell, 1985; Loomes & Sugden, 1984, 1986), the disappointment or elation is not added to the decision-maker’s utility function but increases the event’s subjective probability by prompting the decision-maker to simulate that event more frequently. Unlike in previous theories, this distortion was not introduced to describe human behavior but derived from first principles of resource-rational information processing: Importance sampling over-simulates extreme outcomes to minimize the mean-squared error of its estimate of the action’s expected utility gain. It tolerates the resulting bias because it is more important to shrink the estimate’s variance.
Unfortunately, importance sampling with qvar is intractable, because it presupposes the expected utility gain that importance sampling is supposed to approximate. However, the average utility of the outcomes of previous decisions made in a similar context could be used as a proxy for the expected utility gain . That quantity has been shown to be automatically estimated by model-free reinforcement learning in the midbrain (Schultz, Dayan, & Montague, 1997). Therefore, people should be able to sample from the approximate importance distribution
| (11) |
This distribution weights each outcome’s probability by the extremity of its utility. Thus, on average, extreme events will be simulated more often than equiprobable outcomes of moderate utility. We therefore refer to simulating potential outcomes by sampling from this distribution as utility-weighted sampling.
Utility-weighted sampling
Having derived the optimal way to simulate a small number of outcomes (Equation 11), we now turn to the question how those simulated outcomes should be used to make decisions under uncertainty. The general idea is to estimate each action’s expected utility gain from a small number of simulated outcomes, and then choose the action for which this estimate is highest.
If the simulated outcomes were drawn representatively from the outcome distribution p, then we could obtain an unbiased expected utility gain estimate by simply averaging their utilities (Equation 2). However, since the simulated outcomes were drawn from the importance distribution rather than p, we have to correct for the difference between these two distributions by computing a weighted average instead (Equation 5). Concretely, we have to weight each simulated outcome oj by the ratio of its probability under the outcome distribution p over its probability under the importance distribution from which it was sampled. Thus, the extreme outcomes that are overrepresented among the samples from will be down-weighted whereas the moderate outcomes that are underrepresented among the samples from will be up-weighted. Because , the weight wj of outcome oj is for some constant z. Since the weighted average in Equation 5 is divided by the sum of all weights, the normalization constant z cancels out. Hence, given samples o1, … ,os from the utility-weighted sampling distribution , the expected utility gain of an action or prospect can be estimated by
| (12) |
If no information is available a priori, then there is no reason to assume that the expected utility gain of a prospect whose outcomes may be positive or negative should be positive, or that it should be negative. Therefore, in these situations, the most principled guess an agent can make for the expected utility gain in Equation 10 – before computing it – is . Thus, when the expected utility gain is not too far from zero, then the importance distribution qvar for estimating the expected utility gain of a single prospect can be efficiently approximated by
| (13) |
This approximation simplifies the UWS estimator of a prospect’s expected utility gain (Equation 12) into
| (14) |
where sign(x) is −1 for x < 0, 0 for x = 0, and +1 for x > 0.
This utility-weighted sampling mechanism succeeds where representative sampling failed. For Russian roulette, the probability that a sample drawn from the utility-weighted sampling distribution (Equation 13) considers the possibility of death (o2) is
| (15) |
Consequently, utility-weighted sampling requires only 1 rather than 51 samples to recommend the correct decision at least 99.99% of the time, because the first sample is almost always the most important potential outcome (i.e., death). In this case, the utility estimate defined in Equation 14 would be 1/|109|·−1 = −109 and its expected value for a single sample is also very close to −109. While this mechanism is biased to overestimate the risk of playing Russian roulette , that bias is beneficial because it makes it easier to arrive at the correct decision. Likewise, a single utility-weighted sample suffices to consider the potential disaster (Equation 3) at least 99.85% of the time, whereas even 700, 000 representative samples would miss the disaster almost half of the time. Thus, utility-weighted sampling would allow people to make good decisions even under extreme time pressure. This suggests that to achieve the optimal bias-variance tradeoff (Hastie et al., 2009) the sampling distribution has to be biased towards extreme outcomes. This bias reduces the variance of the utility estimate enough to enable better decisions than representative sampling whose expected utility gain estimate is unbiased but has high variance.
To apply the utility-weighted sampling model to decisions people face in life and experiments, we have to specify the utility u(o) of the outcomes o. To do so, we interpret an outcome’s utility as the subjective value that the decision-maker’s brain assigns to it in the choice context. Concretely, we follow the proposal of Summerfield and Tsetsos (2015) that the brain represents value in an efficient neural code. This proposal is based on psychophysical and neural data (Louie, Grattan, & Glimcher, 2011; Louie, Khaw, & Glimcher, 2013; Mullett & Tunney, 2013) and fits into our resource-rational framework: The brain’s representational bandwidth is finite, because the possible range of neural firing rates is limited. Efficient coding makes rational use of the brain’s finite representational bandwidth by adapting the neural code to the range of values that have to be represented in a given context. This implies rescaling the values of potential outcomes such that all of them lie within the representational bandwidth. If the representational bandwidth is 1 and the largest and the smallest possible values in the current context c are and respectively, then the utility of an outcome o should be represented by
| (16) |
where is neural noise that reflects uncertainty about the outcome’s value. Since it is the neural representation of value rather than value itself that drives choice, we interpret u(o) as the subjective utility of outcome o in context c. We will consistently use this formal definition of utility (Equation 16) in this and all following sections.
Our basic UWS model of how people estimate a prospect’s expected utility thus has only two parameters: the number of samples s and the unreliability of the decision-maker’s representation of utility.
Utility-weighted sampling in binary choices yields a simple heuristic
Having derived a resource-rational mechanism for estimating expected utilities, we now translate it into a decision strategy. Many real-world decisions and most laboratory tasks involve choosing between two actions a1 and a2 with uncertain outcomes and that depend on the unknown state of the world. Consider, for example, the choice between two lottery tickets: the first ticket offers a 1% chance to win $1000 at the expense of a 99% risk to lose $1 (O(1))∈{−1,1000}) and the second ticket offers a 10% chance to win $1000 at the expense of a 90% risk to lose $100 (O(2) ∈{−100, 1000}). According to expected utility theory, one should choose the first lottery (taking action a1) if and the second lottery (action a2) if This is equivalent to taking the first action if the expected utility difference is positive and the second action if it is negative. The latter approach can be approximated very efficiently by focusing computation on those outcomes for which the utilities of the two actions are very different and ignoring events for which they are (almost) the same. For instance, it would be of no use to simulate the event that both lotteries yield $1000 because it would not change the decision-maker’s estimate of the differential utility and thus have no impact on her decision. To make rational use of their finite resources, people should thus use utility-weighted sampling to estimate the expected value of the two actions’ differential utility ΔU = u(O(1) – u(O(2)) as efficiently as possible. This is accomplished by sampling pairs of outcomes from the bivariate importance distribution
| (17) |
integrating their differential utilities according to
| (18) |
and then choosing the first action if the estimated differential utility is positive, that is
| (19) |
Note that each simulation considers a pair of outcomes: one for the first alternative and one for the second alternative. This is especially plausible when the outcomes of both actions are determined by a common cause. For instance, the utilities of wearing a shirt versus a jacket on a hike are both primarily determined by the weather. Hence, reasoning about the weather naturally entails reasoning about the outcomes of both alternatives simultaneously and evaluating their differential utilities in each case (e.g. rain, sun, wind, etc.) instead of first estimating the utility of wearing a shirt and then starting all over again to estimate the utility of wearing a jacket.
Given that there is no a priori reason to expect the first option to be better or worse than the second option, is 0 and the equation simplifies to
| (20) |
This distribution captures the fact that the decision-maker should never simulate the possibility that both lotteries yield the same amount of money– no matter how large it is. It does not overweight extreme utilities per se, but rather pairs of outcomes whose utilities are very different. Its rationale is to focus on the outcomes that are most informative about which action is best. For instance, in the example above, our UWS model of binary choice overweights the unlikely event in which the first ticket wins $1000 and the second ticket loses $100. Plugging the optimal importance distribution (Equation 20) into the UWS estimate for the expected differential utility yields an intuitive heuristic for choosing between two options. Formally, the optimal importance sampling estimator for the expected value of the differential utility is
| (21) |
where sign(x) is +1 for positive x and −1 for negative x. If the heightened availability of extreme events roughly corresponded to the utility-weighted sampling distribution (Equation 20), then the decision rule in Equation 21 could be realized by the following simple and psychologically plausible heuristic for choosing between two actions:
Imagine a few possible events (e.g., 1. Ticket 1 wins and ticket 2 loses. 2. Ticket 2 wins and ticket 1 loses. 3. Ticket 1 winning and ticket 2 losing comes to mind again. 4. Both tickets lose.).
For each imagined scenario, evaluate which action would fare better (1. ticket 1, 2. ticket 2, 3. ticket 1, 4. ticket 1).
Count how often the first action fared better than the second one (3 out of 4 times).
If the first action fared better more often than the second action, then choose the first action, else choose the second action (Get ticket 1!).
As a quantitative example, consider how UWS would choose between a ticket with a 10% chance of winning $99 and a 90% chance of losing $1 versus winning $1 for sure. If, the frequency with which events come to mind reflects utility-weighted sampling, then people could simply tally whether winning came to mind more often than losing. According to UWS, winning should came to mind about 86% of the time whereas losing should come to mind only about 14% of the time (the derivation of these simulation frequencies is provided in Appendix B). Hence, if the decision-maker imagined the outcome of choosing the gamble twice, there would be a 71.4% chance that winning came to mind twice, a 26.2% chance that winning and losing each came to mind once, and an only 2.4% chance of imagining losing twice. In the first case, the heuristic would always choose the gamble, in the second case it would choose it half of the time, and in the last case it would always decline the gamble. Hence, simply tallying which option (gambling vs. playing it safe) the imagined outcomes favored more frequently (and breaking ties at random) would be sufficient to make the correct decision 84% of the time despite having imagined the outcome only twice. Appendix B provides a complete description of this worked example, and Appendix C applies UWS to the general case of choosing between a gamble and its expected value.
The overweighting of outcomes that strongly favor one action over another in UWS is similar to the effect of anticipated regret in regret theory (Loomes & Sugden, 1982), but in UWS extremity changes the frequency with which an event is simulated and does not affect its utility. Magnifying the subjective probabilities of extreme events makes UWS more similar to salience theory (Bordalo, Gennaioli, & Shleifer, 2012) according to which pairs of payoffs that are very different receive more attention than pairs of payoffs that are similar. Yet, while salience theory provides a descriptive account of binary choice frequencies in decisions from description, UWS additionally provides a resource-rational mechanistic account of decisions from experience, memory recall, and frequency judgments.
Summary and outlook
In summary, our analysis suggested that the rational use of finite cognitive resources implies that extreme events should be overrepresented in decision-making under uncertainty. Utility-weighted sampling is a rational process model that formalizes this prediction. This biased mechanism leads to better decisions than its unbiased alternative (i.e. representative sampling). Utility-weighted sampling thereby enables robust decisions under time constraints that prohibit the careful consideration of many possible outcomes.
We have derived two versions of utility-weighted sampling: The first version estimates the expected utility gain of a single action. The second version chooses between two actions. Although both mechanisms overweight extreme events their notions of extremity are different. The UWS mechanism for estimating the expected utility gain of a single action overweights individual outcomes with extreme utilities. By contrast, the UWS mechanism for choosing between two actions overweights pairs of outcomes whose utilities are very different. In the remainder of this article, we will use the first mechanism to simulate frequency judgment, pricing, and decisions from experience and the second mechanism to simulate binary decisions from description. Despite this difference, we can interpret the first mechanism as a special case of the second one, because its importance distribution (Equation 11) compares the utility of the prospect’s outcomes against the average utility of alternative actions. Hence, UWS always overweights events that entail a large difference between the utility of the considered action and some alternative. The frequency with which a state has been experienced or its stated probability also influence how often it will be sampled. Thus, impossible and highly improbable states are generally unlikely to be sampled. However, states with high differential utility are sampled more frequently than is warranted by how often they have been experienced or their stated probability. This increases the probability that improbable states with extreme differential utility will be considered. We support the proposed mechanism by showing that it can capture people’s memory biases for extreme events, the overestimation of the frequency of extreme events, biases in decisions from description, and biases in decisions from experience.
Biases in frequency judgment confirm predictions of UWS
If people remembered the past as if they were sampling from the UWS distribution (Equation 11), they would recall their best experience and their worst experience much more frequently than an unremarkable one (cf. Madan et al., 2014). If people relied on such a biased memory system to estimate frequencies and assess probabilities, then their estimate of the frequency fk = p(ok) of the event ok would be
| (22) |
where is the utility-weighted sampling distribution. Since over-represents each event ok proportionally to its extremity , that is , we predict that people’s relative over-estimation is a monotonically increasing function of the event’s extremity , Formally, the bias (Equation 6) of utility-weighted probability estimation (Equation 22) implies that the relative amount by which people overestimate an event’s frequency (i.e., ) should increase with the event’s extremity , according to
| (23) |
where c is an upper bound on people’s relative overestimation. This predicts that people should overestimate the frequency of an event more the more extreme it is regardless of its frequency. In this section, we test this prediction against people’s judgments: we first report an experiment suggesting that frequency overestimation increases with perceived extremity, and then we show that UWS can capture the finding that overestimation occurs regardless of the event’s frequency (Madan et al., 2014).
Frequency overestimation increases with perceived extremity
Lichtenstein et al. (1978) and Pachur, Hertwig, and Steinmann (2012) found that people’s estimates of the frequencies of lethal events are strongly correlated with how many instances of each event they can recall. Furthermore, Lichtenstein et al. (1978) also found that overestimation was positively correlated with the number of lives lost in a single instance of each event, the likelihood that an occurrence of the event would be lethal, and the amount of media coverage it would typically attract. We hypothesize that extremity-weighted memory encoding contributed to these effects. If this were true, then overestimation should increase with perceived extremity. Here, we test this prediction of UWS in a new experiment that measures perceived extremity and correlates it with the biases in people’s frequency estimates.
Methods
We recruited 100 participants on Amazon Mechanical Turk. Participants received a baseline payment of $1.25 for about 30 minutes of work. Participants were asked to estimate how many American adults had experienced each of 39 events in 2015 as accurately as possible and accurate frequency estimation was incentivized by a performance dependent bonus of up to $2. In addition, participants judged each event’s valence (good or bad) and extremity (0: neutral – 100: extreme). The 39 events comprised 30 stressful life events from Hobson et al. (1998), four lethal events (suicide, homicide, lethal accidents, and dying from disease/old age), three rather mundane events (going to the movies, headache, and food-poisoning), and two attention-checks. As a reference, participants were told the total number of American adults and how many of them retire each year.
To assess overestimation we compared our participants’ estimates to the true frequencies of the events according to official statistics.2 The complete experiment can be inspected online.3 Out of 100 participants 22 failed one or more attention checks (number of Americans elected president, number of Americans who slept between 2h and 10h at least once) and were therefore excluded.
Results and Discussion
A significant rank correlation4 between the average extremity judgments of the 37 events and average relative overestimation confirmed our model’s prediction (Spearman’s ρ = 0.46, p = .0045, see Figure 1), and we observed the same effect at the level of individual judgments (Spearman’s ρ = 0.14, p < 10−12). The frequencies of the five most extreme events, that is murder (93.3%), suicide (92.6% extreme), dying in an accident (90% extreme), the death of one’s partner (86% extreme), and suffering a major injury or serious illness (85% extreme) were overestimated by a factor of 159 (p = 0.0001), 9 (p = 0.0026), 35 (p = 0.0035), 1.01 (p = 0.03), and −0.22 (p = 0.25) respectively. By contrast, the prevalences of the five least extreme events, that is headache (20% extreme), change in work responsibilities (21% extreme), getting a traffic ticket (26% extreme), moving flat (26% extreme), and career change (32% extreme) were underestimated by 4% (p = 0.42), 1% (p = 0.95), 10% (p = 0.52), 52% (p < 0.0001), and 24% (p = 0.0211) respectively. Like Rothman et al. (1996), we found that people overestimate the frequency of suicide (overestimated by 927%) more heavily than the frequency of divorce (overestimated by 27%). According to our theory, this is because suicide is perceived as more extreme than divorce (92.6% extreme vs. 59% extreme).
Figure 1.
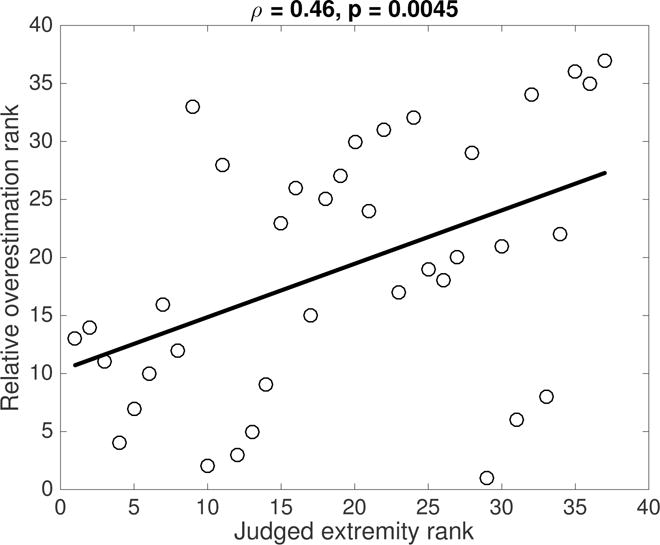
Relative overestimation increases with perceived extremity . Each circle represents one event’s average ratings.
Furthermore, we found that the effect of extremity on overestimation also holds across the three categories the events were drawn from (see Figure 2): people significantly underestimated the frequency of mundane events (t(233)=−3.66,p=0.0003) while overestimating the frequency of stressful life events (t(2338) = 2.02, p = 0.0433) and lethal events (t(311) = 5.46, p < 10−7). Two-sample t-tests confirmed that relative overestimation was larger for stressful life events than for mundane events (t(2571) = 3.16, p = 0.0016) and even larger for lethal events t(544) = 12.70, p < 10−15). Figure 2 illustrates that overestimation and perceived extremity increased together.
Figure 2.
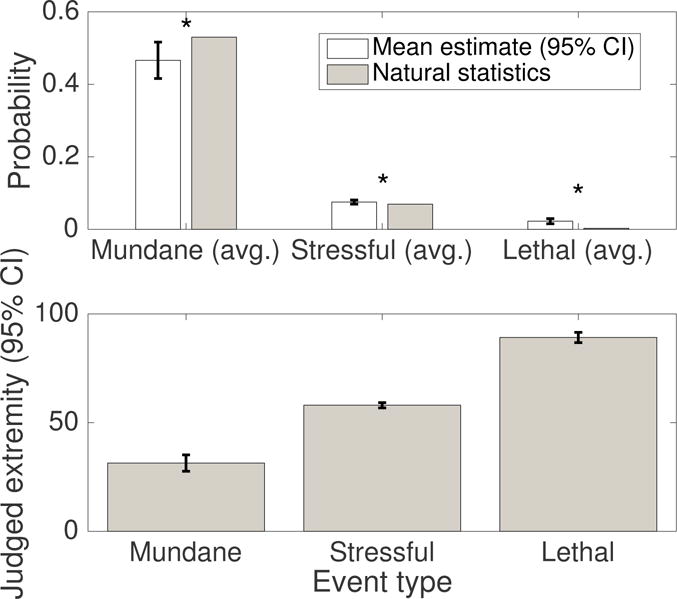
Judged frequency and extremity by event type.
While people’s judgments were biased for the events studied here, there are many quantities, such as the length of poems, for which people’s predictions are unbiased (Griffiths & Tenenbaum, 2006). This is consistent with UWS because unlike monetary gains and losses they impart no (dis)utility on their observer. For instance, hearing that a poem is 8 lines long carries virtually the same utility as hearing that another poem is 25 lines long. Hence, for such quantities, UWL would predict effectively unbiased memory encoding, recall, and prediction. Our theory’s ability to differentiate situations where human judgment is biased from situations where it is unbiased speaks to its validity.
In conclusion, the experiment confirmed our theory’s prediction that an event’s extremity increase the relative overestimation of its frequency. However, additional experiments are required to disentangle the effects of extremity and low probability, because these two variables were anti-correlated (ρ(36) = −0.67, p < 0.0001). To address this problem, we examined our model’s predictions using two published studies that kept frequency constant across events (Madan et al., 2014).
UWS captures that extreme events are overestimated regardless of frequency
The results reported above supported the hypothesis that people overestimate the frequency of extreme events, but most extreme events in that experiment were also rare. Therefore our findings could also be explained by postulating that people overestimate extreme events only because they are rare (Hertwig, Pachur, & Kurzenhäuser, 2005). This possibility is supported by empirical evidence for regression to the mean effects in frequency estimation (Attneave, 1953; Lichtenstein et al., 1978; Hertwig et al., 2005; Zhang & Maloney, 2012). Yet, extremity per se also contributes to overestimation: Madan et al. (2014) found that people overestimate the frequency of an extreme event relative to a non-extreme event even when both were equally frequent. The hypothesis that people overestimate the frequency of extreme events because those events are rare cannot account for this finding, but utility-weighted sampling can. To demonstrate this, we simulated the experiments by Madan et al. (2014) using utility-weighted sampling.
In the first experiment by Madan et al. (2014) participants repeatedly chose between two doors. Each door probabilistically generated one of two outcomes, and different doors were available on different trials. There were a total of four doors generating a sure gain of +20 points, a sure loss of −20 points, a risky gain offering a 50/50 chance of +40 or 0, and a risky loss offering a 50/50 chance of 0 or −40 points. In most trials participants either chose between the risky and the sure gain (gain trials) or between the risky and the sure loss (loss trials). After each choice, participants were shown the number of points earned, and they received no additional information about the options. After 6 blocks of 48 such choices participants were asked to estimate the probability with which each door generated each of the possible outcomes and to report the first outcome that came to their mind for each of the four doors. In their second experiment Madan et al. (2014) shifted all outcomes from Experiment 1 by +40 points.
We estimated the two parameters of the UWS model (i.e., the number of samples s and the noisiness σε of the utility function) from the choice frequencies reported by Madan et al. (2014) using the maximum-likelihood principle. While participants had to learn the outcome probabilities from experience, the model developed so far assumes known probabilities. We thus restricted our analysis to the last block of each experiment. For each experiment, our model defines a likelihood function over the number of risky choices in gain trials and the number of risky choices in loss trials. We maximized the product of these likelihood functions with respect to our model’s parameters using grid search over possible numbers of samples and global optimization with respect to σε. The resulting parameter estimates were s = 4 samples and σε = 0.05.
With these parameters, utility-weighted sampling correctly predicted that extreme outcomes come to mind first more often than the equally frequent moderate outcomes; see Table 1A. Next, we simulated people’s frequency estimates according to Equation 22. UWS correctly predicted that people overestimate the frequency of extreme outcomes relative to the equally frequent moderate outcome; see Table 1B. In addition, UWS captured that participants were more risk-seeking for gains than for losses (see Table 2), and a later section investigates this phenomenon in more detail.
Table 1.
UWS simulation of people’s memory recall (A) and frequency estimates (B) after the Experiments by Madan et al. (2014).
| A | ||
|---|---|---|
| Comes to mind first: | Extreme Gain vs. Neutral | Extreme Loss vs. Neutral |
| Experiment 1 | 64.5% vs. 35.5% | 71% vs. 29% |
| Experiment 2 | 70.0% vs. 30% | 72.6% vs. 27.4% |
| B | ||
| Estimated Frequency of … | Extreme Gain vs. Neutral | Extreme Loss vs. Neutral |
|
| ||
| Experiment 1 | 83.0% vs. 17.0% | 87.5% vs. 12.5% |
| Experiment 2 | 87.5% vs. 12.5% | 90.0% vs. 10.0% |
Table 2.
UWS captures people’s risk preferences in the Experiments by Madan et al. (2014).
| Risky Choices in | Gain Trials | Loss Trials |
|---|---|---|
| Experiment 1: | UWS: 54% People: 45% | UWS: 36%, People: 35% |
| Experiment 2: | UWS: 60%, People: 55% | UWS: 31%, People: 14% |
Summary and Discussion
The findings presented in this section provide strong support for our hypothesis that utility-weighting is the reason why people over-represent extreme events: First, Experiment 1 showed that there is a significant correlation between an event’s utility and the degree to which people overestimate its frequency. Second, the data from Madan et al. (2014) rule out the major alternative explanation that people overestimate the frequency of extreme events only because they are rare and also demonstrate that the overestimation is mediated by a memory bias for events with extreme utility. Furthermore, we found that the adaptive bias predicted by our theory exists not only in decision-making but also in frequency estimation and memory.
A parsimonious explanation for these three phenomena could be that the over-representation of extreme events results from a known bias in learning: emotional salience enhances memory formation (Cruciani et al., 2011). While overestimation has been previously explained by high “availability” of salient memories (Tversky & Kahneman, 1973), our theory specifies what exactly the availability of events should correspond to – namely their importance distribution (Equation 13) – and why this is useful. Our empirical findings were consistent with utility-weighted sampling but inconsistent with the hypothesis that the bias in frequency estimation is merely a reflection of the regression to the mean effect (Hertwig et al., 2005). While alternative accounts of why people overestimate the frequency of extreme events, such as selective media coverage (Lichtenstein & Slovic, 1971), can explain the overestimation of certain lethal events, they cannot account for the data of Madan et al. (2014). Thus at least part of the overestimation of extreme events appears to be due to utility-weighted sampling. Hence, an event’s extremity may sway people’s decisions by increasing their propensity to remember it, and this is clearly distinct from extremity’s potential effects on the subjective utility of anticipated outcomes (Loomes & Sugden, 1982; Bell, 1985; Loomes & Sugden, 1984, 1986).
Our model’s predictions are qualitatively consistent with the data of Madan et al. (2014) but often more extreme. This difference might result from the idealistic assumption that there is no forgetting. We revisit this issue with a more realistic learning model later in the paper.
Biases in decisions from description
According to decision theory, an event’s probability determines its weight in decision-making under uncertainty. Therefore, the biased probability estimates induced by utility-weighted sampling suggest that people should overweight extreme events in decisions under uncertainty. We will test this prediction in the domain of decisions from experience. Since this will require a model of learning, we model decisions from description as an intermediate step towards building a model of decisions from experience.
In the decisions from description paradigm participants choose between gambles that are described by their payoffs and outcome probabilities (Allais, 1953; Kahneman & Tversky, 1979). Typically participants make binary choices between pairs of gambles or between a monetary gamble and a sure payoff. While people could, in principle, make these decisions by computing and comparing the gamble’s expected values, ample empirical evidence demonstrates that they do not. Instead, people might reuse their strategies for everyday decisions. Everyday decisions are usually based on memories of past outcomes in similar situations. Hence, if people reused their natural decision strategies, then their decisions from description should be affected by the availability biases that have been observed in memory recall and frequency judgments. Our section on utility-weighted learning in decision from experience provides a precise, mechanistic account of how these biases arise from biased memory encoding. Here, we assume that similar mechanisms are at play in decisions from description. For instance, it is conceivable that the high salience of large differential payoffs in decisions from description (Bordalo et al., 2012) attracts a disproportionate amount of people’s attention, making them more memorable, and increasing the frequency with which they will be considered. We think that such mechanisms could roughly approximate the utility-weighting prescribed by our model, at least for simple gambles whose outcomes are displayed appropriately.
In this section, we therefore apply UWS to decisions from description, validate the resulting model on the data from the Technion choice prediction competition (Erev et al., 2010), and demonstrate that it can capture three classic violations of expected utility theory.
Validation on decisions from description
We validated the utility-weighted sampling model of binary choices (Equations 18–21) with the stochastic normalized utility function defined in Equation 16 against people’s decisions from description in the Technion choice prediction tournament (Erev et al., 2010). There are many factors that influence people’s responses that are outside the scope of our model. These include accidental button presses, mind-wandering, misperception, and the occasional use of additional decision strategies that might be well adapted to the specific problems to which they are applied (Lieder & Griffiths, 2015, under review). We therefore extended UWS to allow for an unknown proportion of choices (prandom) that are determined other factors. We model the net effect of those choices as choosing either option with a probability of 0.50.
We fitted the number of samples s, the noisiness σε of the utility function, and the percentage of trials in which people choose at random to the training data of the Technion choice prediction competition. The maximum likelihood estimates of these model parameters were s = 10 samples, σε = 0.1703, and prandom = 0.07. We then used these parameter estimates to predict people’s choices in the decision problems of the test set of the Technion choice prediction competition. Figure 3 shows our model’s predictions and compares them to people’s choice frequencies. On average across the 60 problems, people chose the risky option about 46.75 ± 3.98% of the time and the UWS model chose the risky option about 48.92 ± 2.56% of the time. This difference was not statistically significant (t(59) = −1.03, p = 0.31) suggesting that the predictions of UWS were unbiased. While there was no bias—on average—the predictions of UWS were regressed towards 50/50 compared to people’s choice frequencies: On problems where people were risk-seeking UWS chose the risky option less often than people (66.11% vs. 79.20%, t(24) = −6.48, p < .0001). But on problems where people were risk-averse, UWS chose the risky option more often than people (35.54% vs. 21.97%, p < .0001).
Figure 3.

Predictions of UWS on the test set of the Technion choice prediction tournament for decisions from description according to the parameters estimated from the training set. Each data point reports the frequency with which UWS (horizontal axis) versus people (vertical axis) chose the risky option in one of the 60 decision problems of the Technion competition, and the solid line is the identity line.
Our model predicted people’s choice frequencies more accurately than cumulative prospect theory (CPT; Tversky, & Kahneman, 1992) or the priority heuristic (Brandstätter, Gigerenzer, & Hertwig, 2006): Its mean squared error (MSDUWS = 0.0266) was significantly lower than for cumulative prospect theory (MSDCPT = 0.0837, t(59) = − 5.4, p < .001) or the priority heuristic (MSDpriority = 0.1437, t(59) = −4.9,p < .001). Furthermore, the predicted risk preference agreed with people’s risk preferences in 87% of the trials (CPT: 93%, priority heuristic: 81%) and the predicted choice frequencies were highly correlated with people’s choice frequencies (rUWS(59) = 0.88, p < 10−15 versus rCPT = 0.86 and rpriority = 0.65). Our model’s predictive accuracy was similar to those of the best existing models, namely stochastic cumulative prospect theory with normalization (r = 0.92, MSD = 0.0116) and Haruvy’s seven parameter logistic regression model that won the competition (r = 0.92, MSD = 0.0126), although the differences were still statistically significant (t(59) = 3.5, p < .001 and t(59) = 3.97, p < .001). In addition to performing about as well as the best existing models our model is distinctly principled: UWS is the only accurate mathematical process model that is derived from first principles. All alternative models that perform similarly well were tailored to capture known empirical phenomena or fail to specify the mechanisms of decision-making.
Having estimated our model’s parameters and validated it, we now proceed to demonstrate that it can explain three paradoxes in risky choice, namely the Allais paradox (Allais, 1953), the fourfold pattern of risk preferences (Tversky & Kahneman, 1992), and preference reversals (Lichtenstein & Slovic, 1971).
The Allais paradox
In the two lotteries L1(z) and L2(z) defined in Table 3 the chance of winning z dollars is exactly the same. Yet, when z = 2400 most people prefer lottery L2 over lottery L1, but when z = 0 the same people prefer L1 over L2. This inconsistency is known as the Allais paradox (Allais, 1953).
Table 3.
The Allais gambles: Participants choose between lottery L1 and lottery L2 for z = 2400 versus z = 0.
| (ol, pl) | (o2, p2) | (o3, p3) | |
|---|---|---|---|
| L1(z): | (z, 0.66) | (2500, 0.33) | (0, 0.01) |
| L2 (z): | (z, 0.66) | (2400, 0.34) |
We simulated people’s choices between both pairs of lotteries according to utility-weighted sampling with the parameters estimated from the Technion training set. To do so, we computed the probability p and utility difference ΔU for each possible pair of outcomes of the first lottery L1 and the second lottery L2. Since the outcomes of the two lotteries are statistically independent, the probability that the first lottery yields outcome O1 while the second lottery yields O2 is P(O1) · P(O2). To apply UWS to predict people’s choices between the two lotteries, we determined all possible values of the differential utility ΔU and their respective probabilities. For instance, when z = 0, then the possible differential utilities are 0, −u(2400), u(2500) − u(2400), and u(2500) (see Tables 3 and 4). In this case, ΔU is −u(2400) if the first or the third outcome is drawn for the first lottery and the second outcome is drawn for the second lottery. The probability of the first scenario is p1 · p2 = 0.66 · 0.34 and the probability of the second scenario is p3 · p2 = 0.01 · 0.34; hence the probability of ΔU = −u(2400) is 0.67 · 0.34. Next, we computed the simulation frequency which is proportional to p(ΔU) · |Δu|. For instance, in this example, and normalizing this probability distribution yields suggesting that this extreme eventuality would occupy half of the decision-maker’s mental simulations even though its probability is less than 23%. This corresponds to overweighting this event by a factor of 2.19. Table 4 presents these numbers for all differential utilities possible with z = 2400 or z = 0.
Table 4.
Utility-weighted sampling explains the Allais paradox.
| ΔU | p |
|
/p | ||
|---|---|---|---|---|---|
|
|
|||||
| 0 | 0.66 | 0 | 0 | ||
| z = 2400: | |||||
| u(2500) − u(2400) | 0.33 | 0.58 | 1.8 | ||
| −u(2400) | 0.01 | 0.42 | 42 | ||
| ΔU | p |
|
/p | ||
|
|
|||||
| 0 | 0.66 · 0.67 | 0 | 0 | ||
| z = 0 : | −u(2400) | 0.67 · 0.34 | 0.5 | 2.19 | |
| u(2500) −u(2400) | 0.33 · 0.34 | 0.01 | 0.08 | ||
| u(2500) | 0.33 · 0.66 | 0.49 | 2.26 | ||
Note: The agent’s simulation yields ΔU = Δ u with probability where p is Δ u’s objective probability.
Our simulations with UWS predicted people’s seemingly inconsistent preferences in the Allais paradox. For the first pair of lotteries (z = 2400), UWS preferred the second lottery to the first one, choosing L2 55.66% of the time and L1 only 44.34% of the time. But for the second pair of lotteries (z = 0), UWS choose the first lottery more often than the second one (50.38% vs. 49.62%). Table 4 shows how our theory explains why people’s preferences reverse when z changes from 2400 to 0: According to the importance distribution (Equation 13), people overweight the event for which the utility difference between the two gambles’ outcomes (O1 and O2) is largest (ΔU = u(O1) − u(O2)). Thus when z = 2400, the most over-weighted event is the possibility that gamble L1 yields o1 = 0 and gamble L2 yields o2 = 2400 (ΔU = −u(2400)); consequently the bias is negative and the first gamble appears inferior to the second ( which corresponds to $ − 75.54). But when z = 0, then L1 yielding o1 = 2500 and L2 yielding o2 = 0 (ΔU = +u(2500)) becomes the most over-weighted event making the first gamble appear superior which corresponds to $3.25). Our model’s predictions are qualitatively consistent with the empirical findings by Kahneman and Tversky (1979) but less extreme; this is primarily because fitting the model to the data from the Technion choice prediction Tournament led to large number of samples (s = 10) and the predicted availability biases decrease with the number of samples; for a smaller number of samples, the model predictions would have been closer to the empirical data.
The fourfold pattern of risk preferences
Framing outcomes as losses rather than gains can reverse people’s risk preferences (Tversky & Kahneman, 1992): In the domain of gains people prefer a lottery (o dollars with probability p) to its expected value (risk seeking) when p < .5, but when p > .5 they prefer the expected value (risk aversion). In contrast, in the domain of losses, people are risk averse for p < .5 but risk seeking for p > .5. This phenomenon is known as the fourfold pattern of risk preferences. Formally, decision-makers are risk seeking when they prefer a gamble (p, o; 0) which yields $o with probability p and nothing otherwise to its expected value p · o dollars, and risk averse if they prefer receiving the expected value for sure to playing the gamble. We therefore determined the risk preferences predicted by utility-weighted sampling by simulating choices between such gambles and their expected values. Concretely, we used the gambles (p, o; 0) for 0 < p < 1 and −1000 < o < 1000 and applied UWS with the parameters estimated from the Technion choice prediction tournament. Appendix C illustrates how utility-weighted sampling makes these decisions and how this leads to inconsistent risk preferences.
We found that utility-weighted sampling predicts the fourfold pattern of risk preferences (Tversky & Kahneman, 1992); see Figure 4. To understand how utility-weighted sampling explains this phenomenon, remember that it estimates the expected value of the differential utility ΔU by sampling from the importance distribution . The differential utility of choosing a gamble that yields o with probability p over its expected value p · o is
| (24) |
Utility-weighted sampling thus overweights the gain/loss o of the lottery if p is small, because then |u(o) − u(p · o)| > |u(p · o)|. Conversely, it underweights the gain/loss o if p is large, because then |u(o) − u(p · o)| < |u(p · o)|. Concretely, when choosing between a two-outcome gamble and its expected value, UWS simulates the outcome of the gamble as if winning and losing were equally probable even when the probability of winning is much larger or much smaller than 0.5 (see Appendix C). On top of this over-simulation of the more extreme outcome, the noise term of the utility function (Equation 16) stochastically flips the sign of the differential utilities of some of the simulated outcomes. When the probability of winning is close to 0 or 1, then this happens almost exclusively for the outcome whose differential utility is closer to zero. Combined with the over-simulation of the more extreme outcome this asymmetry renders the decision-maker’s bias positive (risk-seeking) for improbable gains and probable losses but negative (risk-aversion) for probable gains and improbable losses (see Figure 4). Appendix C elaborates this explanation with detailed worked examples.
Figure 4.
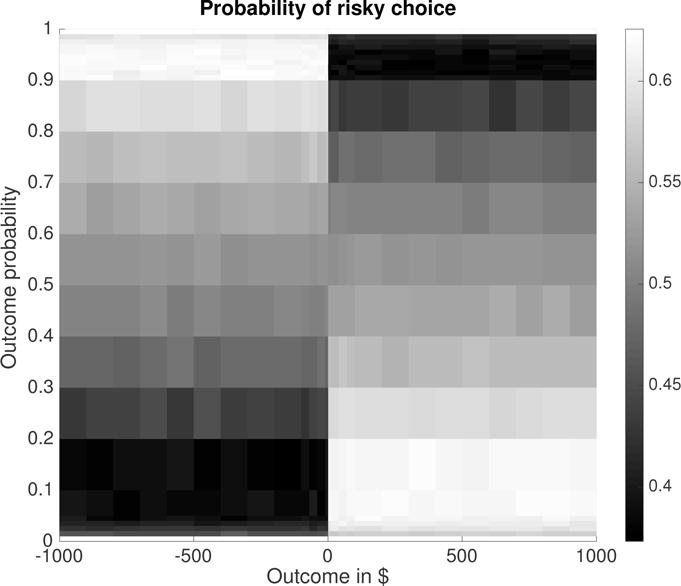
Utility-weighted sampling predicts the fourfold pattern of risk preferences. The color scale indicates the probability people make the risky choice as a function of the probability and dollar value of the outcome.
In everyday life the fourfold pattern of risk preferences manifests itself in the apparent paradox that people who are so risk-averse that they buy insurance can also be so risk-seeking that they play the lottery. Our simulations resolved this apparent contradiction: First, we simulated the decision whether or not to play the Powerball lottery.5 The jackpot is at least $40 million, but the odds of winning it are less than 1:175 million. In brief, people pay $2 to play a gamble whose expected value is only $1. We simulated how much people would be willing to pay for a ticket of the Powerball lottery according to UWS. We found that UWS overestimates the value of a lottery ticket by more than a factor of 2 more than 36% of the time. Thus, a person who evaluates lottery tickets often should consider them underpriced about one third of the time. Applied to choice, UWS predicts that people buy lottery tickets almost every second time they consider it (PUWS(buy lottery ticket) = 0.497), because they over-represent the possibility of winning big. Next, we applied UWS to predict how much the same people would be willing to pay for insurance. Our simulation assumed that the total insured loss follows the heavy-tailed power-law distribution of debits (N. Stewart et al., 2006) over the range from $1 to $1 000 000. To simplify the application of UWS to this continuous distribution, we set the reward expectancy ū to zero and assumed that the simulation distribution is not affected by noise. We determined the certainty equivalents of the utility-weighted sampling estimates of the utility of an insurance against a loss drawn from this distribution. To do so, we applied the inverse of the utility function to the UWS estimates of the expected disutility of the hazard. We found that UWS overestimates the expected hazard about 80% of time, and it overestimates it by a factor of at least 2 in 64% of all cases. Therefore, most people should be motivated to buy insurance even when they just bought a lottery ticket. The prediction of utility-weighted sampling for whether people actually decide to buy an overpriced insurance policy are more moderate, because the high price of insurance makes the possibility of paying nothing and losing nothing more salient. Nevertheless, UWS predicts that people would be willing to buy insurance for 130% of its expected value about 37.3% of the time. Thus 90% of customers would buy 130% overpriced insurance after considering at most 5 offers.
Utility-weighted sampling thereby resolves the paradox that people who are so risk-seeking that they buy lottery tickets can also be so risk-averse as to buy insurance by suggesting that people overweight extreme events regardless of whether they are gains (as in the case of lotteries) or losses (as in the case of insurance).
Preference reversals
When people first price a risky gamble and a safe gamble with similar expected value and then choose between them, their preferences are inconsistent almost 50% of the time: most people price the risky gamble higher than the safe one, but many of them nevertheless choose the safer one (Lichtenstein & Slovic, 1971). This inconsistency does not result from mere randomness, as preference reversals in the opposite direction are rare.
To evaluate whether our theory can capture this inconsistency, we simulated the pricing of a safe gamble offering an 80% chance of winning $1 and a risky gamble offering a 40% chance of winning $2, and the subsequent choice between them according to UWS with the parameters estimated from the Technion choice prediction tournament for decisions from description. Since the largest and the smallest possible outcome are omax = 2 and omin = 0 respectively, the utility function from Equation 16 becomes with .
We assumed that people price a gamble by estimating its expected utility gain according to Equation 14 and then convert the resulting utility estimate into its monetary equivalent. Plugging the payoffs and outcome probabilities of the safe gamble in to Equation 14 reveals that, for the safe gamble, winning (o = 1) and losing (o = 0) would be simulated with the frequencies
| (25) |
| (26) |
respectively. For the risky gamble the possibility of winning is over-represented more:
| (27) |
| (28) |
Each simulated decision-maker sampled 10 possible outcomes. We then applied Equation 14 to translate the 10 samples from qsafe into the UWS estimate of the expected utility gain of playing the safe gamble and the 10 samples from qrisky into the UWS estimate of the expected utility gain of playing the risky gamble . Finally, we converted each estimated utility gain into the equivalent monetary amount m by inverting the utility function u without adding any noise, that is
| (29) |
| (30) |
Each value of mrisky corresponds to one participant’s judgment of the fair price for the risky gamble and likewise for the values of msafe.
To simulate choice, we applied the UWS model for binary decisions from description (Equations 20–21) with the parameters estimated from the Technion choice prediction tournament. To choose between the risky versus the safe gamble, this model estimates the expected differential utility directly instead of estimating the gambles’ expected utilities and separately. Consequently, it overweights pairs of outcomes whose utilities are very different instead of individual outcomes whose utilities are far from 0. Concretely, it simulates pairs of outcomes (i.e., one outcome for the risky gamble and one outcome for the safe gamble) according to the distribution qΔ defined in Equation 20, which weights their joint probability by the absolute value of their difference in utility. The differential utilities Δu1,…, Δu10 of the simulated outcome pairs are then translated into an estimate of the difference between the expected utility of the risky gamble versus the safe gamble according to Equation 21. If the resulting decision variable is positive, the simulated decision-maker chooses the risky gamble, if it is negative they choose the safe gamble, and if it is 0 then they choose randomly.
Since the utilities u(o) that drive the overweighting of extreme outcomes are stochastic (Equation 16), we conducted 100 000 simulations to average over a large number of utility-weighted sampling distributions q. Each simulation generated one price for the safe gamble, one price for the risky gamble, and one simulated choice between the two. At the beginning of each simulation, the utilities u(0), u(1), and u(2) were drawn from for each possible outcome o ∈ {0,1, 2} and plugged into Equations 25–28 to yield the distributions the decision-maker would sample from in that simulation. Within each simulation, the sampled outcomes were evaluated by independent applications of the noisy utility function (Equation 16). Hence, even when the same outcome was sampled multiple times in a simulation, its subjective utility could be different every time.
UWS predicted that 42% of participants should reverse their risk preference from pricing to choice. In 66% of these reversals the model prices the risky gamble higher but choose the safe one. As a result, utility-weighted sampling typically prices the risky gamble higher than the safe gamble (67% of the time), but it choses the safe gamble almost every second time (49% of the time). The rational decision mechanism of utility-weighted sampling weights events differently depending on whether it is tasked to perform pricing versus choice. Given that its shift in attention is a rational adaption to the task, the inconsistency between people’s apparent risk preferences in pricing versus choice is consistent with resource-rationality.
While the laboratory experiments that demonstrated the effects simulated above can be criticized as artificial because their stakes were low or hypothetical, the overweighting of outcomes with extreme differential utility has also been observed in high-stakes, financial decisions whose outcomes do count (Post, Van den Assem, Baltussen, & Thaler, 2008), and UWS can capture those effects as well (see Section “Deal or No Deal: Overweighting of extreme events in real-life high-stakes economic decisions” of the Supplemental Online Material).
Summary
In this section, we have shown that utility-weighted sampling accurately predicts people’s decisions from description across a wide range of problems including those that elicit inconsistent risk preferences. Our utility-weighted sampling model of decisions from description rests on three assumptions: Its central assumption is that expected utilities are estimated by importance sampling. In addition, we assumed that binary choices from description are made by directly estimating the differential utility of choosing the first option over the second option. This assumption was important to predict the fourfold pattern of risk preferences, preference reversals, and the Allais paradox. Finally, we assumed that the mapping from payoffs to utilities is implemented by efficient coding. This assumption is not critical to the simulations reported here, but it will become important in our simulations of decisions from experience in the next section.
Overweighting of extreme events in decisions from experience
In decisions outside the laboratory we are rarely given a list of all possible outcomes and their respective probabilities. Instead, we have to estimate these probabilities from past experience. When people learn outcome probabilities from experience their risk preferences are systematically different than when the probabilities are described to them (Hertwig & Erev, 2009). For instance, people overweight rare outcomes in decisions from description but tend to underweight them in decisions from experience (Hertwig, Barron, Weber, & Erev, 2004).
A common paradigm for studying decisions from experience is repeated binary choices with feedback. In this paradigm, the outcomes and their probabilities are initially unknown and must be learned from experience. Madan et al. (2014) discovered an interesting memory bias in this paradigm: people remember extreme outcomes more often than moderate ones and overestimate their frequency. Ludvig et al. (2014) showed that people also overweight the same extreme outcomes in their decisions when their probability is . Above we showed that utility-weighted sampling can account for the memory biases discovered by Madan et al. (2014), and in this section we investigate whether utility-weighted sampling can also account for the corresponding biases in decisions from experience by simulating the experiments by Ludvig et al. (2014). Our analysis suggests that biased memory encoding serves to help people make future decisions more efficiently by making the most important desiderata come to mind first.
Ludvig et al. (2014) conducted a series of four experiments. In each of the four experiments people made a series of decisions from experience. For instance, Experiment 1 comprised 5 blocks with 48 choices each. There were a total of four options: a sure gain of +20 points, a sure loss of −20 points, a risky gain offering a 50/50 chance of +40 or 0, and a risky loss offering a 50/50 chance of 0 or −40 points. In most trials participants either chose between the risky and the sure gain (gain trials) or between the risky and the sure loss (loss trials). After each choice subjects were shown the number of points earned, and they received no additional information about the options. Experiments 2–4 used different outcomes but were otherwise similar. In Experiment 2 the absolute values of all outcomes of Experiment 1 were shifted by 5 points. In Experiment 3 the gain and loss trials were supplemented by extreme gain trials and extreme loss trials whose outcomes were double the outcomes in Experiment 1. Experiment 4 had a loss condition in which all outcomes were losses (4L) and a gain condition in which all outcomes were gains (4G). Both conditions comprised risky gambles in which only the high outcome was extreme (HX), gambles in which only the low outcome was extreme (LX), and gambles in which both outcomes were extreme (BX).
To simulate these experiments, we assumed that Ludvig et al.’s participants had learned the outcome probabilities in the first four blocks and modeled their choice frequencies in the final block of each experiment. We can therefore model each individual decision as the choice between two lotteries each of which is defined by the value of the high outcome ohigh, the probability phigh of receiving it, and the low outcome olow:
| (31) |
| (32) |
We model utility-weighted sampling as simulating s possible outcomes of each action a by sampling from the importance distribution defined in Equation 11:
| (33) |
where is the average outcome experienced by the participant. The simulated utilities are then combined into estimates of each action’s expected utility gain according to Equation 12, and the option with the highest expected utility gain estimate is chosen. Our model defines the likelihood of individual choices in terms of two parameters: the number of samples s, and the noise variance of the brain’s representation of utilities. We estimated these parameters from the choice frequencies in the final blocks of each condition of Experiments 1–4 by the maximum-likelihood method.
The results of fitting our model to the data of Ludvig et al. (Figure 5) revealed that utility-weighted sampling can capture the effects in all of the experiments with a single set of parameters (i.e. s = 2 samples, and a noise standard deviation of σε = 0.65) and the fit is robust to small changes in these parameters. Most importantly, utility-weighted sampling predicts that people are more risk seeking when the extreme outcome is high than when the extreme outcome is low. This explains why participants were more risk seeking for gains than for losses (Experiments 1–2). Experiment 3 combined trials in which the outcomes were twice the outcomes in Experiment 1 (3X) with the original trials from Experiment 1 (3NX). Our model correctly predicted the two main effects: more risk seeking on extreme gain trials than on extreme loss trials (3X) and a substantially smaller difference in risk seeking between their non-extreme counterparts (3NX).
Figure 5.
Differential risk preferences in the experiments by Ludvig et al. (2014). (A) Observed and predicted patterns of risk preferences. (B) Scatterplot combining all experimental conditions.
UWS also captured the finding that the effect for the non-extreme outcomes is substantially smaller than in Experiment 1 even though the options were identical. According to our model, the context of the extreme outcomes in Experiment 3 suppresses the difference between the non-extreme gain and loss trials, because each outcome is divided by the range of all outcomes that need to be represented; see Equation 16. Since the range of outcomes is twice as large in Experiment 3 than in Experiment 1, the difference between the rewards of the non-extreme outcomes in Experiment 3 is only half as large as in Experiment 1. Consequently the noise in the reward signals can overturn the signal in Experiment 3NX more often than in Experiment 1. For Experiment 4 utility-weighted sampling correctly predicted more risk seeking when the high outcome was extreme and the low outcome was moderate (HX; prisky choice = 0.61) than vice versa (LX; prisky choice = 0.39), and an intermediate amount of risk seeking when both outcomes were extreme (BX, prisky choice = 0.49). Utility-weighted sampling predicted this pattern of risk preferences regardless of whether all outcomes were gains (Experiment 4G) or all outcomes were losses (Experiment 4L). Utility-weighted sampling predicts all of these effects from the assumption that the brain’s simulation mechanism is biased towards outcomes with extreme utility. Future models might be able to achieve a better fit, but to our knowledge utility-weighted sampling is the only theory to date that captures at least the qualitative effects observed by Ludvig et al. (2014).
In the experiments by Ludvig et al. (2014) all outcome probabilities were equal to 0.5. In prospect theory (Kahneman & Tversky, 1979) probability weighting only depends on the magnitude of the probability. Hence, it cannot overweight the 50% chance of one event and underweight the 50% chance of the other event at the same time. UWS, by contrast, can explain the effects, because it predicts that extreme events will always be overweighted regardless of their probability. This highlights a critical difference between UWS and prospect theory: In prospect theory over- versus under-weighting depends on the value of the probability but is independent of the utility. By contrast, in UWS the over- or under-weighting is determined by the outcome’s utility but is independent of its probability. Cumulative prospect theory (Tversky & Kahneman, 1992) captures the effect of extremity on overweighting in principle, but it doesn’t capture this effect when there are only two possible outcomes.
To apply our theory to the empirical data, we had to choose a utility function. We chose the stochastic normalized utility function defined in Equation 16 because of its neuroscientific underpinnings and its ability to explain context-sensitive preferences in value-based decision-making (Summerfield & Tsetsos, 2015). Concretely, UWS combined with a context-insensitive utility function, such as a simple linear function of the outcome, or the concave utility function of prospect theory, would be unable to explain why people’s preference for the risky gamble +40/0 over the safe option +20 is lower in Experiment 3 than in Experiment 1 even though the choices are exactly the same. In addition to the normalization by the dynamic range, the noise term is also necessary, because otherwise any scaling of the utility function is canceled out by the normalization of the sampling distribution. Therefore, there appears to be no simpler or more conventional utility function that can explain the qualitative features of the data of Ludvig et al. (2014) than the normalized stochastic utility function defined in Equation 16. Given this utility function, UWS predicts that the overweighting of the gain (+40) in the choice between a 50/50 chance to gain 40 or 0 vs. 20 for sure in Experiment 1 would disappear if there were only gain trials so that the average outcome would be 20 which is exactly in the middle between 0 and 40.
Utility-weighted learning from experience
So far, we have shown that utility-weighted sampling can capture biases in frequency judgment, decision-making, and memory recall. Our explanation postulates that the brain samples from an importance distribution that weights each outcome’s probability by the absolute value of the extremity of the outcome’s utility, but it remains unclear whether and how the brain could implement this mechanism. We have speculated that there may be a common root to these biases: the enhancement of learning by emotional salience. Consistent with this mechanism, memory consolidation is enhanced when the reward associated with an experience is larger (Adcock, Thangavel, Whitfield-Gabrieli, Knutson, & Gabrieli, 2006). Adcock et al. (2006) found that this modulation of memory consolidation is mediated by the release of dopamine from the ventral tegmental area. The enhancement of learning by emotional salience implies that extreme events, such as the terrorism, natural disasters, and traumatic accidents, are engraved more deeply into our memory than mundane events. A single extreme experience, such as a traumatic event, in a neutral context can instill an enduring association that is much stronger than the association formed with a mundane event that occurred more frequently in the same context. Based on this idea we propose a biologically-plausible learning mechanism that tunes neural networks to sample from the importance distribution of utility-weighted sampling.
UWS can emerge from reward-modulated associative plasticity
Utility-weighted sampling can be implemented using a stochastic winner-take-all network (c.f. Nessler, Pfeiffer, Buesing, & Maass, 2013) whose units represent potential outcomes and receive inputs from units representing the alternatives of the choice (a). The weight wa,o of connection between the input units representing alternative a and the output units representing outcome o encode the strength of the association between alternative a and outcome o. The weights w thereby determine the relative frequency with which the network simulates each outcome for each alternative. In this section, we propose a learning rule for the weights w that tunes the network to simulate outcomes according to utility-weighted sampling (Equation 33).
We assume that the initial association strengths w are zero, and that choosing an alternative a and receiving a rewarding outcome o reinforces their association wa,o. The association strengthens more the more surprising the outcome is (Courville, Daw, & Touretzky, 2006). Our model captures this effect by updates that are proportional to the absolute value of the reward prediction error PE(o):
| (34) |
where A(t) and O(t) are the chosen alternative and the outcome in trial t, α is the learning rate, and γ is the forgetting rate. The reward prediction error is the difference between the experienced reward r(o) and reward expectancy :
| (35) |
where r (o(t)) is the subjective utility of outcome o defined in Equation 16, and is the reward expectancy associated with any trial in the experiment. It can therefore be thought of as a recency-weighted average over all rewards regardless of the choices that generated them. We assume that this expectancy is learned independently from the alternative-outcome associations by temporal difference learning, that is
| (36) |
where is a learning rate and the reward prediction error PE is conveyed by phasic dopamine signals from the ventral tegmental area to the ventral striatum and the frontal lobe (Niv, 2009). This concludes the learning part of our model.
To model decision-making we assume that the rate at which units representing alternative a activate units representing outcome o is proportional to the strength of their connection, that is
| (37) |
The learning rule (Equation 34) increases the weight wa,o with probability p(o|a) by an increment proportional to |PE(o)|. Therefore, the probability that outcome o will be simulated when considering action a (i.e, P(Ô = o|A = a)) converges to p(o|a) · |PE(o)| = p(o|a) · |u(o) − u| ∝ qUWS, where u(o) = r(o). In this way, the network gradually learns to perform utility-weighted sampling (Equation 11). The simulated outcomes could be read out by a decision network that chooses the alternative with the highest value of the utility estimate defined in Equation 12. Thus, after sufficient learning the simulation network and the decision network jointly perform utility-weighted sampling. The above equations are meant as an abstract specification of network properties rather than the definition of a concrete neural network, but they suggest a way in which the brain might learn to perform utility-weighted sampling.
Having proposed a learning mechanism that can give rise to utility-weighted sampling, we will now evaluate its predictions against the temporal dynamics of people’s risk preferences in repeated decisions from experience.
Temporal dynamics of risk preferences
Above, we simulated people’s risk preferences in the final blocks of the experiments by Ludvig et al. (2014) assuming that the participants had already learned the utility-weighted sampling distribution. Here, we test whether the utility-weighted learning (UWL) model can predict this learning outcome and capture the temporal evolution of people’s risk preferences from the first block through the last block. The utility-weighted learning model predicts participants’ choice probabilities as a function of seven parameters: the number of samples s, the uncertainty σε about utilities, the learning rate α, the forgetting rate γ, the initial reward expectancy , the rate η at which the reward expectancy is being updated, and the probability of random choice prandom. To estimate these parameters, we fitted the block-by-block choice frequencies reported by Ludvig et al. (2014) by maximum-likelihood estimation.
The parameter estimates were s = 1 samples, learning rate α = 1, forgetting rate γ = 0.375, noise standard deviation σε = 0.1, initial reward expectancy 3, TD learning rate η = 0.05, probability of random choice prandom = 0.64. We found that utility-weighted learning captures several qualitative properties of how people’s risk preferences changes with experience: Our simulations of Experiments 1–2 captured that people gradually become more risk-averse on loss trials but more risk-seeking on gain trials (Figure 6A). Our simulations of Experiment 3 captured that this effect is reduced when gains and losses are non-extreme in the context in which they occur (Figure 6B), and the simulation of Experiment 4 captured that more experience makes people more risk-seeking when the high outcome is extreme, but more risk-averse when the low outcome is extreme, even if all outcomes are gains or all outcomes are losses (Figure 6C). According to utility-weighted learning the determinant of risk-seeking is that the high outcome is farther away from the learned reward expectancy than the low outcome. The reward expectancy tracks to average across all recent outcomes. Thus, UWL predicts risk seeking when the high outcome is farther away from the average outcome than the low outcome.
Figure 6.
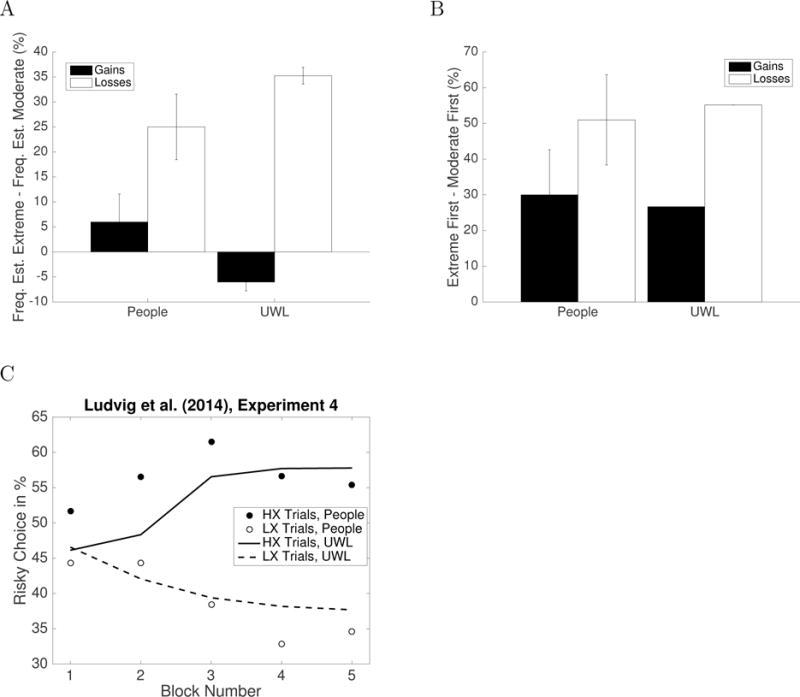
The utility-weighted learning (UWL) model captures the temporal evolution of people’s risk preferences in the experiments by Ludvig et al. (2014). (A) UWL captures that participants in Experiments 1–2 became increasingly more risk seeking on gain trials but more risk averse on loss trials. (B) UWL captures that in Experiment 3 risk seeking increased primarily on trials with extreme outcomes. (C) UWL captures that in Experiment 4 people became risk seeking when the larger outcome was extreme and risk averse when the smaller outcome was extreme regardless of whether the outcomes were gains or losses.
Predicting memory biases
Earlier in this paper we simulated the experiments by Madan et al. (2014) according to utility-weighted sampling. We found that UWS correctly predicted the qualitative differences between moderate and extreme events in frequency estimation and memory recall, but its predictions were more extreme than the biases observed in people. In this section we revisit these effects with the utility-weighted learning model. In addition, the utility-weighted learning model also allows us to simulate the relationship between memory biases and risk preferences, as well as the effect of recent outcomes on risky choice.
Concretely, we fitted the UWL model to the block-by-block choice frequencies in Experiments 1 and 2 by Madan et al. (2014) using the maximum-likelihood method. We then used the resulting parameter estimates to predict participants’ frequency estimates and memory biases. To do so, we modeled people’s frequency estimates according to utility-weighted sampling as defined in Equation 22. Likewise, participants’ answers to the memory recall question were modeled by the outcome that was sampled most frequently; if two or more outcomes occurred equally frequently one of them was chosen at random.
The maximum likelihood parameter estimates indicated increased accuracy motivation: more simulations (s = 2), faster learning (α = 9), and slower forgetting (γ = 0). The estimated standard deviation of the noise was σε = 0.1, the estimated initial reward expectancy was 7, the estimated rate at which the reward expectancy is updated was 0.5, and the estimated probability of random choice was 0. With these parameters our model captured people’s memory biases (see Figure 7) and their relationship with risk seeking: Even though the risky choice generated the moderate outcome (0 points) and the extreme outcome (±40 points) equally often, for most people the extreme outcome came to mind first (Figure 7B), and their frequency estimates were significantly higher for the extreme loss than for the moderate outcome (Figure 7A). This was not the case for the high gain (+40), because according to the parameter estimates participants entered the experiment with the expectation that outcomes would average 560 points. As a comparison with Table 1 shows, the predictions of UWL are closer to the empirical data than the predictions of the basic UWS model.
Figure 7.
Utility-weighted learning (UWL) predicts the biased memory recall and frequency estimates observed by Madan et al. (2014). Error bars denote 95% confidence intervals. (A) Difference between estimated frequencies of extreme versus moderate outcomes. (B) Proportion of people who recalled the extreme outcome first minus proportion who recalled the moderate one first.
In addition, our model correctly predicted that people who recalled the extreme gain first were more risk seeking on gain trials than people who remembered the moderate outcome first (56.32 ± 0.24% vs. 50.83 ± 0.26% risky choices) whereas people who remembered the extreme loss first were less risk seeking on loss trials than people who remembered the moderate outcome first (31.83% ± 0.34% vs. 33.67 ± 0.34% risky choices). The simulated frequency estimates were significantly correlated with the model’s preference for the risky option: The higher the model estimated the frequency of the extreme loss to be the fewer risky choices it made on loss trials (r = − 0.4419, p < 10−15). Conversely, risk seeking on gain trials increased with the estimated frequency of the extreme gain (r = 0.23, p < 10−15). Utility-weighted learning also captured that people were more risk seeking when the most recent risky choice in the same context yielded the good outcome than when it yielded the bad outcome: For gain trials UWS predicted 8.6% higher risk seeking after receiving the high gain (+40) than after winning nothing on the previous risky gain trial. Conversely, UWS predicted 6.0% less risk seeking following the large loss (−40) compared to no loss on the previous risky loss trial.
Finally, we simulated Experiment 2 from Madan et al. (2014) according to the same parameters. This experiment was identical to Experiment 1 except that all outcomes were shifted by +40 points so that there were no negative outcomes. Our model correctly predicted that this manipulation changes none of the qualitative effects observed in Experiment 1, and our model now correctly predicted that people overestimate the frequency of the extreme gain relative to the neutral outcome (UWS: 56.4% versus 43.2%).
Validation on decisions from experience
Having shown that UWL predicts people’s biases in memory recall and frequency estimation more accurately than the original UWS model and captures the temporal dynamics of people’s risk preferences in repeated decisions from experience and the effect of recent outcomes on risky choice, we now evaluate UWL against alternative models of repeated decisions from experience. To do so, we use data from the Technion choice prediction tournament as we did for our basic utility-weighted sampling model of decisions from description. As before, we fit our utility-weighted learning model to the training set by maximum-likelihood estimation, evaluate its predictive accuracy on the test set, and perform formal model comparisons against the best models from the competition. The only difference is that we now use the data sets and models from the Technion tournament on repeated decisions from experience rather than decisions from description.
The parameter estimates were as follows: learning rate α = 2, number of samples s = 9, forgetting rate γ = 0, standard deviation of the noise σε = 0.1, probability of random choice prandom = 0.12, initial reward expectancy , and η = 0.05. We set our model’s parameters to these values and evaluated its predictions against people’s choice frequencies on the test set; see Figure 8. Our model’s predictions agreed with people’s risk preferences for 90% of the decision problems. The correlation between the predicted and observed choice frequencies was r = 0.80, and the mean-squared error of the predicted choice frequencies was MSD = 0.0120. Our model thereby explained the data substantially better than the basic reinforcement learning model that Erev et al. (2010) considered as a baseline (66% agreement, r = 0.51, MSD = 0.0263; t(59) = −3.2, p = .002), and not significantly worse than the best model in the competition: the explorative sampler with recency (MSD = 0.0066, t(59) = 1.65, p = .1, 86% agreement, r = 0.89). While the best model was provided as a baseline, the best submission was the ACT-R model of instance-based learning (MSD: 0.08, r = 0.89). After the competition, Lejarraga, Dutt, and Gonzalez (2010) introduced an improved instance-based learning model that performed slightly better than the exploratory sampler with recency (MSD = 0.006, 86% agreement, r = 0.89) and its mean-squared error was significantly lower than that of our model (t(118) = −2.21, p = 0.01). The predictive accuracy of the normalized reinforcement learning model was comparable to the performance of our model (MSD: 0.0087, 84% agreement, r = 0.84). Additional analyses comparing the risk preferences of UWL to those of people are provided in the Online Supplemental Material.
Figure 8.
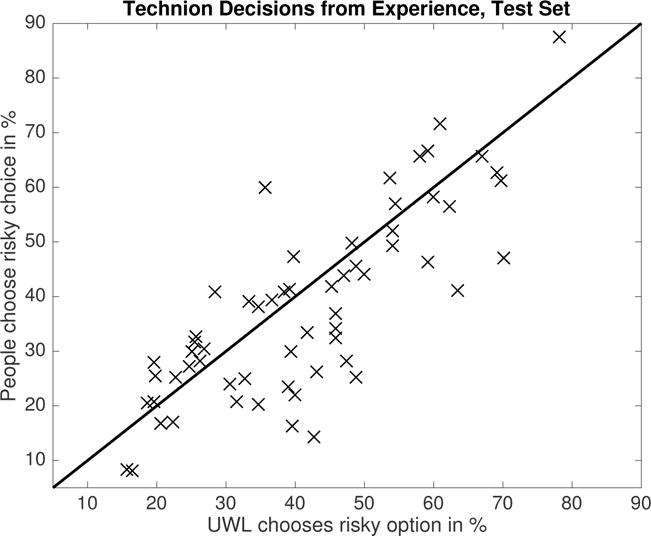
Utility-weighted learning (UWL) predictions for test set of Technion prediction tournament for repeated decisions from experience. Each data point reports the risky choice frequency of UWL (horizontal axis) versus people (vertical axis) for one of the 60 decision problems, and the solid line is the identity line.
Discussion
We hypothesized that utility-weighted sampling arises from biased memory encoding. In this section, we formalized this proposal by a biologically-plausible learning rule that we call utility-weighted learning (UWL). The empirical data of Ludvig et al. (2014) and Madan et al. (2014) provides four strong pieces of evidence for our hypothesis that the over-representation of extreme events results from utility-weighted memory encoding: First, people overweight outcomes with extreme utilities in decisions from experience relative to equally probably outcomes with moderate utilities. Second, this overweighting emerged gradually through learning and the time course of learning matched the predictions of our utility-weighted-learning model. Third, participants displayed biases in memory recall that matched the biases of their decisions and our model captured both. Fourth, as predicted by our model, there was a significant correlation between the magnitude of each participant’s bias in memory recall and the bias in their choice frequencies. This is consistent with our model’s assumption that the overweighting of events with extreme utilities and their heightened availability in memory have a common cause: utility-weighted memory encoding. While the correlation between biases in memory and choice does not imply causation, our model’s assumption that utility-weighted memory encoding causes memory biases that in turn cause biases in decision-making does offer a plausible explanation for this phenomenon. Under this assumption the covariation of the ease with which extreme events come to mind could plausible arise from individual differences in the sensitivity to reward and punishment (Corr, 2004): The higher a person’s reward sensitivity, the more biased their memory encoding will be. The more biased the strengths of a person’s memories are in favor of extreme events, the more easily they will be recalled, and this in turn increases their decision weights.
We found that our model explained the temporal dynamics of of people’s risk preferences and memory biases in repeated decisions from experience and evaluated the utility-weighted learning model against people’s choice frequencies in a wide range of decisions problems. UWL was competitive with the best existing models of decisions from experience. Together with the findings presented in previous sections, the results in this section show that utility-weighted sampling can provide a unifying, mechanistic explanation for a wide range of biases in decisions from description and decisions from experience. This is important for two reasons. First, it is often implied that decisions from description and decisions from experience rely on separate mechanisms, and second our most influential theories of decision-making are not mechanistic.
Although the experiments simulated here had only two possible outcomes, the UWL learning model is equally applicable to decisions with many possible outcomes and one example thereof can be found in the Section “Payoff-variability effects in decisions with very many possible outcomes” of the Online Supplemental Material.
The proposed learning mechanism is similar to the Pearce-Hall model of classical conditioning (Pearce & Hall, 1980) in that both update the strength of a stimulus-reward association by an amount proportional to the absolute value of a reward prediction error. However, there are several important differences. Most importantly, our model learns the conditional probabilities of multiple possible outcomes given a single cue whereas the Pearce-Hall model learns to predict the intensity of a single reward or punishment given multiple cues. Consequently, in the Pearce-Hall model, the reward prediction is derived from the learned associations. By contrast, in our model the reward prediction is learned independently of the cue-outcome associations. Furthermore, the Pearce-Hall model uses the reward prediction error from the previous trial whereas our model uses the reward prediction error from the current trial. The two models also differ in the remaining terms of their learning rules.
To fit the temporal dynamics of risk preferences with learning, we had to make a number of assumptions about the underlying learning mechanisms. The details of this proposal are not essential to our theory and may be revised and simplified in future versions of the utility-weighted learning model. Instead, the utility-weighted learning model should be seen as a proof of principle that utility-weighted sampling can emerge from reward-modulated associative learning in the brain.
General Discussion
Our resource-rational analysis of decision-making in high-risk situations suggested that people should decide by utility-weighted sampling. Utility-weighted sampling explains not only how we are able to make sensible decisions under severe time pressure but also why we overestimate the frequency of extreme events and have inconsistent risk preferences. Utility-weighted sampling explains why extreme events come to mind first and why people overestimate their frequencies and overweight them in decisions under uncertainty. Our model captures how people’s risk preferences depend on valence (gains versus losses), probability, the elicitation method (pricing versus choice), and on whether probabilities are described or experienced. Utility-weighted sampling can thus explain preference reversals, the Allais paradox, and the fourfold pattern of risk preferences. In addition, our utility-weighted learning model captures the temporal dynamics of people’s risk preferences during repeated decisions from experience, the effect of recent outcomes on risky choice, and the relationship between memory biases and risk preferences.
Our model’s predictive validity in the Technion choice prediction tournaments for repeated decisions from description and decisions from experience was competitive with, although not quite as good as, the fit of the models that won these competitions. Yet, while most of these models were specific to their competition, our model was derived from first principles, it also applies to more complex decisions with (infinitely) many possible outcomes, and it can simultaneously explain a much wider range of biases in decision-making, judgment, and memory than ever attempted before. In addition, our model does not just describe risk preferences but specifies the underlying (neuro)computational mechanisms. The biases explained by our model include newly discovered phenomena (Madan et al., 2014; Ludvig et al., 2014) that have not been modeled before as well as classic findings that were previously explained separately.
In the remainder of this paper we synthesize and discuss the results presented above. We start by showing that the difference between our theory’s predictions for decisions from description versus decisions from experience captures the description-experience gap. We then discuss the similarities and differences between UWS and previous theories of inconsistent risk preferences. Afterwards, we take a step back and discuss how the work presented here instantiates the general resource-rational approach to modeling cognitive mechanisms. Next, we discuss the connections between our theory and theory of ecological rationality. Finally, we acknowledge the limitations of our analysis, discuss directions for future work, and conclude.
Utility-weighted sampling captures the description-experience gap
People’s risk preferences in decisions from description and decisions from experience are systematically different. This difference is known as the description-experience gap (Hertwig & Erev, 2009). Most prominently, people appear to overweight small probabilities in decisions from description but underweight them in decisions from experience. Having applied utility-weighted sampling to decisions from description and decisions from experience, we are now in a position to evaluate whether the difference between the UWS model of binary decisions from description (Equations 20–21) and the utility-weighted learning model (Equations 34–37) captures the description experience gap. To do so, we computed the difference between the two models’ predictions on the test set of the Technion choice prediction tournament (Figure 3 versus Figure 8) and compared it against the difference between people’s choice frequencies in these two conditions.
Figure 9 shows that the difference between the two models correctly predicted the sign of the description-experience gap on 95% of the decision problems in the test set of the Technion choice prediction tournament. The correlation between the predicted and the actual description-experience gaps was r = 0.8853 (p < 10−15), and the mean squared deviation was 0.0361. Our model of decisions from experience captures the effects of either not experiencing, or gradually forgetting rare outcomes. This explains why rare events tend to receive less weight in decisions from experience than in decisions from description. For instance, in problems 1–5 where the probability of the high outcome is at most 0.1, people and utility-weighted sampling are more risk-seeking when the probabilities are described than when they are experienced. According to our models, there is another difference: In decisions from description people over-simulate eventualities in which the outcomes of two choices are extremely different. In decisions from experience, by contrast, people simulate the possible outcomes of each option independently, so that utility-weighted sampling over-simulates each option’s most extreme outcome even when they are identical. Thus, when choosing between losing a moderate amount for sure and the chance of winning a small amount or losing a large amount, UWS is more risk seeking in decisions from description than in decisions from experience, and this correctly predicts the positive description-experience gap in problems 30–34 (see Figure 9 and Erev et al., 2010). According to our theory, the description-experience gap is not only due to the fact that rare events in decisions from experience sometimes go unnoticed or are gradually discounted or forgotten but also due to difference between overweighting unusually large and unusually small outcomes in decisions from experience versus overweighting of pairs of outcomes with large utility differences in binary decisions from description. Recent empirical evidence for the important contribution of memory biases in favor of extreme events to the description-experience gap (Madan, Ludvig, & Spetch, 2016) strongly supports our model’s explanation. Furthermore, Kellen, Pachur, and Hertwig (2016) found that people are more sensitive to the payoffs and less sensitive to their probabilities in decisions from experience than in decisions from description even when the difference between experienced frequencies and described probabilities is controlled for. This too is consistent with the overweighting of extreme payoffs in decisions from experience.
Figure 9.
Utility-weighted sampling captures the gap between people’s risk preferences in decisions from description and decisions from experience. 95% agreement, r = 0.8853, mean-squared error 0.0361.
Comparison to previous theories of judgment and decision-making
Unlike previous theories of decision-making, our model is both normative and mechanistic. In contrast to descriptive theories of choice, our approach has been to explore the implications of limited cognitive resources for the mechanisms by which people should make decisions under uncertainty. In contrast to most normative theories of choice, we have engaged with people’s limited cognitive resources and derived a process model. This makes our theory the first rational process model (Griffiths et al., 2015) of cognitive biases in decision-making. The proposed mechanism for decisions from experience is psychologically plausible in that it relies on the well-known availability bias in memory recall (Tversky & Kahneman, 1973). Furthermore, we have shown that UWS naturally emerges from a biologically-plausible reward-modulated associative plasticity mechanism that is driven by the reward prediction error conveyed by dopamine (Schultz et al., 1997). But unlike most process models, UWS was derived from first principles and instantiates rational information processing.
Our theory provides the first rational perspective on the heightened availability of extreme events and the cognitive biases in judgment and decision-making that result from it. We have shown that it can explain a wide range of phenomena in memory, judgment, learning, decisions from description, and decisions from experience. Subsets of these phenomena, such as the simulated violations of expected utility theory in decisions from description were already accounted for by previous theories, but our model is the first to provide a unifying explanation for all of them, and none of the previous theories could explain why events with extreme utilities should be remembered first and sway people’s decisions. As far as we know, UWS is the first theory that can simultaneously explain decisions from description and decisions from experience, and it reconciles the discrepancies between them. In particular, no previous theory was able to reconcile the reflection effect in decisions from description (risk aversion for a 50% chance of a large gain but risk seeking for a 50% chance of a large loss) with the exact opposite of this effect in decisions from experience (Ludvig et al., 2014; Madan et al., 2016). We think that our theory is unique in providing the first rational process model of availability biases in judgment and decision-making and offering a unifying explanation for a very wide range of seemingly disparate phenomena, but it builds on previous work (Griffiths et al., 2015; Vul et al., 2014; Ludvig et al., 2014; Madan et al., 2014; Tversky & Kahneman, 1973; Bordalo et al., 2012; N. Stewart et al., 2006; Lichtenstein et al., 1978; Hertwig et al., 2005; Pachur et al., 2012) and has commonalities with many existing theories of judgment and decision-making. We provide a detailed discussion of how our theory is similar to and different from previous accounts of memory, frequency judgment, decisions from description, and decisions from experience in the Online Supplemental Material. Table 5 summarizes these comparisons in terms of the range of phenomena explained by UWS and some previous models and theories, namely the availability-by-recall model (Hertwig et al., 2005; Pachur et al., 2012), the regressed-frequency model (Hertwig et al., 2005), the value-assessment model (Barron & Erev, 2003), instance-based learning theory (T. C. Stewart, West, & Lebiere, 2009), the exploratory sampler with recency (Erev et al., 2010), the contingent average and trend (CAT) model (Plonsky, Teodorescu, & Erev, 2015), the decision-by-sampling model (N. Stewart et al., 2006), salience theory (Bordalo et al., 2012), the priority heuristic (Brandstätter et al., 2006), regret theory (Loomes & Sugden, 1982), prospect theory (Kahneman & Tversky, 1979), stochastic cumulative prospect theory (SCPT; Erev, et al., 2010), dynamic prospect theory (Post et al., 2008), disappointment theory (Bell, 1985; Loomes & Sugden, 1984, 1986), and the 3-moments model (Hagen, 1979; Allais, 1979). These and other comparisons suggest that UWS is the first mathematical theory to provide a unifying explanation for availability biases in frequency judgment, memory, decisions from experience, and decisions from description.
Table 5.
Comparison of the range of phenomena explained by UWS versus previous theories.
| UWS | Availability-by-recall | Regressed-frequency | Value assessment |
Instance-based learning |
Exploratory-sampler with recency |
CAT | Decision by Sampling |
Salience theory | Priority Heuristic |
Regret theory |
Prospect Theory |
SCPT | Dynamic Prospect Theory |
Disappointment theory |
3-moments model |
||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||||||||
| Memory & Judgement | Memory bias for extreme events | ✓ | |||||||||||||||
| Overestimation of rare extreme events | ✓ | ✓ | ✓ | ||||||||||||||
| Overestimation of frequent extreme events | ✓ | ✓ | |||||||||||||||
|
| |||||||||||||||||
| Decision from experience | Reversed reflection effect | ✓ | |||||||||||||||
| Temporal dynamics of risk preferences | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||
| Underweighting of rare events | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||
| Payoff variability effect | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||
| Wavy recency effect | ✓ | ||||||||||||||||
|
| |||||||||||||||||
| Decision from description | Reflection Effect | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| Allals paradox | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| Preference reversals | ✓ | ✓ | |||||||||||||||
| Intransitivity | ✓ | ✓ | ✓ | ✓ | |||||||||||||
| Common-ratio effects | ✓ | ✓ | ✓ | .5 | ✓ | ✓ | ✓ | .5 | ✓ | ||||||||
| Gradual effect of choice difficulty | ✓ | ✓ | ✓ | ✓ | |||||||||||||
|
| |||||||||||||||||
| Dscription-experience gap | ✓ | ||||||||||||||||
Note: A checkmark means that theory can qualitatively account for the phenomenon, and ‘.5′ means that theory can qualitatively account for a subset of the phenomena.
Resource-rationality
We derived utility-weighted sampling by resource-rational analysis (Griffiths et al., 2015): We first defined the function of decision-making. Second, we modeled people’s cognitive capacities by an abstract computational architecture that can simulate outcomes by sampling, evaluate their utility, combine the simulated utilities into an estimate of each action’s expected utility by a weighted average, and choose the action with the highest utility estimate. In addition, we assumed that time constraints and cognitive capacity severely limit the number of simulations the mind can perform. Third, we derived an approximately optimal strategy for allocating the architecture’s computational resources. Finally, we evaluated our original proposal (Lieder, Hsu, & Griffiths, 2014) against empirical data and alternative models of decision-making under uncertainty and refined it by making the utility-function context sensitive. Consistent with previous results (Vul et al., 2014), we also found that people appear to perform more simulations for high-stakes decisions (see Section“Deal or No Deal: Overweighting of extreme events in real-life high-stakes economic decisions” of the Supplemental Online Material) than for low-stakes decisions (Technion choice prediction tournament). Furthermore, simulations reported in the Online Supplemental Material showed that UWS captures that people’s decision quality approaches optimality as the difference between their options increases. Overall, we found that the availability biases and inconsistent risk preferences modeled in this article can be reconciled with the rational use of cognitive resources (Griffiths et al., 2015).
Our rational analysis assumed that people’s judgments and decisions are based on sampling. We view sampling as a rational computational mechanism for approximating the expected utilities in decision problems with many possible outcomes whose probabilities have to be estimated from experience. This characterization holds for most everyday decisions. This suggests that utility-weighted sampling might be a resource-rational strategy for the decisions people make in real life. By contrast, when choosing between simple gambles with numerically stated outcome probabilities and payoffs, people could, in principle, compute each gamble’s expected value and choose the gamble with the highest expected value. When the stakes are high enough to offset the additional time and effort required to compute expected values then the expected value strategy would become resource-rational and participants should apply it. Is it therefore a sign of irrationality when people use utility weighted sampling in decisions from description? On the one hand, it appears suboptimal that people use sampling in simple decisions from description instead of relying on arithmetic. On the other hand, decisions from description are very rare outside the laboratory and resource-rationality is defined with respect to the distribution of problems in the agent’s natural environment. Furthermore, the payoffs used in the decisions from description paradigm are usually small or hypothetical, and people’s application of mathematical procedures is often error prone, slow, and effortful. We therefore believe that people’s use of utility-weighted sampling in the simulated decisions from description is not necessarily inconsistent with resource-rationality.
Our results should be taken with a grain of salt, because there is no guarantee that the parameter estimates for which our model captures empirical phenomena accurately reflect the resource-limitations of the human brain. We cannot rule out that the actual opportunity cost of simulating an outcome is so low that it would be resource-rational for people to generate so many samples that their availability biases should be much smaller than they are. Hence, without independent measurements of the available cognitive resources we cannot conclude that people are resource-rational but only that the simulated cognitive biases could be resource-rational in principle. To complete our theory of resource-rational decision-making, future work will have to provide a precise specification of the available cognitive resources and their costs as well as a mechanism that determines the optimal number of samples. We will discuss these limitations and future directions in more detail below.
Pushing our abstract computational model further towards the algorithmic and implementational level (Marr, 1982), we have shown that utility-weighted sampling can emerge from reward-modulated associative learning during repeated decisions from experience. Our learning rule assumes that synaptic plasticity is modulated by the absolute value of the reward prediction error (Equation 34) which can be interpreted as surprise or emotional salience. The success of the utility-weighted learning model might suggest that people gradually learn to make more rational use of their finite cognitive resources and that emotion contributes to the emergence of resource-rational decision-making. A recent neuroimaging study discovered a neural correlate of the absolute reward prediction error in the basolateral amygdala (Roesch, Esber, Li, Daw, & Schoenbaum, 2012) – an area known to mediate the impact of emotional salience on associative learning in the dorsal and ventral striatum (McGaugh, McIntyre, & Power, 2002; McGaugh, 2004; Cador, Robbins, & Everitt, 1989). This suggests that the learning mechanism of our UWL model could be implemented via the amygdala’s control over the neuromodulation of synaptic plasticity. Our work on utility-weighted sampling thereby illustrates how resource-rational analysis can be used to connect the computational level of analysis to the algorithmic and the implementation level (Marr, 1982; Griffiths et al., 2015). Future work might be able to leverage insights from neuroscience to quantify the resource-constraints and cost of computation in models of rational information processing (Lieder, Goodman, & Griffiths, 2013).
Connection to fast-and-frugal heuristics and ecological rationality
Interestingly, our resource-rational analysis led to simple and psychologically plausible decision strategies that resemble two fast-and-frugal heuristics (Gigerenzer, 2008). Biased mental simulation (stochastically) considers the most important consequence first - like take-the-best - and binary choices are made by tallying if there are more positive than negative simulated outcomes - as in the tallying heuristic. The fact that we derived this strategy as a resource-efficient approximation to normative decision-making (resource-rational analysis) sheds light on why fast-and-frugal heuristics work and how they can be generalized to harder problems (cf. Lieder, Griffiths, & Goodman, 2013).
Pleskac and Hertwig (2014) point out that natural decision environments often exhibit and inverse relationships between probability and reward, such as power-law distributions. It is these reward structures for which representative sampling fails and utility-weighted sampling becomes necessary. This suggests that utility-weighted sampling is an ecologically rational heuristic, and this might be why it is so effective and predictive of people’s decisions and biases. Although we derived utility-weighted sampling for complex real-life decisions with infinitely many possible outcomes, we found that it also captures the simpler two-outcome choices people make in laboratory experiments that could be solved by computing and maximizing expected value. This is consistent with the view that people’s heuristics are adapted to the structure of the problems they face in real-life rather than those posed in the laboratory (Gigerenzer, 2015). This highlights the value of deriving theories from an analysis of the problems people have to solve in real life instead of building them in a bottom-up fashion from empirical findings in artificial laboratory experiments.
Importantly, utility-weighted sampling works not despite its bias but because of it (cf. Gigerenzer & Brighton, 2009). The underlying principle is the bias-variance tradeoff (Hastie et al., 2009). Fast-and-frugal heuristics tolerate bias to make good inferences from incomplete, noisy observations, and utility-weighted sampling tolerates bias to make good decisions based on incomplete, noisy simulations of possible outcomes. Thus, biased minds can not only make better inferences but also better decisions. However, our results highlight a tension between good inference and good decision-making: To make good decisions bounded sample-based agents should over-sample extreme events even though this leads to bad inferences such as the overestimation of event frequencies, and people appear to do the same. In more general terms, the human mind should, and appears to, sacrifice the rationality of its beliefs (theoretical rationality) for the rationality of its actions (practical rationality, Harman, 2013), because limited computational resources necessitate tradeoffs. Concretely, our analysis suggested that the availability bias is a manifestation of resource-rational decision-making. Being biased can be resource-rational.
Limitations and future work
In addition to the many phenomena that our model captures there are others that it does not capture. For instance, UWS with the parameters estimated from the Technion choice prediction competition for decisions from description does not capture the common-ratio effects observed by Starmer and Sugden (1989). Consistent with the failure of UWS to capture these effects, Starmer and Sugden (1989) demonstrated that at least some common-ratio effects are partly driven by a distortion of stated probabilities that is independent of the outcome. Furthermore, UWS with the parameters estimated from the Technion choice prediction competition for decisions from description also cannot capture the violation of weak stochastic transitivity demonstrated by Tversky (1969) as this effect appears to be driven by people’s limited sensitivity to small differences in outcome probability. For both experiments, UWS predicted that people would always choose the gamble with higher expected value. These discrepancies highlight that probability weighting in decisions from description is impacted not only by the extremity of the associated outcomes but also by the probabilities themselves. UWS fails to capture these effects because it cannot account for outcome-independent distortions of probability. Incorporating this distortion into the UWS model of decisions from description is a potential direction for future research.
It is important to keep in mind that our goal was not to test a specific computational mechanism but rather to explore the implications of finite time and limited cognitive resources for decision-making under uncertainty. We explored these implications under specific simplifying assumptions about people’s utility function, resources, and cognitive operations that may have to be revised in the future. The empirical data we examined supported the conclusion that the neural mechanisms of decision-making share some of the abstract properties of utility-weighted sampling, but there additional intricacies that remain to be captured. The following discrepancies between our models’ predictions and human behavior could be a starting point for making the utility-weighted sampling mechanism more realistic: Although our model’s predictions of the Allais paradox are qualitatively correct, the predicted effect was much smaller than the one observed by Kahneman and Tversky (1979). Furthermore, despite its large number of parameters, the utility-weighted learning model does not fully capture the experimental data of Ludvig et al. (2014); in particular, our model could not predict that participants in Experiment 3 were more risk seeking for non-extreme loss trials than for non-extreme gain trials. Another avenue towards identifying the computational mechanism that underly availability biases could be to investigate their neural implementation. Although the utility-weighted learning model is inspired by neuroscientific findings, our hypotheses about the neural basis of utility-weighted learning remain to be tested.
Unlike most laboratory experiments, many real-world decisions involve many possible alternatives. This makes extending UWS to multi-alternative decisions an important direction for future research. One way to extend UWS to multi-alternative choice is to apply the UWS mechanism defined in Equation 12 to efficiently estimate the expected utility gain of each option separately and choose the alternative whose utility estimate is highest:
| (38) |
| (39) |
where ranges from the first to the last alternative, and can be thought of as the average utility gain obtained in past decisions or the reward expectancy conveyed by dopamine, as discussed above. This mechanism could be very efficient for decisions from experience because it allows multiple alternatives to be evaluated in parallel. Given the resulting estimates of the expected utility gain, the brain could read out the preferred action with a winner-take-all network (Maass, 2000). Alternatively, it is conceivable that decision-makers sometimes reduce multi-alternative decisions into a series of binary choices and make those choices with the UWS heuristic for binary decisions (Equations 18–21). Finally, it is also conceivable that decision-makers would first identify which alternatives are most promising by evaluating them separately according to Equation 38 and then apply the UWS heuristic for binary decisions (Equations 18–21) to choose between the two actions with the highest estimated utility gains. Future work should evaluate which of these alternative extensions best predicts people’s multi-alternative decisions from experience.
Our resource-rational analysis assumed that the limited resource is the number of samples that can be generated. This assumption appears justified for memory-based decisions where sampling by memory retrieval is the primary cognitive operation. But in decisions from description other cognitive and perceptual operations, such as inspecting the probabilities, or gauging the differential utilities of pairs of outcomes also consume a non-negligible amount of time and cognitive resources. In particular, the cost of determining the differential utility of all pairs of outcomes becomes prohibitive as the number of outcomes increases. Since our analysis ignores these computational costs, the applicability of our original model of decisions from descriptions is limited to choices with a small number of possible outcomes. However, this limitation does not apply to our model of decisions from experience, and a recent resource-rational analysis of multi-alternative, multi-outcome decisions from description captured important aspects of people’s adaptive decision strategies in the Mouselab paradigm (Lieder, Krueger, & Griffiths, under review).
While the simulation and integration mechanisms of UWS were derived from first principles, the choice of the utility function in Equation 16 was less principled. We chose it because it is the simplest instantiation of the efficient coding theory proposed by Summerfield and Tsetsos (2015) that captures our findings. It thus remains to be validated independently. Consistent with this normalized representation of utility, there is neural evidence that the human brain encodes relative value rather than absolute value (Mullett & Tunney, 2013). Yet, this evidence equally consistent with a rank-dependent utility function. Neurophysiological data from animal studies (Louie et al., 2011) and psychophysical data from humans (Louie et al., 2013) speak to the encoding of normalized value, but further research is needed to determine the exact nature of the brain’s relative utility representation and its variability.
While we focused on one particular strategy for mitigating resource constraints, namely adjusting the simulation distribution, the brain also appears to adjust the number of samples. Our own and other recent findings suggest that people draw more samples when the stakes are high (Vul et al., 2014) and when they are very uncertain (Hamrick, Smith, Griffiths, & Vul, 2015). The models presented here capture neither of these effects, but future versions of UWS will accommodate them according to the principle that people make rational use of their finite cognitive resources (Griffiths et al., 2015). Recent work has developed a mechanism for determining the optimal number of samples (Tajima, Drugowitsch, & Pouget, 2016), and future work should integrate this mechanism into UWS.
Testing whether the magnitude of the simulated availability biases is resource-rational will additionally require independent measurements of people’s cognitive resources. Therefore, measuring resource constraints independently and using these measurements to derive and test quantitative predictions of human performance as a function of incentives and time pressure is an important direction for future research. A first step towards deriving these predictions could be to measure how long it takes to generate a single sample using psychophysical methods (Lengyel, Koblinger, Popovic, & Fiser, 2015). It might also be possible to measure how long it takes to generate a sample by investigating the relationship between the time available to make a choice and the resulting choice variability. Alternatively, a lower bound on how long it takes to generate a sample could be derived from spiking neural network models of how the brain generates samples (Buesing, Bill, Nessler, & Maass, 2011). This bound on how fast samples can be generated could then be translated into an upper bound on how much the availability biases simulated here can be reduced by financial incentives. The estimated time per sample could also be used to derive the cost of sampling in scenarios where people have to trade off how much computation to invest in a decision against the number of choices they can make (Vul et al., 2014). The resulting model of the cost of sampling could inform a rational mechanism for choosing the number of samples (Hay, Russell, Tolpin, & Shimony, 2012; Tajima et al., 2016; Vul et al., 2014) to be generated by utility-weighted sampling. Future experiments should also test the assumption that the number of mental simulations is a critical limiting factor to the quality of people’s decisions. This assumption predicts that time pressure and cognitive load should make people’s risk preferences more inconsistent between gains versus losses. Conversely, instructing or incentivizing participants to simulate their decision more often should reduce the impact of extreme events.
Another avenue for future research is to investigate whether people use utility-weighted sampling adaptively. Three mechanisms of adaptivity are conceivable: First, people might adapt the number of simulations to the decision problem’s incentives for speed and accuracy. Second, people might use their current estimate of the expected utility gain to adapt their simulation distribution from one simulation to the next as in adaptive importance sampling (Oh & Berger, 1992):
| (40) |
Third, people might use utility-weighted sampling selectively only for those problems in which they expect it to work well (Lieder & Griffiths, 2015, under review).
Finally, utility-weighted sampling makes a number of novel predictions that can be tested empirically: Because the predicted availability biases increase with the extremity of the event, the probability-weighting function (Tversky & Kahneman, 1992) should be monotonic in the outcome’s payoff relative to other outcomes. According to our UWL model, the rate at which action-outcome associations are learned is proportional to the absolute value of the reward’s utility. This assumption could be tested by measuring the temporal evolution of memory biases as a function of outcome extremity in a modified version of the paradigm by Madan et al. (2014). In addition, the utility-weighted learning model predicts that whether an outcome becomes overweighted and how strongly depends on what the decision-maker expected when they experienced that outcome: A person who expected a large reward will come to overweight a neutral outcome whereas a person whose reward expectation was zero would come to underweight it. Likewise, people with a negative reward expectation should come to overweight positive outcomes much more strongly than people with a positive reward expectation and vice versa. In terms of individual differences, UWL predicts that people with lower sensitivity to rewards and punishments (Corr, 2004) should be less susceptible to develop availability biases in memory recall, frequency estimation, and decision-making than people with higher reinforcement sensitivity. Furthermore, people who are more sensitive to punishment than to reward should be more prone to develop such biases for losses than for gains, and the opposite should be true for people who are more sensitive to reward than to punishment. Perhaps the most counterintuitive prediction of UWS is that for certain decisions, such as the one illustrated in the Online Supplemental Material, where people’s risk preferences should become more biased the more people think about them.
Conclusion
A wide range of cognitive biases in judgment and decision-making may result from the rational use of finite computational resources. We derived the implications of two bounds on human rationality: First, limited time and finite processing speed restrict the number of simulations that can be performed. This makes biased simulation necessary to guarantee that important outcomes are taken into account. Second, a finite representational bandwidth limits the fidelity of each simulation. The rational use of this finite representational bandwidth by efficient coding scales reward values by their dynamic range and this limits the discriminability of similar outcomes in the context of extreme eventualities (Summerfield & Tsetsos, 2015). Our results show that utility-weighted sampling is a promising rational process model of judgment and decision-making: UWS predicts a wide range of cognitive biases in memory recall, learning, frequency estimation, decisions from experience, and decisions from description. According to our model all of these availability biases result from the rational use of limited time and bounded cognitive resources. From this perspective, cognitive biases are a window on resource-rational information processing rather than a sign of human irrationality.
Supplementary Material
Acknowledgments
We are grateful to Sam Gershman, Elliot Ludvig, Christopher Madan, Marta Kryven, Ido Erev, Nisheeth Srivastava, Thomas Icard, and Phoebe Lin for their helpful pointers, discussion, and assistance.
Appendix A
Derivation of the optimal importance distribution for self-normalized importance sampling One way to derive the optimal importance distribution q for estimating the expected value of f with respect to p, that is , is to minimize the asymptotic variance (Equation 7) of the self-normalized importance sampling estimator (Equation 5) subject to the constraints that and q(x) > 0 for all x using variational calculus (Gelfand & Fomin, 2000). To solve this constrained optimization problem we minimize its Lagrangian
| (41) |
where λ is the Lagrange multiplier. To minimize the Lagrangian L(q) we compute its functional derivative
| (42) |
and set it to zero. Solving that equation for q yields
| (43) |
Therefore, the optimal importance distribution for self-normalized importance sampling is proportional to .
Appendix B
Worked Example of UWS applied to binary decisions from description Here we provide a worked example of how UWS makes the decision whether or not to accept a gamble. We consider the choice between a gamble with a 90% chance of losing $1 (o1 = −1) and a 10% chance of winning $99 (o2 = 99) versus $1 for sure. Thus, the largest and the smallest possible outcome are omax = 99 and omin = −1. For the sake of illustration, let’s assume that the utility function is like the one defined in Equation 16, but deterministic:
| (44) |
Hence, the utility of the sure gain is u(1) = 0.01, the probability of the gamble’s likely loss is u(−1) = −0.01 and utility of the gamble’s unlikely gain is u(99) = 0.99.
If the gamble is chosen, then its first outcome o1 = −1 has a differential utility of ΔU(ol) = u(−1) − u(1) = −0.02 whereas its second outcome has a large positive differential utility of ΔU(o2) = u(99) − u(1) = 0.98. Given these differential utilities, we can now compute the distribution the decision-maker should sample from to decide whether or not to take the sure gain by applying Equation 20:
| (45) |
| (46) |
To normalize this probability distribution we divide each value by their sum. This yields
| (47) |
| (48) |
This means that UWS would simulate the possibility of losing out on the $99 prize more than 80% of the time even though its probability is only 10%. If the decision-maker generates two samples, then there are four possible simulations results: (ol, ol), (ol, o2), (o2, ol), (o2, o2). After the outcomes have been simulated, the UWS heuristic for binary decisions from description determines their utilities and tallies how often the utility is positive minus how often it is negative. If the resulting count is positive, then UWS accepts the gamble. If the count is negative, then it declines the gamble, and if the count is zero, then UWS has no preference and chooses at random. All possible outcomes of this process and their respective probabilities are summarized in Table B1. Summing up the probability of the simulations that lead UWS to accept the gamble reveals that it predicts that about 84.48% of people who are offered the gamble should accept it. This illustrates that UWS can identify the correct decision with high probability using only two simulations.
Table B1.
UWS applied to the decision between a gamble with a 90% chance of losing $1 and a 10% chance of winning $99 versus a sure gain of $1.
| Simulated Outcomes | Utilities | Count | Decision | Frequency |
|---|---|---|---|---|
| (01,01) | (−0.02, −0.02) | −2 | decline gamble | 0.1552 · 0.1552 = 2.41% |
| (o1,o2) | (−0.02, +0.98) | 0 | accept with prob. 0.5 | 0.1552 · 0.8448 = 13.11% |
| (o2, o1) | (+0.98, −0.02) | 0 | accept with prob. 0.5 | 0.8448 · 0.1552 = 13.11% |
| (o2,o2) | (+0.98, +0.98) | +2 | accept gamble | 0.8448 · 0.8448 = 71.37% |
|
| ||||
| P(choose gamble) | 84.48% | |||
Appendix C
Detailed explanation of how UWS explains the fourfold pattern of risk preferences In this appendix we explain how UWS chooses between a two-outcome gamble and its expected value and show how this gives rise to the fourfold-pattern of risk preferences. These decisions can be formalized as the choice between a p · 100% chance of winning $x and winning nothing otherwise versus the gamble’s expected value p· x dollars for sure. As a first step towards explaining UWS we assume that each outcome’s utility was equal to its monetary value, that is u(x) = x.6 In this case, the differential utility of choosing a gamble that yields x with probability p over its expected value p · x is
| (49) |
Thus, the utility-weighted sampling distribution becomes
| (50) |
| (51) |
Note that the two terms are equal. Therefore, if we normalize the distribution we find that
| (52) |
As our first concrete example, let’s consider the choice between a 1% chance of winning $100 versus $1 for sure. In this case, the differential utility of winning is $99 and the differential utility of losing is −$1. Hence, the differential utility of winning the gamble is 99 times as extreme as the differential utility of losing the gamble. Thus, we would intuitively expect UWS to over-simulate winning relative to losing. This is indeed the case since UWS will simulate winning and losing as if they were equally probable (Equation 52). In this example UWS over-simulates winning because the differential utility of winning ($99 dollars) is more extreme than the disutility of losing (−$1). As our second concrete example, let’s consider the choice between a 99% chance of winning $100 versus $99 for sure. Now the differential utility of winning is $1 whereas the differential utility of losing is minus $99. The sampling distribution is still 50/50. Thus, now UWS over-simulates losing the gamble because the differential utility of losing is 99 times as extreme as the utility of winning. This illustrates that UWS always over-simulates the event whose differential utility is most extreme.
Next, let’s work through how the simulations are translated into decisions. For simplicity, let’s assume that the decision-maker generates only two samples. In our examples there are two possible outcomes of each of the two simulations. So there are four possibilities in total. Intuitively, these possibilities correspond to (lose, lose), (lose, win), (win, lose), and (win, win). In the first case, the decision-maker would decline the gamble and choose the sure outcome instead. In the second and the third case the decision-maker would not have a systematic preference and their decision would be determined by noise. In the fourth case, that is (win,win), the decision-maker would choose the gamble. Critically, these four simulation results occur with different probabilities. These probabilities depend on the simulation distribution , which in turn depends on the probability p of winning the gamble. Concretely, the probability that UWS will choose the gamble over the sure payoff is the probability of sampling (win, win) plus one half of the probability of sampling (win, lose) or (lose, win).
Table C1 summarizes the probabilities of the four possible outcomes and the resulting choice frequencies for the general case and the two examples. As this table shows, the probabilities of the four scenarios add up such that the probability of choosing the gamble based on two simulations is equal to the probability to simulate winning the gamble. Consequently, when offered the choice between a 1% chance of winning $100 versus $1 for sure, UWS is risk neutral because it chooses the gamble 50% of the time. When offered the choice between a 99% chance of winning $100 versus $99 for sure, UWS is also risk neutral and chooses the gamble only 50% of the time. However, when the utility function is non-linear or noisy then the resulting judgments appear to be risk-seeking or risk-averse depending on the problem posed to the decision-maker.
To illustrate this, let’s see what happens when we take into account that the brain’s representation of value is noisy so that where . The utility affects two stages of the decision-process: It biases the probability distribution according to which different outcomes will be simulated and it is used to judge the value of the simulated outcomes. Since the utility is noisy, both stages are subject to noise. In this example the noise has no systematic effect on the simulation frequencies because and . However, the noise in the utility function does systematically bias how the simulated outcomes are translated into a decision. The reason is that the noise ε is more likely to flip the sign of values that are close to zero than the sign of values that are far from zero.
Concretely, for p = 0.01, the differential payoff of winning is $99 whereas the differential payoff for losing is only −$1. The utility function u divides these differential payoffs by the range of possible payoffs (xmax − xmin = 100). This transforms these two differential payoffs into +0.99 and −0.01 respectively. Next, the noise ε is sampled from a normal distribution with mean zero and standard deviation σ = 0.17. Thus, for each simulation of losing there is a roughly 48% chance that the sign of its differential utility will be flipped from negative to positive, but the probability that the sign will flip for a simulated win is less than 2 in one billion. This means that if losing is simulated k times, then the probability that the sign will be flipped for at least one of those simulations is 1 − (1 − 0.48)k.
From the Technion data set we estimated that the number of samples is s = 10. Winning and losing are simulated with equal probability. So a typical value for k would be 5, and when 5 losses are simulated then there is a 96% chance that the sign flips for at least one of them. When this happens in the example where the person simulated 5 wins and 5 losses, then there will be more simulations in favor of the gamble than against it. So the UWS heuristic for binary decisions from description will choose the gamble. This induces risk seeking in the domain of gains when p < .5.
By contrast, when the probability of winning is 99% the differential payoff for winning (i.e. $1) is closer to zero than the differential payoff for losing (i.e. −$99). Therefore, now the noise has exactly the opposite effect, and this induces risk-aversion. Thus, like people, UWS is risk-seeking for improbable gains but risk averse for probable gains. These effects become less extreme as the probability of winning approaches 50% but they do persist. For instance, for the choice between a 30% chance of winning $100 versus $30 for sure, the normalized differential payoff for losing is −0.3, which is still less than two standard deviations of the noise. Consequently, there is an almost 4% chance that its sign will be flipped for a single simulation of losing. This probability is small but its cumulative effect is non-negligible: it entails that when 5 losses are simulated then there is an 18% chance that the sign will be flipped for at least one of them, and this could be enough to make the decision-maker prefer the risky gamble.
Next, let’s see how UWS makes decisions in the domain of losses. Let’s start by considering the choice between the 1% risk to lose $100 and losing $1 for sure. In this case, the differential utilities for choosing the gamble are −$99 when the loss occurs versus $ + 1 when the loss does not occur. The corresponding normalized differential payoffs are +0.01 and −0.99. Thus, it is very likely that the addition of noise will flip the sign of the positive outcome into a minus but very unlikely that it would flip the sign of the negative outcome. Therefore, the noise tilts the balance towards negative outcomes and thereby induces risk aversion. Conversely, if we were choosing between a 99% risk of loosing $100 and a sure loss of $99, then the normalized differential payoffs would be −0.01 for the big loss and 0.99 for its absence. Hence, the noise would be very likely to flip the sign of the negative outcome into a plus, but it would almost never flip the sign of the positive outcome. This tilts the balance towards positive outcomes, and thereby induces risk-seeking. Thus, as for people, the risk preferences of UWS flip when the outcomes are framed in terms of losses instead of gains. These examples illustrate that UWS correctly predicts the fourfold pattern of risk preferences. Note that while the noise in the utility function is necessary to get these effects, none of them would occur if the outcomes were simulated according to their actual frequencies. Therefore, the over-simulation of extreme outcomes plays an important role in utility weighted sampling’s explanation of the fourfold pattern of risk preferences.
Furthermore, our model makes the counterintuitive prediction that for choices between a gamble and its expected value the inconsistencies in people’s risk preferences increase with the number of simulations. Thus, although increased stakes seem to increase the number of simulations, our model predicts that this will exacerbate people’s inconsistent risk preferences rather than ameliorate them. Therefore, in this particular case incentives should increase ‘irrationality’ instead of reducing it. This is very counterintuitive because it means that people should become more irrational the more they think, and the way to make them more rational would be to encourage them to think less. Testing this prediction is an interesting direction for future research.
Table C1.
Two worked examples of UWS applied to the choice between a gamble ($x with probability p) versus its expected value (p · × dollars for sure) for a linear utility function without noise. These predictions change significantly when UWS takes into account that outcome valuation is noisy, as discussed in the text.
| Samples | Decision | Frequency | Freq. if p = 0.01 | Freq. if p = 0.99 | |
|---|---|---|---|---|---|
| (win, win) | gamble |
|
0.5 · 0.5 = 0.25 | 0.5 · 0.5 = 0.25 | |
| (lose, lose) | sure option |
|
0.5 · 0.5 = 0.25 | 0.5 · 0.5 = 0.25 | |
| (win, lose) | choose randomly |
|
0.5 · 0.5 = 0.25 | 0.5 · 0.5 = 0.25 | |
| (lose, win) | choose randomly |
|
0.5 · 0.5 = 0.25 | 0.5 · 0.5 = 0.25 | |
|
| |||||
| P(choose gamble) : |
|
0.5 | 0.5 | ||
Footnotes
People often cope with this complexity by partitioning possible outcomes into chunks like “stock goes up” vs. “stock goes down”. We do not consider this approximation to be an inherent component of the problem itself, but rather as useful component of many heuristic strategies.
This data was obtained from Hobson & Delunas (2001), www.cdc.gov/nchs/fastats/deaths.htm, www.mpaa.org/resources/3037b7a4-58a2-4109-8012-58fca3abdf1b.pdf, www.cdc.gov/foodborneburden/, and Rasmussen, Jensen, Schroll, & Olesen (1991).
We analyzed this relationship using Spearman’s rank correlation, since we cannot assume that people’s extremity judgments follow a ratio scale.
The payoffs and probabilities of this lottery were modeled according to http://www.calottery.com/play/draw-games/powerball.
We will soon return to the stochastic, normalized utility function we used for the simulations reported in the Main Text.
Author Note
A preliminary version of our simulations of decisions from description was presented at the 36th Annual Meeting of the Cognitive Science Society and appeared in the conference proceedings. This work has been updated and extended for inclusion in the current manuscript.
Contributor Information
Falk Lieder, Helen Wills Neuroscience Institute, University of California, Berkeley.
Thomas L. Griffiths, Department of Psychology, University of California, Berkeley
Ming Hsu, Haas School of Business, University of California, Berkeley.
References
- Adcock RA, Thangavel A, Whitfield-Gabrieli S, Knutson B, Gabrieli JD. Reward-motivated learning: mesolimbic activation precedes memory formation. Neuron. 2006;50(3):507–517. doi: 10.1016/j.neuron.2006.03.036. [DOI] [PubMed] [Google Scholar]
- Allais M. Le comportement de l’homme rationnel devant le risque: Critique des postulats et axiomes de l’école américaine. Econometrica: Journal of the Econometric Society. 1953;21(4):503–546. [Google Scholar]
- Allais M. The foundations of a positive theory of choice involving risk and a criticism of the postulates and axioms of the american school. In: Allais M, Hagen O, editors. Expected utility hypotheses and the allais paradox: Contemporary discussions of the decisions under uncertainty with allais’ rejoinder. Dordrecht: Springer Netherlands; 1979. pp. 27–145. 1952. [Google Scholar]
- Anderson JR. The adaptive character of thought. Psychology Press; 1990. [Google Scholar]
- Anderson JR, Schooler LJ. Reflections of the environment in memory. Psychological science. 1991;2(6):396–408. [Google Scholar]
- Ariely D. Predictably irrational. New York: Harper Collins; 2009. [Google Scholar]
- Attneave F. Psychological probability as a function of experienced frequency. Journal of Experimental Psychology. 1953;46(2):81. doi: 10.1037/h0057955. [DOI] [PubMed] [Google Scholar]
- Barron G, Erev I. Small feedback-based decisions and their limited correspondence to description-based decisions. Journal of Behavioral Decision Making. 2003;16(3):215–233. [Google Scholar]
- Bell DE. Disappointment in decision making under uncertainty. Operations research. 1985;33(1):1–27. [Google Scholar]
- Bhatia S. Associations and the accumulation of preference. Psychological Review. 2013;120(3):522. doi: 10.1037/a0032457. [DOI] [PubMed] [Google Scholar]
- Bordalo P, Gennaioli N, Shleifer A. Salience theory of choice under risk. Quarterly Journal of Economics. 2012;127(3):1243–1285. [Google Scholar]
- Brandstätter E, Gigerenzer G, Hertwig R. The priority heuristic: Making choices without trade-offs. Psychological Review. 2006;113(2):409–432. doi: 10.1037/0033-295X.113.2.409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown R, Kulik J. Flashbulb memories. Cognition. 1977;5(1):73–99. [Google Scholar]
- Buesing L, Bill J, Nessler B, Maass W. Neural dynamics as sampling: a model for stochastic computation in recurrent networks of spiking neurons. PLOS Computational Biology. 2011;7(11):e1002211. doi: 10.1371/journal.pcbi.1002211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cador M, Robbins TW, Everitt BJ. Involvement of the amygdala in stimulus-reward associations: interaction with the ventral striatum. Neuroscience. 1989;30(1):77–86. doi: 10.1016/0306-4522(89)90354-0. [DOI] [PubMed] [Google Scholar]
- Christianson Så, Loftus EF. Memory for traumatic events. Applied Cognitive Psychology. 1987;1(4):225–239. [Google Scholar]
- Corr PJ. Reinforcement sensitivity theory and personality. Neuroscience & Biobehavioral Reviews. 2004;28(3):317–332. doi: 10.1016/j.neubiorev.2004.01.005. [DOI] [PubMed] [Google Scholar]
- Courville AC, Daw ND, Touretzky DS. Bayesian theories of conditioning in a changing world. Trends in Cognitive Sciences. 2006;10(7):294–300. doi: 10.1016/j.tics.2006.05.004. [DOI] [PubMed] [Google Scholar]
- Cruciani F, Berardi A, Cabib S, Conversi D. Positive and negative emotional arousal increases duration of memory traces: common and independent mechanisms. Frontiers in Behavioral Neuroscience. 2011;5 doi: 10.3389/fnbeh.2011.00086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Denison S, Bonawitz E, Gopnik A, Griffiths T. Rational variability in children’s causal inferences: The sampling hypothesis. Cognition. 2013;126(2):285–300. doi: 10.1016/j.cognition.2012.10.010. [DOI] [PubMed] [Google Scholar]
- Dickhaut J, Rustichini A, Smith V. A neuroeconomic theory of the decision process. Proceedings of the National Academy of Sciences. 2009;106(52):22145–22150. doi: 10.1073/pnas.0912500106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards W. Subjective probabilities inferred from decisions. Psychological review. 1962;69(2):109. doi: 10.1037/h0038674. [DOI] [PubMed] [Google Scholar]
- Erev I, Ert E, Roth AE, Haruvy E, Herzog SM, Hau R, Lebiere C. A choice prediction competition: Choices from experience and from description. Journal of Behavioral Decision Making. 2010;23(1):15–47. [Google Scholar]
- Fiser J, Berkes P, Orbán G, Lengyel M. Statistically optimal perception and learning: from behavior to neural representations. Trends in Cognitive Sciences. 2010;14(3):119–130. doi: 10.1016/j.tics.2010.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelfand IM, Fomin S. Calculus of variations. Mineola, N.Y: Courier Corporation; 2000. [Google Scholar]
- Geweke J. Bayesian inference in econometric models using Monte Carlo integration. Econometrica. 1989;57(6):1317–1339. [Google Scholar]
- Gigerenzer G. Why heuristics work. Perspectives on Pschological Science. 2008;3(1):20–29. doi: 10.1111/j.1745-6916.2008.00058.x. [DOI] [PubMed] [Google Scholar]
- Gigerenzer G. Simply rational: Decision making in the real world. New York: Oxford University Press; 2015. [Google Scholar]
- Gigerenzer G, Brighton H. Homo heuristicus: Why biased minds make better inferences. Topics in Cognitive Science. 2009;1(1):107–143. doi: 10.1111/j.1756-8765.2008.01006.x. [DOI] [PubMed] [Google Scholar]
- Gonzalez C, Dutt V. Instance-based learning: Integrating sampling and repeated decisions from experience. Psychological review. 2011;118(4):523. doi: 10.1037/a0024558. [DOI] [PubMed] [Google Scholar]
- Gonzalez C, Lerch JF, Lebiere C. Instance-based learning in dynamic decision making. Cognitive Science. 2003;27(4):591–635. [Google Scholar]
- Gonzalez R, Wu G. On the Shape of the Probability Weighting Function. Cognitive Psychology. 1999;38(1):129–166. doi: 10.1006/cogp.1998.0710. [DOI] [PubMed] [Google Scholar]
- Griffiths TL, Lieder F, Goodman ND. Rational use of cognitive resources: Levels of analysis between the computational and the algorithmic. Topics in Cognitive Science. 2015;7(2):217–229. doi: 10.1111/tops.12142. [DOI] [PubMed] [Google Scholar]
- Griffiths TL, Tenenbaum JB. Optimal predictions in everyday cognition. Psychological Science. 2006;17(9):767–773. doi: 10.1111/j.1467-9280.2006.01780.x. [DOI] [PubMed] [Google Scholar]
- Griffiths TL, Vul E, Sanborn A. Bridging levels of analysis for probabilistic models of cognition. Current Directions in Psychological Science. 2012;21(4):263–268. [Google Scholar]
- Hagen O. Towards a positive theory of preferences under risk. In: Allais M, Hagen O, editors. Expected utility hypotheses and the allais paradox: Contemporary discussions of the decisions under uncertainty with allais’ rejoinder. Dordrecht: Springer Netherlands; 1979. pp. 271–302. [Google Scholar]
- Hammersley DC, Handscomb JM. Monte Carlo methods. London: Methuen & Co Ltd; 1964. [Google Scholar]
- Hamrick JB, Smith KA, Griffiths TL, Vul E. Think again? the amount of mental simulation tracks uncertainty in the outcome. In: Noelle DC, et al., editors. Proceedings of the 37th Annual Meeting of the Cognitive Science Society. Austin, TX: Cognitive Science Society; 2015. [Google Scholar]
- Harman G. Rationality. In: LaFollette II, Deigh J, Stroud S, editors. International Encyclopedia of Ethics. Hoboken: Blackwell Publishing Ltd; 2013. [Google Scholar]
- Hastie T, Tibshirani R, Friedman J. The elements of statistical learning. 2nd. New York: Springer; 2009. [Google Scholar]
- Hawkins GE, Camilleri AR, Heathcote A, Newell BR, Brown SD. Proceedings of the 36th Annual Meeting of the Cognitive Science Society. Austin, TX: Cognitive Science Society; 2014. Modeling probability knowledge and choice in decisions from experience; pp. 595–600. [Google Scholar]
- Hay N, Russell S, Tolpin D, Shimony S. Selecting Computations: Theory and Applications. In: de Freitas N, Murphy K, editors. Proceedings of the twenty-eighth conference on uncertainty in artificial intelligence. Corvallis: AUAI Press; 2012. [Google Scholar]
- Herrnstein RJ, Loveland DH. Maximizing and matching on concurrent ratio schedules. Journal of Experimental Analysis of Behavior. 1975;24(1):107–116. doi: 10.1901/jeab.1975.24-107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hertwig R, Barron G, Weber EU, Erev I. Decisions from experience and the effect of rare events in risky choice. Psychological Science. 2004;15(8):534–539. doi: 10.1111/j.0956-7976.2004.00715.x. [DOI] [PubMed] [Google Scholar]
- Hertwig R, Erev I. The description-experience gap in risky choice. Trends in Cognitive Sciences. 2009;13(12):517–523. doi: 10.1016/j.tics.2009.09.004. [DOI] [PubMed] [Google Scholar]
- Hertwig R, Pachur T, Kurzenhäuser S. Judgments of risk frequencies: tests of possible cognitive mechanisms. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2005;31(4):621. doi: 10.1037/0278-7393.31.4.621. [DOI] [PubMed] [Google Scholar]
- Hobson CJ, Delunas L. National norms and life-event frequencies for the revised social readjustment rating scale. International Journal of Stress Management. 2001;8(4):299–314. [Google Scholar]
- Hobson CJ, Kamen J, Szostek J, Nethercut CM, Tiedmann JW, Wojnarowicz S. Stressful life events: A revision and update of the social readjustment rating scale. International Journal of Stress Management. 1998;5(1):1–23. [Google Scholar]
- Jarvstad A, Hahn U, Rushton SK, Warren PA. Perceptuo-motor, cognitive, and description-based decision-making seem equally good. Proceedings of the National Academy of Sciences. 2013;110(40):16271–16276. doi: 10.1073/pnas.1300239110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson EJ, Häubl G, Keinan A. Aspects of endowment: a query theory of value construction. Journal of experimental psychology: Learning, memory, and cognition. 2007;33(3):461. doi: 10.1037/0278-7393.33.3.461. [DOI] [PubMed] [Google Scholar]
- Kahneman D, Tversky A. Prospect theory: An analysis of decision under risk. Econometrica. 1979;47(2):263–291. [Google Scholar]
- Kass R, Raftery A. Bayes factors. Journal of the American Statistical Association. 1995;90(430):773–795. [Google Scholar]
- Kawaguchi K, Kaelbling LP, Lozano-Pérez T. Bayesian optimization with exponential convergence. In: Cortes C, Lawrence ND, Lee DD, Sugiyama M, Garnett R, editors. Advances in Neural Information Processing Systems. Vol. 28. 2015. pp. 2809–2817. [Google Scholar]
- Kellen D, Pachur T, Hertwig R. How (in) variant are subjective representations of described and experienced risk and rewards? Cognition. 2016;157:126–138. doi: 10.1016/j.cognition.2016.08.020. [DOI] [PubMed] [Google Scholar]
- Krajbich I, Armel C, Rangel A. Visual fixations and the computation and comparison of value in simple choice. Nature neuroscience. 2010;13(10):1292–1298. doi: 10.1038/nn.2635. [DOI] [PubMed] [Google Scholar]
- Krajbich I, Rangel A. Multialternative drift-diffusion model predicts the relationship between visual fixations and choice in value-based decisions. Proceedings of the National Academy of Sciences. 2011;108(33):13852–13857. doi: 10.1073/pnas.1101328108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lejarraga T, Dutt V, Gonzalez C. Instance-based learning: A general model of repeated binary choice. Journal of Behavioral Decision Making. 2010;25(2):143–153. [Google Scholar]
- Lengyel M, Koblinger Á, Popović M, Fiser J. On the role of time in perceptual decision making. arXiv preprint arXiv:1502.03135 2015 [Google Scholar]
- Lichtenstein S, Slovic P. Reversals of preference between bids and choices in gambling decisions. Journal of Experimental Psychology. 1971;89(1):46–55. [Google Scholar]
- Lichtenstein S, Slovic P, Fischhoff B, Layman M, Combs B. Judged frequency of lethal events. Journal of Experimental Psychology: Human Learning and Memory. 1978;4(6):551–578. [PubMed] [Google Scholar]
- Lieder F, Goodman ND, Griffiths TL. Reverse-engineering resource-efficient algorithms; Paper presented at NIPS-2013 Workshop Resource-Efficient ML; Lake Tahoe, USA. 2013. [Google Scholar]
- Lieder F, Griffiths TL. When to use which heuristic: A rational solution to the strategy selection problem. In: Noelle DC, et al., editors. Proceedings of the 37th annual conference of the cognitive science society. Austin, TX: Cognitive Science Society; 2015. [Google Scholar]
- Lieder F, Griffiths TL. Strategy selection as rational metareasoning. doi: 10.1037/rev0000075. (under review) [DOI] [PubMed] [Google Scholar]
- Lieder F, Griffiths TL, Goodman ND. Burn-in, bias, and the rationality of anchoring. In: Bartlett P, Pereira FCN, Bottou L, Burges CJC, Weinberger KQ, editors. Advances in Neural Information Processing Systems. 2013. p. 26. [Google Scholar]
- Lieder F, Hsu M, Griffiths TL. Proceedings of the 36th Annual Meeting of the Cognitive Science Society. Austin, TX: Cognitive Science Society; 2014. The high availability of extreme events serves resource-rational decision-making. [Google Scholar]
- Lieder F, Krueger PM, Griffiths TL. An automatic method for discovering rational heuristics for risky choice. In: Gunzelmann G, Howes A, Tenbrink T, Davelaar E, editors. Proceedings of the 39th Annual Meeting of the Cognitive Science Society. Austin, TX: Cognitive Science Society; (under review) [Google Scholar]
- Lin D, Donkin C, Newell BR. The exemplar confusion model: An account of biased probability estimates in decisions from description. In: Noelle DC, et al., editors. Proceedings of the 37th Annual Meeting of the Cognitive Science Society. Austin, TX: Cognitive Science Society; 2015. [Google Scholar]
- Loomes G, Sugden R. Regret theory: An alternative theory of rational choice under uncertainty. The Economic Journal. 1982;92(368):805–824. [Google Scholar]
- Loomes G, Sugden R. Progress in utility and risk theory. Springer; 1984. The importance of what might have been; pp. 219–235. [Google Scholar]
- Loomes G, Sugden R. Disappointment and dynamic consistency in choice under uncertainty. The Review of Economic Studies. 1986;53(2):271–282. [Google Scholar]
- Louie K, Grattan LE, Glimcher PW. Reward value-based gain control: divisive normalization in parietal cortex. Journal of Neuroscience. 2011;31(29):10627–10639. doi: 10.1523/JNEUROSCI.1237-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Louie K, Khaw MW, Glimcher PW. Normalization is a general neural mechanism for context-dependent decision making. Proceedings of the National Academy of Sciences. 2013;110(15):6139–6144. doi: 10.1073/pnas.1217854110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ludvig EA, Madan CR, Spetch ML. Extreme outcomes sway risky decisions from experience. Journal of Behavioral Decision Making. 2014;27(2):146–156. [Google Scholar]
- Maass W. On the Computational Power of Winner-Take-All. Neural Comput. 2000;12(11):2519–2535. doi: 10.1162/089976600300014827. [DOI] [PubMed] [Google Scholar]
- Madan CR, Ludvig EA, Spetch ML. Remembering the best and worst of times: Memories for extreme outcomes bias risky decisions. Psychonomic Bulletin & Review. 2014;21(3):629–636. doi: 10.3758/s13423-013-0542-9. [DOI] [PubMed] [Google Scholar]
- Madan CR, Ludvig EA, Spetch ML. The role of memory in distinguishing risky decisions from experience and description. The Quarterly Journal of Experimental Psychology. 2016:1–12. doi: 10.1080/17470218.2016.1220608. [DOI] [PubMed] [Google Scholar]
- Marchiori D, Di Guida S, Erev I. Noisy retrieval models of over-and undersensitivity to rare events. Decision. 2015;2(2):82. [Google Scholar]
- Marcus G. Kluge: The haphazard evolution of the human mind. Boston: Houghton Mifflin Harcourt; 2009. [Google Scholar]
- Marr D. Vision: A computational investigation into the human representation and processing of visual information. San Francisco: W. H. Freeman and Company; 1982. [Google Scholar]
- McGaugh JL. The amygdala modulates the consolidation of memories of emotionally arousing experiences. Annual Review of Neuroscience. 2004;27(1):1–28. doi: 10.1146/annurev.neuro.27.070203.144157. [DOI] [PubMed] [Google Scholar]
- McGaugh JL, McIntyre CK, Power AE. Amygdala modulation of memory consolidation: Interaction with other brain systems. Neurobiology of Learning and Memory. 2002;78(3):539–552. doi: 10.1006/nlme.2002.4082. [DOI] [PubMed] [Google Scholar]
- McRaney D. You are not so smart. Sherryl Woods; 2011. [Google Scholar]
- Mulder G. The concept and measurement of mental effort. In: Hockey G, Gaillard AW, Coles M, editors. Energetics and human information processing. Heidelberg: Springer; 1986. pp. 175–198. [Google Scholar]
- Mullett TL, Tunney RJ. Value representations by rank order in a distributed network of varying context dependency. Brain and cognition. 2013;82(1):76–83. doi: 10.1016/j.bandc.2013.02.010. [DOI] [PubMed] [Google Scholar]
- Nessler B, Pfeiffer M, Buesing L, Maass W. Bayesian computation emerges in generic cortical microcircuits through spike-timing-dependent plasticity. PLOS Computational Biology. 2013;9(4):e1003037. doi: 10.1371/journal.pcbi.1003037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nilsson H, Rieskamp J, Wagenmakers EJ. Hierarchical bayesian parameter estimation for cumulative prospect theory. Journal of Mathematical Psychology. 2011;55(1):84–93. [Google Scholar]
- Niv Y. Reinforcement learning in the brain. Journal of Mathematical Psychology. 2009;53(3):139–154. [Google Scholar]
- Noguchi T, Stewart N. Multialternative decision by sampling. Manuscript submitted for publication; 2016. [Google Scholar]
- Oaksford M, Chater N. Bayesian rationality: The probabilistic approach to human reasoning. Oxford University Press; 2007. [DOI] [PubMed] [Google Scholar]
- Oh MS, Berger JO. Adaptive importance sampling in Monte Carlo integration. Journal of Statistical Computation and Simulation. 1992;41(3–4):143–168. [Google Scholar]
- Pachur T, Hertwig R, Steinmann F. How do people judge risks: availability heuristic, affect heuristic, or both? Journal of Experimental Psychology: Applied. 2012;18(3):314. doi: 10.1037/a0028279. [DOI] [PubMed] [Google Scholar]
- Payne JW, Bettman JR, Johnson EJ. Behavioral decision research: A constructive processing perspective. Annual review of psychology. 1992;43(1):87–131. [Google Scholar]
- Pearce JM, Hall G. A model for Pavlovian learning: variations in the effectiveness of conditioned but not of unconditioned stimuli. Psychological Review. 1980;87(6):532. [PubMed] [Google Scholar]
- Pleskac TJ, Hertwig R. Ecologically rational choice and the structure of the environment. Journal of Experimental Psychology: General. 2014;143(5):2000. doi: 10.1037/xge0000013. [DOI] [PubMed] [Google Scholar]
- Plonsky O, Teodorescu K, Erev I. Reliance on small samples, the wavy recency effect, and similarity-based learning. Psychological review. 2015;122(4):621. doi: 10.1037/a0039413. [DOI] [PubMed] [Google Scholar]
- Post T, Van den Assem MJ, Baltussen G, Thaler RH. Deal or no deal? decision making under risk in a large-payoff game show. The American Economic Review. 2008;98:38–71. [Google Scholar]
- Quiggin J. A theory of anticipated utility. J Econ Behav Organ. 1982;3(4):323–343. [Google Scholar]
- Rasmussen BK, Jensen R, Schroll M, Olesen J. Epidemiology of headache in a general population—a prevalence study. Journal of Clinical Epidemiology. 1991;44(11):1147–1157. doi: 10.1016/0895-4356(91)90147-2. [DOI] [PubMed] [Google Scholar]
- Rieskamp J. The probabilistic nature of preferential choice. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2008;34(6):1446. doi: 10.1037/a0013646. [DOI] [PubMed] [Google Scholar]
- Robert C, Casella G. Introducing Monte Carlo methods with R. New York: Springer Science & Business Media; 2009. [Google Scholar]
- Roesch MR, Esber GR, Li J, Daw ND, Schoenbaum G. Surprise! Neural correlates of Pearce-Hall and Rescorla-Wagner coexist within the brain. European Journal of Neuroscience. 2012;35(7):1190–1200. doi: 10.1111/j.1460-9568.2011.07986.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rothman AJ, Klein WM, Weinstein ND. Absolute and relative biases in estimations of personal risk. Journal of Applied Social Psychology. 1996;26(14):1213–1236. [Google Scholar]
- Schultz W, Dayan P, Montague PR. A neural substrate of prediction and reward. Science. 1997 Mar 14;275(5306):1593–1599. doi: 10.1126/science.275.5306.1593. [DOI] [PubMed] [Google Scholar]
- Shadlen MN, Shohamy D. Decision making and sequential sampling from memory. Neuron. 2016;90(5):927–939. doi: 10.1016/j.neuron.2016.04.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi L, Griffiths T. Neural implementation of hierarchical Bayesian inference by importance sampling. In: Bengio Y, Schuurmans D, Lafferty J, Williams CKI, Culotta A, editors. Advances in Neural Information Processing Systems. Vol. 22. 2009. pp. 1669–1677. [Google Scholar]
- Shi L, Griffiths T, Feldman N, Sanborn A. Exemplar models as a mechanism for performing Bayesian inference. Psychonomic Bulletin and Review. 2010;17(4):443–464. doi: 10.3758/PBR.17.4.443. [DOI] [PubMed] [Google Scholar]
- Shteingart H, Neiman T, Loewenstein Y. The role of first impression in operant learning. Journal of Experimental Psychology: General. 2013;142(2):476. doi: 10.1037/a0029550. [DOI] [PubMed] [Google Scholar]
- Simon HA. Rational choice and the structure of the environment. Psychological Review. 1956;63(2):129–138. doi: 10.1037/h0042769. [DOI] [PubMed] [Google Scholar]
- Sims CA. Implications of rational inattention. Journal of monetary Economics. 2003;50(3):665–690. [Google Scholar]
- Starmer C. Developments in non-expected utility theory: The hunt for a descriptive theory of choice under risk. Journal of economic literature. 2000;38(2):332–382. [Google Scholar]
- Starmer C, Sugden R. Probability and juxtaposition effects: An experimental investigation of the common ratio effect. Journal of Risk and Uncertainty. 1989;2(2):159–178. [Google Scholar]
- Stewart N. Decision by sampling: the role of the decision environment in risky choice. Quarterly Journal of Experimental Psychology. 2009;62(6):1041–1062. doi: 10.1080/17470210902747112. [DOI] [PubMed] [Google Scholar]
- Stewart N, Chater N, Brown GD. Decision by sampling. Cognitive Psychology. 2006;53(1):1–26. doi: 10.1016/j.cogpsych.2005.10.003. [DOI] [PubMed] [Google Scholar]
- Stewart N, Reimers S, Harris AJ. On the origin of utility, weighting, and discounting functions: How they get their shapes and how to change their shapes. Management Science. 2015;61:687–705. [Google Scholar]
- Stewart N, Simpson K. In: A decision-by-sampling account of decision under risk. Chater N, Oaksford M, editors. Oxford University Press; Oxford, UK: 2008. pp. 261–276. [Google Scholar]
- Stewart TC, West R, Lebiere C. Applying cognitive architectures to decision making: How cognitive theory and the equivalence measure triumphed in the technion prediction tournament. In: Taatgen N, Rijn H van, Schomaker L, Nerbonne J, editors. Proceedings of the 31st annual meeting of the cognitive science society. Houston, TX: Cognitive Science Society; 2009. pp. 561–566. [Google Scholar]
- Stott HP. Cumulative prospect theory’s functional menagerie. Journal of Risk and uncertainty. 2006;32(2):101–130. [Google Scholar]
- Summerfield C, Tsetsos K. Do humans make good decisions? Trends in Cognitive Sciences. 2015;19(1):27–34. doi: 10.1016/j.tics.2014.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sunstein CR, Zeckhauser R. Overreaction to fearsome risks. Environmental and Resource Economics. 2011;48(3):435–449. [Google Scholar]
- Sutherland S. Irrationality: The enemy within. Constable and Company 1992 [Google Scholar]
- Tajima S, Drugowitsch J, Pouget A. Optimal policy for value-based decision-making. Nature Communications. 2016;7:12400–12411. doi: 10.1038/ncomms12400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thaler RH, Johnson EJ. Gambling with the house money and trying to break even: The effects of prior outcomes on risky choice. Management science. 1990;36(6):643–660. [Google Scholar]
- Tierney L, Kadane JB. Accurate approximations for posterior moments and marginal densities. Journal of the American Statistical Association. 1986;81(393):82–86. [Google Scholar]
- Todd PM, Gigerenzer G. Ecological rationality: Intelligence in the world. OUP USA: 2012. [Google Scholar]
- Tsetsos K, Moran R, Moreland J, Chater N, Usher M, Summerfield C. Economic irrationality is optimal during noisy decision making. Proceedings of the National Academy of Sciences. 2016;113(11):3102–3107. doi: 10.1073/pnas.1519157113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tversky A. Intransitivity of preferences. Psychological review. 1969;76(1):31. [Google Scholar]
- Tversky A, Kahneman D. Availability: A heuristic for judging frequency and probability. Cognitive Psychology. 1973;5(2):207–232. [Google Scholar]
- Tversky A, Kahneman D. Judgment under uncertainty: Heuristics and biases. Science. 1974;185(4157):1124–1131. doi: 10.1126/science.185.4157.1124. [DOI] [PubMed] [Google Scholar]
- Tversky A, Kahneman D. Advances in prospect theory: Cumulative representation of uncertainty. Journal of Risk and Uncertainty. 1992;5(4):297–323. [Google Scholar]
- Von Neumann J, Morgenstern O. The theory of games and economic behavior. Princeton: Princeton University Press; 1944. [Google Scholar]
- Vul E, Goodman ND, Griffiths TL, Tenenbaum JB. One and done? Optimal decisions from very few samples. Cognitive Science. 2014;38(4):599–637. doi: 10.1111/cogs.12101. [DOI] [PubMed] [Google Scholar]
- Vulkan N. An economist’s perspective on probability matching. Journal of Economic Surveys. 2000;14(1):101–118. [Google Scholar]
- Weber EU, Johnson EJ, Milch KF, Chang H, Brodscholl JC, Goldstein DG. Asymmetric discounting in intertemporal choice a query-theory account. Psychological science. 2007;18(6):516–523. doi: 10.1111/j.1467-9280.2007.01932.x. [DOI] [PubMed] [Google Scholar]
- Wiederholt M. Rational inattention. In: Durlauf Steven N, Blume Lawrence E., editors. The new Palgrave dictionary of economics. Basingstoke: Palgrave Macmillan; 2010. [Google Scholar]
- Zabaras N. Importance sampling (Tech Rep) Cornell University; 2010. Retrieved from http://mpdc.mae.cornell.edu/Courses/UQ/ImportanceSampling.pdf. [Google Scholar]
- Zhang H, Maloney LT. Ubiquitous log odds: a common representation of probability and frequency distortion in perception, action, and cognition. Frontiers in Neuroscience. 2012;6(1):1–14. doi: 10.3389/fnins.2012.00001. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


