Abstract
The structure of the superconducting gap in unconventional superconductors holds a key to understand the momentum-dependent pairing interactions. In superconducting FeSe, there have been controversial results reporting nodal and nodeless gap structures, raising a fundamental issue of pairing mechanisms of iron-based superconductivity. Here, by utilizing polarization-dependent laser-excited angle-resolved photoemission spectroscopy, we report a detailed momentum dependence of the gap in single- and multi-domain regions of orthorhombic FeSe crystals. We confirm that the superconducting gap has a twofold in-plane anisotropy, associated with the nematicity due to orbital ordering. In twinned regions, we clearly find finite gap minima near the vertices of the major axis of the elliptical zone-centered Fermi surface, indicating a nodeless state. In contrast, the single-domain gap drops steeply to zero in a narrow angle range, evidencing for nascent nodes. Such unusual node lifting in multi-domain regions can be explained by the nematicity-induced time-reversal symmetry breaking near the twin boundaries.
The superconducting gap structure of FeSe remains a debated issue. Here, Hashimoto et al. report momentum dependence of the gap in single- and multi-domain regions of orthorhombic FeSe crystals, revealing an unusual node lifting of the gap structure in multi-domain regions.
Introduction
Since the discovery of Fe-based superconductors1, they have been actively investigated to fully understand their superconducting (SC) mechanisms. Among the several kinds of Fe-based superconductors discovered so far, FeSe has the simplest crystal structure consisting only of SC layers2. After high-quality single crystals grown by the vapor transport method became available3, intrinsic properties of FeSe have attracted much attention. One of the noticeable properties of FeSe is its SC transition temperature (Tc). While Tc of bulk FeSe is ∼10 K at ambient pressure4 and it increases to 37 K under applied pressure of 9 GPa5, it has been reported that superconductivity above 100 K is observed for single-layer FeSe grown on SrTiO36. Another prominent feature of FeSe is its small Fermi energy (εF), and thus, FeSe has been proposed to be in the crossover regime between weakly coupled Bardeen–Cooper–Schrieffer (BCS) and strongly coupled Bose–Einstein-condensate (BEC) limits4, where εF is comparable to the SC gap, as well as the bands around the Γ point of FeSe1−xTex7,8.
The other features that may be directly related to the mechanism of superconductivity in FeSe are the existence of the structural transition from the tetragonal phase to the orthorhombic phase at Ts ∼ 90 K and the absence of the antiferromagnetic ordering9 unlike other Fe-based superconductors. It has been discussed based on the angle-resolved photoemission spectroscopy (ARPES) measurements10–14 that the structural transition is accompanied by orbital ordering. They reported that the splitting of the Fe 3dyz and 3dzx bands emerges at the M point around Ts and it increases as large as 50 meV. This large splitting has been considered to be too large for the crystal field splitting due to the structural transition, and thus regarded as the evidence of an electronically driven orbital ordering. On the other hand, however, several recent reports have interpreted this splitting as that of 3dyz/zx and 3dxy15,16, or that due to the spin–orbit coupling17. At the Γ point, it has been confirmed that the 3dyz and 3dzx bands split, and one of the bands sinks below EF and the other forms an elliptical hole Fermi surface (FS) by ARPES on the detwinned FeSe18. Similar inequivalent electron occupation of the Fe 3dyz and 3dzx orbitals has been observed by ARPES in Ba(Fe,Co)2As219 and NaFeAs20,21. However, the interplay of this band splitting accompanied with the orbital ordering and superconductivity is still elusive. Revealing the SC gap anisotropy of the elliptical FS at the Γ point of FeSe should be crucial for understanding the role of the orbital ordering in superconductivity. In addition, the existence of line nodes in the SC gap of FeSe has been suggested from the thermal conductivity and scanning tunneling microscopy/spectroscopy (STM/STS) measurements4, although some reports suggest a fully gapped state without nodes22–25. Determination of the positions of the SC gap nodes is important for clarifying the SC mechanism.
In this paper, a study on the SC gap anisotropy of the zone-centered hole FS is presented based on the laser-excited ARPES measurements26,27 of single-crystal FeSe. We observe that the fourfold symmetry is significantly broken in the SC gap anisotropy, which is considered to be due to the orbital ordering, and find that while the SC gap node is not observed for multi-domain samples, it exists at the vertices of the major axis of the elliptical FS for single-domain samples. This can be attributed to breaking of time-reversal symmetry at the twin boundaries and our results reveal the effects of time-reversal symmetry breaking on the nodal SC gap anisotropy.
Results
Fermi surfaces and band dispersions of the twinned FeSe
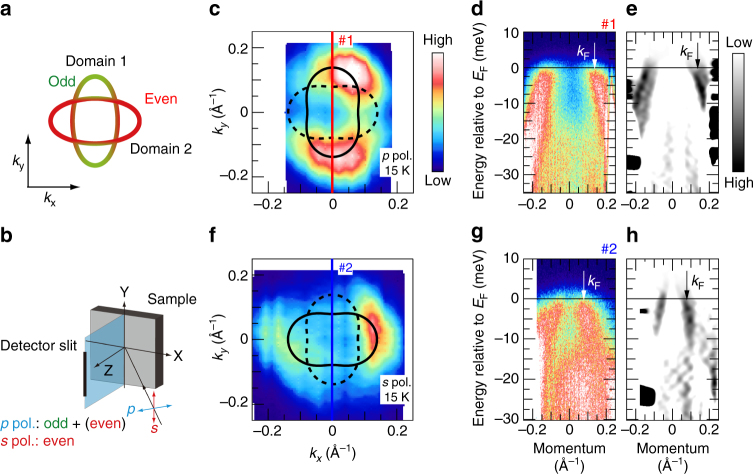
Figure 1c and f shows the FS maps at the Brillouin-zone (BZ) center measured at 15 K (>Tc), taken with p- and s-polarized incident light. Two FSs were observed and their shapes were twofold symmetric and elliptical. They are rotated to each other by 90° and elongated along the ky and kx directions, respectively. Photoemission intensity of the FS elongated along the ky (kx) direction was higher for p-(s-) polarization. Below Ts, the crystal symmetry is transformed from the tetragonal phase to the orthorhombic phase, and therefore, the formation of structural twins is generally inevitable. Observed polarization dependence can be explained by the orbital character of these two FSs due to twinning. Each Fe 3d orbital can be classified into even or odd parity with regard to the mirror plane which is parallel to the detector slit (see Supplementary Fig. 1 and Supplementary Note 1 for details). Due to the parity selection rule, p- (s-) polarized light predominantly observes orbital with odd (even) parity. Considering orbital components of the FS determined by the previous work18, the FS of two domains can be selectively observed by p- (s-) polarized light as shown in Fig. 1c, f. Figure 1d and g shows energy–momentum (E–k) images in cut #1 in Fig. 1c and cut #2 in Fig. 1f taken with p- and s-polarized light, respectively. Figure 1e and h are their momentum second derivatives. One can see that a hole band crosses the Fermi level (EF) at different Fermi wavevector kF positions for each polarization. The different kF positions of the observed bands correspond to those of the major and minor axes of the elliptical FS. The kF positions are determined from momentum distribution curves (MDCs) at EF (see Supplementary Fig. 6 and Supplementary Note 6 for details).
Fig. 1.
Electronic structure of the twinned FeSe at 15 K in the orbital ordered state. a Schematic FSs at the zone center. x and y are coordinates along the crystal axes of the orthorhombic setting. Due to the orbital ordering, two elliptical FSs are overlapped. Portions of the orbital contributions in those FSs are indicated by red and green for even and odd parity with respect to the mirror plane defined in b, respectively. b Experimental configuration. A mirror plane is defined to be parallel to the detector slit. Definition of p- and s-polarized light and sample axes is shown. c Plots of the ARPES intensity at EF as a function of the two-dimensional wavevector measured with p-polarized light. The intensity is obtained by integrating the spectra within ±3 meV with respect to EF. The experimental FS (solid ellipse) and a duplicate rotated by 90° caused by twin domains (dashed ellipse) are shown. d ARPES intensity plot, e momentum second derivative of d at #1 in c. The arrow indicates a kF position. f–h The same as c–e but taken with s-polarized light reflecting the other domain
SC gap structure of the twinned FeSe
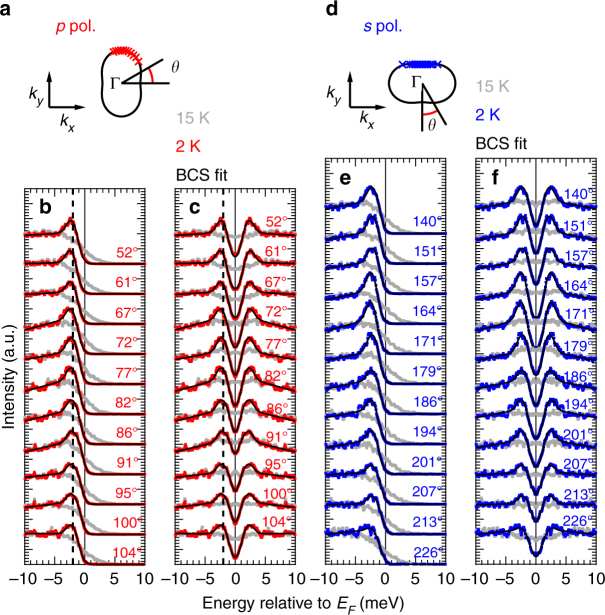
Figure 2b and e shows the energy distribution curves (EDCs) at kF below Tc and above Tc taken with p- and s-polarized light, respectively. Each EDC is identified with a FS angle θ, and the kF positions are shown in Fig. 2a, d. To cancel out the effect of the Fermi–Dirac cutoff, the EDCs were symmetrized with respect to EF, and the results are shown in Fig. 2c, f. Sharp SC coherence peaks can be recognized very clearly in the spectra below Tc. The vertical dashed line in Fig. 2c indicates the peak position of the EDC at θ = 91°, which is at the end of the major axis of the elliptical FS. The EDC at θ = 61°, for example, has a higher peak energy, indicating a finite SC gap anisotropy. Previous STM/STS measurements reported a two-peak structure4 indicating two SC gaps (Δ ∼ 2.5 and 3.5 meV). Current results correspond to the smaller gap, and the larger gap may exist at the zone corner. In order to quantify the SC gap sizes, we fitted the spectra to the BCS spectral function and the results are shown as solid lines (see Supplementary Note 7 for details of the fitting function). The observed spectra are well reproduced by the fitting function, indicating reliability of the obtained SC gap sizes.
Fig. 2.
Superconducting gap anisotropy of twinned FeSe. a Definition of FS angle in case of p-polarized light. Red points indicate the kF positions where energy distribution curves (EDCs) in b and c are taken. b EDCs at various kF points along the FS at 15 K (gray) and 2 K (red). Black lines show the fits to the BCS fitting function. FS angle defined in a is shown for each EDC. c The same as b but symmetrized with respect to EF. d–f The same as a–c but taken with s-polarized light
SC structure of single-domain FeSe
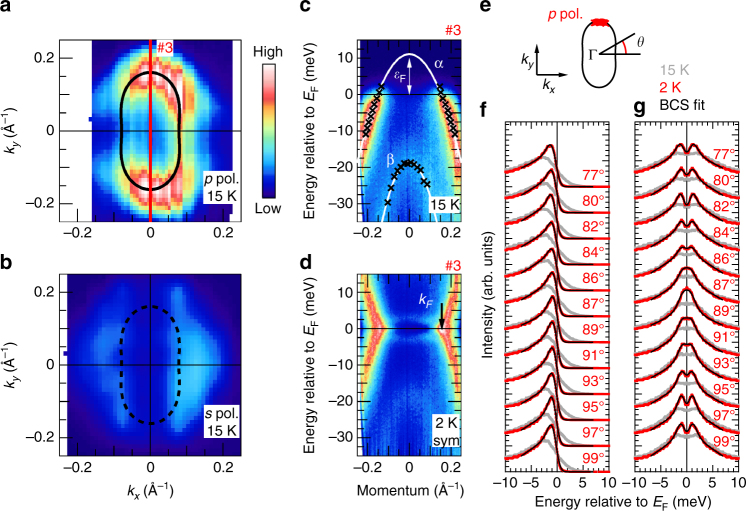
Figure 3 shows the results for another sample, which has a different intensity ratio between two polarizations from Fig. 1. The observed FSs are shown in Fig. 3a, b. The intensity of the FS observed by s-polarized light is much weaker compared to that by p-polarized light, and this intensity difference is similar to that of the detwinned sample (Supplementary Fig. 2 and Supplementary Note 2). By contrast, Fig. 1c, f shows similar intensity of the FS between s- and p-polarized light. Considering this difference, the results shown in Fig. 3 can be interpreted as observation of the single-domain region, although any intentional uniaxial tensile strain was not applied to the sample. This is probably owing to the small laser spot size (∼200 μm) and the large domain size of the cleaved surface (see Supplementary Fig. 5 and Supplementary Note 5 for the position dependence of the spectra). Similar results for the observation of the single-domain region have been reported for FeSe by Raman scattering28 and ARPES29.
Fig. 3.
Superconducting gap anisotropy of single-domain FeSe without uniaxial tensile strain. a Plots of the ARPES intensity at EF of FeSe as a function of the two-dimensional wavevector measured with p-polarized light. The intensity is obtained by integrating the spectra within 3 meV with respect to EF. Black ellipse indicates the experimental FS. b The same as a but measured with s-polarized light. c ARPES intensity plot above Tc (15 K) at the momentum line shown in a, taken with p-polarized light. Black markers represent the experimental band dispersion determined from momentum distribution curves and energy distribution curves (EDCs) for the α and β band. The Fermi energy εF is shown for the α band. d The same as c but taken below Tc (2 K) and the data are symmetrized with respect to EF. The black arrow indicates the kF position. e Definition of FS angle. The red points indicate the kF values where EDCs in f and g are taken. f EDCs at different kF values along the FS at 15 K (gray) and 2 K (red). Black lines show the fits to the BCS fitting function. The FS angles defined in e are shown for each EDC. g Same as f but symmetrized at EF
The clear image in Fig. 3c enables a discussion about the band dispersions. The value of kz for the present results obtained with 7-eV laser can be estimated from the position of the β band, which lies below EF as shown in Fig. 3c. The top of the β band is located at ∼18 meV below EF. Watson et al. have reported that the top of the β band is located at ∼25 and 16 meV below EF for the Γ and Z point, respectively12. Therefore, kz for 7 eV can be estimated to be closer to the Z point than the Γ point according to the results of Watson et al. As mentioned above, FeSe has been suggested to be in a BCS–BEC crossover regime4. The present result shows εF ∼ 10 meV for the α band (Fig. 3c). This corresponds to 0.2 for the hole band at the BZ center. This is almost consistent with the previous report of 0.3 from the STM/STS measurements4, which is smaller than the criteria of the BCS–BEC crossover regime, and should be an evidence that our results are reasonable and reliable. The electron band at the BZ corner might have 1 and satisfy this criterion, as suggested from the STS/STM measurements4.
Figure 3d shows the E–k image below Tc (2 K) of cut #3 indicated in Fig. 3a, symmetrized with respect to EF. This shows no detectable gap, which may demonstrate the existence of SC gap nodes. Figure 3f and g shows the EDCs at kF and symmetrized EDCs with respect to EF, respectively, taken with p-polarized light. Each EDC is identified with a FS angle θ, and the momentum positions in the FS are shown in Fig. 3e. Some of the symmetrized EDCs above Tc (15 K) seem to have a pseudogap. This might correspond to the preformed Cooper pairing associated with the BCS–BEC crossover regime reported by Kasahara et al30. They reported that the experimental signatures of the preformed Cooper pairing were observed below 20 K. It is clear from the spectra that the SC gap becomes smaller as θ reaches to 90°. Furthermore, the spectra around θ = 90° show an undetectable gap, and thus, nodes may exist around θ = 90°. On the other hand, since the experimental observation limit is estimated to be ∼0.2 meV, the SC gap minimum is at least smaller than 0.2 meV. The BCS spectra fitting is shown in Fig. 3f, g as solid lines.
Figure 4 shows the obtained SC gap anisotropy. The results from the multi- and single-domain samples are shown together. For the multi-domain samples, the results with p- and s-polarized light are shown together, considering that each polarization shows a higher intensity for the domain rotated to each other by 90°. We fitted the results of the multi-domain samples to the following twofold symmetric formula of the summation of harmonic series:
| 1 |
and the obtained fitting parameters were A = 1.19 meV, B = 0.079 meV, C = 0.02 meV, D = 0.228 meV, and E = –0.141 meV.
Fig. 4.
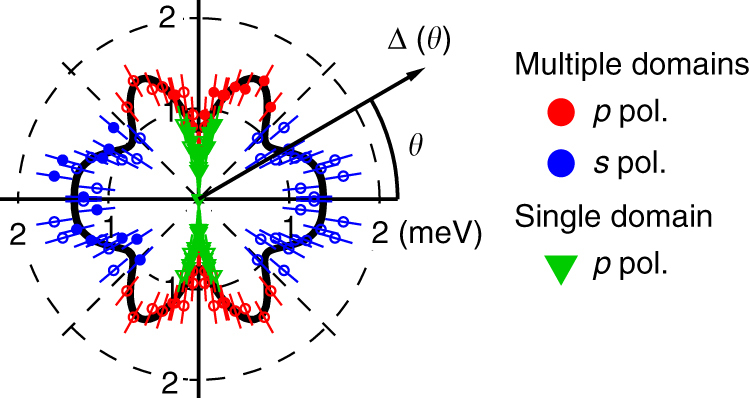
Superconducting gap anisotropy of the elliptical Fermi surface. Results of the multi-domain sample with p- (red circle) and s- (blue circle) polarized light are shown together, considering that each polarization predominantly probes different domains. Results of the single-domain sample (green triangle) are also shown together. Solid symbols are obtained from BCS spectra fitting and open symbols are symmetrized by taking into account the orthorhombic crystal symmetry. Error bars are determined by the systematic and statistical error of the calibrated EF positions, as explained in Supplementary Note 8. The black curve is fitting to the observed anisotropy of the multi-domain sample, considering the twofold orthorhombic symmetry. The fitting function is
The observed SC gap anisotropy shows two major characteristics. First, it shows twofold symmetry. The orbital ordering makes the electronic structure twofold symmetric, and the SC gap anisotropy follows the symmetry. The SC gap at θ = 90° shows a minimum, while that at θ = 0° shows a maximum. This clearly demonstrates the breaking of the fourfold symmetry of the SC gap anisotropy. Fitting of the SC gap anisotropy also shows the breaking of the fourfold symmetry as well. Second, the observed SC gap anisotropy shows sharp anisotropy around θ = 90°. The gap shows a sharp drop toward θ = 90°. In contrast, the anisotropy becomes very weak around θ = 180°. These two observations show the necessity for considering the fourfold symmetry breaking due to the orbital ordering when one pursues the mechanism of superconductivity in FeSe. Additionally, there are local minima around θ = ±45° and ± 135°. The breaking of fourfold symmetry in SC gap anisotropy is basically consistent with very recent reports of ARPES on a similar compound FeSe0.93S0.0731, and Bogoliubov quasiparticle interference (BQPI) on FeSe32. Theoretically, twofold symmetry of SC gap anisotropy is explained based on spin fluctuations33,34, cooperation between spin and orbital fluctuations35, competition between nematic order and superconductivity36, or orbital nematic fluctuations37.
The observed SC gap anisotropy summarized in Fig. 5a shows a considerable difference between the multi- and single-domain samples. The results for the multi-domain samples show finite gaps at any θ, while those for the single-domain samples show an undetectable gap around θ = 90°. The difference of the SC gap size between the multi- and single-domain samples away from θ = 90° becomes small and is almost within error bars at θ = 80° and 100°.
Fig. 5.
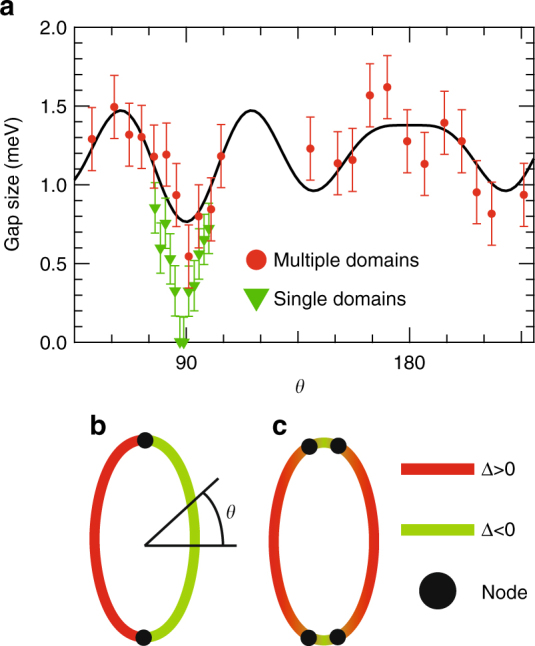
Superconducting gap anisotropy of multi- and single-domain FeSe. a Superconducting gap anisotropy of the elliptical FS, shown in Cartesian coordinates. Results of the multi-domain samples (red circle) and single-domain samples (green triangle) are shown together. Error bars are determined by the systematic and statistical error of the calibrated EF positions, as explained in Supplementary Note 8. The black curve is fitting to the observed anisotropy of the multi-domain samples, considering the twofold orthorhombic symmetry. The fitting function is . Schematic description of gap signs on the Γ-centered FS assuming b a single node and c two nodes. The red (green) line indicates Δ > 0 (<0), and the black circles are the positions of nodes. Definition of θ is shown
Discussion
It is not likely that this different gap anisotropy is caused by the difference of disorder level among the pieces of samples. Teknowijoyo et al. have reported from the London penetration depth measurements that the gap minimum increases by ∼0.05 meV after introducing point-like disorder by electron irradiation24, when the created Frenkel pairs of interstitial vacancies are estimated to be ∼0.05% per Fe and per Se (0.1% total pairs per formula). For our single crystals, the number of impurities and defects was confirmed to be <0.05% per Fe by scanning tunneling microscope topography4,38, and thus, the increase of the gap minimum due to impurities and defects is expected to be less than ∼0.05 meV, which is much smaller than the difference of the gap minimum at θ = 90° between the multi- and single-domain samples (∼0.5 meV).
Alternatively, SC gap anisotropy could be affected by the existence of twin boundaries. According to Watashige et al., it has been suggested that twin boundaries induce a twist of the order parameter, and accordingly, time-reversal symmetry is broken and a fully gapped state is observed over a distance several times larger than the coherence length near twin boundaries38. Because there should exist many twin boundaries within the laser spot for the multi-domain samples, the SC gap anisotropy for the multi-domain samples could reflect a fully gapped state due to time-reversal symmetry breaking. This could settle a contradiction between the different results for the thermal conductivity measurements. While Kasahara et al. observed a large (a residual linear term in the thermal conductivity as T → 0 K) and suggested line nodes in the SC gap4, Bourgeois-Hope et al. observed a very small 22, although a residual resistivity is not significantly different between these two studies. This difference might be due to the density of twin boundaries. Moreover, the difference of the SC gap anisotropy between the multi- and single-domain samples around θ = 90° is consistent with the theoretically calculated node disappearance due to time-reversal symmetry breaking39. Therefore, the difference of the SC gap anisotropy between the multi- and single-domain samples is considered as the effect of time-reversal symmetry breaking near twin boundaries.
According to the SC gap determined from BQPI32, significantly anisotropic gap has been suggested for the zone-centered hole FS. Although the gap nodes were not observed by BQPI, since its reason might be due to the finite scanned area for the Fourier transform, our results should be totally consistent with the gap anisotropy determined from BQPI. If a single node is assumed at the vertex, this means that a sign change occurs at each vertex of the major axis (θ = ±90°) as schematically shown in Fig. 5b. Although the signed values of the SC gap should become more continuous at θ = ±90° in this case, the SC gap symmetry is considered to be a p-wave. This would be difficult to expect because there is no theoretical argument for p-wave pairing in this system and this seems inconsistent with the temperature dependence of the upper critical field40,41. Thus, two nodes are assumed to exist at each vertex of the major axis (θ = ±90°) as shown in Fig. 5c, similar to KFe2As2, which shows an octet-line node structure where two nodes exist within the narrow FS angle range26. In this case, the sign changes occur twice around the vertices and the sign of the gap is consistent with the s-wave symmetry.
Methods
Sample preparation
High-quality single crystals were grown by the chemical vapor transport method using KCl/AlCl3 as transport agent as described in ref. 3.
Laser-ARPES measurements
ARPES data were collected using a laser-ARPES apparatus at ISSP with 6.994 eV, sixth harmonics of Nd:YVO4 quasi-continuous-wave (repetition rate = 960 MHz) laser, and VG-Scienta HR8000 electron analyzer as described in ref. 26. This apparatus achieves a maximum energy resolution of 70 μeV and the lowest cooling temperature of 1.5 K, which enables a direct measurement of the SC gap of FeSe. The overall energy resolution was set to ∼1.2 meV and the angular resolution was 0.1°. The Fermi edge of an evaporated gold film was measured to calibrate EF energy positions. The error bars of the SC gap size were determined from the stability of EF position, and evaluated to be 200 μeV. More details for the accuracy of the measured gap size were described in the previous reports26,42. Polarization of the incident excitation laser was adjusted using half-wave (λ/2) and quarter-wave (λ/4) plates. Samples were cleaved in situ under ultrahigh vacuum and measurements were carried out at pressures better than 5 × 10−11 Torr. The measurements were limited to the hole FS at the zone center due to the relatively low excitation energy of 6.994 eV, with which the momentum around the electron FS at the zone corner cannot be accessed.
Data availability
The data supporting the findings of this study are available from the corresponding author on request.
Electronic supplementary material
Acknowledgements
We would like to thank H. Kontani, R. Arita, and P. Zhang for valuable discussions and comments, and also S. Kawachi and M. Tokunaga for technological support of polarization microscope and for enlightening comments. This work was supported by the Photon and Quantum Basic Research Coordinated Development Program of MEXT and partially supported by Grants-in-Aid for Scientific Research (KAKENHI) (Grant Numbers JP25220707, JP16K17741, JP25220710, JP15H02106, JP15H03688), and on Innovative Areas Topological Material Science (Grant Number JP15H05852) from Japan Society for the Promotion of Science (JSPS). T.H. acknowledges financial support from JSPS through Program for Leading Graduate Schools (MERIT).
Author contributions
T.H., Y.O., and H.Q.Y. performed the ARPES measurements. T.H. and K.O. analyzed the data. Y.S. and T. Shimojima designed a sample folder for the ARPES measurements on detwinned samples. S.W. and C.C. developed a VUV laser system. Samples were grown and characterized by S.K., Y.M., and T. Shibauchi. The manuscript was written by T.H., K.O., and S.S. All the authors discussed and contributed to the manuscript. K.O. and S.S. designed the project.
Competing interests
The authors declare that they have no competing financial interests.
Footnotes
Electronic supplementary material
Supplementary Information accompanies this paper at 10.1038/s41467-017-02739-y.
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Kozo Okazaki, Email: okazaki@issp.u-tokyo.ac.jp.
Shik Shin, Email: shin@issp.u-tokyo.ac.jp.
References
- 1.Kamihara Y, Watanabe T, Hirano M, Hosono H. Iron-based layered superconductor La[O1−xFx]FeAs (x=0.05-0.12) with Tc=26 K. J. Am. Chem. Soc. 2008;130:3296–3297. doi: 10.1021/ja800073m. [DOI] [PubMed] [Google Scholar]
- 2.Hsu FC, et al. Superconductivity in the PbO-type structure α-FeSe. Proc. Natl Acad. Sci. USA. 2008;105:14262–14264. doi: 10.1073/pnas.0807325105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Böhmer AE, et al. Lack of coupling between superconductivity and orthorhombic distortion in stoichiometric single-crystalline FeSe. Phys. Rev. B. 2013;87:180505. doi: 10.1103/PhysRevB.87.180505. [DOI] [Google Scholar]
- 4.Kasahara S, et al. Field-induced superconducting phase of FeSe in the BCS-BEC cross-over. Proc. Natl Acad. Sci. USA. 2014;111:16309–16313. doi: 10.1073/pnas.1413477111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Medvedev S, et al. Electronic and magnetic phase diagram of β-Fe1.01Se with superconductivity at 36.7K under pressure. Nat. Mater. 2009;8:630–633. doi: 10.1038/nmat2491. [DOI] [PubMed] [Google Scholar]
- 6.Ge JF, et al. Superconductivity above 100K in single-layer FeSe films on doped SrTiO3. Nat. Mater. 2014;14:285–289. doi: 10.1038/nmat4153. [DOI] [PubMed] [Google Scholar]
- 7.Lubashevsky Y, Lahoud E, Chashka K, Podolsky D, Kanigel A. Shallow pockets and very strong coupling superconductivity in FeSexTe1−x. Nat. Phys. 2012;8:309–312. doi: 10.1038/nphys2216. [DOI] [Google Scholar]
- 8.Okazaki K, et al. Superconductivity in an electron band just above the Fermi level: possible route to BCS-BEC superconductivity. Sci. Rep. 2014;4:4109. doi: 10.1038/srep04109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.McQueen TM, et al. Tetragonal-to-orthorhombic structural phase transition at 90 K in the superconductor Fe1.01Se. Phys. Rev. Lett. 2009;103:057002. doi: 10.1103/PhysRevLett.103.057002. [DOI] [PubMed] [Google Scholar]
- 10.Shimojima T, et al. Lifting of xz/yz orbital degeneracy at the structural transition in detwinned FeSe. Phys. Rev. B. 2014;90:121111. doi: 10.1103/PhysRevB.90.121111. [DOI] [Google Scholar]
- 11.Zhang P, et al. Observation of two distinct dxz/dyz band splittings in FeSe. Phys. Rev. B. 2015;91:214503. doi: 10.1103/PhysRevB.91.214503. [DOI] [Google Scholar]
- 12.Watson MD, et al. Emergence of the nematic electronic state in FeSe. Phys. Rev. B. 2015;91:155106. doi: 10.1103/PhysRevB.91.155106. [DOI] [Google Scholar]
- 13.Nakayama K, et al. Reconstruction of band structure induced by electronic nematicity in an fese superconductor. Phys. Rev. Lett. 2014;113:237001. doi: 10.1103/PhysRevLett.113.237001. [DOI] [PubMed] [Google Scholar]
- 14.Fanfarillo L, et al. Orbital-dependent Fermi surface shrinking as a fingerprint of nematicity in FeSe. Phys. Rev. B. 2016;94:155138. doi: 10.1103/PhysRevB.94.155138. [DOI] [Google Scholar]
- 15.Watson MD, et al. Evidence for unidirectional nematic bond ordering in FeSe. Phys. Rev. B. 2016;94:201107. doi: 10.1103/PhysRevB.94.201107. [DOI] [Google Scholar]
- 16.Fedorov A, et al. Effect of nematic ordering on electronic structure of FeSe. Sci. Rep. 2016;6:36834. doi: 10.1038/srep36834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Borisenko SV, et al. Direct observation of spin-orbit coupling in iron-based superconductors. Nat. Phys. 2016;12:311–317. doi: 10.1038/nphys3594. [DOI] [Google Scholar]
- 18.Suzuki Y, et al. Momentum-dependent sign inversion of orbital order in superconducting FeSe. Phys. Rev. B. 2015;92:205117. doi: 10.1103/PhysRevB.92.205117. [DOI] [Google Scholar]
- 19.Yi M, et al. Symmetry-breaking orbital anisotropy observed for detwinned Ba(Fe1−xCox)2As2 above the spin density wave transition. Proc. Natl Acad. Sci. USA. 2011;108:6878–6883. doi: 10.1073/pnas.1015572108. [DOI] [Google Scholar]
- 20.Zhang Y, et al. Symmetry breaking via orbital-dependent reconstruction of electronic structure in detwinned NaFeAs. Phys. Rev. B. 2012;85:085121. doi: 10.1103/PhysRevB.85.085121. [DOI] [Google Scholar]
- 21.Yi M, et al. Electronic reconstruction through the structural and magnetic transitions in detwinned NaFeAs. New J. Phys. 2012;14:073019. doi: 10.1088/1367-2630/14/7/073019. [DOI] [Google Scholar]
- 22.Bourgeois-Hope P, et al. Thermal conductivity of the iron-based superconductor FeSe: nodeless gap with a strong two-band character. Phys. Rev. Lett. 2016;117:097003. doi: 10.1103/PhysRevLett.117.097003. [DOI] [PubMed] [Google Scholar]
- 23.Jiao L, et al. Superconducting gap structure of FeSe. Sci. Rep. 2017;7:44024. doi: 10.1038/srep44024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Teknowijoyo S, et al. Enhancement of superconducting transition temperature by pointlike disorder and anisotropic energy gap in FeSe single crystals. Phys. Rev. B. 2016;94:064521. doi: 10.1103/PhysRevB.94.064521. [DOI] [Google Scholar]
- 25.Li M, et al. Superfluid density and microwave conductivity of FeSe superconductor: ultra-long-lived quasiparticles and extended s -wave energy gap. New J. Phys. 2016;18:082001. doi: 10.1088/1367-2630/18/8/082001. [DOI] [Google Scholar]
- 26.Okazaki K, et al. Octet-line node structure of superconducting order parameter in KFe2As2. Science. 2012;337:1314–1317. doi: 10.1126/science.1222793. [DOI] [PubMed] [Google Scholar]
- 27.Shimojima T, Okazaki K, Shin S. Low-temperature and high-energy-resolution laser photoemission spectroscopy. J. Phys. Soc. Jpn. 2015;84:072001. doi: 10.7566/JPSJ.84.072001. [DOI] [Google Scholar]
- 28.Hu Y, et al. Nematic magnetoelastic effect contrasted between Ba(Fe1−xCox)2As2 and FeSe. Phys. Rev. B. 2016;93:060504. doi: 10.1103/PhysRevB.93.060504. [DOI] [Google Scholar]
- 29.Watson MD, Haghighirad AA, Rhodes LC, Hoesch M, Kim TK. Electronic anisotropies revealed by detwinned angle-resolved photo-emission spectroscopy measurements of FeSe. New J. Phys. 2017;19:103021. doi: 10.1088/1367-2630/aa8a04. [DOI] [Google Scholar]
- 30.Kasahara S, et al. Giant superconducting fluctuations in the compensated semimetal FeSe at the BCS-BEC crossover. Nat. Commun. 2016;7:12843. doi: 10.1038/ncomms12843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Xu HC, et al. Highly anisotropic and twofold symmetric superconducting gap in nematically ordered FeSe0.93S0.07. Phys. Rev. Lett. 2016;117:157003. doi: 10.1103/PhysRevLett.117.157003. [DOI] [PubMed] [Google Scholar]
- 32.Sprau PO, et al. Discovery of orbital-selective Cooper pairing in FeSe. Science. 2017;357:75–80. doi: 10.1126/science.aal1575. [DOI] [PubMed] [Google Scholar]
- 33.Kreisel A, et al. Orbital selective pairing and gap structures of iron-based superconductors. Phys. Rev. B. 2017;95:174504. doi: 10.1103/PhysRevB.95.174504. [DOI] [Google Scholar]
- 34.She, J.-H., Lawler, M. J. & Kim, E.-A. Mechanism for nematic superconductivity in FeSe. Preprint at http://arxiv.org/abs/1701.07813 (2017).
- 35.Yamakawa Y, Kontani H. Nematicity, magnetism, and superconductivity in FeSe under pressure: Unified explanation based on the self-consistent vertex correction theory. Phys. Rev. B. 2017;96:144509. doi: 10.1103/PhysRevB.96.144509. [DOI] [Google Scholar]
- 36.Mishra V, Hirschfeld PJ. Effect of disorder on the competition between nematic and superconducting order in FeSe. New J. Phys. 2016;18:103001. doi: 10.1088/1367-2630/18/10/103001. [DOI] [Google Scholar]
- 37.Agatsuma T, Yamase H. Structure of the pairing gap from orbital nematic fluctuations. Phys. Rev. B. 2016;94:214505. doi: 10.1103/PhysRevB.94.214505. [DOI] [Google Scholar]
- 38.Watashige T, et al. Evidence for time-reversal symmetry breaking of the superconducting state near twin-boundary interfaces in FeSe revealed by scanning tunneling spectroscopy. Phys. Rev. X. 2015;5:031022. [Google Scholar]
- 39.Maiti S, Chubukov AV. s+is state with broken time-reversal symmetry in Fe-based superconductors. Phys. Rev. B. 2013;87:144511. doi: 10.1103/PhysRevB.87.144511. [DOI] [Google Scholar]
- 40.Terashima T, et al. Anomalous Fermi surface in FeSe seen by Shubnikov de Haas oscillation measurements. Phys. Rev. B. 2014;90:133517. [Google Scholar]
- 41.Vedeneev SI, Piot BA, Maude DK, Sadakov AV. Temperature dependence of the upper critical field of FeSe single crystals. Phys. Rev. B. 2013;87:134512. doi: 10.1103/PhysRevB.87.134512. [DOI] [Google Scholar]
- 42.Ota Y, et al. Unconventional superconductivity in the Bis2-based layered superconductor NdO0.71F0.29Bis2. Phys. Rev. Lett. 2017;118:167002. doi: 10.1103/PhysRevLett.118.167002. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data supporting the findings of this study are available from the corresponding author on request.