Network Features and Dynamical Landscape of Naive and Primed Pluripotency

Abstract

Although the broad and unique differentiation potential of pluripotent stem cells relies on a complex transcriptional network centered around Oct4, Sox2, and Nanog, two well-distinct pluripotent states, called “naive” and “primed”, have been described in vitro and markedly differ in their developmental potential, their expression profiles, their signaling requirements, and their reciprocal conversion. Aiming to determine the key features that segregate and coordinate these two states, data-driven optimization of network models is performed to identify relevant parameter regimes and reduce network complexity to its core structure. Decision dynamics of optimized networks is characterized by signal-dependent multistability and strongly asymmetric transitions among naive, primed, and nonpluripotent states. Further model perturbation and reduction approaches reveal that such a dynamical landscape of pluripotency involves a functional partitioning of the regulatory network. Specifically, two overlapping positive feedback modules, Klf4/Esrrb/Nanog and Oct4/Nanog, stabilize the naive or the primed state, respectively. In turn, their incoherent feedforward and negative feedback coupling mediated by the Erk/Gsk3 module is critical for robust segregation and sequential progression between naive and primed states before irreversible exit from pluripotency.

Introduction

Pluripotent stem cells retain a broad range of differentiation potential in contrast to lineage-restricted cells. This ability is regulated by an extended transcriptional program centered around a core set of pluripotent factors known as Oct4, Sox2, and Nanog. Pluripotency has further been subdivided into two main states characterized by distinct developmental potential and regulatory machineries (1). The naive state of pluripotency characterizes pluripotent stem cells that are able to differentiate into lineages of all germ layers and the germline and to contribute to blastocyst chimeras. Naive cells are typically mouse embryonic stem cells (mESC) derived by in vitro culture from the inner cell mass of the blastocyst. They are long-term propagated in vitro in the presence of LIF and pharmacological inhibitors of diverse signaling pathways (2). In contrast, the primed state of pluripotency corresponds to pluripotent cells that do not contribute to blastocyst chimeras and present some differentiation bias due to their expression of some lineage-specific differentiation factors or to their sensitivity to differentiation signals that is higher than in naive cells. Mouse epiblast stem cells (mEpiSC) derived from the epiblast of the prestreak postimplantation embryo and stabilized in vitro by adding Activin and FGF in the culture medium are a common model of primed pluripotency (3, 4). These two states can also be interconverted in vitro under various procedures (5).

The possibility of culturing and monitoring pluripotent stem cells in different states has allowed comparative studies and has helped to reveal markedly different expression profiles and regulatory mechanisms. Although naive/mESC and primed/mEpiSC cells share significant expression levels of the core Oct4, Sox2, and Nanog pluripotent factors, they also drastically differ in the expression levels of some factors, especially the naive-specific factors such as Klfs, Esrrb, Dax1, and Tbx3 that are strongly downregulated in primed/mEpiSC cells (3, 4). However, the recurrent interactions between all these pluripotent and naive-specific factors and their sensitivity to a multiplicity of signaling cues give rise to a highly complex signaling and transcriptional network (6). How such a densely interconnected network can drive the developmental progression through well-distinct pluripotent states before lineage-specific differentiation is not clear, but nevertheless suggests a functional level of network organization in terms of modules (7) and loop motifs (8).

Diverse mathematical modeling approaches have proven valuable to investigate the key features of the pluripotency regulatory network (9, 10). On the one hand, mechanistic approaches typically consist of translating regulatory network models into dynamical system models whose deterministic and stochastic behaviors can be thoroughly analyzed using tools and concepts from numerical analysis, dynamical system theory and statistical physics. Dynamical models of the Oct4-Nanog-Sox2 transcriptional network have contributed to identify key regulatory and stochastic mechanisms that underlie cell fate decisions in mESCs (11, 12, 13, 14, 15, 16, 17). However, the poor quantitative knowledge of biochemical kinetic constants associated with the numerous regulatory mechanisms restricts the possibility of reliable dynamical modeling of detailed regulatory networks. On the other hand, descriptive approaches begin with systematic analysis of large sets of genomic, expression, and phenotypic data to extract relevant information about the regulatory design (18, 19, 20, 21) or the heterogeneity of the cell population (22, 23, 24) without necessarily requiring mechanistic assumptions and quantitative knowledge regarding regulatory kinetics.

This modeling study couples these descriptive and mechanistic approaches to extract pluripotency network regulatory features that are inferred from experimental data and required for a specific cell-fate decision pattern. In this interplay, the choices of experimental data and of ordinary differential equation formalism are motivated by our restricted focus on the deterministic regulatory mechanisms underlying pluripotency decisions, leaving aside the sources of intracellular stochasticity and population heterogeneity (25). Starting with a pluripotency network model of intermediate complexity and a set of perturbation experiments, we use an evolutionary computation method to explore model parameter sets that optimally match these data. Systematic analysis of optimized parameter statistics and sensitivities allows us to assign relative degrees of significance to diverse regulations and to identify a core network architecture. Further dynamical analysis of optimized models reveals the existence of signal-dependent multistability and asymmetric transitions, not only between pluripotent and nonpluripotent states, but also between naive and primed states of pluripotency. Finally, perturbation and reduction approaches recapitulate the modular, feedforward, and feedback organization of the pluripotency network that underlies these pluripotent cell fate decision properties.

Methods

Pluripotency network structure

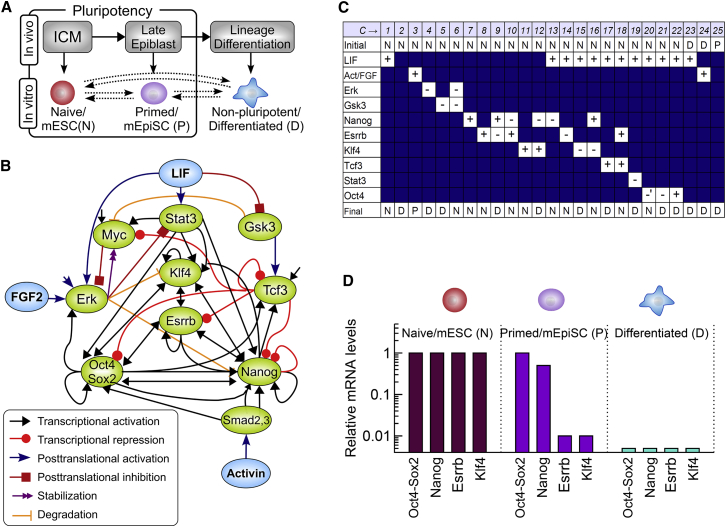
The dichotomy and transitions between the naive and primed states of pluripotency (Fig. 1 A) are studied in a network model (Fig. 1 B) whose architecture is composed of a selected set of proteins and their well-documented posttranslational and transcriptional interactions (Supporting Material; Table S1). Specifically, the network comprises a set of signaling cues (LIF, FGF, and Activin), signaling proteins (Erk, Stat3, Smad2/3, and Gsk3), and pluripotency factors (Oct4-Sox2, Nanog, Esrrb, Klf4, Tcf3, and Myc), most of which have been included in previous pluripotency network models (16, 19, 20, 26) and have been targets of informational perturbation experiments (Fig. 1 C) including reprogramming experiments. This design can be seen as an intermediate level of description (Fig. S1 A) that strikes a balance between the aim to analyze some detailed and nontrivial features of pluripotency network complexity and the need to keep such analysis computationally tractable, given our mechanistic and continuous modeling framework. In striking this balance, it was necessary to leave aside some pluripotency factors often included in larger-scale network representation (such as Dax1, Tbx3, Tcfp2l1, Rex1, Sall4, Mbd3, and Jarid2; see Fig. S1 B) whose signal-mediating or feedback-regulatory roles in pluripotency are presumed either to be comparatively less central or to be more involved in larger-scale epigenetic regulations.

Figure 1.

The pluripotency model: network architecture and cell fate data. (A) Pluripotency displays specific in vitro and in vivo transition patterns among a naive/mESC pluripotent state, N; a primed/mEpiSC pluripotent state, P; and a nonpluripotent differentiated state, D. (B) The regulatory network model is based on a selected set of signaling and transcription factors interacting with each other through various regulatory mechanisms (arrow legend box). (C) A set of perturbation experiments is used as target experimental dataset for the model optimization procedure. These experiments describe the fate outcome j′ = N,P,D of cells that are initially in a state j = N,P,D and then subjected to specific culture conditions (LIF, Activin, FGF) or to upregulation/downregulation (±) of specific factors. (D) Typical relative mRNA levels of pluripotency factors (Oct4-Sox2, Nanog, Esrrb, and Klf4) are associated with naive/mESC, primed/mEpiSC, and nonpluripotent states, which are determined from experiments (Fig. S4) and used for model optimization. To see this figure in color, go online.

Differential equation model

The dynamics of this pluripotency regulatory network is described by a set of deterministic differential equations (see the Supporting Material):

$$\frac{d\overrightarrow{X}}{dt}=\overrightarrow{F}\left(\overrightarrow{X},\overrightarrow{S},\overrightarrow{\mathcal{P}},\overrightarrow{\alpha }\right),$$ (1)

where the 10 components of $\overrightarrow{X}$ are the time-dependent concentrations of the Oct4-Sox2, Klf4, Nanog, Esrrb, Tcf3, Myc, Smad2/3, Erk, Gsk3, and Stat3 proteins. The model parameters consist of signaling parameters $\overrightarrow{S}$ associated to the extracellular concentration of LIF, Activin, and FGF2 signaling factors, in 60 regulatory parameters $\overrightarrow{\mathcal{P}}$ associated to the basal or regulated rates of degradation, transcription, or posttranslational modifications (Tables S1 and S2), and perturbation parameters $\overrightarrow{\alpha }$ used for simulating overexpression, knock-down or pharmacological perturbation experiments. Mechanistic assumptions, steady-state approximation, and normalization procedures are made to keep a restricted number of parameters where each regulatory edge is quantified by a single parameter. The lack of quantitative knowledge of many regulatory parameters and their effective description requires us to infer most regulatory parameters $\left(P_{i=1,N_P=49}\subset \overrightarrow{\mathcal{P}}\right)$ from a target set of experimental data.

Data-driven model inference

The target dataset is provided by a collection of in vitro studies describing the fate outcome of naive/mESC cells or primed/mEpiSC cells following the manipulation of proteins that are included in the network model (Fig. 1 C; and see the Supporting Material). In these data, the naive/mESC cells cultured with LIF are considered to a first approximation as a homogeneous phenotype, disregarding the small pool of cells in transition toward the primed state commonly observed in the presence of serum in addition to LIF. Such expression heterogeneity in single-cell data is difficult to address within a mechanistic modeling framework, especially in the absence of knowledge or consensus about the main source of stochasticity. The initial and final cellular states in these experimental studies are therefore restricted to the three classes of naive, primed, and differentiated states, for which we also define typical expression levels estimated from another set of experimental data (Fig. 1 D; Fig. S4; Supporting Material): whereas the naive/mESC state is characterized by the high expression of Oct4, Nanog, Klf4, and Esrrb, the primed/mEPISCs state retains only a high expression of Oct4 and Nanog, which both become downregulated upon exit from pluripotency and lineage-specific differentiation. These datasets define N_C = 25 experimental conditions $C_{i=1,N_C}$ that can be simulated using Eq. 1 with appropriate initial conditions $\left({\overrightarrow{X}}_0\right)$, signaling inputs $\left(\overrightarrow{S}\right)$, and perturbation factors $\left(\overrightarrow{\alpha }\right)$ (Table S3). The difference between data and model simulations is quantified by measuring and summing the distances ϕ_i between the experimental behavioral outputs ${\overrightarrow{Y}}^{N,P,D}$ and the model behavioral outputs $\overrightarrow{Y}(.)$ for each experimental conditions C_i:

$$\text{Φ}=N_c^{-1}\sum _i{\varphi }_i,$$ (2)

where

$${\varphi }_i=\left|{\overrightarrow{Y}}^{N,P,D}\left(C_i\right)-\overrightarrow{Y}({\overrightarrow{X}}_{\infty }S\left(C_i\right),{\overrightarrow{X}}_0\left(C_i\right),\overrightarrow{P},\alpha \left(C_i\right)\right|.$$ (3)

The use of least-absolute errors rather than least-square errors aims to provide more robust solutions with respect to the possible outliers in the target dataset. The global error Φ is used as the objective or score function to be minimized in the parameter optimization procedure to generate optimal model parameter sets ${\overrightarrow{P}}^k$ that best match the target data set. Parameter optimization is performed via a population-based metaheuristic algorithm called “evolution strategy” (see the Supporting Material for details). Evolution strategy is a global and stochastic optimization method that is appropriate to a nonconvex derivative-free optimization problem. In this case, nonconvexity (i.e., multiple local optima) is due to the high nonlinearity of the dynamic network system and the use of a large data sets, and the derivative of the score with respect to parameter variations is difficult to obtain for a score obtained from numerical simulations and for a high-dimensional parameter space.

Sensitivity and similarity measures

The parameter sensitivity measure γ_i is defined as the relative change of the global error score Φ upon a parameter change P_i → 0 (i.e., disrupted regulation):

$${\gamma }_i^{\left(k\right)}=\frac{{\text{Φ}}^{\left(k\right)}\left(P_i=0\right)-{\text{Φ}}^{\left(k\right)}}{{\text{Φ}}^{\left(k\right)}}.$$ (4)

The value ${\gamma }_i^{\left(k\right)}\ll 1$ indicates that the regulation i of strength P_i^k in the model k can be neglected without significant impact on the model performance in matching experimental data.

The identification of clusters or subclasses within a set of models is performed by computing distance matrices containing the distances, taken pairwise, between specific quantitative features of distinct models (27). In this study, the degree of similarity between optimized models is analyzed by measuring the distances between their condition-specific error scores (ϕ) as well as the parameter and sensitivity values (P and γ) on a logscale. A distance measure between models k and l is defined by

$$D_{kl}\left(y\right)=Z^{-1}\sqrt{\sum _{i=1,N}{\left(y_i^l-y_i^k\right)}^2},$$ (5)

where y_i = {ϕ_i,log₁₀(P_i), log₁₀(γ_i)}, and N = {N_C, N_P} depending on the feature considered, whereas the normalization factor Z is the largest distance within the set of optimal models so that D_kl ranges between 0 and 1. The number of clusters or classes is evaluated by measuring the percentage of variance explained.

Results

Regulatory hierarchies and core circuitries in data-driven network models

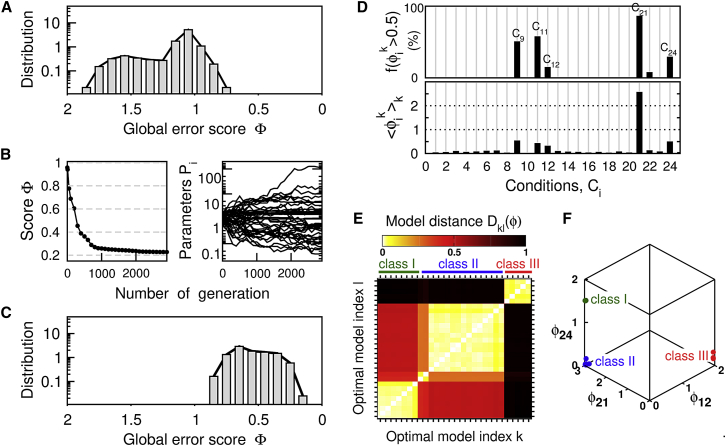
The pluripotency network model exhibits a complex regulatory architecture and its ability to match experimental behaviors is expected to be highly sensitive to the parameter values that set the strength of each regulatory link. As a matter of fact, pluripotency models with random parameters $P_i^k={10}^{{\eta }_k+{\eta }_i}$, where η_i,k are uniformly distributed between [−1:1] exhibit a broad distribution of error score values Φ ranging from ∼2 for the worst scores to only ∼0.8 for the best scores (Fig. 2 A). Due to the high dimensionality of the parameter space, a parameter optimization procedure is definitively required to identify the model parameter sets that are the most consistent with the target dataset. Starting from these randomized-parameter models and then optimizing using the evolutionary algorithm significantly decreases the error scores Φ (Fig. 2 B), which now range between ∼0.8 and ∼0.2 for the 10³ evolutionary trials (Fig. 2 C). The broad distribution of Φ for parameter-optimized models nevertheless emphasizes the difficulty to reach a global optimum because of the likely existence of many local optima related to the high dimension of the parameter space, the nonlinearity of the network, and a cost function based on heterogeneous datasets.

Figure 2.

Model optimization through computational evolution. (A) The statistical distribution of the global error score Φ is computed over 10³ randomized-parameter models. (B) An example of a computational evolutionary trial showing the decreasing score Φ from 0.8 to 0.2 and the parameter set of the fittest model individual of the family of the ith generation. The generation 0 is composed of N_I = 20 model individuals k of parameter $P_i^k={10}^{{\eta }_k+{\eta }_i}$, where η_i,k values are uniformly distributed between [−1:1]. (C) The statistical distribution of the global error score Φ is computed for the fittest individuals of 10³ evolutionary trials. (D) Given here are condition-specific scores ϕ_i^k of a set of optimal models satisfying Φ < 0.21: model-averaged value (lower panel) and fraction of models with ϕ_i^k > 0.5 (upper panel). (E) Three main classes of optimal models (green, class I; blue, class II; red, class III) are evidenced by the distance matrix of their condition-specific scores (Eq. 5). (F) The three model classes differ in their worst-condition-specific scores. To see this figure in color, go online.

To overcome this difficulty, we investigate and compare the features of a subset of N_M = 29 optimized models that have the lowest error scores (Φ_k < 0.21 that is below ∼10% of the lowest error score). The distribution of their condition-specific scores ${\varphi }_i^{k=1,N_M}$ confirms the existence of several local optima. Most sets of experimental conditions are properly adjusted by all these optimal models 〈ϕ_i^k〉_k ∼ 0, whereas a few conditions (C₉, C₁₁, C₁₂, C₂₁, C₂₄) are suitably adjusted only by a subset of optimal models (Fig. 2 D). The analysis of similarity between the score patterns ϕ_i^k of the optimal models reveals in fact the existence of three main classes of models (Fig. 2 E; Table S5), which can be distinguished by their worst-adjusted conditions (Fig. 2 F).

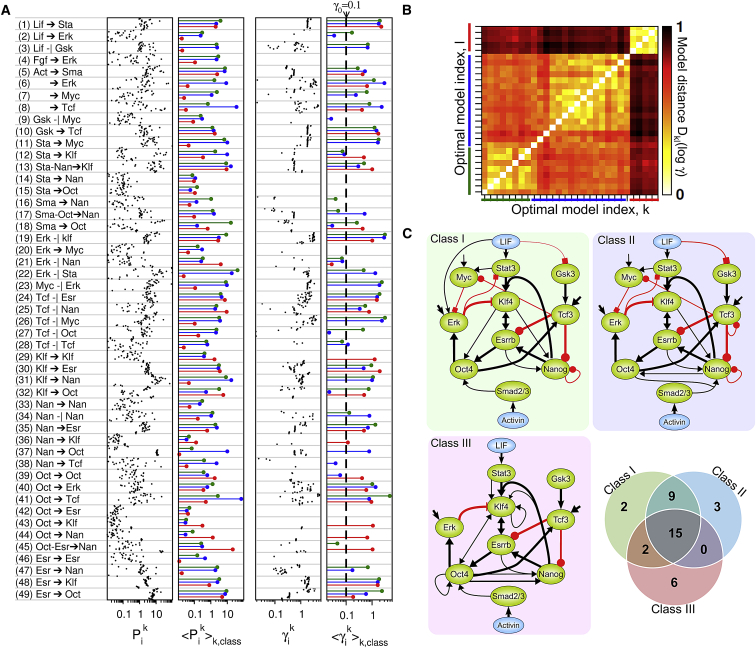
To determine the common and class-specific regulatory properties of this set of optimal models, we perform an extensive statistical and sensitivity analysis of their parameter values P_i^k (Fig. 3). For each optimal model, distribution and uncertainty of parameters reveals the existence of both highly sensitive and neutral parameters (Fig. 3 A; Fig. S5), which indicates that core networks of reduced complexity can fit the data equally well. Furthermore, a comparative variance and similarity analysis between optimized models (Fig. 3, A and B; Fig. S6 A) shows that the parameter values P_i^k and sensitivities γ_i^k are much more similar between models of a same class than between models of different classes, which indicates that networks of well-distinct topologies are equally consistent with the data. The core network topologies associated to each class are drawn by removing the network edges associated with the most insensitive parameters 〈γ_i^k〉_k⊂Class < γ₀ (Fig. 3 C; Fig. S6 B). These class-specific core circuits share a common set of 15 regulations, but also display some subtle differences. Despite the systematic presence of at least one signaling pathway from LIF or Activin toward pluripotency factors, some models differ in the nature of the main signaling paths, for instance whether the main target of Activin/Smad is Oct4 or Nanog, or in the presence of signaling cross talk such as among the Gsk3/Tcf3, Stat/Myc, and Erk pathways. And although several positive feedback loops are systematically implemented in most models through the reciprocal interactions among Klf4, Esrrb, and Nanog, the self-activation of Klf4 and Oct4 and their reciprocal activation occur only in class-III models. Addressing the significance of both the common and the distinctive topological features in the optimal network models requires us to scrutinize and compare their dynamical properties, beyond their ability to match the target experimental dataset.

Figure 3.

Parameter distribution and core topologies of optimized models. The systematic analysis of the $i=\mathrm{1,49}$ optimized parameters is made for the k = 1,29 optimal models segregated into the three classes identified in Fig. 2E (green, class I; blue, class II; red, class III). (A) The two left panels show parameter values P_i^k (k points in the ith line) and their class-averaged values 〈P_i〉_k⊆class. The two right panels show parameter sensitivities γ_i^k (Eq. 4) and their class-averaged values 〈γ_i^k〉_k⊆class, where the dashed line shows the threshold γ₀ = 0.1 between relevant and irrelevant regulations (Fig. S6). (B) The three classes of optimal model differ in their topology, as evidenced by the distance matrix of model parameter sensitivities D_kl(log γ_i) (Eq. 5). (C) Core pluripotent circuitries for each model class are drawn by including only regulations whose removal results in a significant increase of error score Φ (〈γ_i〉_k⊆class > γ₀ in (A)). Model classes share 15 common regulations (thick network edges). To see this figure in color, go online.

Multistability and transitions among naive, primed, and nonpluripotent states

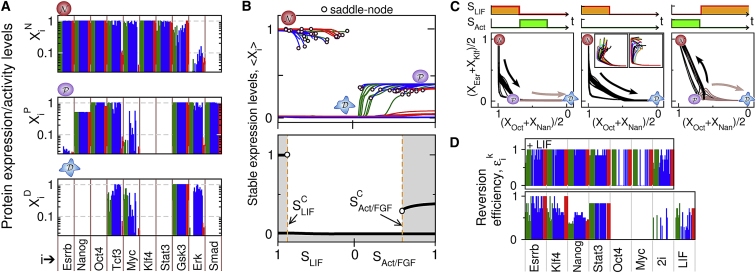
The model adjustment procedure is based on a restricted set of experiments describing the fate outcome of pluripotent cells subjected to specific and discrete perturbations. However, the differential equation framework not only enables parameter fitting of experimental behaviors, but can also provide a broader picture of network dynamics by computing the whole set of stable expression states ${\overrightarrow{X}}_{\infty }\left(\overrightarrow{S}\right)$ (solutions of $\overrightarrow{F}\left({\overrightarrow{X}}_{\infty },\overrightarrow{S},\overrightarrow{P},\overrightarrow{1}\right)=0$) and transitional trajectories (Fig. 4). The protein concentration phenotypes ${\overrightarrow{X}}_{\infty }$ of the naive, primed, and differentiated states in their classical signaling contexts are very similar across the optimal models, especially for Oct4, Nanog, Klf, and Esrrb in agreement with the mRNA targets (Fig. 4 A). The manner in which these distinct phenotypic states depend upon signals S_LIF and S_Act/FGF reveals a very specific pattern of signal-dependent multistability common to most optimal models (Fig. 4 B). A gradual decrease in signaling factor levels has little impact on the concentrations of the stable naive and primed pluripotent states. Instead, such decrease leads to a sudden destabilization of these states through a saddle node bifurcation occurring for some critical signal levels S^C_LIF and S^C_AF, toward an always stable nonpluripotent state. Therefore, all optimized models display two distinct bistability domains between each pluripotent state and the nonpluripotent differentiated state (except class-I models that display an ultrasensitive switch from ${\overrightarrow{X}}^P$ to ${\overrightarrow{X}}^D$ states) with differences only in the signaling threshold values.

Figure 4.

Multistability domains and asymmetric transitions between naive and primed states. Color code represents the three classes of optimal models (green, class I; blue, II; red, class III). (A) Normalized expression/activity levels X^j_∞,j of the i protein species are associated with the stable states j = N,P,D (top, naive state with S_LIF = 1; middle, primed state with S_Act/_FGF = 1; bottom, differentiated state with S_LIF = S_Act/FGF = 0). (B) Distinct multistable subdomains between these three states are depicted by their average expression levels of pluripotency factors 〈X_i^k〉_{i = Oct, Nan, Esr, Klf} as a function of S_LIF (and S_Act/_FGF = 0) and S_Act/FGF (and S_LIF = 0). (Lower panel) An example of multistable property with two bistability domains (shading) and two saddle-node bifurcation points (circles) is illustrated for one optimal model. (C) Dynamical trajectories of optimal models in a 2D section of the concentration space are shown for distinct transition scenarios between naive and primed pluripotent states. (Middle panel, insets) A set of trajectories from a heterogeneous naive state $\left({\overrightarrow{X}}_0={\overrightarrow{X}}_{\infty }^N+\overrightarrow{\eta }\right)$ seems attracted to a slow manifold through the primed state. (D) Primed-to-naive reversion efficiencies ϵ_i^k = 1/θ_i^k are given for the strategy i (overexpression of a given pluripotency factor or 2i, with or without LIF) and optimal model k, where θ_i is the critical level of upregulation or downregulation α_i or of S_LIF that is required for successful reversion. To see this figure in color, go online.

Such multistable properties raise the question of the transition dynamics between these diverse states (Fig. 4 C). In particular, the bifurcation diagram alone does not indicate whether naive and primed states can be easily converted upon reciprocal change of their stabilizing signaling cues (S_LIF versus S_Act/FGF), or instead would be trapped in the strongly stable differentiated steady state. Simulations first show that the naive pluripotent state systematically transits toward a primed state upon the signaling change from S_LIF = 1 to S_Act/FGF = 1, whereas further removal of Activin/FGF (S_Act/FGF → 0) leads, as expected, to a transition toward the differentiated state (Fig. 4 C, left panel). Interestingly, the dynamical trajectory from the destabilized naive state (S_LIF → 0) seems to be canalized along a similar path in the concentration space through a primed-like state in a manner that is very robust to heterogeneous initial conditions (Fig. 4 C, insets of middle panel). In sharp contrast with the likely naive-to-primed transition, the opposite primed-to-naive transition is not systematically induced by a signaling change from S_Act/FGF = 1 to S_LIF = 1 as the outcome is found to be model-dependent (Fig. 4 C, right panel). This result suggests that the primed state of steady-state concentration ${\overrightarrow{X}}_{\infty }^P$ sits close to the state-space boundary separating the basin of attraction of the naive state and differentiated state in the presence of LIF. Accordingly, the primed-to-naive reversion is sensitive to specific model features, and, more importantly, can be promoted through perturbations that extend the attraction basin of the naive state, such as the overexpression of any naive-specific pluripotent factors. For all optimal models, measuring the reversion efficiency E shows that the overexpression of Esrrb, Klf4, or Stat3 are the most efficient strategies to drive primed-to-naive transition as compared with the limited efficiency of overexpressing Nanog or the null-efficiency of overexpressing Myc or Oct4 (Fig. 4 D). Furthermore, a strong synergetic effect is observed by combining LIF with another input, even with those that are weakly efficient alone such as Oct4 or Myc overexpression, or Erk/Gsk3 inhibition (2i).

Despite their possible structural differences, optimized pluripotency network models share a similar qualitative dynamical landscape characterized with signal-dependent multistability and asymmetric transition between naive and primed states with only minor quantitative discrepancies in signaling thresholds and transition timescales.

Network design principles for segregation of pluripotent states

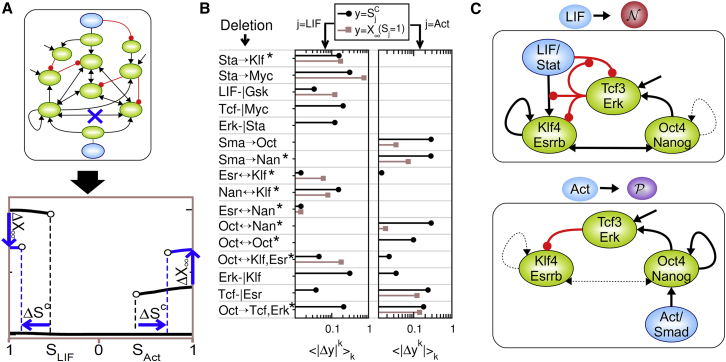
A challenging issue is now to determine the relationship between, on the one hand, the maintenance and transition properties of naive and primed pluripotent states, and, on the other hand, the core regulatory circuitries that have been identified. To address this issue, we evaluate the effect of network perturbations on the attractor landscape of naive and primed pluripotency. The changes of expression state and signaling thresholds associated with naive and primed identity are measured upon the deletion of single or several network edges and averaged over all optimal models (Fig. 5, A and B). The results show that most edge/motif deletions are prone to influence only the naive/mESC state or only the primed/mEpiSC state, suggesting a functional segregation between diverse regulatory motifs. The signaling control of the naive state depends on several LIF-dependent signaling pathways distributed among the Stat3-dependent activation of Klf4, the inhibition of the Gsk3 pathway, and the reciprocal interaction between Stat and Erk, notably through Myc. Its intrinsic regulation is also distributed between various regulatory motifs such as the reciprocal activation between Esrrb and Klf4 and their respective interactions with Nanog and Oct4. In contrast, the primed state is exclusively dependent on regulations centered on Oct4 and Nanog, as likely targets of Activin/Smad signaling, and through their reciprocal interaction or through Oct4 self-activation. Finally, only the inhibitory actions of Erk and Tcf3 toward Klf4 and Esrrb, respectively, and their activation by Oct4, significantly influence the stability and the expression phenotypes of both naive and primed states. The naive/mESC and primed/mEpiSC states are thus proposed to rely on the segregated operations of two regulatory modules featured with their own stabilizing positive-feedback and signaling inputs, and subtly coupled through reciprocal positive interactions and negative interactions mediated by an inhibitory Tcf3/Erk module (Fig. 5 C).

Figure 5.

Identification of a modular network through systematic perturbation approach. (A) The approach consists in quantifying the effect of diverse network motif perturbations on the signaling thresholds and expression levels of the naive and primed states. (B) Model-average alterations 〈|ΔY^k|〉_k of expression levels ($Y={\langle X_{\infty ,i}\rangle }_{i=\text{Oct},\text{Nan},\text{Klf},\text{Esr}}\left(S_j=1\right)$ and signaling thresholds (Y = S^C_j) of the naive state (left, j = LIF) and the primed state (right, j = Act/FGF) are computed upon the deletion of a single or multiple (^∗) regulatory links (a ↔ b: a → b ∪ b → a; a → b,c : a → b ∪ a → c). (C) Functional modular circuits are inferred from (B) regulating the naive and primed states. (Black arrows) Activatory regulation; (red circles) inhibitory regulation. (Solid lines) Effective regulation; (dashed line) ineffective regulation. To see this figure in color, go online.

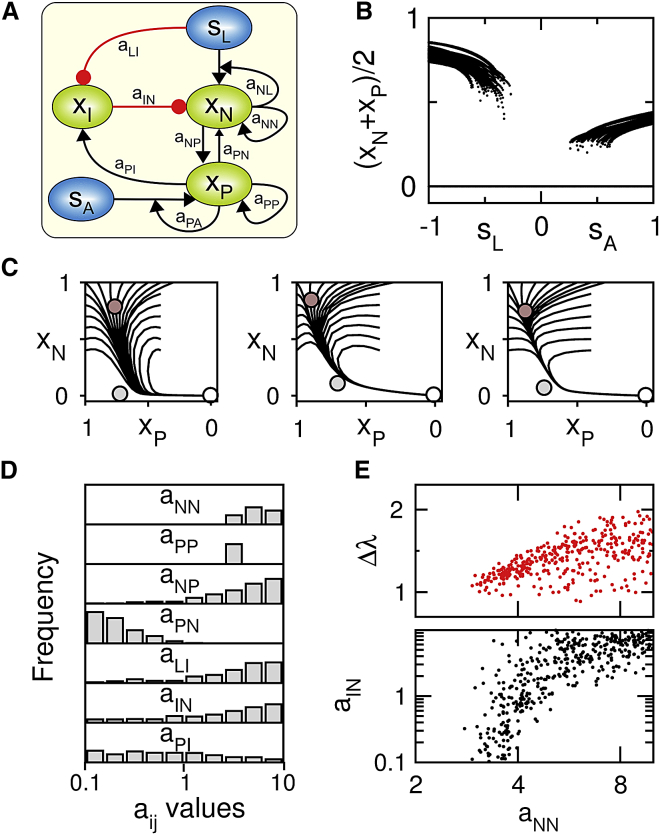
To assess the significance of the modular architecture depicted in Fig. 5 C, a computational strategy consists in designing a coarse-grained model of such architecture (Fig. 6 A) where the activities of the naive module N (Klf/Esrrb), the primed module P (Nanog/Oct4/Sox2), and the inhibitory module I (Tcf3/Erk) are described by normalized variables x_N,I,P, whereas their interactions are described by effective transcriptional activations and repressions (Supporting Material):

$$\begin{array}{l}\frac{d{x}_N}{dt}=\frac{s_L^2{x}_N^{a_{NL}}+a_{NN}{x}_N^2+a_{PN}{x}_P^2}{1+s_L^2{x}_N^{a_{NL}}+a_{NN}{x}_N^2+a_{PN}{x}_P^2+a_{IN}{x}_I^2}-x_N,\\ \frac{d{x}_I}{dt}=\frac{1+a_{PI}{x}_P^2}{2+a_{LI}{s}_L^2+a_{PI}{x}_P^2}-x_I,\\ \frac{d{x}_P}{dt}=\frac{s_A^2{x}_P^{a_{PA}}+a_{NP}{x}_N^2+a_{PP}{x}_P^2}{1+s_A^2{x}_P^{a_{PA}}+a_{NP}{x}_N^2+a_{PP}{x}_P^2}-x_P.\end{array}$$ (6)

The differential equation system of Eq. 6 contains few parameters which quantify the strength of the various regulatory edges and loop motifs. Systematic exploration of the parameter space identifies a subset of model parameters for which the modular model exhibits a signal-dependent multistability among three states (high x_N and x_p; high x_N and low x_p; low x_N and x_p) that is very similar to that observed in the optimal set of detailed models (compare Fig. 6 B with Fig. 4 B; Fig. S7). It turns out that these suitably parameterized modular models also display similar transition dynamics from a heterogeneous naive state toward a differentiated state canalized through the primed state (compare Fig. 6 C with middle panel insets of Fig. 4 C). The distribution of their model parameters is relatively broad, but always peaks around high values (except a_PN) (Fig. 6 D). These high parameter values support the premise that this modular circuit design is both necessary and sufficient to achieve the signal-dependent multistability observed in detailed and optimized pluripotent models, which is confirmed by the significant alterations of the dynamical landscape when any parameter is set to zero (Fig. S7). The broadness of the parameter distribution reflects in part the existence of correlation between parameters, especially between a_NN and a_IN, whose concomitant high values also coincide with a higher signal-dependent stability of the naive-like state (Fig. 6 E; Fig. S7). The coexistence of strong naive-specific positive feedback loop (a_NN high) counterweighted by tightly regulated inhibitory pathways of strength a_IN thus promotes the possibility to switch the naive state from being very stable to very unstable upon suitable signal changes (Fig. S7 C).

Figure 6.

A low-dimensional modular model reproduces the pluripotent dynamics of detailed models. (A) Minimal circuit corresponding to Eq. 6 consists of regulatory modules x_{i = N,I,P}, extrinsic signals s_{i = L,A}, and regulatory parameters a_ii′. (Black arrows) Activatory regulation (red circles) inhibitory regulation. (B) A signal-dependent multistability among three discrete states similar to Fig. 4B is found for 381 parameter sets from a sample of 10⁶ random parameter sets for which log₁₀(a_ii′) values are uniformly distributed between [−1:1] except a_NL = 1 and a_PA = 1. (See Fig. S7A for the quantitative multistability criteria used for parameter set selection.) (C) Three examples of canalized trajectories where heterogeneous initial conditions around the naive-like state (dark shaded circle) are quickly attracted to a slow 1D manifold that passes near the primed-like state (light shaded circle) toward the differentiated-like state (blank circle). (D and E) The 381-parameter set satisfying the multistability criteria in (B) shows specific distribution profiles for each parameter with peaks for high values (D), and significant positive correlations between the parameters a_NN and a_IN (lower panel of E) and between the parameters a_NN and Δλ (upper panel of E). Δλ is a measure of stability of the naive state (Fig. S7, B and C). To see this figure in color, go online.

The ability of the reduced model to capture the dynamical landscape confirms the notion that the subset of detailed model of slightly distinct parameterization and topologies share a common high-level network organization. The critical feature of this organization is the manner in which two positive-feedback modules are differentially controlled by signaling inputs, and are reciprocally coupled through both mutual activation and negative feedback interaction.

Discussion

This modeling study dissects the complexity of the pluripotency network to extract the core regulatory properties that underlie its naive and primed pluripotent cell decisions. Data-driven network inference approaches have proven valuable to hierarchize, clusterize, and reevaluate the functional role of many pluripotent factors (19, 20, 21, 23). This study further seeks to evaluate how the large-scale feedback and feedforward organization of the pluripotency network shapes its dynamical landscape including multistable and transitional properties. This issue requires the use of a dynamical modeling framework that is confronted, for large-scale networks, to the difficult challenge of the determination of relevant parameter regimes (28, 29). Parameter optimization and sensitivity methods were first devoted to identifying a subset of model parameters and network topologies consistent with experimental data. Bifurcation analysis and reduction methods then established some dynamical and network mechanisms underlying pluripotent decisions that are shared within this subset of models despite and beyond their structural differences. This two-step approach has proved to be very effective to identify a modular regulatory pattern within the densely interconnected pluripotency networks, and to assign a dynamic and functional role to this pattern in underlying robust and controllable transition from a naive to a primed state of pluripotency before lineage differentiation.

Feedforward and feedback topology of the pluripotency network

Computational studies have focused on diverse topological aspects of pluripotency network ranging from core circuitries, functional clusters, regulatory hubs, feedback motifs, sensitive reprogramming nodes, and concurrent topologies (13, 14, 17, 19, 20, 21, 26, 30). In this study, the emphasis is made on the functional interplay and hierarchy among a plethora of feedback loops, either positive or negative, and feedforward loops, either coherent or incoherent. In the context of cell-fate decisions, the common interplay of multiple positive feedback loops has been proposed to contribute either to robust switches using dual time mechanisms (31) or to binary fate decisions based on tristability (32, 33). In the case of the pluripotency regulatory network, the many reciprocal activatory regulations between several transcriptional factors give rise to a particularly large number of intricate positive feedback loops. Some of these loops are shown to be functionally segregated between redundant naive-stabilizing loops, consisting in the many reciprocal activatory interactions among Esrrb, Klf4, and Nanog, and the primed-stabilizing loops, involving the self- and reciprocal interactions of Oct4/Sox2 and Nanog. Such a segregation was not apparent in the network architecture, and is shown to rely in fact on how these distinct modules are differentially coupled with activatory (Stat3 and Smad2/3) and inhibitory (Erk and Gsk3) signaling pathways. First, some positive feedback loops operate in synergy with signaling pathways consistently with the acknowledged interaction between Smad2/3 and Oct4 (34) or between Stat3 and Nanog (35), which allows a sharper signal-dependent maintenance and exit of naive or primed pluripotent states toward an attracting nonpluripotent state. Second and even more important, the Erk and Gsk3/Tcf3 pathways play a pivotal role by inhibiting only the naive-specific factors Klf4 and Esrrb, respectively (36, 37), while being regulated negatively by LIF signals and positively by Oct4. This set of regulations contributes to several feedforward and feedback motifs that counterweight the strong stabilizing role of the many naive-specific positive feedback loops. In particular, coherent feedforward loops in LIF signaling pathways contribute to restricting the naive state stability to a LIF signaling context. In addition, the incoherent feedforward and negative feedback loops mediated by Oct4-dependent upregulations of the Erk/Tcf3 pathways promote naive-state destabilization toward a well-distinct primed state upon LIF removal.

Although these network design principles explain some key multistable and transitional properties in pluripotency, their implementation by a specific set of factors and regulations can nevertheless differ between models depending on prior network design assumptions. This is the case for the Oct4-dependent negative feedback and incoherent feedforward loops whose presence and role have been acknowledged to account for culture-dependent expression profile and variability in mESCs (12, 13, 14, 17, 21, 38). Yet, these models propose diverse realizations of these loops where the main inhibitory regulation either consists in the Oct4-dependent repression of Nanog (12, 16), the Oct4-dependent repression of Tcfp2l1 (20), the Nanog-dependent repression of Sall4 (21), the Tcf3-dependent repression of Oct4 (19), or the Erk-dependent inhibition of Nanog (17), to compare with the Tcf3-dependent repression of Esrrb and Erk-dependent degradation of Klf4 in this study. These discrepancies between models support the notion that the functional organization of complex regulatory networks can be reliably inferred without necessarily identifying with certainty the full set of regulatory mechanisms or factors involved.

Distinct and ambivalent roles for Oct4 and Nanog

Although Nanog and Oct4 are expressed at significant levels in both mESC and mEpiSC states (3), these two master pluripotent factors perform markedly distinct regulatory functions. Nanog is part of a large number of mutual activatory interactions with many other pluripotent factors, whereas Oct4 exerts both activatory and inhibitory influences, which are restricted to a subset of pluripotency factors and are tuned in a context-dependent manner. Besides their participation to a sophisticated feedback and feedforward network organization required for specific pluripotency decision making, these distinct regulatory roles make sense to a large number of experimental observations among which some are apparently paradoxical. The contribution of Nanog distributed into multiple positive feedback loops suggests a role in fine-tuning the level of pluripotency stability, while being dispensable for both mESC maintenance (39) and mEpiSC maintenance (40). In sharp contrast, the role of Oct4 drastically changes throughout pluripotency, from an ambivalent dose-dependent role in mESC self-renewal to a strongly supporting role in mEpiSC maintenance. The importance of an inhibitory role of Oct4 toward naive-specific factors in the model coincides with the two key assumptions that its overexpression promotes mESC differentiation while its moderate downregulation stabilizes the mESC state (41, 42), and that Oct4 is likely to upregulate Tcf3 (43) and Erk (44, 45). In contrast, the pluripotency-sustaining role of Oct4 becomes the most effective, and apparent mainly toward supporting the primed/mEpiSC state, consistent with the observation that Oct4 mediates Activin/Smad signaling as both a target (46) and a coactivator (34) of Smad2/3 transcriptional activity. Supplementing the model with regulations of the targets of Oct4 and their redistribution between mESCs and mEpiSCs (47, 48) should refine the mechanisms contributing to the dose-dependent and stage-dependent roles of Oct4.

Developmental and induced pluripotent transitions

The robust developmental progression from a naive to a primed state before differentiation has been corroborated by in vitro observations that the forward naive-to-primed transition is much more likely than the reverse primed-to-naive transition (5). In particular, the naive/mESC cells subjected to LIF removal are prone to transiently acquire a phenotype resembling primed/mEpiSC cells before differentiation, as evidenced by the transient upregulation of Fgf5 and the maintenance or reactivation of Oct4 and Nanog expression (40, 49). Without intending to match these data, optimized models are nevertheless found to exhibit a transitional trajectory through a primed-like state, which is highly robust to heterogeneities and where the primed state stability can be finely tuned by extrinsic signals. This dynamical behavior reflects the existence of a low-dimensional attracting slow manifold, which is prone to occur in a network with multiple strong and antagonistic feedback regulations and which has been proposed to contribute to the developmental canalization through successive states against extrinsic and intrinsic sources of noise (50, 51). Methods for reconstructing global potential landscapes would be valuable for a more comprehensive analysis of transition paths and rates (26, 52).

In sharp contrast, the reverse primed-to-naive transition is performed in vitro by a fastidious process that requires multiple passaging of mEpiSC in mESC signaling culture conditions (53) and whose efficiency can be increased by using 2i (54) or upregulating specific pluripotent factors such as Klf4 (55), Esrrb (56), or Stat3 (57, 58). Model simulations confirm that LIF stimulation in primed/mEpiSCs cells is often not sufficient to restore a naive/ESC state and needs to be supplemented with 2i or overexpression of naive-specific factors to optimally succeed. However, the reversion efficiency seems much lower in experiments than in simulations, which may be explained by the acknowledged role of epigenetic locks and barriers opposing the reversion toward the naive/mESC state (59). The control of pluripotency factor expression by various epigenetic mechanisms operating at the level of gene transcription (60) or of mRNA stability (61) has been proposed to contribute to the stringent temporal control of sequential and irreversible pluripotency decisions. In this respect, it is conceivable that the modular organization of the pluripotency transcriptional network would also facilitate dynamic interplay with epigenetic mechanisms to drive both flexible and robust fate decisions during development, notably by avoiding spurious states (30).

Author Contributions

B.P., C.K., and B P. designed the research and wrote the manuscript. B.P. performed the research, developed analytic tools, and analyzed the data.

Editor: Reka Albert.

Supporting Citations

References (62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95) appear in the Supporting Material.