Abstract
Investigation of folding/unfolding DNA duplexes of various size and composition by superprecise calorimetry has revised several long-held beliefs concerning the forces responsible for the formation of the double helix. It was established that: 1) the enthalpy and the entropy of duplex unfolding are temperature dependent, increasing with temperature rise and having the same heat capacity increment for CG and AT pairs; 2) the enthalpy of AT melting is greater than that of the CG pair, so the stabilizing effect of the CG pair in comparison with AT results not from its larger enthalpic contribution (as expected from its extra hydrogen bond), but from the larger entropic contribution of the AT pair that results from its ability to fix ordered water in the minor groove and release it upon duplex unfolding; 3) the translation entropy, resulting from the appearance of a new kinetic unit on duplex dissociation, determines the dependence of duplex stability on its length and its concentration (it is an order-of-magnitude smaller than predicted from the statistical mechanics of gases and is fully expressed by the stoichiometric correction term); 4) changes in duplex stability on reshuffling the sequence (the “nearest-neighbor effect”) result from the immobilized water molecules fixed by AT pairs in the minor groove; and 5) the evaluated thermodynamic components permit a quantitative expression of DNA duplex stability.
Introduction
Although more than half a century has passed since it was recognized that the DNA double helix is formed from two complementary strands and the sequence of AT and CG basepairs carries genetic information, the forces stabilizing this molecular construction are still under discussion, as are attempts to predict stabilities of DNA duplexes in practical applications.
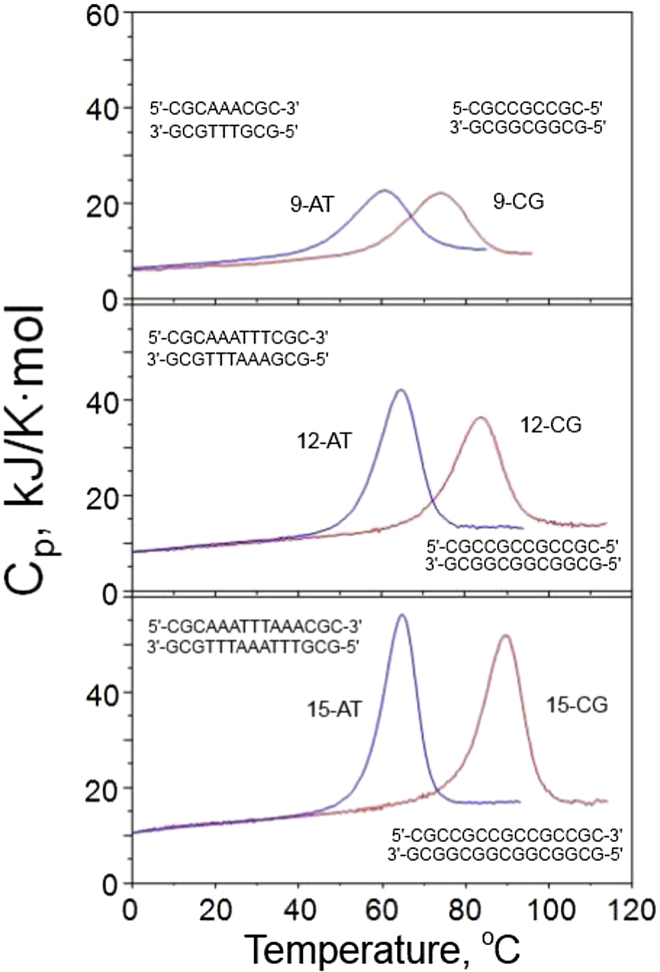
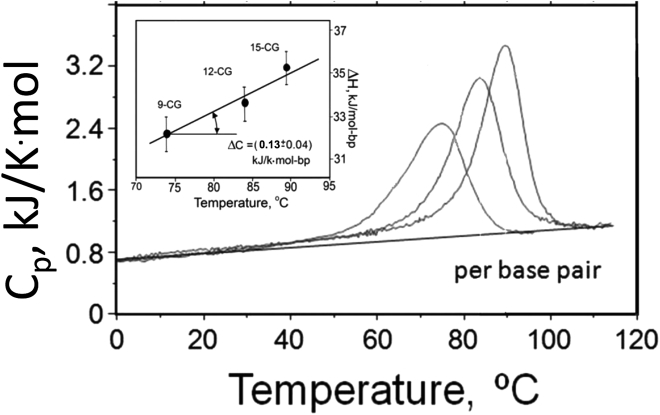
Originally it was supposed that an essential role in maintaining the double helix is played by hydrogen bonding between basepairs: two between AT and three between CG (1). This was supported by the observation that the stability of the DNA double helix rises with an increase in the CG content (2). Subsequent studies of thermal unfolding synthetic DNA duplexes using various physical methods led to the conclusion that the enthalpic and entropic contribution of CG basepairs significantly exceeds those of AT and both are temperature independent, i.e., unfolding of the duplex proceeds without any heat capacity increment (3, 4, 5, 6, 7). However, later detailed investigation of dissociation/association of DNA duplexes of various length and composition by highly precise differential scanning calorimetry and isothermal titration calorimetry (i.e., nano-DSC and nano-ITC (8)) showed that the enthalpy of dissociation/association of the DNA duplex is temperature dependent (i.e., proceeds with a heat capacity increment and, moreover, the enthalpic and entropic contribution of the AT pair significantly exceeds that of CG (9, 10)). This is illustrated in Fig. 1, showing that although the thermal stability of the duplexes containing AT basepairs are lower than CG duplexes of the same size, as expected, their heats of melting are larger. Plotting the heat capacities of CG duplexes of various length, expressed per basepair, against their melting temperatures showed that the specific heat of duplex melting increases with a rise in the melting temperature: the slope of this dependence (inset in Fig. 2) represents the heat capacity increment on duplex unfolding, which amounts to (0.13 ± 0.04) kJ/K⋅mol-bp.
Figure 1.
Comparison of the partial molar heat capacities of 9-, 12-, and 15-basepair CG duplexes (in red) and the same length duplexes having AT pairs in the central region (in blue). All measurements are at the identical duplex concentration of 283 μM in 150 mM NaCl, 5 mM Na-Phosphate, pH 7.4. Reproduced from (10). To see this figure in color, go online.
Figure 2.
The partial heat capacities of the three CG duplexes in 150 mM NaCl, 5 mM Na-phosphate, pH 7.4, calculated per mole of basepair. (Inset) Given here is the dependence of the excess enthalpy on the transition temperature, the slope of which gives the heat capacity increment (from (10)).
One might be surprised that duplex thermostability increases with the number of basepairs. If the enthalpy and entropy of duplex formation are additive functions, the duplex unfolding temperature should not depend on its size. As shown in Fig. 2, the enthalpy of unfolding the all-CG duplexes is indeed a linear function of length. It appears therefore that the entropy of duplex unfolding cannot be an additive function. Indeed, although the conformational entropy also increases linearly with the number of basepairs in the CG duplexes, the total entropy additionally includes the translation entropy term that results from the appearance of a new kinetic unit on dissociation of the strands and that does not depend on the number of bases nor on the temperature.
Translational entropy
According to the original proposal by Gurney (11), the translational entropy is expressed by the cratic term, δScratic, which is just the entropy of mixing the additional kinetic unit that appears upon complex dissociation with the solvent. This cratic entropy is assumed to be independent of the solution composition and the molecular weight of the solute. For the formation of a dimer in 1 M standard aqueous solution (55 molar water), δScratic = Rln(1/55) = −8.02 cal/K⋅mol = −33.3 J/K⋅mol. However, this cratic entropy later became the target of severe criticism by physicists as being physically ungrounded.
Assuming that the translational entropies of macromolecules in aqueous solution do not differ from those of small molecules in the gaseous phase and can be calculated by the simple Sackur-Tetrode equation, Finkelstein and Janin (12) found that the translational entropy of dissociating a typical dimeric protein at 300 K is 180–230 J/K⋅mol, depending on the molecular weight of the protein. According to these authors, the rotational entropy increase is of the same order of magnitude. Therefore, the total value of (ΔStrans + ΔSrot) amounts to 400 J/K⋅mol, with a positive sign for the dissociation of a dimer and a negative sign for its association. Very similar values for the entropy effects of dimer dissociation were obtained by Tidor and Karplus (13) using the statistical-thermodynamic approach of Chandler and Pratt (14). According to these authors, dimerization of insulin should result in a decrease of the translational entropy by 180 J/K⋅mol and a decrease of the rotational entropy by 200 J/K⋅mol, but this should be accompanied by an increase of the vibrational entropy by 110 J/K⋅mol; thus, the overall change in the external entropy (i.e., the entropy not associated with changes in conformation or hydration) upon dimerization of insulin should amount to ΔStrans = 270 J/K⋅mol. Translation entropy values in the range from 300 to 400 J/K⋅mol have been widely used by many authors in the thermodynamic analysis of forming protein/protein and protein/DNA complexes (see e.g., (15, 16, 17, 18)). However, early calorimetric studies of unfolding an S-S cross-linked and non-cross-linked dimeric globular protein and also an α-helical coiled-coil in aqueous solution showed that the translation entropy appears much lower than suggested by the statistical mechanics of gases (19, 20). The question is then: what is the translation entropy of DNA duplex dissociation? Without knowing its magnitude, it is not possible to properly predict the stabilities of DNA duplexes.
Materials and Methods
See the Supporting Material for Materials and Methods.
Results and Discussion
The entropy of DNA duplex dissociation
Consider two cases: the 15- and 9-basepair CG duplexes (seen in Figs. 1 and 2) unfold cooperatively at temperatures 362.7 and 347.2 K, with enthalpies of 408 and 223 kJ/mol (see Table 1 of (10)). Thus, the total entropies of their unfolding at their transition temperatures are
| (1) |
and
| (2) |
Extrapolating these entropies to the standard temperature of 25°C (using ΔCp = 0.13 kJ/K⋅mol-bp; (10)) and expressing the total entropy as the sum of the conformational and translational components, we have
| (3) |
| (4) |
Bearing in mind that both experiments were carried out at the same duplex concentration, i.e., the translational entropies are the same for both cases and assuming the conformational entropies are additive like the enthalpies, subtracting one from the other and dividing by the difference in the number of basepairs, we obtain
| (5) |
With an accurate value of the conformational entropy of a CG pair in hand, the translational entropy is best evaluated by analyzing the dependence of duplex thermostability (the melting temperature, Tt) on the number of basepairs. Bearing in mind that the heat capacity increment on duplex dissociation, ΔCp, does not depend on temperature (10), the transition temperature can be expressed by the straightforward equation
| (6) |
The magnitudes of the total enthalpy and entropy of the CG pair at 25°C are 26.5 kJ/mol-bp and 64.0 J/K⋅mol-bp, respectively, as given in Table 3 of (10). In Eq. 6, these are corrected to Tt using ΔCp = 0.13 kJ/K⋅mol-bp.
From Eq. 6, we have for ΔStrans
| (7) |
The derived values of ΔStrans are very sensitive to the magnitude of the conformational entropy, , which comes from calorimetrical measurements carrying significant error: Table 1 therefore shows ΔStrans calculated for the three all-CG duplexes using several values of the conformational entropy close to 46.5 J/K⋅mol-bp. However, the translational entropy should not depend on the number of basepairs in the duplexes, nor on the conformational entropy of the bases: a requirement realized for the considered three CG duplexes at a conformational entropy value of 44.6 J/K⋅mol-bp—and for which the translational entropy is calculated to be ΔStrans = (73.2 ± 0.5) J/K⋅mol. This analysis therefore permits optimization of both the conformational entropy of a CG pair and also gives the translational entropy for dissociation of the duplexes under these conditions.
Table 1.
Using the 9-, 12-, and 15-CG Basepair DNA Duplex Data To Calculate Translational Entropies, ΔStrans, for Variable Magnitudes of the Conformational Entropy of a CG Pair, ΔSconf, at 25°C Lying within the Experimental Error of 46.5 ± 3.0 J/K⋅mol-bp
| J/K⋅mol-bp | 9-CG |
12-CG |
15-CG |
|---|---|---|---|
| ΔStrans J/K⋅mol | ΔStrans J/K⋅mol | ΔStrans J/K⋅mol | |
| 44.0 | 78.4 | 80.5 | 82.3 |
| 44.5a | 73.9a | 74.5a | 74.8a |
| 44.7a | 72.1a | 72.1a | 71.8a |
| 45.0 | 69.4 | 68.5 | 67.3 |
| 45.3 | 66.7 | 64.9 | 62.8 |
| 45.5 | 64.9 | 62.5 | 59.8 |
| 45.8 | 62.2 | 58.9 | 55.3 |
| 46.0 | 60.4 | 56.5 | 52.3 |
| 46.3 | 57.6 | 52.9 | 47.8 |
| 46.5 | 55.9 | 50.5 | 31.4 |
Closest fit to a constant value of ΔStrans.
It is notable that the translational entropy thus obtained for separation of the DNA strands is at least five times smaller than that derived by statistical mechanics for the dissociation of dimeric macromolecules in the gas phase (12, 13, 14, 15, 16) and also differs from the cratic entropy value proposed by Gurney (11). However, it is essentially identical to the stoichiometric correction term used when considering the entropy of heterodimer dissociation:
| (8) |
where [No] = No/Nst is the dimensionless initial concentration of the complex and R = 8.31 J/K⋅mol is the universal gas constant (8). At the DNA concentration of 283 μM used in many of our experiments, this correction term amounts to 73.7 J/K⋅mol, a magnitude corresponding accurately to the above calorimetrically determined value of the translational entropy ΔStrans = (73.2 ± 0.5) J/K⋅mol. It thus appears that the translation entropy is fully expressed by the stoichiometric correction term. It is important to note that the translational entropy does not include the hydration effects associated with unfolding the DNA duplex; these are included in the conformational entropy term.
Contributions of AT basepairs to duplex stabilization
The enthalpic and entropic contributions of the AT basepairs in duplexes containing AT runs—flanked by CGC/GCG triplets for thermal reinforcement and the avoidance of end-effects (see Table 2)—were estimated by first extrapolating the measured enthalpies of all the AT-containing duplexes to the standard temperature of 25°C. The enthalpy of the smallest, the 9-bp AT duplex, consisting of 6CG and 3AT basepairs (210 kJ/mol), was then subtracted from the enthalpies of each of the longer AT duplexes and the result divided by the difference in the number of their AT pairs—giving the enthalpic contribution of a single AT pair at 25°C, as seen in column 5 of Table 2. The same procedure was adopted with the entropies: subtracting the cooperative entropy of the 9-bp AT duplex from that of the longer duplexes gives the conformational entropy of an AT basepair (Table 2, last column). The most notable feature of the AT pairs is that their enthalpic, and particularly their entropic, contributions are substantially larger than those of the CG basepair (summarized in Table 3).
Table 2.
Enthalpic and Entropic Contributions of the AT Basepair to DNA Duplex Stabilization
| DNA Duplex | Tt °C | kJ/mol | kJ/mol | kJ/mol-bp | J/K⋅mol | J/K⋅mol-bp |
|---|---|---|---|---|---|---|
| 5′-CGCAAACGC-3′ | 60.4 | 251 | 210 | 621 | ||
| 3′-GCGTTTGCG-5′ | ||||||
| 5′-CGCAAAAAACGC-3′ | 63.0 | 360 | 301 | 30.3 | 884 | 87.7 |
| 3′-GCGTTTTTTGCG-5′ | ||||||
| 5′-CGCAAATTTCGC-3′ | 64.5 | 350 | 288 | 26.0 | 844 | 74.3 |
| 3′-GCGTTTAAAGCG-5′ | ||||||
| 5′-CGCTTTAAACGC-3′ | 60.8 | 327 | 271 | 20.3 | 801 | 60.0 |
| 3′-GCGAAATTTGCG-5′ | ||||||
| 5′-CGCATATATCGC-3′ | 60.3 | 326 | 271 | 20.3 | 802 | 60.3 |
| 3′-GCGTATATAGCG-5′ | ||||||
| 5′-CGCAAATTTAAACGC-3′ | 64.8 | 440 | 362 | 25.3 | 1058 | 72.8 |
| 3′-GCGTTTAAATTTGCG-5′ | ||||||
| 5′-CGCAAAAAAAAACGC-3′ | 65.1 | 443 | 365 | 25.8 | 1063 | 73.7 |
| 3′-GCGTTTTTTTTTGCG-5′ | ||||||
| Averaged | 25 ± 3 | 72 ± 10 | ||||
Results in this table were obtained by subtracting the 9-bp duplex (top row) from those of the longer six duplexes. All measurements were at a duplex concentration of 283 μM in 0.15 mM NaCl, pH 7.4. Original data was from (10). represents the total enthalpy of the cooperative transition at the dissociation temperature Tt and is its magnitude corrected to 25°C. is the enthalpy of a single AT pair at 25°C. The corresponding entropies are denoted by and .
Table 3.
Optimized Contributions of the CG and AT Basepairs to the Enthalpy, Entropy, and Heat Capacity Increment of Double Helical DNA Dissociation at 25°C
| Basepair | ΔCp kJ/K⋅mol-bp | ΔStrans J/K⋅mol | ΔHcoop kJ/mol-bp | ΔSconf J/K⋅mol-bp |
|---|---|---|---|---|
| CG | 0.13 ± 0.01 | a | 18.8 ± 0.3 | 44.7 ± 0.2 |
| AT | 25 ± 3 | 72 ± 10 |
Data from this analysis and from (10) were all obtained at a duplex concentration of 283 μM in 0.15 mM NaCl, pH 7.4.
ΔStrans (403 μM) = 70.7 J/K⋅mol; ΔStrans (337 μM) = 72.2 J/K⋅mol; ΔStrans (283 μM) = 73.7 J/K⋅mol; ΔStrans (214 μM) = 76.0 J/K⋅mol; ΔStrans (107 μM) = 81.7 J/K⋅mol; ΔStrans (87 μM) = 83.4 J/K⋅mol; and ΔStrans (40 μM) = 90.0 J/K⋅mol.
Prediction of DNA duplex stability
The conformational and translational entropies obtained, together with the enthalpies, can then be used for estimating the expected melting temperatures of the considered duplexes. For example, using Eq. 6 and the parameters specifying the contributions of the CG basepairs, one can calculate the expected melting temperatures for the duplexes consisting only of CG basepairs. The main obstacle in using this equation is that the quantity to be obtained, Tt, is also included in the right-hand side. The equation can, however, be solved by stepwise consecutive iterations. This can be done bearing in mind that melting of the DNA duplexes in 0.15 NaCl solutions takes place at temperatures between 50 and 95°C, depending on their sequence. Therefore, to a first approximation, one can take Tt1 = 75°C = 348 K, i.e., 50 K above the standard temperature. The value of Tt obtained on this assumption can then be used for a second approximation. Usually the second iteration gives a value of Tt, which is close to that experimentally observed—as seen for the 9-, 12-, and 15-CG duplexes (Table 4). As seen in Table 4, increasing the number of CG basepairs from 9 to 25 leads to the duplex melting temperature increasing by 25 K, a change entirely due to inclusion of the translational contribution in the total entropy.
Table 4.
The Melting Temperatures of Various DNA Duplexes Calculated Using the Data Given in Table 3 for CG and AT Pairs
| DNA Duplexes | Composition | References | Concentration μM | Tt °C Experiment | Tt °C Calculated |
|---|---|---|---|---|---|
| 5′-CGCCGCCGC-3′ | 9-CG | (10) | 283 | 74.0 | 73.5 |
| 3′-GCGGCGGCG-5′ | |||||
| 5′-CGCCGCCGCCGC-3′ | 12-CG | (10) | 283 | 83.6 | 83.1 |
| 3′-GCGGCGGCGGCG-5′ | |||||
| 5′-CGCCGCCGCCGCCGC-3′ | 15-CG | (10) | 283 | 89.5 | 89.3 |
| 3′-GCGGCGGCGGCGGCG-5′ | |||||
| 5′-CGCCGCCGCCGCCGCCGCCG-3′ | 20-CG | N/Aa | 283 | N/A | 94.2 |
| 3′-GCGGCGGCGGCGGCGGCGGC-5′ | |||||
| 5′-CGCCGCCGCCGCCGCCGCCGCGCGC-3′ | 25-CG | N/Aa | 283 | N/A | 98.7 |
| 3′-GCGGCGGCGGCGGCGGCGGCGCGCG-5′ | |||||
| 5′-CGCAAACGC-3′ | 6CG, 3AT | (10) | 283 | 60.4 | 60.3 |
| 3′-GCGTTTGCG-5′ | |||||
| 5′-CGCAAATTTCGC-3′ | 6CG, 6AT | (10) | 283 | 64.5 | 62.1 |
| 3′-GCGTTTAAAGCG-5′ | |||||
| 5′-CGCAAAAAACGC-3′ | 6CG, 6AT | (10) | 283 | 63.0 | 62.1 |
| 3′-GCGTTTTTTGCG-5′ | |||||
| 5′-CGCTTTAAACGC-3′ | 6CG, 6AT | (10) | 283 | 60.8 | 62.1 |
| 3′-GCGAAATTTGCG-5′ | |||||
| 5′-CGCATATATCGC-3′ | 6CG, 6AT | (10) | 283 | 60.3 | 62.1 |
| 3′-GCGTATATAGCG-5′ | |||||
| 5′-CGCAAATTTAAACGC-3′ | 6CG, 9AT | (10) | 283 | 64.8 | 63.3 |
| 3′-GCGTTTAAATTTGCG-5′ | |||||
| 5′-CGCAAAAAAAAACGC-3′ | 6CG, 9AT | (10) | 283 | 65.1 | 63.3 |
| 3′-GCGTTTTTTTTTGCG-5′ | |||||
| 5′-CGCAGAGAGAGACGC-3′ | 10CG, 5AT | N/Ab | 283 | 72.2 | 73.6 |
| 3′-GCGTCTCTCTCTGCG-5′ | |||||
| 5′-CGCACACACACACGC-3′ | 10CG, 5AT | N/Ab | 283 | 75.9 | 73.6 |
| 3′-GCGTGTGTGTGTGCG-5′ | |||||
| 5′-CGAACAATCG-3′ | 5CG, 5AT | (9) | 214 | 51.3 | 57.1 |
| 3′-GCTTGTTAGC-5′ | |||||
| 5′-CGAACAATCG-3′ | 5CG, 5AT | (9) | 107 | 49.0 | 53.8 |
| 3′-GCTTGTTAGC-5′ | |||||
| 5′-GCGAACAATCGG-3′ | 7CG, 5AT | (9) | 403 | 64.8 | 67.3 |
| 3′-CGCTTGTTAGCC-5′ | |||||
| 5′-GCGAACAATCGG-3′ | 7CG, 5AT | (9) | 87 | 60.6 | 61.5 |
| 3′-CGCTTGTTAGCC-5′ |
To determine the transition temperature of DNA duplexes containing not only CG basepairs but also AT basepairs and not necessarily at the concentration of 283 μM used in many of our experiments but at any other [No], one has to expand Eq. 6 to include AT pairs (see Table 4) and solve it by consecutive iterations using Eq. 9:
| (9) |
The enthalpy, entropy, and heat capacity increment on dissociation of AT and CG basepairs used in the calculation of melting temperatures are all given in Table 3. Calculated values of Tt for duplexes of various compositions and concentrations are compared with experimentally determined melting temperatures in Table 4.
Considering Table 4, one can see that the correspondence between the calculated and experimentally determined melting temperatures is much better for duplexes consisting only of CG basepairs, for which the deviation between the predicted and measured melting temperatures is within ±0.3 K, whereas for the duplexes containing AT basepairs, it is one order larger. Because for duplexes containing AT pairs the melting temperatures were determined using different sequences (see Table 2), it appears that the enthalpic and entropic contributions of the AT basepair are sequence dependent.
The fact that the stability of a DNA duplex depends not only on the composition of AT and CG basepairs forming the duplex, but also on their arrangement, was first noted by Tinoco et al. (21) and is usually explained by the effects of nearest-neighbor interactions. However, the nature of these nearest-neighbor interactions has so far been quite obscure. It now appears that this is an AT effect and the physical basis for this must be the unique ability of AT pairs to fix waters by binding the polar groups of A and T bases in the minor groove of DNA (10).
Author Contributions
Both P.L.P. and C.C.-R analyzed data and wrote the manuscript.
Acknowledgments
Initiation of this work was funded by National Institutes of Health (NIH) grant 105365.
Editor: Wilma Olson
Footnotes
Supporting Materials and Methods are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(17)31210-9.
Supporting Material
References
- 1.Watson J.D., Crick F.H.C. Genetical implications of the structure of deoxyribonucleic acid. Nature. 1953;171:964–967. doi: 10.1038/171964b0. [DOI] [PubMed] [Google Scholar]
- 2.Marmur J., Doty P. Determination of the base composition of deoxyribonucleic acid from its thermal denaturation temperature. J. Mol. Biol. 1962;5:109–118. doi: 10.1016/s0022-2836(62)80066-7. [DOI] [PubMed] [Google Scholar]
- 3.Breslauer K.J., Frank R., Marky L.A. Predicting DNA duplex stability from the base sequence. Proc. Natl. Acad. Sci. USA. 1986;83:3746–3750. doi: 10.1073/pnas.83.11.3746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sugimoto N., Nakano S., Honda K. Improved thermodynamic parameters and helix initiation factor to predict stability of DNA duplexes. Nucleic Acids Res. 1996;24:4501–4505. doi: 10.1093/nar/24.22.4501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.SantaLucia J., Jr. A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics. Proc. Natl. Acad. Sci. USA. 1998;95:1460–1465. doi: 10.1073/pnas.95.4.1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Holbrook J.A., Capp M.W., Record M.T., Jr. Enthalpy and heat capacity changes for formation of an oligomeric DNA duplex: interpretation in terms of coupled processes of formation and association of single-stranded helices. Biochemistry. 1999;38:8409–8422. doi: 10.1021/bi990043w. [DOI] [PubMed] [Google Scholar]
- 7.Chalikian T.V., Völker J., Breslauer K.J. A more unified picture for the thermodynamics of nucleic acid duplex melting: a characterization by calorimetric and volumetric techniques. Proc. Natl. Acad. Sci. USA. 1999;96:7853–7858. doi: 10.1073/pnas.96.14.7853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Privalov P.L. Wiley and Sons; Hoboken, NJ: 2012. Microcalorimetry of Macromolecules; pp. 59–60. [Google Scholar]
- 9.Jelesarov I., Crane-Robinson C., Privalov P.L. The energetics of HMG box interactions with DNA: thermodynamic description of the target DNA duplexes. J. Mol. Biol. 1999;294:981–995. doi: 10.1006/jmbi.1999.3284. [DOI] [PubMed] [Google Scholar]
- 10.Vaitiekunas P., Crane-Robinson C., Privalov P.L. The energetic basis of the DNA double helix: a combined microcalorimetric approach. Nucleic Acids Res. 2015;43:8577–8589. doi: 10.1093/nar/gkv812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gurney R.W. McGraw-Hill; New York, NY: 1953. Ionic Processes in Solution. [Google Scholar]
- 12.Finkelstein A.V., Janin J. The price of lost freedom: entropy of bimolecular complex formation. Protein Eng. 1989;3:1–3. doi: 10.1093/protein/3.1.1. [DOI] [PubMed] [Google Scholar]
- 13.Tidor B., Karplus M. The contribution of vibrational entropy to molecular association. The dimerization of insulin. J. Mol. Biol. 1994;238:405–414. doi: 10.1006/jmbi.1994.1300. [DOI] [PubMed] [Google Scholar]
- 14.Chandler D., Pratt L.R. Statistical mechanics of chemical equilibria and intermolecular structures of nonrigid molecules in condensed phase. J. Chem. Phys. 1976;65:2925–2940. [Google Scholar]
- 15.Janin J., Chothia C. The structure of protein-protein recognition sites. J. Biol. Chem. 1990;265:16027–16030. [PubMed] [Google Scholar]
- 16.Janin J. Elusive affinities. Proteins. 1995;21:30–39. doi: 10.1002/prot.340210105. [DOI] [PubMed] [Google Scholar]
- 17.Spolar R.S., Record M.T., Jr. Coupling of local folding to site-specific binding of proteins to DNA. Science. 1994;263:777–784. doi: 10.1126/science.8303294. [DOI] [PubMed] [Google Scholar]
- 18.Searle M.S., Williams D.H. The cost of conformational order: entropy changes in molecular associations. J. Am. Chem. Soc. 1992;114:10697–10704. [Google Scholar]
- 19.Tamura A., Privalov P.L. The entropy cost of protein association. J. Mol. Biol. 1997;273:1048–1060. doi: 10.1006/jmbi.1997.1368. [DOI] [PubMed] [Google Scholar]
- 20.Yu B.Y., Lavigne P., Privalov P.L. Contribution of translational and rotational entropy to the unfolding of dimeric coiled-coil. J. Phys. Chem. 1999;103:2270–2278. [Google Scholar]
- 21.Tinoco I., Jr., Borer P.N., Uhlenbeck O.C. Stability of ribonucleic acid double-stranded helices. J. Mol. Biol. 1974;86:843–853. doi: 10.1016/0022-2836(74)90357-x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.