Dynamic Model for Characterizing Contractile Behaviors and Mechanical Properties of a Cardiomyocyte

Abstract

Studies on the contractile dynamics of heart cells have attracted broad attention for the development of both heart disease therapies and cardiomyocyte-actuated micro-robotics. In this study, a linear dynamic model of a single cardiomyocyte cell was proposed at the subcellular scale to characterize the contractile behaviors of heart cells, with system parameters representing the mechanical properties of the subcellular components of living cardiomyocytes. The system parameters of the dynamic model were identified with the cellular beating pattern measured by a scanning ion conductance microscope. The experiments were implemented with cardiomyocytes in one control group and two experimental groups with the drugs cytochalasin-D or nocodazole, to identify the system parameters of the model based on scanning ion conductance microscope measurements, measurement of the cellular Young’s modulus with atomic force microscopy indentation, measurement of cellular contraction forces using the micro-pillar technique, and immunofluorescence staining and imaging of the cytoskeleton. The proposed mathematical model was both indirectly and qualitatively verified by the variation in cytoskeleton, beating amplitude, and contractility of cardiomyocytes among the control and the experimental groups, as well as directly and quantitatively validated by the simulation and the significant consistency of 90.5% in the comparison between the ratios of the Young’s modulus and the equivalent comprehensive cellular elasticities of cells in the experimental groups to those in the control group. Apart from mechanical properties (mass, elasticity, and viscosity) of subcellular structures, other properties of cardiomyocytes have also been studied, such as the properties of the relative action potential pattern and cellular beating frequency. This work has potential implications for research on cytobiology, drug screening, mechanisms of the heart, and cardiomyocyte-based bio-syncretic robotics.

Introduction

The heart, as the most important organ in the human blood circulation system, is the source of the power needed to pump blood through the entire body. Damage to the dynamic balance in the system caused by a diseased heart leads to a significant portion of human deaths (1). Some heart diseases that can damage the normal contraction and relaxation behavior of heart cells, even in the early stages (2), may result from differences in contractile forces and mechanical properties between healthy and diseased cells. Therefore, analyzing the contractile force, mechanical properties, and dynamic beating behavior of heart cells is of great significance for the quantitative understanding of the mechanism of heart disease and the molecular alterations that occur in diseased heart cells (3). Moreover, cardiomyocytes have been used as actuators in the development of bio-syncretic robots in recent years (4, 5, 6, 7, 8, 9) for their advantageous functional features, including spontaneous contraction, high energy conversion efficiency, and high energy density (10). Therefore, understanding the mechanical dynamics of heart cells is essential for designing, actuating, and controlling cardiomyocyte actuation-based bio-syncretic robots. Hence, research on the contractility and physical properties of living heart cells is of great interest for both biomedicine and robotics. In recent decades, scientists have studied the mechanism of heartbeat generation, the control of cardiac contraction, and the relationship between cardiac structure and function (11).

The effects of the extra- and intracellular physiological microenvironments on the contraction of heart cells have been investigated to understand the pathology of cardiomyocyte function. For example, experiments have been conduction to understand the relationship between the contractility of cardiomyocytes and the concentration of calcium ions in the sarcoplasmic cytoplasm (12, 13), and it was concluded that heart cells with a low concentration of calcium ions express less contractility than those with normal calcium ion concentration. A mathematical model was also derived to describe the coupling between excitation and contraction in cardiomyocytes (14, 15, 16, 17). The influence of the external biophysical environment, such as the organization in vivo and the substrate in vitro, was studied in research on heart contractility (18, 19, 20, 21), and the results showed that the stiffness of the extracellular physical environment, in addition to biochemical and genetic factors, can affect the phenotype and contractile properties of heart cells.

The contractility of heart cells, as a label-free biomarker for heart diseases such as heart failure and cardiac arrhythmia, has been regarded as another important factor, leading to investigations of cardiac muscle mechanics directly in single, isolated heart cells (22, 23). Single heart cells also work as the basic actuation elements of cardiomyocyte-based bio-syncretic robots, and the contractility and mechanics of single cardiomyocytes are fundamental to understanding the dynamics of bio-syncretic robots. To study the contractility and mechanical properties of single and multiple heart cells, many novel methods have been reported. The stretching method is the most direct measuring approach. This method is implemented by holding onto both ends of a cell with microclamps, beads, or hooks, and then measuring the contractility of the living beating cell (3, 24, 25). Another simple method is to use a micrometer-scale, elastic pillar array as a substrate to culture heart cells. The cells grow and extend to cover several posts and then drive the pillars to bend rhythmically with their contraction. According to the mechanics of materials, the contractility on each independent micro-pillar can be calculated to describe the local force of the beating cells (26, 27). To measure the stress induced by cell contraction, scientists have developed the flexible, thin-film measuring method (28, 29, 30, 31). In this method, living heart cells are cultured on a prefabricated elastic substrate that can be deformed rhythmically by the contraction force of the cells, and the cellular contraction stress can be calculated by measuring the deformation of the substrate film based on Stoney’s equation (32). Using this method, the stress of heart cells was found to vary between 2 and 5 kPa.

These studies in theoretical analysis, mathematical modeling, and experimental measurements have improved our understanding of the mechanism of cellular contraction and the pathology of heart disease. However, most of these achievements have focused on the cellular movement and mechanical properties of entire cells, although few have paid close attention to the dynamic characteristics of subcellular structures, which may fundamentally impact cellular function. Furthermore, most current measurement approaches may induce some effects in the cell membranes and cellular functions due to the mechanical contact force during the measurement (3), and few have adopted a noncontact measurement method to reduce the influence on cellular contraction. In this study, a linear dynamic mechanical model of a single, living beating cardiomyocyte was proposed based on subcellular structures, to study the relationship between the cellular characteristics and subcellular structures, such as the sarcomeres and cytoskeleton. The system parameters of the model representing the mechanical properties, such as the elasticity and viscosity of the corresponding subcellular structures, were identified based on the beating patterns of living cardiomyocytes measured by a scanning ion conductance microscope (SICM) in noncontact mode. Simulation of the model was carried out to study the effect of the cytoskeleton viscoelasticity on cellular beating amplitude. To validate the proposed model, the cells were divided into one control group and two experimental groups with cytochalasin-D (CD) and nocodazole (Noc) respectively, and experiments were carried out to identify the system parameters of the model based on SICM measurement, to measure the cellular Young’s modulus using atomic force microscopy (AFM) indentation and the cellular contraction forces using the micro-pillar technique, and to image the cytoskeleton with immunofluorescence staining. The equivalent comprehensive elasticity of a whole cardiomyocyte was calculated based on the identified elasticity parameters of the subcellular structures. The variation in the cytoskeleton, beating amplitude, and contractility of cardiomyocytes among the control and experimental groups indirectly and qualitatively verified the proposed model. Furthermore, the relationship between the identified elasticity of the cytoskeleton and the beating amplitude of cardiomyocytes was in line with the result obtained by the simulation, and the ratio between the comprehensive elasticity and the Young’s modulus of cells in the experimental groups to those of the cells in the control group displayed a significant consistency of 90.5%. These consistencies directly and quantitatively validated the proposed model. In addition to the mechanical properties (mass, elasticity, and viscosity) of the subcellular structures, other properties of cardiomyocytes were also studied, including the relative action potential pattern and contraction frequency, based on the proposed model. This work not only has potential implications for understanding heart functional mechanisms and heart disease, but also has potential applications in drug screening and the development of cardiomyocyte actuation-based bio-syncretic robots.

Materials and Methods

Theoretical model

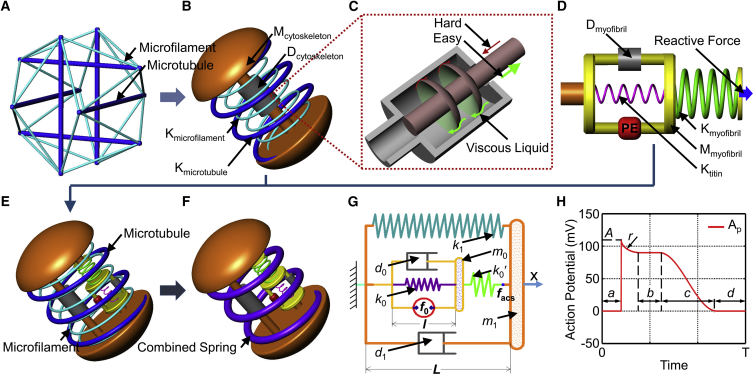
The proposed dynamic model was established based on two cellular structures of cardiomyocytes, the cytoskeleton and the active contractile structure. With respect to the cytoskeleton, cardiomyocytes are adherent cells, and their cytoskeleton arrangement displays a disorderly crisscross structure of microtubules and microfilaments, as shown in confocal fluorescence images of the cytoskeleton (Fig. S1). The line tensegrity model (Fig. 1 A) has been widely used to model the cytoskeleton structure of various adherent cells (33), such as endothelial cells (34) and cardiomyocytes (35); therefore, it was used to develop the mechanical model of cytoskeleton of a cardiomyocyte in this study. However, the regular tensegrity model was not directly adopted, and some modifications were made so that the complicated dynamic beating behaviors of cardiomyocytes were taken into account. Inspired by the tensegrity model, the proposed mechanical model (Fig. 1 B) of the cytoskeleton of a cardiomyocyte contains a thick spring (K_microtubule, with a parameter k_microtubule) and a thin spring (K_actin, with a parameter k_actin) describing the elasticity properties of the microtubules and the microfilaments of the cytoskeleton, respectively (Fig. 7 A; Fig. S1), which are inspired by the thick lines (microtubule) and the thin lines (microfilament) in the tensegrity model. In addition, a mass point (M_cytoskeleton, with a parameter m₁) was adopted to provide the inertia force of the beating cell. According to the Newtonian liquid drop model (36), when a cell flows into a micropipette, the liquid-like cytoplasm appears viscid. A damper (D_cytoskeleton, with a parameter of d₁) was added into the cytoskeleton to describe the resistance against deformation of the cell (Fig. 1 B). According to the modified muscle model by Zahalak et al. (37) the viscosity of the cells changes with the movement state; thus, the damper in this work was defined to have a variable damping coefficient during cell beating (Fig. 1 C).

Figure 1.

Mechanical model of the cytoskeleton and the active contractile structure of a cardiomyocyte. (A) Tensegrity model, where the thick and thin lines represent the microtubules and microfilaments, respectively. (B) Mechanical model of cytoskeleton structure, where the K_microtubule represents the microtubules with a spring constant of k_microtubule, and K_actin represents the microfilaments with a spring constant of k_actin, M_cytoskeleton provides the inertial force induced by variable motion with a parameter of m₁, and D_cytoskeleton provides the resistance against the deformation velocity of the cell with a damping coefficient of d₁. (C) Schematic diagram of the damper with a variable damping coefficient. (D) Mechanical model of sarcomeres (myofibril) as the active contractile structure of a cardiomyocyte: D_myofibril provides the resistance during sarcomere contraction with a damping coefficient of d₀; K_titin provides the static passive tension of the cell with a spring constant of k₀; M_myofibril describes the equivalent mass of the myofibrils with a parameter of m₀; PE is the power element of the cardiomyocyte; K_myofibril can transmit the contraction force from the sarcomere to the cytomembrane, and its spring constant is k₀′; the reactive force is the resistance of the cytoskeleton. (E) Mechanical model of a cardiomyocyte. (F) Simplified mechanical model of a cardiomyocyte. (G) Two-dimensional mechanical model of a cardiomyocyte: k₁ is the parameter of the integrated spring constant including the microtubule, microfilaments, and substrate-induced elasticity; l is the length of the sarcomere with an original value (relaxed phase) of l₀; L is the length of the cell with an original value (relaxed phase) of L₀; f_acs is the force of the active contractile structure of the cardiomyocyte. (H) Schematic model of internal relative action potential triggering the cell to regularly contract, where A, a, b, c, d, and r are the parameters to define the relative action potential pattern and will be identified based on the cellular beating patterns measured with SICM. To see this figure in color, go online.

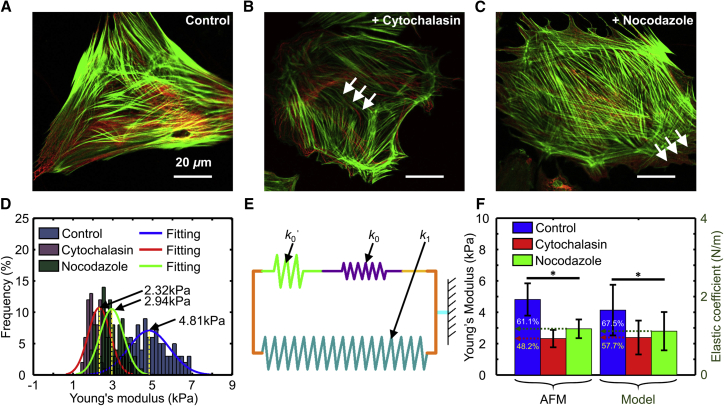
Figure 7.

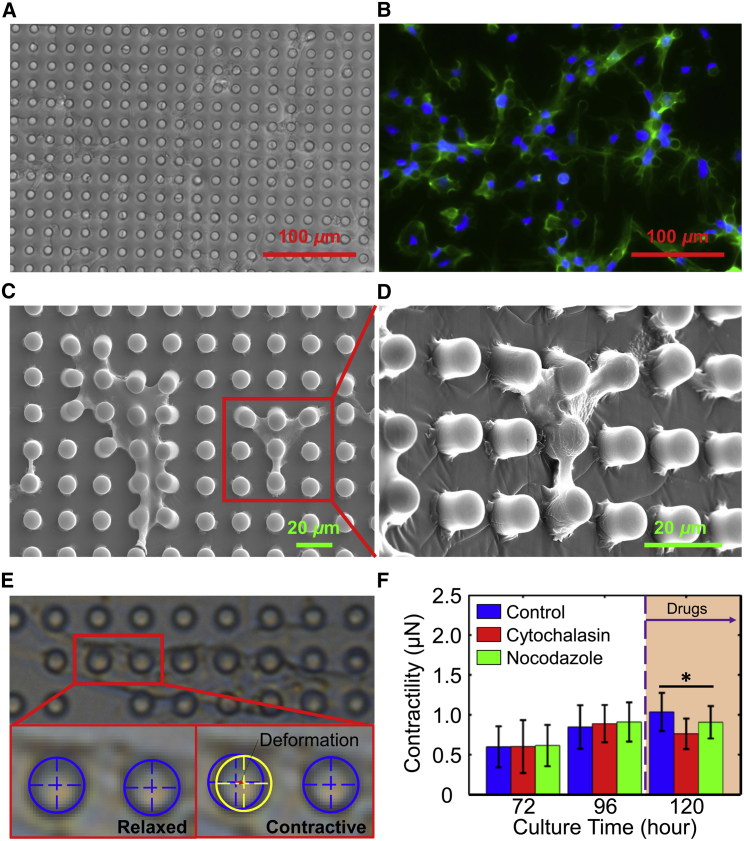
Fluorescence images of cells in (A) the control group, (B) the experimental group treated with CD for 12 h, and (C) the experimental group treated with Noc for 12 h. The arrows in (B) indicate the microfilaments and the arrows in (C) indicate the microtubules. The green areas are microfilaments stained with Actin-Tracker Green, and the red areas are microtubules stained with Tubulin-Tracker Red. The scale bar represents 20 μm. (D) Comparison of statistical histograms of the Young's modulus of the cells in the experimental and control groups, measured by AFM. (E) Schematic diagram of an integrated spring from three springs in the mechanical model. (F) Comparison of the Young’s modulus and the elastic coefficient of the cells in the three groups measured by AFM and the proposed model. Significant differences were assessed at ^∗p < 0.05. To see this figure in color, go online.

The cellular contractility depends on the active contractile structure, which contains clusters of myofibrils made up of a series of sarcomeres. The sarcomeres are composed of overlapping thick and thin filaments and provide the contraction force of the cell through filament displacement, powered by cross-bridge switching by consuming ATP (38). The Hill model is a basic macroscopic model that mimics the relationship between energetic events and the intrinsic mechanical elements of skeletal muscles (39); many modified Hill-type models have been proposed to analyze the characteristics of living muscles, such as the energetic-viscoelastic model (40) and the bi-directional Hill-type muscle model (41). However, few of them focus on the mechanism of a single beating cardiomyocyte at the subcellular scale. In this article, a mass-spring-damper mechanical system was proposed to model the active contractile structure (myofibril) of a cardiomyocyte (Fig. 1 D). The actuation force (f₀) of the power element (PE) of the active contractile structure is influenced by various factors, such as the action potential and the concentration of free calcium in the cell (14, 15, 16, 17). Cardiomyocytes are under a passive force (or tension), which is an important factor because it determines the cellular shortening property (42). This passive tension is primarily governed by the sarcomeric protein titin, which acts as a mechanical spring (43). Therefore, a titin spring (K_titin, with a parameter of k₀) in parallel with the PE was used in the model, to act as the titin to resist passive stretching from the substrate. Because f₀ is generated by the relative motion between the overlapping thick and thin filaments, a variable damping element (D_myofibril, with a parameter of d₀) was used to provide resistance to the moving myofibrils (44). The elasticity of a myofibril consisting of a myosin globular portion, a lever domain, a long tail, and actin (45) was described by a myofibril spring (K_myofibril, with a parameter of k₀′). The equivalent mass of the myofibrils was replaced by a mass point (M_myofibril, with a parameter of m₀) in the middle of the active contractile structure.

By combining the cytoskeleton model and the active contractile structure model proposed above, a complete mechanical model of a cardiomyocyte was demonstrated, as shown in Fig. 1 E. Because cardiomyocytes can grow adhering to a substrate, the stiffness will have an effect on the contractile behavior of the cardiomyocyte, as described in a previous article (46). Therefore, the influence of the substrate was described by a spring with the spring constant k_substrate in parallel with the cytoskeleton springs. According to Hooke's law, the springs in the cytoskeleton (K_microtubule and K_actin in Fig. 1 B) and the substrate influence can be combined into one spring (K₁) with an equivalent spring constant of k₁ (Fig. 1, F and G), as shown in Eq. 1:

$$k_{\text{microtubule}}+k_{\text{actin}}+k_{\text{substrate}}=k_1,$$ (1)

where k_microtubule and k_actin are the spring constants of the microtubule (K_microtubule) and the action network (K_actin) of the cytoskeleton, respectively; k_substrate is the substrate-induced spring constant; and k₁ is the equivalent synthesis spring constant of the simplified mechanical model.

In the tetanic contraction state, repeated excitement produces an additional activation before the relaxation of the contractive cell (47); thus, the inertial force of the mass and the damping force of viscidity can be ignored in the kinetic equilibrium. Then, the relationship between the force of PE and the cellular length change (static state) can be described by the following equations.

The force of the active contractile structure can be described as

$$f_{\text{acs}}=\left[\left(l-l_0\right)-\left(L-L_0\right)\right]\times k_0^{\prime }$$ (2)

where l₀ is the original length of the myofibril, and L₀ is the cellular original length.

The equilibrium equation of the active contractile structure is

$$f_0-\left(l-l_0\right)\times k_0-\left[\left(l-l_0\right)-\left(L-L_0\right)\right]\times k_0^{\prime }=0,$$ (3)

where f₀ is the force of PE.

The equilibrium equation of the cell is

$$f_{\text{acs}}-\left(L-L_0\right)\times k_1=0.$$ (4)

The intermediate variables are defined as

$$\overline{l}=l-l_0;\overline{L}=L-L_0.$$ (5)

Then, the static relationship between f₀ and the change of L is established by combining Eqs. 2, 3, 4, and 5, and can be expressed as

$$\overline{L}=f_0\times \frac{k_0^{\prime }}{k_0^{\prime }\times k_0+k_0^{\prime }\times k_3+k_0\times k_1}.$$ (6)

If a cardiomyocyte beats at a relatively low frequency (less than 3 Hz normally), the cell can obviously display a normal dynamic beating pattern including contracting and relaxing phases, and otherwise the cell behaves with a tetanic contraction pattern. Therefore, dynamic forces, including the viscous resistances of the cytoplasm and filaments and the inertial forces of the myofibril and cytoskeleton, cannot be omitted. For the dynamic movement of the system, the mechanical process is described using a series of general differential equations. The active force generated by the active contractile structure is written as Eq. 2.

The equilibrium equation of the active contractile structure can be described as

$$-f_{\text{acs}}+f_0-d_0\times \frac{\text{d}\overline{l}}{\text{d}t}-k_0\times \overline{l}-\frac{{\text{d}}^2\overline{l}}{\text{d}{t}^2}\times m_0=0,$$ (7)

where d₀ is a variable damping coefficient, which changes with the sarcomere contraction state and can be described as

$$d_0=\{\begin{array}{c}{d}_{00},\left(\frac{\text{d}\overline{l}}{\text{d}t}\ge 0\right)\\ d_{01},\left(\frac{\text{d}\overline{l}}{\text{d}t}<0\right)\end{array}.$$ (8)

The equilibrium equation of the cell is

$$f_{\text{acs}}-k_1\times \left(L-L_0\right)-d_1\frac{\text{d}L}{\text{d}t}-\frac{{\text{d}}^{2}L}{\text{d}{t}^2}\times m_1=0,$$ (9)

where d₁ is a variable damping coefficient that changes with the cell beating state and can be expressed as

$$d_1=\{\begin{array}{c}{d}_{10},\left(\frac{\text{d}\overline{L}}{\text{d}t}\ge 0\right)\\ d_{11},\left(\frac{\text{d}\overline{L}}{\text{d}t}<0\right)\end{array}.$$ (10)

Because of the complexity of the biology, an approximate assumption is established that f₀ linearly depends on the relative cellular action potential (A_p), which is obtained through translation of the real action potential of cardiomyocytes, by setting the minimum potential as 0 V (Fig. 1 H). There have been many studies on the coupling between cardiac muscle contraction and A_p (14, 15, 16, 17) that can be adopted to support the approximation. Therefore, the f₀ of the myofibril is defined as Eq. 11. According to the action potential in contractile cells (48, 49, 50, 51), and for the purpose of easy calculation, the parameter of peak value A in the model of the assumptive A_p is set to be 110 mV, and the conversion factor α in Eq. 11 is 0.01.

$$f_0=\alpha \times A_{\text{p}}.$$ (11)

Then, the dynamic relationship between f₀ and cellular deformation is established by combining Eq. 7, 8, 9, 10, and 11:

$$Y=\left\{\begin{array}{c}\overline{l}\\ \overline{L}\\ \frac{d\overline{l}}{dt}\\ \frac{d\overline{L}}{dt}\end{array}\right\},\dot{Y}=\left[\begin{array}{cccc}0& 0& 1& 0\\ 0& 0& 0& 1\\ -\frac{k_0^{\prime }+k_0}{m_0}& \frac{k_0^{\prime }}{m_0}& -\frac{d_0}{m_0}& 0\\ \frac{k_0^{\prime }}{m_1}& -\frac{k_0^{\prime }+k_1}{m_1}& 0& -\frac{d_1}{m_1}\end{array}\right]Y+\left[\begin{array}{c}0\\ 0\\ \frac{\alpha }{m_0}\\ 0\end{array}\right]A_{\text{p}}.$$ (12)

Cell culture and reagents

The complete growth medium consisted of Dulbecco's Modified Eagle Medium: Nutrient Mixture F-12 (1:1) (Gibco BRL, Gaithersburg, MD), 10% fetal bovine serum (Gibco BRL), 100 U mL⁻¹ penicillin, and 0.17 mM streptomycin (Gibco BRL). The cardiomyocytes were obtained from 1- to 3-day-old Sprague-Dawley rats (purchased from Liaoning ChangSheng Biology Co., Ltd.). Briefly, the hearts were extracted from the rats and immediately placed in ice-cold Hank’s balanced salt solution (HBSS) (HyClone, Logan, UT). Then, the ventricles were minced into 1 mm³ pieces with sterile small scissors in ice-cold HBSS and gently digested in 0.05% trypsin (HyClone) for 1 h at 4°C on a shaker. The tissue was transferred to fresh complete growth medium to inhibit the trypsin digestion, warmed in a water bath at 37°C for 5 min, and rinsed twice in HBSS. The tissue was then digested in warm 0.1% (w/v) type II collagenase (Sigma Aldrich, St. Louis, MO) in HBSS on a rocker for 45 min at 37°C. The tissues were triturated to mechanically dissociate the cells, and passed through a 75 μm cell strainer to filter out undigested connective tissues. The cells were centrifuged at 150 × g for 5 min to remove the supernatant with trypsin and type II collagenase, and were resuspended in fresh warm complete growth medium. Then, the cells were preplated twice for 30 min each to purify the cardiomyocytes, which needed more time to adhere than did cardiac fibrocytes. The cells were counted and seeded onto the micro-pillar chips and target petri dishes at different concentrations, and were then cultured for 48 h at 37°C and 5% carbon dioxide before changing the medium for fresh normal complete growth medium. To validate the theoretical model, four experiments were carried out: confocal fluorescence imaging of the cytoskeleton, measurement of Young’s modulus by AFM, determination of beating patterns by SICM, and measurement of the cellular contraction force with micro-pillars. Cells in each experiment were divided into one control group and two experimental groups treated with the drugs CD and Noc. The drugs can influence only the mechanical properties of the cellular structure, but hardly the f₀ of the sarcomeres. This is because drugs can depolymerize, preventing microfilaments and microtubules from aggregating further, and thereby breaking the dynamic balance of the cytoskeleton (52, 53, 54). However, the drugs would hardly influence sarcomere contractility, because the actin in the myofibril has a stable structure without aggregation and depolymerization dynamic balance. In this work, for Young’s modulus measurement, beating pattern acquisition, and confocal fluorescence imaging of the cardiomyocyte cytoskeleton, after culturing for 72 h, the medium was changed to fresh normal complete growth medium in the control group, and to functional complete growth medium containing 0.98 μM CD or 0.66 μM Noc (medium-containing drugs are termed functional medium in this article) in each of the experimental groups, respectively. However, for the measurement of cellular contraction force, the normal medium was changed for fresh normal complete growth medium in the control group, and for functional medium in the experimental group, after 108 h of culture.

Immunofluorescence staining

To mark the microfilaments and microtubules in the cells, Actin-Tracker Green (Beyotime Biotechnology, Jiangsu, China) and Tubulin-Tracker Red (Beyotime Biotechnology) were used, and the process was as follows: 1) the culture medium was removed from the dish, and the cells were washed three times with phosphate-buffered saline (PBS) (HyClone), each for 5 min; 2) the cells were fixed with Immunol Staining Fix Solution (Beyotime Biotechnology) for 10 min; 3) the cells were then washed three times with Immunol Staining Wash Buffer (Beyotime Biotechnology), each for 5 min; 4) the cells were covered with Actin-Tracker Green solution 1/50 attenuated with Immnol Fluorence Staining Secondary Antibody Dilution Buffer (Beyotime Biotechnology), with a volume one fifth that of the primary complete growth medium; 5) the cells were incubated in staining solution and avoiding light for 1 h; 6) the staining solution was removed, and the cells were washed three times with Immunol Staining Wash Buffer, each for 5 min; 7) the cells were covered in Tubulin-Tracker Red solution 1/250 attenuated with Immnol Fluorence Staining Secondary Antibody Dilution Buffer, the volume of the solution was one fifth of primary complete growth medium; 8) the cells were incubated in staining solution in the absence of light for 1 h; 9) the staining solution was removed, and the cells were washed three times with Immunol Staining Wash Buffer, each for 5 min; and 10) the sample cells were covered with PBS and imaged using a commercial laser scanning confocal microscope (Nikon C2 Plus, Tokyo, Japan).

Acquisition and processing of the cellular beating data with SICM

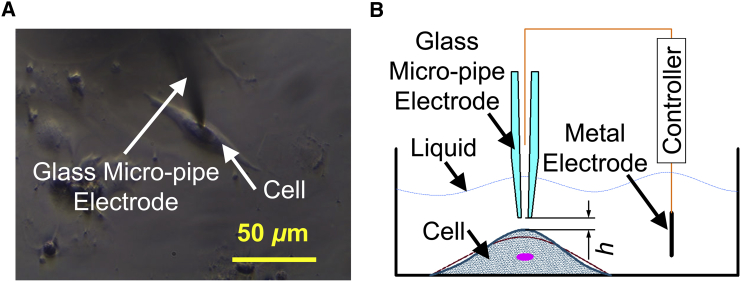
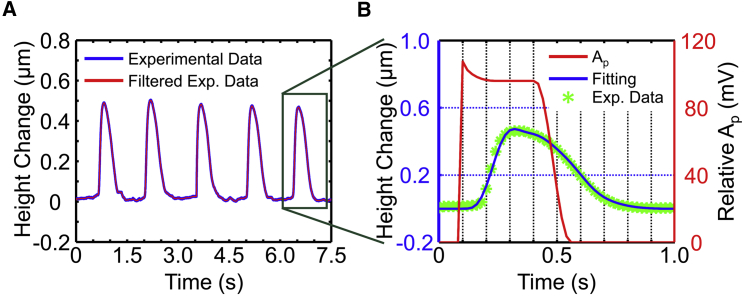
To decrease the effect of uncertainties occurring in SICM measurement such as temperature drift, a novel (to our knowledge) noncontact phase modulation mode developed in our laboratory (55) was adopted to acquire the beating patterns of cardiomyocytes growing on the bottom of the petri dish. To decrease the effect of the shape variability of cells on the cellular beating pattern and therefore on the parameters of the model, single cells with similar shapes were selected to identify parameters based on pattern measurements using SICM. As shown in Fig. 2 A, the glass micro-pipe electrode was located on the beating cardiomyocyte and maintained a micro distance h from the cytomembrane (Fig. 2 B) by a controller that can control the glass micro-pipe electrode to move with a cellular beating motion in the vertical direction, which can describe the contraction of the living cell (56) by maintaining a changing current within 2% error. Twenty cells from each group were selected for the measurement of beating patterns, and five waves were obtained for each cell. The experimental data recorded from the beating cells were filtered to remove noise through an available median filtering function, medfilt, of MATLAB with a “window” modulus of 100 according to the size of the data.

Figure 2.

Acquiring beating data of a single beating cardiomyocyte by SICM. (A) Brightfield diagram of a single beating cell and the glass micro-pipe electrode. (B) Schematic diagram of acquiring data by SICM. To see this figure in color, go online.

Measurement of the cellular stiffness with AFM

The AFM experiments were conducted using a Bioscope Catalyst AFM (Bruker, Santa Barbara, CA) that was set on an inverted fluorescence microscope. The probe was an MLCT-type (Bruker), and a cantilever with a nominal spring constant of 0.01 N/m was used. The process of obtaining force curves with the AFM was as follows: 1) the AFM tip was controlled to enter the liquid in a petri dish containing living cells growing on the bottom, 2) force curves were obtained on the bare area of the dish substrate to calibrate the deflection sensitivity of the cantilever, 3) a thermal tuning method was used to calibrate the spring constant of the cantilever, and 4) the AFM tip was moved to a single cardiomyocyte to obtain force curves on the central area of the cell. Ten cells were randomly selected from each group to obtain the force curves, and 10 force curves were collected at different points on a cell at the same loading rate (3 μm/s). Subsequently, the cellular Young’s modulus was calculated based on the Hertz model with the force curves (57, 58, 59, 60).

Measurement of the cellular contractility with micro-pillars

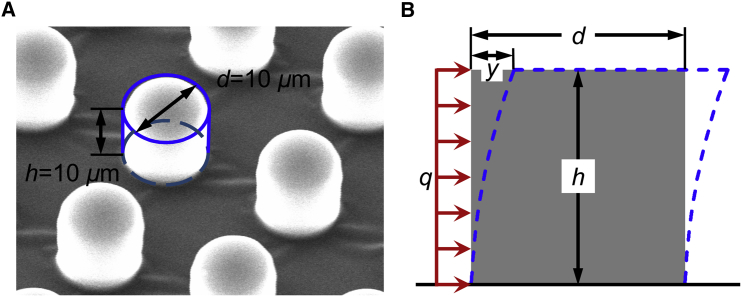
In this work, arrays of micro-pillar chips made of polydimethyl siloxane (PDMS) were adopted. These arrays were pulled by the cellular contractility for calculating the contraction force according to the material mechanics. PDMS micro-pillars were fabricated by casting PDMS from silicon wafers with patterned SU-8 structures using traditional lithography. The Young’s modulus of the PDMS micro-pillars used in this experiment was defined as 750 kPa, and the Poisson’s ratio was 0.49, as described in our previous report (27). Each micro-pillar was 10 μm in diameter and 10 μm in height, and the center-to-center spacing between pillars was 20 μm (Fig. 3 A). The micro-pillar chip was washed with 75% alcohol three times and then washed using PBS (HyClone) twice for 5 min. Thereafter, the chips were transferred into 35 mm petri dishes with 0.24 μM laminin solution for 4 h, and air-dried in a sterile manner. To study the effect of the drugs CD and Noc on the cellular contraction force, cardiomyocytes from the same batch of neonatal rats were divided into three groups (one control group, and two experimental groups with CD and Noc) at the same cellular concentration (2000 cells/mm²). The contraction forces of the cells in the control group were measured after culturing for 72, 96, and 120 h in the normal medium. For the experimental groups, cellular contraction forces were first measured after 72 and 96 h of culture in normal medium, and subsequently measured after exchanging normal medium for the corresponding functional medium for 12 h (for a total culture time of 120 h). For each of the groups, 10 pillars were randomly selected to measure pillar deformation, and 10 contraction-relaxation periods for each pillar were recorded to calculate the cellular contraction force. Based on the consideration that the living cells grow and contract around micro-pillars (Fig. 8 D), the cellular force actuating on the micro-pillar is a uniformly distributed load (Fig. 3 B), and can be described as

$$q=\frac{8yEI}{h^4},$$ (13)

where E is the Young’s modulus of the PDMS, and I is the inertia moment of the cylinder, which can be defined as

$$I=\frac{\pi d^4}{64}.$$ (14)

According to Eqs. 13 and 14, cellular contractility can be calculated as

$$F=\frac{yE\pi d^4}{8h^3}.$$ (15)

Figure 3.

Micro-pillars for cellular contractility measurement. (A) Scanning electron microscope (SEM) image of micro-pillars made of PDMS, by commercial SEM (Zeiss EVO MA). (B) Schematic diagram for the calculation of the cellular contractility. q is the uniformly distributed load of the cellular force on a micro-pillar; y is the deformation of the micro-pillar pulled by beating cells; d and h are the diameter and height of each micro-pillar, respectively. The red arrows describe the cellular force. The blue dotted line describes the deformation of the micro-pillar.To see this figure in color, go online.

Figure 8.

Measurement of the contractilities of the cells in the experimental and control groups. (A) Image of cells growing on a chip with arrays of micro-pillars that are 10 μm high and 10 μm in diameter. (B) Fluorescence image of cells stained with Actin-Tracker Green and DAPI. (C) Scanning electron microscope (SEM) image of cells growing on a chip with arrays of micro-pillars that are 10 μm in high and 10 μm in diameter. (D) SEM image, enlarged and tilted 45°, of the cells growing on chips. (E) Measurement of the deformation of the top of the micro-pillar for the calculation of the contractility of the beating cells. (F) Contractilities of cells at different culture times and in different medium. ^∗ indicates a significant difference between the control and experimental groups, p < 0.05. To see this figure in color, go online.

Statistical data analysis

In this work, to statistically study the mechanical properties of cells in the control and experimental groups, hypothesis testing (two-sample t-test) has been used. Differences were assessed as being significant at p < 0.05. The error bars in the figures represent the SD.

Results

Simulation of the theoretical model

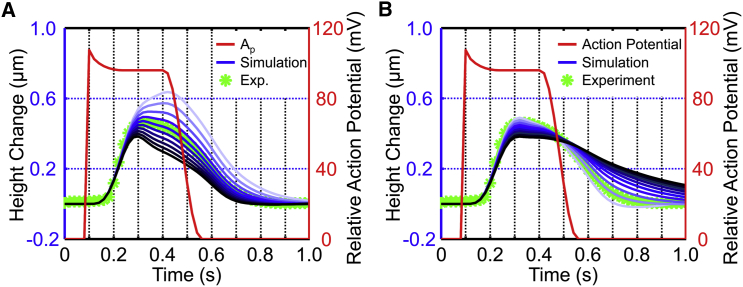
Elasticity and viscidity are the two main mechanical properties of cells; therefore, the relationship between cellular beating properties and the values of cellular viscoelasticity, arranged around the corresponding identified parameters (k₁ = 1.6 and d₁ = 0.02, measured as described in Parameter Identification and Characterization of Beating Cells with SICM in this article), have been simulated based on the proposed mathematical model. Under the same stimulation action potential, the cellular beating amplitude decreases (from 0.6 to 0.4) with increasing cellular elasticity (k₁ is from 0.8 to 2.6) (Fig. 4 A). In contrast, the beating amplitude decreases slightly (from 0.5 to 0.4) with increasing cellular viscidity (d₁ is from 0.01 to 0.1) (Fig. 4 B).

Figure 4.

Simulation of the cellular beating movement with increasing cellular viscoelasticity. (A) Simulation of the cellular beating movement with increasing cellular elasticity, where a darker blue line represents greater elasticity. (B) Simulation of the cellular beating movement with increasing cellular viscidity, where a darker blue line represents greater viscosity. To see this figure in color, go online.

Parameter identification and characterization of beating cells with SICM

Fig. 5 A is the beating pattern of a randomly selected living cardiomyocyte measured by SICM with the phase modulation mode. As shown in Fig. 5 B, based on the median-filtered beating pattern (blue curve) of the living cardiomyocyte, the parameters of the proposed mechanical model for the cell and the assumptive stimulation power (red curve) were identified with the proposed model.

Figure 5.

Identification of the cellular mechanical parameters. (A) Beating pattern of a randomly selected, living cardiomyocyte obtained by SICM. (B) Result of identification parameters of the theoretical model based on the median-filtered beating pattern of the cardiomyocyte. To see this figure in color, go online.

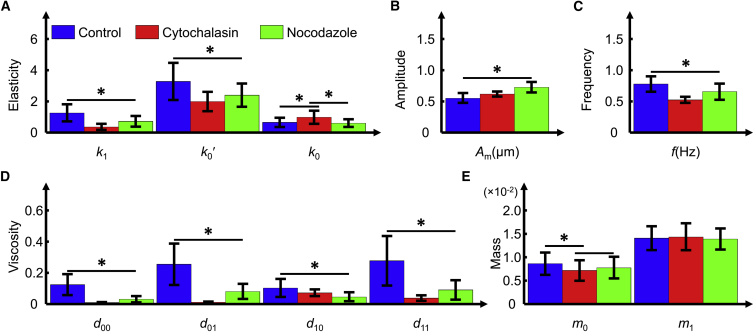
Twenty cardiomyocytes from each group were randomly selected for the measurement of beating patterns using SICM, and to identify the parameters of the proposed model after 84 h of culture. The SICM measurement results showed that the beating amplitude (A_m) of the cells in the experimental groups was higher than that of the control group cells. Moreover, the beating frequency (f) of the cells in the experimental group was slower than that of the control group cells. Based on the measurement results, the parameters of the model were identified: the parameters k₁, k₀′, d₀, d₁, and m₀ of the cells in the experimental groups were smaller than those of the control group. However, the parameters m₁ and actuation force during time (r + b + c) of the cells in the three groups were similar. The statistical results of the identified parameters based on 20 cells in each group are shown in Fig. 6. For an intuitive demonstration of the system parameters of individual cells identified with the proposed model based on measured beating patterns, important mechanical characteristic parameters of five cells randomly selected from each group are listed in Tables S1–S3.

Figure 6.

Comparison of the identification parameters of cells from the control and experimental groups using the proposed model based on beating data acquired by SICM. (A) Elasticity parameters in the model. (B) Beating amplitude of the cardiomyocytes. (C) Beating frequency of the cardiomyocytes. (D) Viscosity parameters in the model. (E) Mass parameters in the model. ^∗ indicates a significant difference between the control and experimental groups, p < 0.05. To see this figure in color, go online.

Immunofluorescence staining of cytoskeleton

To study the effect of CD and Noc on the cytoskeleton of cardiomyocytes, microfilaments and microtubules were labeled after 84 h of culture. The cells in the experimental groups were observed to have weaker cytoskeletons than the cells in the control group (Fig. 7, A–C; Fig. S2). Moreover, the microfilament intensity of the cells treated with CD was lower than that seen in the cells in the control group (arrows in Fig. 7 B; Fig. S2), and the microtubule intensity in cells treated with Noc was lower than that in the cells in the control group (arrows in Fig. 7 C; Fig. S2). These observations mean that the cells in the control group had stronger cytoskeletons than those in the experimental groups. Moreover, as shown in Figs. 7, A–C and S2, CD affected not only the microfilaments but also the microtubules of cardiomyocytes, whereas Noc mainly affects the microtubules and hardly influences the microfilaments, particularly when the cells were cultured for 48 h with the respective drugs. This observation implied that the cells treated with Noc had stronger cytoskeletons than those treated with CD.

Measurement of the mechanical properties of living cells with AFM

To quantitatively validate the proposed model by comparing the measurement results of cellular mechanical parameters obtained through the model with those obtained by the traditional method, the Young’s modulus of the cells in the three groups were obtained using the AFM indentation technique according to the available indentation depth conditions (400 nm < indentation depth < 1/10 of the cellular thickness) (61, 62). From the Gaussian fitting (Fig. 7 D), we can see that the mean Young’s modulus of cells cultured with CD and Noc for 12 h were 2.32 and 2.94 kPa, respectively, which were much lower than that of the cells in the control group (4.81 kPa). The ratios of the Young’s modulus of the cells in the experimental groups (with CD and Noc) to that of the cells in the control group were 48.2 and 61.1%, respectively (Fig. 7 F).

The equivalent comprehensive cellular elasticity can be synthesized approximately with the elasticity parameters (k₁, k₀, and k₀′) of subcellular components, identified based on the proposed model according to Hooke’s law (Fig. 7 E), as the equation

$$k_2=k_1+\left(\frac{k_0{k}_0^{\prime }}{k_0+k_0^{\prime }}\right),$$ (16)

where k₂ is the calculation integrated elasticity, which was regarded as the approximate cellular elasticity.

The ratios of the comprehensive cellular elasticity (obtained with the proposed model) of the cells in the experimental groups (with CD and Noc) to that of the cells in the control group were 57.7 and 67.5%, respectively (Fig. 7 F). On comparing the ratios of the comprehensive cellular elasticity of the cells in the control group to that of the cells in the experimental groups obtained using the proposed model with those of the Young’s modulus obtained using AFM, the maximal difference was found to be 9.5%.

Measurement of the cellular contractility of living cardiomyocytes

The cellular contractilities of the cells in the three groups were measured with an array of micro-pillar chips according to the method mentioned above. The cells were grown on the chip containing micro-pillars that were 10 μm in height and 10 μm in diameter (Fig. 8, A and B). Most of the cells cultured in medium for 10 h were able to beat synchronously, and bent the PDMS micro-pillars rhythmically (Fig. 8 C). The deformation of the tops of micro-pillars was measured using a MATLAB procedure written by us (see Supporting Material) to record reference positions on the micro-pillars in continuous frames of a video that recorded the bending movement of the pillars (Fig. 8 E), and the contraction force of a cell could then be calculated based on the deformation, according to Eq. 15. It was shown that the contraction forces of the cells in the control group increased (0.60, 0.85, and 1.04 μN) with respect to the culturing time (72, 96, and 120 h). The cellular contraction forces of cells in the experimental groups also increased with culturing time, before the normal media were replaced with the functional media (0.60 and 0.89 μN for the cells in the experimental group with CD, and 0.61 and 0.91 μN for the cells in the experimental group with Noc), and were not significantly different from that of the cells in the control group at each measurement time point (at 72 and 96 h of culture) (Fig. 8 F), indicating that the cells in the control and experimental groups were statistically the same. However, at 120 h of culture (with drug treatment for 12 h), the contraction forces of the cells in the experimental groups were smaller than those in the control group (0.76 μN for the cells with CD, 0.91 μN for the cells with Noc, and 1.04 μN for the cells in control group). This result demonstrated that treatment with CD and Noc can weaken the cellular force acting on the micro-pillars.

Discussion

To study the relationship between cellular characteristics and subcellular structures, in this work, a linear dynamic mechanical model of a single beating cardiomyocyte has been proposed based on subcellular structures. The mechanical properties of cardiomyocytes can be described by the system parameters, which can be identified by the cellular beating patterns measured by SICM based on the proposed model. To validate the model, a series of necessary simulations and experiments, including measurement of the cellular beating pattern by SICM, of the cytoskeleton by immunofluorescence, of cellular stiffness by AFM, and of cellular contractility by micro-pillars, have been implemented.

The result obtained based on the proposed model is consistent with the theoretical simulation result that cells with lower k₁ and d₁ would show greater A_m. The experimental results are also well in line with a previous report of myocardial contraction performance under the effect of CD (63).

The Young’s modulus of cardiomyocytes obtained by AFM showed that the cells in the control group (4.81 kPa) are stiffer than those treated with CD (2.32 kPa) and with Noc (2.94 kPa). This result is in line with previous reports (64, 65, 66, 67, 68). Moreover, this result is consistent with that obtained by SICM based on the proposed model that the elasticity of the cells in the control group is higher than those treated with CD and Noc, and that the elasticity of the cells with CD is even smaller than those with Noc (Fig. 7 F). The maximal difference in the ratios of the elasticity of cells in the experimental groups to that of the cells in control group obtained with the proposed model, and that measured with AFM, was 9.5%, which could be attributed to 1) the measurement error of Young’s modulus using AFM based on the Hertz model with the assumption of infinite plane and thickness, 2) the effect of the viscidity of the cells on the measurement of elasticity, and 3) the inaccuracy of the proposed theoretical model in describing real cellular physiological characters.

The measurement of cellular contraction force shows that the cells in the control group display a greater cellular contraction force (1.04 μN) than those in the experimental groups treated with CD (0.76 μN) and with Noc (0.91 μN). These contractility values are consistent with previous reports that individual and clustered mammalian cells, such as cardiac and skeletal cells, can produce even higher contractile forces between 80 nN and 3.5 μN (10). Although the cells in the experimental groups express greater beating amplitudes measured by SICM than control cells, they have a smaller cellular contractility measured by micro-pillars than the cells in the control group. The reason for this ostensible divergence can be attributed to the fact that the cytoskeletons of the cells in the experimental groups are weakened by CD and Noc, so that they provide a smaller anchorage force onto the micro-pillars than do the cells with stronger cytoskeletons in the control group. Therefore, the results of contraction force measurements of cardiomyocytes are in line with the results of cellular elasticity by AFM and SICM based on the proposed model (Fig. 7 F). This result is also consistent with the observation, through confocal immunofluorescence imaging, that cells treated with CD or Noc have weaker cytoskeletons than those in the control group (Fig. 7, A–C; Fig. S2).

In addition, the comparison between the two experimental groups with CD and Noc shows that the contraction force of the cells treated with Noc is greater than those treated with CD (Fig. 8 F), which is in line with the result that the cells treated with Noc are stiffer than cells treated with CD, as measured by AFM and SICM based on the proposed model (Fig. 7 F). This is also consistent with the observation, through confocal immunofluorescence imaging, that cells treated with Noc have stronger cytoskeletons than cells treated with CD (Fig. S2) and the underlying reason is that the drug CD can damage both microtubules and microfilaments of cells, whereas Noc may mainly damage microtubules.

The above consistencies in the variations of cytoskeleton, beating amplitude, contractility, comprehensive elasticity, and Young’s modulus of cells among the control and experimental groups validate the proposed model. Although the mechanical properties of the cells obtained using the proposed model-based method are not accurate for each structure of the living cell, they are valuable for analyzing the different mechanical properties of the subcellular structures between beating cells in different statuses for pathological analysis and drug screening. In addition, this work is useful to achieve optimal control of bio-syncretic robots, which may possess greater potential intrinsic safety and self-repair capability than traditional electromechanical robots (69), through the control of cellular performance such as beating frequency, amplitude, and contraction force, by adjusting the cells’ structural characteristics using a targeted drug such as adrenaline, CD, Noc, colchicine, and paclitaxel (Taxol). The accuracy of these findings will be improved in further work, in which the fixed peak actuation force will be described by the action potential measured via patch clamp or artificial electric pulse stimulation; furthermore, system science theory will be adopted to study cells treated as mechanical systems stimulated by external import signals, such as vibration, electricity, and drug treatment.

Conclusions

Most of the research on cardiac muscle cells concerns only the whole cellular movements and mechanical properties, and few have paid close attention to the state and properties of subcellular structures. To remedy this shortcoming, in this work, a linear dynamic mathematical model has been derived based on the corresponding mechanical model of single living beating cardiomyocytes according to the subcellular structures. One control group and two experimental groups of cells treated with the drugs CD and Noc were used for experiments for identifying the system parameters of the model based on SICM measurement, measuring the cellular Young’s modulus using AFM indentation, and cellular contraction forces using the micro-pillar technique, and imaging cytoskeleton of cells with immunofluorescence staining. Moreover, the proposed model has been validated by consistencies among the results of the theoretical simulation, cytoskeleton staining, the measurement of beating amplitude, cellular contraction force, comprehensive elasticity, and Young’s modulus of cells among the control group and the experimental groups. In addition to the mechanical properties (mass, elasticity, and viscosity) of the subcellular structures, other properties of cardiomyocytes have also been studied, such as the properties of the relative action potential pattern and the cellular beating frequency. The proposed mechanical model will be useful for the development of clinical medicine, research on cardiovascular disease and relative drug screening for identifying the specificity influence on special cellular structure proteins under different medicines, and provides the foundation for the development of bio-syncretic robots, such as controlling the bio-actuation force and frequency by adjusting the mechanical properties and contractility of actuation cells using an appropriate drug.

Author Contributions

All authors participated in discussions and the writing of the manuscript. C.Z., W.W., and L.L. conceived the research and designed the experiments. C.Z. and W.H. performed the experiments. C.Z. performed the experiment setup and data analysis. W.W., Y.W., N.X., and L.L. supervised the project.

Editor: Mark Cannell.