Essential Role of the ε Subunit for Reversible Chemo-Mechanical Coupling in F₁-ATPase

Abstract

F₁-ATPase is a rotary motor protein driven by ATP hydrolysis. Among molecular motors, F₁ exhibits unique high reversibility in chemo-mechanical coupling, synthesizing ATP from ADP and inorganic phosphate upon forcible rotor reversal. The ε subunit enhances ATP synthesis coupling efficiency to > 70% upon rotation reversal. However, the detailed mechanism has remained elusive. In this study, we performed stall-and-release experiments to elucidate how the ε subunit modulates ATP association/dissociation and hydrolysis/synthesis process kinetics and thermodynamics, key reaction steps for efficient ATP synthesis. The ε subunit significantly accelerated the rates of ATP dissociation and synthesis by two- to fivefold, whereas those of ATP binding and hydrolysis were not enhanced. Numerical analysis based on the determined kinetic parameters quantitatively reproduced previous findings of two- to fivefold coupling efficiency improvement by the ε subunit at the condition exhibiting the maximum ATP synthesis activity, a physiological role of F₁-ATPase. Furthermore, fundamentally similar results were obtained upon ε subunit C-terminal domain truncation, suggesting that the N-terminal domain is responsible for the rate enhancement.

Introduction

F_oF₁-ATP synthase (F_oF₁) is one of the most ubiquitous enzymes, which mediates energy conversion among heterogeneous energy sources; in particular, by catalyzing ATP synthesis from ADP and inorganic phosphate (P_i) by using the proton motive force (pmf) across biomembranes (1, 2, 3, 4, 5). The prominent feature of F_oF₁ is that mechanical rotation of the inner rotor complex mediates heterogeneous energy conversion with high efficiency and reversibility. F_oF₁ comprises two rotary motors (6), F_o and F₁. F_o, the membrane-embedded component of F_oF₁, is a rotary motor driven by the proton flux down the pmf (7, 8). F₁, the water-soluble element of F_oF₁, is an ATP-driven rotary motor protein, in which the rotary shaft rotates against the surrounding stator upon ATP hydrolysis. In a cell, F_o and F₁ are connected by a common rotary shaft and peripheral stalk that transmit their competing rotary torques. When the pmf is sufficiently large, F_o rotates the rotor against F₁, leading to ATP synthesis in F₁. When the pmf is diminished, F₁ hydrolyses ATP to rotate the rotor complex in reverse, enforcing F_o to pump the protons.

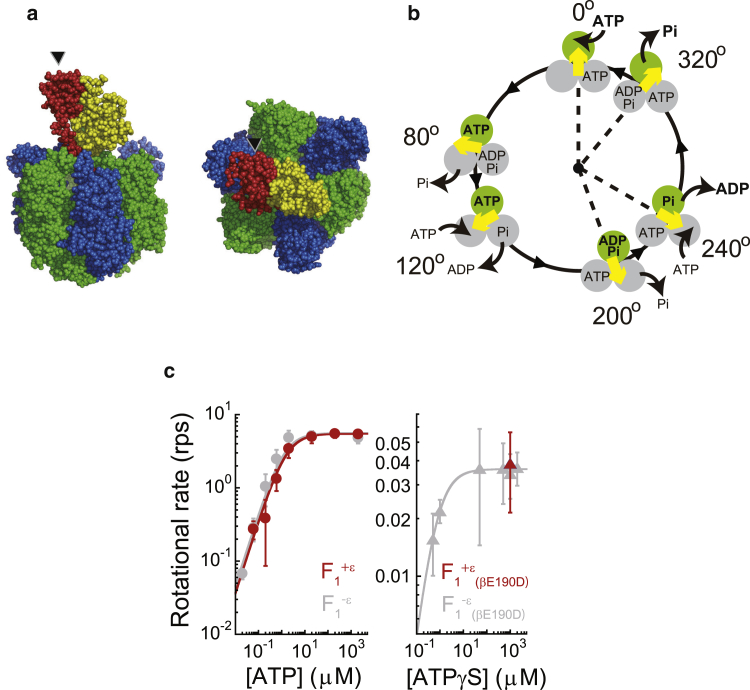
F₁, the main target of this study, is composed of α₃β₃γδε; the minimum complex as a rotary motor is the α₃β₃γ subcomplex (Fig. 1 a). Of these, three α and three β subunits form the α₃β₃ stator ring with a central cavity that accommodates the central rotary shaft γ (9, 10, 11). The catalytic reaction centers for ATP hydrolysis/synthesis reside at the αβ interfaces, mainly on the β subunit. Upon ATP hydrolysis, F₁ rotates in the anticlockwise direction (12) (when viewed from the membrane side), in which the three β subunits cooperatively change their conformation (13), generating a rotary torque of 40 pN·nm for the F₁ from thermophilic Bacillus PS3 (14) and 20–74 pN·nm for the F₁ from Escherichia coli (15, 16, 17). The energy required for the mechanical work for one γ rotation is mostly equivalent to the hydrolysis of three ATP molecules (14, 18). Therefore, F₁ is extremely efficient in converting chemical energy to mechanical work; i.e., the catalysis is tightly coupled to the mechanical work. To elucidate the fundamental rotation properties, single-molecule studies have been extensively carried out for F₁ from thermophilic Bacillus PS3 (19), which was also used in this study. Fig. 1 b shows the presently accepted scheme of chemo-mechanical coupling of F₁ from thermophilic Bacillus PS3 (20). Hydrolysis or turnover of a single ATP molecule at each catalytic site is coupled to one revolution of the γ subunit, with the angle between the three catalytic sites differing by 120° during each catalytic phase. The unitary step size of the rotation of F₁ is 120° and each step is coupled to a single turnover of ATP hydrolysis (14). The 120° step is further divided into 80 and 40° substeps (21, 22). The 80° substep is triggered by ATP binding and ADP release, each of which occurs on different β subunits. The 40° substep is triggered by ATP hydrolysis and the release of P_i, which also occurs on different β subunits. The angular positions of F₁ before the 80 and 40° substeps are referred to as the ATP-binding and catalytic angles, respectively. When the β subunit ATP-binding angle is 0° (green circle in Fig. 1 b), it executes a hydrolysis reaction after the γ subunit rotates by 200° and releases ADP and P_i at 240 and 320°, respectively (20, 23, 24, 25). When the γ subunit returns to the original angular position, the β subunit initiates the next round of catalysis by binding to a new ATP. Thus, the reaction sequences among the three β subunits are well coordinated at the resolution of elementary reaction steps, which contributes to the reversibility of the chemo-mechanical coupling on F₁.

Figure 1.

Rotary catalysis of F₁-ATPase. (a) Crystal structure of the α₃β₃γε complex, F₁^+ε, from thermophilic Bacillus PS3 (PDB: 4XD7). The α, β, γ, and ε subunits are colored in blue, green, yellow, and red, respectively. The black arrowheads indicate the ε subunit. (b) Chemo-mechanical coupling scheme of F₁ at low ATP concentration. The circles and yellow arrows represent the catalytic state of the β subunits and the angular positions of the γ subunit. Each β subunit completes one turnover of ATP hydrolysis in a turn of the γ subunit, where the three β subunits vary in their catalytic phase by 120°. Regarding the catalytic state of the top β subunit (green), ATP binding, hydrolysis, ADP release, and inorganic phosphate (P_i) release occur at 0, 200, 240, and 320°, respectively. (c) The rotational velocity (V) of F₁^+ε (red, left panel), F₁^−ε (gray, left panel), F₁^+ε_(βE190D) (red, right panel), and F₁^−ε_(βE190D) (gray, right panel) obtained using magnetic beads at various ATP or ATPγS concentrations. The curves represent Michaelis–Menten fits with V = V_max[ATP]/([ATP] + K_m), where V_max = 5.5 and 5.6 s⁻¹, K_m = 2.0 and 1.2 μM, and the corresponding ATP-binding rate, k_on = 3 × V_max/K_m; 0.8 × 10⁷ and 1.4 × 10⁷ M⁻¹·s⁻¹ for F₁^+ε and F₁^−ε, respectively. To see this figure in color, go online.

The reversible chemo-mechanical coupling is regulated by several mechanisms that differ among species (26); e.g., in bacteria, the ε subunit functions as a main regulator of the reversible coupling. The ε subunit, which is intrinsically bound to the γ subunit as a part of the rotor complex (Fig. 1 a) (10, 27), has been known as an endogenous inhibitor of ATP hydrolysis (28, 29) as well as enhancing the coupling efficiency upon ATP synthesis by almost fivefold (30, 31). The ε subunit has a two-domain structure, N-terminal β-sandwich and C-terminal dual α-helices (32). The C-terminal domain shows a conformational transition between “hairpin-folded” and “extended” states upon ATP association or dissociation, such that the hairpin-folded state is stabilized upon ATP binding (33, 34), whereas the N-terminal domain is itself stable, forming a binding interface toward the protruding part of the γ subunit. The extensive studies related to the ε subunit have shown that, in general, the C-terminal domain inhibits ATP hydrolysis by extending its conformation, whereas conversely, the hairpin-folded state does not affect the kinetic and rotation properties of F₁ in ATP hydrolysis mode; however, the correlation between ε subunit conformation and its effect on ATP synthesis has remained elusive. Moreover, the mechanism by which the ε subunit regulates the chemo-mechanical coupling at the resolution of elementary reaction steps has not been well characterized.

To evaluate kinetic properties during γ rotation, in previous studies we developed, to our knowledge, a novel method, the stall-and-release experiment, to measure the rate and equilibrium constant of the F₁ reaction at an elementary step resolution (20, 35, 36). Through this method, we arrested F₁ in the transient conformation using magnetic tweezers and observed the behavior of F₁ immediately after release from arrest. The analysis of the behavior of F₁ allowed us to simultaneously determine the rate constant for each forward and reverse step of the reaction at various rotational angles; e.g., ATP binding and release, or hydrolysis and synthesis. Thus, we could also measure the equilibrium constant of each reaction step in the catalytic cycle. Because the equilibrium constant is a measure of the difference in the free energy of the pre- and postreaction states, ΔG(θ) = −k_BT·lnK_E(θ), the torque generated during each reaction step could also be estimated from the derivative of the free energy, dΔG(θ)/dθ.

In this study, we performed the stall-and-release experiment to elucidate how the ε subunit modulates or its conformation affects the rate and equilibrium constants of hydrolysis or synthesis at an elementary step resolution to achieve the highly reversible chemo-mechanical coupling. The results revealed that the ε subunit increased the rate constants of the reverse reaction steps, and ATP release and synthesis, by two- to fivefold, which was also observed using ε without its C-terminal domain (εΔc), whereas it did not affect those of the forward reaction steps, i.e., ATP binding and hydrolysis (29, 37). These findings have important implications for the molecular mechanisms of the highly reversible chemo-mechanical coupling of F₁, as exclusively achieved among molecular motor proteins driven by ATP hydrolysis.

Materials and Methods

Rotation assay

The samples of F₁ and ε subunits were prepared as previously reported (31). To visualize the rotation of F₁, the stator subunits (α₃β₃), which carried His-tags at the N-terminus, were fixed on a glass surface modified with Ni-nitrilotriacetic acid, and a streptavidin-coated magnetic bead (ϕ = ∼0.2 μm; Seradyn, Indianapolis, IN) was attached on the top of a biotinylated rotor subunit (γ) to probe rotation. The procedures were as follows. First, the flow chamber was constructed from an uncoated top coverglass and a bottom coverglass modified with Ni-nitrilotriacetic for immobilization of His-tagged F₁. F₁ was diluted with buffer A (50 mM 3-(N-morpholino)propanesulfonic acid-KOH and 50 mM KCl, pH 7.0) to a final concentration of 200 pM and then infused into the flow chamber. After 5 min, unbound F₁ molecules were washed out with buffer A containing 10 mg/mL bovine serum albumin, then streptavidin-coated beads in buffer A were infused. After 10 min, unbound beads were washed out with buffer A. Finally, buffer A containing the indicated amount of Mg-ATP and Mg-ATPγS was infused. The rotating beads were observed under a phase-contrast microscope (IX-70 or IX-71; Olympus, Tokyo, Japan) with a 100× objective lens. The rotation assay was performed at 25 ± 3°C.

Manipulation with magnetic tweezers

The microscope stage was equipped with magnetic tweezers controlled by custom software (Celery, Library, Japan) (36). The rotary motion of the bead was imaged at 30 frames/s (FC300M; Takex America, Inc., Takex, Kyoto, Japan) for the experiments in Figs. 3, 4, and 5 or at 1000 frames/s (FASTCAM 1024PCI-SE; Photron, Tokyo, Japan) for the experiments in Fig. 1 d. Images were stored in the hard disk drive of a computer as audio video interleave files and analyzed using custom software (36).

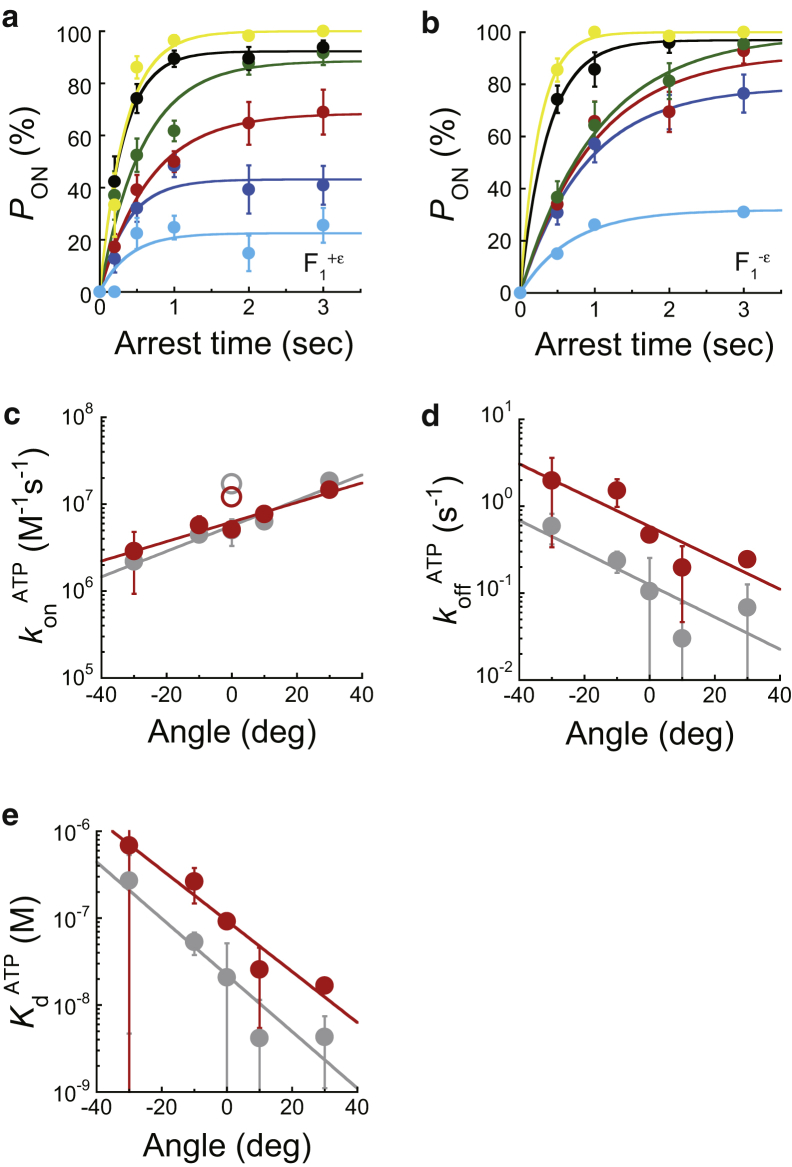
Figure 3.

Angle dependence of ATP binding and release. (a and b) Time courses of p_ON of F₁^+ε (a) and F₁^−ε (b) at 200 nM ATP after stalling at −30° (cyan), −10° (blue), 0° (red), +10° (green), +30° (black), or +50° (yellow) from the original ATP-binding angle. k_on^ATP and k_off^ATP were determined by fitting to a single exponential function: p_ON = (k_on^ATP·[ATP]/(k_on^ATP[ATP] + k_off^ATP)) × (1 − exp(−(k_on^ATP[ATP] + k_off^ATP) × t)), according to the reversible reaction scheme, F₁ + ATP ⇄ F₁∙ATP. Each data point was obtained from 29 to 80 trials using more than five molecules. The error in p_ON is given as $\sqrt{p_{\text{ON}}\left(100-p_{\text{ON}}\right)/N}$, where N is the number of trials for each stall measurement. (c–e) Angle dependence of k_on^ATP, k_off^ATP, and K_d^ATP plotted against the arrest angle. Zero degrees corresponds to the ATP-binding angle in Fig. 1b. The open symbols represent the k_on^ATP determined from freely rotating F₁. Red and gray symbols represent the values for F₁^+ε and F₁^−ε, respectively. deg, degree. To see this figure in color, go online.

Figure 4.

Angle dependence of ATPγS hydrolysis, synthesis, and Thio-Pi release. (a and b) Time courses of p_ON of F₁^+ε_(βE190D) (a) and F₁^−ε_(βE190D) (b) at 1 mM ATPγS after stalling at −50° (blue), +10° (red) or +50° (green) from the original hydrolysis waiting angle (200° in Fig. 1b). k_hyd^ATPγS, k_syn^ATPγS, K_E^ATPγS, and k_off^Thio-Pi were determined by fitting to a consecutive reaction model. Each data point was obtained from 12 to 78 trials using more than five molecules. The error in p_ON is given as $\sqrt{p_{\text{ON}}\left(100-p_{\text{ON}}\right)/N}$, where N is the number of trials for each stall measurement. (c–f) Angle dependence of k_hyd^ATPγS, k_syn^ATPγS, K_E^ATPγS, and k_off^Thio-Pi plotted against arrest angle. Zero degrees corresponds to the hydrolysis angle in Fig. 1b. Red and gray symbols represent the values for F₁^+ε_(βE190D) and F₁^−ε_(βE190D), respectively. deg, degree. To see this figure in color, go online.

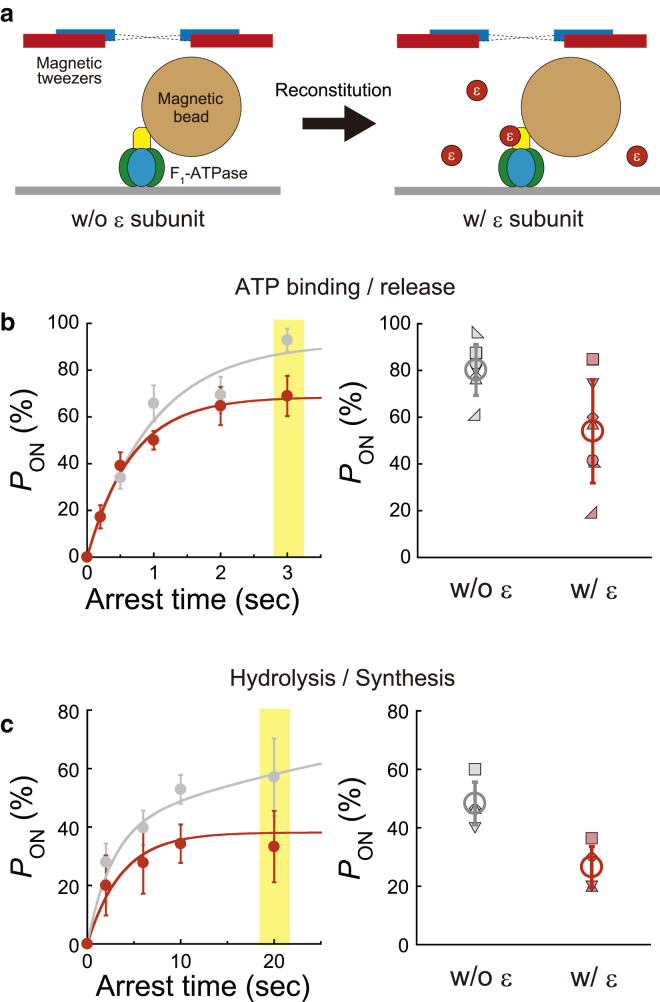
Figure 5.

Buffer exchange experiments. (a) Schematic of buffer exchange experiments: p_ON measured for a target F₁ molecule, exchanged with the buffer including 50 nM ε subunits for the reconstitution of F₁^+ε or F₁^+ε_(βE190D) complex, and then p_ON measured again. (b) Left panel shows the time course of p_ON of F₁^+ε (red) and F₁^−ε (gray) at 200 nM ATP determined from the ensemble average at ± 0°. p_ON at 3 s was highlighted using a yellow bar. Right panel shows p_ON determined by buffer exchange experiments, with a stall at ± 0° for 3 s for the same rotating molecules before (gray) and after reconstitution of the ε subunit (red). The p_ON for each molecule is displayed using different symbols. The open circles represent the averages of seven molecules. (c) Left panel shows the time course of p_ON of F₁^+ε_(βE190D) (red) and F₁^−ε_(βE190D) (gray) at 1 mM ATPγS determined from the ensemble average at ± 0°. p_ON at 20 s was highlighted using a yellow bar. Right panel shows P_ON determined by buffer exchange experiments, with a stall at ± 0° for 20 s for the same rotating molecules before (gray) and after reconstitution of the ε subunit (red). The p_ON for each molecule is displayed using different symbols. The open circles represent the averages of four molecules. w/o, without; w/, with. To see this figure in color, go online.

Results

Rotary motion of F₁ in the presence of the ε subunit

All of the subunit components for F₁ used in this study were originated from F₁ from thermophilic Bacillus PS3 (TF₁). The α₃β₃γε complex of F₁, which is referred as to F₁^+ε for simplicity, was reconstituted by mixing the ε subunit with the α₃β₃γ complex (Fig. 1 a). The α₃β₃γ complex is subsequently referred as to F₁^−ε. The binding of the ε subunit to F₁^−ε was confirmed using gel-filtration chromatography and single-molecule fluorescence analysis (Figs. S1 and S2). In the rotation assay with magnetic beads as a rotation probe (ϕ = ∼200 nm), actively rotating particles that showed continuous rotation without lapsing into ε inhibition were selectively observed in the presence of ATP in the range from 60 nM to 2 mM. The rotation rate of F₁^+ε obeyed a Michaelis–Menten curve with a maximum rotational rate, V_max, of 5.5 s⁻¹ and a Michaelis constant, K_m, of 1.5 μM (red, Fig. 1 c). The rate constant of ATP binding, k_on^ATP, was determined as 3 × V_max/K_m to be 1.1 × 10⁷ M⁻¹·s⁻¹, which is almost the same as that for F₁^−ε, 1.4 × 10⁷ M⁻¹·s⁻¹ (gray, Fig. 1 c); i.e., the ε subunit does not affect the kinetic property of freely rotating F₁.

In this study, we used the βE190D mutant, F_{1 (βE190D)}, which retards the rate constant of ATP hydrolysis by 300-fold, to facilitate the stall-and-release experiment for the hydrolysis step (21, 36). To investigate the effect of the ε subunit on this mutant, we conducted a rotation assay for F₁^+ε_(βE190D). At 1 mM ATPγS, where the rate-limiting step is the hydrolysis of ATPγS, the rotational rate of F₁^+ε_(βE190D) was 0.039 revolutions/s (Fig. 1 c), which is almost the same as that for F₁^−ε_(βE190D). Thus, it was shown that the ε subunit does not affect the kinetic property of the hydrolysis step for the freely rotating βE190D mutant.

Manipulation of single F₁ rotation

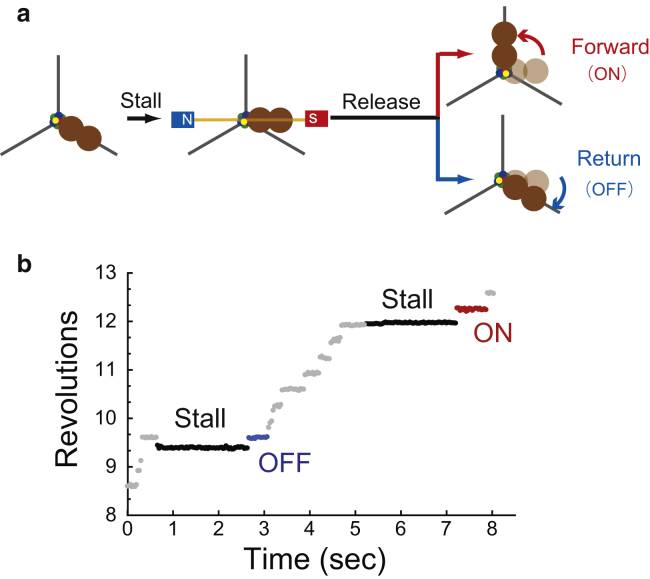
To investigate how the ε subunit affects the angle-dependent affinity change of ATP binding and equilibrium change of hydrolysis, we conducted stall-and-release experiments using F₁^+ε to measure ATP binding and F₁^+ε_(βE190D) to measure hydrolysis. Experimental procedures were essentially the same as for previous stall-and-release experiments (Fig. 2 a) (36, 38). First, we turned on the magnetic tweezers to arrest F₁ at the target angle when F₁ paused for ATP binding or hydrolysis (Fig. 2 a). At the designated time, we turned off the magnetic tweezers to release F₁ from arrest. After release, F₁ showed one of two behaviors: a forward 120° step (“ON” event) or a resumed pause at the original pause angle (“OFF” event) (Fig. 2). The ON event indicates that F₁ completed the waiting reaction and exerted a torque on the magnetic probes (red, Fig. 2); conversely, the OFF event shows that the waiting reaction had not been completed (blue, Fig. 2). F₁ was stalled at the angle range of ± 50°. Note that we defined the stall angle of “0°” as the original pause angle, which corresponds to 0 and 200° in Fig. 1 b for ATP binding and hydrolysis, and assigned the positive value to the stall angle in counterclockwise fashion. The subsequent sections discuss analysis of the probability of ON events against total trials, p_ON.

Figure 2.

Single-molecule manipulation with magnetic tweezers. (a) Schematic of manipulation procedures. When F₁ paused at the ATP-binding or hydrolysis dwell, the magnetic tweezers were turned on to stall F₁ at the target angle then turned off to release the motor after the set time. Released F₁ either steps forward (ON) or returns to the original pause angle (OFF). These behaviors indicate that the reaction under investigation has completed or not, respectively. (b) Examples of stall-and-release traces for ATP binding of F₁^+ε at 200 nM ATP. During a pause, F₁^+ε was stalled for 2 s and then released. After release, F₁^+ε stepped to the next binding angle without moving back (red), indicating that ATP had already bound to F₁^+ε before release. When stalled for 2 s, F₁^+ε rotated back to the original binding angle (blue), indicating that no ATP binding had occurred. To see this figure in color, go online.

Angle dependence of ATP binding/release

The stall-and-release experiments were conducted using F₁^+ε at 200 nM ATP where the ATP-waiting time was 0.41 s (yellow, Fig. S3 a). As shown in Fig. 3 a, p_ON increased with both the stall angle and stall time, which is similar to our previous finding of ATP binding by F₁^−ε (36). In addition, p_ON was not always 100% saturated, although it converged to a certain value within 3 s. The values of p_ON at 3 s obtained using F₁^+ε were smaller than those of F₁^−ε; e.g., 69 and 93% for ± 0° stall of F₁^+ε and F₁^−ε, respectively (red lines in Fig. 3, a and b). These observations imply that ATP binding is reversible in this time range, such that ATP release also occurs during stalling. Accordingly, the plateau level indicates the equilibrium level between ATP binding/release.

To confirm that F₁ transits the catalytic states between the ATP-waiting or ATP-bound state without lapsing into an unexpected state such as ADP or ε inhibition, we analyzed the dwell time of F₁^+ε to spontaneously conduct a 120° step after an OFF event (blue, Fig. 2 b). Here, only experiments with longer stalling times in which p_ON achieved a plateau were analyzed to avoid including data before the equilibrium. The obtained dwell time histogram showed a single exponential decay, providing the rate constant (green, Fig. S3 a). As expected, the determined rate constant corresponded to that for free rotation (yellow, Fig. S3 a). This correspondence excluded the possibility of unexpected inactivation; e.g., ε inhibition. We also plotted a histogram of the dwell time to conduct the second 120° step after the ON event (red, Fig. 2 b). The histogram was also in good agreement with that of free rotation (red, Fig. S3 a), confirming that manipulation did not alter the kinetic properties of F₁^+ε at the ATP hydrolysis condition.

By fitting time courses of p_ON based on a reversible reaction scheme, F₁ + ATP ⇄ F₁·ATP, the rate constants of ATP binding and release, k_on^ATP and k_off^ATP, were determined for each stall angle. The k_on^ATP increased exponentially with stall angle by 1.7-fold per 20° (red, Fig. 3 c), the k_off^ATP decreased exponentially by 2.2-fold per 20° (red, Fig. 3 d), and the dissociation constant of ATP, K_d^ATP, accordingly decreased 3.9-fold per 20° (red, Fig. 3 e), which was a similar trend as that of F₁^−ε (gray, Fig. 3, c–e). In contrast to the similar angle dependence, the k_off^ATP of F₁^+ε was almost fivefold larger than that of F₁^−ε, independent of the rotary angle, showing that the ε subunit enhances the rate constant of ATP release; i.e., inclines the equilibrium toward ATP release.

Angular dependence of hydrolysis/synthesis

For the wild-type F₁, the dwell time for ATP hydrolysis is only 1 ms, which is too short for stalling with magnetic tweezers. Therefore, we conducted the stall-and-release experiment using the hydrolysis reaction of the ATP analog, ATPγS, and a mutant, F₁^+ε_(βE190D), both of which retard the hydrolysis rate by 10,000-fold (21), such that F₁^+ε_(βE190D) showed a 120° stepping rotation, yielding hydrolysis-waiting pauses of 9.3 s (yellow, Fig. S3 b) (21, 36). Then, F₁^+ε_(βE190D) in the hydrolysis pause was stalled for 2–60 s with magnetic tweezers to determine p_ON. As shown previously (36), p_ON increased in two phases (Fig. 4 a); however, the slope of the second increase was more gradual than that obtained using F₁^−ε_(βE190D) (Fig. 4 b). The first increase was nearly complete within 20 s, which is consistent with the time constant of ATPγS hydrolysis. The subsequent increase was extremely slow for an effective catalytic reaction. We previously showed that this slow increase results from the release of thio-phosphate (Thio-Pi) by the β subunit that hydrolyzed the bound ATPγS (Fig. 1 b, 200° state) during stalling (36). To confirm that F₁ does not lapse into an unexpected state before Thio-Pi release, we analyzed the dwell time of F₁ to spontaneously conduct a 120° step after an OFF event. Here, experimental stalling for 20 s, in which the first increase of p_ON achieved a plateau whereas the second increase rarely occurred, was analyzed to avoid including data under a nonequilibrium state owing to Thio-Pi release. The obtained dwell time histogram showed a single exponential decay, providing the rate constant (green, Fig. S3 b). As expected, the determined rate constant corresponded to that for free rotation (yellow, Fig. S3 b). This correspondence excluded the possibility of unexpected inactivation; e.g., ADP inhibition. We also plotted a histogram of the dwell time to conduct the second 120° step after the ON event. The histogram was also in good agreement with that of free rotation (red, Fig. S3 b), confirming that manipulation did not alter the kinetic properties of F₁^+ε_(βE190D) in the hydrolysis condition.

By fitting time courses of p_ON based on a consecutive reaction model with a reversible hydrolysis step followed by irreversible Thio-Pi release at 200°, F_1(βE190D)·ATPγS ⇄ F_1(βE190D)·(ADP + Thio-Pi) → F_1(βE190D)·ADP + Thio-Pi, the rate constants of ATPγS hydrolysis, synthesis, and Thio-Pi release—k_hyd^ATPγS, k_syn^ATPγS, and k_off^Thio-Pi—were determined for each stall angle. The k_hyd^ATPγS increased exponentially with stall angle (red, Fig. 4 c), whereas the k_syn^ATPγS remained constant (red, Fig. 4 d). The equilibrium constant of hydrolysis, (k_hyd^ATPγS/k_syn^ATPγS = K_E^ATPγS) showed relatively weak angle dependence when compared with that of ATP binding K_d^ATP (red, Fig. 4 e), which was a similar trend as that of F₁^−ε_(βE190D) (gray, Fig. 4, c–e). In contrast to the similar angle dependence, the k_syn^ATPγS was almost twofold larger than that of F₁^−ε_(βE190D), independent of the rotary angle, showing that the ε subunit enhances the rate constant of ATPγS synthesis; that is, inclines the equilibrium to ATPγS synthesis. The k_off^Thio-Pi was constant around 0.01 s⁻¹; i.e., almost fourfold smaller than that of F₁^−ε_(βE190D) (Fig. 4 f), showing that the ε subunit suppresses the Thio-Pi release at around 200°.

Buffer exchange experiment

To confirm the equilibrium shift owing to the ε subunit, we measured p_ON, a barometer of the equilibrium level, before and after reconstitution of the ε subunit for F₁ molecules under observation by conducting buffer exchange experiments: we measured p_ON for a target F₁ molecule (F₁^−ε or F₁^−ε_(βE190D) complex), exchanged the buffer including 50 nM ε subunits for reconstitution of the F₁^+ε or F₁^+ε_(βE190D) complex, and then again measured p_ON (Fig. 5 a). For the ATP-binding step, we conducted the stall-and-release experiment at ± 0° for 3 s, where the ensemble averages of p_ON were 93% and 69% for F₁^−ε and F₁^+ε, respectively (left, Fig. 5 b). The buffer exchange experiment showed that all F₁ molecules exhibited decreased p_ON for ATP binding by ∼26% after reconstitution of the ε subunit (right, Fig. 5 b), which corresponds to the ensemble results (left, Fig. 5 b). In addition, we conducted the stall-and-release experiment for the hydrolysis step of F₁^−ε_(βE190D) at +10° for 20 s, where the ensemble averages of p_ON were 52 and 34% for F₁^−ε_(βE190D) and F₁^+ε_(βE190D), respectively (left, Fig. 5 c). The buffer exchange experiment showed that all F_1(βE190D) molecules exhibited decreased P_ON for hydrolysis by ∼22% after reconstitution of the ε subunit (right, Fig. 5 c), which also coincided with the ensemble results (left, Fig. 5 c). Thus, it was again confirmed that the ε subunit inclined the equilibrium toward ATP synthesis at the resolution of elementary reaction steps, which would contribute to highly efficient synthesis of ATP, a prominent feature of F₁ among molecular motor proteins.

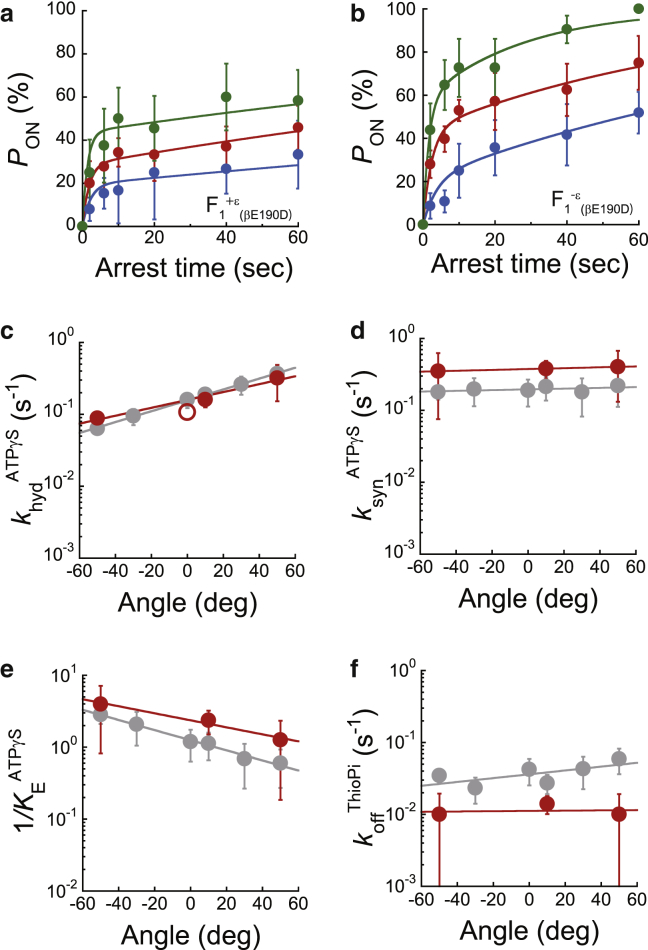
The role of individual domains on the ε subunit for rotary catalysis

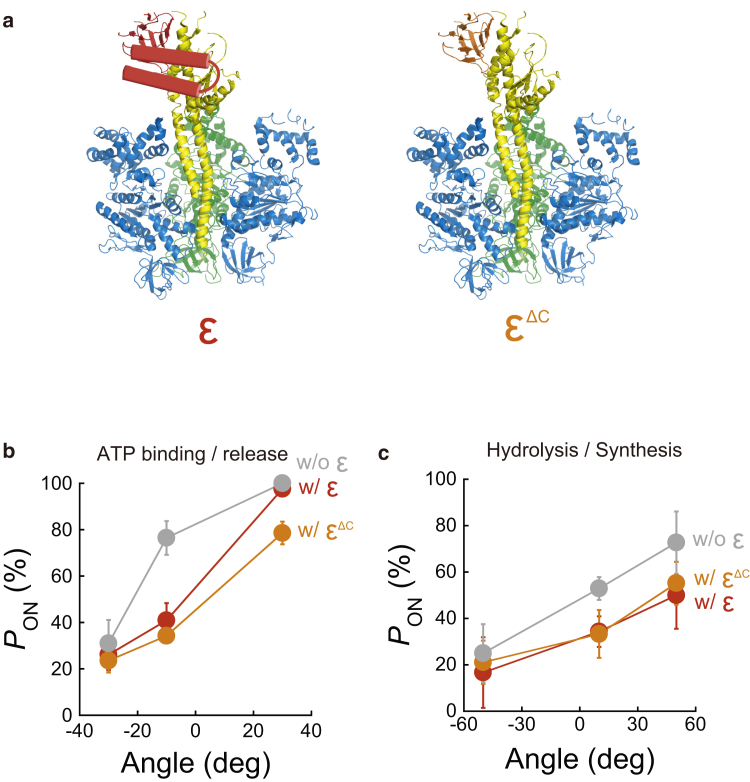
The ε subunit has a two-domain structure consisting of an N-terminal β-sandwich and C-terminal α-helices (Fig. 6 a). To understand the role of individual domains on the regulatory mechanism, we again measured p_ON using a truncated ε subunit (εΔc) that did not contain the C-terminal α-helices (orange in Fig. 6 a) (39). For the ATP-binding step, we conducted the stall-and-release experiment at ± 30° for 3 s, where the equilibrium of ATP binding achieved a plateau level as mentioned above (Fig. 3 a). The p_ON of F₁^+εΔc almost coincided with that of F₁^+ε, being smaller than F₁^−ε (Fig. 6 b). In addition, we conducted the experiment for the hydrolysis step of F₁^−ε_(βE190D) at ± 50° for 20 s, where the equilibrium of hydrolysis also achieved a plateau level (Fig. 4 a). The p_ON of F₁^+εΔc_(βE190D) also coincided with that of F₁^+ε_(βE190D) (Fig. 6 c), showing that the N-terminal β-sandwich of the ε subunit contributes to highly efficient synthesis of ATP, whereas the C-terminal α-helices do not. This result is consistent with that of a previous biochemical study using chloroplast F₁, in which the effect of the N-terminal domain of the ε subunit was found to be higher than that of the C-terminal domain (40).

Figure 6.

C-terminal domain of the ε subunit. (a) Cross section view of F₁^+ε (left) and F₁^+εΔc (right) from thermophilic Bacillus PS3 (PDB: 4XD7). The C-terminal α-helices of the ε subunit are illustrated using cylindrical diagrams. The ε subunits with (ε) or without C-terminal α-helices (ε^Δc) are colored in red and orange, respectively. (b) p_ON at 200 nM ATP for F₁^−ε (gray), F₁^+ε (red), and F₁^+εΔc (orange) were plotted against the arrest angle. (c) p_ON at 1 mM ATPγS for F₁^−ε_(βE190D) (gray), F₁^+ε_(βE190D) (red), and F₁^+εΔc_(βE190D) (orange) were plotted against the arrest angle. deg, degree; w/o, without; w/, with. To see this figure in color, go online.

Discussion

The ε subunit modulates the catalytic reaction rate of F₁ in an asymmetric manner; i.e., ATP release and the phosphoester bond formation of ATP on the catalytic site are accelerated, whereas ATP binding and the cleavage of ATP are not significantly changed. As previously reported, the major rate-limiting step of ATP synthesis is thought to be the ATP release step (41). Thus, the enhancement of ATP release by the ε subunit should improve the overall chemo-mechanical coupling efficiency of ATP synthesis. Consistent with this, it was previously reported that the coupling efficiency of ATP synthesis on F₁ during the forcible reverse rotation at 10 Hz was enhanced by almost fivefold when F₁ was reconstituted with the ε subunit (31).

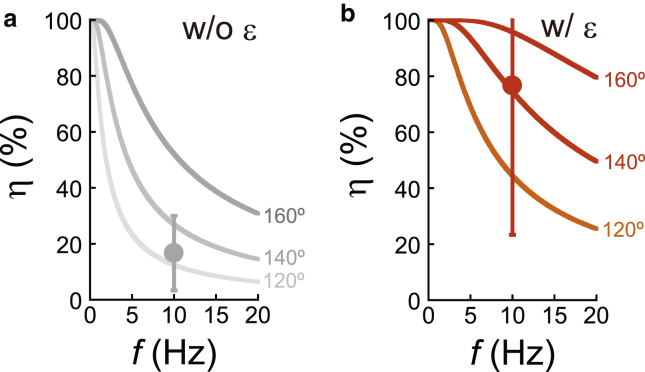
Here, we quantitatively estimated how the ε subunit enhances the probability of ATP release (η) during the forcible reverse rotation of F₁, using the determined angle dependence of k_off^ATP in the presence of the ε subunit (Fig. 7). The calculation is similar to our previous numerical analysis of the ATP-binding probability upon forcible forward rotation (42). In this calculation, we assume that F₁ has a chance to release bound ATP until γ reaches 120–160° in the clockwise direction (synthesis direction) from the ATP-binding angle. This assumption is based on the observation that the catalytic site again enhances the affinity toward ATP or ADP from −160° to −120° (200–240° in Fig. 1 b) (20, 43). Hereafter, the maximum angle displacement from the ATP-binding angle where F₁ can release ATP is expressed as θ_off. When the forcible rotation is considered as a stepwise rotation with a step size of Δθ, the probability that F₁ releases ATP at θ is expressed as p_off(θ) = 1 − exp(−k_off^ATP(θ)·Δt), where k_off^ATP(θ) is the angle dependence of k_off^ATP determined in this study; k_off^ATP(θ) = 0.12 × exp(−0.043·θ) and 0.58 × exp(−0.042·θ) for F₁^−ε and F₁^+ε, respectively (Fig. 3 d); and Δt is the step duration at f Hz rotation; Δt = Δθ/(360·f). The coupling efficiency (η) is accordingly expressed as η = $1–\text{exp}-\left(k_{\text{off}}^{\text{ATP}}\left(0°\right)\cdot \left(1-\text{exp}\left(-{\theta }_{\text{off}}\cdot \alpha \right)\right)/360\cdot \alpha \cdot f\right)$, where k_off^ATP(θ) is given as k_off^ATP(θ) = k_off^ATP(0°) × exp(−α·θ). The solid lines in Fig. 7 represent the calculated coupling efficiencies (η) for F₁^−ε and F₁^+ε at θ_off = 120, 140, and 160, which were markedly enhanced by incorporation with the ε subunit from 13–52 to 45–96% for F₁^−ε and F₁^+ε at f = 10 Hz. We previously reported that the ε subunit enhanced the net efficiency of ATP synthesis from 17 ± 13% to 77 ± 53% when the γ subunit was forcibly rotated in the clockwise direction at 10 Hz (31). Thus, the numerical estimation based on this study well explains our previous ATP synthesis experiment with the ε subunit. We further note that the maximum rate of ATP synthesis for thermophilic F_oF₁ at room temperature was biochemically determined to be ∼30 ATP molecules s⁻¹ (44), which corresponds to ∼10 Hz rotation of the γ subunit, assuming that the rotation and catalysis are tightly coupled. Our result therefore implies that the enhancement of ATP release by the ε subunit is critical for the maximum ATP synthesis activity.

Figure 7.

Chemo-mechanical coupling efficiency during ATP synthesis. (a) The coupling efficiency of forcible rotation with ATP release in the absence of the ε subunit. The gray lines represent the results of numerical calculation based on k_off^ATP(θ) = 0.12 × exp(−0.043·θ) determined for F₁^−ε in Fig. 3d at θ_off = 120° (light gray), 140° (gray), and 160° (thick gray). The gray circle represents the net coupling efficiency of F₁^−ε during ATP synthesis, as experimentally determined in the previous study (31). (b) The coupling efficiency of forcible rotation with ATP release in the presence of the ε subunit. The colored lines represent the results of numerical calculation based on k_off^ATP(θ) = 0.58 × exp(−0.042·θ) determined for F₁^+ε in Fig. 3 d at θ_off = 120° (orange), 140° (pink), and 160° (red). The red circle represents the net coupling efficiency of F₁^+ε as determined in the previous study (31). w/o, without; w/, with. To see this figure in color, go online.

This study determined the equilibrium constants of ATP binding/release and hydrolysis/synthesis as the function of the rotary angle (Figs. 3 e and 4 e). As previously reported, the slopes of the equilibrium constants reflect the magnitude of torque generated upon each reaction step, N ∝ dΔG(θ)/dθ = $\left(d/d\theta \right)$k_BT·[ln(K_E(θ))], where N represents the generated torque (38, 45). These results show that $\left(d/d\theta \right)$k_BT·[ln(K_E(θ))] for the ATP-binding or hydrolysis process is not different between F₁^−ε and F₁^+ε, whereas k_off or k_syn was enhanced in the presence of the ε subunit. This suggests that the ε subunit does not affect torque generation, which is consistent with the previous report (46). For further understanding, direct measurement of the thermodynamic efficiency of F₁^+ε using single molecule manipulation is awaited in future studies (18, 47).

The chemo-mechanical coupling of F₁ is mediated via interfaces between rotor and stator subunits (9, 48, 49, 50). It was revealed that when the rotor-stator interface is engineered and the resultant rotary potential of the rotor in the stator ring is largely affected (38, 51), the rate and equilibrium constants of catalysis are also significantly modulated (52, 53). Considering these reports, one possible molecular mechanism of the ε-assisted kinetic modulation of ATP binding and synthesis is the enhancement of rotor stiffness by the ε subunit, which presumably improves the chemo-mechanical coupling efficiency via rotor-stator interactions by the enhancement of rotary potential. Although the comparison of rotary potentials between F₁^−ε and F₁^+ε (Fig. S4) did not support this explanation, we consider that this possibility is not completely excluded as our analysis might not be sensitive enough to detect a subtle change in the stiffness or the rotary potential. We note that the apparent rotary fluctuation should include not only the rotary diffusion or the stiffness of the rotor in the stator ring, but also the rotary fluctuation of the whole F₁ molecule owing to the flexible His-tag linkers. On the other hand, chloroplast F₁ may provide some insights regarding this issue. It is known that F₁ from chloroplast or photosynthetic bacteria significantly modulates the catalytic activity of hydrolysis or synthesis upon disulphide bond formation or cleavage between two intrinsic cysteines of the γ subunit (54, 55, 56). However, because the cysteine residues are located at the distal part from the stator-ring interface, how the disulphide bond formation can affect the catalytic activity remains elusive (54).

A possible role of the C-terminal domain in the observed ε subunit-associated ATP release and synthesis rate enhancement may be considered because it is well recognized that the ε subunit C-terminal domain blocks ATP hydrolysis and resultant rotation by extending into the cleft between the γ subunit and the stator ring (27, 28). However, it should be emphasized that the ε subunit should not assume the inhibitory extended state under our experimental conditions, because we selectively investigated only the actively rotating molecules. In addition, it should be noted that the noninhibitory state of the ε subunit should be very stable within the observation time according to the previous kinetic analysis of the conformational transition of the ε subunit from TF₁ (33). Thus, the extended state of the C-terminal domain of the ε subunit is unlikely to be involved in the observed rate enhancement. Consistent with this argument, the mutant ε subunit from which the C-terminal domain was truncated exhibited similar rate constant enhancement as observed for the intact ε subunit.

F₁ frequently lapses into MgADP inhibition, a common feature of F₁-ATPases from various species. We previously proposed the following reaction scheme for ADP inhibition: TF₁ lapses into the MgADP inhibited form when Pi or Thio-Pi, which should be released at around 320° during active turnover, are occasionally released before ADP release at around 240° (57). These results showed that the ε subunit suppresses the occasional release of Thio-Pi release at around 200° by almost fourfold. This finding is suitably consistent with the previous biochemical study that the MgADP inhibition of TF₁ was suppressed by incorporation with a truncated ε subunit (εΔc) (39). The effect of the ε subunit on MgADP inhibition is different among species (58) and, therefore, single-molecule analysis for other species would help to understand the universal principle underlying the mechanism of MgADP inhibition.

In vivo, F₁ forms F_oF₁-ATP synthase and synthesizes ATP by coupling with a rotary motion driven by F_o. Recently, the rotary motion and proton translocation of the F_oF₁ complex on a lipid bilayer membrane was visualized at the single-molecule level (7, 8, 59). For further understanding of the effect of the ε subunit on catalysis at physiological conditions, verification by single-molecule measurement of the F_oF₁ complex is desirable in the future.

Author Contributions

R.W. and M.G. designed and performed experiments and analyzed data. Y. K. provided technical support. H.N. designed experiments. H.N. and R.W wrote the article.

Editor: Kazuhiro Oiwa.