Abstract
The addition of salt to protein solutions can either increase or decrease the protein solubility, and the magnitude of this effect depends on the salt used. We show that these effects can be captured using a theory that includes attractive and repulsive electrostatic interactions, nonelectrostatic protein-ion interactions, and ion-solvent interactions via an effective solvated ion radius. We find that the ion radius has significant effects on the translational entropy of the salt, which leads to salt specificity in the protein solubility. At low salt, the dominant effect comes from the entropic cost of confining ions within the aggregate, whereas at high concentrations, the salt drives a depletion attraction that favors aggregation. Our theory explains the reversal in the Hofmeister series observed in lysozyme cloud point measurements and semi-quantitatively describes the solubility of lysozyme and chymosin crystals. We present a comparison of the contributions to the free energy and give guidelines for when salting in or salting out should be expected.
Introduction
The effects of salt on protein solubility are one of the oldest problems in protein chemistry. Early experiments showed that salts can increase or decrease solubility depending on the pH, salt used, and the protein studied (1, 2, 3, 4). More than a century later, these effects are still poorly understood, yet the problem has taken on new importance with the realization that protein aggregation is a primary determinant of many neurodegenerative diseases, such as Alzheimer’s, Huntington’s, and prion diseases (5, 6, 7, 8). Considerable qualitative insight can be drawn from simple colloidal models (9, 10), but proteins have been difficult to model, because salts have many effects on the solubility. For example, the addition of salts weakens electrostatic interactions by screening charges. This means that at pH values where the protein is strongly charged, the addition of salt reduces electrostatic repulsion, decreasing the solubility (salting out). However, near the isoelectric point, the net charge is small, allowing for attractive interactions through the alignment of patches with complementary charge. In this case, the addition of salt will weaken attractive interactions, resulting in increased solubility (salting in) (3). Proteins that show salting in have nonmonotonic solubilities, with salting-out behavior returning as the salt concentration approaches 1 M. At these concentrations, electrostatic interactions are negligible, so this salting-out regime is attributed to a salt-mediated enhancement of the hydrophobic effect (11, 12).
More than a century ago, Hofmeister ranked salt ions on the basis of their effectiveness to precipitate proteins. His ranking, now known as the Hofmeister series, is for anions and for cations. The same ranking of ions has been observed in many circumstances, such as in the surface tension of electrolytes (13, 14, 15), double-layer force measurements (16, 17), the charge of globular proteins (18), and, of course, the solubility of proteins (19, 20). In recent years, several elegant theoretical studies have shown that Hofmeister effects on interfacial tension are due to differential depletion or absorption of ions to the interface. The differing affinities of ions to the interface are driven by a combination of solvophobic, polarization, image-charge, and dispersion effects (13, 21, 22, 23, 24, 25, 26, 27, 28, 29). These same effects undoubtedly play a role in protein systems as well (30), but are complicated by the heterogeneity of the protein-water interface. In addition, the Hofmeister series has been observed to reverse under some conditions that have been related to whether the pH of solution is below or above the isoelectric point (17, 31) and whether salt concentration is low or high (32, 33).
Hofmeister effects are intimately related to the solvation properties of ions. To explain this, ions have been classified as either kosmotropes, which increase solvent structure by tightly binding water, or chaotropes, which disrupt water structure (34, 35). Although experiments have shown that the perturbation to water structure does not extend past the first solvation shell (36), these effects have profound consequences on the solvophobic and polarization interactions that determine the interfacial affinity (13, 14, 23). Furthermore, simulations of a coarse-grained water model have shown that salts drive a depletion interaction between nonpolar solutes. This interaction is sensitive to the excluded volume, which in turn depends on the size of the ion solvation shell (37, 38).
In this article, we show that only three contributions are necessary to capture the important features of salt effects on protein solubility: the Coulomb energy, the translational entropy of the salt, and a nonelectrostatic contribution to the protein-ion interaction. Furthermore, salt-specific effects emerge naturally by accounting for the excluded volume of the ions in the translational entropy. The salt entropy has two effects that in many ways dominate the solubility. The first arises from the entropy of the bulk solution and gives rise to an ion-mediated depletion force. The second arises from the entropy of confining counterions within a protein aggregate. This contribution dominates the free energy of dense aggregates (39), but it has received little attention for its role in salt specificity because most previous work has focused on planar geometries or two-body interactions where confinement effects are minimal.
Materials and Methods
The model free energy includes Coulomb energy, salt entropy, protein-protein, and protein-ion interactions
Theoretical descriptions of salt effects are complicated by the disparate length scales involved. Ion-specific effects necessarily involve microscopic interactions of the ion with its environment, whereas solubility is determined by minimizing the global free energy of the solution. To bridge this gap, we construct a mesoscopic model that consists of a Poisson-Boltzmann (PB)-level treatment of the solution free energy with modifications to account for microscopic effects. This allows us to observe how microscopic perturbations affect the overall free energy.
Protein solubility is defined by the concentration, , where the chemical potentials are equal for proteins in the solution state and aggregated phase, . This condition is equivalent to
| (1) |
The first term comes from the translational entropy of proteins in the solution state. and are the salt-dependent free energies in the solution and aggregated states, respectively, and is the salt-independent protein-protein interaction in the aggregated state. This last term accounts for short range interactions like H-bonds and the hydrophobic effect. We show below that the effect of salt on hydrophobic interactions can be captured by the salt-dependent terms. These terms are given by
| (2) |
where or . Here, is the Coulomb energy of the system:
| (3) |
where E is the local dielectric and is the electrostatic potential.
The second term in Eq. 2 is the entropy of mobile salt ions. This term contributes a free energy density, , for each salt species i, where is the ion concentration in a bulk reservoir (40, 41, 42). This density is integrated over the system volume, V. For monovalent salt at a bulk concentration, , we have
| (4) |
where are the local ion concentrations. In writing Eq. 4, we have split the volume integration into regions where the ion concentration is nonzero and ion-excluded regions, where either or is zero. The integration over these excluded regions can be done trivially, resulting in the final term. The excluded volumes, and , depend on the ion size, which requires distinct values for each ion. The excluded volume is also a function of protein size and shape and protein-protein separation, resulting in a depletion attraction. Importantly, we take the ion size to be an effective parameter that includes the effects of bound water, thereby implicitly capturing solvent structuring.
The final term in Eq. 2 is the free energy of transient ion-protein binding. To model this binding, we write the partition function for binding sites on the protein surface that can either be unoccupied or bound to an ion.
| (5) |
where is the number of bound ions and μ is the ion chemical potential. The binding of ions has two energetic contributions; an electrostatic component, , that we will calculate from the electrostatic potential, and a nonelectrostatic component, . These are opposed by the translational entropy cost of removing the ion from solution, which is captured by the chemical potential , where is a reference concentration taken to be 1 M. Due to the uncertainty in the location of the binding sites, we assume that the number of bound ions is equal in the soluble and aggregated states. Therefore, does not change upon aggregation and the contribution of this term is to modify the charge on the protein.
The Coulomb energy and salt entropy terms comprise the usual PB free energy, and functional minimization of with respect to the local salt concentration yields the well-known PB equation (41, 42, 43). PB theory provides the starting point for most methods for modeling protein solubility, including the Derjaguin-Landau-Verwey-Overbeek theory of colloid stability and many subsequent refinements (18, 44, 45, 46, 47, 48). Our approach modifies PB theory to capture the key physics identified by two distinct approaches to explaining ion-specific effects. The first of these is the nonelectrostatic component to the protein-ion interaction (21), which we include via the two-state binding model in Eq. 5. Second, we include ion size and hydration effects (34, 35) through the mutual excluded volume of the proteins and ions. This has profound effects on the electro-neutrality requirement on the aggregate, but it also gives rise to a depletion attraction that emerges naturally from PB theory simply by accounting for the excluded volume in the entropy term (Eq. 4). By neglecting the microscopic details of the protein-ion interaction and ion hydration, our model is able to focus on the big-picture aspects of how these effects influence the solution free energy.
The soluble protein is modeled as a sphere with monopole and dipole charges
We approximate the protein charge distribution using a first-order spherical harmonic expansion (see Fig. 1). The resulting distribution, , is the simplest one that gives both attractive and repulsive contributions. Here, and are the monopole and dipole charge densities and R is the effective radius of the protein, which we calculate from the crystal structure using
| (6) |
where a, b, and c are the dimensions of the unit cell, is the number of proteins in the unit cell, and is the volume fraction of protein in the crystal.
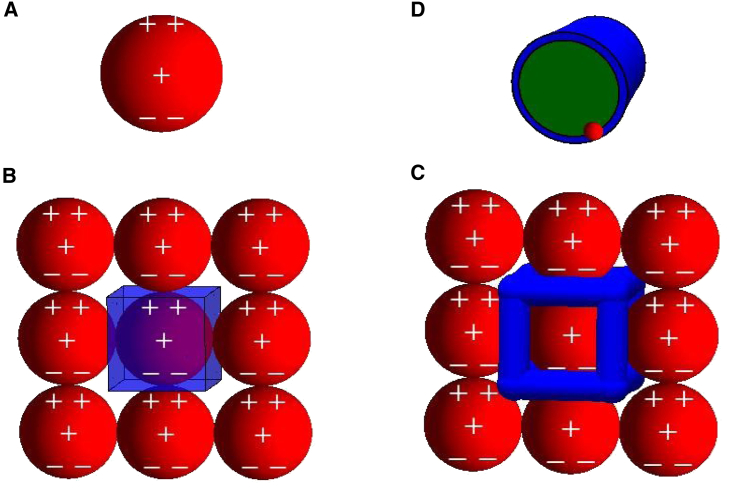
Figure 1.
Cartoon representation of the geometry used in our model. (A) The protein is modeled as a sphere embedded in an aqueous environment. The charge distribution is described by a monopole and dipole, schematically shown as charges at the sphere center and poles, respectively. (B) Each protein in the aggregate is surrounded by a Wigner cell consisting of the protein (red spheres) and surrounding water (blue). (C) We approximate the surrounding water as cylindrical channels. (D) The volume accessible to ions in the channels depends on the ionic radius. Smaller ions have a larger accessible volume (green). To see this figure in color, go online.
To solve for the electrostatic free energy, we linearize the PB equation for the region outside the protein and employ the Laplace equation for . The resulting potentials outside and inside of the sphere are
| (7) |
and
| (8) |
where is the Debye screening length. , , and are the permittivities of water, protein, and vacuum, respectively. is the net protein charge and is an effective “dipole charge” that we obtain by matching the protein dipole moment, p, to the moment of . and p are calculated from the protein crystal structure and the Henderson-Hasselbach equation using average pKa values (49). These “bare” charges will be modified to effective charges by ion binding, as described below.
To limit the number of free parameters, we consider the nonelectrostatic protein-ion interaction for anions only. Experimental and theoretical evidence shows that the interaction for anions is much stronger than that for cations (50, 51). For our two reference systems, anion binding has obvious effects; it has been directly measured in lysozyme (50) and it explains the displacement of the solubility minimum away from the calculated isoelectric point of chymosin (52). Several experiments have reported the number of anion-binding sites on lysozyme, with widely varying results: , , , and (53, 54, 55, 56). Here, we report results for the average of these values, , although the best fits to experimental solubilities are found for . For chymosin, we use based on the fact that the surface area of chymosin is roughly double the surface area of lysozyme. Using protein radii of and for lysozyme and chymosin, this corresponds to one binding site per .
The average number of bound ions is determined from the binding-site partition function (Eq. 5),
| (9) |
with
| (10) |
Here, the potential is written as a function of the monopole and dipole charges as modulated by anion binding. The dipole correction is an approximation that assumes that anions bind primarily to the positive hemisphere, where gives a median value for the potential. Solving for the number of bound ions requires a summation over protein surface potentials (Eq. 10). However, the solubility is determined by the difference of and , which can be found by evaluating Eqs. 3 and 4 with the modified charge.
The aggregate is modeled as cylindrical water channels surrounded by protein
We assume that the proteins align within the aggregate so that complementary charges are paired in the aggregate, thereby neutralizing the dipole charge. The resulting charge symmetry allows us to neglect the Coulomb energy within the protein where the electric field vanishes by symmetry (48). Thus, we require only the potential within the aqueous cavities of the aggregate. As a rough approximation, we assume that each protein is surrounded by channels with a total length of , as would be expected in a crystal with cubic packing symmetry (see Fig. 1 C). We further approximate these channels as cylinders with radius , chosen to match the solvent content of the aggregate. The cylinder geometry was chosen because previous calculations have shown an insensitivity to cavity geometry (45, 48, 57) and the cylinder provides a better representation of the cavity surface/volume ratio for excluded volume effects than does a traditional spherical Wigner cell. Since each channel is surrounded by four proteins (see Fig. 1, B and C), the solvent volume per protein is . To obtain the ion-accessible volume, we use , where is the effective radius of the ion and its solvation shell.
The dimensionless potential within a protein aggregate, , often exceeds the threshold for linearization of the PB equation. However, since the cavities are small, on the order of , the variation in the potential is small. Under these conditions, it is an excellent approximation to linearize the PB equation around a nonzero potential, (39). Linearization of the PB equation around a nonzero potential gives
| (11) |
where , , and . To eliminate numerical issues at , we model the cavity as concentric cylinders trapping ionic solvent. With the boundary conditions
| (12) |
the solution to Eq. 11 in cylindrical coordinates is
| (13) |
where K and I are modified Bessel functions, , , and the dimensionless electric field at the cylinder surface is
| (14) |
The inner cylinder radius, , is set to the small value in the numerical calculations. Note that Eq. 13 has a finite limit when . Accordingly, our calculations are insensitive to inner radius values <∼0.1 Å. A suitable reference potential, , is the average potential needed for charge neutrality,
| (15) |
where and are the accessible volumes for positive and negative ions in the cavity, respectively, and are the ion concentrations in the presence of the average potential.
Upon rearranging Eq. 1, the expression for the protein solubility is
| (16) |
where is a constant determined by fitting. We solve for the Coulomb energy and ion entropy, and hence the solubility, by numerically evaluating the integrals (Eqs. 3 and 4) using the potentials given in Eqs. 7, 8, and 13.
Crystals provide a model system with known parameters
The solubility is a sensitive function of the solvent content within the aggregate state. To facilitate the comparison of our theory with experiments, we focus on crystalline aggregates where the solvent content is readily obtained from the crystal structure. Protein and cavity radii are chosen to match the protein and solvent volumes reported in the crystal structures of lysozyme (58) and chymosin (59). Following Eq. 6, the radius of the cylindrical cavities is determined from the solvent content of the crystal according to
| (17) |
Ion excluded volumes were obtained using the University of California at San Francisco’s Chimera to compute the accessible volume for varying probe sizes in the crystal and monomer states (60).
We use published values for the solvated ionic radii: 1.50 Å for chloride, 1.50 Å for potassium, 1.25 Å for ammonium (61), and 1.67 Å for sodium (17). The parameters that require fitting are the prefactor A and , the nonelectrostatic anion-protein interaction. mg/mL and are obtained by fitting to lysozyme solubility (Fig. 2), whereas mg/mL is fit to the data in Fig. 3. Since the ion interaction is expected to be a general effect with protein surfaces, we use the same value, , obtained from lysozyme. Note that the A prefactors simply provide a vertical shift on the semi-log plots, so is the only fitting parameter that affects the shape of the calculated solubility trends.
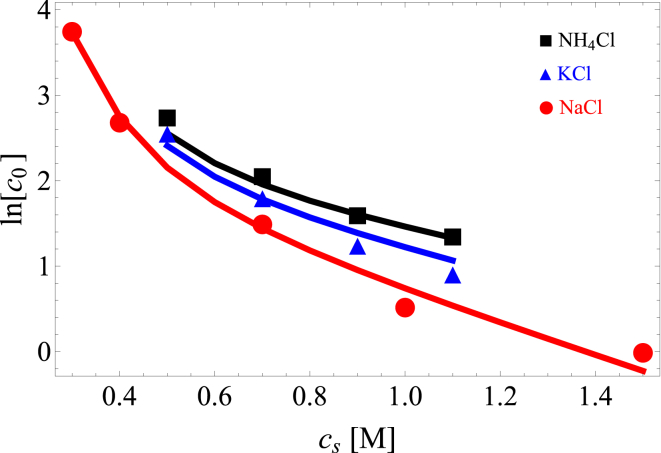
Figure 2.
Comparison of lysozyme solubility, measured in mg/mL (data points) (19), to the theoretical model (Eq. 16) (lines) as a function of salt concentration, . The salt specificity comes from the preferential exclusion of large coions from the crystal interior. R = 16.1 Å, Rc = 6 Å, , , , and . The fitted parameters are mg/mL and . No experimental error bars are given in (19). To see this figure in color, go online.
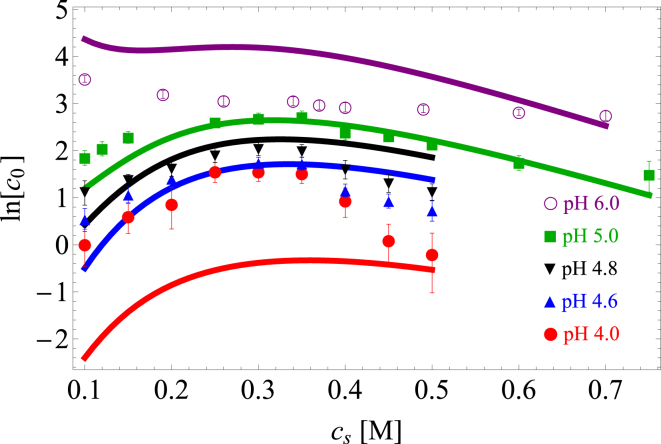
Figure 3.
Comparison of chymosin solubility, measured in mg/mL (data points) (52), to the theoretical model (Eq. 16) (lines) as a function of NaCl concentration, . The model captures the transition from pure salting out at pH 6 to nonmonotonic solubility at lower pH. The maximum deviation between theory and experiment is at pH 4.0, closest to the isoelectric point. At this pH value, the ratio has a maximum value of 11.5 at M and remains between 6.4 and 8.5 over the range cs = 0.15–0.35 M. , , , , and . The fitted parameter is mg/mL. To see this figure in color, go online.
The calculated monopole and dipole charges of chymosin are tabulated in Table 1. Since there is little variation in the dipole parameter, , we use the average value at all pH values, which is equivalent to a moment of 653 Debye (137e Å).
Table 1.
Calculated Monopole and Dipole Charges of Chymosin
| pH | Monopole Charge | Dipole Parameter |
|---|---|---|
| 4.0 | 4.77 | 17.49 |
| 4.6 | 17.47 | |
| 4.8 | 17.62 | |
| 5.0 | 17.74 | |
| 6.0 | 17.92 |
Results and Discussion
Theory captures salt specificity, salting in, and salting out
Fig. 2 compares our theory to the solubility of lysozyme at pH 4.5 (19). At this pH value, and , so the dominant effect of salt is monopole screening, resulting in salting out. The solubility is shown for three different coions. Our theory shows that the salt specificity is a result of the enhanced depletion effect along with preferential exclusion of larger ions from the aggregate cavities, which reduces the entropy penalty of recruiting neutralizing counterions. Note that hydration effects reverse the relative size rankings of and , demonstrating the importance of water-ion interactions in salt specificity (62).
Fig. 3 shows the solubility of chymosin near the isoelectric point (52) as a function of NaCl concentration. The theory captures the qualitative trends of salting in and salting out. These trends are a result of several competing terms in the free energy. In the next sections we examine these contributions individually, beginning with the electrostatic terms. Note that the maximum deviation between the experiment and theory is ∼2 kBT, or kcal/mol at pH 4.0. Although the origin of this discrepancy is not clear, we note that carboxylate residues are expected to protonate in this region, which renders the model particularly sensitive to pKa perturbations. In addition, the predicted solubility is very sensitive near the isoelectric point, where small uncertainties in the model parameters are magnified.
Electrostatic contributions are a competition between monopole versus dipole and energy versus entropy
To simplify our analysis of the contributions to the free energy, we begin by examining a version of the model in which the salt-specific features of ionic volume and ion-protein binding have been removed. This model is equivalent to a PB analysis and gives a view of the behavior expected from purely electrostatic interactions.
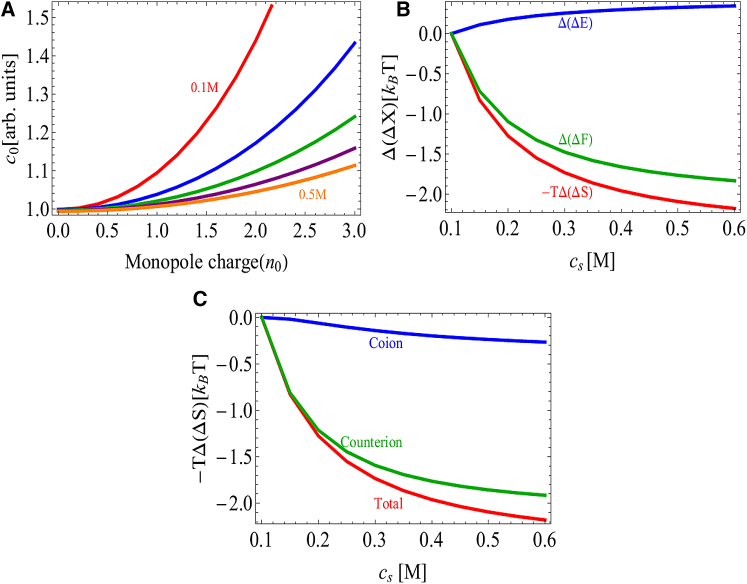
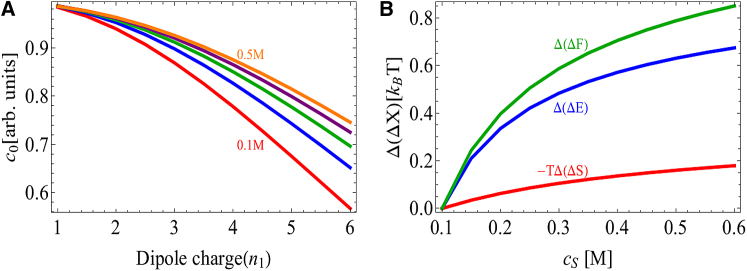
Fig. 4 A shows the solubility of a model protein containing only a monopole charge (). Increasing the charge increases the repulsion between proteins, thereby increasing the solubility. Adding salt reduces the repulsion, resulting in salting-out behavior. Although it is intuitively convenient to think of the repulsive interaction as arising from the Coulomb interaction between the identical protein charges, in fact, the Coulomb energy of aggregation is actually attractive and the repulsive behavior arises from the entropic cost of confining counterions within the aggregate (39, 48). This can be seen in Fig. 4 B, which shows a dramatic reduction in the entropic penalty of aggregation with the addition of salt, with the bulk of the entropy change coming from the counterions (Fig. 4 C). In contrast, the Coulomb energy becomes less favorable with the addition of salt. This is because the favorable energy of aggregation is due to the closer association of counterions with the protein in the crystal state; at high salt, the screening layer is already compact, so the change upon aggregation is minimal.
Figure 4.
(A) Solubility of charged spherical proteins as a function of monopole charge and salt concentration. The dipole moment and nonelectrostatic effects have been omitted . Repulsion between proteins stabilizes the solution state and increases the solubility. Adding salt screens the repulsion and leads to salting out. Salt concentration is increased from 0.1 m (top curve) to 0.5 M (bottom curve) in 0.1 M increments. (B) Change in the Coulomb energy, entropy, and free energy of aggregation relative to 100 mM salt, , for spheres with charge . The repulsive interaction is dominated by the ion entropy, so adding salt leads to a large decrease in the entropy penalty. (C) The salt entropy can be further separated into coion and counterion terms, demonstrating that the dominant contribution comes from the confinement of counterions. To see this figure in color, go online.
Fig. 5 A shows the opposite case of a protein with dipole and an insignificant monopole (). Here, the electrostatic interactions are favorable for aggregation, so increasing the dipole charge decreases solubility and adding salt leads to salting in. Another significant difference is that both the energy and entropy terms contribute to the attraction. This is because the association of proteins leads to both the release of counterions and the close association of complementary charges between proteins. In this case, the free energy is dominated by the Coulomb energy term, as shown in Fig. 5 B.
Figure 5.
Electrostatics-only model , showing the solubility of a nearly ideal dipole . (A) Dipole attraction decreases the solubility and the addition of salt increases solubility. Salt concentration is increased from 0.1 M (bottom curve) to 0.5 M (top curve) in 0.1 M increments. (B) Variation of the energy, entropy and free energy of aggregation of a pure dipole . Both the energy and entropy are favorable for aggregation and become less favorable with the addition of salt. To see this figure in color, go online.
Since the protein monopole and dipole moments have opposite effects on the solubility, it is important to know which effect dominates to determine whether salting in or salting out will occur. Fig. 6 shows the protein solubility as a function of the ratio . When the ratio is <∼0.2, the system is dipole dominated and salting in occurs. Monopole-dominated salting-out behavior is seen for , with intermediate values of giving nonmonotonic solubility (Fig. 6, shaded regions). Within these shaded regions, the initial effect of adding salt is to screen the long-ranged monopole repulsion, leading to salting out (63). At higher salt, the dominant effect is screening of the dipole, resulting in salting in. However, this analysis does not include the depletion effect that emerges from the finite ion size. This effect will always result in salting out at high concentrations, although the onset of this behavior will depend on the salt used and the geometry of the aggregate.
Figure 6.
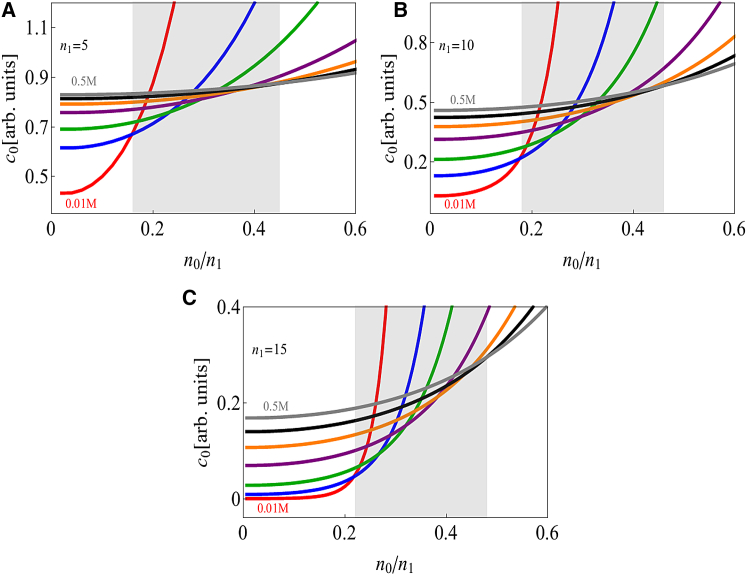
Competition between the monopole and dipole leads to salting in and salting out in an electrostatics-only model . Holding the dipole fixed at (A) , (B) , and (C) , the system shows pure salting in behavior for , pure salting out for , and nonmonotonic dependence on the salt concentration for intermediate values of the monopole/dipole ratio (shaded regions). These crossover points depend weakly on the magnitude of the dipole and strongly on the aggregate solvent fraction. In these plots, the salt concentrations are 0.01, 0.05, 0.1, 0.2, 0.3, 0.4, and 0.5 M. To see this figure in color, go online.
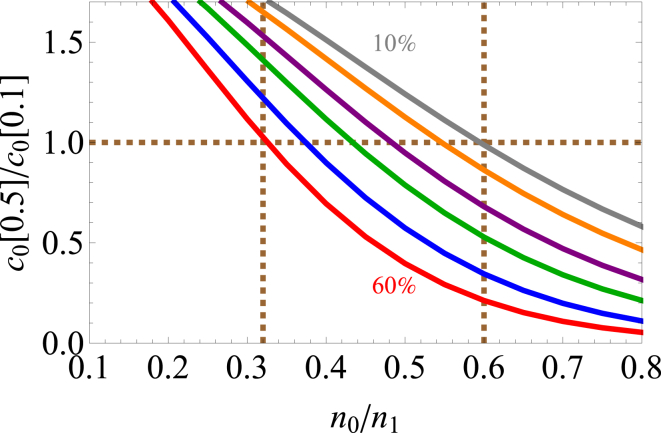
Fig. 6 shows that the crossover between salting in and salting out occurs at a ratio for 40% aggregate solvent content. This means that the dipole charge has to be substantially larger than the monopole for salting in to occur. This crossover point can vary due to the distinct mechanisms underlying the dipole and monopole interactions; although the dipole interactions are driven by the energetic gain of pairing charged patches, the monopole repulsion is dominated by counterion confinement entropy. Therefore, increasing the solvent content of the aggregate will reduce the monopole repulsion with minimal effect on the dipole attraction. This can be seen in Fig. 7, which shows the salting-in/salting-out crossover shifting to larger values of as the aggregate solvent content increases.
Figure 7.
Competition between the monopole and dipole leads to salting in and salting out in an electrostatics-only model . The crossover point depends strongly on the protein and solvent volume fractions. The protein volume fraction is varied from 10% (top curve) to 60% (bottom curve) in 10% intervals. Here, we plot the ratio of the solubility at 0.5 M salt to the solubility at 0.1 M. Ratios greater than unity (horizontal dashed line) indicate salting in over this range of salt concentrations. As the protein volume fraction increases from 10 to 60%, smaller monopoles are required for salting out to dominate. For this range of aggregate densities, the maximum monopole/dipole ratio at which to observe salting in ranges from 0.32 to 0.6 (vertical dashed lines). . To see this figure in color, go online.
The nonelectrostatic protein-ion interaction and ion excluded volume result in salt specificity
Now we take a closer look at the salt-specific contributions to the solubility, beginning with nonelectrostatic protein-ion binding. The nonelectrostatic protein-ion interaction has received considerable attention and has been attributed to dispersion, solvophobic, and image charge interactions (21, 22, 30). Within our model, these various contributions are combined into a single parameter and the net interaction is assumed to be sufficiently short-ranged that it can be approximated using a two-state model. Importantly, this binding parameter is expected to depend on the ion used, thereby giving rise to salt-specific effects (33). This mechanism for salt specificity is not explored further in this work, because the available experiments on lysozyme and chymosin crystal model systems all used chloride as the anion (19, 52).
We find that the binding parameter is small, , indicating that these are low-affinity, transient binding events rather than specific binding pockets for the ions. Obviously, there will be a distribution of affinities on the protein surface, so the value that we obtain is best interpreted as the affinity of sites that significantly change their binding occupancy over the concentration range where electrostatic effects are significant. Since these are nonspecific sites, we use the same binding energy for both proteins and we assume that their number should scale roughly with the protein surface area.
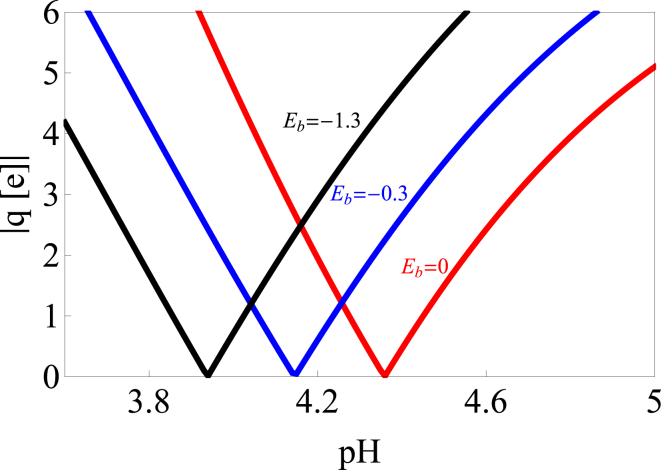
The inclusion of the nonelectrostatic binding has two important effects on the solubility. First, the association of ions with the protein means that the effective charge depends on the number of bound ions, which in turn depends on the binding affinity and the salt concentration. Fig. 8 shows how the isoelectric point of the protein shifts with increasing ion affinity. This effect is important for our modeling of chymosin, which has a calculated isoelectric point at pH 4.6 (Table 1), whereas the solubility minimum is closer to pH 4.0 (Fig. 3).
Figure 8.
Anion binding shifts the isoelectric point of chymosin. Charge versus pH is shown at different values of the binding affinity. Anions that are more strongly bound shift the isoelectric point toward lower pH. To see this figure in color, go online.
Second, the binding of ions to the protein upon the addition of salt alters the protein monopole charge, which can have dramatic effects on the solubility. Since anions are the binding species, the effective charge of the protein will decrease with added salt. This means that the magnitude of the protein charge will increase if the pH is above the isoelectric point. Fig. 9 shows this increase in the absolute protein charge along with the beginnings of a saturation at high salt as the sites become occupied. Between the saturation of binding sites and the enhanced screening at high salt, the effects of ion binding on the solubility are confined to the low-salt regime (<0.3 M). This is demonstrated in Fig. 10, which shows that the inclusion of ion binding dramatically enhances the salting-in effect below 0.3 M salt. This is because the addition of charge to the protein happens faster than the enhancement of the screening effect. At higher salt, the effect dissipates as the salt becomes concentrated enough to screen the addition of further charges.
Figure 9.
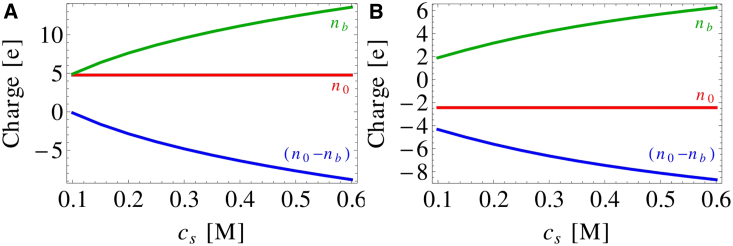
Charge of chymosin versus salt concentration. The red horizontal line shows the original monopole charge, , reported in Table 1. The green line shows the number of anions bound to the protein, , whereas the blue line shows the net protein charge, , after anion binding. (A) At pH 4.0, anion binding results in a reversal in the protein charge. (B) At pH 4.6, anion binding enhances the monopole charge as the salt concentration increases. . To see this figure in color, go online.
Figure 10.
Ion binding enhances the salting-in effect. Shown is the free-energy change of chymosin crystallization with respect to salt at pH 4.0 and 4.6 with (solid lines) and without (dotted lines) anion binding ( and ). The inclusion of anion binding increases the magnitude of the monopole, resulting in a stronger salting-in effect. To see this figure in color, go online.
A second source of salt specificity comes from the varying ion size. Intuitively, we expect the finite ion size to be important when the ions, and their associated solvation layers, occupy a significant fraction of the solution volume. This condition can be trivially satisfied by adding large amounts of salt to the system. Under these conditions, the screening length is so short that electrostatic interactions can be reasonably neglected. In this case, the dominant contribution to the free energy is a salt-mediated depletion interaction arising from the final term of Eq. 4. The attraction is proportional to the salt concentration and the change in the ion-accessible volume upon aggregation. The accessible volume depends on both the ion size and the size of the protein-protein interaction sites. These effects can be seen in the excluded volumes listed in Table 2.
Table 2.
Change in Ion-Accessible Volume per Protein in Lysozyme and Chymosin Crystals
| Size of Ions () | Lysozyme () | Chymosin () |
|---|---|---|
| 800 | 1820 | |
| 1200 | 3200 | |
| 2000 | 4800 |
Even at low bulk salt concentration, the ion volume fraction can reach significant values within the aggregate cavities. This is because of the high concentration of counterions needed to neutralize the protein monopole. Clearly, large counterions will occupy more space within the crystal, thereby increasing the entropic penalty of achieving neutrality. Therefore, large counterions will be less effective at salting out the protein in the low-salt regime. Coions will have the opposite effect in that large ions will enhance salting out. This is because large ions will be preferentially excluded from the aggregate. This reduces the number of counterions that must be confined, thereby reducing the entropic cost of achieving charge neutrality. This exclusion of coions is the source of the salt specificity in the low-salt range of Fig. 2. Since electrostatic effects are insignificant in this regime, nonelectrostatic theories like Setchenow coefficients and preferential interaction parameters can be successfully applied to capture the salting-out effect (11, 64).
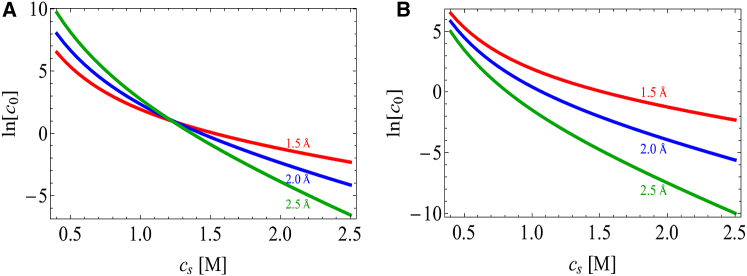
The contributions from the ion size are complicated when varying the size of counterions. At low concentration, larger counterions result in higher solubility than smaller ones, because it is more difficult for the aggregate to accommodate the ions needed for charge neutrality. However, at high salt concentration, electrostatic interactions are negligible, so large counterions reduce solubility due to the enhanced depletion effect. For positively charged proteins, this leads to a reversal in the anion Hofmeister series, with the reverse series observed at low salt and the direct series at high salt (Fig. 11 A). This trend has been observed in cloud-point measurements in lysozyme (32) and simulations of simple water models (65). Previous theory has attributed the reversal to the nonelectrostatic association of anions with the protein surface (33). However, Boström et al. did not consider the ionic excluded volume, suggesting that ion-protein association and excluded-volume effects both contribute to the salt-concentration-dependent reversal.
Figure 11.
Comparison of the effect of excluded volume on counterions and coions. (A) Variation in the counterion size leads to a reversal in the Hofmeister series, with large ions more effective at salting out at high salt concentrations and small ions more effective at salting out at low salt concentrations. (B) Coions do not show a reversal since the exclusion of large ions and the depletion effect both favor aggregation. In both (A) and (B), the protein charge is , the common ion size is , and ion binding effects have been removed to highlight the excluded-volume effect. To see this figure in color, go online.
The situation is simpler for coions. Fig. 11 B shows that large coions lead to lower solubility at all concentrations, with the nonlinear screening behavior giving way to a linear depletion effect at high salt concentration.
Conclusions
The central role of salt entropy has long been appreciated in polymer systems (66) but has received much less attention in the protein community. Salt-confinement entropy is the dominant electrostatic contribution in the aggregation of strongly charged proteins (48), but we find that this gives way to a more energy-driven mechanism near the isoelectric point. These distinct mechanisms behind electrostatic repulsion and attraction can possibly be exploited for controlling protein phase behavior. The dominant role of ion entropy in highly charged and/or dense aggregates means that small perturbations, such as differences in the hydrated radii, can have a significant effect. We show that these effects are consistent with observed Hofmeister effects, but other works have shown that salt-solute interactions can also lead to comparable effects (13, 17, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33). We have been unable to assess the relative magnitude of these contributions due to the scarcity of systematic studies of ion specificity on protein crystal solubility (the only form of protein aggregate where density is fixed and known). However, our approach does account for these ion binding effects, which are essential for capturing perturbations to the isoelectric point. Notably, these ion binding events are individually weak and transient, but they occur in sufficient number to be statistically significant.
Salt effects are a combination of electrostatic screening and finite size contributions. Direct electrostatic effects are easy to understand. Like charges repel, so when the monopole dominates, adding salt reduces the solubility. If the monopole is small enough, then attractions between complementary charges (due to dipole and higher moments) can be screened away, leading to salting in (3). This qualitative picture comes with two notes of caution. First, although it is useful to think in terms of the Coulomb interaction between proteins, the dominant contribution to the free energy actually comes from the entropy of distorting the screening layers (39). Second, charge repulsion is amenable to mean-field treatments like the one presented here due to the dominant role of the nonlocal ion entropy (48). However, attractive electrostatic interactions depend strongly on the arrangement of charges within the aggregate. In particular, the formation of salt bridges can cause large pKa shifts, resulting in anomalous behavior when the pH is changed. Fortunately, monopole interactions usually dominate the free energy, and these interactions can be modeled using a variety of geometries for the aqueous cavities (44, 45, 48). Care is required, however, if the aggregate is sufficiently diffuse that there is substantial variation in the electric potential within the cavities. In these cases, the electrostatics are best calculated using two-body models or lower-dimensional structures (39). Gels represent an obvious case of an aggregate with large aqueous cavities, although in general, noncrystalline aggregates can have a heterogeneous internal density and will need to be evaluated for whether the best model is a dense cluster, an open network, or something else entirely. Similarly, the solution-state protein model will need to be modified if the protein deviates strongly from a spherical shape.
Nonelectrostatic interactions, responsible for the Hofmeister series, arise from the fact that ions are not point charges. The finite size of the ions has many effects that must be accounted for. First, the ion size correlates with polarizability, which affects the protein-ion interaction (51). Second, the ion radius determines its affinity to water, resulting in nontrivial corrections to the effective ion volume (67). This effective size in turn determines the entropic cost of trapping ions within the aggregate and the strength of the salt-mediated depletion attraction. Our work shows that modest perturbations in the ion radius lead to solubility perturbations consistent with Hofmeister effects. Notably, the parameters we use for the solvated ion volume are conservative compared to others in the literature, whereas the relative ordering is consistent (68, 69). This suggests that our model may, in fact, be an underestimate of these excluded volume effects. This mechanism is independent of salt specificity arising from protein-ion interactions, and further work will be required to assess the relative influence of these contributions.
The model we have presented is a simplified representation of protein aggregation and therefore neglects features that will contribute to the solubility. However, the ability of the model to capture salting-in/salting-out trends and the correct magnitude of these phenomena suggests that the model elements of Coulomb energy, salt entropy, and protein-ion binding are the most important contributions to the solubility. The simplicity of our approach has the advantage that it allows a detailed analysis of the various contributions, which leads to improved intuition as to which effects are likely to be most important. It also allows the model to be used to estimate the solubility change for any aggregate for which the protein charge, dipole, volume, and overall aggregate density are known. In practice, the difficulty is determining the aggregate density and having confidence that the protein-protein interaction sites do not significantly change with solution conditions. These two concerns are negligible in crystals that maintain constant morphology. Although some tuning was required to reach quantitative agreement with protein solubility measurements, the qualitative features are insensitive to model choices like the protein and cavity geometry, ion size, and binding parameters. We expect that better agreement could be obtained by applying the same physics to higher-resolution models.
Author Contributions
Y.R.D. and J.D.S. designed the research and wrote the article. Y.R.D. performed the research and analyzed the data.
Acknowledgments
We thank A. Lenhoff and K. Dill for valuable comments on the manuscript.
This work was supported by National Institutes of Health grant R01GM107487.
Editor: Rohit Pappu.
References
- 1.Hofmeister F. Zur Lehre von der Wirkung der Salze. Arch. Exp. Pathol. Pharmakol. 1888;24:247–260. [Google Scholar]
- 2.Cohn, E. J., and J. T. Edsall. 1943. Proteins, Amino Acids and Peptides as Ions and Dipolar Ions. Reinhold, New York.
- 3.Tanford C. John Wiley & Sons; Hoboken, NJ: 1961. Physical Chemistry of Macromolecules. [Google Scholar]
- 4.Green A.A. Studies in the physical chemistry of the proteins: IX. The effect of electrolytes on the solubility of hemoglobin in solutions of varying hydrogen ion activity with a note on the comparable behavior of casein. J. Biol. Chem. 1931;93:517–542. [Google Scholar]
- 5.Shammas S.S.L., Knowles T.P.J., Glyn L. Perturbation of the stability of amyloid fibrils through alteration of electrostatic interactions. Biophys. J. 2011;100:2783–2791. doi: 10.1016/j.bpj.2011.04.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Buell A.K., Galvagnion C., Dobson C.M. Solution conditions determine the relative importance of nucleation and growth processes in α-synuclein aggregation. Proceedings of the National Academy of Sciences of the United States of America. 2014;111:7671–7676. doi: 10.1073/pnas.1315346111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Pedersen J.T., Borg C.B., Hemmingsen L. Aggregation-prone amyloid-β⋅CuII species formed on the millisecond timescale under mildly acidic conditions. ChemBioChem. 2015;16:1293–1297. doi: 10.1002/cbic.201500080. [DOI] [PubMed] [Google Scholar]
- 8.Ciryam P., Kundra R., Vendruscolo M. Supersaturation is a major driving force for protein aggregation in neurodegenerative diseases. Trends Pharmacol. Sci. 2015;36:72–77. doi: 10.1016/j.tips.2014.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Derjaguin B.V., Landau L.D. Theory of the stability of strongly charged lyophobic sols and of the adhesion of strongly charged particles in solutions of electrolytes. Prog. Surf. Sci. 1941;14:633–662. [Google Scholar]
- 10.Verwey E.J.W., Overbeek J.T.G. Courier Dover Publications; Mineola, NY: 1948. Theory of the Stability of Lyophobic Colloids. [Google Scholar]
- 11.Setchenow M. Action de l’acide carbonique sur les solutions des sels a acides forts. Etude absortiometrique. Ann. Chim. Phys. 1892;25:226–270. [Google Scholar]
- 12.Baldwin R.L. How Hofmeister ion interactions affect protein stability. Biophys. J. 1996;71:2056–2063. doi: 10.1016/S0006-3495(96)79404-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Levin Y., Flores-Mena J.E. Surface tension of strong electrolytes. Europhys. Lett. 2001;56:187–192. [Google Scholar]
- 14.Levin Y., dos Santos A.P., Diehl A. Ions at the air-water interface: an end to a hundred-year-old mystery? Phys. Rev. Lett. 2009;103:257802. doi: 10.1103/PhysRevLett.103.257802. [DOI] [PubMed] [Google Scholar]
- 15.Boström M., Williams D.R.M., Ninham B.W. Surface tension of electrolytes: specific ion effects explained by dispersion forces. Langmuir. 2001;17:4475–4478. [Google Scholar]
- 16.Pashley R.M., Ninham B.W. Double-layer forces in ionic micellar solutions. J. Phys. Chem. 1987;91:2902–2904. [Google Scholar]
- 17.Parsons D.F., Boström M., Ninham B.W. Why direct or reversed Hofmeister series? Interplay of hydration, non-electrostatic potentials, and ion size. Langmuir. 2010;26:3323–3328. doi: 10.1021/la903061h. [DOI] [PubMed] [Google Scholar]
- 18.Curtis R.A., Ulrich J., Blanch H.W. Protein-protein interactions in concentrated electrolyte solutions. Biotechnol. Bioeng. 2002;79:367–380. doi: 10.1002/bit.10342. [DOI] [PubMed] [Google Scholar]
- 19.Ries-Kautt M.M., Ducruix A.F. Relative effectiveness of various ions on the solubility and crystal growth of lysozyme. J. Biol. Chem. 1989;264:745–748. [PubMed] [Google Scholar]
- 20.Carbonnaux C., Ries-Kautt M., Ducruix A. Relative effectiveness of various anions on the solubility of acidic Hypoderma lineatum collagenase at pH 7.2. Protein Sci. 1995;4:2123–2128. doi: 10.1002/pro.5560041018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ninham B.W., Yaminsky V. Ion binding and ion specificity: the Hofmeister effect and Onsager and Lifshitz theories. Langmuir. 1997;13:2097–2108. [Google Scholar]
- 22.dos Santos A.P., Levin Y. Ion specificity and the theory of stability of colloidal suspensions. Phys. Rev. Lett. 2011;106:167801. doi: 10.1103/PhysRevLett.106.167801. [DOI] [PubMed] [Google Scholar]
- 23.dos Santos A.P., Levin Y. Ions at the water-oil interface: interfacial tension of electrolyte solutions. Langmuir. 2012;28:1304–1308. doi: 10.1021/la204036e. [DOI] [PubMed] [Google Scholar]
- 24.Flores S.C., Kherb J., Cremer P.S. Direct and reverse Hofmeister effects on interfacial water structure. J. Phys. Chem. C. 2012;116:14408–14413. [Google Scholar]
- 25.Medda L., Barse B., Salis A. Hofmeister challenges: ion binding and charge of the BSA protein as explicit examples. Langmuir. 2012;28:16355–16363. doi: 10.1021/la3035984. [DOI] [PubMed] [Google Scholar]
- 26.Lund M., Jungwirth P. Patchy proteins, anions and the Hofmeister series. J. Phys. Condens. Matter. 2008;20:494218. [Google Scholar]
- 27.Tadeo X., López-Méndez B., Millet O. Protein stabilization and the Hofmeister effect: the role of hydrophobic solvation. Biophys. J. 2009;97:2595–2603. doi: 10.1016/j.bpj.2009.08.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bye J.W., Falconer R.J. Thermal stability of lysozyme as a function of ion concentration: a reappraisal of the relationship between the Hofmeister series and protein stability. Protein Sci. 2013;22:1563–1570. doi: 10.1002/pro.2355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sedlák E., Stagg L., Wittung-Stafshede P. Effect of Hofmeister ions on protein thermal stability: roles of ion hydration and peptide groups? Arch. Biochem. Biophys. 2008;479:69–73. doi: 10.1016/j.abb.2008.08.013. [DOI] [PubMed] [Google Scholar]
- 30.Zhou H.-X. Interactions of macromolecules with salt ions: an electrostatic theory for the Hofmeister effect. Proteins. 2005;61:69–78. doi: 10.1002/prot.20500. [DOI] [PubMed] [Google Scholar]
- 31.Boström M., Tavares F.W., Ninham B.W. Why forces between proteins follow different Hofmeister series for pH above and below pI. Biophys. Chem. 2005;117:217–224. doi: 10.1016/j.bpc.2005.05.010. [DOI] [PubMed] [Google Scholar]
- 32.Zhang Y., Cremer P.S. The inverse and direct Hofmeister series for lysozyme. Proc. Natl. Acad. Sci. USA. 2009;106:15249–15253. doi: 10.1073/pnas.0907616106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Boström M., Parsons D.F., Monduzzi M. Possible origin of the inverse and direct Hofmeister series for lysozyme at low and high salt concentrations. Langmuir. 2011;27:9504–9511. doi: 10.1021/la202023r. [DOI] [PubMed] [Google Scholar]
- 34.Hribar B., Southall N.T., Dill K.A. How ions affect the structure of water. J. Am. Chem. Soc. 2002;124:12302–12311. doi: 10.1021/ja026014h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Dill K.A., Truskett T.M., Hribar-Lee B. Modeling water, the hydrophobic effect, and ion solvation. Annu. Rev. Biophys. Biomol. Struct. 2005;34:173–199. doi: 10.1146/annurev.biophys.34.040204.144517. [DOI] [PubMed] [Google Scholar]
- 36.Zhang Y., Cremer P.S. Interactions between macromolecules and ions: The Hofmeister series. Curr. Opin. Chem. Biol. 2006;10:658–663. doi: 10.1016/j.cbpa.2006.09.020. [DOI] [PubMed] [Google Scholar]
- 37.Vlachy V., Blanch H.W., Prausnitz J.M. Liquid-liquid phase separations in aqueous solutions of globular proteins. AIChE J. 1993;39:215–223. [Google Scholar]
- 38.Hribar-Lee B., Vlachy V., Dill K.A. Modeling Hofmeister effects. Acta Chim. Slov. 2009;56:196–202. [PMC free article] [PubMed] [Google Scholar]
- 39.Schmit J.D., Whitelam S., Dill K. Electrostatics and aggregation: how charge can turn a crystal into a gel. J. Chem. Phys. 2011;135:085103. doi: 10.1063/1.3626803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Theodoor J., Overbeek G. The role of energy and entropy in the electrical double layer. Colloids Surf. 1990;51:61–75. [Google Scholar]
- 41.Sharp K.A., Honig B. Calculating total electrostatic energies with the nonlinear Poisson-Boltzmann equation. J. Phys. Chem. 1990;94:7684–7692. [Google Scholar]
- 42.Andelman D. Electrostatic properties of membranes: the Poisson-Boltzmann theory. In: Lipowski R., Sackmann E., editors. Structure and Dynamics of Membranes From Cells to Vesicles. Elsevier; 1995. pp. 603–642. [Google Scholar]
- 43.Holm C. Volume 2001. Springer; Berlin, Germany: 2001. Electrostatic Effects in Soft Matter and Biophysics. [Google Scholar]
- 44.Prinsen P., Odijk T. Optimized Baxter model of protein solutions: electrostatics versus adhesion. J. Chem. Phys. 2004;121:6525–6537. doi: 10.1063/1.1786915. [DOI] [PubMed] [Google Scholar]
- 45.Warren P.B. Simple models for charge and salt effects in protein crystallization. J. Phys. Condens. Matter. 2002;14:7617–7629. [Google Scholar]
- 46.Lima E.E.R.A., Biscaia E.C., Boström M. Osmotic second virial coefficients and phase diagrams for aqueous proteins from a much-improved Poisson-Boltzmann equation. J. Phys. Chem. C. 2007;111:16055–16059. [Google Scholar]
- 47.Boström M., Lonetti B., Ninham B.W. Why pH titration in protein solutions follows a Hofmeister series. J. Phys. Chem. B. 2006;110:7563–7566. doi: 10.1021/jp051025t. [DOI] [PubMed] [Google Scholar]
- 48.Schmit J.D., Dill K.A. The stabilities of protein crystals. J. Phys. Chem. B. 2010;114:4020–4027. doi: 10.1021/jp9107188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Grimsley G.R., Scholtz J.M., Pace C.N. A summary of the measured pK values of the ionizable groups in folded proteins. Protein Sci. 2009;18:247–251. doi: 10.1002/pro.19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Gokarn Y.R., Fesinmeyer R.M., Brems D.N. Effective charge measurements reveal selective and preferential accumulation of anions, but not cations, at the protein surface in dilute salt solutions. Protein Sci. 2011;20:580–587. doi: 10.1002/pro.591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Parsons D.F., Ninham B.W. Importance of accurate dynamic polarizabilities for the ionic dispersion interactions of alkali halides. Langmuir. 2010;26:1816–1823. doi: 10.1021/la902533x. [DOI] [PubMed] [Google Scholar]
- 52.Maurer R.W., Sandler S.I., Lenhoff A.M. Salting-in characteristics of globular proteins. Biophys. Chem. 2011;156:72–78. doi: 10.1016/j.bpc.2011.02.002. [DOI] [PubMed] [Google Scholar]
- 53.Poznański J., Wszelaka-Rylik M., Zielenkiewicz W. Concentration dependencies of NaCl salting of lysozyme by calorimetric methods. Thermochim. Acta. 2004;409:25–32. [Google Scholar]
- 54.Poznański J., Wszelaka-Rylik M., Zielenkiewicz W. HEW lysozyme salting by high-concentration NaCl solutions followed by titration calorimetry. Biophys. Chem. 2005;113:137–144. doi: 10.1016/j.bpc.2004.08.007. [DOI] [PubMed] [Google Scholar]
- 55.Boncina M., Lah J., Vlachy V. Thermodynamics of the lysozyme-salt interaction from calorimetric titrations. J. Phys. Chem. B. 2010;114:4313–4319. doi: 10.1021/jp9071845. [DOI] [PubMed] [Google Scholar]
- 56.Sibille L., Pusey M.L. Investigation of nucleating lysozyme solutions. Acta Crystallogr. D Biol. Crystallogr. 1994;50:396–397. doi: 10.1107/S0907444993013447. [DOI] [PubMed] [Google Scholar]
- 57.Prinsen P., Odijk T. Fluid-crystal coexistence for proteins and inorganic nanocolloids: dependence on ionic strength. J. Chem. Phys. 2006;125:074903. doi: 10.1063/1.2336423. [DOI] [PubMed] [Google Scholar]
- 58.Vaney M.C., Maignan S., Ducriux A. High-resolution structure (1.33 Å) of a HEW lysozyme tetragonal crystal grown in the APCF apparatus. Data and structural comparison with a crystal grown under microgravity from SpaceHab-01 mission. Acta Crystallogr. D Biol. Crystallogr. 1996;52:505–517. doi: 10.1107/S090744499501674X. [DOI] [PubMed] [Google Scholar]
- 59.Newman M., Safro M., Andreeva N. X-ray analyses of aspartic proteinases. IV. Structure and refinement at 2.2 Å resolution of bovine chymosin. J. Mol. Biol. 1991;221:1295–1309. [PubMed] [Google Scholar]
- 60.Pettersen E.F., Goddard T.D., Ferrin T.E. UCSF Chimera—a visualization system for exploratory research and analysis. J. Comput. Chem. 2004;25:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- 61.Kielland J. Individual activity coefficients of ions in aqueous solutions. J. Am. Chem. Soc. 1937;59:1675–1678. [Google Scholar]
- 62.Boncina M., Rescic J., Vlachy V. Solubility of lysozyme in polyethylene glycol-electrolyte mixtures: the depletion interaction and ion-specific effects. Biophys. J. 2008;95:1285–1294. doi: 10.1529/biophysj.108.128694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Tavares F.W., Bratko D., Prausnitz J.M. Phase behavior of aqueous solutions containing dipolar proteins from second-order perturbation theory. J. Chem. Phys. 2004;120:9859–9869. doi: 10.1063/1.1697387. [DOI] [PubMed] [Google Scholar]
- 64.Timasheff S.N. The control of protein stability and association by weak interactions with water: how do solvents affect these processes? Annu. Rev. Biophys. Biomol. Struct. 1993;22:67–97. doi: 10.1146/annurev.bb.22.060193.000435. [DOI] [PubMed] [Google Scholar]
- 65.Kalyuzhnyi Y.V., Vlachy V. Explicit-water theory for the salt-specific effects and Hofmeister series in protein solutions. J. Chem. Phys. 2016;144:215101. doi: 10.1063/1.4953067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Oosawa F. Marcel Dekker; New York: 1971. Polyelectrolytes. [Google Scholar]
- 67.Collins K.D., Neilson G.W., Enderby J.E. Ions in water: characterizing the forces that control chemical processes and biological structure. Biophys. Chem. 2007;128:95–104. doi: 10.1016/j.bpc.2007.03.009. [DOI] [PubMed] [Google Scholar]
- 68.Nightingale R. Phenomenological theory of ion solvation. effective radii of hydrated ions. J. Phys. Chem. 1959;63:1381–1387. [Google Scholar]
- 69.Conway B. Elsevier Science; Amsterdam, the Netherlands: 1981. Ionic Hydration in Chemistry and Biophysics. [Google Scholar]