Microtubule Polymerization and Cross-Link Dynamics Explain Axonal Stiffness and Damage

Abstract

Axonal damage is a critical indicator for traumatic effects of physical impact to the brain. However, the precise mechanisms of axonal damage are still unclear. Here, we establish a mechanistic and highly dynamic model of the axon to explore the evolution of damage in response to physical forces. Our axon model consists of a bundle of dynamically polymerizing and depolymerizing microtubules connected by dynamically detaching and reattaching cross-links. Although the probability of cross-link attachment depends exclusively on thermal fluctuations, the probability of detachment increases in the presence of physical forces. We systematically probe the landscape of axonal stretch and stretch rate and characterize the overall axonal force, stiffness, and damage as a direct result of the interplay between microtubule and cross-link dynamics. Our simulations reveal that slow loading is dominated by cross-link dynamics, a net reduction of cross-links, and a gradual accumulation of damage, whereas fast loading is dominated by cross-link deformations, a rapid increase in stretch, and an immediate risk of rupture. Microtubule polymerization and depolymerization decrease the overall axonal stiffness, but do not affect the evolution of damage at timescales relevant to axonal failure. Our study explains different failure mechanisms in the axon as emergent properties of microtubule polymerization, cross-link dynamics, and physical forces. We anticipate that our model will provide insight into causal relations by which molecular mechanisms determine the timeline and severity of axon damage after a physical impact to the brain.

Introduction

Billions of neurons provide the basis for all communication with and within our brain. A neuron consists of the cell body from which a long and slender axon protrudes to connect it to other neurons cells or to another cell types in the body. In humans, the axon can be up to a meter in length (1). The structure of the axon is made up of longitudinally aligned microtubules surrounded by an actin cortex (2). Neuronal microtubules are 10–100 μm long and are cross-linked by proteins, including dynein and tau (3). Similarly, the actin filaments in the cortex are cross-linked by spectrin and myosin (4). Recent studies have shown that physical forces are constantly present in the axon, and that these forces play an important role in axon physiology (5, 6, 7). For example, moderate axonal forces during development trigger axonal elongation and towed growth (8, 9, 10), whereas extreme axonal forces during impact may lead to axonal damage and diffuse axonal injury (11, 12). The various cross-links that connect individual microtubules and actin filaments are key players in generating active mechanical forces within the axon (13, 14, 15) and in determining the mechanical response of the axon as a whole (14, 16, 17). A common feature of all cross-links is that they are highly dynamic and constantly attach to, detach from, pull on, or push on the axonal cytoskeleton (18, 19, 20). The polymerization and depolymerization of microtubules adds another level of dynamics to the axon physiology (21, 22, 23, 24).

Understanding the biophysics of the axon requires a proper recognition of its individual constituents and their highly dynamic character. Computational simulations can provide powerful insights into the interplay of these different mechanisms and elucidate cause-effect relations that may be extremely difficult to obtain by experiments alone (25). Early models consider the axon as a one-dimensional viscoelastic structure that behaves as a solid at short timescales and as a fluid at longer timescales (26, 27). These models accurately reproduce the axonal response in relaxation and creep experiments. More recent models recognize the importance of active force generation through molecular motors (17). In normal physiology, force equilibrium in the axon is a competition between the tension and compression in the actin cortex and in the microtubule bundle. Deviations from this equilibrium result in stall, collapse, or growth of the axon (28, 29). A recent trend is to explicitly model the axon as a system of discrete microtubules and cross-links. This approach provides insight into the static and dynamic response of the axon (30, 31, 32, 33), the effects of cross-link and microtubule breakage (34, 35), and internal force generation by dynein cross-links (36). Recently, we developed a general computational framework that additionally allows to explicitly model the dynamic character of cross-links within the standard, finite element method (37). This framework provides a general and modular interface to assign any molecular mechanism to a cross-link or microtubule in the axon.

The objective of this study is to explore the interplay of different axonal mechanisms and their collective impact on the biophysical behavior of the axon. Toward this objective, we establish a mechanistic axonal model that consists of a network of dynamically polymerizing and depolymerizing microtubules connected by dynamically detaching and reattaching cross-linking proteins. Using the classical Bell model (38) for chemical bonds, we characterize cross-link detachment in response to an external force applied at a characteristic loading rate. We systematically vary the axonal stretch and stretch rate, and characterize the overall axonal force, stiffness, and damage as emergent properties of the interplay between microtubule and cross-link dynamics.

Methods

Axon model

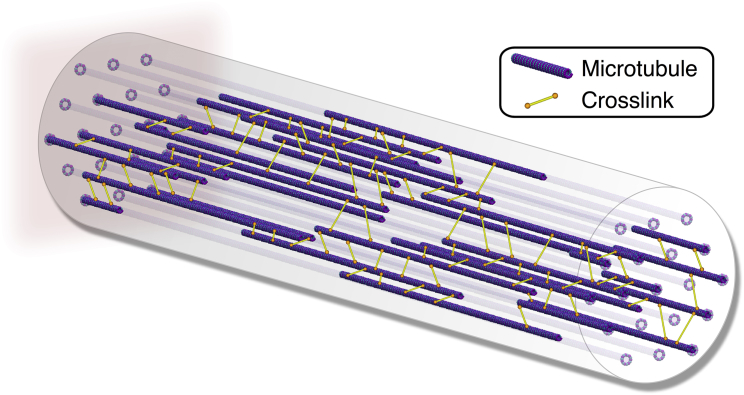
We model the axon as an assembly of longitudinally aligned microtubules that are connected by discrete cross-links (37). Fig. 1 shows our axon model with 19 potential microtubule sites per cross section arranged in a triangular grid. On average, only half of these sites are occupied by microtubules. Neighboring microtubules within the grid are interconnected by cross-links. We randomly add cross-links to the model based on a cross-link density input parameter. On average, the cross-links are evenly distributed within each cross section as well as along the axon length. Every cross-link in our model can detach from and reattach to its microtubules according to the phenomenological Bell model for chemical bond strength (38).

Figure 1.

Axon model. The axon is made up of triangularly arranged, longitudinally aligned microtubules connected by discrete cross-links. Microtubules polymerize and depolymerize dynamically at their distal ends. Cross-links detach and reattach dynamically from and to their microtubules according to the Bell model for chemical bond strength. To see this figure in color, go online.

Fig. 1 illustrates the boundary conditions of our axon. The left, proximal ends of all microtubules are fixed in space. The right, distal ends of the rightmost microtubules are constrained to have an equal longitudinal displacement. Microtubules can only move longitudinally and are embedded in a viscous fluid with an estimated viscosity of 5 mPa/s that mimics the axonal cytosol (39). We load the axon at its distal end with a maximum stretch λ, a loading rate $\dot{\lambda }$, and a characteristic holding period at maximum stretch. Table 1 summarizes all model parameters of our axon model.

Table 1.

Model Parameters of the Axon Model, the Microtubule Model, and the Cross-Link Model

	Value	Unit	Reference
Axon model
Axon length	40	μm	(57)
Axon diameter	540	nm	(58)
Microtubules per cross section	9.5	–	(59)
Cytosol viscosity	5	mPa/s	(39)
Mircotubule model
Microtubule length	10	μm	(60)
Microtubule stiffness	1200	MPa	(61)
Microtubule area	400	nm2	(62)
Polymerization rate	1	nm/ms	(42)
Depolymerization rate	2	nm/ms	(42)
Polymerization time	2000	ms	(42)
Depolymerization time	1000	ms	(42)
Cross-link model
Cross-link distance	1	nm	(58)
Cross-link angle	45	deg	(58)
Cross-link stiffness	10	MPa	(63)
Cross-link area	1	nm2	(37)
Cross-link bond force, $F_0$	10	pN	[estimated]
Cross-link attachment rate, $k_0$	4	1/s	(64, 65)

Microtubule model

Microtubules are highly dynamic structures that continuously polymerize and depolymerize at their plus or distal ends (40). Experiments have shown that microtubule dynamics have significant effects on macroscopic properties of the axon. To include polymerization dynamics in our model, we allow each microtubule to polymerize and depolymerize at its plus end (41). The rates of microtubule polymerization and depolymerization are input parameters to our model. Polymerization and depolymerization are complex phenomena, which depend on microtubule microstructure (22), the presence of tau protein (42), and other proteins in the near environment (43). Although it is conceptually straightforward to include these effects, here, we use constant polymerization and depolymerization rates to reduce the complexity of our model. To account for the short microtubules in our simulations, we select our rates about an order of magnitude slower than reported in the literature (42). For simplicity, we chose a random duration between zero and the characteristic polymerization and depolymerization time (see Table 1).

Cross-link model

All cross-links in our model can dynamically detach from and reattach to their microtubules. We model the attachment and detachment of chemical bonds under an applied force using the Bell model (38), which characterizes attachment and detachment rate k under a constant external force F as

$$k\left(F\right)=\{\begin{array}{ll}{k}_0\hfill & \text{attach}\hfill \\ k_0\text{exp}\left(F/F_0\right)\hfill & \text{detach}\hfill \end{array},$$ (1)

where $k_0$ is the attachment and detachment rate caused exclusively by thermal fluctuations at zero force and $F_0=k_{\text{B}}T/\xi$ is the characteristic bond force in terms of the Boltzmann constant $k_{\text{B}}$, the temperature T, and the characteristic bond separation distance ξ.

Cross-link model: cross-link detachment at constant force F

Using the Bell model (Eq. 1), we can compute the probability $p\left(F,t\right)$ that a cross-link subjected to the force F will detach at time t,

$$p\left(F,t\right)=k\left(F\right)\text{exp}\left(-k\left(F\right)t\right).$$ (2)

The expected attachment time of a single cross-link T then becomes

$$T={\int }_0^{\infty }\overline{t}p\left(F,\overline{t}\right)\text{d}\overline{t}=\frac{1}{k\left(F\right)},$$ (3)

which is consistent with the definition of $k_0$ as the detachment rate at zero force. In our simulations, we keep track of the total attachment time $t_0$ of each cross-link and determine the probability P that a cross-link subjected to the constant force F will detach within the current time interval $\Delta t$ as

$$P\left(F,\Delta t\right)=\frac{{\int }_{t_0}^{t_0+\Delta t}p\left(F,\overline{t}\right)\text{d}\overline{t}}{{\int }_{t_0}^{\infty }p\left(F,\overline{t}\right)\text{d}\overline{t}}=1-\text{exp}\left(-k\left(F\right)\Delta t\right).$$ (4)

Cross-link model: cross-link detachment at constant loading rate $r_f$

The detachment probabilities in Eqs. 2, 3, and 4 assume that the cross-link is subjected to a constant force F, which is not the case during the loading phase of our simulations. To include nonconstant forces (44), we assume that each cross-link is subjected to a constant loading rate $r_f$ and experiences a linear increase of force in time, $F=r_{f}t$. For an arbitrary, general force-time relation, $F=g\left(t\right)$, the Bell model would predict a probability distribution $p\left(t\right)=-\text{d}\left(\text{exp}{\int }_0^t{k}_0\text{exp}\left(g\left(\overline{t}\right)/F_0\right)\text{d}\overline{t}\right)/\text{d}t$, which we can only solve analytically for a very limited number of force-time relations. For the linear assumption that we adopt here, $F=r_{f}t$, we can use a convolution integral and reparameterize the probability density function of cross-link detachment in Eq. 2 in terms of the loading rate $r_f$ as

$$p\left(F,r_f\right)=\frac{k\left(F\right)}{r_f}\text{exp}\left(-\frac{1}{r_f}{\int }_0^{F}k\left(\overline{F}\right)\text{d}\overline{F}\right)=\frac{k\left(F\right)}{r_f}\text{exp}\left(-\frac{F_0}{r_f}\left[k\left(F\right)-k_0\right]\right).$$ (5)

The expected attachment time of a single cross-link T becomes

$$\text{T}={\int }_0^{\infty }\frac{\overline{F}}{r_f}p\left(\overline{F},r_f\right)\text{d}\overline{F}=\frac{F_0}{r_f}\text{exp}\left(\frac{k_0{F}_0}{r_f}\right)\mathit{\Gamma }\left(0,\frac{k_0{F}_0}{r_f}\right),$$ (6)

where $\mathit{\Gamma }\left(a,b\right)={\int }_b^{\infty }\text{exp}\left(-x\right)x^{a-1}\text{d}x$ is the upper incomplete Γ function. The probability P that a cross-link subjected to the initial force $F_0=r_f{t}_0$ will detach within the current loading interval $\Delta F=r_f\Delta t$ is

$$P\left(F,\Delta F\right)=\frac{{\int }_{F_0}^{F_0+\Delta F}p\left(F\right)\text{d}F}{{\int }_{F_0}^{\infty }p\left(F\right)\text{d}F}.$$ (7)

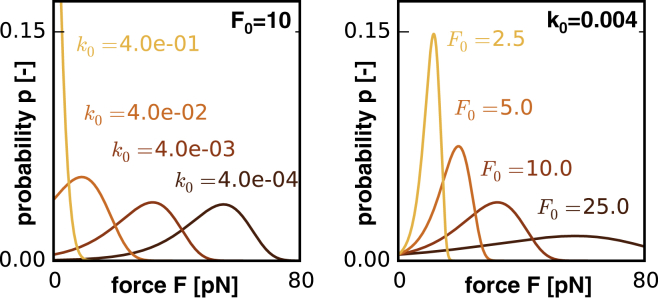
Fig. 2 illustrates the probability $p=k/r_f\text{exp}\left(-F_0/r_f\left[k-k_0\right]\right)$ of cross-link detachment or reattachment at a constant loading rate of r_f = 1 pN/ms according to Eq. 5 (cross-link model). The graphs illustrate the effects of varying the detachment and reattachment rate caused exclusively by thermal fluctuations $k_0$ at a constant characteristic bond force $F_0=10$ pN (left), and of varying the characteristic bond force $F_0$ at a constant rate k₀ = 0.004/ms (right), for a range of external forces F. Fig. 2, left, shows that increasing the cross-link detachment rate $k_0$ decreases the detachment force F and promotes axonal damage. Fig. 2, right, shows that increasing the bond force $F_0$ increases the detachment force F and reduces axonal damage.

Figure 2.

Cross-link model. All cross-links can dynamically detach from and reattach to their microtubules. The probability of cross-link detachment or reattachment $p=k/r_f\text{exp}\left(-F_0/r_f\left[k-k_0\right]\right)$ at a constant loading rate of $r_f$ is a function of the detachment or reattachment rate $k=k_0\text{exp}\left(F/F_0\right)$. The graphs illustrate the effects of varying the detachment and reattachment rate caused exclusively by thermal fluctuations $k_0$ and the characteristic bond force $F_0$ for a range of external forces F at a constant loading rate of r_f = pN/ms. To see this figure in color, go online.

Computational model

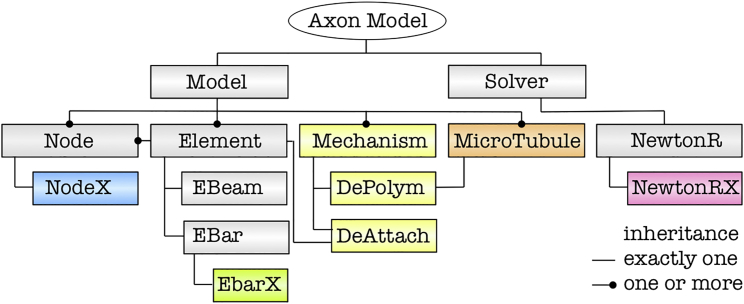
Our computational model is an extension of the finite element method. It preserves the functionality of a standard, finite element algorithm and allows the user to assign mechanisms to a single element or to a collection of multiple elements (37). We model cross-link detachment/reattachment as a single-element mechanism and microtubule polymerization/depolymerization as a multiple-element mechanism.

Fig. 3 summarizes the organization of our computational model. The gray boxes Model, Solver, Node, Element, EBeam, EBar, and NewtonR are part of every standard finite element framework; the colored boxes highlight our extensions. The NodeX and EBarX objects are extensions of the standard node and bar elements. They contain additional information about the mechanism assigned to the element and about its current state. The main addition is the Mechanism object, a general interface to define the single-element mechanism DeAttach for detachment/reattachment and the multiple-element mechanism DePolym for polymerization/depolymerization. To facilitate easy handling of our multiple-element mechanisms, we also created a separate MicroTubule object. Finally, to apply all mechanisms throughout the simulation, we introduced NewtonRX, an extension of the standard Newton Raphson solver that allows us to execute all mechanisms at the beginning of each time step throughout the entire course of the simulation. In this study, we consider two different mechanisms: the first mechanism, DePolym, is applied to MicroTubule objects and it facilitates polymerization and depolymerization of microtubules at their plus ends; the second mechanism, DeAttach, is assigned to every cross-link and is modeled by the Bell model for chemical bond strength (38).

Figure 3.

Computational model. Gray boxes are part of every standard finite element framework; colored boxes highlight mechanism-specific extensions. The NodeX and EBarX objects contain information about the assigned mechanism and its current state. The Mechanism object contains the single-element mechanism DeAttach for detachment/reattachment and the multiple-element mechanism DePolym for polymerization/depolymerization. The NewtonRX object executes all mechanisms before executing the regular time step. To see this figure in color, go online.

Computational model: microtubule polymerization/depolymerization

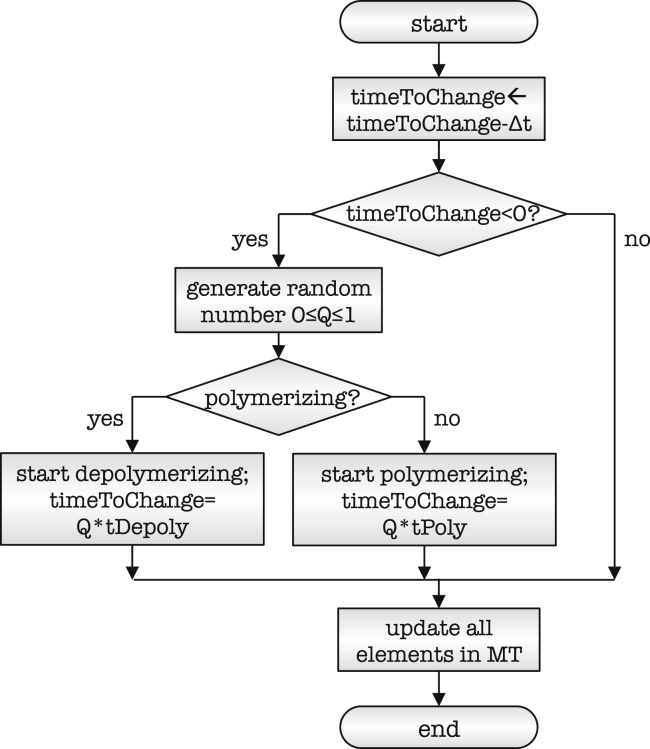
Fig. 4 shows a flowchart of our microtubule model. In our model, throughout the entire simulation, each microtubule is continuously polymerizing or depolymerizing. This implies that, although its proximal end is fixed, its distal end is continuously moving. Every time a microtubule switches from polymerization into depolymerization or vice versa, we randomly select a new duration time guided by the characteristic values in Table 1. We provide a detailed description of the microtubule model in the Supporting Material.

Figure 4.

Microtubule model. Flowchart of polymerization and depolymerization mechanism. The time variable timeToChange is decremented at the beginning of every time step in the simulation. If parameter timeToChange becomes negative, the microtubule switches from polymerization into depolymerization, or vice versa. During the switch, timeToChange is updated based on the characteristic duration of polymerization, tPoly, or depolymerization, tDepoly. All elements in the microtubule are updated according to the current dynamic state of the microtubule.

Computational model: cross-link attachment/detachment

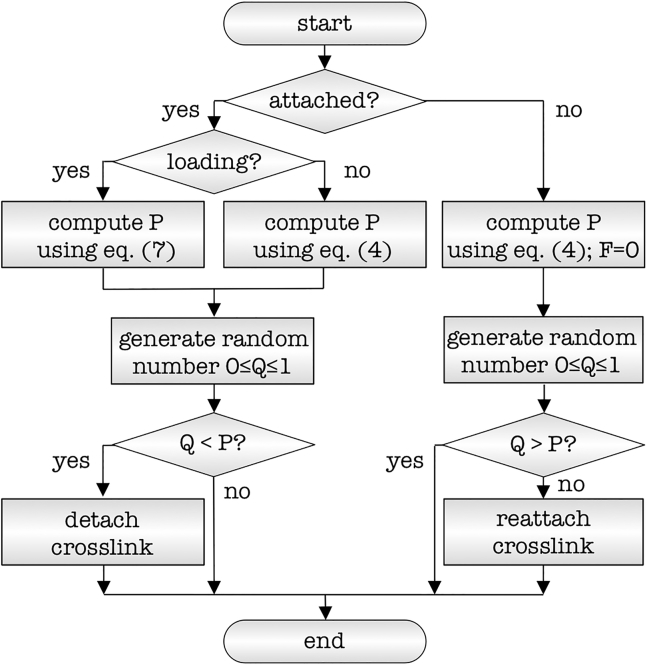
Fig. 5 shows a flowchart of the cross-link model that is applied to each cross-link at the beginning of each time step in the simulations. We compute the force in each cross-link from its individual stretch and stiffness properties. For each cross-link, we then calculate the loading rate from its current stretch divided by its duration of attachment. Using Eqs. 4 or 7, we determine the individual probability of cross-link detachment or reattachment. With this probability, we determine whether the cross-link will detach or reattach and perform the corresponding updates into our computational model (37).

Figure 5.

Cross-link model. Flowchart of cross-link detachment and reattachment mechanism. Depending on the current state, attached or detached, loading or holding, we determine the probability of cross-link detachment or reattachment P and compare it against a randomly generated number Q to determine the next state of the cross-link.

Damage model

In continuum damage mechanics, structural integrity is characterized through a scalar-valued damage parameter d, which varies from $d=0$ for the intact material to $d=1$ for the fully damaged material (45). The damage parameter is associated with an excessive detachment of cross-links and manifests itself directly in a loss of stiffness,

$$E=\left[1-d\right]E_0,$$ (8)

where E and $E_0$ are the stiffnesses of the damaged and undamaged material. If the cross-link detachment and reattachment rates are in equilibrium and at the baseline level $k_0$, the stiffnesses are equal, $E=E_0$, and there is no damage $d=0$. Damage increases with increasing stretch λ, where the stretch $\lambda =l/L$ is the ratio between the current, deformed axonal length l and the initial, undeformed axonal length L. Motivated by these definitions, we characterize axonal damage through the scalar-valued damage parameter d at every stretch level λ as a function of the secant stiffnesses $E\left(\lambda \right)$ of the damaged axon and the baseline stiffness $E_0\left(\lambda \right)$ of the undamaged axon,

$$d\left(\lambda \right)=1-E\left(\lambda \right)/E_0\left(\lambda \right).$$ (9)

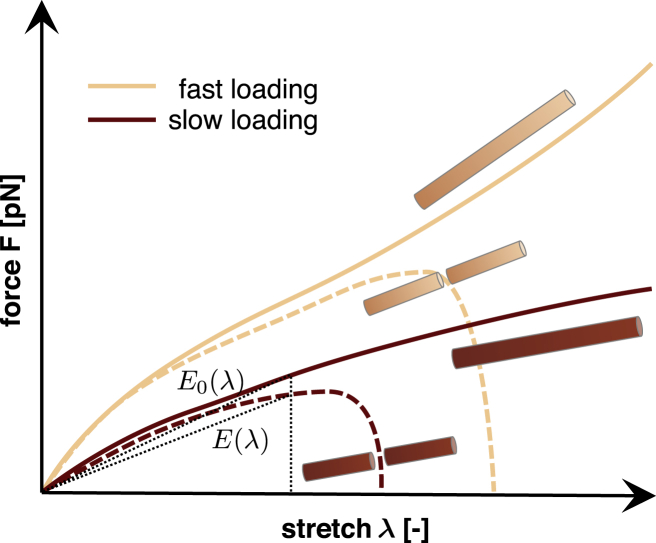
Fig. 6 illustrates four characteristic force-displacement curves of our simulations for fast and slow loading, both without and with damage. The thin dotted lines highlight the secant and baseline stiffnesses $E\left(\lambda \right)$ and $E_0\left(\lambda \right)$ that define the amount of damage $d\left(\lambda \right)$. To calculate the secant stiffness of the damaged axon, $E\left(\lambda \right)=F\left(\lambda \right)/A^{\text{axon}}-1]$, we determine the overall force-stretch relation of the axon $F\left(\lambda \right)$, the axonal cross section area $A^{\text{axon}}$, and the axonal stretch λ. To calculate the baseline stiffness of the undamaged axon, we follow the same steps, but enforce the no-damage condition by assuming that $F_0\to \infty$, such that the detachment rate of cross-links, $k\left(F\right)=k_0$, is identical to the attachment rate $k_0$ (Eq. 1). Our model naturally allows for finite deformations, which induce geometric nonlinearities associated with a rotation of cross-links. We further explain and discuss this effect by means of a simple analytical model in the Supporting Material. For fast loading, this cross-link rotation is the main source of nonlinearity. For slow loading, viscous effects due to random detachment and reattachment of cross-links also contribute to the nonlinearity of the force-stretch curve. To account for differences between fast and slow loading, we simulate the baseline force-displacement curves for the intact, undamaged axon individually for each loading rate. Fig. 6 highlights this difference by means of the beige and red solid lines for fast and slow loading.

Figure 6.

Damage model. Force versus. stretch relations of the undamaged axon (solid lines) and of the damaged axon (dashed lines) under fast and slow loading (beige and red colors, respectively). At every stretch level λ, damage $d\left(\lambda \right)=1-E\left(\lambda \right)/E_0\left(\lambda \right)$ is a function of the current secant stiffnesses $E\left(\lambda \right)=F\left(\lambda \right)/A^{\text{axon}}-1]$ and $E_0\left(\lambda \right)$ of the damaged and undamaged axon (thin dotted lines). To see this figure in color, go online.

To model the force-stretch behavior of the damaged axon, we apply a characteristic force of $F_0=10$ pN. The detachment rate of the cross-links will then increase significantly when we apply an external displacement to the axon. Consequently, the total number of cross-links will decrease and induce a loss in stiffness, which we interpret as axonal damage. Fig. 6 illustrates characteristic force-stretch curves of the damaged axon by means of dashed lines for fast and slow loading. If the force-stretch curve follows the simulation without damage, $E\left(\lambda \right)=E_0\left(\lambda \right)$, the damage parameter is zero, $d\left(\lambda \right)=0$; if the axon separates into two entirely disconnected segments, $E\left(\lambda \right)=0$, the damage parameter is one, $d\left(\lambda \right)=1$.

Results

Cross-link model

First, we verified the implementation of our cross-link model into our axon model by comparing discrete detachment histograms to the analytical detachment probability of Eq. 5 (cross-link model). To create histograms of detachment from our axon model simulation, for every event of cross-link detachment, we store the associated force and time at detachment. We assume that the cross-link force increases linearly in time, such that the loading rate at detachment is simply the force divided by time. We can then create histograms of the force at detachment F for any particular loading rate $r_f$. These detachment histograms should be consistent with the detachment probability $p=k/r_f\text{exp}\left(-F_0/r_f\left[k-k_0\right]\right)$ as a function of the loading rate $r_f$ and the detachment rate $k=k_0\text{exp}\left(F/F_0\right)$, which is a function of the force F.

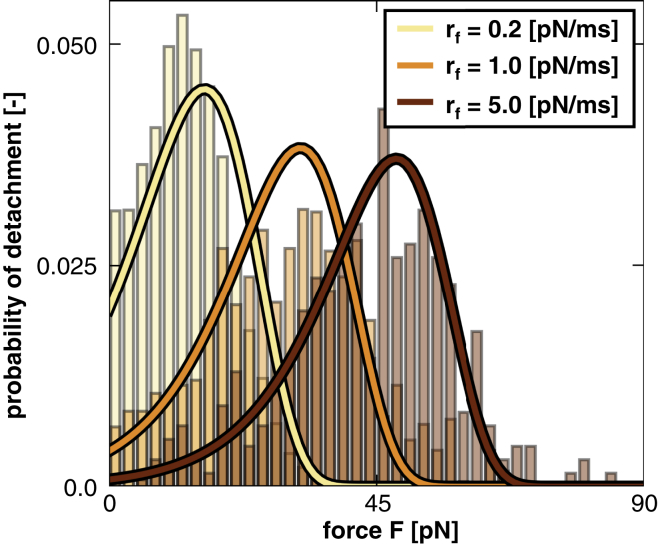
Fig. 7 illustrates the probability of cross-link detachment or reattachment for three different loading rates $r_f$ at varying external force levels F. Increasing the loading rate shifts the probability of detachment into the higher force regime. The detachment histograms of the discrete axon model agree well with the analytical detachment probability of Eq. 5 (cross-link model), especially for larger loading rates $r_f$. Discrepancies are most likely a result of nonlinear increase of the cross-link force with time, as discussed in detail in the Supporting Materials.

Figure 7.

Cross-link model. All cross-links can dynamically detach from and reattach to their microtubules. The probability of cross-link detachment or reattachment $p=k/r_f\text{exp}\left(-F_0/r_f\left[k-k_0\right]\right)$ is a function of the detachment or reattachment rate $k=k_0\text{exp}\left(F/F_0\right)$ and the loading rate $r_f$. The detachment histograms illustrate the effects of varying the loading rate $r_f$ and the external force F in our discrete axon model in comparison to the solid lines of the analytical detachment probability p. To see this figure in color, go online.

Axon model

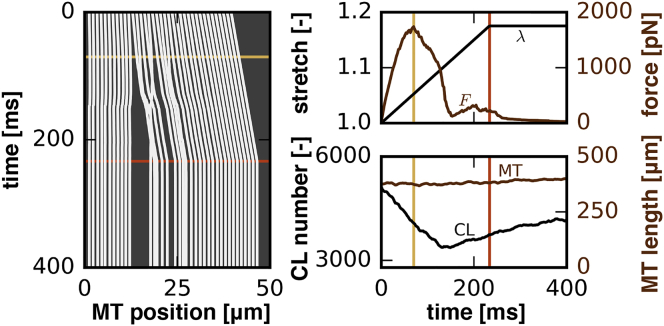
Fig. 8 illustrates a representative output of a single simulation with our axon model. We performed a displacement-controlled simulation and prescribed a stretch of $\lambda =1.15$ at a stretch rate of $\dot{\lambda }=0.075/\text{ms}$. The output consists of the external force F required to generate the prescribed stretch λ (top right) and the associated total number of cross-links and total microtubule length (bottom right), monitored throughout the entire simulation as functions of time. To provide an illustrative summary of the simulation, we also create kymographs of the microtubule positions as a function of time (left). The kymograph shows the spatio-temporal position of all microtubules, represented through their centers, with respect to the longitudinal position along the axon. The beige and brown lines highlight the time points associated with the maximum force and maximum stretch. In the kymograph, these time points are associated with progressive axonal damage and with the complete separation of the proximal and distal ends.

Figure 8.

Axon model. Representative output of a single simulation with a prescribed stretch of $\lambda =1.15$ at a stretch rate of $\dot{\lambda }=0.075/\text{ms}$. External force required to generate the prescribed displacement (top right), total number of cross-links and total microtubule length (bottom right), and kymographs of the microtubule positions (left), all monitored throughout the entire simulation as functions of time. Beige and brown lines highlight maximum force and maximum stretch associated with progressive axonal damage and with the complete separation of the proximal and distal ends. To see this figure in color, go online.

Axonal force, stiffness, and damage

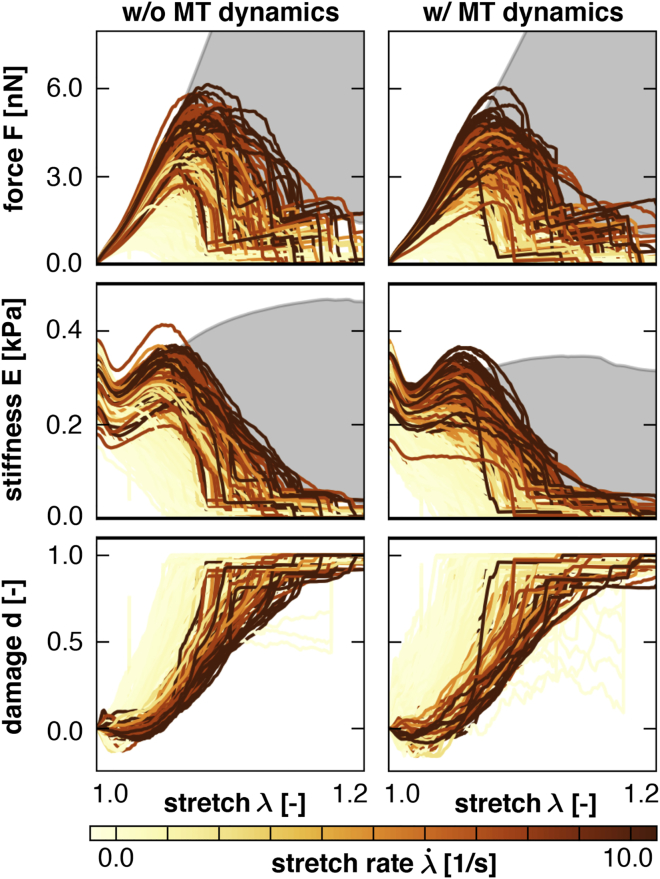
Fig. 9 summarizes the result of $n=1440$ axon model simulations at varying stretch rates $\dot{\lambda }$, both without and with microtubule dynamics. The horizontal axis in all plots represents the applied stretch λ at the distal end of the axon. The gray background region highlights the response of the undamaged elastic axon model according to the solid lines in Fig. 6; the colored curves summarize the response of the damaged axon model according to the dashed lines in Fig. 6. Every colored curve is associated with a single simulation and its color indicates the applied stretch rate. As cross-links detach, the colored curves begin to deviate from the elastic response.

Figure 9.

Force F, stiffness E, and damage d versus stretch λ for $n=1440$ axon model simulations with varying stretch rates $\dot{\lambda }$, without and with microtubule dynamics. The boundary of the gray region indicates the undamaged elastic response $E_0$. Every colored curve is associated with a different stretch rate and begins to deviate from the elastic response as cross-links detach. The accumulation of cross-link detachment gradually results in a decrease in force, a decrease in stiffness, and an increase in damage. Including microtubule (MT) dynamics decreases the elastic force and stiffness, whereas the damage characteristics remain virtually unaffected. To see this figure in color, go online.

Fig. 9, top, shows the force F required to maintain the prescribed stretch λ. All simulations display an initial increase in force as the stretch increases. Each curve begins to deviate from the elastic regime at its own characteristic stretch level, experiences a peak at its own characteristic stretch, and undergoes gradual softening. Geometric nonlinearities, as explained in the Supporting Material, create a brief hardening regime before all force-stretch curves decay rapidly as the proximal and distal ends of the axon separate completely. Fig. 9, middle, displays the secant stiffness E versus applied stretch λ. These curves are a result of the force-stretch curves as depicted in Fig. 6. Again, the gray background and the curves represent the stiffness of the axons without and with damage, respectively.

Fig. 9, bottom, summarizes the accumulation of damage d with increasing stretch λ. At each stretch level, we can calculate damage $d\left(\lambda \right)=1-E\left(\lambda \right)/E_0\left(\lambda \right)$ using Eq. 9. We can interpret damage visually as the deviation of each secant stiffness curve E from its undamaged elastic stiffness $E_0$ in the gray background. The individual damage curves demonstrate that the higher the loading rate $\dot{\lambda }$, the higher the required stretch λ to initiate axonal damage. This trend is consistent with the cross-link model in Fig. 7. Finally, the left and right columns of the force, stiffness, and damage graphs in Fig. 9 represent simulations without and with microtubule dynamics. Interestingly, the undamaged, elastic force-stretch and stiffness-stretch curves in the gray backgrounds are markedly different with and without microtubule depolymerization: both force and stiffness decrease when allowing for the dynamic polymerization and depolymerization of individual microtubules.

Damage contours

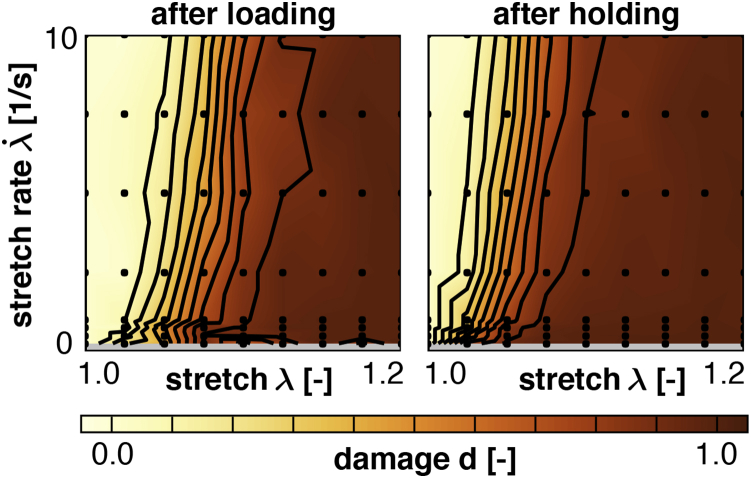
To illustrate the effects of varying stretch and stretch rates on the accumulation of axonal damage, we systematically varied the stretch $\lambda =\left[1.0,\dots ,1.2\right]$ and stretch rates $\dot{\lambda }=\left[0,\dots ,100\right]/\text{s}$. For each combination of λ and $\dot{\lambda }$, we performed $n=10$ discrete axon model simulations and quantified the amount of axonal damage for each simulation. We summarize the result of all $n=720$ simulations in contour plots of the damage parameter d.

Fig. 10 shows the damage contours d for $n=720$ axon model simulations without microtubule dynamics at the end of the loading period and at the end of the holding period. The contours clearly show that damage increases with increasing stretch λ and decreases with increasing stretch rate $\dot{\lambda }$. Both observations are consistent with the cross-link model as illustrated in Fig. 7. By comparing the damage contours after loading and holding, we conclude that damage further increases during the holding period. This increased vulnerability to damage is particularly visible in regions of moderate stretch, on the order of $\lambda =1.02$ to $\lambda =1.10$, where damage further increased up to 30% during holding. This is consistent with the cross-link model: cross-links continue to be stretched during holding, their detachment rate is larger than their attachment rate, and the overall number of cross-links decreases.

Figure 10.

Damage contours d from $n=720$ axon model simulations with varying stretch λ and stretch rates $\dot{\lambda }$, without microtubule dynamics. Damage increases with increasing stretch and decreases with increasing stretch rate. Damage is initiated during loading, $\dot{\lambda }>0$(left), and continues to accumulate during holding, $\dot{\lambda }=0$ (right). As the cross-links remain stretched during holding, $\lambda >1$, the cross-link detachment rate is greater than the attachment rate, resulting in an overall increase in damage. To see this figure in color, go online.

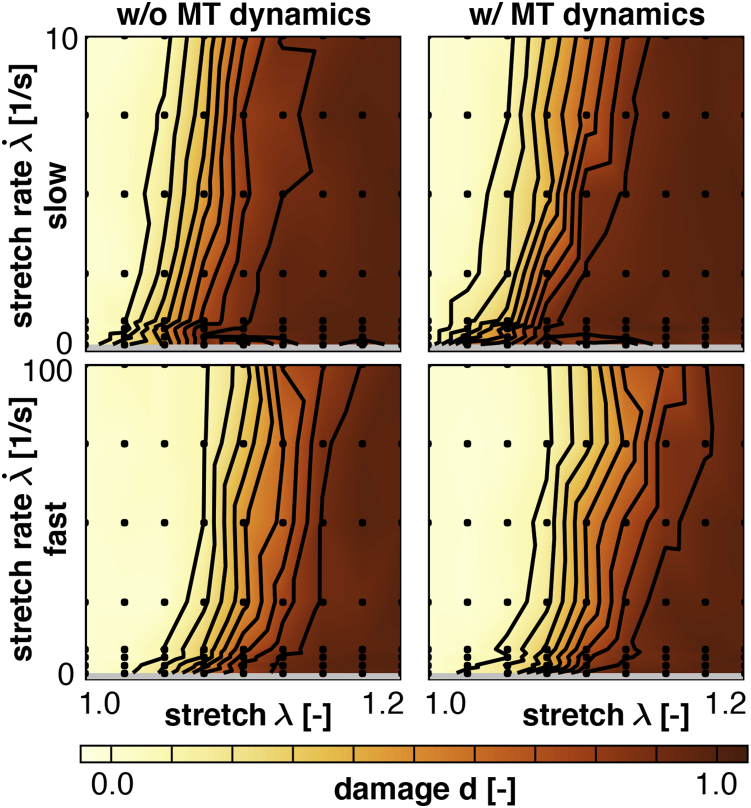
Fig. 11 shows the damage contours d for $n=2880$ axon model simulations at slow and fast loading, without and with microtubule dynamics. For reference, Fig. 11, top left, is the same as Fig. 10, left. The bottom row confirms that increased loading rates lead to a lower damage at the end of the loading period. The right column indicates that axonal damage increases margninally with microtubule dynamics, and that this effect is more pronounced at low loading rates. In regions of moderate stretch, on the order of $\lambda =1.10$, damage increased up to 20% with microtubule dynamics. These findings are consistent with our model: microtubule depolymerization causes an immediate removal of cross-links, whereas microtubule polymerization initiates a delayed reattachment of cross-links. As a consequence, with microtubule dynamics, the axon becomes more susceptible to damage. At low loading rates, when there is more time for microtubules to polymerize and depolymerize, this effect is more pronounced.

Figure 11.

Damage contours d from $n=2880$ axon model simulations with varying stretch λ and stretch rates $\dot{\lambda }$, for slow and fast loading, without and with microtubule dynamics. Damage increases with increasing stretch and decreases with increasing stretch rate. Including microtubule (MT) dynamics increases damage, especially at lower stretch rates. To see this figure in color, go online.

Cross-link stretch

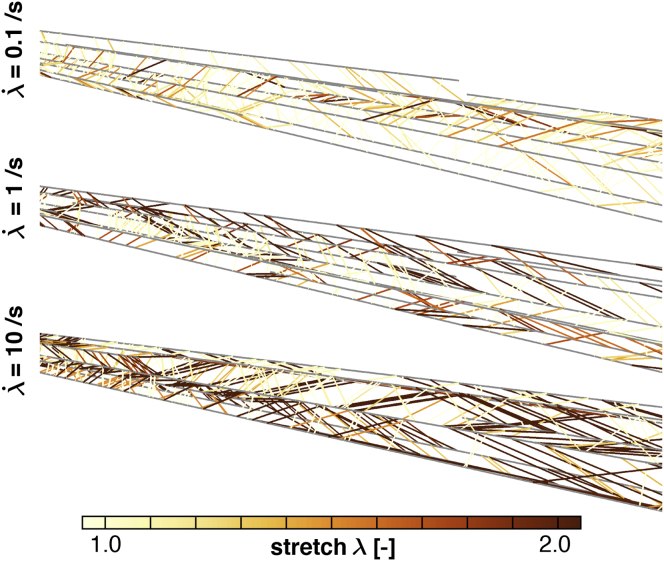
Fig. 12 illustrates the effect of varying stretch rates on the molecular-level stretch of individual cross-links. We stretched three axons to $\lambda =1.05$, but applied the stretch at different stretch rates $\dot{\lambda }$, and plotted representative sections along the axon. At lower stretch rates $\dot{\lambda }$, the axonal response is dominated by cross-link dynamics, a net reduction of cross-links, and a gradual accumulation of damage. The few remaining cross-links do indeed experience less stretch, which confirms the viscous trends in Fig. 9. At higher stretch rates $\dot{\lambda }$, the axonal response is dominated by cross-link deformations, a rapid increase in stretch, and an immediate risk of rupture. The many remaining cross-links undergo large stretching, which agrees with the viscous observations in Fig. 9. Consistent with viscous effects, the cross-link stretch is low at low stretch rates and increases with increasing stretch rate.

Figure 12.

Cross-link stretch λ in representative sections of three axons at a prescribed stretch $\lambda =1.05$, applied at varying stretch rates $\dot{\lambda }$. Slow loading (top) is dominated by cross-link dynamics, a net reduction of cross-links, and a gradual accumulation of damage. Fast loading (bottom) is dominated by cross-link deformations, a rapid increase in stretch, and an immediate risk of rupture. To see this figure in color, go online.

Discussion

The axon is a highly dynamic system of microtubules cross-linked by tau and other proteins and surrounded by an actin and spectrin cortex. Understanding the dynamic interplay of these components is essential to gain better insight into the physiological integrity of the axon and its pathological degradation by a biochemical or mechanical insult. We have previously demonstrated how to identify macroscopic axonal stiffness and viscosity as emergent properties from microscopic cross-linking mechanisms. Here, we extend this concept to characterize macroscopic axonal damage. We establish a mechanistic axonal model that consists of a network of dynamically polymerizing and depolymerizing microtubules connected by dynamically detaching and reattaching cross-linking proteins. We explore axon damage as a result of an external mechanical stimulus that triggers in excessive detachment of cross-links. Although the probability of cross-link attachment is governed exclusively by thermal fluctuations, the probability of cross-link detachment also depends on physical forces and on the loading rate. It increases with increasing forces and decreases with the rate of loading. In addition, our model allows microtubules to polymerize and depolymerize, which further increases the probability of cross-link detachment. With these mechanisms in mind, the objective of this study was to relate the microscale dynamics of microtubules and cross-links to macroscopic damage accumulation within the axon. Ultimately, this will allow us to identify different safety level thresholds (liberal, conservative, or optimal) to characterize the risk of axonal failure.

In Fig. 7, we verified the implementation of the cross-linking mechanism into our computational model of Fig. 3. We summarized the results in a detachment histogram and showed that the probability of detachment as a function of force and force rate follows the analytical prediction of the Bell model (38), in agreement with Eq. 5. The general trend is that when increasing the loading rate, cross-links require a larger force to detach, which is consistent with earlier computational observations (34). At the same time, the expected attachment time decreases with increasing loading rates. We confirmed these trends by comparing damage contour plots for varying stretch and stretch rates in Fig. 11.

In Fig. 8, we illustrated a representative output of a single axon model simulation at prescribed stretch and stretch rate. Most illustrative is the initial nonlinear increase in force followed by a gradual decrease in force that indicates damage in Fig. 8 (top right). Our peak force at a stretch level of $\lambda =1.18$ agrees well with reported in vitro damage thresholds of 1.18 for functional damage and 1.21 for morphological damage in white matter tissue (46), and with the in vivo damage thresholds of 1.16 in a traumatic axonal injury model in adult rats (47). Initial nonlinearities of the force-displacement curves arise from viscous effects (48) and from geometric effects associated with a rotation of cross-links. These nonlinearities show remarkable qualitative agreement with reported force-displacement curves of the axon, both from experimental (49) and numerical (31) studies. The subsequent gradual decrease is a result of the excessive loss of cross-links and is consistent with the Bell model (38). This loss of cross-links leads to total failure of the axon when the proximal and distal ends of the axon separate into two unconnected bundles of microtubules. This separation is clearly visible in the kymograph in Fig. 8 (left). Fig. 8, bottom right, confirms that the total number of cross-links decreases during the first 150 ms of the simulation. However, after a short plateau, the number of cross-links begins to increase again. This effect is a result of the drop in axonal force that reduces the detachment rate to $k_{\text{detach}}\approx k_0$. Detached cross-links are still present in the cytosol and try to reattach to the axon. More cross-links are now trying to reattach than to detach. The net effect is that the total number of cross-links increases, although macroscopically, the axon is already separated into two parts. Fig. 8 also shows that the total microtubule length remains approximately constant, which is consistent with the choice of parameters in Table 1: the product of rate and time is equal for microtubule polymerization and depolymerization.

Fig. 9 shows the axonal force, stiffness, and damage as functions of stretch for $n=1440$ axon model simulations. These simulations were performed for a range of stretch rates of $\dot{\lambda }=\left[0,\dots ,10\right]/\text{s}$. The viscous response of the axon is apparent from Fig. 9 (top), showing that higher axonal forces are required at higher stretch rates. This trend is consistent with experimental findings on the viscous characterization of the axon (26). Our results clearly demonstrate the gradual accumulation of axonal damage in response to external loads. Fig. 9, bottom, highlights the evolution of the axon damage parameter d for each simulation. For low stretch rates, indicated by the light yellow curves, damage develops at a lower stretch, which is a direct result of our chosen cross-link mechanism. This trend agrees well with alternative axonal injury models in the literature that predicted a failure strain of 4% at a loading rate of 1/s, 5% at 10/s, and 6% at 50/s (35). In addition, our model predicts that damage accumulates rapidly within a narrow range of stretch at lower stretch rates, and more gradually within at higher stretch rates. Note, this trend is reversed if we consider damage development as function of time instead of stretch. A comparison of the simulations without and with microtubule dynamics reveals that, for our selected range of rate constants and stretch rates, axonal damage is sensitive to microtubule polymerization and depolymerization: depolymerization causes an immediate detachment of cross-links, whereas polymerization only results in a delayed attachment of cross-links. Consequently, including microtubule dynamics results in a net loss of cross-links, which manifests itself in a reduced axonal viscosity. At the same time, the undamaged elastic force-stretch curves without damage in the gray background do experience a significantly reduced stiffness in the presence of microtubule dynamics.

In Fig. 10, we present damage contours for varying stretch and stretch rates at the end of the loading and holding periods. The damage contours confirms our earlier observation of reduced damage at increased stretch rates, both after loading and holding. Notably, these observations agree with experimental findings on mechanical insults of axons for different stretch rates and magnitudes (50, 51). Our results demonstrate that damage further develops during the holding period as we maintain the applied stretch. This trend is a natural result of our cross-link mechanism, for which a cross-link force increases the detachment rate k and, with a constant attachment rate $k_0$, results in a net loss of cross-links. Our predicted gradual accumulation of damage agrees with an in vitro model of traumatic brain injury in which cell death accumulated gradually over time and increased by ∼50% from day 3 to day 4 (52).

Fig. 11 contains additional damage contour plots immediately after loading for different loading rates and without and with microtubule dynamics. Our model predicts an onset of damage at stretches as low as $\lambda =1.05$, which agrees with observed mild traumatic axonal injury thresholds of cortical axons in culture (53). Damage continues to accumulate until $\lambda =1.14$, a value that agrees with the conservative white matter tissue level threshold observed at strain rates of 30–60/s (46). Again, we observe clear and consistent differences in axon damage for the different loading regimes, whereas the effect of microtubule dynamics is marginal. At first sight, this observation seems counter intuitive. At low loading rates, we could expect that microtubule dynamics accelerate axonal damage since microtubules would have enough time to polymerize and depolymerize during the simulation. However, even at low loading rates, damage seems only marginally sensitive to the presence of microtubule dynamics. This observation can, at least in part, be explained by the displacement controlled simulations. Indeed, even though microtubule dynamics induce a net reduction of cross-links, the remaining cross-links do not have to compensate by carrying more force because of displacement controlled loading. This implies that the probability of detachment is not affected by microtubule dynamics. The impact of microtubule dynamics is, therefore, captured by a reduction in axonal viscosity alone. On a general note, our microtubules polarize only at their plus ends, which are oriented toward the distal side of the axon. However, our overall results in Fig. 11 are not sensitive to microtubule orientation. Our current model could therefore be directly applied to dendrites, which display randomly oriented microtubules.

Fig. 12 shows a representative section of our axon model for three simulations in which the axon is loaded at different stretch rates up to the same stretch magnitude. This figure captures the two main trends that we have observed and discussed in this section. First, Fig. 12 shows that cross-links experience more stretch at higher applied stretch rates, which illustrates the viscous character of the axon (48). Indeed, the probability that cross-links have released energy by detaching from the microtubules is smaller at high, applied stretch rates. Second, Fig. 12 illustrates a lower cross-link density at lower stretch rates. This observation is indicative of excessive cross-link detachment at low stretch rates, and thereby, of increased axon damage d. Ultimately, it would be interesting to derive a single analytical expression for the damage parameter d. In practice, this is extremely difficult because axonal damage is always governed by the weakest cross section and by the number of available load paths. Identifying these load paths is a highly combinatorial problem, as described by percolation theory (36).

Limitations

Although our model is a promising first step toward understanding the interaction of different failure mechanisms within the axon, we recognize several limitations that should be addressed in future models. First, our current axon model consists of idealized microtubules and cross-links, which is a great simplification of the real axonal anatomy. Although microtubules and cross-links are undoubtedly the mechanically most relevant substructures of the axon, we have not yet included the actin cortex, which could provide additional mechanical support to stabilize the axon against damage. Our current model also only accounts for longitudinal motion of microtubules and neglects lateral, bending, and twisting motions, which may increase the likelihood of axonal damage. Second, so far, we have modeled all cross-linking proteins collectively using the phenomenological Bell model. Although this model has been verified for a wide range of chemical bonds, it is not specific to the axon and to mechanisms related to tauopathies or traumatic brain injury, and other models could be more appropriate. Third, experimental evidence suggests that breaking of microtubules further accelerates axonal degeneration (54). Our model currently lacks a mechanism by which microtubules can break. The inherent modularity of our axon model allows us to address these three limitations by simple local modifications. Fourth, our external loading consists of axonal stretch at varying stretch rates. We have long known the devastating effects of shear loadings to the human brain (55, 56), and recent molecular level studies suggest that axonal shear can be equally, if not more damaging to the axon than axonal stretch alone (35). In future studies, we will explore the effect of different types of loading, including stretch, shear, bending, and twist. However, many microscopic mechanisms of axonal damage are yet unknown and therefore require more experimental research or molecular level simulations.

Conclusions

Taken together, our results demonstrate how molecular level mechanisms associated with cross-link and microtubule dynamics modulate cellular level force, stiffness, and damage, and how axonal damage changes in response to physical forces. Our simulations predict axonal damage for varying stretches and stretch rates and provide quantitative insight into the molecular failure mechanisms within the axon. We anticipate that our axon model could become a powerful tool to simulate, understand, and predict individual failure mechanisms in response to traumatic impact to the brain.

Author Contributions

R.d.R. designed the research, performed the research, developed the computational tools, analyzed the data, and wrote the manuscript. E.K. designed the research, performed the research, and wrote the manuscript.

Editor: Philip LeDuc.