Collective Cell Migration in Embryogenesis Follows the Laws of Wetting

Abstract

Collective cell migration is a fundamental process during embryogenesis and its initial occurrence, called epiboly, is an excellent in vivo model to study the physical processes involved in collective cell movements that are key to understanding organ formation, cancer invasion, and wound healing. In zebrafish, epiboly starts with a cluster of cells at one pole of the spherical embryo. These cells are actively spreading in a continuous movement toward its other pole until they fully cover the yolk. Inspired by the physics of wetting, we determine the contact angle between the cells and the yolk during epiboly. By choosing a wetting approach, the relevant scale for this investigation is the tissue level, which is in contrast to other recent work. Similar to the case of a liquid drop on a surface, one observes three interfaces that carry mechanical tension. Assuming that interfacial force balance holds during the quasi-static spreading process, we employ the physics of wetting to predict the temporal change of the contact angle. Although the experimental values vary dramatically, the model allows us to rescale all measured contact-angle dynamics onto a single master curve explaining the collective cell movement. Thus, we describe the fundamental and complex developmental mechanism at the onset of embryogenesis by only three main parameters: the offset tension strength, α, that gives the strength of interfacial tension compared to other force-generating mechanisms; the tension ratio, δ, between the different interfaces; and the rate of tension variation, λ, which determines the timescale of the whole process.

Introduction

The miracle of life starts with a movement. In zebrafish, this movement is called epiboly and consists of a continuous spreading motion of the blastoderm—the cluster of ∼1000 cells that forms the early embryo—over the spherical yolk cell (Fig. 1 a). During epiboly the cluster spreads toward the opposite pole until the yolk is fully covered by cells (1, 2). The onset of epiboly is a key event for correct development and hence, it is very important for the organism that it is driven by a robust mechanism (2). As illustrated in Fig. 1 a, epiboly starts ∼4 h post-fertilization (hpf), at a time when the embryo/yolk system is of spherical shape. At this stage, one can already distinguish three cell populations in the blastoderm: the enveloping layer (EVL), which covers the embryo by forming the epithelial layer enclosing the blastoderm; the yolk syncytial layer (YSL), situated at the interface between the yolk and the blastoderm; and the deep cells, which are enclosed by the EVL and the YSL (3, 4).

Figure 1.

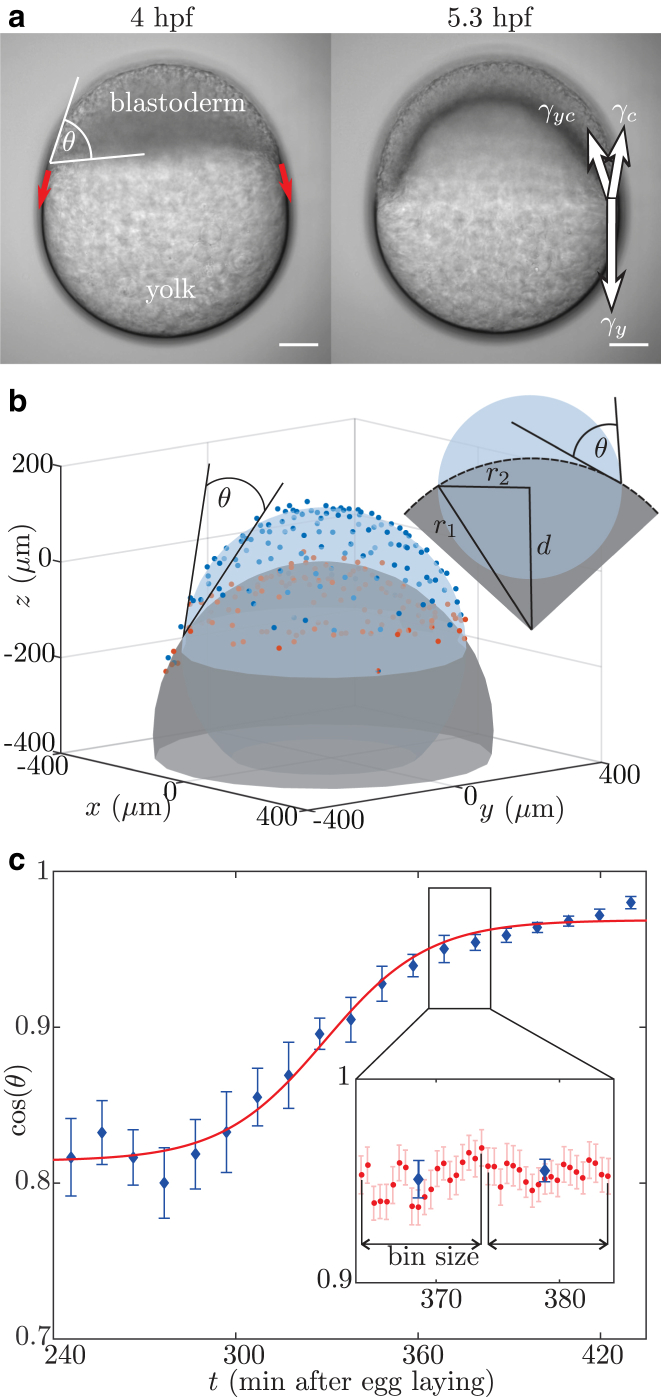
The contact angle is measured over time. (a) Beginning at 4 hpf (left), the cells forming the blastoderm move from the animal pole toward the vegetal pole of the yolk (red arrows). During this process, there are three different materials—yolk, cells, and medium—in contact, leading to interfaces carrying tension (right, white arrows). Scale bars, 100 μm. (b) The nuclei defining the yolk-blastoderm (red) and the nuclei defining the cells-medium (blue) interfaces are extracted from detected spots by filtering for nuclei close and away from the yolk. Spheres are fitted to these two sets of nuclei, and from the radii, $r_{\mathrm{1,2}}$, and distance, d, of the two spheres, the contact angle, θ, is calculated. (c) The measured contact-angle dynamics shows a clear time dependence. Although it stays constant at the beginning of the experiments, the angle becomes smaller, corresponding to an increase in the $cos\left(\theta \right)$, which finally reaches a plateau. Such a behavior corresponds to a wetting model (8), which is fitted to the experimental data (red curve). The time is displayed in minutes after egg laying. (Inset) To reduce the plotted data, 20 points (red) are binned and the mean and error (blue) are presented. To see this figure in color, go online.

The controlled collective cell migration during epiboly suggests a major role of mechanics (5, 6, 7), and previous studies have identified rearrangement of the deep cells, pushing forces in the yolk, and the integrity of the EVL as important elements for epiboly (2, 8, 9, 10). In a recent work, an active expansion of the EVL layer in combination with anisotropic stresses in the blastoderm was identified to be important for epiboly, and crucial for doming (11), which is the bulging motion of the yolk toward the vegetal side. This recent analysis successfully modeled the upward bulging of the yolk, but connecting simple experimentally accessible parameters such as the contact angle between the blastoderm and yolk cell to the spreading motion of epiboly was only possible by combining it with active stress within the epiblast. The robust nature of epiboly suggests that it is at least partially driven by fundamental forces such as a continuous change in surface tension acting in combination with pulling forces generated by an actomyosin ring at the contact line (6) (Fig. 3 a). Here, we show that the complex collective motion of more than 1000 cells in the early embryo can indeed be quantitatively described by the physics of wetting (12). Our approach is motivated by previous work that has employed wetting to successfully model collective cell migration in the context of cancer aggregates spreading on a solid surface, where typical features such as precursor films are observed (13, 14). Conceptually, the analogy between cells spreading and a liquid wetting a surface is based on the presence of three different materials with different properties—the cells, the yolk, and the surrounding medium (Fig. 1 a)—that meet at a three-phase contact line. Here, the role of a precursor film is taken by the few leading cells that extend over the yolk, called external YSL (Fig. 3 a). The wetting approach assumes that the system can be described as a liquid, so that only scales that are large compared to the single cell length are considered in the tissue-level description.

Figure 3.

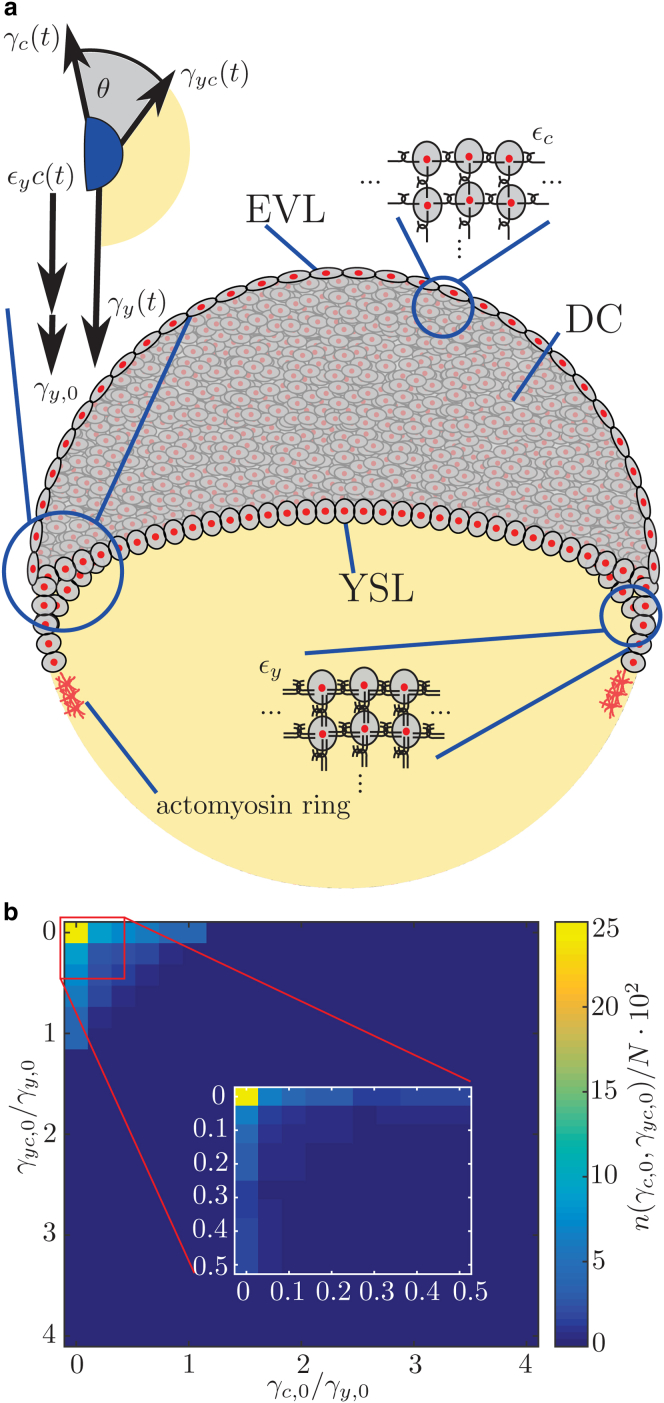
The wetting model for epiboly. (a) At the onset of epiboly, the embryo consists of the cell cluster at the animal pole of the embryo (gray) and the yolk at the vegetal pole (yellow). The cells at the cells-medium and the yolk-cells interface interact mechanically with adjacent cells, resulting in net forces of ${\gamma }_{\text{c}}\left(t\right)$ and ${\gamma }_{\text{yc}}\left(t\right)$, respectively. The mechanical interaction of the cells of the precursor film leads to the contribution ${\mathit{ϵ}}_{\text{y}}c\left(t\right)$ to ${\gamma }_{\text{y}}\left(t\right)$. In addition, the actomyosin ring exerts a pulling force ${\gamma }_{\text{y,0}}$, that also contributes to ${\gamma }_{\text{y}}\left(t\right)$. The region where the interfaces meet is the contact zone (blue), which consists of several cells to maintain the tissue scale. The EVL, YSL, and deep cells (DC) are labeled. (b) Scanning of parameter values and applying general conditions to the according solutions. First, the parameters ${\mathit{ϵ}}_j{c}_{\text{s}}/{\gamma }_{\text{y,0}}$ and ${\gamma }_{i,0}/{\gamma }_{\text{y,0}}$ are picked from the interval $\left[0,{10}^4\right]$ using logarithmic spacing. After applying general conditions to the functions of each parameter combination, a maximum of the number of valid solutions, $n\left({\gamma }_{\text{c,0}},{\gamma }_{\text{yc,0}}\right)$, is found for small ${\gamma }_{\text{c,0}}/{\gamma }_{\text{y,0}}$ and ${\gamma }_{\text{yc,0}}/{\gamma }_{\text{y,0}}$. A total of $N=1.3\times {10}^6$ valid combinations is found after evaluating $1.2\times {10}^8$ parameter combinations. Then, the search is refined by picking equidistant values from the interval $\left[\mathrm{0,4}\right]$ for the parameters ${\gamma }_{\text{c,0}}/{\gamma }_{\text{y,0}}$ and ${\gamma }_{\text{yc,0}}/{\gamma }_{\text{y,0}}$. The parameters ${\mathit{ϵ}}_j{c}_{\text{s}}/{\gamma }_{\text{y,0}}$ are chosen from the interval $\left[0,{10}^4\right]$ using logarithmic spacing between values. Again, a clear maximum is found for small ${\gamma }_{\text{c,0}}/{\gamma }_{\text{y,0}}$ and ${\gamma }_{\text{yc,0}}/{\gamma }_{\text{y,0}}$ (inset). Here, a total of $N=55\times {10}^6$ valid combinations is found after evaluating $6.4\times {10}^9$ parameter combinations. In each instance, the function $f\left(t\right)$ is evaluated for 20 time points $t^{\prime }=\lambda \left(t-t_{1/2}\right)$ in the interval $\left[-\mathrm{10,10}\right]$. To see this figure in color, go online.

The scope of this report is to present and experimentally test a minimal model that only uses surface tension to describe the dynamics of the contact angle, thus providing a simple model that explains epiboly without including the more complex process of doming. A key difference from previous work is the definition of the contact angle on a tissue scale, as well as a systematic approach to simplify the law of wetting, which eventually leads to successful rescaling of the contact-angle dynamics of different embryos and collapsing them into a master curve. Furthermore, the presented model predicts a stringent relation between its fit parameters, which is demonstrated in the measurements.

Materials and Methods

Embryo preparation

To investigate collective cell migration in the context of epiboly, we image the embryo during a 4 h time span starting with the onset of migration at 4 hpf and ending at 8 hpf, where epiboly is at 75%, hence covering three-fourths of the yolk (1). Tg(ßactin:H2AmCherry) transgenic embryos expressing mCherry fluorophore in all nuclei are raised and imaged under physiological conditions at 28°C using selective plane illumination microscopy (15). The zebrafish are handled according to the regulations of the state of North Rhine-Westphalia, supervised by the veterinarian office of the city of Münster.

Microscopy and three-dimensional cell tracking

Three-dimensional image stacks are acquired with a z-step of $2\mu \text{m}$ and a lateral resolution of $0.37\mu \text{m}$, sufficient to resolve and track the marked nuclei of single cells. The nuclei positions are detected subsequently in the acquired stacks by adapting a modified version of standard detection algorithms (16) using a Laplacian of Gaussian detector (17) and an estimated nucleus diameter of $8\mu \text{m}$. To reliably detect nuclei, filters are applied to the quality and the mean intensity of the detected spots.

Contact-angle measurements

The nuclei defining the yolk-cells interface and the nuclei defining the cells-medium interface are extracted from the list of detected nuclei (Fig. 1 b) by dividing the xy-plane in $50$ × $50\mu {\text{m}}^2$ sections and looking for the nuclei closest to and farthest away from the yolk, respectively. The contact angle, θ, can be efficiently determined by fitting a sphere to each group of nuclei. Then, knowing the distance, d, between the origin of the spheres and their radii, $r_{\mathrm{1,2}}$, gives the contact line as their intersection, and straightforward trigonometry determines θ (Fig. 1 b).

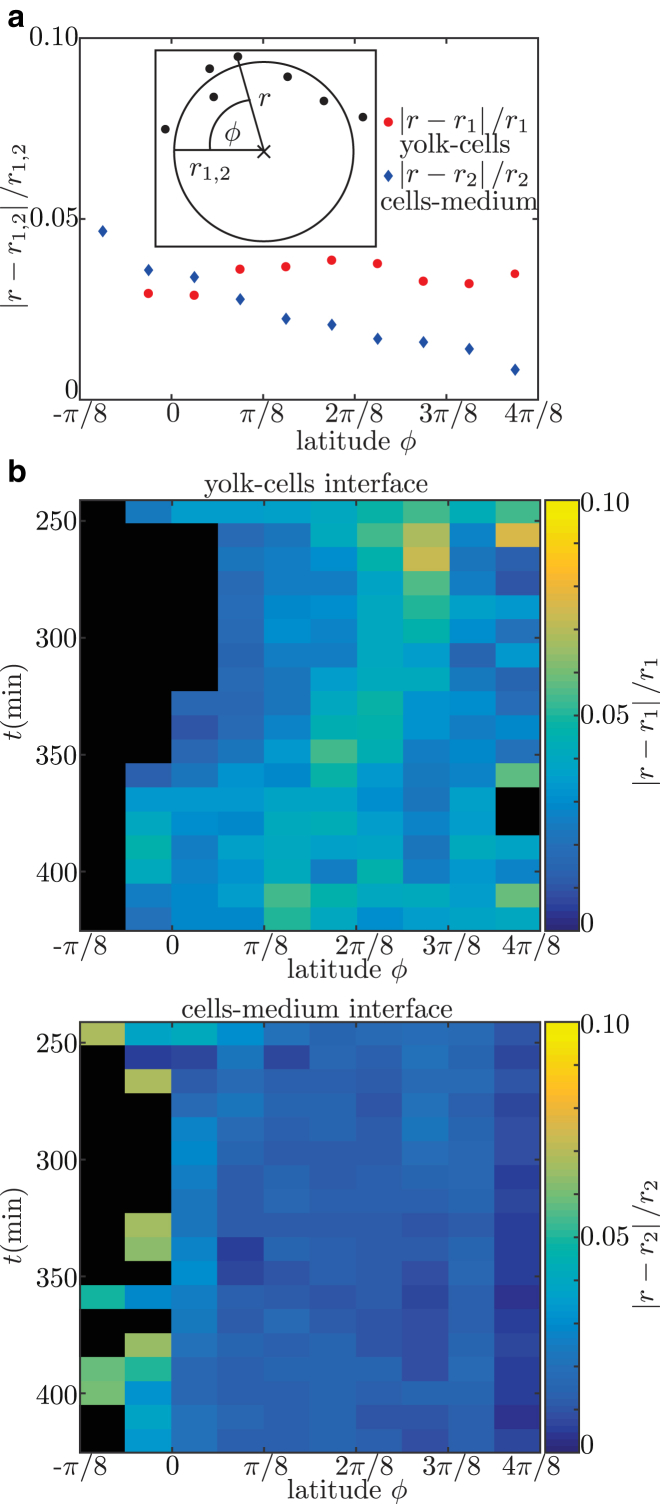
This implies that the contact angle is defined using the tissue scale, and is independent of the details at the single cell level near the contact point. Fitting spheres to the interfaces requires a constant curvature, which is a key assumption for a purely surface-tension-based model as proposed here. The validity of this assumption was checked by calculating the relative error $\left|r-r_{\mathrm{1,2}}\right|/r_{\mathrm{1,2}}$ between the fitted spheres and experimentally measured cell positions for all performed contact-angle measurements (Fig. 2 a). This relative error is evaluated depending on the latitude, ϕ, along the sphere. In the case of uniform curvature, one expects no dependence of relative error on latitude. This is the case for the yolk-cells interface (red). For the cells-medium interface (blue), a linear dependence of relative error and latitude is observed. Nevertheless, given the difference of 4% between a point at the equator and a point at the pole, the local change in curvature is small. To check whether the described situation is valid for all observed developmental stages, the relative error is plotted over time for a single embryo (Fig. 2 b). There is no observable systematic dependence of relative error on time. This allows us to evaluate the variation in the contact-angle measurements due to the curvature error. The variation of curvature is estimated by $\Delta r_{\mathrm{1,2}}/r_{\mathrm{1,2}}=\text{max}\left(\left|r-r_{\mathrm{1,2}}\right|/r_{\mathrm{1,2}}\right)<0.05$ (Fig. 2 a). Classical error propagation yields $\Delta \text{cos}\theta /\text{cos}\theta <\Delta r_{\mathrm{1,2}}/r_{\mathrm{1,2}}<0.05$. This is neglectable, since the variation of $\text{cos}\theta$ over time is of the order of 25% and the error has no time dependence.

Figure 2.

The error due to assuming constant curvature is estimated. (a) The relative error, $\left|r-r_{\mathrm{1,2}}\right|/r_{\mathrm{1,2}}$, of each nucleus defining the yolk-cells interface $\left(r_1\right)$ and the cells-medium interface $\left(r_2\right)$ is calculated (inset). This relative error is evaluated in dependence of latitude, ϕ, by averaging over the values in bins of size $\Delta \varphi =\pi /16$. The plot shows data of all performed contact-angle measurements of $n=14$ embryos for the yolk-cells (red circles) and cells-medium (blue diamonds) interfaces. (b) To check a possible time dependence of the relative error, it is plotted here for an individual embryo with color-coding depending on time and latitude. This is done for yolk-cells (top) and cells-medium (bottom) interfaces. The same embryo is used as in Fig. 1. Black indicates areas for which no data were available. To see this figure in color, go online.

To ensure a precise measurement of the contact-angle dynamics, the time interval between three-dimensional stacks was 30–37 s and remained fixed for each embryo. In the data presented here, the detected contact angle, $\theta \left(t\right)$, is averaged in bins of 20 measurements (Fig. 1 c), and in the following, all data are presented as the mean $\pm$ SD, unless otherwise stated. However, fits of the contact-angle data are performed using the unbinned data.

Volume measurements

The image data of the embryos used for the contact-angle measurements are analyzed to obtain the total volume of the cell cluster located at the animal pole of the embryo. The surface of the cell cluster is segmented using image analysis software (Imaris 9.0, Bitplane AG) by applying a threshold to intensity and connecting close voxels. The volume enclosed by the segmented surface is calculated. To measure cell-cluster volume over time, measurements are started at $t=240\text{min}$ and repeated every 30 min. Please note that one embryo used for the contact-angle measurements is excluded from volume measurements, since it partly drifts out of the field of view.

Parameter search

The performed parameter search aims at identifying regions in the parameter space of the general model presented here that are consistent with the experimentally found characteristics. These features are formalized as the conditions that 1) $0<\text{cos}\theta \left(t\right)<1$, and 2) that $\text{cos}\left(\theta \right)$ is an increasing function $\partial \text{cos}\left(\theta \right)/\partial t>0$ in time.

Initially, the parameter space is roughly scanned by varying ${\mathit{ϵ}}_j{c}_{\text{s}}/{\gamma }_{\text{y,0}}$ and ${\gamma }_{j,0}/{\gamma }_{\text{y,0}}$ over four orders of magnitude in the interval $\left[0,{10}^4\right]$ using logarithmic spacing between evaluated parameter values and checking against formalized features 1 and 2. Only parameter combinations including small values of ${\gamma }_{\text{c,0}}/{\gamma }_{\text{y,0}}$ and ${\gamma }_{\text{yc,0}}/{\gamma }_{\text{y,0}}$ fulfill both conditions. To further refine the search of valid parameter combinations, in a second step, equidistant values for ${\gamma }_{\text{c,0}}/{\gamma }_{\text{y,0}}$ and ${\gamma }_{\text{yc,0}}/{\gamma }_{\text{y,0}}$ are chosen from the interval $\left[\mathrm{0,4}\right]$. Again, ${\mathit{ϵ}}_j{c}_{\text{s}}/{\gamma }_{\text{y,0}}$ is varied in the interval $\left[0,{10}^4\right]$ using logarithmic spacing. By applying conditions 1 and 2 to the functions obtained for the different parameter combinations, a maximal number of solutions is found for ${\gamma }_{\text{c,0}}/{\gamma }_{\text{y,0}}\ll 1$ and ${\gamma }_{\text{yc,0}}/{\gamma }_{\text{y,0}}\ll 1$ (Fig. 3 b).

Numerical simulation

We performed direct numerical time simulations of the model using the open-source flow solver Gerris (18, 19), which numerically solves the incompressible Navier-Stokes equation on a non-uniform flow-adaptive grid. The interface-tracking volume of fluid implementation in Gerris facilitates the efficient solution of multiphase problems. Here, three phases are taken into account: cells, yolk, and the surrounding medium. The code provides a combination of a quad/octree discretization, a generalized height-function curvature estimation and a balanced-force surface-tension scheme and has been validated to give accurate results for surface-tension-driven flows (http://gfs.sourceforge.net/tests/tests/).

We solve the equations in a non-dimensional form for a Reynolds number, $\text{Re}=0.001$, which defines the ratio of inertial forces to viscous forces within a fluid and a Weber number, We$=0.001$, which measures the relative importance of the fluid’s inertia compared to its surface tension. As the dynamics in zebrafish epiboly is strongly over-damped, the exact values Re and We only set an arbitrary timescale, for which the dynamics takes place quasi-statically. After a relaxation of the initial condition, the relative strengths of the interfacial tensions at the three different interfaces are chosen according to Eqs. 2, 3, and 4 with the parameters ${\gamma }_{\text{yc,0}}={\gamma }_{\text{c,0}}=0$, $\alpha =0.05$, $\delta =0.53$, $t_0=5.4$ and $\lambda =2.2$, which correspond to the mean values of the experimentally estimated parameters.

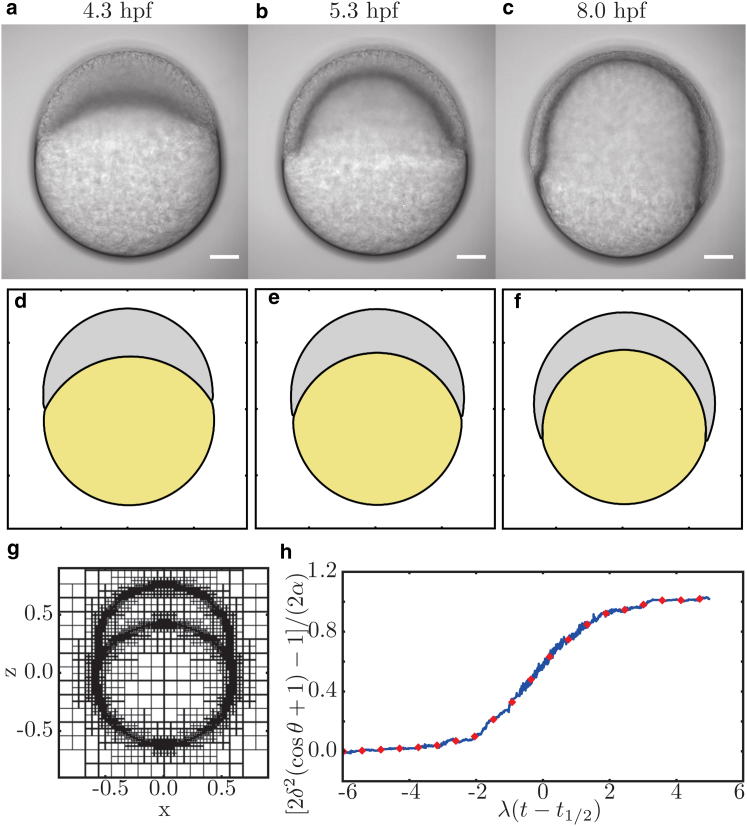
The size of the (square) simulation domain is 1.5 embryo diameters, with Neumann conditions applied at the boundaries of the two-dimensional simulation box. The discretization is controlled adaptively every 100th time step, with a refinement at the interfaces and a maximal resolution of $2^8$ grid points per box length (see Fig. 5 g for exemplary grid). The contact angle is measured by the same fitting procedure that is used for the experimental data. To reduce the data, the measured contact-angle data are binned and the mean of the intervals is presented (see Fig. 5 h).

Figure 5.

Comparison of (a–c) embryonic development and (d–f) DNSs. (a and d) At 4.3 hpf, directly after the onset of epiboly movements, the DNS is in perfect agreement with embryonic development. (b and e) When development proceeds to 50% epiboly at 5.3 hpf, the first deviations occur. For instance, the thickness of the cell layer at the animal pole relative to a position close to the contact line is larger in silico compared to in vivo. (c and f) This trend continues when epiboly reaches 75% at 8 hpf. The scale bar represents $100\mu \text{m}$. The units of simulations are arbitrary for space and time. The pictures used for comparison are chosen according to epiboly progression. (g) Exemplary visualization of the used grid refinement. (h) Reduction of the measured contact-angle data (blue) to binned mean values (red). To see this figure in color, go online.

Results

Contact angle changes characteristically over time

The time evolution of the cosine of the contact angle $\text{cos}\left(\theta \right)$ measured in experiments is shown in Fig. 1 c. After an initial stationary phase, we find a fast increase of $\text{cos}\left(\theta \right)$, which eventually levels off into a second plateau that corresponds to a pointed contact angle with a cosine close to 1. These characteristics are shared by all recorded data sets $\left(n=14\right)$. Such contact-angle dynamics is in sharp contrast to a recent measurement of the contact angle (11). The reason for the discrepancy can be found in the different employed definitions of the contact angle. We define it on the macro scale that is here the tissue scale, whereas the authors of that study (11) define it on the micro scale given by individual cells. Please note that for an interpretation in the context of wetting, the tissue scale is the relevant one, whereas for interpretation of the forces acting on the cells at the contact line, the cell scale is relevant. The described change in the contact angle during epiboly suggests that the interfacial force balance shifts during the onset of epiboly movements. Since the relaxation time of embryonic zebrafish tissue is of the order of $\approx 5$ min (20), we assume a quasi-static process where the collective cell dynamics acts on a fast timescale and is enslaved to a slower change of the interfacial tensions.

General wetting model

According to the general physics of wetting, the force balance at the contact line between three liquid media can be expressed in terms of the interfacial tensions and the macroscopic contact angle (21)

$$\text{cos}\theta =\frac{{\gamma }_{\text{y}}^2-{\gamma }_{\text{c}}^2-{\gamma }_{\text{yc}}^2}{2{\gamma }_{\text{c}}{\gamma }_{\text{yc}}},$$ (1)

where ${\gamma }_i$ $\left(i=\text{c,}\text{y,}\text{yc}\right)$ denotes the interfacial tensions of the cells-medium $\left(i=\text{c}\right)$, yolk-medium $\left(i=\text{y}\right)$, and cells-yolk $\left(i=\text{yc}\right)$ interfaces (Fig. 3 a). To model the time-dependent nature, we assume that the interfacial tension ${\gamma }_i\left(c\right)$ depends on the concentration, c, of a molecule mediating mechanical interaction between cells. In this general approach, any molecule that will affect the tension in a linear way is a potential candidate. Note that the cell cluster is directly located between the cells-medium and yolk-cells interfaces. At the yolk-medium interface close to the contact line is the external YSL, which connects the cell cluster with the actomyosin ring. Overall, we assume that all interfacial tensions depend on the same concentration c of protein. Additionally, we expect concentration-independent offset tension to be generated, e.g., by the actomyosin ring (6). Mathematically, this is reflected by the constant term in the Taylor expansion of ${\gamma }_i\left(c\right)$. All expansions are up to first order in c. As a result, we obtain the following equations for the interfacial tensions:

$${\gamma }_{\text{c}}\left(t\right)={\gamma }_{\text{c,0}}+{\mathit{ϵ}}_{\text{c}}c\left(t\right)$$ (2)

$${\gamma }_{\text{yc}}\left(t\right)={\gamma }_{\text{yc,0}}+{\mathit{ϵ}}_{\text{yc}}c\left(t\right)$$ (3)

$${\gamma }_{\text{y}}\left(t\right)={\gamma }_{\text{y,0}}+{\mathit{ϵ}}_{\text{y}}c\left(t\right).$$ (4)

Here, we include the effect of the protein on the different interfaces in the prefactor ϵ. The time dependence is introduced by the general rate equation for proteins. The concentration of any protein depends on its production and degradation, which are commonly described by a rate equation with production and degradation rates k and $-\lambda c$, respectively:

$$\frac{\text{d}c}{\text{d}t}=-\lambda c+k=-\lambda \left(c-c_{\text{s}}\right),$$ (5)

with timescale λ and final stationary concentration $c_{\text{s}}=k/\lambda$. Solving Eq. 5 for $c\left(t\right)$ with starting concentration $c\left(t_0^{\prime }\right)$ and inserting the solution in Eq. 1 results in the general model for the contact angle θ:

$$\text{cos}\theta \left(t\right)=\frac{1}{2}\frac{{\gamma }_{\text{y,0}}^2-{\gamma }_{\text{c,0}}^2-{\gamma }_{\text{yc,0}}^2+2\left({\gamma }_{\text{y,0}}{\mathit{ϵ}}_{\text{y}}-{\gamma }_{\text{yc,0}}{\mathit{ϵ}}_{\text{yc}}-{\gamma }_{\text{c,0}}{\mathit{ϵ}}_{\text{c}}\right)c_{\text{s}}f\left(t\right)+\left({\mathit{ϵ}}_{\text{y}}^2-{\mathit{ϵ}}_{\text{yc}}^2-{\mathit{ϵ}}_{\text{c}}^2\right)c_{\text{s}}^{2}f{\left(t\right)}^2}{{\gamma }_{\text{c,0}}{\gamma }_{\text{yc,0}}+\left({\gamma }_{\text{c,0}}{\mathit{ϵ}}_{\text{yc}}+{\gamma }_{\text{yc,0}}{\mathit{ϵ}}_{\text{c}}\right)c_{\text{s}}f\left(t\right)+{\mathit{ϵ}}_{\text{c}}{\mathit{ϵ}}_{\text{yc}}{c}_{\text{s}}^{2}f{\left(t\right)}^2},$$ (6)

with $f\left(t\right)=\left[\left(c\left(t_0^{\prime }\right)-c_{\text{s}}\right)/c_{\text{s}}\right]\text{exp}\left(-\lambda t\right)+1$.

Minimal wetting model

To simplify the obtained general law, we check which combination of parameters is consistent with the phenomenological features of the contact-angle evolution. These features are formalized as the conditions that 1) $0<\text{cos}\theta \left(t\right)<1$, and 2) $\text{cos}\left(\theta \right)$ is an increasing function, $\partial \text{cos}\left(\theta \right)/\partial t>0$, in time. We independently vary the six parameters ${\gamma }_{i,0}$ and ${\mathit{ϵ}}_i$. Then, we apply the aforementioned conditions to the solutions, which leads to a further reduction of complexity. The two-step parameter search scanned possible combinations over four orders of magnitude (see Materials and Methods for details) and checked the resulting contact-angle dynamics against the formalized features 1 and 2. This showed that only parameter combinations where ${\gamma }_{\text{c,0}}/{\gamma }_{\text{y,0}}\ll 1$ and ${\gamma }_{\text{yc,0}}/{\gamma }_{\text{y,0}}\ll 1$ (Fig. 3 b) need be considered to reflect the experimental characteristics. This result justified simplifying the set of equations by neglecting the constant offsets ${\gamma }_{\text{yc,0}}={\gamma }_{\text{c,0}}=0$. This yields

$$\text{cos}\theta =\frac{1}{2}\left(\frac{{\alpha }^2}{{\delta }^2}\frac{{\mathit{ϵ}}_{\text{c}}}{{\mathit{ϵ}}_{\text{yc}}}\frac{1}{f{\left(t\right)}^2}+\frac{2\alpha }{{\delta }^2}\frac{{\mathit{ϵ}}_{\text{c}}}{{\mathit{ϵ}}_{\text{yc}}}\frac{1}{f\left(t\right)}+\frac{{\mathit{ϵ}}_{\text{y}}^2-{\mathit{ϵ}}_{\text{yc}}^2-{\mathit{ϵ}}_{\text{c}}^2}{{\mathit{ϵ}}_{\text{c}}{\mathit{ϵ}}_{\text{yc}}}\right),$$ (7)

with $\alpha ={\gamma }_{\text{y,0}}/\left({\mathit{ϵ}}_{\text{y}}{c}_{\text{s}}\right)$ and $\delta ={\mathit{ϵ}}_{\text{c}}/{\mathit{ϵ}}_{\text{y}}$. Fitting this reduced model to the experimental $\text{cos}\theta \left(t\right)$ data of $n=14$ embryos shows that the best fits are obtained when ${\mathit{ϵ}}_{\text{yc}}/{\mathit{ϵ}}_{\text{c}}=1.0\pm 0.1$ and when $\alpha =0.05\pm 0.02$ is small. This motivates the final simplification of setting ${\mathit{ϵ}}_{\text{yc}}\equiv {\mathit{ϵ}}_{\text{c}}$, whereas the small value of α justifies neglecting terms $\propto {\alpha }^2$ in the reduced Eq. 7. Hence, by use of a phenomenological inspection, the initial general description of wetting has been transformed into a simplified model equation that fully describes all experimental data sets with only four independent parameters that can be intuitively interpreted:

$$\text{cos}\theta =\frac{\alpha }{{\delta }^2}\frac{1}{\text{exp}\left(-\lambda \left(t-t_{1/2}\right)\right)+1}+\frac{1-2{\delta }^2}{2{\delta }^2},$$ (8)

where $\alpha ={\gamma }_{\text{y,0}}/\left({\mathit{ϵ}}_{\text{y}}{c}_{\text{s}}\right)$ is the offset tension strength quantifying the ratio between the constant ${\gamma }_{\text{y,0}}$ and the final time-dependent tension ${\mathit{ϵ}}_{\text{y}}{c}_{\text{s}}$, $t_{1/2}=t_0^{\prime }+\text{ln}\left(\left[c\left(t_0^{\prime }]\right)-c_{\text{s}}\right]/c_{\text{s}}\right)/\lambda$ represents an offset time that depends on the moment the experiment was started, λ is the rate of tension variation, and $\delta ={\mathit{ϵ}}_{\text{c}}/{\mathit{ϵ}}_{\text{y}}$ is the tension ratio between the cells and precursor film represented by the external YSL. It is important to note that the experimental sigmoid curves provide information for four parameters (plateau values at the beginning and end of the experiment, the maximal slope, and the time offset of the increase) that correspond to the four parameters in our model.

Master curve of contact-angle dynamics

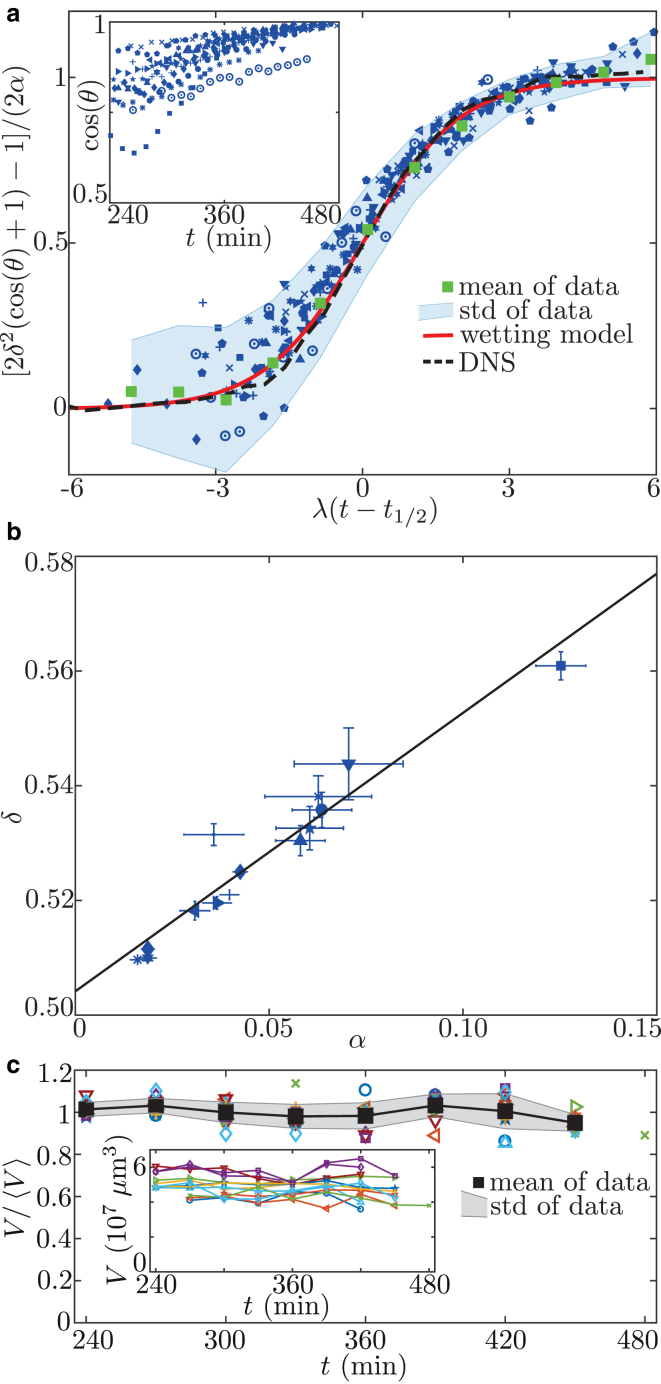
Our final model (Eq. 8) provides excellent fits for all $n=14$ data sets quantified by an average $r^2$ value of $0.88\pm 0.08$. Although each embryo follows an individual curve (Fig. 4 a, inset), the common law for the dynamics of $\text{cos}\left(\theta \right)$ suggests an underlying principle that allows one, by rescaling time and contact angle, to collapse all data points onto a single master curve (Fig. 4 a, green squares), which is predicted by the model (Fig. 4 a, red curve). The mean fit values of the 14 experiments are displayed in Table 1.

Figure 4.

Rescaling of experimental data. (a) The contact angle of $n=14$ embryos is measured in experiments (inset). The model described by Eq. 8 is fitted to each curve. The raw data are rescaled using the fit parameters (blue symbols, main plot) and averaged in bins of size $\Delta t^{\prime }=1$ (mean $\pm$ SD, green squares and shaded area), providing excellent agreement with our simple model (red curve). Also, the time evolution of the contact angle obtained from DNSs (dashed curve) is in very good accordance with the model curve and the data. (b) To further validate the model, parameter δ is plotted over α (blue symbols) showing the expected linear dependence. Linear regression gives the black line. (c) The total volume of the cell cluster is measured (inset). To compare different-sized embryos, the volume is normalized by the mean volume of each curve (colored symbols, main plot). This normalized volume is averaged at each time point (mean $\pm$ SD, black squares and shaded area). No systematic change of cell-cluster volume is observed. To see this figure in color, go online.

Table 1.

Mean of Extracted Parameter Values

$\text{cos}\left(\theta \right)$		$\delta \left(\alpha \right)$
α	δ	m
$0.05\pm 0.03$	$0.53\pm 0.01$	$0.49\pm 0.09$
$t_0$	λ	n
$\left(5.4\pm 0.5\right)\text{h}$	$\left(2.2\pm 0.5\right){\text{h}}^{-1}$	$0.504\pm 0.005$

Values are expressed as the mean ± SD of the fit parameters of $n=14$ embryos $\left(\text{cos}\left(\theta \right)\right)$ and parameters of the line fit according to Eq. 9, with confidence interval $\left(\delta \left(\alpha \right)\right)$.

Universal dependence among final tensions

Although the four parameters are independent in the fit, their definition in the introduced model implies a hidden dependence between the tension ratio, δ, and the offset tension strength, α. Introducing the final tensions of the cells-medium interface, ${\gamma }_{\text{c,s}}={\mathit{ϵ}}_{\text{c}}{c}_{\text{s}}$, and the yolk-medium interface, ${\gamma }_{\text{y,s}}={\gamma }_{\text{y,0}}+{\mathit{ϵ}}_{\text{y}}{c}_{\text{s}}$, this is analytically expressed by

$$\delta =\frac{{\gamma }_{\text{c,s}}}{{\gamma }_{\text{y,s}}}\left(\alpha +1\right),$$ (9)

which predicts a linear relation with equal offset and slope. Indeed, Fig. 4 b shows that such a relation holds for the obtained δ and α values. A linear regression of the form $\delta =m\alpha +n$ confirms that slope $m=0.49\pm 0.09$ and offset $n=0.504\pm 0.005$ are equal within the error (Table 1; the error represents a 95% confidence interval).

Simulating the minimal wetting model

The presented quasi-static model exclusively describes the contact-angle dynamics and does not allow for a full prediction of the shape changes, which the embryo and the yolk experience during epiboly. To overcome this, we compare both the simple model and the developmental stages of the embryo to direct numerical simulations (DNSs) of a hydrodynamic model that incorporates the experimentally obtained fit parameters (Fig. 5). As the relaxation time of the tissue is small compared to the timescale of the epiboly process, an over-damped, quasi-static dynamics is assumed. Furthermore, it is assumed that the cell-cluster volume is conserved, which is experimentally verified (Fig. 4 c). We study the surface-tension-driven flows and shape transformations that result from the temporal variation of ${\gamma }_{\text{c}}$, ${\gamma }_{\text{y}}$, and ${\gamma }_{\text{yc}}$ given by the parameters displayed in Table 1 (for details see Materials and Methods). Hence, no fit parameters were used or adjusted to confirm the experimental measurements. In the simulation, the contact angle is measured employing the same fitting procedure as used for the experimental data. Fig. 5 shows that overall, the DNS conforms to the embryonic development during early epiboly. However, the DNS shows that there exist experimental features that are beyond the simple model, such as the more complex interface shapes in the contact-line region. This is consistent with recent experimental results suggesting that anisotropic stresses in the blastoderm, exerted, for example, by active contraction, are required for a more detailed understanding of the embryo shape during epiboly (11).

Discussion

The introduced simple wetting model has resulted from a phenomenological reduction scheme using an extended parameter search and systematic comparison to the measurements. To gain a deeper understanding of the model, we seek an interpretation of the fitting parameters in the context of the biological system.

Molecular mechanisms controlling tension

Potential molecular mechanisms giving rise to the interfacial tensions are cell-cell adhesion and cell cortex tension or an interplay between the two (22). Although the model presented here is independent of the exact molecular mechanism generating tension, it allows prediction of relations between the underlying molecular or cellular properties. This requires an interpretation of the used parameters in light of the potential model. As listed in Table 2, the concentrations used in the model need to be interpreted either as the surface density of adhesion molecules (when assuming an adhesion-based tension) or as cortical density of active myosin motor proteins in the cell cortex (when assuming actomyosin contractility as the tension-generating mechanism). The prefactor ${\mathit{ϵ}}_{\text{y,c}}$ needs then to be interpreted as either adhesion energy (in the adhesion interpretation) or contractile energy per motor protein (in the contraction interpretation). The model itself holds independent of the nature of the molecular mechanism generating interfacial tension. In a recent experiment on cell-cell interaction, it was demonstrated that the cell tension is mainly generated by the contractility of the actomyosin network (22), pointing toward an interpretation in the context of active tension generation. However, in the situation of epiboly, adhesion might still provide a contribution to the contractility, and from the data provided in this analysis, the two different mechanisms cannot be differentiated.

Table 2.

Different Interpretations of the Model Parameters Assuming Different Mechanisms for Interfacial Tensions

	Cell-Cell Adhesion	Cortex Tension
c	surface density of cadherine adhesion molecule	cortical concentration of myosin motor protein
${\mathit{ϵ}}_{y,c}$	molecular adhesion energy	contractile energy
${\gamma }_{y,0}$	pulling force by actomyosin ring

Interpretation of the model independent parameters

Although the initial approach allows static offset tensions for all three interfaces, the parameter search yields that a single constant offset tension at the yolk ${\gamma }_{\text{y,0}}$ is required to explain measurements. Indeed, it is well known that a contractile ring formed by an actomyosin network provides an active pulling force at the external YSL, just at the surface of the yolk. This pulling force is essential for epiboly, as demonstrated recently (6) (Fig. 3). By performing laser cutting experiments (6) it has been found, furthermore, that the actomyosin-based pulling tension remains constant, supporting the assumption that the constant offset tension ${\gamma }_{\text{y,0}}$ corresponds to the tension generated by this actomyosin network. Using this interpretation, the model presented here can predict the ratio of the final yolk-medium interfacial tension to the tension of the actomyosin ring via $\alpha ={\gamma }_{\text{y,0}}/\left({\mathit{ϵ}}_{\text{y}}{c}_{\text{s}}\right)$. The determined value of $\alpha =0.05\pm 0.03$ suggests that interfacial tension arising from mechanical cell-cell interaction dominates over the pulling force by the actomyosin ring. In the initial phase of epiboly, this effect is even stronger, since the tension resulting from cell-cell interaction decreases over time. Hence, the offset tension becomes more important the further epiboly has progressed. This is also consistent with the finding that the actomyosin ring commonly forms only at 40% epiboly (5 hpf), and is hence not yet present at the onset of epiboly (23), when the model predicts that the offset tension is not yet required for the force balance.

The tension ratio, $\delta ={\mathit{ϵ}}_{\text{c}}/{\mathit{ϵ}}_{\text{y}}$, is a key parameter that quantifies the ratio of interfacial tension of the blastoderm to the precursor film equivalent, the external YSL. The measured value of $\delta =0.53\pm 0.01$ suggests that interfacial tension of the precursor film is twice as strong as that of the blastoderm. This tension increase is supported by the presence of tight junctions that provide strong adhesion between the EVL and the external YSL (24, 25), but it might also be generated by a stronger contractility of these cells. It should be noted that other interpretations also would lead to the same conclusion, such as introducing different stationary concentrations, $c_{\text{s}}$, for the different interfaces.

Inherent dependence of stationary tensions

The check of the model prediction presented here, namely, that δ depends in a well-defined way on α, and that the δ-intercept is close to the slope, suggests that the ratio ${\gamma }_{\text{c,s}}/{\gamma }_{\text{y,s}}$ between the final stationary tensions at the cells-medium and yolk-medium interfaces is conserved throughout different embryos. Thus, the model suggests an inherent regulation ensuring this crucial balance by a yet unknown, probably biochemical process. Alternatively, it is possible that these parameters both depend on the same underlying process, which would explain such a robust relation found in our experiments.

Predicting dynamic changes in tension

The implicit assumption that the involved tensions decrease over time is supported by several experiments. Tension of the yolk measured shortly before the beginning of epiboly is of the order of 200 $\text{pN}/\mu \text{m}$ (11), whereas at 80–90% epiboly, it decreases to 110 $\text{pN}/\mu \text{m}$ (26). Moreover, this measured tension at the end of epiboly allows one to estimate the final stationary tensions. Combining the measured ${\gamma }_{\text{y,s}}=110\text{pN}/\mu \text{m}$ with our model predicts that ${\gamma }_{\text{y,0}}=5\text{pN}/\mu \text{m}$ and ${\gamma }_{\text{c,s}}=56\text{pN}/\mu \text{m}$.

Limitations of the pure wetting model

Although the minimal wetting model presented here can successfully explain the time evolution of the contact angle, it is not sufficient to describe the temporal changes of the epiblast thickness during early epiboly. The possibility that such changes are caused by an increasing volume of the cell cluster in experiments, whereas theory assumes a constant volume, can be ruled out, as the volume is found to also be constant in the experiments. This suggests that an additional mechanism is required to explain the process of doming. Indeed, anisotropic stresses have been recently proposed to explain doming (11). Interestingly, the contact angle in that study was measured on the cell scale, and it was found that it varies only marginally, which could be seen to be in conflict with the measurements presented here. However, since we measure the contact angle on the tissue scale, it is not surprising to find such differences. The definition on the tissue scale, however, can describe the system very accurately, as demonstrated by the small relative error we find when we compare the actual cell position with the implied property of constant curvature as imposed by fitting spheres to the embryo shape. Note that in mesoscopic hydrodynamics, it is well known that the contact angle on a small and a large scale may differ depending on the particular height dependence of wetting energies (27, 28).

Conclusions

Overall, the proposed wetting model characterizes the measured contact-angle evolution surprisingly well. Such a simple description is not expected, as the blastoderm is a complex tissue consisting of several thousand cells and as such differs sharply from a simple liquid. In consequence, the model presented here should not be employed beyond the here-discussed stages of epiboly, as an increasing deviation between the data and the model can already be observed at the final stage presented (Fig. 4 a). Although the model predicts a plateau, the data keep increasing slightly, but significantly. This deviation is not surprising, because parallel to epiboly, further gastrulation movements start at 5.3 hpf, thus leading to the formation of different germ layers that represent a new material not currently included in the model. Additionally, our model does not cover additional anisotropic stresses that might be generated within the embryo, as recently suggested (11). Still, it was shown that epiboly also happens when the deep cells are partially removed, suggesting that only changes at the interfaces eventually lead to epiboly, similar to the predictions of our model. The complexity of the process might also be driven by more than one force generating mechanisms that work together, and rescue the system in case a single process fails to drive the key developmental step of epiboly.

Author Contributions

B.W., S.Y., and T.B. designed the experimental research. B.W. performed and analyzed the experiments. B.W., S.T., U.T., and T.B. developed the presented model. S.T. performed the simulations. B.W. and T.B. wrote the manuscript. All authors together developed the interpretation and progression of experiments and modelling.

Editor: Laurent Blanchoin.