Low‐dose CT perfusion with projection view sharing

Abstract

Purpose

CT Perfusion (CTP) is a widely used clinical imaging modality. However, CTP typically involves the use of substantial radiation dose (CTDI _vol ≥~200 mGy). The purpose of this study is to present a low‐dose CTP technique using a projection view‐sharing reconstruction algorithm originally developed for dynamic MRI — “K‐space Weighted Image Contrast” (KWIC).

Methods

The KWIC reconstruction is based on an angle‐bisection scheme. In KWIC, a Fourier transform was performed along each projection to form a “k‐space”‐like CT data space, based on the central‐slice theorem. As a projection view‐sharing technique, KWIC preserves the spatiotemporal resolution of undersampled CTP data by progressively increasing the number of projection views shared for more distant regions of “k‐space”. KWIC reconstruction was evaluated on a digital FORBILD head phantom with numerically simulated time‐varying objects. The numerically simulated scans were undersampled using the angle‐bisection scheme to achieve 50%, 25%, and 12.5% of the original dose (288, 144, and 72 projections, respectively). The area‐under‐the‐curve (AUC), time‐to‐peak (TTP), and full width half maximum (FWHM) were measured in KWIC recons and compared to fully sampled filtered back projection (FBP) reconstructions. KWIC reconstruction and dose reduction was also implemented for three clinical CTP cases (45 s, 1156 projections per turn, 1 s/turn, CTDI _vol 217 mGy). Quantitative perfusion metrics were computed and compared between KWIC reconstructed CTP data and those of standard FBP reconstruction.

Results

The AUC, TTP, and FWHM in the numerical simzulations were unaffected by the undersampling/dose reduction (down to 12.5% dose) with KWIC reconstruction compared to the fully sampled FBP reconstruction. The normalized root‐mean‐square‐error (NRMSE) of the AUC in the FORBILD head phantom is 0.04, 0.05, and 0.07 for 50%, 25%, and 12.5% KWIC, respectively, as compared to FBP reconstruction. The cerebral blood flow (CBF) and cerebral blood volume had no significant difference between FBP and 50%, 25%, and 12.5% KWIC reconstructions (P > 0.05).

Conclusions

This study demonstrates that KWIC preserves perfusion metrics for CTP with substantially reduced dose. Clinical implementation will require further investigation into methods of rapid switching of a CT x‐ray source.

1. Introduction

CT brain perfusion (CTP) is a widely used imaging technique for the evaluation of hemodynamic changes in stroke and cerebrovascular disorders as well as neoplasm.¹ In acute stroke imaging, CTP of the brain is valuable for the detection of ischemic lesions, and for distinguishing infarct core from penumbra brain tissue in acute stroke.² However, CTP involves a high radiation dose for the patients as the CTP scan continuously images the same anatomical region for approximately 60 s in order to capture the full passage of the contrast bolus. This has been raised as a concern by the FDA,³ especially when multiple successive CTPs are performed on the same patient, for example, to monitor reperfusion following recanalization.

Recently, several techniques have been applied for radiation dose reduction in CTP scans, including reduction in tube current and tube voltage, as well as the use of novel noise reduction techniques such as iterative reconstruction (IR).^{3, 4} The standard CTP protocols now employ a reduced tube voltage of ~80 kV while keeping the tube current below 200 mA (typically 150 mA), without deterioration of quantitative perfusion values.⁵ However, the resultant radiation dose of existing CTP scans (≥~200 mGy) is still about two to three times higher than that of a standard head CT scan (~60 mGy).⁶ More recently, different IR methods for reducing radiation dose without sacrificing image quality have been developed by all major CT manufacturers (e.g., iDose by Phillips Healthcare, ASIR by GE Healthcare, SAFIRE (Sinogram Affirmed Iterative Reconstruction) by Siemens Healthcare, and AIDR by Toshiba Medical Systems).⁷ Although the application of IR in standard CT scans has been improving due to enhanced computational power, its application in CTP is very limited due to the high complexity and computational burden for processing dynamic CTP image series (e.g., Siemens does not offer IR options for CTP). A recent study showed that it is feasible to reduce radiation dose of CTP by 50% using the IR algorithm called iDose^{1, 8, 9} developed by Philips, however, the subjective image quality of the resultant CTP with IR is still inferior in about a quarter of the patients.¹⁰ There is a critical and unmet need to develop effective dose reduction techniques for dynamic CTP scans, without sacrificing image quality and speed (i.e., clinical workflow).

In recent years, a number of sparse sampling and reconstruction algorithms have been developed for dynamic MRI with radial trajectories, such as highly constrained back projection (HYPR),¹¹ k‐space weighted image contrast (KWIC),¹² and compressed sensing.¹³ Since CT projection data can be converted into “k‐space” data according to the central‐slice theorem, these MRI algorithms can potentially be adapted for dose reduction in dynamic CT scans such as CTP by acquiring reduced number of projections for each image. As a proof‐of‐concept, HYPR has been applied for low‐dose CTP^{11, 14, 15} that allows for reduced image noise and streaking artifacts from undersampled datasets.

Here, we present an alternative strategy to reduce the radiation dose of existing CTP methods by ~75% by adapting a projection view‐sharing technique originally developed for accelerated dynamic MRI–k‐space weighted image contrast (KWIC)^{12, 16} We present the theory and provide a proof‐of‐concept of the proposed technique with numerically simulated phantom data and retrospectively undersampled clinical CTP data.

2. Theory

As shown in Fig. 1(a), the standard CT scan involves continuous rotation and exposure of the x‐ray source around the patient. According to the Nyquist criterion and standard CT acquisition scheme, a total of π * X_res (where X_res is the number of detectors; π takes into account two projections 180° apart) projection views are acquired to form one CT image. For dynamic CT scans, the total number of x‐ray projection views will be π * X_res * N_frame (number of temporal frames, typically 45–60 for CTP), resulting in a high level of radiation dose. As shown in Fig. 1(b), the proposed technology reduces the radiation dose of CTP scans by controlling the x‐ray source to be on intermittently (instead of continuously) at prespecified rotation angles (e.g., programmed pulsed x ray). The dynamic CTP image series can then be reconstructed using algorithms that preserve high spatial and temporal resolutions as well as image quality comparable to those of standard CTP scans.

Figure 1.

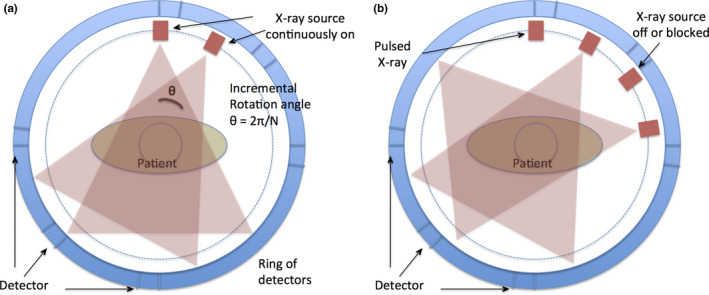
(a) The standard CT acquisition has the x‐ray tube continuously on and acquires projections at 2π/N increments. For KWIC implementation the x‐ray tube needs to be intermittently on, (b), during gantry rotation at specified angles. [Color figure can be viewed at wileyonlinelibrary.com]

Many algorithms can be applied for this purpose by exploiting the redundancy of information in four‐dimesional (4D) dynamic imaging data. In this work, we focus on a projection view‐sharing technique called KWIC which was originally developed for accelerated 4D dynamic MRI with radial trajectories.^{12, 16} KWIC exploits the oversampling of the k‐space center in the radial acquisition by using drastically fewer views in the central region of k‐space, while progressively larger numbers of views are used toward the outer k‐space regions in a fashion of subapertures (Fig. 2). The image contrast is primarily determined by the central region of k‐space (i.e., low spatial frequencies), therefore relatively few projection views are required to maintain the image contrast with a high temporal resolution. The radius of the central region (ρ ₁), and subsequent subaperture regions (ρ _n), is based on the Nyquist sampling criteria to minimize undersampled streaking artifacts and is calculated by

$${\mathit{\rho }}_n=\frac{N}{\mathit{\pi }\left(\mathit{\alpha }-n+1\right)}$$ (1)

where N is the total number of projections, α is the number of subapertures used, and n is the region number (n = 1 is central region).¹² The number of projections in each subaperture region (ρ _n*π) increases progressively with number of subapertures toward the outer k‐space regions.^{12, 16} A voronoi diagram is then used for density compensation.¹⁷

Figure 2.

Illustration of the CT‐KWIC workflow. Raw CT projection data are Fourier transformed along the detector rows (column direction in this figure depiction) and combined with a KWIC mask, which selects and weights projections into subapertures. The masked sinogram is then regridded into 2D Cartesian k‐space; a grid is overlaid in this diagram to indicate the relative density of projections in each subaperture (fewest at the center “view‐core,” where contrast info lies, most at the outer, high‐frequency regions). The outer subapertures will contain the largest amount of view sharing. Finally, the gridded k‐space image will be Fourier transformed into final 2D image.

As a projection view‐sharing technique, KWIC is able to preserve high spatial and temporal resolutions of undersampled 4D dynamic contrast‐enhanced MRI and MR angiography.^{18, 19, 20} Projection imaging data such as CT can be related to the frequency domain (e.g., k‐space in MRI) through the central‐slice theorem by performing 1‐D FT of the projection of an object, which is the same as the line drawn through the center of the 2‐D FT plane (i.e., k‐space). By converting the CT sinogram into “k‐space” data, we can apply KWIC to preserve high spatial and temporal resolutions of undersampled CTP data by progressively increasing the number of projection views for more distant regions of “k‐space” (Fig. 2). Under this paradigm, contrast information, most important for quantitative CTP measures such as CBV, CBF, etc., maintains high temporal resolution, and temporal blurring is relegated to high‐frequency image details that do not impact perfusion measurements.

While the central‐slice theorem provides the key connection between CT projection data and k‐space used for KWIC reconstructions, parallel‐beam CT geometry (e.g., “pencil beam” or translate‐rotate geometry²¹) is required for correct mapping. Modern CTP studies are typically conducted using third‐generation CT scanners with cylindrical detector geometry, which is not immediately suitable for a KWIC reconstruction. To achieve the correct geometry, rebinning algorithms originally developed for helical reconstruction were applied to the projection data, transforming the fan‐beam data into “pseudo‐parallel” data.^{22, 23} The rebinning portion of the FreeCT_wFBP reconstruction software was utilized to accomplish this.²⁴

It should be noted that rebinning involves interpolation and mapping of data from nearby projections in the study. In the case of CTP, this means that the rebinning process itself could result in some amount of temporal blurring, even prior to the temporal blurring one expects to see from the KWIC algorithm. While this is an important effect to be aware of, it is limited to approximately 0.2 s (See appendix for explanation and derivation of this value) at the edge of the scanner field of view, where it is most severe. Near the center of the scanner field of view, where a head would be placed for a perfusion study, data are interpolated from at most 50–100 nearby projections, or < 0.1 s of acquisition data. This is substantially less than the temporal blurring induced by KWIC and has not been observed to be a source of deviation in perfusion measurements.

The rebinning approach provides benefits as well. Many modern CT scanners employ “flying focal spots” to improve in‐plane and z‐direction spatial resolution and the rebinning process and software routines used in this work allows for a robust approach to reconstruct scans acquired with flying focal spots using KWIC reconstruction. This requires little to no modification of the KWIC algorithm and allows for improved spatial resolution of the flying focal spot scan. Additionally, once the data are in a parallel geometry, convolution filters can readily be applied to the parallel projection data to modify the spatial and contrast properties of the final reconstruction, as is done in FBP reconstruction; this direct application is not possible in the unmodified diagnostic fan‐beam geometry.²² While not investigated in this work, further dose reduction could be achievable via the careful selection and application of these filters.

3. Materials and Methods

3.A. Adapting KWIC for CTP

A modified KWIC algorithm for reconstruction of CTP data was implemented in MATLAB (The MathWorks Inc., Natick, MA, USA), that consisted of five main modules/steps: (a) rebinning of fan‐beam CT data into parallel‐beam sinogram data; (b) performing 1D FFT of the projection along the detector row direction; (c) multiplication with a KWIC filter that selects and weights projections into subapertures; (d) gridding of KWIC‐filtered sinogram into 2D Cartesian k‐space using the VORONOI algorithm²⁰; and finally (e) performing 2D FFT of the regridded k‐space data into 2D images (see Fig. 2 for diagram of the workflow). Step (1) was implemented using a modified version of freely available, open‐source weighted filtered backprojection (FBP) for CT, FreeCT_wFBP.²⁴

K‐space weighted image contrast (KWIC) divides the k‐space into subapertures [Fig. 3(b)]: the subaperture covering the central region of k‐space is updated every time frame (or rotation of CT gantry), while progressively larger numbers of projections are used in the subapertures toward the outer k‐space regions and shared between neighboring time frames (Fig. 2). The number of projections in the central subaperture (or the number of x‐ray projections per rotation of CT gantry) is determined by the desired dose reduction. For example, if the standard number of projections is 576 per 180 degrees, and the desired dose reduction is 75%, then the number of projections in the central subaperture is 144. The total number of subapertures required is also determined by the amount of desired dose reduction as well as the Nyquist sampling criterion in the outer regions of k‐space. In this study the minimum number of projections needed in the outmost subaperture of k‐space is 576 in order to meet the Nyquist criterion. Therefore, to achieve 50%, 25%, and 12.5% of the original dose the central subaperture would comprise 288, 144, and 72 projections, respectively; to satisfy the Nyquist criterion, two, four, and eight subapertures are used, respectively.

Figure 3.

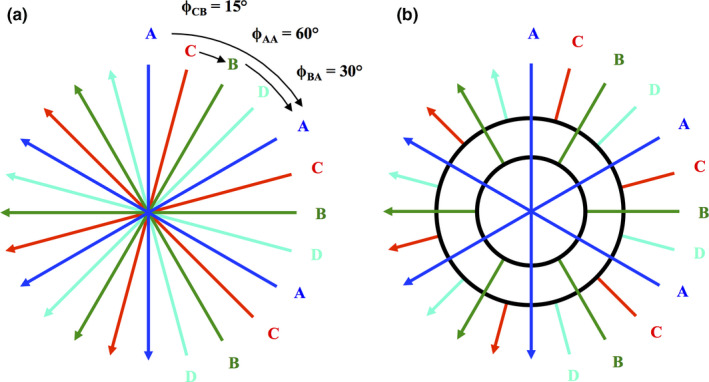
Angle‐bisection (a) and KWIC reconstruction techniques (b). A, B, C, and D represent subapertures that are acquired in an angle‐bisection scheme (a). In this example, the time frame projections, A, acquires three projections within one gantry rotation with each projection being 60° apart from each other. The next time frame, B, is then acquired such that each projection bisects the angle separation so that the angle between an A and B projection is 30°. C and D subapertures are acquired at angles that bisect A to B and B to A projections, respectively. The KWIC reconstruction divides the k‐space into subapertures (b). The subaperture in the central region of k‐space is updated every time frame (A,B,C,D), while progressively larger numbers of views are used in the subapertures toward the outer k‐space regions and shared between neighboring time frames. [Color figure can be viewed at wileyonlinelibrary.com]

As mentioned, a clinical implementation of KWIC algorithm also requires a custom acquisition scheme. One potential realization of this is a high speed x‐ray switching (e.g., pulsed x ray) at prespecified rotation angles to which different sampling sequences of rotation angles can be applied. In the present work, an angle‐bisection (or “bit‐reverse”) sequence of rotation angles for sampling patterns was applied for KWIC. As shown in Fig. 3(a), the projections were acquired in an interleaved fashion (A, B, C, D). During the first gantry rotation, only one downsampled set of evenly distributed projection angles were acquired (A). During subsequent gantry rotations, the projections that bisect the previous set of projections were acquired (B, C, D) until a full set of projections at all angles were acquired. In other words, one quarter of the projection views are acquired each rotation, corresponding to a 25% dose level per gantry rotation assuming perfect x ray switching. Data from the different gantry rotations is then assembled by the KWIC reconstruction algorithm into the subapertures to achieve complete sampling of k‐space. Alternative sampling sequences of rotation angles such as the golden ratio scheme^{25, 26} may be applied and will be discussed below.

3.B. FORBILD phantom CTP

A FORBILD head phantom containing numerically simulated time‐varying objects (5, 10, and 50 mm in size) was developed to create a parallel‐beam dynamic CT projection dataset. The goal was to assess the types of artifacts only the KWIC algorithm will produce. Therefore, the FORBILD head phantom was numerically simulated with no added noise. The time‐varying object contrast was simulated using the following gamma variate equation²⁷

$$C\left(t\right)=C_0{t}^{\mathit{\alpha }}{e}^{\mathit{\alpha }\left(1-t\right)}$$ (2)

where C(t) is the contrast signal, C ₀ is an arbitrary constant (C ₀ = 1), t is time and α is a constant that affects the contrast uptake rise and fall (α = 11). The simulated scans were 60 s long with 1 gantry rotation per second and 576 projections per 180° rotation. Reduced‐dose cases were simulated by down‐sampling the number of projections per 180° rotation from 576 to 288 (50% dose), 144 (25%), and 72 (12.5%) based on the angle‐bisection scheme. One image per second was reconstructed using FBP and KWIC, respectively. KWIC reconstructions utilized 72, 144, and 288 projections per gantry rotation and four, three, and two subapertures, for the 12.5%, 25%, and 50% dose cases, respectively. On all sets of reconstructed images (FBP 100% dose, KWIC 50% dose, KWIC 25% dose, KWIC 12.5% dose), an ROI was placed on the time‐varying object (red ROI dot, online version only) and time‐to‐peak (TTP), area‐under‐the‐curve (AUC), and the full width at half maximum (FWHM) of the corresponding dynamic curves were calculated. Perfusion curves produced using the KWIC reconstructions were compared against reference values from the full‐dose FBP data.

To assess the effects of the streaking artifacts near the edge of the image, the time‐varying object was placed near the back of the FORBILD head phantom. KWIC reconstruction was also performed down to 6.25% of the original dose to show when KWIC reconstruction begins to break down. This was only performed with a 5‐mm size object, to assess the more extreme case of a lesion in clinical practice. The ROI was drawn on the time‐varying object (red ROI dot, online version only) and TTP, AUC, and FWHM were measured. To better highlight the artifacts, image subtraction was performed between full‐dose KWIC reconstruction and the respective low‐dose KWIC reconstruction. Due to reconstruction algorithm difference, image subtraction was not performed with full‐dose FBP because it could create spurious artifacts not relevant to the study.

3.C. In vivo CTP data

Three clinical CTP cases were scanned on a Definition AS (Siemens Healthineers, Erlangen, Germany) CT scanner. The scanning parameters are listed in Table 1. The CTP protocols used were the standard clinical protocols for patients with potential strokes, with dose level (217 mGy) over 20% lower compared to that of the AAPM recommended protocol (281 mGy).⁵

Table 1.

Imaging and reconstruction parameters

Imaging and reconstruction parameters	FBP recon	KWIC recon
Scan time (s)	45	45
CTDIV01 (mGy)	217	N/A
Gantry rotation (s/turn)	1	1
# Projections/turn	1152	576,288, 144, 72
FOV (cm2)	50 × 50	50 × 50
# Subapertures	1	2,4,8,16
Projections/subaperture	1152	576, 288, 144, 72
Effective CTDIvol (mGy)	217	109,55,28, 14

The CTP images were reconstructed using an in‐house FBP reconstruction using MATLAB and were compared to KWIC reconstruction at 50%, 25%, and 12.5% dose reduction based on the angle‐bisection scheme. Images using all of the projections were also reconstructed using the KWIC algorithm, which is the same as performing gridding reconstruction. For this proof‐of‐concept study, the central four detector slices of the fan‐beam dataset were averaged together and utilized to achieve an effective slice thickness of 4.8 mm, which AAPM recommends as the slice thickness for a Definition AS CT scanner CTP scan protocol.⁵ The software used for CTP analysis was SCAN4, which has been used in large‐scale clinical trials.²⁸ Postprocessing of CT perfusion images yielded multiparametric perfusion maps including cerebral blood flow (CBF) and cerebral blood volume (CBV) by using the delay‐insensitive block‐circulant singular‐value decomposition (bSVD) method according to previously described procedures.²⁹ Regions‐of‐interest (ROI) were drawn in the motor cortex (see Fig. 6 white ROI) for all three cases in the CBV and CBF maps to compare between all the reconstructed perfusion maps. A two‐tailed t‐test was used to compare the mean values of the ROI's for CBF and CBV. The arterial input function (AIF) was extracted from the anterior cerebral artery (see Fig. 6 blue ROI, online version only), venous output function (VOF) from the sagittal sinus vein (see Fig. 6 red ROI, online version only), and the tissue density signals from manually drawn ROI within the brain parenchyma. The KWIC‐reconstructed dynamic curves for AIF, VOF, and tissue density signals were compared to those by the full‐dose FBP reconstructions using least squares linear regression.

4. Results

4.A. Simulated FORBILD phantom CTP data

The reconstructed images of the FORBILD head phantom using the full‐dose FBP and KWIC with different dose reduction levels (100%, 50%, 25%, 12.5%) are shown in Fig. 4(a). The quality of FBP‐reconstructed images is degraded by streaking artifacts (blue arrows, online version only) at reduced‐dose levels, while the streaks are drastically reduced in KWIC‐reconstructed images down to 12.5% dose level. A numerically simulated time‐varying object (red arrow in Fig. 4, 5 mm size, online version only) for CTP is clearly visible at all dose reduction levels for FBP and KWIC (10 mm and 50 mm objects are not shown because they were separate simulations with the object in the same place). At 12.5% dose the FORBILD resolution fiducials (white arrows) are barely visible in the FBP‐reconstructed images while they are still detectable in KWIC‐reconstructed images. Figure 4(b) shows the gamma variate signal curves from the 5 mm object using FBP and KWIC reconstructions down to 12.5% dose. The KWIC‐reconstructed signal curves down to 12.5% dose are virtually equivalent to that of the full‐dose FBP reconstruction. In Table 2, the FWHM, TTP, and AUC measurements show that FBP and KWIC reconstructions are comparable for simulated objects of 5 mm, 10 mm, and 50 mm in size. The largest variation occurs at 12.5% dose KWIC reconstruction, however, the normalized root‐mean‐square‐error (NRMSE) of the AUC between 12.5% KWIC and FBP is 0.07. The NRMSE of the AUC between 50% KWIC and FBP and 25% KWIC and FBP is 0.04 and 0.05, respectively. The maximum temporal blurring occurred at 50% dose reduction with 0.02 s increase in the FWHM.

Figure 4.

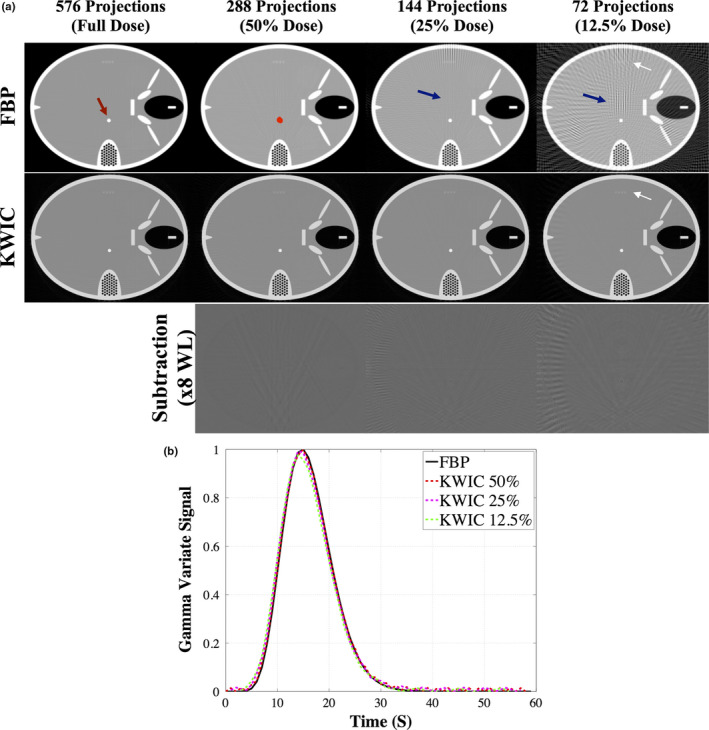
FORBILD CT phantom, a), with a 5‐mm object (red arrow, online version only) reconstructed using FBP and KWIC. Streaking artifacts (blue arrows, online version only) are present in FBP but not KWIC reconstructed images down to 25% dose level. The resolution fiducials (white arrows) are still visible at 12.5% dose in the KWIC reconstruction while in the FBP they are not visible. The red dot, online version only, is the ROI drawn to obtain the dynamic curve of the time‐varying object. The subtraction images show the artifacts from the KWIC. The gamma variate dynamic time curve, b), is similar at all dose reconstruction levels. [Color figure can be viewed at wileyonlinelibrary.com]

Table 2.

Measure TTP, AUC, and FWHM for numerically simulated time‐varying object near the middle of the phantom

	FBP full	KWIC 50%	KWIC 25%	KWIC 12.5%
TTP(s)
5 mm	15	15	14	14
10 mm	15	15	15	14
50 mm	15	15	15	15
AUC
5 mm	0.0253	0.0310	0.0285	0.0294
10 mm	0.0253	0.0271	0.0271	0.0264
50 mm	0.0253	0.0270	0.0271	0.0272
FWHM (s)
5 mm	10.712	10.732	10.729	10.696
10 mm	10.712	10.705	10.703	10.785
50 mm	10.712	10.712	10.712	10.708

The time‐varying object (red arrow, online version only) and the ROI (red dot, online version only) drawn are shown in Fig. 5. The subtraction image shows that there are streaking artifacts most prominent near the back of the FORBILD head phantom. At 12.5% of the original dose there is presence of temporal blurring the in subtraction images (blue arrow), and is more prominent in 6.25% of the original dose image. Table 3 shows that there is not a significant difference in the measured TTP, AUC, and FWHM up to 12.5% of the original dose despite the streaking artifacts. However, at 6.25% dose the measured AUC, TTP, and FWHM vary about 30–40% compared to the corresponding FBP measurements. The maximum temporal blurring occurred at 6.25% dose reduction with 2.3 s increase in the FWHM.

Figure 5.

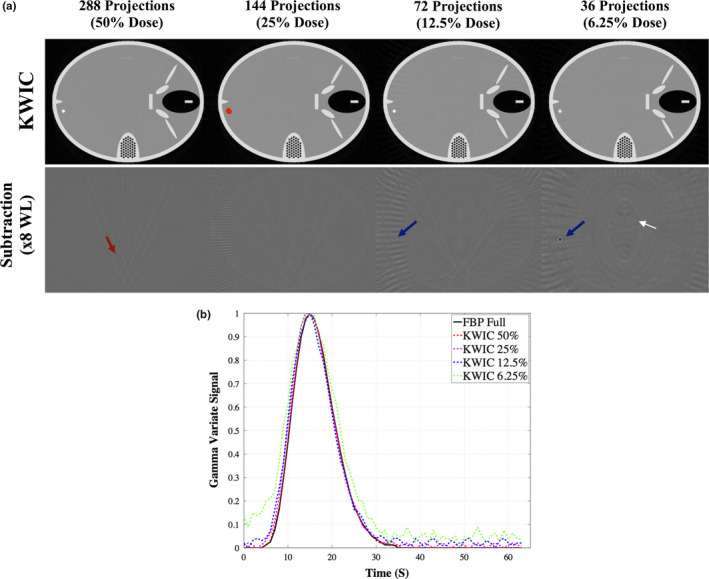
FORBILD CT phantom, (a), with a 5‐mm object near the back edge of the phantom. The subtraction images show the artifacts from the KWIC. The red dot, online version only, is the ROI drawn to obtain the dynamic curve of the time‐varying object. Streaking artifacts (red and white arrows, online version only) where the time‐varying object are seen and introduce more noise into the time curves. The blue arrows, online version only, identify a temporal blurring artifact due to higher amounts of view sharing at 12.5% and 6.25% KWIC.The gamma variate dynamic time curve, b), is similar at all dose reconstruction levels, except at KWIC 6.25% (green dotted line, online version only). [Color figure can be viewed at wileyonlinelibrary.com]

Table 3.

Measure TTP, AUC, and FWHM for numerically simulated time‐varying object near the back edge of the phantom

5mm	FBP full	KWIC 50%	KWIC 25%	KWIC 12.5%	KWIC 6.25%
TTP(s)	15	15	14	15	15
AUC	0.0253	0.0254	0.0270	0.0280	0.0354
FWHM (s)	10.714	10.731	11.022	10.914	13.054

4.B. Clinical CTP data

Figure 6 shows the CTP images reconstructed using FBP and KWIC with 50%, 25%, and 12.5% dose levels for one of the three clinical cases. All CTP images of the KWIC reconstructions are comparable to that of the full‐dose FBP reconstructions, however, at 12.5% dose there are some streaking artifacts. The image quality is significantly improved using KWIC compared to FBP at lower doses, with identifiable brain structures and blood vessels. At 25% and 12.5% dose, the FBP‐reconstructed images are not viable for diagnostic imaging. In the 50% and 25% dose KWIC images, the blood vessels are better delineated mostly due to the windowing and leveling of the images. Due to reconstruction method differences between FBP and KWIC (i.e., kernel size), the images do not have the same signal‐to‐noise ratios and thus comparable contrast in the images can be difficult to achieve. Also, the kernel used in FBP could smooth out finer structures compared to KWIC reconstruction. Difference images between the KWIC images and full‐dose reconstructed images (bottom row). The window and leveling was increased by ×8 to show the difference. The noise becomes more grainy as the dose reduction increases, and there are visible streaking artifacts near the edge of the head.

Figure 6.

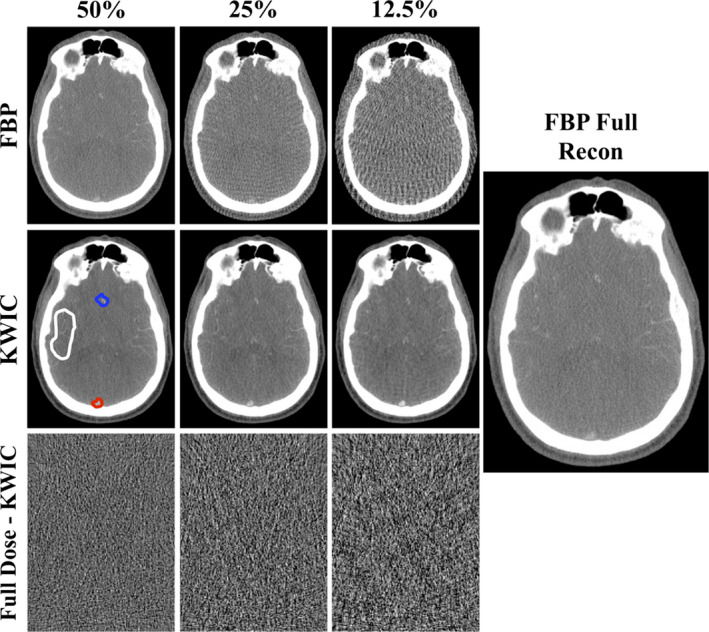
FBP and KWIC reconstructed STP cases at 50%, 25%, and 12.5% dose levels. The image quality shows slight degrading in the KWIC reconstructions while the FBP images show a greater increase in streaking artifacts as the dose reduction increases. Difference images between the KWIC images and full‐dose reconstructed images (bottom row). The window leveling (WL) and width (WW) was decreased by ×8 to show the difference (WL: 67, WW: 1800). The window leveling and width for the FBP and KWIC images are 11,000 and 8500, respectively. (The noise becomes more grainy as the dose reduction increases, and there are visible streaking artifacts near the edge of the head. The white, blue, and red ROIs, online version only, are where the ROIs were drawn to generate tissue, arterial, and venous time curves. The white ROI was also used to measure CBF and CBV in the tissue. [Color figure can be viewed at wileyonlinelibrary.com]

The AIF, VOF, and tissue density signals are shown in Fig. 7 for FBP and KWIC reconstructions, respectively. The signal curves from the KWIC reconstructions down to 25% dose level are virtually identical to those of FBP. However, slight deviation is observed for the 12.5% dose KWIC curves compared to the reference curves of FBP. The scatter plots of Fig. 8 further show the strong correlations between the full‐dose FBP signals and those by KWIC reconstructions for AIF, VOF, and tissue density curves, respectively. The maximum temporal blurring between all three CTP cases occurred at 12.5% dose reduction for case 2 with 0.5‐s increase in the FWHM.

Figure 7.

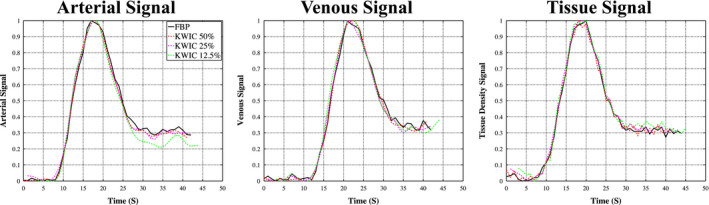
Dynamic contrast curves for arterial, venous, and tissue ROIs generated with FBP full‐dose reconstruction, 50%, 25%, and 12.5% KWIC reconstruction. The noise in the signal minimally increases as the dose reduction increases. [Color figure can be viewed at wileyonlinelibrary.com]

Figure 8.

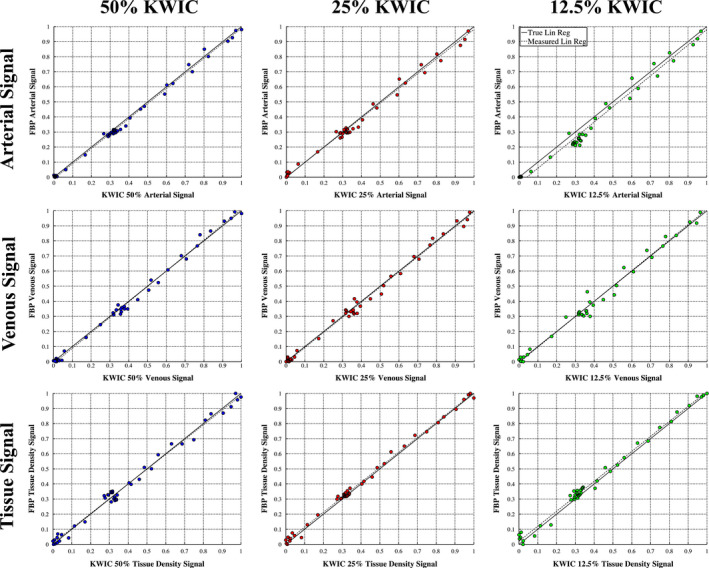
Correlation plots for Arterial (first row), Venous (second row), and Tissue (third row) signal curves comparing FBP and the KWIC reconstruction. There is high correlation at all dose reconstruction levels. [Color figure can be viewed at wileyonlinelibrary.com]

Figure 9 shows the quantitative CBF maps for one of the clinical CTP cases (case 3). The CBF maps generated with KWIC reconstructions are comparable to those by full‐dose FBP. However, some variations of CBF maps can be observed across different dose levels, for example, the CBF maps of full radial and 12.5% KWIC have a lower intensity compared to full‐dose FBP and 50% and 25% KWIC CBF maps. Table 4 shows the measured CBF and CBV in the motor cortex region of the brain. There is no significant difference of CBV and CBF values between KWIC and FBP reconstructed images. The quantitative perfusion metrics (CBF and CBV) are not significantly different (P > 0.05) between FBP and KWIC reconstructions (only CBF maps are shown).

Figure 9.

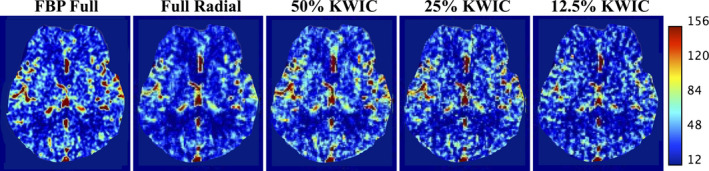
CBF maps generated from a clinical case using FBP and radial gridding with all projections (Full Radial), KWIC reconstruction at 50%, 25%, and 12.5% dose reduction levels. The CBF maps of full radial and 12.5% KWIC have a lower intensity compared to FBP full and 50% and 25% KWIC CBF maps. [Color figure can be viewed at wileyonlinelibrary.com]

Table 4.

Measured CBF and CBV values for all cases. ROl was drawn in the motor cortex region

	FBP Full	Full Radial	KWIC 50%	KWIC 25%	KWIC 12.5%
CBF(ml/100 g/min)
Case 1	40.4 ± 30.3	34.5 ± 26.6	42.8 ±  33.2	51.0 ± 52.7	46.3 ± 40.3
Case 2	49.1 ± 23.2	33.0 ± 15.9	53.1 ± 32.1	52.6 ± 31.8	52.5 ± 38.7
Case 3	56.9 ± 37.9	51.48 ± 33.2	65.5 ±  39.2	59.0 ± 37.2	49.7 ± 29.0
CBV (ml/lOO g)
Case 1	6.4 ± 3.2	5.2 ± 3.1	5.6 ± 3.4	6.7 ± 4.2	6.5 ±  3.6
Case 2	7.9 ± 2.7	5.3 ± 2.1	6.1 ± 2.7	6.4 ± 3.2	7.4 ± 4.1
Case 3	7.9 ± 4.3	6.8 ± 3.3	6.9 ± 3.5	6.9 ± 3.6	6.7 ± 3.2

5. Discussion

In both the simulated and clinical CTP data, KWIC was able to reduce the radiation dose down to 25% of the original dose without significantly affecting the image quality and perfusion quantification. While the original goal of KWIC was for preserving spatial and temporal resolutions in accelerated 4D dynamic MRI, its application in dynamic CT scans results in a reduced number of total x‐ray projections required per gantry rotation. Coupled with fast x‐ray switching and a custom acquisition scheme, it is foreseeable that perfusion exams could be conducted at reduced total radiation doses. This innovation builds on the central‐slice theorem that relates the CT sinogram to “k‐space” data by performing 1D FT of the projection of an object, which is the same as the line drawn through the center of the 2D FT plane (i.e., k‐space). Therefore, many algorithms developed for accelerated dynamic MRI including KWIC can be adapted for low‐dose dynamic CT scans such as CT perfusion and angiography.^{11, 30, 31} The drawback of KWIC is potential temporal blurring of fine objects comprising primarily high spatial frequencies. Based on our simulation, however, there is no apparent temporal blurring of CTP time courses for objects as small as 5 mm in size. Clinical CTP data did not show temporal blurring of the AIF, VOF or tissue density curves. While our initial goal is to reduce the radiation dose of brain CTP, the technology can be expanded to CTP of body organs, which is rarely performed due to excessive radiation dose. Our technique may also be adapted for multiphase CT angiography (CTA) of the brain and heart. One of the limitations of CTA in clinical applications is that the peak of the contrast bolus might not be precisely captured leading to either rescanning of the patient or misdiagnosing the disease.³² With CT‐KWIC more time points can be acquired with the same amount of dose, and thus improving the quality and reliability of CT angiography scans.

In the present study, KWIC was able to reduce the radiation dose down to 25% of the original dose without compromising the image quality of simulated CTP and clinical CTP cases without head motion (case 3). However, in the clinical case presenting head motion, the achievable dose reduction was ~50% (case 1 and 2). Since the higher frequency k‐space regions are shared between neighboring time frames in KWIC, the effect of sudden head motion is propagated to neighboring time frames during reconstruction, affecting the final image quality. While motion was observed to have an impact on reconstruction quality and dose reduction potential, other studies^{13, 33} have proposed methods for autodetection and correction of motion in radial projection acquisitions that would be applicable to the KWIC methods utilized in this work. In the present study, we observed some variations in CBF maps generated across different dose levels (Fig. 9), which may be attributed to variations in the hand drawn ROI's for the VOF and AIF, as well as different amount of view sharing, or potential patient motion. However, there was no significant difference in the measured ROI values (Table 4). Detailed investigation into the effects of motion on KWIC‐reconstructed CTP as well as its correction awaits further investigation in future studies.

Besides the angle‐bisection scheme employed in the present study, alternative sampling sequences may be applied for KWIC such as the golden ratio scheme in which the rotation angles of the x‐ray source are spaced by the golden angle (180°/1.618 = 111.25°). The golden ratio scheme guarantees an optimal projection distribution for any arbitrary number of projections used in reconstruction, especially if the number of total projection views is a Fibonacci number.^{25, 26, 34} To improve the sampling efficiency, a “tiny golden angle” scheme was introduced recently based on a generalized Fibonacci sequence that allows a smaller angle increment while still maintaining the sampling efficiency as the standard golden angle scheme.^{26, 34} It is worth noting that as a pseudo‐random sequence, the (tiny) golden ratio scheme is also ideal for modern sparse sampling techniques with constrained reconstruction such as compressed sensing (CS).

The main competition of KWIC is iterative reconstruction (IR) algorithms currently offered by all major CT vendors. Disadvantages of IR potentially include blotchy image appearance and longer computational time. As mentioned, clinical application of IR for CTP has been very limited due to the high complexity and computational burden for processing dynamic CTP images that impairs clinical workflow. In contrast, KWIC does not prolong reconstruction time and is computationally comparable to FBP. Furthermore, our technology is not exclusive to existing low‐dose CT technologies, and can be combined with IR to dramatically reduce radiation dose of existing CT scans.

Another similar study in reducing the radiation dose by retrospectively reducing the number of projections used is HYPR.^{11, 14} HYPR uses the assumption that the image is a product of the composite image (all projections) and a weighting factor in the image domain. HYPR additionally convolves a low‐pass filtering kernel to smooth out the streaking artifacts in the retrospectively undersampled low‐dose image. The main difference between HYPR and KWIC is the weighting mechanism. HYPR uses a high‐quality composite image of all the projections from the dynamic series to generate low‐noise image frames with high spatial and temporal resolutions. KWIC uses view sharing from immediate neighboring time points in the frequency domain (i.e., local k‐space filter) to minimize streaking artifacts to generate dynamic images with high spatial and temporal resolutions. While HYPR can improve the noise and spatial resolution of the dynamic images, residual artifacts can still occur.^{35, 36} Additional methods may be required to mitigate these artifacts.³⁷ If there is patient motion this can lead to streaking artifacts across all the HYPR images. KWIC reconstruction is also susceptible to streaking motion artifacts, however, the streaking artifacts are limited to the images with motion while HYPR is susceptible to motion artifacts across the dynamic series due to the composite weighted image. HYPR also uses a smoothing kernel and can decrease the spatial resolution of the images, which can affect the perfusion quantification in regions with smaller blood vessels. KWIC does not decrease the spatial resolution because it is sharing information in neighboring time points and does not require the smoothing kernel as HYPR does.

A limitation of the KWIC algorithm is that due to the view sharing in the higher spatial frequencies there will be inherent temporal blurring. It has been shown in this study as well as in MRI KWIC studies^{12, 16, 20} that the effects of temporal blurring are minimal when the projection undersampling (e.g., dose reduction) is less than 75%. The temporal blurring of the contrast uptake is more significant with smaller features (e.g., higher spatial frequencies)¹⁶ because of the higher amounts of view sharing. The temporal blurring can lead to CT number discrepancies in areas where there is contrast uptake. If there is patient motion the angle‐bisection acquisition of the projections can lead to streaking artifacts. Using CS for the undersmapled projections is a promising technique to reduce the streaking artifacts without view sharing, which would reduce the streaking artifacts due to motion and potentially improve the CTP metrics.³¹ Also, due to the interleaved view sharing there is a discontinuity in the projections in the KWIC reconstruction that can lead to streaking artifacts, when there are a higher number of subapertures used. Previous KWIC studies^{12, 16, 20} and this study show that using eight subapertures is the upper limit before reconstruction artifacts are unacceptable.

K‐space weighted image contrast does require sparse sampling through high speed x‐ray switching, which could theoretically be implemented using hardware and/or software approaches. Grid‐controlled x‐ray tube is an existing technology that allows pulsed x‐ray on a very short time scale (micro to milliseconds). It has been applied for pulsed fluoroscopy to reduce radiation dose.³⁸ Grid‐controlled x ray has also been applied for flying focal spot CT to rapidly shift the focal spot of electron beam as a means to increase the slice coverage or resolution.³⁹ Therefore, it could be feasible to adapt grid‐controlled x ray for pulsed CT acquisition as required by KWIC. Currently there are organ‐based tube current modulation techniques that have very rapid changes in mA and are clinically used.⁴⁰ Alternatively, mechanical approaches such as a lead shutter may be applied for implementing pulsed x ray. Software control of intensity‐modulated x ray has been applied for CT with reduced radiation dose, for example, for thoracic imaging to spare lung/breast and cardiac imaging to focus on specific cardiac phases, although the time scale of existing x‐ray intensity modulation is generally on the order of a few hundred milliseconds. Both hardware and software approaches can be explored for the implementation of pulsed x ray in future studies. We recognize that the potential hardware developments required to implement the proposed CTP acquisition/reconstruction approach are substantial, however, the work presented demonstrates the compelling dose reduction benefits that could be possible with such technology, and the potential new applications of low‐dose CTP, that such hardware developments would enable, could be a powerful pathway for improvements in clinical care.

6. Conclusions

In this work, we presented a low‐dose CTP technique by adapting a projection view‐sharing technique named KWIC that was originally developed for accelerated 4D dynamic MRI with radial trajectories.^{10, 11} This study provides a proof‐of‐concept for KWIC reconstruction of CTP to achieve ~75% dose reduction without compromising imaging speed or quality. With high speed x‐ray switching, this technique may be expanded for CTP of body organs and multiphase CTA as well as to include other constrained sparse sampling techniques. Future work will concentrate on further improvement of SNR of the KWIC reconstruction with CT data, further validation of the proposed algorithm in clinical CTP studies, and addressing sampling requirements of the acquisition schemes via new sampling protocols (e.g., tiny golden angle) and hardware and software developments to achieve the required fast x‐ray switching. As demonstrated, KWIC's potential for use in CTP provides another possible pathway to reduce the radiation dose of current CT perfusions exams as well as possible pathways toward clinical body perfusion with CT, and reduced‐dose CT angiography.

Conflict of interest

Thomas Martin, John Hoffman, and Danny Wang are inventors of a patent on low‐dose CTP held by UCLA. Thomas Martin and Danny Wang hold shares in Hura Imaging, LLC.

Appendix 1.

1.1.

Angular rebinning, which induces the temporal blurring, is governed by the equation θ = α + β, where θ is the rebinned angle, α is the unrebinned x‐ray source angle, and β is the detector channel fan angle.²², ²³ Thus, a given projection acquired at angle α, is rebinned into projections of similar source angle, adjusted depending on an individual detector's fan angle. Measurements near the edge of the scanner field of view (i.e., “large” absolute value of β) are rebinned to projections further from its original source angle; measurements near the center of the field (i.e., small β) of view are largely unchanged.

The maximum detector fan angle for the scanner utilized in this is work is 0.436 radians (detectors at the edge of the scanner field of view). A total of 1152 projections are acquired per scanner rotation, which gives an angular increment of 0.00545 rad/projection. Thus, the maximum change in projection index due to rebinning is ±80 projections. With a scanner rotation time of 1 s per rotation, this results in a temporal error of (1/1152)*80 = 0.07 s. Since the blur happens in both the positive and negative directions, all of which will contribute to the reconstruction, we find that at the edge of the field of view, we obtain a temporal blur of 2*0.07 = 0.14~0.2 s due to the angular rebinning. This, however, is still substantially lower than the perfusion sampling rate of 1 sample per second.