Robust optimization in IMPT using quadratic objective functions to account for the minimum MU constraint

Abstract

Purpose

Currently, in clinical practice of intensity‐modulated proton therapy (IMPT), the influence of the minimum monitor unit (MU) constraint is taken into account through postprocessing after the optimization is completed. This may degrade the plan quality and plan robustness. This study aims to mitigate the impact of the minimum MU constraint directly during the plan robust optimization.

Methods and materials

Cao et al. have demonstrated a two‐stage method to account for the minimum MU constraint using linear programming without the impact of uncertainties considered. In this study, we took the minimum MU constraint into consideration using quadratic optimization and simultaneously had the impact of uncertainties considered using robust optimization. We evaluated our method using seven cancer patients with different machine settings.

Result

The new method achieved better plan quality than the conventional method. The D_95% of the clinical target volume (CTV) normalized to the prescription dose was (mean [min–max]): (99.4% [99.2%–99.6%]) vs. (99.2% [98.6%–99.6%]). Plan robustness derived from these two methods was comparable. For all seven patients, the CTV dose–volume histogram band gap (narrower band gap means more robust plans) at D_95% normalized to the prescription dose was (mean [min–max]): (1.5% [0.5%–4.3%]) vs. (1.2% [0.6%–3.8%]).

Conclusion

Our new method of incorporating the minimum MU constraint directly into the plan robust optimization can produce machine‐deliverable plans with better tumor coverage while maintaining high‐plan robustness.

1. Introduction

Intensity‐modulated proton therapy (IMPT) is receiving increased attention in cancer care for its ability to better spare normal tissue compared with intensity‐modulated radiation therapy (IMRT) and the passive scattering proton therapy.^{1, 2, 3} In IMPT, intensities of beamlets are optimized using complicated computer algorithms to deposit adequate tumoricidal dose to targets while depositing as little dose as possible to nearby normal tissues.⁴

IMPT is precise but is sensitive to uncertainties caused by patient setup and range uncertainties, respiratory motion, and anatomic changes.^{5, 6} Several robust optimization methods have been proposed and have been shown to have great advantages by achieving robust plans while maintaining high plan quality.^{2, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24} Unfortunately, in proton therapy besides uncertainties, there are machine hardware constraints, for example, field‐size constraint, minimum–maximum energy constraint, dose‐rate constraint for synchrotron‐based proton therapy systems, and minimum–maximum monitor unit (MU) constraint. Among them, the minimum MU constraint is the most prominent one.²⁵ The minimum MU constraint in proton therapy is mostly due to the minimum charge needed for the spot profile monitor to work properly. Therefore, a small number of protons cannot be delivered reliably, leading to the minimum MU constraint for proton machines.

To date, however, all published robust optimization methods in IMPT ignored the effect of the minimum MU constraint during optimization. To meet the minimum MU constraint, many clinical practices still use the expedient of postprocessing procedure provided by the current commercial treatment planning systems (TPS). This is a procedure that modifies the intensity map to meet the minimum MU constraint after optimization is completed. Different methods are used for postprocessing. A simple one is to round up/down the spots which have intensities lower than minimum MU.^{25, 26} This postprocessing procedure can introduce significant distortions of the dose distributions, thus degrading plan quality.²⁵ Recently, Lin et al. proposed a greedy reassignment method, which reassigned the removed spot's intensity to its neighbor spots to maintain a less distorted dose distribution.²⁷ Compared to the round up/down method, they better mitigated the impact of the minimum MU constraint.

There is a long history in photon therapy to account for the hardware constraints in treatment planning. IMRT uses multiple leaf collimators (MLCs) to form some very complicated dose distributions. Currently, most IMRT plans still need a conversion process (using a leaf‐sequencing algorithm) after a fluence map optimization. This conversion process is very similar to the postprocessing used in IMPT to make the IMPT plans deliverable (as discussed before). Due to the hardware constraints of MLC, plan quality degradation could happen in this conversion process for IMRT. Therefore, the regularization method has been proposed in IMRT to make the optimized fluence map smoother since “smooth profiles are easier to convert into step‐and‐shoot segments than jagged profiles”.²⁸ In addition, nonuniform fluence map usually leads to dose distributions less robust to geometric uncertainties²⁹ and reduces the delivery efficiency³⁰ in IMRT. Several regularization methods have been proposed including variational methods,^{31, 32, 33, 34} filtering methods,^{34, 35, 36, 37} and iterative methods.²⁸ Alternatively, people have developed the direct machine optimization methods (DMPO) to incorporate machine constraints directly in the IMRT optimization so that the distortion to the optimized dose distribution caused by the conversion process can be avoided.^{38, 39, 40}

The minimum MU constraint in proton therapy restricts spot intensities to be either zero or no smaller than the minimum MU, which cannot be solved by smoothing the fluence map as the regularization method does for IMRT. Some methods with the minimum MU constraint considered directly during the plan optimization have also been proposed in proton therapy. Cao et al.⁴¹ proposed one method composed of two optimization stages using linear programming. In the first stage, they performed an optimization to find an intermediately optimized IMPT plan without the minimum MU constraint considered. In the second stage, they performed a boundary‐constrained optimization, in which the optimizer would enforce lower bound constraints for every beamlet that has positive intensity after the first stage. The limitations of this methodology are that plan robustness is not considered and the linear programming is not compatible with the existing commercial TPS. The commercial TPS for proton therapy, Raystation™ (RaySearch Laboratories, Stockholm, Sweden), has the minimum MU constraint considered in the optimization. In the newest version of Eclipse™, the minimum MU constraint has also been considered in the new optimization algorithm [nonlinear proton optimizer (NUPO)]⁴² via two‐phase optimization strategy. In the first phase, optimal fluences are derived with respect to user‐defined objectives. In the second phase, the optimal fluences are converted into deliverable spots, in which spots with smaller intensities are gradually discarded and the left spots are reoptimized. However, this method cannot be straightforwardly integrated into the most popular optimization algorithm of the Eclipse™ [proton convolution superposition optimizer (PCS)], which directly optimizes the spots’ intensities.

In this study, we integrated the minimum MU constraint into robust optimization for IMPT treatment planning based on the conventional quadratic programming. We developed a new robust optimization algorithm and used L‐BFGS‐B optimizer^{43, 44} to incorporate the minimum MU constraint into robust optimization by turning the boundary constraints on and off alternatingly during optimization, so that the algorithm will dynamically apply the boundary constraints to determine whether the intensity of one spot should be either zero or above the minimum MU on the fly. Thus, the optimization explored the full solution domain and led to a better deliverable robust plan compared to the postprocessing method. We further assessed the effectiveness of our new planning method by comparing plan quality and robustness of IMPT plans for seven patients with different spot size and different minimum MU constraint to those achieved with the use of the conventional robust optimization method.

2. Methods

In this study, IMPT plans were retrospectively generated for seven patients with real CT images and clinical structures using both the conventional and new optimization methods with two different machine settings: (a) for a machine with an in‐air, energy‐dependent, large spot size at isocenter (σ: 5–15 mm) and spacing (1.3σ), and (b) for a small spot size (σ: 2–6 mm) and fixed spacing (5 mm). One MU is defined according to the IAEA TRS 398 during our machine commissioning. The minimum MU constraint was 0.003 MU for the small spot machine and 0.005 MU for the large spot machine. For each patient, three plans were generated: the conventional nondeliverable robust plan (plan A), the conventional deliverable robust plan using postprocessing (plan B), and our new deliverable robust plan (plan C). They all use the same objectives and stopping criteria. To illustrate the capability of our proposed method more clearly, we also did the comparison with artificially large (10 times larger than realistic values) minimum MU setting.

2.A. Conventional robust optimization without the minimum MU constraint considered

Robust optimization methods can be implemented by different models: for example, a probabilistic robust optimization model,^{12, 13} an objective‐wise min–max robust optimization model,⁸ a multiple criteria robust optimization model,⁷ or a voxel‐wise worst‐case robust optimization model.^{9, 11, 45} The worst‐case robust optimization model has been verified to simultaneously improve robustness and plan quality, particularly in terms of sparing normal tissues, compared with the conventional planning target volume (PTV) methods.^{22, 46, 47} For brevity, hereafter, we will use the term robust optimization to refer to voxel‐wise worst‐case robust optimization.

In robust optimization, the setup uncertainty and range uncertainty are considered in the optimization process, as shown in the following formula:

$$\begin{array}{c}\hfill F_{\mathit{robust}}({\mathrm{\omega }}_j)=\sum _{i\in CTV}{p}_{CTV,min}{(D_{i,min}-D_{0,CTV})}^2\\ \hfill +\sum _{i\in CTV}{p}_{CTV,max}{(D_{i,max}-D_{0,CTV})}^2\\ \hfill +\sum _{i\in OARs}{p}_{\mathit{OARs}}·H(D_{i,max}-D_{0,OARs}){(D_{i,max}-D_{0,OARs})}^2\end{array}$$

$$D_i^m=\sum _j{k}_{i,j}^m{\mathrm{\omega }}_j^2$$

$$D_{i,min}=\underset{m}{\mathit{min}}(D_i^m)$$

$$D_{i,max}=\underset{m}{\mathit{max}}(D_i^m)$$

Where p denotes the penalty weight of the corresponding term and D ₀ denotes the prescribed dose for the corresponding region of interest (ROI). The Heaviside function, H(D _i −D ⁰ ), is defined conventionally (i.e., its value is unity if D _i  > D ₀ but zero if D _i  ≤ D ₀ ). The terms D _i,min  = min _m ($D_i^m$) and D _i,max  = max _m ($D_i^m$), respectively, indicate the minimum and maximum dose among possible doses $D_i^m$ in voxel i (m = 1…9 here, is the index of the corresponding uncertainty scenario with setup and range uncertainties considered), which are calculated using $D_i^m=\sum _j{k}_{i,j}^m{\mathrm{\omega }}_j^2$ in each iteration. The mth influence matrix $k_{i,j}^m$ incorporates range and setup uncertainties. ${\mathit{\omega }}_j^2$ is the non‐negative intensity map. Dose–volume constraints (DVCs) were used following the method proposed by Wu and Mohan.⁴⁸ In the DVH curves, the DVCs to limit the hot spots in the DVH can be specified as: $V(>D_1)<V_1$, that is, the volume receiving dose $D_{i,max}$ greater than $D_1$ should be less than $V_1$. Then, another dose value $D_2$ can be derived so that in the current DVH, $V\left(D_2\right)=V_1$. Then, the part in the objective function related to DVC can be written as:

$${\sum }_{i\in CTV}{p}_{\mathit{CTV}}H\left(D_2-D_{i,max}\right)H\left(D_{i,max}-D_1\right){\left(D_{i,max}-D_1\right)}^2+\cdots ,$$

Only voxels with $D_{i,max}$ between $D_1$and $D_2$ are penalized. The ellipsis means that additional DVC for the target (also normal tissues) can be specified to have more complete control of the shape of the DVH curves. Similar concepts apply to the DVC to limit the cold spots in the DVH of the targets that can be used. For details of the optimization algorithm, please refer to Liu et al.^{9, 10} The algorithm for robust optimization is shown in Fig. 1 (left). In this treatment‐planning process, no minimum MU constraints are considered. To make the derived robust plan deliverable, a postprocessing procedure (discussed below) is needed.

Figure 1.

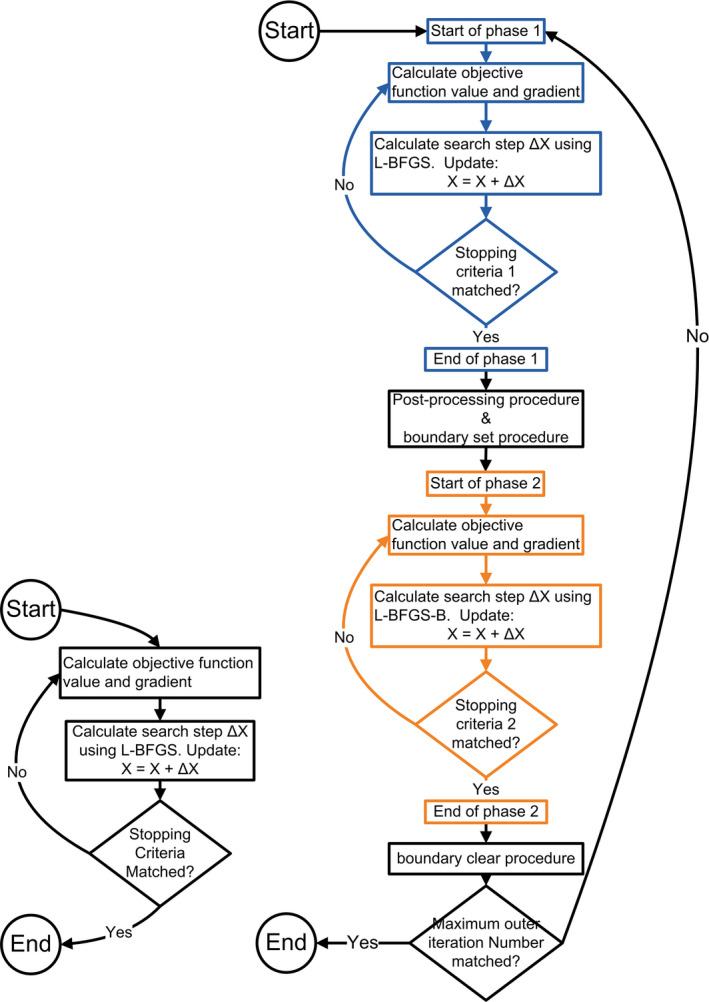
Algorithm diagrams for the conventional robust optimization (left) and the proposed deliverable robust optimization (right). L‐BFGS indicates limited memory Broyden–Fletcher–Goldfarb–Shanno algorithm. [Color figure can be viewed at wileyonlinelibrary.com]

During postprocessing, the system would discard any beamlets with intensities smaller than half of the minimum MU and round the intensities of any beamlets with intensities equal to or larger than half the minimum MU up to the minimum MU. After this procedure, the solution might possibly deviate from the optimal solution. The extent of the deviation depends on the magnitude of the minimum MU constraint and the number of beamlets that are postprocessed.

2.B. Robust optimization with the minimum MU constraint considered

The minimum MU constraint is a lower boundary constraint on the intensity of every beamlet and depends on the proton scanning beam delivery machine. For example, the proton scanning beam machine in our clinic has a minimum MU constraint of 0.003 MU. Thus, the deliverable beamlet intensity is either 0 or ≥ 0.003 MU. The flexibility to have zero intensity for some beamlets is important because it allows optimizers to turn off a beamlet if it is not needed. However, it introduces a discontinuous feasible region to each beamlet: {0}∪[minimum MU, ∞]. In quadratic programming, no optimizers can work on this feasible region directly. To be consistent with current practice, it is important to address this issue in the context of quadratic programming. L‐BFGS is an efficient Quasi‐Newton method to solve an optimization problem with a quadratic objective function with low memory overhead. The L‐BFGS‐B version can apply boundary constraints for its solution variables. Unfortunately, it cannot handle the discontinuous feasible region problem either. To address this problem, we developed a new robust optimization algorithm to dynamically set up the boundary constraints during the optimization process by iteratively turning the boundary constraints on and off. This novel method can effectively find an optimized solution in this discontinuous feasible region composed of zero and values no smaller than the minimum MU constraint.

In our new approach, the form of the objective function remains the same as the conventional robust method. The algorithm for deliverable robust optimization is shown in Fig. 1 (right). More details about the algorithm will be discussed in Section 2.C.

The optimization is based on the in‐house developed analytical dose engine,^{9, 10} using real CT images and clinical structures. Actually, this in‐house developed TPS had been fully validated and clinically commissioned for our proton machines. We had successfully used this TPS to treat five complicated patients, including lung, head and neck, and central nervous system cancers (the final dose calculation was done after optimization still using a commercial TPS),⁴⁹ and regularly used it as secondary MU check for our commercial TPS. The TPS is parallelized using MPI and OpenMP and running on the in‐house high‐performance computing cluster utilizing 48 CPU cores. Each core is Intel Xeon E5‐4650 v2 CPUs at 2.40 GHz.

2.C. Algorithms and procedures

2.C.1. Algorithms

As shown in Fig. 1, in the conventional robust optimization, optimization is performed in one level of loop. When the maximum loop number or other optimization termination criterion is reached, the optimization will terminate. In our deliverable robust optimization, optimization is performed in two levels of loop: the outer loop and the inner loop. For every outer loop, two phases of the inner loop are performed. Phase 1 of the inner loop is performed without boundary constraints, and phase 2 of the inner loop is performed with boundary constraints. Whether to apply the minimum MU constraint for each beamlet in phase 2 is determined by the results of phase 1.

2.C.2. Procedure

Postprocessing procedure

For every beamlet that has intensity ${\mathit{\omega }}_j^2$ equal to or larger than half the minimum MU, its intensity is set to max (${\mathit{\omega }}_j^2$, minimum MU); otherwise, its intensity is set to zero.

Boundary set procedure

For every beamlet that has intensity ${\mathit{\omega }}_j^2$ equal to or larger than half the minimum MU, a lower boundary constraint with the value of the minimum MU will be applied; otherwise, this beamlet is turned off in the following optimization.

Boundary clear procedure

During this step, the boundary constraints for all beamlets, regardless of their intensity, are cleared for the subsequent optimization. All beamlets will be available for the subsequent optimization.

2.D. Patient data and evaluation

We tested our method using seven patients: one with prostate cancer (prescription dose: 76 Gy[RBE]) (RBE indicates Relative Biological Effectiveness), three with head–neck cancer (prescription dose: 66 Gy[RBE], 66 Gy[RBE], and 60 Gy[RBE]), and three with lung cancer (prescription dose: 74 Gy[RBE], 66 Gy[RBE], and 66 Gy[RBE]), as shown in Table 1.

Table 1.

Patient treatment configurations. Energy layers are carefully selected in machine commissioning so that roughly the proton beam range difference between adjacent energy layers is 2 mm in low energy region and 5 mm in high energy region to minimize the ripples in the dose distribution in the beam direction

Pt	Cancer	Field	No. of beamlets	No. of energy layers	Energy range, MeV	Spot spacing, mm	Minimum MU
1	Prostate	1	748	19	148.85–190.55	Energy‐dependent spacing (1.3σ)	0.005
		2	750	19	148.85–190.55
2	Head and neck	1	1,216	20	159.55–206.35	Energy‐dependent spacing (1.3σ)	0.005
		2	1,347	29	141.65–206.35
		3	1,326	25	146.95–203.75
3	Head and neck	1	967	40	72.55–131.05	Energy‐dependent spacing (1.3σ)	0.005
		2	1,114	42	83.15–144.95
		3	1,056	46	72.55–141.65
4	Head and neck	1	7,625	45	78.5–139.1	5	0.003
		2	5,133	65	91.7–185.2
		3	3,243	37	78.5–129.699
		4	5,841	33	80.3–126
5	Lung	1	3,075	49	72.55–122.55	Energy‐dependent spacing (1.3σ)	0.005
		2	3,142	49	72.55–122.55
		3	3,600	67	72.55–155.35
		4	3,657	53	72.55–129.249
6	Lung	1	14,791	56	71.3–147	5	0.003
		2	9,557	69	91.7–191.3
		3	15,061	58	80.3–156.7
7	Lung	1	12,294	68	86.9–183.3	5	0.003
		2	12,391	73	91.7–200.4
		3	16,024	58	71.3–149.2

Pt, patient.

For each patient, we generated three plans based on two optimization methods: plan A is generated by the conventional robust optimization method without the postprocessing procedure. It contains intensities of beamlets smaller than the minimum MU. Plan B is derived from plan A using the postprocessing procedure. It represents the current routine practice in the clinic. Plan C is generated by the new deliverable robust optimization method. We compared plan quality and robustness among these three plans. The proposed method aims to maintain the plan quality and robustness by taking into account the minimum MU constraint.

We do the normalization by dividing the doses with the prescription dose so that different cases with different prescription doses can be compared directly. The following dosimetric parameters were used to compare plan quality and robustness: for any structure, the minimum dose that covers 95% volume of the structure with the highest dose (D_95%); the minimum dose that covers 25% volume of the ROI (D_25%) with the highest dose; the minimum dose that covers 5% volume of the ROI (D_5%) with the highest dose; the minimum dose that covers 1% volume of the ROI (D_1%) with the highest dose; and the normalized volume as a percentage of the ROI that received at least 20 Gy[RBE] or 35 Gy[RBE] (V₂₀, V₃₅).

2.E. Robustness quantification

To evaluate or compare the robustness of IMPT plans, we used a robustness quantification technique that displayed the envelope of all dose–volume histograms in band graphs of the nine dose distributions associated with the corresponding range or setup uncertainties. The width of the band is used to indicate the plan robustness between the competing plans. This robust quantification technique is effective for determining an IMPT plan's sensitivity to setup and range uncertainties.^{9, 10, 50}

3. Results

3.A. Comparison of plan qualities

3.A.1. Comparison of nominal scenario plan qualities

Plan A is the plan without the minimum MU constraint considered. We performed the optimization with the minimum MU as 0.003 and 0.005 MU for the small and large spot machines, respectively. Consistent conclusions are derived from the results of seven patients with different machines. Results are shown in Table 2.

Table 2.

Results for all seven patients^a

Pt	Statistic	Plan A	Plan B	Plan C
1	CTV D95%	0.996 (0.991–0.996)	0.996 (0.990–0.996)	0.996 (0.991–0.996)
	CTV D5%	1.009 (1.006–1.010)	1.009 (1.006–1.010)	1.009 (1.006–1.010)
	Bladder D25%	0.059 (0.017–0.137)	0.059 (0.017–0.137)	0.059 (0.016–0.137)
	Rectum D25%	0.360 (0.170–0.632)	0.360 (0.169–0.634)	0.356 (0.172–0.637)
2	CTV D95%	0.993 (0.961–0.993)	0.986 (0.954–0.987)	0.993 (0.960–0.993)
	CTV D5%	1.040 (1.036–1.046)	1.036 (1.030–1.041)	1.039 (1.037–1.046)
	Brainstem D1%	0.755 (0.639–0.848)	0.751 (0.634–0.842)	0.761 (0.646–0.851)
	Brain D5%	0.446 (0.397–0.506)	0.442 (0.393–0.502)	0.448 (0.399–0.511)
3	CTV D95%	0.992 (0.953–0.992)	0.990 (0.952–0.990)	0.992 (0.949–0.992)
	CTV D5%	1.059 (1.056–1.069)	1.058 (1.054–1.067)	1.059 (1.056–1.070)
	Brain D5%	0.662 (0.599–0.702)	0.660 (0.597–0.700)	0.661 (0.596–0.701)
	Optic chiasm D1%	0.998 (0.976–1.013)	0.995 (0.974–1.010)	1.001 (0.979–1.018)
4	CTV D95%	0.996 (0.989–0.996)	0.992 (0.987–0.992)	0.996 (0.989–0.996)
	CTV D5%	1.021 (1.016–1.023)	1.018 (1.014–1.020)	1.023 (1.018–1.028)
	Spinal cord D1%	0.311 (0.269–0.364)	0.309 (0.266–0.361)	0.316 (0.271–0.368)
	Brain D5%	0.093 (0.062–0.118)	0.092 (0.061–0.116)	0.096 (0.063–0.127)
5	CTV D95%	0.994 (0.974–0.994)	0.988 (0.971–0.988)	0.994 (0.974–0.994)
	CTV D5%	1.044 (1.035–1.051)	1.041 (1.032–1.048)	1.045 (1.036–1.051)
	Right lung V20	0.289 (0.266–0.315)	0.288 (0.265–0.313)	0.298 (0.274–0.324)
	Spinal cord D1%	0.029 (0.023–0.065)	0.029 (0.023–0.065)	0.030 (0.024–0.065)
6	CTV D95%	0.994 (0.981–0.994)	0.992 (0.981–0.992)	0.994 (0.979–0.994)
	CTV D5%	1.050 (1.024–1.060)	1.049 (1.023–1.058)	1.054 (1.027–1.057)
	Lung V20	0.341 (0.321–0.362)	0.342 (0.322–0.362)	0.341 (0.322–0.362)
	Heart V35	0.121 (0.101–0.144)	0.121 (0.101–0.144)	0.121 (0.101–0.144)
7	CTV D95%	0.996 (0.991–0.996)	0.996 (0.991–0.996)	0.996 (0.989–0.996)
	CTV D5%	1.012 (1.005–1.012)	1.012 (1.006–1.013)	1.017 (1.007–1.017)
	Total lung V20	0.281 (0.270–0.290)	0.281 (0.270–0.290)	0.285 (0.275–0.292)
	Spinal cord D1%	0.258 (0.227–0.348)	0.259 (0.224–0.350)	0.240 (0.219–0.351)

CTV, clinical target volume; D_X%, the minimum normalized dose that covers X% of the region of interest with the highest dose; MU, monitor unit; Pt, patient; V_X, the normalized volume as a percentage of the region of interest that received at least X Gy[RBE].

^aValues are norminal (min–max values of uncertainty scenarios).

Figure 2 shows the results for three patients (patient #1, #2, and #5) with two sets of minimum MU settings: realistic (0.005 MU) and artificially large (0.05 MU). In the realistic minimum MU setting, in terms of target coverage, the results from the conventional robust optimization method after postprocessing (plan B) had a notable deviation from plan A, except for patient 1, for whom the effect of the minimum MU was negligible. Thus, compared with the conventional robust optimization method, our novel deliverable robust optimization method can prevent target coverage from degrading due to the impact of the minimum MU, while having organ protections comparable to that of plan A. In the artificially large minimum MU setting, it is more clear that our proposed method can preserve the target coverage while the postprocessing significantly impaired the target coverage.

Figure 2.

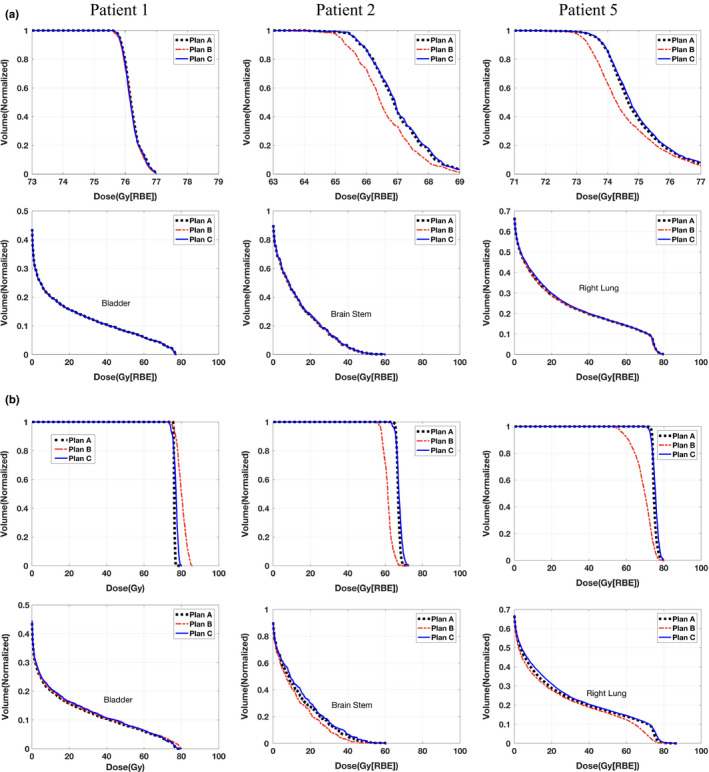
Dose–volume histograms (DVHs) for all three methods in patient 1 with prostate cancer (first column), patient 2 with head–neck cancer (second column), and patient 5 with lung cancer (third column). The first row indicates DVHs for CTVs; the second row indicates DVHs for organ at risk. Part (a) is the test with realistic minimum MU constraint and part (b) is with artificially large (10 times larger than that in part (a)) minimum MU constraint. Please note that figures in the top row are zoomed in. [Color figure can be viewed at wileyonlinelibrary.com]

3.A.2. Comparison of plan robustness

Our method not only minimized the influence of the minimum MU constraint on nominal plan quality but also maintained high plan robustness. A complete comparison of robustness (width of the band of CTV at D_95%) for the seven patients is shown in Fig. 3. Our method prevented the nominal plan quality from degrading while also preserved the plan robustness. This trend was clearer when the method was applied to settings with larger minimum MU constraint.

Figure 3.

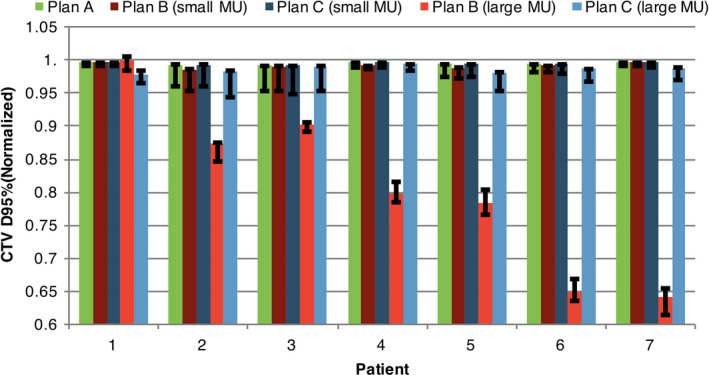
Comparison of CTV D_95% (CTV, clinical target volume; D_95%, the minimum normalized dose that covers 95% of the region of interest with the highest dose of plans A, B, and C with realistic (small) minimum MU constraint and artificially 10 times larger (large) minimum MU constraint, in all seven patients. Error bars indicate the DVH family bandwidth at D_95%, which indicates plan robustness. [Color figure can be viewed at wileyonlinelibrary.com]

3.B. Performance

For a fair comparison of the performance of our new minimum robust optimization method, the time consumed is calculated so that the number of total optimization loops was normalized to 300 for both the deliverable robust optimization and the conventional robust optimization methods. Comparison of the computation time between the two methods showed that the deliverable robust optimization required less time for most patients (Table 3). The unexpected sweetness of faster calculation per inner iteration may be due to the newer implementation of L‐BFGS‐B compared to L‐BFGS.

Table 3.

Total CPU time normalized to 300 loops

Patient	Conventional robust optimization	Deliverable robust optimization
1	2 min, 38 s	2 min, 16 s
2	8 min, 9 s	7 min, 38 s
3	13 min, 43 s	13 min, 15 s
4	500 min, 15 s	438 min, 9 s
5	71 min, 48 s	71 min, 25 s
6	40 min, 21 s	44 min, 0 s
7	66 min, 5 s	62 min, 50 s

4. Discussion

In this study, we developed a new robust optimization method using a quadratic objective function to account for the minimum MU constraint in IMPT. By dynamically turning on and off the boundary constraints of the solution variables directly in the optimization, our new method derived the optimized solution in the discontinuous feasible region and generated deliverable robust plans without the conventional postprocessing procedure.

It is important for the developed methods to be compatible with the current commercial TPS for rapid translation to clinical practice. All the commercial TPS are using nonlinear programming in optimization. Nonlinear programming based on quadratic objective functions (i.e., quadratic optimization) has been used in radiation therapy treatment planning for decades. Compared with linear programming, quadratic optimization usually generates plans with smoother dose–volume histogram curves.⁵¹ Furthermore, because of its simplistic formulations and the capability to use Quasi‐Newton optimization methods, it can achieve clinically acceptable plans much more quickly than linear programming.⁵¹ Therefore, we believe that it is still valuable to develop a method which can integrate the minimum MU constraint into robust optimization for IMPT treatment planning using an optimization algorithm similar to PCS. Therefore, it can be more readily incorporated into the current IMPT treatment planning workflow (such as the most popular version of the optimization algorithm, PCS, in Eclipse^™).

Proton dose distribution is highly sensitive to patient setup and range uncertainties. Therefore, it is important to consider plan robustness in IMPT treatment planning. Recently, many groups have proposed different robust optimization methods that have achieved robust plans while preserving the nominal plan quality compared with the margin‐based method. In this study, we based on the voxel‐wise worst‐case robust optimization which operates on a given set of uncertainty scenarios. Fredriksson et al. have introduced a new robust optimization method which maximizes the possibility of the clinical acceptance with the variable extent of uncertainties that can be incorporated.⁵² This method explored more possibilities in terms of plan quality and demonstrated the relationship between the extent of uncertainties considered and the nominal plan quality. This provides users more control in the tradeoff between nominal plan quality and plan robustness. In our future work, we plan to provide the same control with a different approach.

It is worth noting that, in spite of the fact that our deliverable robust optimization was currently implemented on the basis of the voxel‐wise worst‐case robust optimization method, it is essentially independent of the choice of the optimization model. Therefore, it can be applied to a broad range of optimization models: either robust or nonrobust and either proton or photon therapy. It can also be used in beam angle optimization, optimization in the reduction in energy layers, and spot position optimization since these optimizations all potentially could lead to a substantial number of spots with small intensities. Therefore, integration of the minimum MU constraint into plan optimization could be important for these problems.

Preservation of target coverage while accounting for the minimum MU constraint is important in clinic practice. Degradation of the target coverage, although small, could substantially increase local recurrence. Local recurrence is one of the major causes of patient mortality in many disease sites. In the current clinical practice, the treatment planner sometimes has to adjust the spot spacing and reoptimize the plan by trial‐and‐error if the impact of the minimum MU constraint turns out to be significant (decreasing the target coverage a lot). Our method would relieve the treatment planner from the burden of selecting appropriate spot spacing by trial‐and‐error to minimize the impact of the minimum MU constraint. More importantly, since the minimum MU constraint are directly incorporated into the treatment planning; a postprocessing is not needed as in the current clinical practice; and no dose distribution degradation would take place due to the minimum MU constraint.

The parameters of our proton machines such as spot spacing and discrete energy layers are tuned with great efforts so that the impact of the minimum MU is minimized during the machine commissioning. Therefore, the benefit of deliverable robust optimization is diluted here. We also evaluated our method with larger minimum MU constraint (up to ten times larger). Results showed that our method can still mitigate the effect of the much larger minimum MU constraint (Fig. 3). It suggests that our method is valuable for systems with larger minimum MU constraint and for proton centers, in which the technical support of the careful adjustment of the related configurations to minimize the influence of the minimum MU is not available.

Our method has some limitations. Because of practical considerations, only nine uncertainty scenarios, composed of rigid isocenter shifts due to patient setup uncertainty and minimum–maximum range uncertainty, were considered in the optimization. This could either underestimate or overestimate the effect of uncertainties.⁵³ Also, a study including a larger patient cohort is needed to get statistically significant results.

In summary, compared with the conventional postprocessing methods, our new method of incorporating the minimum MU constraint directly into robust optimization can produce machine‐deliverable plans with better tumor coverage while maintaining high plan robustness.

Conflicts of Interest

The authors have no relevant conflicts of interest to disclose.