Individual Parcellation of Resting fMRI with a Group Functional Connectivity Prior

Abstract

Cortical parcellation based on resting fMRI is an important tool for investigating the functional organization and connectivity of the cerebral cortex. Group parcellation based on co-registration of anatomical images to a common atlas will inevitably result in errors in the locations of the boundaries of functional parcels when they are mapped back from the atlas to the individual. This is because areas of functional specialization vary across individuals in a manner that cannot be fully determined from the sulcal and gyral anatomy that is used for mapping between atlas and individual. We describe a method that avoids this problem by refining an initial group parcellation so that for each subject the parcel boundaries are optimized with respect to that subject’s resting fMRI. Initialization with a common parcellation results in automatic correspondence between parcels across subjects. Further, by using a group sparsity constraint to model connectivity, we exploit group similarities in connectivity between parcels while optimizing their boundaries for each individual. We applied this approach with initialization on both high and low density group cortical parcellations and used resting fMRI data to refine across a group of individuals. Cross validation studies show improved homogeneity of resting activity within the refined parcels. Comparisons with task-based localizers show consistent reduction of variance of statistical parametric maps within the refined parcels relative to the group-based initialization indicating improved delineation of regions of functional specialization. This method enables a more accurate estimation of individual subject functional areas, facilitating group analysis of functional connectivity, while maintaining consistency across individuals with a standardized topological atlas.

Graphical abstract

1. Introduction

Parcellations of the human cerebral cortex representing cyto-, myelo- or chemo-architecture are helpful in understanding the organization and functioning of the brain (Brodmann, 1909; Eickhoff et al., 2002; Von Economo and Koskinas, 1925; Glasser et al., 2016). While we are not yet able to reliably identify architectonic boundaries with in vivo imaging, functional magnetic resonance imaging (fMRI) reveals large-scale correlations in the resting BOLD signal that can be used to identify functional networks (Biswal, 1995). Identification of contiguous areas of cortex that exhibit similar network connectivity can be used to define a functional parcellation (Raichle et al., 2001; Sporns et al., 2005, Smith et al., 2013, Kim et al., 2010; Eickhoff et al., 2011; Eickhoff et al., 2015).

One approach to parcellation is to process each subject separately, subdividing the cortex into a set of functionally homogeneous regions specific to that subject (Blumensath et al., 2013). Limited data available for a single individual can result in instability of the estimated boundaries (Rubinov et al., 2010; Smith et al., 2011). Furthermore, it can be difficult to then determine correspondence between parcels across individuals, as required for group studies of connectivity.

Group analysis is typically performed with respect to a structural coregistration that uses sulcal and gyral features to align the cortices from each subject to a common atlas. Individual parcellations can then be pooled into a single group parcellation with respect to this anatomical correspondence using clustering or other techniques (Yeo et al., 2011; Wig et al., 2014; Craddock et al., 2012; Glasser et al., 2016). Alternative multi-graph K-way clustering methods have been proposed that simultaneously parcellate all subjects in a group (Shen et al., 2010; Arslan et al., 2015). An alternative approach uses group independent component analysis (Beckmann et al., 2009) to directly produce a single parcellation.

These methods are all based on the implicit assumption that all individuals have a common functional parcellation when mapped to the common atlas. However, it is well known that architectonic boundaries and regions of functional specialization do not align precisely with macroscopic morphological features (Brodmann, 1909; von Economo and Koskinas, 1925; Zilles and Amunts, 2010; Amunts et al., 1999; Penfield and Rasmussen, 1950; Honey et al., 2009; Gordon et al., 2015). As a result, a common parcellation will invariably result in errors in defining functionally specialized regions when these areas are mapped back from the atlas to the individual. It can therefore be advantageous to maintain separate parcel boundaries for each subject while still defining correspondence across subjects. Approaches to this joint individual/group parcellation problem include use of shrinkage for each individual towards a group connectivity measure (Shou et al., 2014) and individual parcellation in which connectivity is defined using weighted signal averages over each parcel where the weights are reduced in regions of high inter-subject variability (Wang et al., 2015).

Here we describe GPIP (Group Prior Individual Parcellation), a novel cortical parcellation method based on resting fMRI that performs group-based parcellation but also allows individual variability across subjects in the boundaries of these parcels. As a result, we can retain a single anatomical correspondence across subjects but functional regions and their boundaries can vary from individual to individual with respect to this anatomical correspondence. We use a Bayesian formulation that combines two priors, one on the group connectivity between parcels and one that influences individual parcel boundaries. We use a Markov Random Field (MRF) (Besag, 1986, Geman and Geman, 1984) prior in the form of a Potts model (Boykov et al., 2001) to define a discrete labeling on cortex that represents the set of parcels. This spatial interaction model is defined for each individual. Group data comes into play in the prior on connectivity. We use a group sparsity measure (Cotter et al., 2005), first used in the context of fMRI connectivity estimation by Ng et al. (2012), to represent connectivity between parcels. The measure is applied to the concentration matrix, which is the inverse of the covariance in a multivariate Gaussian model of connectivity between parcels. By using group sparsity we favor a connectivity structure that is common across subjects but allows the strength of this connectivity to vary between subjects. Combining these priors with a Gaussian model of interaction between the mean time-series of each parcel we define a posterior density. Maximization of this posterior using a two-steps iteration process produces our final parcellation. We describe the method below and evaluate performance using a combination of simulation and in vivo data from the Human Connectome Project (Van Essen et al., 2013; Glasser et al., 2013; Smith et al., 2013; Barch et al., 2013; Woolrich et al., 2013).

2. Methods

Individual Functional Parcellation using a Group Sparsity Prior

We assume that the cerebral cortex for each subject can be partitioned into M contiguous functional regions or parcels. This partition is based on a surface representation of cerebral cortex for all subjects, extracted and co-registered using cortical anatomy to a standard atlas with FreeSurfer (Fischl, 2012) or BrainSuite (Shattuck and Leahy, 2002). While each subject has the same M parcels with a common spatial topology, we allow the size and boundaries of these parcels to differ across subjects with respect to the common atlas space.

We represent the functional connectivity between parcels by an M dimensional Gaussian model whose likelihood is computed from the resting fMRI time series averaged over the set of vertices in each of the M parcels. The connection strength between each pair of parcels is then defined as the corresponding element of a sparsified estimate of the inverse covariance or concentration matrix (Whittaker, 2009). We use a group sparsity model to reflect our expectation that the presence or absence of connectivity between parcels is common across subjects although the strength of these connections can vary. A Bayesian framework is used to model spatial contiguity of the cortical parcels and the group sparsity property. GPIP computes a maximum a posterior (MAP) estimate of the individualized parcellations and their respective connectivity as described below.

To initialize GPIP we use a common parcellation with respect to the surface atlas. We show results below for initialization based on a relatively coarse parcellation with 17-networks (Yeo et al., 2011) as well as a more fine-grained atlas with 360 regions (Glasser et al., 2016). The GPIP algorithm then alternates between refining the parcel boundaries for each subject and updating the covariance matrices that describe connectivity between these parcels. We next describe the elements of this model and the optimization algorithm in more detail.

Denote the resting fMRI data as D = {D₁, D₂…D_N} for a group of N subjects with D_i = {D_i(a, t), a = 1…V, t = 1.T} representing the spatio-temporal data for subject i, where V denotes the number of vertices in the surface and T the number of time samples. We subdivide the vertices of the surface tessellation for each subject into M contiguous subsets to obtain parcellations L = {L₁, L₂…L_N} which assigns a label p ∈[1…M] to each surface vertex such that L_i(a) = p for a = 1…V.

The connectivity between the parcels is governed by an M dimensional joint Gaussian distribution for each subject with connection strength given by the elements of the concentration (inverse covariance) matrices C = {C₁,C₂…C_N}. For the case where the data are first normalized to zero mean and unit variance, as we do below, the concentration matrix is identical to the matrix of partial correlations between parcels, with a flipped sign on off-diagonal elements (Whittaker, 2009).

The posterior probability for the parcellation and functional connectivity is given by Bayes theorem as

$$P(L,C|D)=\frac{P(D|L,C)P(L,C)}{P(D)}=\frac{{\displaystyle \prod _{i=1}^{N}P(D_i|L_i,C_i)P(L_i)}}{P(D)}P(C),$$ (1)

where P(D | L, C) represents the probability of the resting fMRI data given L and C and P(L, C) represents the joint prior probability for the group parcellation and functional connectivity. In (1) we assume that the spatial priors for parcellation of each subject, P(L_i), are independent of each other and that each is independent of the connectivity prior. The connectivity prior, P(C), is based on a group sparsity model as defined below and cannot be decoupled into independent terms. We also assume that the resting fMRI data, D_i, are conditionally independent across subjects given the individual parcellations, L_i, and connectivities, C_i.

The parcellation and connectivity can then be computed by maximizing the log posterior.

$$ℒ(L,C|D)={\displaystyle \sum _{i=1}^N\text{ln}P(D_i|L_i,C_i)+{\displaystyle \sum _{i=1}^N\text{ln}P(L_i)+\text{ln}P(C)+\text{const}.}}$$ (2)

We now specify each term in $ℒ(L,C|D)$. for each subject, we assume a zero-mean multi-variate normal likelihood

$$P(D_i|L_i,C_i)=\frac{1}{\sqrt{{(2\pi )}^M\left|C_i^{-1}\right|}}\text{exp}\{-\frac{1}{2}\text{Trace}(Z_i^T{C}_i{Z}_i)\},$$ (3)

where Z_i is an M × T matrix representing the mean signal averaged over all vertices in each of the M parcels in L_i as described. The log likelihood function can be expressed as

$$\text{ln}[P(D_i|L_i,C_i]=\frac{1}{2}\text{ln}(\text{det}{C}_i)-\frac{1}{2}\text{Trace}(Z_i^T{C}_i{Z}_i)+\text{const}.$$ (4)

The group functional connectivity prior P(C) in (2) is designed to favor a sparse concentration matrix whose non-zero entries determine the connectivity between parcels. We assume that subjects will exhibit similar patterns of connectivity but the connection strengths between parcels can vary. To achieve this we use the l_2,1 norm to represent group sparsity (Cotter et al., 2005; Ng et al., 2012):

$$\text{ln}[P(C)]=-\lambda {\displaystyle \sum _{p=1}^M{\displaystyle \sum _{q=1}^M\sqrt{{\displaystyle \sum _{i=1}^N{C}_i^2[p,q]+\text{const}.}}}}$$ (5)

The final term in the model is the spatial prior P(L_i) on the parcellation labels defined on the cerebral cortex. We use a Potts Markov Random Field (MRF) model (Boykov et al., 2001) for this purpose. We denote the labels of each vertex L_i(a) = p ∊ {1…M}, for a = 1…V and subject i ∊ {1…N}. We add a penalty each time a vertex label L_i(a) differs from that of one of its neighbors ${\mathcal{N}}_a$ using the Kronecker delta δ(x). The joint density (Besag, 1986) has the form:

$$P(L_i)=\frac{1}{Z_{\beta }}\text{exp}\{-\beta {\displaystyle \sum _{a=1}^V{\displaystyle \sum _{b\in {\mathcal{N}}_a}(1-\delta [L_i(a)-L_i(b)])\},}}$$ (6)

where β is the Gibbs hyperparameter and Z_β the partition function. The neighborhood ${\mathcal{N}}_a$ for each vertex consists of the set of vertices on the surface tessellation that share an edge with vertex a.

Combining (1)–(6) we can express the solution to the maximum a posterior estimation problem as the minimizer of the negative log posterior density as follows:

$${\{L,C\}}_{\text{GPIP}}=\underset{L,C}{\text{arg}min}\{{\displaystyle \sum _{i=1}^N(-\frac{1}{2}\text{ln}(\text{det}{C}_i)+\frac{1}{2}\text{Trace}(Z_i^T{C}_i{Z}_i)}+\beta {\displaystyle \sum _{a=1}^V{\displaystyle \sum _{b\in {\mathcal{N}}_a}(1-\delta [L_i(a)-L_i(b)]))+\lambda {\displaystyle \sum _{p=1}^M{\displaystyle \sum _{q=1}^M\sqrt{{\displaystyle \sum _{i=1}^{N}C[p,q]\}}}}}}}.$$ (7)

Optimization Method

We use a pre-defined cortical parcellation to initialize all subjects. Here we use those from Yeo, et al. (2011) and Glasser, et al. (2016), but it is also possible to use other atlas or data driven parcellations, e.g. Blumenth, et al. (2013) or Craddock, et al. (2012), for initialization. The resolution of the initial atlas will determine the density of the final parcellation so its selection should be based on the intended application. We assume that an invertible mapping is defined from each subject to the common cortical atlas. As parcellations become increasingly fine, we would expect this assumption to break down and in those cases, the method described here would not be able to correctly identify all functional subdivisions. However, for studies involving larger functional parcels or networks we would expect a reasonable degree of consistency across groups (Kim et al., 2010; Eickhoff et al., 2011). The algorithm below can be applied to data mapped to the common space, with the final results mapped back to define the parcellation with respect to each individual’s cortical anatomy.

We use an alternating method, with guaranteed monotonic decrease of the cost function, to sequentially update the concentration matrices and parcellations:

$$C^{k+1}=\underset{C}{\text{arg}min}\{{\displaystyle \sum _{i=1}^N(-\frac{1}{2}\text{ln}(\text{det}{C}_i)+\frac{1}{2}{\text{Trace(Z}}_i^{k^T}{\mathrm{C}}_i{\mathrm{Z}}_i^k\text{))+}\lambda {\displaystyle \sum _{p=1}^M{\displaystyle \sum _{q=1}^M\sqrt{{\displaystyle \sum _{i=1}^N{C}_i^2[p,q]\}}},}}}$$ (8)

$$L^{k+1}=\underset{\{L_i:i=1\dots N\}}{\text{arg}min}\{{\displaystyle \sum _{i=1}^N(\frac{1}{2}\text{Trace}(Z_i^T{C}_i^{k+1}{Z}_i)+\beta {\displaystyle \sum _{a=1}^V{\displaystyle \sum _{b\in {\mathcal{N}}_a}(1-\delta [L_i(a)-L_i(b)])}})}\}.$$ (9)

In the first step the concentration matrices for each subject are jointly updated given the current parcellation. In the second step, we update the parcellations using the current concentration matrix estimates. Note that in this second step, the parcellations decouple into separate optimization problems, one per subject. Figure 1 illustrates this iterative approach.

Figure 1.

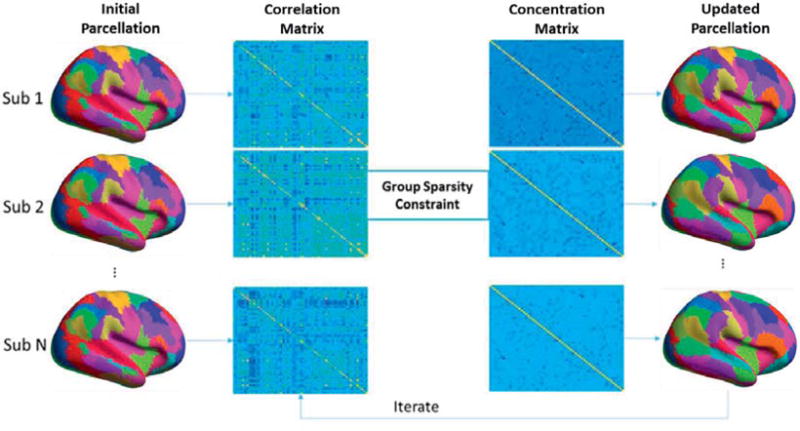
Illustration of the iterative optimization approach. Leftmost column shows the initial parcellation which is identical for all subjects. We use this to compute parcel-wise sample correlation matrices as shown the second column. We then estimate parcel-wise concentration matrices under the group sparsity constraint in the third column. In the right most column we then refine each individual’s parcellation. Iterative sequential updates of the concentration matrices and parcellations are then repeated to convergence.

To update the covariance estimates, at the kth iteration we first compute the average time series in each cortical patch for each subject as the set of matrices $Z_i^k\in {ℛ}^{M\times T}$. We then update the concentration matrix estimates using the group-sparsity regularized cost function in (8). This is a convex problem and can be optimized using the Alternating Direction Method of Multipliers (ADMM) (Boyd et al., 2011). We use the ADMM approach described by (Ng et al., 2012).

To update the parcellations we use a graph theoretic approach as described in detail in the Appendix. By inspection, the optimization in (9) decouples into separate problems, one per subject. We use a graph-cut formulation of the problem of GPIP parcellation over a Markov random field (Byokov et al., 2001). We update parcel labels using an iterative process in which, rather than consider the entire cortex, at each iteration we instead form a graph that contains nodes that correspond only to those vertices in the surface tessellation that lie at the boundaries of the current parcellation. The update procedure then partitions this graph into M subgraphs each corresponding to one parcel label. Each sub-iteration allows the boundary vertices in each parcel to move by at most one vertex, with a guaranteed reduction of the cost function in (9). Iterative repetition of the graph cutting procedure, each time using a new graph based on the latest parcel boundaries, allows the boundaries to move to the positions that jointly minimize the cost function in (9). The purpose of using only boundary vertices is to substantially reduce the time and memory complexity of the problem to an acceptable scale at each iteration. The spatial Markov property we assume and the manner in which the graphs are constructed at each iteration ensures that at convergence the method will select an optimal partition with respect to the entire cortical surface.

The two-steps iteration is repeated until effective convergence at which no more than one vertex is changed in each parcel during the most recent update or 40 iterations have been performed.

In vivo Data

All of the in vivo results below used the minimally preprocessed (ICA-FIX denoised) resting fMRI data from 40 randomly selected subjects (all right handed, age 26–30, 16 male and 24 female), which are publicly available from the Human Connectome Project (HCP) (Van Essen et al., 2013; Glasser et al., 2013; Smith et al., 2013; Barch et al., 2013; Woolrich et al., 2013). These data were acquired for four independent resting fMRI sessions (LR_1, LR_2, RL_1, RL_2) of 15 minutes each (TR = 720ms, TE = 33.1ms, 2 mm × 2 mm × 2 mm voxels) with the subjects asked to relax and fixate on a projected bright cross-hair on a dark background. The phase encoding direction was reversed between (LR_1, LR_2) and (RL_1, RL_2). Here we use the LR_1 sessions to obtain the individual parcellations and the LR_2 sessions to evaluate performance.

HCP’s minimal preprocessing corrects the fMRI data for acquisition artifacts, resamples the data on the cortical surface and performs a non-aggressive spatio-temporal cleanup (Glasser et al., 2013; Smith et al., 2013). The data are then resampled for each subject onto a common standard cortical surface mesh representation (32K Conte-69) in the native subject space (Smith et al., 2013; Van Essen et al., 2012). Additional spatial-temporal processing is then used to remove scanner, motion and other artifacts (Smith et al., 2013). Our only additional preprocessing prior to application of the GPIP parcellation algorithm was to normalize the resting fMRI time series at each vertex to zero mean and unit variance.

The functional parcellation results presented below are compared to task-localizer data also made available by the HCP. Task-based fMRI data were obtained for the same 40 subjects and included seven major task domains: emotion processing, reward & decision making, language processing, motor strip mapping, higher order relation processing, social cognition and working memory. We used HCP’s pre-processed and analyzed task-fMRI data resampled onto the cortical surface, with 4mm Gaussian smoothing, which yielded a total of 15 statistical task-pair activation maps as described in detail by Barch et al. (2013) and Woolrich et al (2013). To identify regions involved in emotion processing, a face versus shape selection scenario was used as the “faces_shapes” contrast. For reward & decision making, gambling punishment and reward tasks were employed and contrasted (“punish_reward”). To identify regions of language processing, interleaved math and story tasks are compared in the “math_story” contrast. The relational processing study contrasts two tasks: the first requiring the subject to identify geometrical relationships among objects, and the second involving matching of objects. The two responses are compared in the “match_rel” contrast. In the study of social cognition, the theory of mind task involved blocks of moving geometric shapes wherein some moved with intention (tom) and were compared to random movement (random). These are compared in the “random-tom” contrast. To sample regions involved in working memory, a 2-back versus 0-back contrast was used (“0bk_2bk”). A number of other contrasts were performed to identify functionally specialized regions, where a certain task is compared to the average of other tasks in that category. In the motor category, regions specific to a particular body part were identified using a contrast of the response of that part to the average response of all other body parts. The contrasts used below involve movement of the tongue (“t_avg”), left hand (“lh_avg”), right hand (“rh_avg”), left foot (“lf_avg”) and right foot (“rf_avg”). Similarly, perception of different categories of images was contrasted with the average response over the other categories as follows: faces (“face_avg”), place processing (“place_avg”), tools (“tool_avg”) and body perception (“body_avg”).

Atlases for Initialization

For the in vivo studies described below, we choose two atlases, Yeo et al., (2011) and Glasser et al., (2016) for initialization. Yeo’s atlas uses resting-fMRI data from a group of 1,000 subjects. These data were resampled onto their respective cortical surfaces and co-registered to a common atlas space. Clustering was used to identify a common set of 17 networks, each consisting of multiple contiguous regions on the cortical atlas¹. We attached a distinct label to each contiguous region, merging those with less than 30 vertices with their neighbors, to produce a final set of 58 cortical parcels. Glasser’s atlas is a more detailed group-based parcellation constructed from both functional and anatomical MRI data from 210 subjects in the HCP database. A machine learning approach was taken to identify a set of 180 cortical parcels per hemisphere². We reduced this number to a total of 338 regions by again merging those with less than 30 vertices with their neighbors.

Evaluation and Metrics

The GPIP parcellation algorithm described above was applied to the 40 HCP subjects’ resting fMRI (LR_1 sessions) initialized with both the Yeo and Glasser atlases. The resulting parcellations, customized to each subject, were then compared to the initial common group atlas parcellation with which the algorithm was initialized. To quantify the degree of refinement required in each subject, we computed the fraction of vertices whose label is changed from initialization to convergence.

For each subject, we used the resting fMRI LR_2 sessions to quantify homogeneity and connectivity variability based on the parcellations obtained from LR_1. As in Craddock et al. (2012), homogeneity of a parcel is defined as the average temporal correlation coefficient between all pairs of vertices in that parcel. A larger homogeneity value indicates greater similarity in time series within that region and is an indication of increased functional homogeneity. As an overall measure, we compute the average homogeneity values over all parcels for each subject and then average these over all subjects. This score is computed with respect to the initial atlas and final parcellation, and as a function of iteration number as an indication of convergence behavior of the algorithm.

We also studied the variability in connectivity across the group, again using the LR_2 data. We first computed the Pearson correlation between each pair of regions using the time series averaged over each region. For each pair of regions we computed the variance of this correlation across the 40 subjects. We then computed the mean of these variances across all region pairs together with its standard error. This variability measure was computed as a function of iteration to indicate convergence behavior as well as allowing a comparison of the initial group atlas and the final individualized parcellations. Lower values of variability will reflect a higher degree of consistency across subjects in the strength of the correlations between parcels. This in turn would indicate improved similarity across the group in network connectivity between the regions making up the parcellated cortices. Conversely, larger variability would suggest inconsistent parcellation across the group. This could be caused by poor accuracy in identification of region boundaries. Alternatively, high variability could be a consequence of mislabeling (i.e. one or more regions in the atlas end up assigned to different functional areas in different subjects).

Finally, we compared resting fMRI parcellations against task-fMRI contrast activation maps for each subject. To compute task variability for a certain task pair, for each subject we computed the variance in each parcel of that activation map’s z-scores as provided by the HCP (Barch et al., 2013; Woolrich et al., 2013). The task variability was then averaged over all regions and all subjects to produce a single task variability metric. We computed task variability for the initial atlas and final parcellation separately for all 15 task contrasts described above. We then applied a Wilcoxon rank-sum test to determine if there was a significant reduction in task variability. Lower task variability would suggest higher functional homogeneity in parcels in terms of a specific task-fMRI contrast and implies better alignment between parcel boundaries and task activation regions.

Perturbation Analysis

We explored the robustness of our algorithm in the case where the perturbed initialization contains regions that do not overlap spatially with the locations of these regions in the original atlas. To do this we choose a parcel in the posterior inferior supramarginal gyrus in Yeo’s atlas. We then perturbed the atlas so that this region was shifted in the posterior direction so that it has zero overlap with its position in the original Yeo atlas. The surrounding parcels were correspondingly modified so that the spatial topography of the parcels remained unchanged. We then applied the parcellation algorithm to the same 40 subjects resting fMRI LR_1 data sets initialized with this perturbed Yeo atlas. To determine the impact on the resulting parcellation, for each subject we computed the Dice coefficient for the right posterior inferior supramarginal gyrus parcel between results obtained using the two versions of Yeo’s atlas. We then computed the mean and standard error of the Dice coefficient across all subjects as a function of iteration.

Simulation Studies

We also explored the performance of our parcellation approach using simulated data. Synthetic data was generated to simulate resting fMRI functional connectivity across a group of subjects with variation in both their cortical parcellations and concentration matrices. We start with a randomly generated sparse symmetric positive definite matrix $\stackrel{\sim }{C}$ representing the mean partial correlation matrix for the population. Individual concentration matrices were obtained by varying each off-diagonal concentration matrix strength (non-zero elements of $\stackrel{\sim }{C}$) by sampling from a normal distribution with mean 1 and standard deviation 0.5. Results were tested for positive definiteness and the sampling repeated in cases where this condition was not met. The resulting matrices C = {C₁, C₂…C_N} were used to define the ground-truth connectivity for each of N = 24 subjects. We used the corresponding correlation matrices to generate synthetic Gaussian data representing resting BOLD interactions between cortical parcels. These were then mapped to a 100 × 100 lattice gridded surface and independent Gaussian spatially and temporally white noise added separately to each vertex. Gaussian smoothing was performed both temporally and spatially. The cortical parcellations for each subject, except subject 1, were based on random perturbations of the boundaries of an initial common parcellation that has 25 square parcels each of size 20 × 20 as shown in figure 8. Individual boundaries were generated by random application of a sequential single-vertex morphological dilation to 12 parcels randomly selected out of 25. Repeating this process 6 times produces a shift of at least 6 vertices between the initial atlas and ground truth parcellations for each subject. Subject 1 was specially designed so that the location of one of the parcel (the red parcel indicated by a black arrow in figure 8) does not overlap with its location in the initial atlas. This allows us to examine the ability of GPIP to correctly identify individual parcels that have no overlap with their initial location in the atlas. The average error rate (percentage of mislabeled vertices) between these ground truth parcels and the regular atlas with which the algorithm was initialized was 27.7%.

Figure 8.

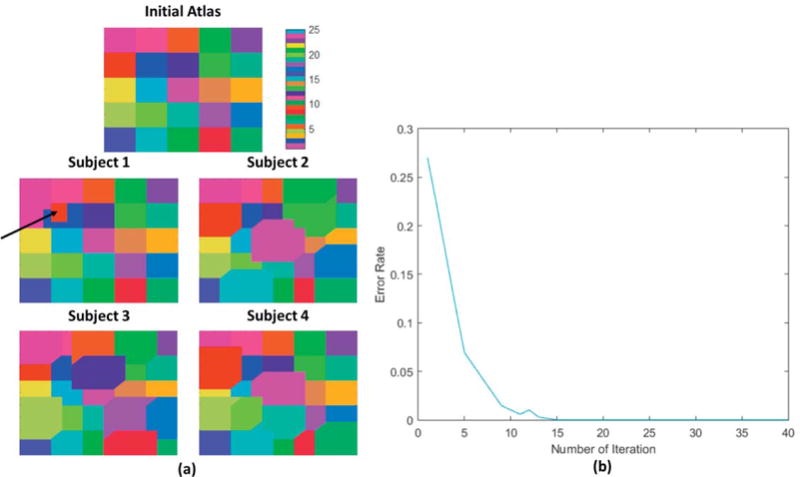
Simulation results: (a) Initial atlas and examples of the final parcellations for four ‘subjects’. Each color represents one of the synthetic parcels which are matched across subjects. The red parcel for subject 1, indicated by a black arrow, has zero overlap with the common initialization. (b) The error rate (fraction of mislabeled vertices) in the parcellations, averaged over all 24 subjects, as a function of iteration number.

3. Results

In vivo data

Figure 2 shows parcellation results for three subjects, selected from a group of 40. Results for all 40 subjects can be found in figures S1 and S2 (supplementary material). For visual comparison, we show all results mapped to the common cortical surface to which each subject is registered. In this common space, the initial parcellations are identical for all subjects. The algorithm then adapts the parcel boundaries using each individual’s resting fMRI to produce the results shown in rows 2–4. The update procedure guarantees that the spatial topology of the original atlas parcels is retained, producing a matched set of regions across subjects that differ only in the locations of their boundaries. The black arrow in figure 2 (row 3, column 3) points to a parcel (green patch) which has no overlap with its initial position in the Glasser atlas. This observation indicates the ability of GPIP to move individual parcels to the point where they no longer overlap with their initial location, a point we return to below in the Discussion. For each subject, the fraction of vertices whose labels changed was computed and resulting statistics over the N = 40 subjects (mean, standard deviation, minimum and maximum) are shown in Table 1 for both the Yeo and Glasser atlas.

Figure 2.

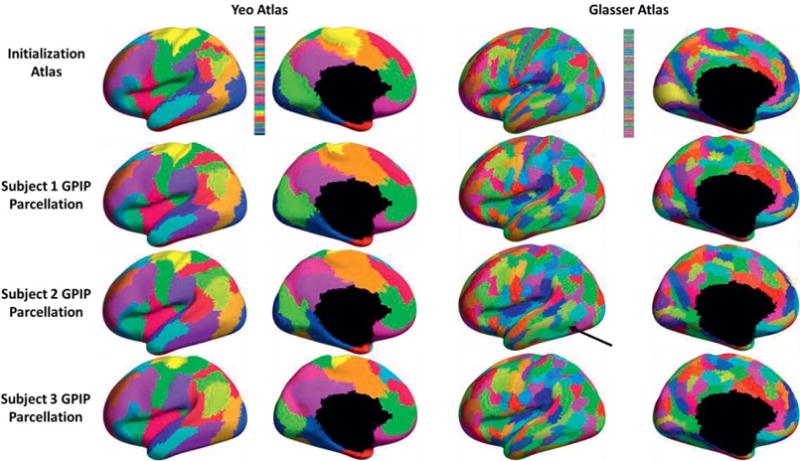
Examples of individualized resting fMRI parcellation, medial and lateral view of left hemisphere. Top row: initialization with Yeo (left) and Glasser (right) atlases. Rows 2–4: Final parcellations for three of 40 subjects. Each color represents a separate parcel, with colors matched across subjects. The black arrow in row 3, column 3 points to a parcel (green patch) which has no overlap with its initial position in the Glasser atlas.

Table 1.

Statistics over n = 40 subjects of the fraction of vertices that were relabeled per subject.

	Mean	Standard deviation	Minimum	Maximum
Yeo’s Atlas	0.3555	0.0156	0.3286	0.3874
Glasser’s Atlas	0.4574	0.0101	0.4364	0.4839

Figure 3 shows changes in homogeneity computed from the LR_2 resting fMRI data using parcellations obtained with LR_1. Homogeneity is averaged across all parcels as a function of iteration and then averaged across all 40 subjects. In both cases there are significant improvements in homogeneity from initialization to the final iteration. Convergence with the Glasser atlas is slower, presumably because of the considerably larger number of regions.

Figure 3.

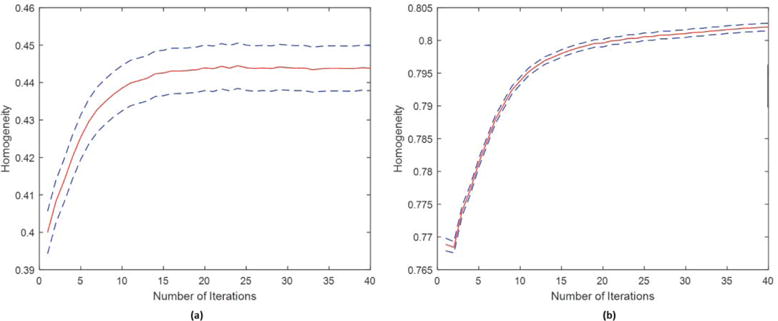
Homogeneity of resting fMRI parcellations as a function of iteration. Shown is mean homogeneity across all regions and subjects (plus/minus the standard error). (a) Initialization using the Yeo atlas; (b) initialization using the Glasser atlas.

Figure 4 shows the variability in connectivity, computed using the LR_2 data, as a function of iteration number for the Yeo and Glasser atlases. In both cases there is a near monotonic reduction in variability with iteration with significant reductions from initialization to the final result.

Figure 4.

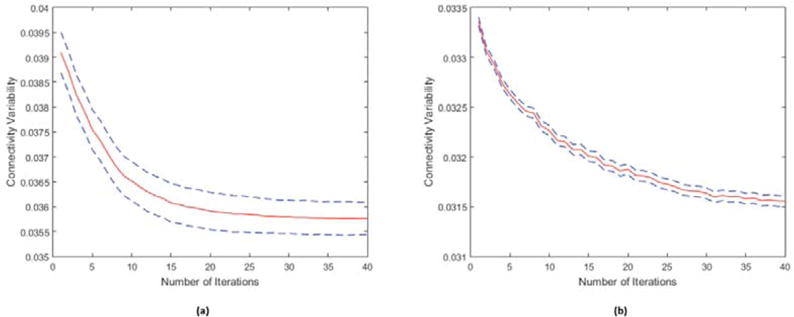
Variability of connectivity (mean plus/minus the standard error) as a function of iteration number computed as the variance of correlation across the population between each pair of regions, averaged over all pairs. (a) Initialization using the Yeo atlas; (b) initialization using the Glasser atlas.

Examples comparing resting fMRI parcellation with task localizers are shown in figures 5 and 6. Quantitative results for all task pairs are included in tables 2 and 3. Figure 5 shows result for the faces vs. shapes visual task pair (Barch et al., 2013) for three individuals. Results for all 40 subjects are included in figures S3 and S4 in the supplemental material. For both initializations, figure 5 shows apparent improvement from the initial atlas to the individualized results in the sense that regions of higher z-score appear better constrained between parcel boundaries after application of GPIP, particularly in the fusiform face area, para-hippocampal gyrus and visual cortex. Figure 6 is an example using the TOM vs. random (theory of mind vs. random motion) social cognition task contrast initialized with the Glasser atlas for two subjects and projected to the medial surface. Results for all 40 subjects are included in figure S5 in the supplemental material. With the high density of the parcellation, the results are perhaps difficult to interpret visually, however bounded parcels in medial prefrontal and parietal regions appear more homogeneous.

Figure 5.

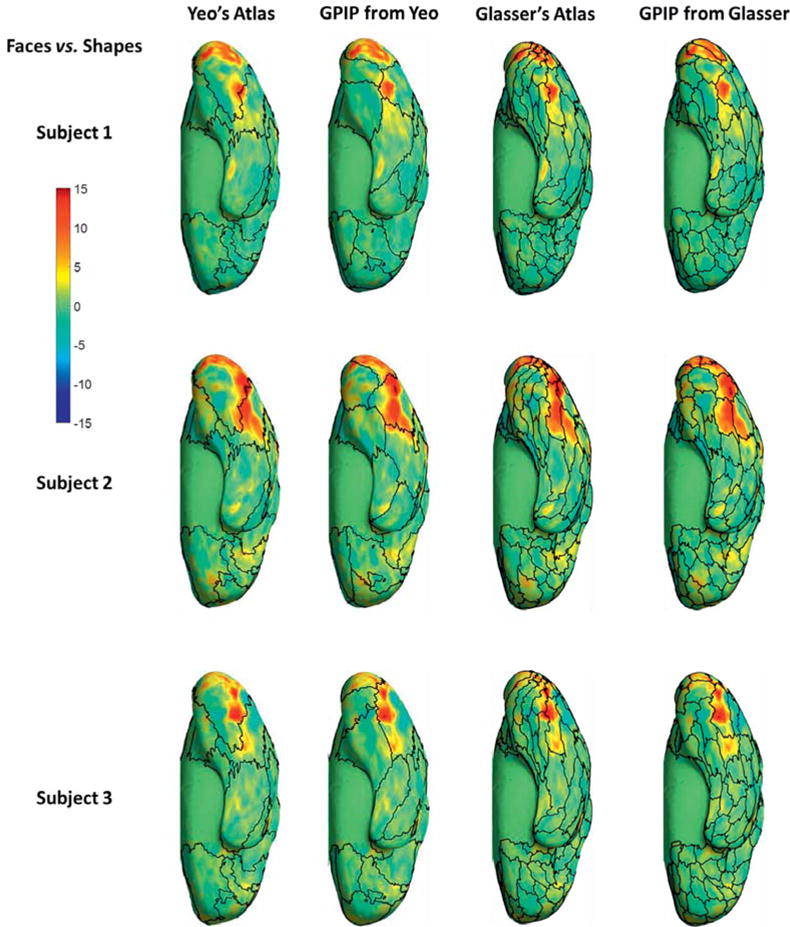
Comparison of resting fMRI parcellation and activation maps for the faces vs. shapes visual task pair, ventral view of right hemisphere. First and third columns: initial parcellations using the Yeo and Glasser atlas, respectively, with boundaries indicated by black curves. These are overlaid with color maps of z-scores computed for the faces vs. shapes contrast for three subjects. Second and Fourth columns: final parcellation boundaries initialized from the Yeo and Glasser atlas respectively.

Figure 6.

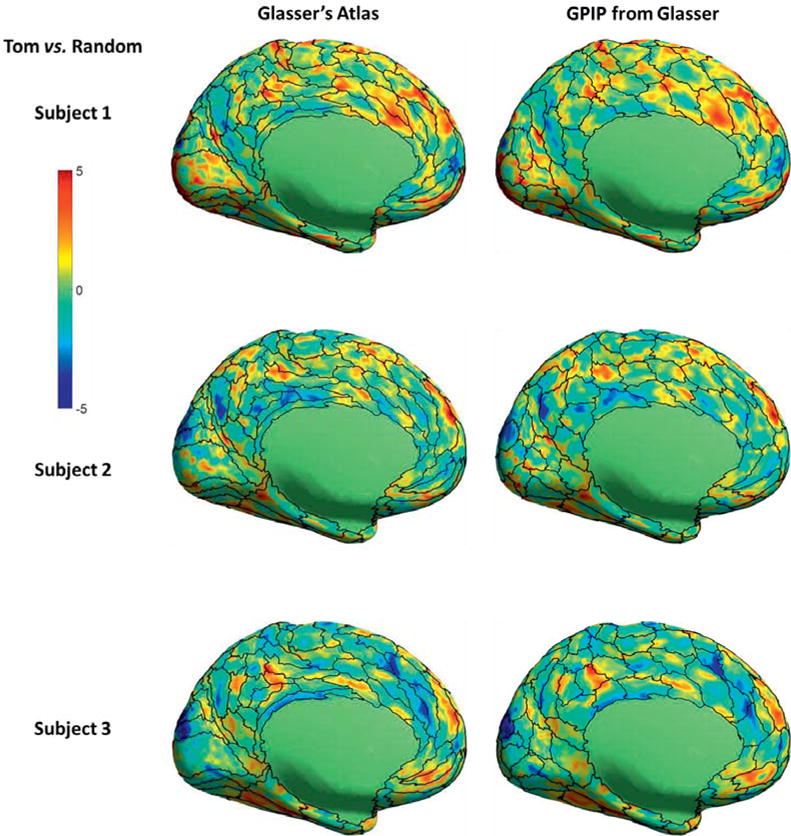
Comparison of resting fMRI parcellation and activation maps for the TOM vs. random social cognition task pair, medial view of left hemisphere. Left column: initialization using the Glasser atlas (black curves) overlaid with color maps of z-scores computed for the TOM vs. random contrast for three subjects. Right column: final individualized parcellation boundaries, again overlaid with task activation maps.

Table 2.

Task variability within each parcel averaged across all parcels and all subjects for each of the 15 task pairs. Shown are task variability computed with respect to the Yeo atlas initialization (column 3) and final result using the GPIP algorithm (column 4). Differences between the two are shown in column 5 and p-values for the Wilcoxon rank-sum test in column 6.

	Contrast	Yeo’s	GPIP from Yeo’s	Difference (Yeo – GPIP)	p-value (ranksum)
EMOTION	faces_shapes	3.269	2.920	0.350	1.01E-10
GAMBLING	punish_reward	2.255	1.795	0.460	1.66E-89
LANGUAGE	math_story	12.180	7.290	4.889	1.33E-200
MOTOR	lf_avg	2.826	2.413	0.414	2.27E-26
	lh_avg	3.240	2.861	0.379	6.72E-10
	rf_avg	2.506	2.115	0.396	1.27E-25
	rh_avg	3.001	2.599	0.402	4.03E-15
	t_avg	7.296	6.393	0.903	6.39E-10
RELATIONAL	match_rel	1.952	1.504	0.443	5.03E-83
SOCIAL	random_tom	3.159	2.279	0.886	2.63E-92
WM	0bk_2bk	7.203	4.860	2.342	9.57E-90
	face_avg	4.948	4.680	0.268	3.24E-02
	place_avg	4.487	4.056	0.425	1.15E-09
	tool_avg	3.817	3.246	0.571	1.05E-40
	body_avg	4.178	3.654	0.525	1.50E-14

Table 3.

Task variability within each parcel averaged across all parcels and all subjects for each of the 15 task pairs. Shown are task variability computed with respect to the Glasser atlas initialization (column 3) and final result using the GPIP algorithm (column 4). Differences between the two are shown in column 5 and p-values for the Wilcoxon rank-sum test in column 6.

	Contrast	Glasser’s	GPIP from Glasser’s	Difference (Glasser – GPIP)	p-value (ranksum)
EMOTION	faces_shapes	2.970	2.220	0.749	3.41E-71
GAMBLING	punish_reward	1.804	1.632	0.172	8.07E-27
LANGUAGE	math_story	6.394	5.114	1.280	6.10E-91
MOTOR	lf_avg	2.340	2.023	0.317	1.67E-44
	lh_avg	2.629	2.387	0.242	9.08E-22
	rf_avg	2.056	1.797	0.258	7.17E-37
	rh_avg	2.444	2.190	0.254	3.75E-26
	t_avg	6.072	5.444	0.628	3.30E-16
RELATIONAL	match_rel	1.469	1.275	0.194	1.05E-57
SOCIAL	random_tom	2.175	1.841	0.333	1.32E-76
WM	0bk_2bk	4.510	3.799	0.711	4.74E-67
	face_avg	4.804	3.902	0.903	3.83E-42
	place_avg	4.024	3.268	0.756	1.03E-67
	tool_avg	3.300	2.874	0.426	1.33E-39
	body_avg	3.637	3.079	0.557	3.11E-54

To quantify the consistency between resting fMRI parcellations and task-fMRI for all task pairs we computed task variability as the variance of each task contrast’s z-score within parcels as described above. In table 2 we tabulate average task variability with respect to the initial Yeo atlas and after application of GPIP. We also performed a Wilcoxon rank-sum test for differences in task variability. Equivalent results for initialization with Glasser’s atlas are shown in table 3. Note that in all cases the difference between initialization and GPIP results are positive, indicating reduced variability with respect to the parcellations for all task pairs for both the Yeo and Glasser atlas. The p-values listed in the final column indicate significant reductions (p<.05, Bonferroni corrected) for all but the face_avg working memory task with the Yeo atlas.

Perturbation Analysis

Figure 7 shows behavior in the cases where the Yeo atlas initialization is modified so that a parcel in the posterior inferior supramarginal gyrus is moved posteriorly so that it no longer overlaps with its original position (red patch, top row of figure 7). Using this as an initialization we again applied the GPIP algorithm to the LR_1 data and compared results with those obtained with the original Yeo atlas. We show the final parcellations for two subjects using the Yeo and perturbed Yeo atlases in figure 7. We also plot the Dice coefficient between the posterior inferior supramarginal gyrus parcels for the two atlases, averaged over all 40 subjects, as a function of iteration. The final average Dice coefficient is 0.65. While this does not indicate an exact overlap, this result does indicate that the algorithm is able to produce large changes in individual parcels when required, and, importantly, that the perturbed parcel is not misaligned to a different adjacent functional region. This robustness stems from the fact that both initializations share the same topography or spatial connectivity between parcels. Movement of the boundaries of the better aligned parcels will affect those of their neighbors, tending to correct initial functional misregistration of individual parcels.

Figure 7.

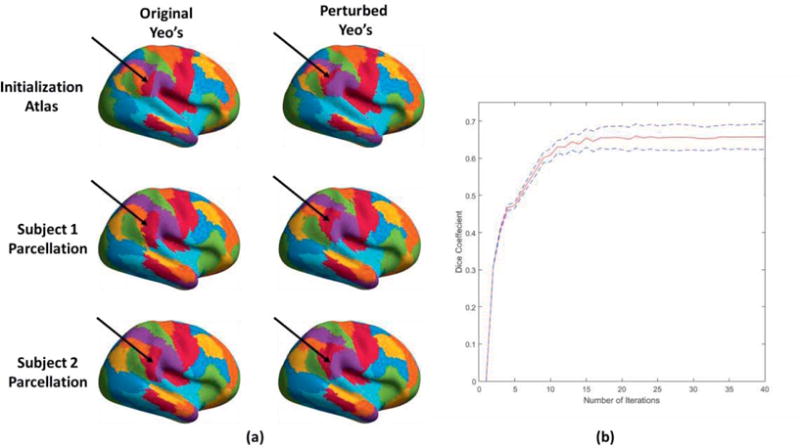
Illustration of parcellation stability to a perturbed initialization: (a) (top row) initialization with Yeo atlas (left) and Yeo atlas perturbed with respect to red parcel in right posterior inferior supramarginal gyrus (right), as indicated by the black arrow; (rows 2 and 3) individualized parcellation results using the two initializations for two of forty subjects; (b) plot of Dice coefficient, averaged over 40 subjects for the posterior inferior supramarginal gyrus parcel, as a function of iteration.

Simulated data

We investigated the convergence properties of the GPIP method using the simulated dataset described above. For each ‘subject’ we computed the error rate in labeling (fraction of vertices that are mislabeled) as a function of iteration by comparing with known ground truth. Figure 8(a) shows examples of the initial and final parcellations for four subjects selected from the group of 24. Final parcellations for all synthetic subjects can be found in figure S6 (supplemental material). The group averaged error rate at each iteration is plotted in Figure 8(b). Since the error rate is zero at the 20^th iteration, the images at convergence also show the degree of variability in spatial structure of the ground truth images. The special case of subject 1 also converged to the ground truth, indicating that GPIP can correctly identify parcels even in cases where the initial and true (final) parcels do not overlap. These results also illustrate converge for data that are consistent with the model described above. Further, the results indicate the ability of the algorithm to adapt individual parcellations to match ground truth that is substantially (27.7% on average) different from the initialization.

4. Discussion

The GPIP algorithm described above takes a common cortical atlas that delineates regions and adapts the boundaries of each region within subject to better fit the individual subject’s regional functional profile from resting fMRI. Through this procedure we are able to produce individualized parcellations but with the property that all subjects have the same labeled parcel topology, facilitating group analysis. Our approach can be viewed as a means of refining a common group atlas. As the results above indicate, this refining process produces consistency, relative to the initial atlas, of regions of functional specialization identified using both independent resting and task fMRI.

In the in vivo results presented, we initialize with two published cortical atlases although the approach could be applied to any parcellation defined with respect to coregistered cortical surfaces. Of the two atlases, the first is based solely on resting functional MRI data (Yeo et al., 2011) while the second uses a combination of anatomical and functional data to define a far denser parcellation (Glasser et al., 2016). Results for both atlases indicate improved homogeneity, reduced inter-subject variability of connectivity, and reduced variability of task-related activation within parcels. However, further work will be needed to validate whether resting fMRI data alone can be used to define dense parcellations which originate from integrated multimodal imaging (e.g. Glasser et al., 2016) especially certain cortical regions that are anatomical driven.

The maps showing individual parcellations mapped on to a common cortical representation in figures 2 (and figures S1 and S2 in supplemental material) show substantial deviation across subjects in region boundaries for both atlases. The statistics in table 1 also indicate the fraction of vertex relabeling required to individualize the atlas boundaries is similar for all subjects. Initializing with the Glasser atlas requires a larger fractional change (mean 0.4574) than does the Yeo atlas (mean 0.3555). Our results also indicate that the GPIP boundaries have improved concordance, relative to the original atlas, with both resting and task related fMRI data. The inter-subject variability in these boundaries, as shown in Figures 2, S1 and S2, indicates the limited accuracy with which functional regions can be identified by anatomically-driven mapping to a common atlas. This in turn will limit the power of analyses based on a common atlas, which have been shown to have moderate inter-subject confidence in peak regions (e.g. Yeo et al., 2011, table 5), and low confidence in boundary regions (e.g. Wang et al., 2015; Wig et al., 2014). The approach described here has the potential to improve statistical power of region-based statistical analysis through improved delineation of functional parcels while retaining a common set of regions across subjects.

Functional areas of the brain demonstrate substantial spatial variability across subjects, and the individual localization of these functional regions optimizes estimation of inter-regional connectivity (e.g. Stevens, et al., 2015). However, task-localizers for functional area identification across cortex exceed the constraints of a single imaging study. Comparisons of the resting fMRI based parcellation with a series of functional localizers shows consistent improvements in concordance with task contrasts. Maps of parcel boundaries overlaid on the z-scores in Figs. 5 and 6 illustrate improved consistency of these boundaries with known areas of functional specialization. Note that for the multiple subjects we presented, each individual subject has its own distinct activation region that cannot be well-delineated by a common atlas. In Fig. 5 the GPIP refinement of the Yeo atlas shows clear changes in boundaries so that we are able to better contain the fusiform face area in a single parcel, rather than splitting into two or more regions. Similarly, although Glasser’s atlas has a different functional resolution from Yeo’s, in figure 5 we see that in the refined parcellation, the medial and posterior boundaries of the fusiform area are frequently consistent for both Yeo and Glasser. This provides some evidence that the regional boundary is indeed determined by the individual’s resting brain activity and can be found consistently even for different initial atlases. Similarly, as shown in Fig. 6, parcels obtained with GPIP using the Glasser atlas may better functionally align parcels to be consistent with individual differences in activation patterns across subjects in the TOM vs. random task contrast (Barch et al., 2013). The quantitative results in tables 2 and 3 confirm these observations across multiple subjects and every task-pair. GPIP consistently shows significantly lower task variability than the corresponding initialization.

While we note that boundary refinement did produce improvement (reduction) in within-parcel task related variability with the Glasser atlas, these results should be interpreted with caution. The original Glasser atlas is based on structural as well as functional features in the data, and certain areas (e.g. motor cortex and visual cortex) are delineated primarily by anatomical features and may not closely reflect regions of functional specialization. The clearest example of this is in primary motor cortex where hand and face areas are combined in a single parcel in the Glasser atlas while they are readily differentiated in resting fMRI data. As a result, refinement of Glasser with GPIP can result in recruiting neighboring parcels to produce a subdivision between hand and face areas, as can be seen in some of the subjects in Figure S2. More generally, some of the parcels may be adapted to locally fit a functional area that differs from the original anatomical-functional region identified in the Glasser atlas. As a result further cross-validation is required to evaluate which regions are most reliably identified when using this atlas.

We also note that the Glasser atlas exhibits lower task variability that Yeo’s in the initial atlas and after GPIP refinement (table 2 vs. table 1). This is expected because the smaller parcel sizes in Glasser will have lower variance than those in Yeo for spatially inhomogeneous z-score maps. Common to both atlases is the significant reduction in variability for all task pairs, with the exception of the face vs. average working memory task for Yeo’s atlas.

The performance of our GPIP algorithm is highly dependent on the initial atlas since this defines the number and arrangement of parcels. Given the range of individual variation, it is important the approach is able to identify equivalent functional regions across subjects even in cases where location of some functional regions are highly perturbed in the initial atlas. To investigate this, we perturbed the Yeo atlas as shown in figure 7 and described above. In this case, despite the fact that one parcel in the perturbed atlas was completely shifted so that it had zero overlap with its original location, the GPIP algorithm was able to produce individualized mapping with an average dice coefficient of 0.65 in the shifted parcel relative to results where the original atlas was used. This indicates a robustness of the approach that likely arises from the constraint we impose of a common atlas topology across subjects. In this way, mislocated regions will be pulled back towards their true location by the refinement of the boundaries of their neighboring parcels. The results shown here is an extreme case since the parcel is mislocalized in the atlas so will be incorrect with respect to most of the individuals. In practice, we may instead expect to see a few subjects whose functional areas are substantially shifted, or even have zero overlap, relative to the initial atlas. This will become increasingly common with finer and finer parcellations. To address the question of whether GPIP will be able to correctly identify parcels in this case, we searched the in vivo results across the 40 subjects shown in figure S2 for cases where GPIP converges with individual parcels that have zero overlap with their initial location. We found three subjects for which this occurred, and show one example in figure 2. We also explored this question in the simulation study, and again found that GPIP is able to identify parcels that do not overlap with their initial location (figure 8). As noted above, this probably follows from the assumption of a common topology across subjects, so that neighboring parcels tend to pull or push the non-overlapping parcel towards its correct location.

A potential disadvantage of the GPIP approach is that the model cannot accommodate differences in the number of functional regions across subjects or functional connectivity that is topological different from the group atlas, for which there is evidence in the literature (Amunts et. al., 1999; Harrison et. al., 2015), limiting some potential applications. Since GPIP adapts an initial atlas to individual resting fMRI data, it is unable to identify functional variability that is systemically absent from the group atlas (Laumann et al., 2016; Gordon et al., 2015; Mueller et al., 2013).

Our individualized GPIP functional parcellation method uses an optimization framework to compute both the parcellation and the connectivity concentration matrix for each subject. This requires solving a large non-convex optimization problem with a mixture of continuous and discrete variables. As a result a globally optimal result is not guaranteed. However, the results of the simulation (Fig. 8) show convergence of the algorithm in the case where the data conforms to the assumed model. The two-steps algorithm, eq. (8) and eq. (9), exhibits monotonic reduction of the cost function in eq. (7), and has the useful property that the function is convex with respect to the concentration matrices that are updated in eq. (8). For the 32K Conte-69 (Smith et al., 2013) surface mesh used here we found that after approximately 20 iterations, less than 1% of vertices are relabeled in any further iteration, irrespective of the number of parcels, when a common initialization is used. Although this may vary with quality of data and mesh size, we found for the HCP data that 40 iterations were sufficient to achieve effective convergence.

Results are dependent on the choice of regularization or hyper parameters, λ and β in eq. (9). For all results in this paper we used λ = 10 with β = 0.1 for GPIP from Yeo’s and λ = 10 with β = 1 for GPIP from Glasser’s, chosen by visual evaluation of results for several in vivo datasets. Further optimization of parameter selection by, for example, modifying parameters to maximize homogeneity by resting-fMRI data cross session validation could further improve performance.

In this paper we present all results for data sampled on the cortical surface. The approach generalizes to volumetric and grayordinate parcellation (Glasser et al., 2013) where minor modifications of the MRF neighborhood system could be used to perform volumetric parcellation of cortical and/or subcortical regions.

5. Conclusion

We have described GPIP, an algorithm that takes an initial cortical atlas representing regions of functional specialization and refines the boundaries of these regions for each subject using that individuals resting fMRI. The approach combines a Markov random field prior, which represents individual parcellations of the cerebral cortex, with a multivariate Gaussian model that uses a group-sparsity prior to model similarity across the population of the connectivity between these parcels. GPIP applied to in vivo data shows distinct individual differences in functional boundaries across subjects with respect to a common anatomical alignment. Validation with a second independent fMRI data set indicates improved functional homogeneity within parcels and reduced variation across subjects of the connectivity between pairs of parcels. These boundaries also appear qualitatively and quantitatively consistent with regions of functional specialization identified using functional task localizers. We assume an invertible mapping exists that maps each subject to the common initial atlas. As parcellations become increasingly fine, we would expect this assumption to break down and in those cases, the method described here would not be able to correctly identify all functional subdivisions. However, for studies involving larger functional parcels or networks we would expect a reasonable degree of consistency across groups. It is at this scale that we envision the proposed approach to be a useful addition, allowing group analysis in which common regions of interest are defined across the population while their boundaries are refined to match the individual’s regions of functional specialization. In these cases, GPIP can be used to individualize functional parcellations of cerebral cortex as a precursor to region-based analysis of either resting or task-related fMRI studies.

Highlights.

• We describe a method for cortical parcellation that adapts a common functional atlas to produce individualized parcellations consistent with each subjects resting fMRI.

• Using a group-sparsity prior we are able to exploit similarities in connectivity across the population to obtain a consistent set of parcels across subjects while also respecting individual differences.

• Quantitative evaluation using HCP data comparing resting fMRI parcellations to functional task localizer data indicates improved consistency between the two relative to use of a common functional atlas.

• The approach has potential to improve statistical power in region-based analysis of either resting or task-related fMRI studies.

APPENDIX

Optimization by graph partitioning

Figure A1.

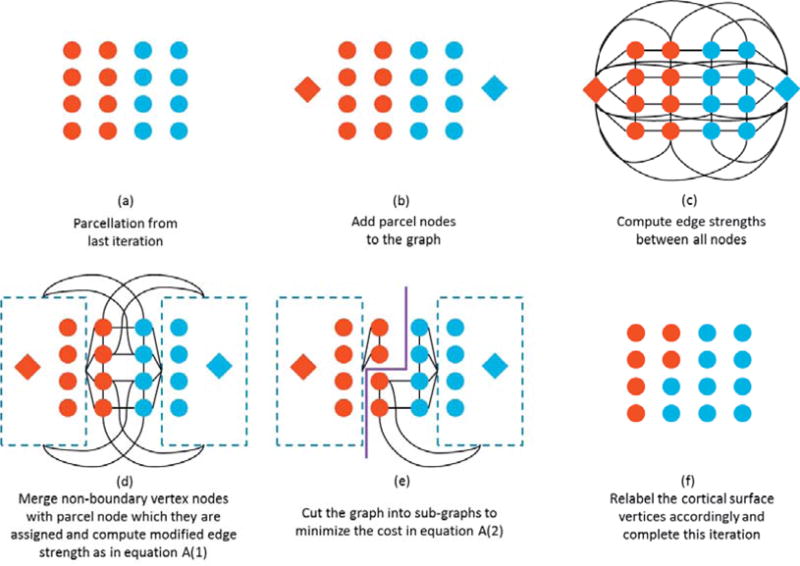
Illustration of the graph formation and partition approach. The red circles in (a)–(e) represent cortical vertices that have been assigned to the red diamond parcel in the previous iteration, similarly for the blue circles and diamond. At that last step (f) a new cut is made, changing the assignment of parcel labels across the set of cortical vertices. See text for detailed description.

The parcel labels for each subject are determined as part of the two-steps procedure summarized in equations (8) and (9). Here we describe the computational approach to solving the optimization subproblem in (9).

We first map the optimization problem to an equivalent graph-cut problem. For each subject, we define a graph G = (Y, E), with nodes Y and edges E. In the node set Y, there are two types of nodes: (a) the surface vertex nodes {b, b ∊ B = [b₁…b_V]}, where B represents the set of all vertices on the cortex as circles in Fig. A1(a), and (b) the set of parcel nodes {p, p ∊ P = [P₁…P_M]}, one node per parcel as diamonds in Fig A1(b). The parcel nodes are used to assign a label to each vertex so that after partitioning each vertex is connected to a single parcel node. Initially each vertex is connected to every parcel node with an edge strength proportional to the log-likelihood for the data at that vertex given that it belongs to each of the parcels in turn. The edge strength between vertex nodes is determined by the MRF model in equation (6) and attaches a weight β between the vertex and each of its neighbors. We could proceed directly to partition this graph by computing the edge strengths as in Fig A1(c) and using a graph partitioning method similar to (Byokov et al, 2001), but the cost would be prohibitive for a problem of this size. We therefore use a modified approach to reduce the size of the graph.

We first prune the vertex nodes to the subset B^k that represents only those vertices on the cortex that lie at the boundary of one of the functional parcels at the previous iteration, k. In other words, all elements of B^k have at least one adjacent vertex with a different label (columns two and three in Fig. A1(a)). The vertices in B that are not in B^k (the first and fourth columns in Fig. A1(a)), will not be changed in the current iteration but since some are mutual neighbors of the boundary vertices, we must still account for their effect on their boundary neighbors, as defined in equation (6), in the reduced graph. Since they are already assigned to a parcel label, we can merge these vertices into the node corresponding to the parcel to which they are currently assigned and modify the edge strength from that parcel node to each of the boundary vertex nodes accordingly, Fig. A1(d). Since the modified graph contains only the parcel and boundary vertex nodes it can be as much as two orders of magnitude smaller than the original graph with corresponding computational savings. Provided the edge strengths are modified appropriately, partitioning this modified graph, Fig. A1(e), provides a locally optimal solution, relative to the original graph, by restricting the movement of parcel boundaries to at most one vertex per iteration, Fig A1(f). A sufficiently large number of iterations can produce an arbitrarily large movement of each boundary.

We define the edge strengths between nodes in the boundary graph as follows (see explanation below):

$$E_i(a,b)=\{\begin{array}{ll}\beta \hfill & b\in {\mathcal{N}}_a,b\in B^k\hfill \\ 0\hfill & b\notin {\mathcal{N}}_a,b\in B^k\hfill \end{array}$$

$$E_i(p,q)=0p,q\in P,p\ne q$$

$$E_i(a,p)=\frac{1}{2}\text{Trace}(\frac{1}{m_i(p)}{\overrightarrow{d}}_i(a){\overrightarrow{l}}_p^T{C}_i^{k+1}{Z}_i^k)+\beta {\displaystyle \sum _{b\in {\mathcal{N}}_a,b\in B^k}(\delta [p-L_i^k(b)])}a\in B^k,p\in P$$ (A1)

We use a normalized multi-way minimum cut algorithm to partition the graph into M subgraphs (Yu and Shi, 2003), which as shown by (Byokov et al., 2001; Von Luxburg, 2007), is equivalent to computing a partitioning for the Potts MRF model. In our case, cutting this graph into M subgraphs using minimum cuts, Fig A1(e), minimizes the cost function (9) over the set of boundary nodes B^k. The restriction to boundary nodes limits the movement of each vertex on the parcel boundaries by at most a single vertex at each iteration, Fig A1(f). The reduced graph size greatly reduces the per iteration cost. Repeatedly updating and cutting the graph using multiple (k) iterations allows the boundaries to move by up to k vertices and minimizes cost with respect to the entire cortex.

Definition of Edge Strengths in the Graph

The optimization problem in (9) has the form:

$$L^{k+1}=\underset{\{L_i:i=1\dots N\}}{\text{arg}min}\{{\displaystyle \sum _{i=1}^N(\frac{1}{2}\text{Trace}(Z_i^T{C}_i^{k+1}{Z}_i)+\beta {\displaystyle \sum _{a=1}^V{\displaystyle \sum _{b\in {\mathcal{N}}_a}(1-\delta [L_i(a)-L_i(b)])}})}\}.$$ (A2)

The edge strengths in (A1) map the cost function on the right to an equivalent graph cut problem. To be consistent with the Potts model, the definition of the edge strength between vertex nodes in (A1) attaches a penalty of β each time a neighboring pair of vertices differ in their parcel labels as a result of a cut. Since we remove vertices from the graph that did not lie on a parcel boundary in the previous iteration, we need to account for the additional cost of moving boundary vertices from the current parcel to a different parcel. This is achieved by the second term in edge strength E_i(a, p), between boundary vertices and parcel nodes, which counts the number of non-boundary vertices that are adjacent to a that currently have the same parcel label.

The first term in E_i(a, p) then computes the contribution of that link to the first term in (A2), the likelihood associated with assigning vertex a to parcel p. The likelihood is computed from the average time series averaged over the vertices in each of the parcels:

$$Z_i={\displaystyle \sum _{a=1}^V\frac{1}{m_i(L_i(a))}{\overrightarrow{l}}_{L_i(a)}{\overrightarrow{d}}_i^T(a),}$$ (A3)

where ${\overrightarrow{l}}_p={[0\dots 010\dots 0]}^T$ is a length M index vector in which the pth element is 1 and 0 otherwise, m_i(p) is the number of vertices with parcel label p and ${\overrightarrow{d}}_i(a)$ is the length T vector representing vertex a’s time series. In order to compute the likelihood as a sum of contributions, one per E_i(a, p) edge, we use the average from the previous iteration, $Z_i^k$, on the right side of the quadratic form based to give the following approximation to the first term in (A2):

$$\frac{1}{2}\text{Trace}(Z_i^T{C}_i^{k+1}{Z}_i)\approx \frac{1}{2}\text{Trace}(Z_i^T{C}_i^{k+1}{Z}_i^k)=\frac{1}{2}\text{Trace}({\displaystyle \sum _{a=1}^V\frac{1}{m_i(L_i(a))}{\overrightarrow{l}}_{L_i(a)}{\overrightarrow{d}}_i^T(a)C_i^{k+1}{Z}_i^k).}$$ (A4)

The contribution of the vertex a to this expression given that it is associated with parcel p is then

$$\frac{1}{2}\text{Trace}(\frac{1}{m_i(p)}){\overrightarrow{l}}_p{\overrightarrow{d}}_i^T(a)C_i^{k+1}{Z}_i^k),$$ (A5)

which gives us the first term in the edge strength E_i(a, p) in (A1).