Acoustofluidic waveguides for localized control of acoustic wavefront in microfluidics

Abstract

The precise manipulation of acoustic fields in microfluidics is of critical importance for the realization of many biomedical applications. Despite the tremendous efforts devoted to the field of acoustofluidics during recent years, dexterous control, with an arbitrary and complex acoustic wavefront, in a prescribed, microscale region is still out of reach. Here, we introduce the concept of acoustofluidic waveguide, a three-dimensional compact configuration that is capable of locally guiding acoustic waves into a fluidic environment. Through comprehensive numerical simulations, we revealed the possibility of forming complex field patterns with defined pressure nodes within a highly localized, pre-determined region inside the microfluidic chamber. We also demonstrated the tunability of the acoustic field profile through controlling the size and shape of the waveguide geometry, as well as the operational frequency of the acoustic wave. The feasibility of the waveguide concept was experimentally verified via microparticle trapping and patterning. Our acoustofluidic waveguiding structures can be readily integrated with other microfluidic configurations and can be further designed into more complex types of passive acoustofluidic devices. The waveguide platform provides a promising alternative to current acoustic manipulation techniques and is useful in many applications such as single-cell analysis, point-of-care diagnostics, and studies of cell–cell interactions.

1 Introduction

Acoustofluidics, merging the fields of acoustics and microfluidics, has recently attracted an increasing amount of attention in research communities (Ding et al. 2013; Friend and Yeo 2011; Yeo and Friend 2014). Acoustofluidic-based particle/cell manipulation methods exhibit several unique advantages over their optical, electrical, and magnetic counterparts (Suri et al. 2013; Voldman 2006; Zhang and Liu 2008). They are simple, noninvasive, contactless, and label-free (Ahmed et al. 2016; Bruus 2011, 2012b; Chen et al. 2013, 2014, 2016; Collins et al. 2015, 2016; Ding et al. 2012a; Gedge and Hill 2012; Glynne-Jones et al. 2012; Goddard et al. 2006, 2007; Guldiken et al. 2012; Guo et al. 2015a, b, c, 2016; Huang et al. 2013; Li et al. 2015; Mao et al. 2016; Ren et al. 2015; Shi et al. 2009a, b; Tang et al. 2016; Wang and Zhe 2011). Among the wide range of applications enabled by acoustofluidic technologies, capturing, patterning, and retaining of biological cells and microparticles in an ordered arrangement is of particular interest as it is of fundamental importance for fields such as microarrays (Flaim et al. 2005; Gresham et al. 2008), regenerative medicine (Khetani and Bhatia 2008; Smith 2007), 3D bio-printing (Kolesky et al. 2014; Murphy and Atala 2014), intercellular communications (Van Nhieu et al. 2003; You et al. 2004), as well as tissue engineering (Ashkin et al. 1987; Puleo et al. 2007).

In many of the previously reported acoustofluidic devices, the harnessing of the acoustic field was realized within a large portion of the microfluidic channel, thereby resulting in a homogeneous patterning and transportation of objects inside the chamber (Collins et al. 2015; Guo et al. 2015a; Shi et al. 2009a). Although tunable particle control can be achieved through changing the frequency (Ding et al. 2012b; Guo et al. 2015a) or relative phase of the signal (Ding et al. 2012a; Guo et al. 2015a, 2016; Li et al. 2014a), these methods still lack the ability to locally manipulate certain particles without influencing neighboring particles. Furthermore, conventional 1D and 2D acoustofluidic techniques could only yield relatively simple field patterns (Collins et al. 2015; Ding et al. 2012a; Guo et al. 2015a, b, c, 2016; Shi et al. 2009a), either in the form of 1D line (Shi et al. 2009a) or 2D dot/net-like distribution (Guo et al. 2015a). The forming of more complex distributions of cells is still urgently needed and is of fundamental importance for a number of applications including tissue engineering (Ashkin et al. 1987) and regenerative medicine (Khetani and Bhatia 2008; Smith 2007).

In order to address the above-mentioned limitations, we introduce acoustofluidic waveguides to guide and localize an acoustic field in a specific region within a microfluidic chamber. The transport of traveling and standing acoustic waves using an additional buffer layer or superstrate has been reported recently for a variety of applications such as particle separation, washing and trapping (Ma et al. 2016; Rambach et al. 2014; Skowronek et al. 2013; Witte et al. 2014), droplet rotating and liquid pumping (Bourquin et al. 2011; Reboud et al. 2012; Wilson et al. 2011), as well as cell sorting and patterning (Guo et al. 2015b; Schmid et al. 2014). With the incorporation of a single uniform layer (Guo et al. 2015b; Ma et al. 2016; Rambach et al. 2014; Schmid et al. 2014; Skowronek et al. 2013; Witte et al. 2014) or a patterned structure such as phononic crystal (Bourquin et al. 2011; Reboud et al. 2012; Wilson et al. 2011), enhanced manipulation of the acoustic fields can be readily realized, which is otherwise difficult to achieve using conventional microfluidic channels. However, despite the significant advancements in this field, the comprehensive study on the effect of acoustofluidic waveguides with different sizes and geometries in shaping and modifying the acoustic fields in fluidics are yet to be demonstrated. In addition, the wide range of subwavelength field localization to wavelength-scale confinement has not been reported, resulting in a gap in the understanding of the trapping and patterning of objects within a region that is comparable to, or much smaller than, the acoustic wavelength scale. Herein, we show that a specifically designed waveguide, with finite scales in all three dimensions, provides an effective approach for confining the acoustic field within a prescribed ultra-small region. The acoustofluidic waveguides studied in this article act as an efficient coupler between the acoustic source and the destination area. With a simple, and easy-to-realize configuration, the acoustofluidic waveguides provide great potential for the efficient manipulation of the acoustic field pattern inside a fluidic chamber.

Our acoustofluidic waveguides enable diverse field distributions within prescribed regions and subwavelength localized control of particles in fluids, thereby making them promising candidates for particle/cell manipulation and other lab-on-a-chip applications. In the following study, we show in detail that by tuning the shape and size of the waveguide structure, as well as the phase and frequency of the excitation wave, the pressure field could be dynamically controlled. Besides conducting comprehensive numerical simulations, we also experimentally characterized and demonstrated patterning for micro-size particles to verify the theoretical predictions. Our studies are expected to pave the way for the development of acoustofluidic waveguide-based lab-on-a-chip devices and may open new avenues for many biomedical applications such as neuroscience and tissue engineering.

2 Working principle of the acoustofluidic waveguides

The schematic of our proposed acoustofluidic waveguide is shown in Fig. 1. The waveguide is a three-dimensional (3D) planar configuration that sandwiches between the microfluidic chamber and the LiNbO₃ substrate. We chose a 128° Y-cut LiNbO₃ wafer due to its optical transparency and high electromechanical coupling. To enable the generation of surface acoustic waves (SAWs), an identical pair of IDTs with homogenous finger spacing (i.e., a quarter of the wavelength of the SAWs) was deposited on the substrate. The pair of IDTs was aligned parallel to the polydimethylsiloxane (PDMS) microchannel as shown schematically in Fig. 1. An RF signal was split and applied to each IDT to generate two identical SAWs propagating along the x-axis. These two SAWs propagate in opposite directions and interfere with each other to form a standing surface acoustic wave (SSAW) field in between the IDTs. With our introduced ultra-thin acoustofluidic waveguides, the acoustic waves could be efficiently and locally transmitted into the microfluidic chamber, resulting in periodic longitudinal pressure waves with pressure fluctuations in a defined region inside the liquid medium. Depending on their elastic properties, microparticles/cells will be pushed toward pressure nodes or pressure antinodes by the acoustic radiation force generated from the pressure fluctuations, similar to the mechanism in previously reported experiments (Guo et al. 2015a, b).

Fig. 1.

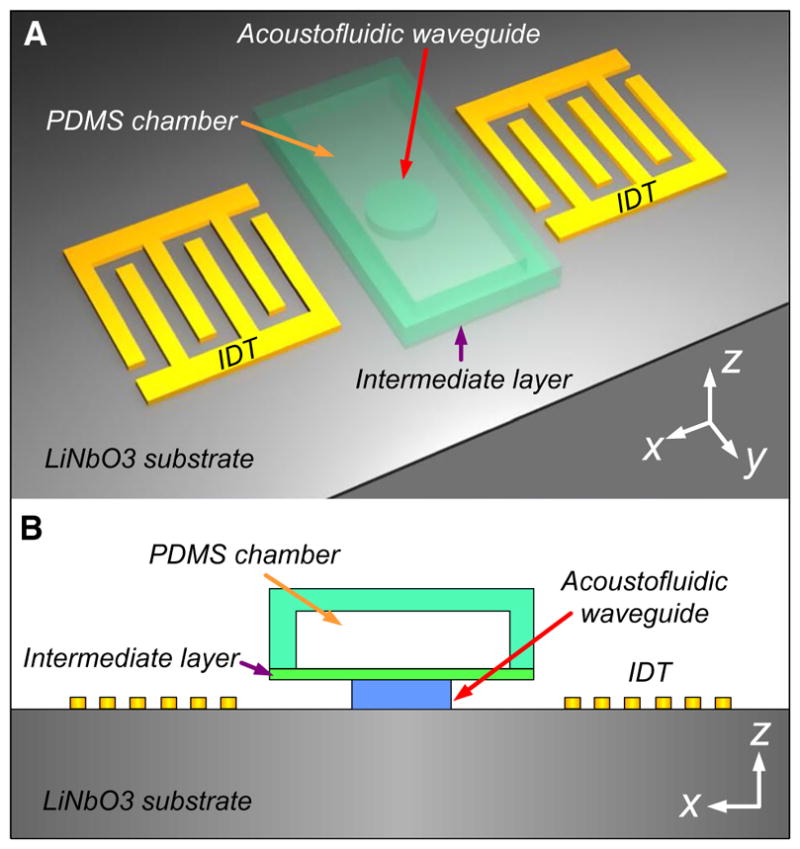
a 3D schematic and b 2D view of the acoustofluidic waveguide configuration within the x–z plane. The waveguide sits between the LiNbO₃ substrate and the upper microfluidic chamber. An ultrathin intermediate layer was introduced to connect the waveguide and the chamber. The waveguide, chamber, and intermediate layer were made of PDMS in our case studies. A pair of IDTs was placed on both sides of the waveguide, acting as the excitation source to generate the SAWs that travel along the LiNbO₃ substrate. The acoustic waves were guided through the waveguide and then transmitted into the fluidic chamber

3 Numerical simulation of the acoustofluidic waveguides

The numerical model for the acoustofluidic waveguides studied throughout this paper was established based on the Helmholtz equation for damped waves. By assuming a harmonic time dependence of the acoustic field (p(r,t) = p(r,t)e^iωt), the lossy Helmholtz equation can be written as (Bruus 2012a; Mao et al. 2016):

$$\frac{{\omega }^2}{c_f^2}p+\left[1+\frac{i\omega (1+\beta )\mu }{{\rho }_f{c}_f^2}\right]{\nabla }^{2}p=0$$ (1)

where p, ρ_f, c_f, ω, β, μ, and i represent the acoustic pressure, density of fluid, acoustic phase velocity of fluid, angular velocity, fluid viscosity ratio, fluid dynamic viscosity, and imaginary unit, respectively.

By selecting appropriate boundary conditions, the acoustic pressure distributions inside the acoustofluidic waveguides and microfluidic channels can be obtained based on Eq. (1). The lower boundary at the interface between the LiNbO₃ substrate and the acoustofluidic waveguide is actuated by the SSAW, which is originated from two leaky Rayleigh SAWs that feature oscillations both parallel and perpendicular to the surface. Owing to the narrow width of the waveguide, the decay of the Rayleigh SAWs is ignored during the study. The parallel component of the leaky Rayleigh SAW is not taken into consideration either, due to the fact that only the perpendicular oscillation can generate compressible acoustic waves and radiate into the waveguide and the fluid domain. Therefore, the harmonic actuation at the lower boundary of the interface is modeled by prescribing the normal component of boundary acceleration (Mao et al. 2016):

$$\begin{gathered} {\mathit{a}}_{\mathbf{PN}}=-\mathit{n}·\left[-\frac{\nabla p}{{\rho }_f}\left(1+\frac{i\omega (1+\beta )\mu }{{\rho }_f{c}_f^2}\right)\right] \\ =\mathit{n}·A_0{\omega }^2[e^{-i{k}_{s}x}-e^{-i{k}_s(w_0-x)}] \end{gathered}$$ (2)

$$\begin{gathered} {\mathit{a}}_{\mathbf{AN}}=-\mathit{n}·\left[-\frac{\nabla p}{{\rho }_f}\left(1+\frac{i\omega (1+\beta )\mu }{{\rho }_f{c}_f^2}\right)\right] \\ =\mathit{n}·A_0{\omega }^2[e^{-i{k}_{s}x}+e^{-i{k}_s(w_0-x)}] \end{gathered}$$ (3)

where A₀, k_s, w₀, and n correspond to the amplitude of leaky SAW displacement, wave number of leaky SAW, channel width, and boundary normal vector, respectively. In Eqs. (2) and (3), the accelerations a_PN and a_AN represent the boundary conditions given for the cases when pressure node (displacement node) and pressure antinode (displacement antinode) of the SSAW are located in the middle of the chamber.

The problem formulated above was solved using the pressure acoustics package of the finite element method (FEM)-based software COMSOL Multiphysics. In order to gain comprehensive observations of the pressure fields inside the chamber, 3D simulations of the acoustofluidic waveguide system were conducted. Convergence tests were performed to ensure that the numerical boundaries and meshing did not interfere with the solutions. In the calculations, the height of the chamber was 120 μm. The thicknesses of the waveguide layer and the intermediate layer were 20 and 10 μm, respectively, unless otherwise stated. The centerline of the waveguide was placed between two pressure antinodes. The densities for water, air, and PDMS are 997, 1.2, and 970 kg/m³, whereas the sound speeds in water, air, and PDMS are 1490, 343 and 1080 m/s, respectively. The acoustic attenuation of PDMS is estimated to be ~80 dB/cm according to the experimentally measured results for PDMS with a mixed ratio of 10:1 (Tsou et al. 2008). The phase velocity of a SAW is 3997 m/s. The operational frequency of the SAWs was fixed at 13.4 MHz unless otherwise stated, corresponding to a working wavelength of 300 μm. In order to demonstrate the ability of our acoustofluidic waveguides in generating versatile field patterns, we not only tuned the size and shape of the waveguiding structure, but also changed the operational frequency of the acoustic waves.

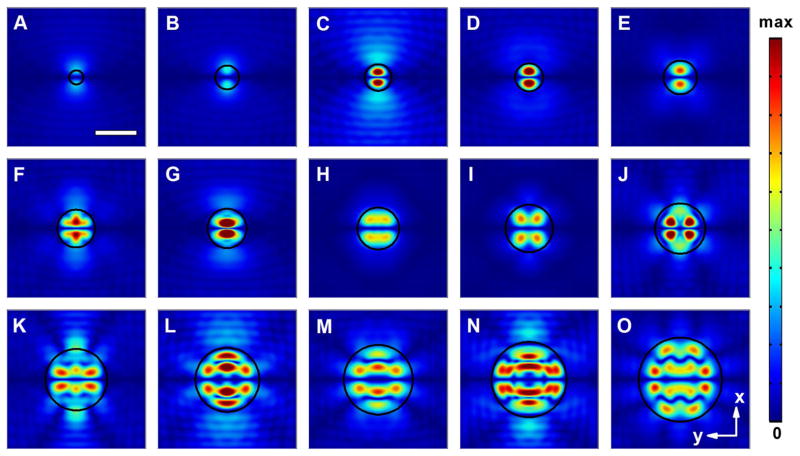
We first considered 3D acoustofluidic waveguides with circular shape. In the simulations, we varied the dimension of the waveguide cross section from subwavelength scale to twice the operational wavelength. In order to better compare the detailed pattern of the waveguide with different dimensions, all the field distributions were normalized. As illustrated from the simulation results in Fig. 2, the pressure field profiles exhibit dramatic change with the variation of the waveguide diameter D. We found that when D is smaller than 100 μm, the field intensity in the center of the PDMS chamber is more than 4 orders of magnitude smaller than that of the incoming boundary of the acoustofluidic waveguides, indicating that the transmission efficiency of the acoustic wave is quite low when the waveguide size is significantly smaller than the working wavelength. With the dimension of the waveguide between 100 and 300 μm, an acoustic field with a single pressure node line was observed (see Fig. 2a–g). In addition, two pressure antinodes with varied intensities exist on each side of the pressure node, along with slightly different field distributions in the rest of the region.

Fig. 2.

Normalized 2D absolute pressure field distribution (Abs(P)) at the center cross section of the microfluidic chamber for circular acoustofluidic waveguides with different diameters (D). a D = 100 μm; b D = 170 μm; c D = 190 μm; d D = 200 μm; e D = 240 μm; f D = 270 μm; g D = 280 μm; h D = 300 μm; i D = 340 μm; j D = 360 μm; k D = 440 μm; l D = 460 μm; m D = 500 μm; n D = 540 μm; o D = 600 μm (Movie 1). Scale bar: 300 μm. The boundary of the waveguide region is highlighted using a black circle. Pressure nodes and pressure antinodes are shown with different field intensities. The corresponding 3D pressure field distributions for typical waveguides are shown in Supplementary Fig. 1

In these scenarios, since the feature size of the field pattern is much smaller than the excitation wavelength, the acoustofluidic waveguide-based devices have the potential to enable the study of the interactions between small populations of cells. When D further increases from λ to 2λ, significant evolution of the field pattern is observable, indicating the notable impact of the waveguide configuration in shaping the pressure field distributions under these conditions. For example, it was seen that with a D around 300 ~ 360 μm (Fig. 2h, j), two pressure antinodes separate into four or even more. In these cases, in addition to the horizontal pressure node line along the center region of the waveguide, vertical pressure nodes also started to appear. The combination of both vertical and horizontal pressure nodes results in more complex 2D field patterns, with curved features incorporated. This interesting profile is obviously different from the field distributions generated by the conventional acoustofluidic platform, where only 1D straight pressure nodes were observed using a single pair of IDTs (Ding et al. 2012b; Shi et al. 2009a). Further increasing the waveguide size could result in the appearance of another two pressure nodes near the bottom and top of the waveguide region, as depicted in Fig. 2k, l. As D exceeds ~500 μm, the pressure nodes on the top and bottom regions within the waveguide boundary change gradually from near-straight lines into curves (Fig. 2m–o). It is also clearly observed that the distance between adjacent horizontal pressure nodes is half of the wavelength of the SAWs, which matches results observed in previous studies (Ding et al. 2012b; Guo et al. 2015b; Shi et al. 2009a).

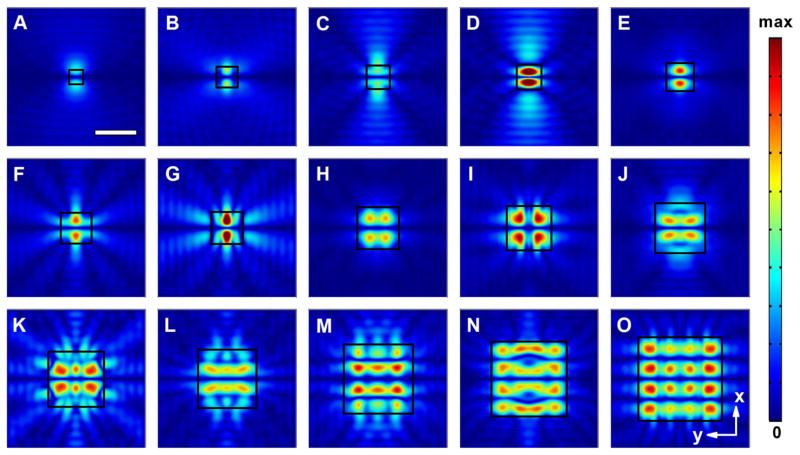
Next, the effect on the pressure gradient of varying the size of a square acoustofluidic waveguide was investigated. As shown in Fig. 3, the width, W, of the square waveguide was varied between 100 and 600 μm. Considering that both the number and position of the pressure nodes yielded by the square waveguide changed with an increasing critical dimension, the evolution of the field patterns with the change in width W is similar to that observed in the circular waveguide case. Single pressure node lines could be maintained for waveguides with subwavelength dimensions (Fig. 3a–g), while the number of the horizontal pressure nodes increases up to three as W exceeds ~360 μm. The interval distances between adjacent nodes are also equal to the half-wavelength of the SAWs.

Fig. 3.

Normalized 2D absolute pressure field distribution (Abs(P)) at the center cross section of the microfluidic chamber for square acoustofluidic waveguides with different widths (W). a W = 100 μm; b W = 150 μm; c W = 170 μm; d W = 180 μm; e W = 200 μm; f W = 220 μm; g W = 230 μm; h W = 300 μm; i W = 320 μm; j W = 360 μm; k W = 400 μm; l W = 420 μm; m W = 500 μm; n W = 540 μm; o W = 600 μm (Movie 2). Scale bar: 300 μm. The boundary of the waveguide region is highlighted using a black square. Pressure nodes and pressure antinodes are shown with different field intensities. The corresponding 3D pressure field distributions for typical waveguides are shown in Supplementary Fig. 2

A further comparison between the square and circular acoustofluidic waveguides reveals differences in the shapes of their pressure field profiles caused by a change in the cross section. For instance, we could observe a significant difference between the field patterns of the square and circular- shaped configurations around 400 μm. In these cases, not only the numbers, but also the shapes of the pressure antinodes are quite different. We also noted that although the square-shaped waveguide has boundaries either parallel or perpendicular to the propagation direction of SSAWs, both the pressure node and pressure antinode distributions are more complex than those of the conventional SSAW devices (Guo et al. 2015a; Shi et al. 2009a), in which the microfluidic chambers are typically significantly larger than the wavelength scale. This phenomenon reveals the unprecedented confinement capability provided by the finite waveguide geometry of our acoustofluidic waveguide- based platform, which is the key to the formation of ultra-small and complex pressure field profiles.

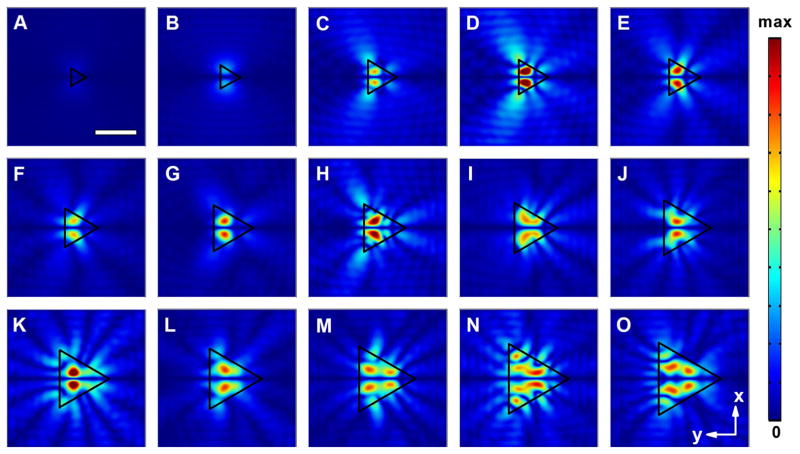
We also studied the acoustic field distributions of the acoustofluidic waveguides with triangular cross-sectional shape, as shown in Fig. 4. The diameter of the circumcircle of the triangle varied from 100 to 600 μm. In significant contrast to the circular- and square-shaped waveguide cases, the unique shape of the triangular acoustofluidic waveguides induces more notable effect on the generated field pattern, as revealed clearly from the evolution of the distributions. Owing to the fact that the area of the cross section for the triangular waveguide is smaller than that of its circular or square counterpart with the same diameter/width, the critical size that allows the efficient transmission of acoustic wave into the chamber is also relatively larger for the triangular configuration. As shown in Fig. 4a, b, the intensity of the acoustic field generated by the triangular acoustofluidic waveguide is lower than its circular- or square-shaped counterpart with the same size.

Fig. 4.

Normalized 2D absolute pressure field distribution (Abs(P)) at the center cross section of the microfluidic chamber for triangular acoustofluidic waveguides with different diameters of their circumcircles (D). a D = 150 μm; b D = 200 μm; c D = 280 μm; d D = 290 μm; e D = 300 μm; f D = 320 μm; g D = 380 μm; h D = 400 μm; i D = 420 μm; j D = 460 μm; k D = 480 μm; l D = 500 μm; m D = 540 μm; n D = 580 μm; o D = 600 μm (Movie 3). Scale bar: 300 μm. The boundary of the waveguide region is highlighted using a black triangle. Pressure nodes and pressure antinodes are shown with different field intensities. The corresponding 3D pressure field distributions for typical waveguides are shown in Supplementary Fig. 3

Another important feature of the triangular configuration is the unique shape of its pressure field distributions. Taking the acoustofluidic waveguide with D = 290 μm as an example, four pressure nodes were observed (Fig. 4d), among which a straight and horizontal one existed in the center of the waveguide, two tilted ones were seen near the bottom and top regions, and a vertical curved node was positioned near the right edge of the triangle. The field distributions could be even more complex for waveguides with dimensions that are much larger than the wavelength scale. In these scenarios, not only the number of the pressure antinodes increased, but also more wavy-like features were incorporated near the boundary of the triangle (Fig. 4m–o). Compared to the symmetric configurations like circular and square ones, the triangular acoustofluidic waveguide provides more freedom for generating unique and more complex field patterns, thereby making itself a promising candidate for shaping and localizing the acoustic fields inside the microfluidic channel.

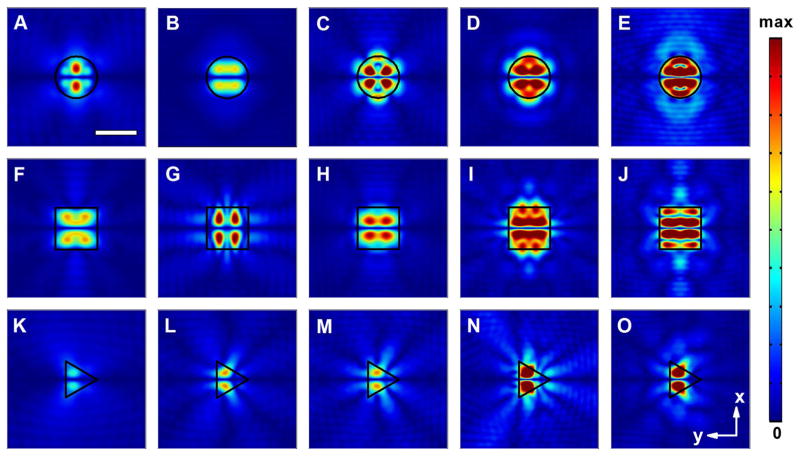
Based on the above discussions, we have shown that both the pattern and size of the pressure field in the microfluidic chamber can be readily controlled by changing the shape and dimension of the acoustofluidic waveguide. We further demonstrated that modifications of the field distributions can be realized through varying the frequency of the involved acoustic wave. Figure 5 shows the field profiles of three types of acoustofluidic waveguides under different operational wavelengths. By varying the working frequency from 12 to 20 MHz, we can observe a dynamic evolution of the pressure fields in the areas above the waveguides for all three cases. Due to the different geometries and shaping effects, the changes in the pressure field of the circular and square acoustofluidic waveguides are more dramatic than in their triangular counterparts. In addition, we found that the coupling efficiency of the acoustic wave into the microfluidic channel could also be well controlled through tuning the operational frequency. The flexible harnessing of the acoustic energy in fluidics is beneficial for controllable engineering of the acoustic forces exerted on the manipulated objects, which could find itself useful to a number of intriguing applications. For example, through tuning the frequency of SAWs, trapping and releasing the cells within a prescribed, localized region may be readily realized. By introducing multiple acoustofluidic waveguide arrays with controlled shape, geometry and distance, separate control of cells within different regions can be realized. This might greatly facilitate the study of the interactions between different groups of cells.

Fig. 5.

Normalized 2D absolute pressure field distribution (Abs(P)) at the center cross section of the microfluidic chamber for acoustofluidic waveguides at different excitation frequencies. a–e Circular acoustofluidic waveguides (300 μm in diameter): a 12 MHz; b 14 MHz; c 16 MHz; d 18 MHz; e 20 MHz (Movie 4); f–j square acoustofluidic waveguides (width of 300 μm): f 12 MHz; g 14 MHz; h 16 MHz; i 18 MHz; j 20 MHz (Movie 5); k–o: triangular acoustofluidic waveguides (diameter of the circumcircle as 300 μm): k 12 MHz; l 14 MHz; m 16 MHz; n 18 MHz; o 20 MHz (Movie 6). Scale bar: 300 μm. The boundary of the waveguide region is highlighted using black lines. Pressure nodes and pressure antinodes are shown with different field intensities. The corresponding 2D pressure field distributions within the x–z plane and 3D pressure field profiles for typical waveguides are shown in Supplementary Fig. 4 and Supplementary Fig. 5, respectively

4 Experimental validation of the acoustofluidic waveguides

To validate the above theoretical predictions, we fabricated several acoustofluidic waveguides with different shapes and demonstrated microparticle patterning based on the acoustofluidic waveguide platform. The device was fabricated by bonding the waveguide-integrated PDMS microchannels onto a LiNbO₃ substrate patterned with IDTs, similar to the fabrication procedure of our previously demonstrated SSAW devices (Guo et al. 2015a, b). In the experiments, 128° YX-cut LiNbO₃ (500 μm thick, double-side-polished) was employed as the piezoelectric substrate. Standard lithography and lift-off processes were utilized to fabricate the IDT. Multiplayer lithographic procedure was followed to obtain the acoustofluidic waveguide-based PDMS device, including the waveguide layer, thin intermediate layer, and the microfluidic chamber (Thorsen et al. 2002). The thicknesses of our fabricated acoustofluidic waveguide layer and intermediate layer were measured to be 22 and 8 μm, respectively, whereas the height of the PDMS chamber was 120 μm.

In the particle patterning experiment, the acoustofluidic waveguide-based device was mounted on the stage of an inverted microscope (TE2000U, Nikon, USA). Solutions of 1-μm-diameter polystyrene particles (Bangs liberates Inc, USA) were injected into the microfluidic chamber of the device using a syringe pump (KDS210, KD Scientific, Germany). The SSAW field was excited by applying two coherent RF signals on the two sets of IDTs, respectively. A signal generator (E4422B Agilent, USA) was used to generate the RF signals, which were amplified by a power amplifier (100A250A, Amplifier Research, USA) before applying to the IDTs. A CCD camera (CoolSNAP HQ2, Photometrics, USA) was used to monitor the motion of the microparticles. The microscopic images were processed with an image processing software (ImageJ, NIH, USA).

For the manipulation of polystyrene beads, RF signals with a frequency of 12.7 MHz and an input power between 200 and 800 mW were applied to the IDTs to generate SSAWs. The bead distributions observed from experiments with and without the presence of SSAW field for acoustofluidic waveguides with circular, rectangular, and triangular shapes are shown in Fig. 6a, b, d, e, g, h, respectively. For the considered waveguides with three different shapes, the particles were driven, trapped, and eventually patterned into the pressure nodes after activating the acoustic field. The interval distance between adjacent nodes was around 150 μm, which is half of the working wavelength. The shape of the pressure nodes was observed to be parallel lines for the square-shaped waveguide, whereas curved features were incorporated into the profiles of the circular- and triangular-shaped configurations, indicating different shaping effect of the acoustic fields enabled by waveguides with varied cross-sectional shapes. Adapting the operational frequency in experiments and the geometric parameters measured, we also simulated the field pattern generated by the corresponding structure, as illustrated in Fig. 6c, f, i. Detailed comparisons between the observed spatial distributions of patterned polystyrene beads and the simulated field patterns indicated an excellent match between the numerical and experimental results, thereby validating our previous predictions. Here, it is worth mentioning that our experimental and simulation results are also in quite good agreement with the experimental observations in (Rambach et al. 2014), where square- and circular-shaped posts have been introduced for particle filtering and washing.

Fig. 6.

Experimental results of the polystyrene bead distributions enabled by acoustofluidic waveguides with different shapes, and the corresponding simulated pressure field patterns. Images of the polystyrene beads on a circular waveguide (600 μm in diameter) a without and b with the presence of SSAW field; c normalized 2D absolute pressure field distribution (Abs(P)) at the center cross section of the microfluidic chamber. Images of the polystyrene beads on a square waveguide (width of 600 μm) d without and e with the presence of SSAW field; f normalized 2D absolute pressure field distribution (Abs(P)) at the center cross section of the microfluidic chamber. Images of the polystyrene beads on a triangular waveguide (diameter of the circumcircle as 600 μm) g without and h with the presence of SSAW field; i normalized 2D absolute pressure field distribution (Abs(P)) at the center cross section of the microfluidic chamber. Scale bar: 100 μm. For simulations and experiments, the thicknesses of the acoustofluidic waveguide layer and intermediate layer are 22 and 8 μm, respectively, while the height of the PDMS chamber is 120 μm

Interestingly, we found that during the bonding process of the PDMS chamber with the substrate, a misalignment of the waveguide with respect to the centerline between the IDT pairs (along the x-axis) could result in a modification of the acoustic field profile. To study this, we fabricated square- and triangular-shaped waveguides on a single device and aligned both waveguides a quarter of the operational wavelength (~75 μm) off the centerline relative to the x-axis. Figure 7 shows the spatial distribution of the particles on the two acoustofluidic waveguides, as well as their corresponding pressure field distributions obtained from numerical simulations. The experimental results exhibit reasonable agreement with the simulations for both acoustofluidic waveguides. Compared to the case without the displacement, not only the numbers of the pressure nodes but also their pressure field distributions varied significantly. For the square-shaped configurations, in contrast to the waveguide without misalignment that has three major pressure nodes (Fig. 6e, f), the introduction of a 75-μm displacement leads to four horizontal pressure nodes, locating symmetrically along the x-axis (Fig. 7b, c). For the triangular-shaped acoustofluidic waveguide, a pressure antinode symmetrically accompanied by two pressure nodes starts to appear along the waveguide center when the displacement occurs (Fig. 6h, i), whereas a symmetric distribution of a single pressure node, and an antinode on each side of the centerline, were observed without the displacement (Fig. 7e, f). Here, it is worth mentioning that the pressure field distributions could also be effectively controlled through tuning the relative phase of the acoustic waves (Ding et al. 2012a; Li et al. 2014a) in addition to changing the position of the waveguide. The phase-changing method provides a more feasible pathway for the dynamic engineering of the acoustic wavefront and could also be leveraged to compensate the pressure field modifications induced by waveguide imperfections during the fabrication process.

Fig. 7.

Experimental results of the polystyrene beads distributions enabled by acoustofluidic waveguides with ~75 μm displacements, and the simulated pressure field profiles. Images of the polystyrene beads on a square waveguide (width of 600 μm) d without and e with the presence of SSAW field; f normalized 2D absolute pressure field distribution (Abs(P)) at the center cross section of the microfluidic chamber. Images of the polystyrene beads on a triangular waveguide (diameter of the circumcircle as 600 μm) g without and h with the presence of SSAW field; i normalized 2D absolute pressure field distribution (Abs(P)) at the center cross section of the microfluidic chamber. Scale bar: 100 μm. Other parameters of the waveguides are the same as those in Fig. 6

5 Discussion

Through comprehensive numerical simulations and experimental verifications, we have demonstrated the unique capability of the acoustofluidic waveguide platform in realizing 2D patterning with only a single pair of IDTs, which is otherwise difficult to achieve using conventional acoustofluidic devices. The acoustofluidic waveguides, with feature sizes comparable to or smaller than the wavelength scale in all three dimensions, could offer ultra-tight confinement and dexterous manipulation of the acoustic potential field and are capable of forming single pressure nodes within subwavelength regions inside the microfluidic chamber, thereby rendering themselves ideal platforms for studying small population of cells even down to the single cell level (Collins et al. 2015; Guo et al. 2016; Kim et al. 2015). In addition, the number, dimension, and distribution of the pressure nodes and pressure antinodes can also be dynamically controlled through tuning the waveguide geometry and the key parameters of the RF signal (frequency, phase, etc.), leading to the formation of reconfigurable patterns of particles and cells. The unprecedented flexibility over the control of cells provided by our acoustofluidic waveguide platform could greatly facilitate the investigation of cell-to-cell interactions and be highly beneficial for applications such as neuroscience and tissue engineering. Specifically, the acoustofluidic waveguide approach can be exploited to produce complex cell patterns, clusters, assembled arrays, and even 3D tissue- like structures based on layer-by-layer positioning of live cells. Another feature of our acoustofluidic waveguide technology is its potential for enabling selective, localized control of the acoustic field in the microfluidic channel. Multiple, spatially separated pressure field distributions can be formed by introducing waveguide arrays with the same or varied shapes/dimensions, facilitating the independent and parallel manipulation of the objects at different positions within the channel. The formation of isolated pressure nodes, with tunable pressure gradients, can also be exploited to adjust the distance between different cell assemblies (Guo et al. 2015a) as well as control the movement of cells and cell matrix (Ding et al. 2012a; Guo et al. 2016).

Although the aforementioned studies were focused exclusively on the 1D standing acoustic waves, our acoustofluidic waveguide concept can be readily applicable to more complex acoustic fields (Collins et al. 2015; Guo et al. 2015a). According to our numerical simulations, 2D acoustic potential field can also be enabled by the acoustofluidic waveguide with two pairs of IDTs. The dimensions of the pressure nodes and pressure antinodes can be further reduced, whereas their numbers will increase as compared to the same configuration leveraging 1D standing acoustic waves. In addition, acoustofluidic waveguides with cross-sectional shapes other than circle, square, and triangle could also be exploited for the localized shaping of the acoustic fields in microfluidics. Our studies revealed that some of these structures are capable of yielding quite unique field profiles, which are extremely sensitive to the geometric modifications and/or the frequency changes, making themselves appealing platforms for some specific biomedical applications (Lee et al. 2014; Liu et al. 2012; Sridharamurthy et al. 2006). Furthermore, through designing more complex structures (e.g., waveguide arrays) and introducing novel configurations like acoustic metasurfaces (Li et al. 2013, 2014b; Xie et al. 2014) and/or phononic crystals (Bourquin et al. 2011; Lin et al. 2009), we envision the exploitation of our acoustofluidic waveguide platform in realizing even more complex and integrated functionalities.

6 Conclusions

In summary, we have proposed and demonstrated compact acoustofluidic waveguides that can efficiently guide and couple acoustic waves from the piezoelectric substrate to prescribed regions inside the microfluidic chamber. Through comprehensive numerical investigations combined with experimental demonstrations, we showed that different pressure field patterns, ranging from subwavelength scale to dimensions much larger than the wavelength, were dynamically achieved using our waveguide structure. By tuning the size and shape of the acoustofluidic waveguide, as well as the frequency of the RF signal, we can conveniently control the number, position, and shape of the pressure nodes. Additionally, we fabricated the waveguide structure and measured the field pattern of specific configuration by using microscale polystyrene beads in our case study. The results showed excellent agreement between numerical simulation results and experimental data, thereby validating our theoretical predictions. The proposed acoustofluidic waveguide is simple, easy-to-fabricate, versatile, and inherently noninvasive for cells and other biological specimens to be manipulated. With these features, it is valuable in a variety of applications such as microarrays, cell studies, and tissue engineering.