A rheological study of the association and dynamics of MUC5AC gels

Abstract

The details of how the mucus hydrogel forms from its primary structural component, mucin polymers, remain incompletely resolved. To explore this, we use a combination of macrorheology and single particle tracking to investigate the bulk and microscopic mechanical properties of reconstituted MUC5AC mucin gels. We find that analyses of thermal fluctuations on the length scale of the micronsized particles are not predictive of the linear viscoelastic response of the mucin gels, and that taken together, the results from both techniques help to provide complementary insight into the structure of the network. In particular, we show that macroscopic stiffening of MUC5AC gels can be brought about in different ways by targeting specific associations within the network using environmental triggers such as modifications to the pH, surfactant, and salt concentration. Our work may be important for understanding how environmental factors, including pathogens and therapeutic agents, alter the mechanical properties of fully-constituted mucus.

1 Introduction

The primary structural component of the biological hydrogel mucus is the large glycoprotein mucin, whose macromonomer subunit is depicted schematically in Figure 1a. Individual subunits consist of an amino acid backbone and bottlebrush-like regions of dense glycosylation¹ and these subunits associate via end-to-end disulphide bonds to form even larger macromonomer chains². The hydrogel network created from an aqueous solution of these high molecular weight molecules, shown schematically in Figure 1b, is formed from a complex series of reversible associations including hydrophobic interactions, and is stabilized by electrostatic repulsion between the negatively charged polysaccharide side chains¹. This rich variety of interaction mechanisms makes mucus an impressively adaptable biological fluid, existing in different forms and serving different purposes across all (non-keratinized) wet epithelial surfaces of the body².

Figure 1.

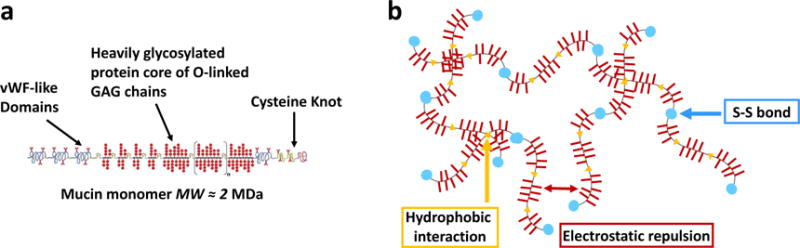
(a) Schematic of a mucin macromonomer adapted with permission from ref 3. Copyright 2005 American Chemical Society. Adapted from ref 4, Copyright 2002, with permission from Elsevier. (b) The mucin network is formed by reversible associations including hydrophobic interactions between the non-glycosylated portions of the molecules, and is stabilized by electrostatic repulsion between the charged sugar side chains.

Mucus gels formed from a specific secretory mucin, MUC5AC, provide a particularly good example of this adaptability⁴. On the ocular surface of the eye, a thin, watery form of these gels known as the tear film is responsible for hydration and lubrication⁵. In the pH-neutral environment of the lungs and respiratory tract, a MUC5AC (and MUC5B) based mucus bilayer serves as a barrier against bacteria and environmental particulate matter⁶. The bottom layer, known as the percilliary fluid, has been modeled as a polymer brush⁶ and permits continuous clearance by the periodic beating action of cilia that line these surfaces, while the superficial mucus gel layer is designed for pathogen containment and transport^6,7. As a final example, the relatively stationary mucus layer lining the stomach is a much stiffer MUC5AC-based gel that serves as a buffer to protect the epithelial lining against the harshly acidic gastric juices (pH ≈ 1 − 2) contained within this organ⁸. Inevitably, however, the same structural adaptability that makes mucus so multifunctional also exposes it to pathological manipulation. For example, in cystic fibrosis (CF), abnormal CFTR and sodium channel activity^9,10 as well as mucin overproduction¹⁰ are among the causes of ‘sticky’ mucus which is less readily cleared by the cilia and hence more susceptible to biofilm formation.

Despite it being well-established that the local milieu plays a major role in determining the viscoelastic properties of mucus, the mechanisms by which this occur remain unclear¹¹. To this end, rheological measurements can be used to obtain quantitative information about both bulk gel properties and their underlying microstructural details. Further, by performing these experiments under a variety of environmental conditions which favour specific classes of interactions, a more holistic picture of how mucin networks change under variations in physiological conditions can be gleaned from the corresponding rheological data. Macroscopic rheological measurements performed with traditional rheometers provide bulk fluid characterizations, i.e. quantification of fluid behaviour over length scales comparable to the size of the attached geometry (typically on the order of 1 – 10 mm)¹². One such technique in particular, small amplitude oscillatory shear (SAOS), has been applied on numerous occasions to the study of mucus and mucin gels. Using this method, Critchfield et al.¹³ have shown that the macrorheological response of cervical mucus is indicative of high- or low-risk pregnancy states. In addition, Wang et al.¹⁴ have demonstrated that the mechanical properties of cervicovaginal mucus are pH-dependent. Celli et al.⁸ have assessed the effect of pH on the bulk response of reconstituted MUC5AC gels, and have demonstrated from their results that the ulcer-causing bacterium H. Pylori enhances its motility in the stiff mucus lining of the stomach by locally hydrolyzing urea, which raises the pH of the gel and reduces its storage and loss moduli^8,15. In all of these cases, however, the ubiquity of slowly varying dependencies of the storage and loss moduli on the oscillation frequency, which may arise as a consequence of a very broad spectrum of relaxation modes¹⁶, complicates the deciphering of specific structural rearrangements and mechanisms that may be contributing to these macroscopic viscoelastic changes.

With this in mind, microrheological techniques, and Single Particle Tracking (SPT) in particular, are becoming increasingly popular tools with which to characterize the microscale features of biological fluids, partially as a result of the very limited sample volume (e.g. microliters) that they require¹⁷. In principle, if the particles are significantly larger than the characteristic length scale of heterogeneity within the gels and they do not interact with the gel components, then the thermal fluctuations measured using SPT should be directly related to the linear viscoelastic measurements obtained from macrorheology, as initially shown by Mason and Weitz^17,18. Recently, however, Bansil et al.¹¹ have found that the storage and loss moduli predicted from SPT with micron sized beads in MUC5AC gels at pH2 were significantly lower than those obtained using SAOS. Regardless of whether quantitative agreement is obtained between the results of SPT and linear viscoelastic measurements, microrheology provides an independent microstructural characterization of complex biological fluids that is inaccessible at the length scale probed by standard macroscopic rheological techniques. As such, Hill et al. have employed this technique to assess the impact of elevated mucus solids concentration on the diffusion of micron sized particles in respiratory mucus samples¹⁹, and Georgiades et al. have studied the mean squared displacement of micron probes in reconstituted MUC2 and MUC5AC gels at different pH levels, as well as at different concentrations of mucin, urea, and ECEG (a plant polyphenol)²⁰.

In this paper, we use a combination of macroscopic (SAOS) and microscopic (SPT) rheological studies to investigate the effect of a series of perturbations, including modifications of the pH, surfactant, and salt concentration, on the structure and mechanical response of purified MUC5AC gels. We demonstrate that the results from SPT, including the degree of trajectory heterogeneity and the statistical distribution of step sizes, can provide independent and complementary information about the gel microstructure to that obtained from bulk rheological measurements, which is pertinent even when the results from these two techniques are not in quantitative agreement.

2 Methods

2.1 Mucin preparation

MUC5AC was purified from fresh pig stomach scrapings following the method detailed in Lieleg et al.²¹. Briefly, the isolated mucus layer was solubilized in sodium chloride buffer containing protease inhibitors and sodium azide to prevent mucin degradation and bacterial proliferation, respectively²². Following centrifugation to remove insoluble components, the mucins were isolated using gel filtration chromatography on a Sepharose column (CL2B), and then concentrated and lyophilized²². Mucins were then solubilized overnight in deionized (Milli-Q) water, and gels were prepared the same day as the experiments were performed by combining the solubilized mucins with the appropriate buffers (and surfactant or salt solutions when appropriate). The pH of the gels was modulated through the addition of a phosphate and sodium citrate buffer to a final concentration of 10mM. The salt concentration was modified through the addition of NaCl dissolved in deionized water, while the surfactant used was 1,2-hexanediol (Sigma-Aldrich, St. Louis, MO). This particular surfactant was chosen as a result of previous studies that have shown that a similar compound, the mild detergent trans-cyclohexane-1,2-diol, can reversibly interfere with hydrophobic interactions in the nuclear pore complexes (NPCs) of eukaryotic cells²³. Gels were vortex mixed to ensure adequate mixing following addition of all components, and kept on ice until experimental use. All gels in this manuscript contain 10 mg/ml or 1 wt % of purified MUC5AC.

To assess the potential impact of the presence of non-mucin proteins on the properties of MUC5AC gels, we repeated the microrheological and macrorheological measurements at pH2 and pH7 using mucins prepared with an additional cesium chloride (CsCl) gradient centrifugation step, as described by Smith and Lamont²⁴. These results are shown and analyzed in Section S1 of the supporting information (SI).

2.2 Macrorheology

All shear rheology tests were performed using a stress controlled AR-G2 (TA Instruments, New Castle, DE, USA) or a DHR-3 rheometer (TA Instruments, New Castle, DE, USA) with a 20 mm, 4° cone-and-plate fixture. All experiments were performed on a Peltier plate at a constant temperature T = 25 °C. SAOS measurements were performed at a strain amplitude within the linear viscoelastic regime (γ₀ ≤ 10%) of each mucin gel as determined from separate strain sweep experiments (presented in Section S2 of the supporting information (SI)).

2.3 Microrheology

Samples for single particle tracking experiments were prepared by combining 30 μl of the prepared mucin gels with 0.5. μl of a solution of 1 μm diameter, fluorescent, negatively charged (carboxylated) microspheres (Magsphere Inc) in deionized water at a dilution ratio of 1: 200 by volume (resulting in an overall dilution ratio of 1: 12,000 for the microspheres). Negatively charged particles were selected as a result of previous findings of increased charge-mediated diffusion impairment for positively charged (amine functionalized) particles as compared to negatively charged (carboxylated) ones in mucus and mucin gels^19,21,25. Specimens were subsequently vortexed to ensure adequate mixing, then loaded via pipette into borosilicate square capillaries 0.9 mm × 0.9 mm × 15 mm in dimension (Vitrocom 8290). The capillaries were sealed on either end using a 1 :1 :1 mixture of Vaseline, lanolin, and paraffin to prevent evaporation, and then mounted onto microscope slides for imaging.

Imaging was performed at 30.3 frames per second for 10 seconds at room temperature with an Axio Observer D.1 inverted microscope using a Zeiss LD Plan-Neofluar 20×/0.4 Corr Ph2 objective lens and a Hamamatsu Flash 4.0 C11440-22CU camera. An average of 160 particles were imaged for each sample from an average of ten movies recorded at different spatial locations within the glass capillaries.

For each resulting image frame, particles were identified using publicly available Matlab (Natick, MA) code which identifies candidate features using high intensity matches and filters them using criteria such as maximum feature eccentricity and radius of gyration^26,27.

2.4 Mathematical details for microrheological analysis

The x and y positions of every validated particle in each frame were recorded using the same publicly available Matlab code by the center of mass of the localized image intensity. A drift correction code from the same publicly available source²⁶ was subsequently applied to all SPT data. This correction subtracts the center of mass motion of all of the particles in a given frame from each individual trajectory. Using these drift-corrected data, the time-averaged mean squared displacement (in one dimension) of the k^th particle for a movie N images in length is given by^21,28

$$\begin{gathered} \overline{\mathrm{\Delta }{x}_k^2(\mathrm{\Delta }\tau )} \\ =\frac{1}{N-\mathrm{\Delta }\tau /\mathrm{\Delta }t}{\displaystyle \sum _{i=1}^{N-\mathrm{\Delta }\tau /\mathrm{\Delta }t}[x(i\mathrm{\Delta }t+\mathrm{\Delta }\tau })-x(i\mathrm{\Delta }t)]{ }^2, \end{gathered}$$ (1)

where Δt is the time between successive frames and Δτ is the lag time. The ensemble averaged mean squared displacement (MSD) over all K particles is then²⁸

$$\langle \mathrm{\Delta }{x}^2(\mathrm{\Delta }t)\rangle =\frac{1}{K}{\displaystyle \sum _{k=1}^K\overline{\mathrm{\Delta }{x}_k^2(\mathrm{\Delta }\tau )}}.$$ (2)

For normal diffusive motion such as that occurring in a homogeneous Newtonian medium with no fluid memory and with which the microspheres do not interact, the MSD is expected to scale linearly with lag time, and in one dimension the explicit form of this scaling is²⁸

$$\langle \mathrm{\Delta }{x}^2(\mathrm{\Delta }\tau )\rangle =2D\mathrm{\Delta }\tau ,$$ (3)

where D is the translational diffusion coefficient of the microsphere in the medium. This normal diffusion is known as Brownian motion, and when this scaling does not hold, the diffusion is termed anomalous or non-Brownian²⁸, and the mean squared displacement is generally expressed as an arbitrary, monotonically increasing function of the lag time, often assigned a power-law form as

$$\langle \mathrm{\Delta }{x}^2(\mathrm{\Delta }\tau )\rangle =2D_{\alpha }\mathrm{\Delta }{\tau }^{\alpha },$$ (4)

where D_α is a generalized diffusion coefficient²⁹. When α < 1, the motion of the particle is subdiffusive, and when α > 1, the motion is superdiffusive²⁸. Although in general the functional form of the MSD varies with lag time, the approximately power-law nature of our experimental data allowed a single characteristic anomalous diffusion exponent α and generalized diffusion coefficient D_α to be defined by fitting Eq. (4) to the MSD data for lag times 0.1 ≤ Δτ ≤ 2 s.

Anomalous diffusive motion is encountered in a wide range of fields³⁰, from particle diffusion in biological gels²⁰ to transport in semi-conductors³¹. The underlying mechanisms leading to these deviations from normal Brownian motion are system-specific, but generally arise in conjunction with anomalies in one or both of the following: (i) the distribution of waiting times between steps and (ii) the distribution P(Δx, Δτ) of step sizes Δx at a given lag time Δτ (known as the van Hove distribution function)^29,32. Anomalies in both distributions have been observed in a number of experimental systems including the diffusion of probe particles in F-actin gels³³ and the motion of potassium channels in cell plasma membranes³⁴ for the former case (i), and the diffusion of colloidal beads on lipid tubes³⁵ as well as particle dynamics in random-energy landscape³⁶ for the latter case (ii). In the present study, we focus our attention on van Hove correlations as a tool with which to study subdiffusion. In particular, the onedimensional step size distribution for a random walk at a given lag time Δτ is a Gaussian distribution about a displacement Δx = 0²⁹

$$P(\mathrm{\Delta }x,\mathrm{\Delta }\tau )=\frac{1}{\sqrt{4\pi D\mathrm{\Delta }\tau }}\text{exp}\left(-\frac{\mathrm{\Delta }{x}^2}{4D\mathrm{\Delta }\tau }\right),$$ (5)

where, as before, D is the diffusion coefficient of the walker in the medium. For a Gaussian distribution, the kurtosis (or ratio of the 4^th moment to the 2^nd moment of the distribution) is calculated to be

$$\beta =\frac{\langle \mathrm{\Delta }{x}^4\rangle }{{\langle \mathrm{\Delta }{x}^2\rangle }^2}=3,$$ (6)

and hence following Evers et al.³⁶, we can define a suitable non-Gaussian parameter κ as

$$\kappa =\frac{\langle \mathrm{\Delta }{x}^4\rangle }{3{\langle \mathrm{\Delta }{x}^2\rangle }^2}-1.$$ (7)

For a normal Brownian motion, we expect |κ| ≪ 1. Deviations from this expression are frequently attributed to heterogeneity of the surrounding medium³⁶, and have been observed using SPT in several systems including Laponite clay dispersions³⁷ and colloidal gels³⁸.

In the section to follow, we study the microscopic and macroscopic rheology of the mucin gels in response to imposed environmental perturbations using these methods of analysis. All reported microrheological data reflect the average of two or three experimental replicates. For clarity, error bars are omitted from the van Hove distributions, but the magnitude of the statistical uncertainty is conveyed in the reported value of the non-Gaussian parameter κ.

3 Results and Discussion

3.1 Effect of pH and salt concentration on rheology of MUC5AC gels

3.1.1 Decreasing the pH and increasing the salt concentration at neutral pH increase MUC5AC gel macroscopic viscoelastic moduli

The macroscopic linear viscoelastic response for 10mg/mL MUC5AC gels at pH2, pH4 and pH7 is shown in Figure 2a, and for pH7 gels with salt concentrations of 0mM, 50 mM, 200 mM (near-physiologic condition³⁹) and 400 mM in Figure 2b.

Figure 2.

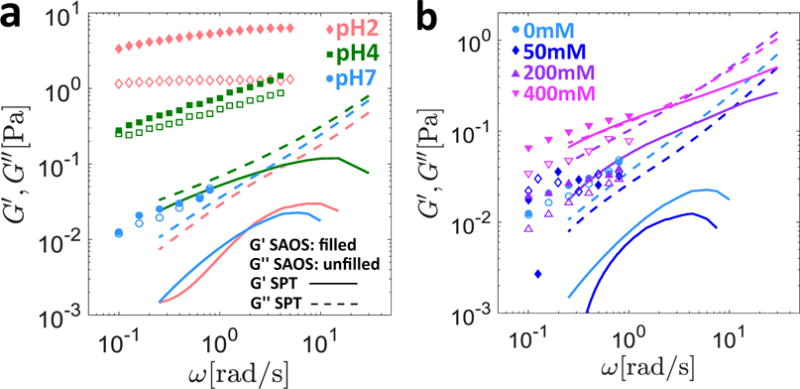
Effect of pH and salt on the rheology of 10mg/mL MUC5AC gels. The linear viscoelastic response measured macroscopically (symbols) as well as the predicted moduli from the MSD data (lines) are presented. Filled symbols and solid lines represent the elastic property G′(ω), while the hollow symbols and dashed lines represent the viscous property G″(ω). The aggregate MSD of all particle trajectories was used to calculate the viscoelastic moduli for all gels except the pH2 sample, for which only the MSD of a specific subset of ‘exponential’ particles (see text for details) was used. In (a) the pH is varied with no added salt, and data is presented at pH2, pH4, and pH7. In (b), the pH is maintained at pH7 and data is presented for salt concentrations of 0 mM, 50 mM, 200 mM and 400 mM.

Consistent with previous findings⁸, as seen in Figure 2a, both the storage (G′) and loss (G″) moduli measured rheometrically increase uniformly as the pH is decreased. In particular, at pH7 the close agreement between G′ and G″ resembles sticky Rouse relaxation of an unentangled reversible gel⁴⁰. As the pH is decreased, the response of the MUC5AC gels becomes increasingly solid-like as seen by the relative increase of the storage modulus compared to the loss modulus, which is suggestive of additional crosslinks with longer lifetimes under acidic conditions. Although the data in Figure 2b is somewhat noisier (due to the low torque values exerted by these very soft gels) we observe an increase in both the storage and loss moduli of the MUC5AC gels as the salt concentration is increased to 400 mM.

From a biochemical perspective, at pH7 the carboxylate side groups of the amino acid backbone are largely deprotonated, and correspondingly the mucin chains possess a net negative charge. Under these conditions, the conformation of the mucin molecules is random coil-like, as estimated by Cao et al.⁴¹ by fitting a theoretical formulation for the friction coefficient of a worm-like chain⁴² to dynamic light scattering data. Further, the zwitterionic mucin molecules are stabilized by electrostatic interactions known as salt bridges between oppositely charged residues on the globular, non-glycosylated portions of the polymer backbone^2,43. These salt bridges maintain the flexible hydrophobic regions of the mucin chains (indicated schematically as gray and yellow loops between the red bottle-brush like segments of the polymer in Figure 1a) in folded conformations, thus sequestering them to the interior of the molecules². Upon lowering the pH of the system to pH2, the carboxylate groups of the negatively charged amino acid residues (such as aspartic and glutamic acid) become protonated, resulting in destruction of the salt bridges and a subsequent unfolding of the mucin chains². This unfolding is thought to expose additional moieties including hydrophobic sites within each mucin chain that were previously hidden², permitting phase separation of these near neutrally charged molecules into mucin-rich domains maintained by hydrophobic interactions and diminished electrostatic repulsion⁴⁴. A schematic depicting this transition for the case of mucin gels in response to an acidic pH environment is depicted in Figures 3a and 3b, with the location of the additional interaction sites indicated by yellow triangles.

Figure 3.

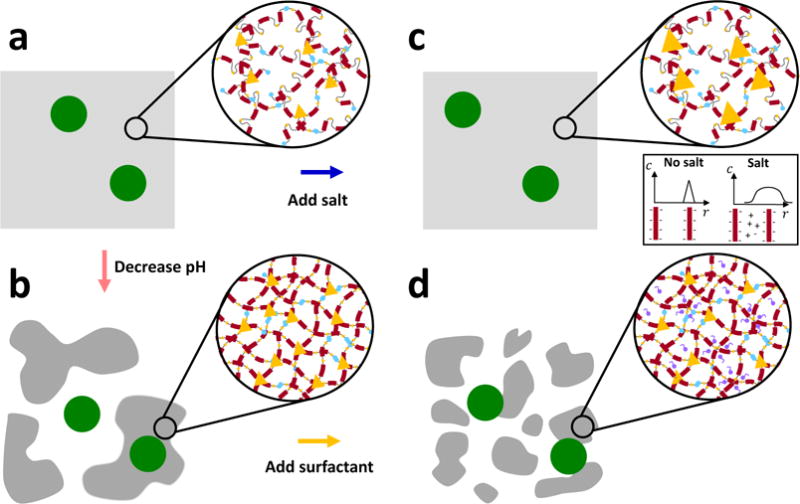
Schematic illustration of the proposed effects of the various environmental modifications on the supramolecular structure of the mucin network. The mesoscopic porous structure of the mucin gels is represented by the gray regions and the diffusing probe particles are shown by large green circles. At neutral pH (a), the mucin molecules possess a net negative charge and are semi-flexible. Under acidic conditions (b), the protonated mucin molecules possess a nearly neutral net charge, and stiffen via breaking of salt bridges, exposing additional moieties including hydrophobic domains which associate to form additional crosslinks (shown by yellow triangles). Collectively, this induces local mesoscopic phase separation into mucin-rich and mucin-poor regions. When salt is added at neutral pH (c), the screening of electrostatic interactions reduces the degree of repulsion between the sugar side chains which permits stronger and longer-lived associations between mucin molecules (indicated schematically by the increased size of the yellow triangles). Finally, when surfactant is added under acidic conditions (d), the hydrophobic domains are out-competed by the small surfactant molecules, which loosens and disrupts the aggregates in the mucin-rich regions prompting the return towards a single phase.

The net negative charge of the mucin molecules at pH7 suggests that under neutral pH conditions, increasing the ionic strength through the addition of NaCl (which screens electrostatic interactions between the mucin chains by lowering the Debye length³⁹) should be an effective means with which to modify the viscoelastic network. For polyampholytic molecules such as mucin, the addition of salt can either increase or decrease the viscosity or viscoelastic moduli of the gel depending on the environmental pH and corresponding charge-state of the molecule^45,46. In general, however, the screening of electrostatic interactions at the intra-molecular level should result in a decrease in the persistence length of the mucin chains and hence a reduction in their bending rigidity. At the inter-molecular level, the presence of salt decreases the strength of repulsive forces between the negatively charged sugar side chains, which allows for stronger and potentially longer lived associative interactions between mucin molecucles. These structural changes are depicted schematically in Figures 3a and 3c by the increased size of the yellow triangles which symbolically represent the reversible interactions.

3.1.2 Modulation of pH and salt concentration alters MUC5AC gel viscoelasticity through different microstructural mechanisms

The biochemical changes to the mucin gels described above suggest that fundamentally different structural rearrangement may occur in response to a change in the pH level or salt concentration. To verify this, we performed single particle tracking on the same gels, and in Figures 4a and 4b the mean squared displacement (MSD) as a function of lag time is presented for the various pH levels and salt concentrations, respectively. As seen in Figure 4a, when the pH is initially lowered from pH7 to pH4, the motion of the particles becomes increasingly confined, with the anomalous diffusion exponent decreasing from α = 0.85 ± 0.17 at pH7 to α = 0.61 ± 0.08 at pH4. As the pH is further decreased to pH2, however, the anomalous diffusion exponent appears to increase to α = 0.92 ±0.49. At neutral pH, the particle mobility initially increases slightly at 50 mM NaCl as seen in Figure 4b, but the overall effect of salt addition is to decrease the anomalous diffusion exponent nearly monotonically from α = 0.85 ± 0.17 at 0mM NaCl, to α = 0.86 ± 0.27 at 50 mM NaCl, α = 0.70 ± 0.05 at 200 mM NaCl, and α = 0.51 ± 0.18 at 400 mM NaCl.

Figure 4.

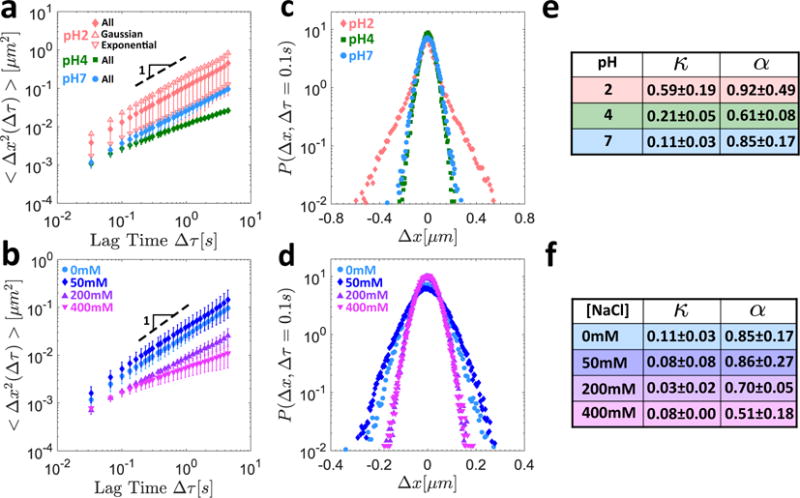
Microrheological response of 10mg/mL MUC5AC gels to pH variations at zero salt concentration (a,c,e) and salt addition at neutral pH (b,d,f). The MSD as a function of the lag time is shown at different pH levels in (a) and for different salt concentrations at neutral pH in (b). The MSD is that of the aggregate particle populations for all gels. In addition, the individual MSDs corresponding to just the Gaussian and just the exponential particle populations are shown for the pH2 gel, with the error bars omitted for clarity. The van Hove correlations for the aggregate particle populations are shown at different pH levels in (c) and at different salt concentrations in (d). Summary tables of the non-Gaussian parameters κ and the anomalous diffusion exponents α are presented for the different pH levels and salt concentrations in (e) and (f), respectively.

The trend of decreasing particle mobility with increasing salt concentration is consistent with the observation of increasing MUC5AC gel viscoelastic moduli (Figure 2b). The apparent contradiction between the macroscopic determination of greatest mucin gel stiffness at pH2 and the microscopic observation of largest particle mobility under the same conditions can be partially resolved by considering the individual, time averaged MSD results for each particle (Eq. (1)) as opposed to their ensemble average (Eq. (2)). Rich et al.³⁷ define the lag-time dependent spatial heterogeneity of a medium (HR) as the quotient of the variance and squared average of the MSDs of all of the individual particle trajectories, i.e.

$$HR(\mathrm{\Delta }\tau )=\frac{\text{var}\left(\overline{\mathrm{\Delta }{x}_k^2(\mathrm{\Delta }\tau )}\right)}{{\langle \mathrm{\Delta }{x}^2(\mathrm{\Delta }\tau )\rangle }^2}.$$ (8)

At a characteristic lag time of Δτ = 0.1s, the HR for water is HR = 0.03, while the corresponding values for the MUC5AC gels are HR = 0.07 ± 0.02 at pH7, HR = 0.22 ± 0.02 at pH4, and HR = 0.64 ± 0.21 at pH2. At neutral pH, the heterogeneity ratio at all salt concentrations is low, with HR ≲ 0.1 for each gel. These results are consistent with the proposed physical mechanism of a local phase separation into mucin-rich and mucin-poor domains (Figures 3a and 3b) under acidic conditions, which would result in the observation of a heterogeneous population of slow, trapped particles and freely-diffusing fast particles. In contrast, a single particle population would be expected based on the proposed uniform biochemical response to salt (Figures 3a and 3c) in which a single gel phase is preserved. The degree of heterogeneity is also reflected in the corresponding van Hove distributions for the MUC5AC gels as seen in Figures 4c and 4d for the pH and salt conditions, respectively. It is clear in Figure 4c that the shape of the distribution at pH2 deviates significantly from the expected parabolic profile (on a semi-log plot) for a Gaussian distribution (e.g. at pH7), with the probability of large steps significantly greater than would be predicted for normally distributed step sizes. This deviation is also reflected in the value of the non-Gaussian parameter κ which increases from κ = 0.11 ± 0.03 at pH7 to κ = 0.21 ± 0.05 at pH4 and κ = 0.59 ± 0.19 at pH2. In contrast, as seen in Figure 4d, the step size distributions in response to increased salt concentration remain Gaussian, with κ ≲ 0.11 ± 0.03 for all of the gels. The values of κ and α for the various gels are summarized in tabular form in Figures 4e and 4f for the different values of pH and salt concentrations, respectively.

We note that in addition to affecting the charge and conformation of the mucin chains, the environmental pH and salt concentration also influence the surface charge of the carboxylated probe particles^47,48. At pH2, protonation of the carboxylate groups on the surfaces of the beads increases their zeta potential⁴⁸, rendering them less negatively charged. Further, as the concentration of salt increases, the width of the electrical double layer decreases, permitting attractive van der Waals interactions over shorter and shorter distances⁴⁷. The effect of this screening on the zeta potential ζ of the beads is unclear however. By comparing atomic force microscopy (AFM) curves with theoretical predictions of Derjaguin-Landau-Verwey-Overbeek (DLVO) theory, Assemi et al.⁴⁷ measured an increase in the zeta potential of 1μm carboxylate modified polystyrene (PS) latex beads as the concentration of NaCl was increased. Conversely, Barany et al.⁴⁸ reported a decrease in ζ of 1.43 μm carboxylated PS beads at constant pH as the concentration of KCl was increased. Nevertheless, at particle length scales ≥ 500 nm, the effect of surface functionalization such as PEGylation to reduce particle-mucus interactions has been shown to be minimal^19,49, and steric interactions between the mucin network and the beads principally determine the particle trajectories. As such, it is our expectation that the variations in probe particle diffusion that we observe under different environmental conditions are dominated by the mechanical properties of the environment that the particles experience, and that interactions with the mucin chains play only a minimal role.

3.1.3 Definition of Gaussian and exponential particle populations for heterogeneous MUC5AC gels at pH2

High levels of heterogeneity have been observed in mucin gels under strongly acidic conditions¹¹, which suggests that an ensemble average is not a suitable choice to faithfully characterize the displacement of all of the individual particles at pH2. In their studies of particle tracking in porcine respiratory mucus, Murgia et al.⁵⁰ noted that analysis of the individual time-averaged MSDs allowed for the specification of two distinct particle populations: ‘immobile particles’ (defined by these authors as those with MSD slope α < 0.5) which are trapped within the mucus, and ‘diffusive particles’ (α > 0.5) which are not trapped and consequently diffuse much more quickly. Similar observations have been reported in a number of other systems, including colloidal gels³⁸ and aqueous Laponite dispersions³⁷ near the sol-gel transition, but the sorting approach for the individual particles has generally been study-specific.

In this paper, we base our approach on the method of Gao and Kilfoil³⁸ and fit a mixed probability distribution function constructed as the weighted sum of a Gaussian and an exponential distribution to the van Hove distribution of all of the particles in a given experimental replicate at an early lag time of Δτ = 0.1 s, i.e.

$$P_{\text{fit}}(\mathrm{\Delta }x,\mathrm{\Delta }\tau )=\frac{A(\mathrm{\Delta }\tau )}{\sqrt{2\pi {\sigma }^2}}\text{exp}\left(-\frac{\mathrm{\Delta }{x}^2}{2{\sigma }^2}\right)+\frac{(1-A(\mathrm{\Delta }\tau ))}{2\lambda }\text{exp}\left(-\frac{\left|\mathrm{\Delta }x\right|}{\lambda }\right).$$ (9)

The lag time dependent weights 0 ≤ A(Δτ) ≤ 1 and (1 − A(Δτ)) signify the fraction of steps distributed normally and exponentially, respectively, and sum to unity for a normalized probability distribution. This fit is shown as the thick solid line in Figure 5a, while the van Hove distribution itself is denoted by the pink diamond symbols.

Figure 5.

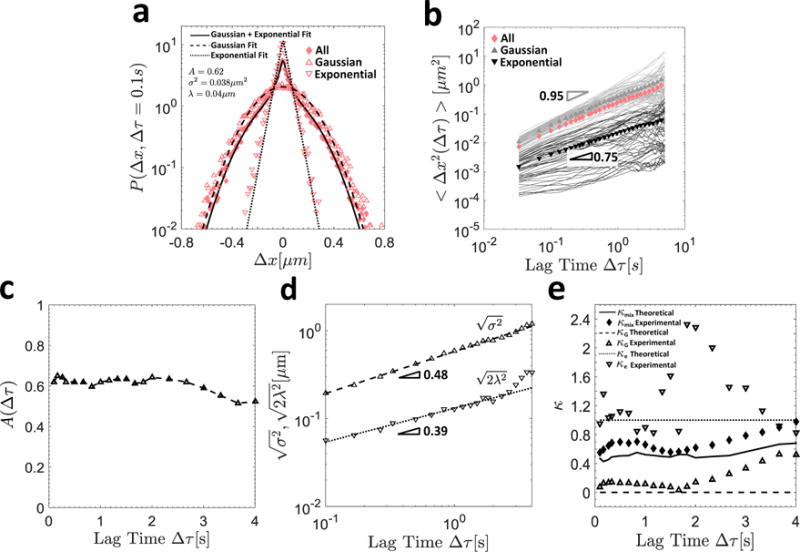
In (a), the van Hove distribution for all particles is shown by the diamond symbols, and the thick solid line indicates the composite Gaussian and exponential fit defined in Equation (9). The hollow triangles and inverted triangles denote the van Hove distributions of the Gaussian and exponential particles, respectively, and their respective Gaussian (dashed) and exponential (dotted) fits are also shown. In (b), the individual particle MSDs sorted into Gaussian (gray) and exponential (black) trajectories are shown, as well as their ensemble averages (filled symbols of the same color) and that of the aggregate population (solid pink diamonds). In (c), the fraction of Gaussian particles A(∆τ) is shown as a function of the lag time ∆τ. In (d), the characteristic Gaussian and exponential length scales $\sqrt{{\sigma }^2(\mathrm{\Delta }\tau )}$ and $\sqrt{2{\lambda }^2(\mathrm{\Delta }\tau )}$, respectively, are plotted as a function of the lag time, and the slope of the resulting power-law fit is indicated. In (e), the experimental (symbols) and theoretical (lines) values of the non-Gaussian parameters κ (Equation (7)) for the exponential (dotted lines and hollow inverted triangles), Gaussian (dashed lines and hollow triangles), and aggregate (solid lines and solid diamonds) populations are shown as a function of lag time ∆τ.

Using these fitting parameters, we can sort the particles into Gaussian and exponential subpopulations with van Hove distributions corresponding to the appropriate component of the mixed probability distribution presented in Equation (9). This sorting procedure is outlined in detail in Section S3 of the supporting information (SI).

In Figure 5b, the time averaged MSDs (given by Equation (1)) for each individual particle are shown by thin solid lines, with particles classified as Gaussian and exponential shown in gray and black respectively. Using this approach, it is clear that the ensemble average MSDs for these subpopulations (gray triangles and inverted black triangles, respectively) are far more representative of their individual constituents than the aggregate ensemble average (solid pink diamonds). Further, the average motion of the particles in these two subgroups is indeed quite distinct, with the exponential population undergoing subdiffusive motion characterized by α = 0.75, and the Gaussian population appearing to diffuse nearly normally with exponent α = 0.95 characterizing their ensemble average MSD. Indeed, these data for the Gaussian particles are quite comparable to our control results for the same size carboxylated particles diffusing in water (α_water = 0.95 and D_water = 0.41 μm²/s^α). We note that although the van Hove distribution is in general a function of the lag time, the fraction of Gaussian particles in this system remains nearly invariant up to lag times of Δτ_max = 4s, as seen in Figure 5c. This justifies our choice of performing this sorting at an early lag time Δτ = 0.1s which maximizes statistical power for the individual particle trajectories (since each trajectory contains a significantly reduced number of steps compared to the combined trajectories of the aggregate population of particles). Further, the time-independence of the fraction of Gaussian particles also implies that within our limited experimental time window (Δτ ≲ 4s), particles essentially remain exponential or Gaussian throughout the entire experiment.

To demonstrate the consequences of this statistical sorting of individual trajectories, in Figure 4a we have also shown the mean ensemble average MSDs across all experimental replicates for the Gaussian (hollow triangles) and exponential (hollow inverted triangles) particle populations as a function of lag time for the MUC5AC gels at pH2. Although the standard deviation is large between replicates in these heterogeneous gels, the MSD across all experimental replicates is again quite distinct between these two populations, with the Gaussian particles diffusing nearly normally with α = 0.95 ± 0.48, and the exponential particles undergoing subdiffusive motion characterized by α = 0.78 ± 0.35.

In addition to these differences in the ensemble average MSDs of the Gaussian and exponential particle populations, their van Hove distributions are also fundamentally distinct. In Figure 5a, these distributions are presented for the Gaussian (hollow triangles) and exponential (inverted hollow triangles) populations at a lag time of Δτ = 0.1s. The step sizes of the Gaussian particles are normally distributed with κ = 0.07, and this distribution is well fit by the unweighted Gaussian portion of the mixed probability distribution in Equation (9) shown as the dashed line in Figure 5a. Further, in Figure 5d, the characteristic Gaussian length scale $\sqrt{{\sigma }^2}$ is plotted as a function of the lag time. The nearly square root dependence of this quantity on $\mathrm{\Delta }\tau (\sqrt{{\sigma }^2}\sim \mathrm{\Delta }{\tau }^{0.48})$ is in good agreement with the near linear dependence of the MSD on Δτ previously reported for the Gaussian population (Figure 5b), and thus both metrics confirm that this population of particles is undergoing nearly regular, diffusive Brownian motion for all lag times considered.

In contrast, the step sizes of the exponential particles follow an exponential distribution with κ = 0.95, as confirmed by the goodness of fit with the dotted line indicating the unweighted exponential portion of the distribution in Equation (9). Further, the exponential length scal $\sqrt{2{\lambda }^2(\mathrm{\Delta }\tau )}$ exhibits a power-law dependence on the lag time characterized by $\sqrt{2{\lambda }^2}\sim \mathrm{\Delta }{\tau }^{0.39}$, as seen in Figure 5d. The origin of this scaling can easily be understood by considering the second moment of an exponential distribution of step sizes, i.e.

$${\langle \mathrm{\Delta }{x}^2\rangle }_{\text{exp}}={\displaystyle {\int }_{-\infty }^{+\infty }\frac{\mathrm{\Delta }{x}^2}{2\lambda (\mathrm{\Delta }\tau )}}\text{exp}\left(-\frac{\left|\mathrm{\Delta }x\right|}{\lambda (\mathrm{\Delta }\tau )}\right)d\mathrm{\Delta }x=2{\lambda }^2(\mathrm{\Delta }\tau ).$$ (10)

Hence, equating this result to the assumed power law form for the MSD in Equation (4), we obtain the result 2λ²(Δτ) ~ Δτ^α, which is in excellent agreement with our experimental values of α = 0.75 and $\sqrt{2{\lambda }^2}\sim \mathrm{\Delta }{\tau }^{0.39}$. This analytical result is also consistent with the recent experimental findings of Wang et al.³⁵ who studied the diffusion of colloidal beads along linear phospholipid bilayer tubes as well as through entangled F-actin networks. In both systems, these authors reported a square root dependence of the exponential length scale on the lag time, i.e. $\sqrt{{\lambda }^2}\sim \mathrm{\Delta }{\tau }^{1/2}$, as well as Brownian experimental MSDs (α = 1). Taken together then, the results from the present study as well as those from Wang et al.³⁵ suggest that the scaling $\sqrt{{\lambda }^2(\mathrm{\Delta }\tau )}\sim \mathrm{\Delta }{\tau }^{\alpha /2}$ may be even more general than the previously reported square root dependence³⁵, as it can also be extended to anomalous diffusive motion (α ≠ 1).

Using the definition of the non-Gaussian parameter presented in Equation (7), the theoretical value for exponentially distributed step sizes is κ_e = 1, where the 4^th moment is obtained by replacing Δx² in the integral of Equation (10) with Δx⁴. In addition, a theoretical prediction for the non-Gaussian parameter corresponding to the mixed distribution presented in Equation (9) can also be obtained in a similar fashion, resulting in the expression

$${\kappa }_{\text{mix}}=\frac{A+8(1-A){(\lambda /\sigma )}^4}{{(A+2(1-A){(\lambda /\sigma )}^2)}^2}-1.$$ (11)

In Figure 5e, the theoretical (lines) and experimental (symbols) values of κ for the Gaussian population (with theoretical value κ_G = 0, dashed lines and hollow triangles) and exponential population (with theoretical value κ_e = 1, dotted lines and inverted hollow triangles) are presented as a function of the lag time. In addition, κ for the aggregate population (solid lines and diamonds) is shown, with κ_mix from Equation (11) calculated using the fitted values of A, σ², and λ from Equation (9) at each lag time Δτ. The theoretical predictions and experimental values and are found to be in good agreement. Further, as with the fraction of Gaussian particles (shown in Figure 5c), these quantities are found to be nearly invariant with lag time, although the fluctuations increase in magnitude at larger values of Δτ where there are fewer total steps over which to calculate these statistical measures.

3.1.4 Comparison of mechanical response predicted by thermal fluctuations and macrorheology

As a final consideration for this section, we note that in their studies of F-actin gels, Wong et al.³³ have observed a similar distinction between diffusive and confined particles, and have shown that bulk linear viscoelastic data can be recovered from the study of thermal fluctuations using the well-known result

$$G(s)=\frac{d{k}_{B}T}{3\pi as\langle \mathrm{\Delta }{x}^2(s)\rangle }$$ (12)

from Mason and Weitz¹⁸ when only the confined or ‘slow’ particles are considered. In Equation (12), s is the Laplace variable, G(s) is the Laplace transform of the relaxation modulus, 〈Δx²(s)〉 is the Laplace transform of the MSD, d is the dimensionality of the MSD data, a is the particle radius, k_B is Boltzmann’s constant, and T is the absolute temperature. Consequently, in Figure 2a, we also plot the storage (solid line) and loss (dashed line) moduli predicted from Equation (12) for just the exponential particles at pH2, as well as the same results from the aggregate populations for pH4 and pH7. However, consistent with the findings in Bansil et al.¹¹, even with this separation into Gaussian and exponential populations, there is a significant discrepancy between the macroscopic and microscopic linear viscoelasticity, and this difference increases in magnitude as the pH is lowered. This mismatch suggests that the exponential population of particles do not sample the entire range of microenvironments in the gel, and/or that the mucin molecules and probe particles interact in additional ways that are not considered in the theoretical framework used to derive Equation (12)¹⁸. One possible explanation may be that the viscoelastic moduli measured macroscopically are dominated by the mechanical properties of the stiffest portions of the mucin-dense phase. At the microscopic scale, it is possible that the tracer particles are unable to penetrate these stiffest regions, and as such the exponential particles only probe the softer portions of the heterogeneous mucin-dense phase, while the Gaussian particles diffuse quite freely in the mucin-poor parts of the gel.

The limited electrostatic interaction expected between the negatively charged tracer particles and the negatively charged, flexible mucins at pH7 as well as the presence of a single gel phase suggest that improved agreement between the microscopic and macroscopic rheology should be observed upon salt addition. Indeed, as seen in Figure 2b, although the SPT prediction underestimates the macroscopic viscoelastic moduli at the two lowest salt concentrations, reasonably good agreement between the two methods is recovered for the 200 mM and 400 mM gels. The disagreement observed at the two lowest salt concentrations suggests that a certain degree of heterogeneity may still be present at pH7. However, the low value of the heterogeneity ratio for all salt concentrations (HR ≲ 0.1) suggests that at neutral pH, the mucin gel does not appear to be heterogeneous to the particles: any stiff mucin-rich regions that may influence the macroscopic rheology are highly localized and impenetrable to the micron sized probes. At large salt concentrations, the near complete screening of intermolecular interactions may eliminate these microscopic heterogeneities, resulting in the observed agreement between the macroscopic and microscopic rheological measurements. Altogether then, these results are suggestive of increasingly viscoelastic yet homogeneous gels at neutral pH as salt is added. This is verified by the measured increase in the macrosopic viscoelastic moduli of the gels as well as the decreasingly Brownian (or increasingly subdiffusive) motion of the tracer particles, while homogeneity is inferred from the Gaussian step size distributions of these particles at all salt concentrations investigated.

3.2 Effect of surfactant on rheology of MUC5AC gels

Ribbeck and Gorlich have shown that the mild detergent trans-cyclohexane-1,2-diol can be used to interfere with hydrophobic interactions in the nuclear pore complexes (NPCs) of eukaryotic cells, reversibly eliminating their selectivity towards specific classes of molecules²³. Motivated by this, we hypothesized that adding a similar non-ionic surfactant molecule also composed of an ethylene glycol polar group and an apolar butylene moiety²³, 1,2-hexanediol, to the MUC5AC gels at low pH would have the effect of disrupting the hydrophobic crosslinks and decreasing the viscoelastic moduli of the gels through a third and distinct structural rearrangement mechanism. This experiment was carried out under acidic conditions as a result of the increased number of hydrophobic interaction sites that have been measured using fluorescent probes by Cao et al. in MUC5AC gels at pH2 compared to pH7⁴¹, consistent with the biochemical pictures presented in Figures 3a and 3b.

In Figure 6a, the macroscopic SAOS results for surfactant addition to 10 mg/ml MUC5AC gels at pH2 are reported, and a monotonic decrease in the storage and loss moduli above a critical concentration of c* ≈ 10 wt % is observed. At the microscopic level, a first effect of surfactant addition is to decrease the heterogeneity of the particle trajectories (as captured by the value of the heterogeneity ratio at Δτ = 0.1 s reported in Figure 6b) from a value of HR = 0.64 ± 0.21 at 0 wt % of added surfactant to HR = 0.60 ± 0.49 at 5 wt %, HR = 0.36 ± 0.10 at 10 wt %, and HR = 0.10 ± 0.07 at 20 wt % hexanediol. This trend is also reflected in the shapes of the step size distributions (presented in Figure 6c) and the associated non-Gaussian parameters, which decrease close to monotonically from κ = 0.59 ± 0.19 for no added surfactant to a near Gaussian value of κ = 0.11 ± 0.09 at 20 wt % hexanediol.

Figure 6.

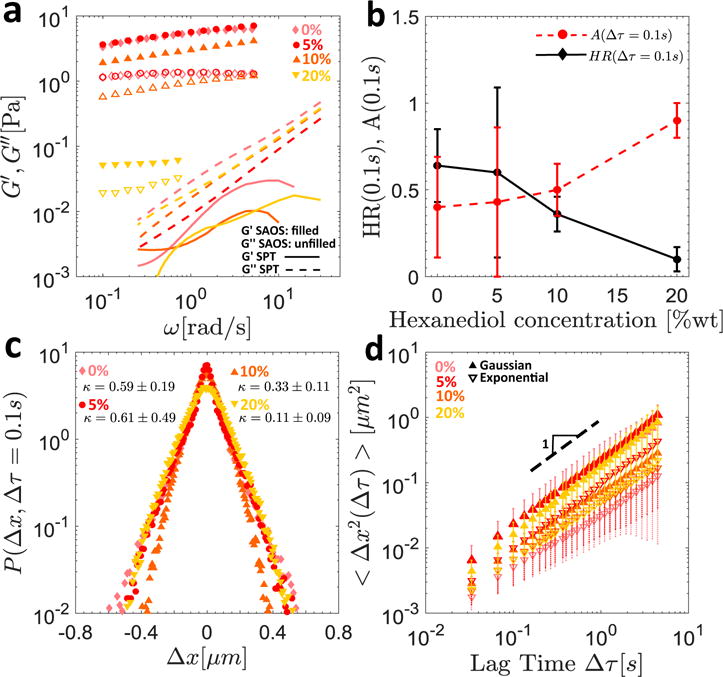
The effect of added surfactant on the rheology of 10 mg/ml MUC5AC gels at pH2. In (a), the SAOS results for the pH2 gels with 0 wt %, 5 wt %, 10 wt %, and 20 wt % hexanediol are shown for the macrorheological measurements (symbols) and the SPT predictions (lines) based on the MSDs of the exponential particle populations. In (b), the heterogeneity ratio HR(∆τ) (black diamonds and solid lines) and fraction of Gaussian particles A(∆τ) (red circles and dashed lines) at a lag time of ∆τ = 0:1 s are shown as a function of hexanediol concentration, and in (c), the van Hove distributions and associated non-Gaussian parameters κ are presented for all surfactant concentrations. In (d), the MSDs evaluated from SPT for the exponential (hollow inverted triangles and dashed error bars), and Gaussian (filled triangles and solid error bars) populations, as sorted at a lag time of ∆τ = 0:1 s, are plotted as a function of lag time for the same gels.

Further, by applying the sorting algorithm outlined in Section 3.1.3 at the characteristic early lag time of Δτ = 0.1 s, the trajectory statistics and MSDs can once again be analyzed using two distinct subgroups consisting of Gaussian and exponential particles. With the exception of the 10 wt % hexanediol gel, the anomalous diffusion exponents α associated with the Gaussian populations remain approximately constant at the Brownian exponent α = 1. Further, as seen in Figure 6b, the fraction of Gaussian particles A(Δτ = 0.1 s) increases nearly uniformly as a function of surfactant concentration, from A = 0.40 ± 0.29 with no added surfactant to A = 0.90 ± 0.10 at 20 wt % hexanediol. It is clear then that at this highest surfactant concentration, a nearly single or aggregate population undergoing normal Brownian motion is regained, as evidenced from the values of A, κ, and α. We note that it is more difficult to discern a clear trend in the values of α associated with the exponential populations, which vary from α = 0.78 ± 0.35 at 0 wt % of added surfactant to α = 1.00 ± 0.49 at 5 wt %, α = 0.86 ± 0.22 at 10 wt %, and α = 0.91 at 20 wt % hexanediol. However, the generally subdiffusive motion implied by these results is consistent with the biochemical picture for this subpopulation of less mobile particles confined to the mucin-rich phases of the gel.

Piculell et al.⁵¹ have reviewed existing experimental data on the effect of surfactant addition to solutions of polymers containing hydrophobic groups, and have found that above a threshold surfactant concentration, the viscosity of the solution generally decreases with added surfactant. For certain polymer/surfactant combinations, this threshold concentration curiously corresponds to the critical micelle concentration (CMC) of the surfactant in the polymer-free solution, while in other cases, in particular for charged systems, this decrease in viscosity occurs at a lower surfactant concentration known as the critical aggregation concentration (CAC)⁵¹. The mechanism behind this observed decrease in viscosity has been attributed to associations between surfactant complexes and the polymer molecules, which crowd out the hydrophobic sites within the network and disrupt the crosslinks that previously held it together⁵¹. This phenomenon has also been observed and clearly illustrated in schematic form by Kjøniksen et al. in their studies of chitosan⁵².

The expected effect of disrupting the hydrophobic interactions between individual mucin molecules using surfactant molecules at concentrations greater than the CAC is to loosen the mucin-rich phase of the gel, eventually returning it to a single phase. Macroscopically, as seen in our rheological data in Figure 6a, this manifests as a monotonic decrease in the elastic modulus of the gel for surfactant concentrations above the CAC of 1,2-hexanediol and MUC5AC. Although quantitative measures of the CAC are often difficult to obtain as a result of the uncertainty associated with the structure of the surfactant/polymer complexes that form in solution, it is generally smaller than the CMC of the surfactant in polymer-free solution⁵¹, which has been measured by Hajji et al. to be CMC= 8.9 wt % for 1,2-hexanediol⁵³. Additionally, this physical picture of gradually loosening mucin-rich domains and elimination of the largest pores created by the pH-induced mesoscopic phase separation as the surfactant molecules crowd out the hydrophobic sites (Figure 3d) is also consistent with our observations at the microscopic level. As surfactant is added, the heterogeneity ratio is observed to decrease as the hydrophobic crosslinks maintaining the mucin dense regions are disrupted, until a single population (A = 0.9 ± 0.1) undergoing nearly Brownian motion, as confirmed by the slope of the MSD (α = 1.04 ± 0.37) as well as the value of the non-Gaussian parameter (κ = 0.11 ±0.09), is observed at 20 wt % hexanediol. Despite this apparent return to homogeneity on the microscopic level as the concentration of surfactant is increased, the viscoelastic moduli predicted from thermal fluctuations of the exponential particles still disagree with those measured macroscopically for all hexanediol concentrations as seen in Figure 6a. This suggests that our explanation proposed previously of the tracer particles being unable to penetrate the densest local mucin regions which dominate the macrorheology may still be in effect despite the progressive elimination of hydrophobic crosslinks upon surfactant addition.

4 Conclusion

In summary, we have analyzed the effect of pH, added salt, and surfactant on the macroscopic and microscopic rheological response of 10 mg/ml MUC5AC gels in order to gain additional insight into the structure and associative dynamics of mucin gels. The values of the viscoelastic moduli we measure macroscopically using cone-and-plate rheometry are largest at pH2, and the greatest degree of heterogeneity within the trajectories of the tracer particles is also observed at this pH, as measured by both the heterogeneity ratio (HR) and the non-Gaussian parameter (κ). Through the introduction of a novel sorting method, we have shown that, on average, the Gaussian particles diffuse nearly normally, but with a diffusion coefficient approximately 4 times smaller than that in water. By contrast, the exponential step size distribution of the trapped anomalously diffusing particles, with distribution width increasing as a power law of the lag time $(\sqrt{{\lambda }^2(\mathrm{\Delta }\tau )}\sim \mathrm{\Delta }{\tau }^{\alpha /2})$, is suggestive of interactions between the particles and the mucin molecules and/or geometric confinement.

Our combined observations on both length scales are suggestive of mesoscopic phase separation, which may simultaneously increase the overall elastic modulus of the gel as well as the heterogeneity of the measured MSDs of the embedded tracer particles through the creation of mucin-rich regions as well as mucin-poor ones through which some particles can easily diffuse. From a biophysical perspective, these findings are consistent with previous work which has shown that under acidic conditions, additional hydrophobic interaction sites are exposed on mucin chains as salt bridges are destroyed, which creates additional interaction points within the network that can promote and maintain the coexistence of two phases within the mucin gel^2,41,44. This hypothesis is further supported by the rheological changes that are induced by the addition of hexanediol. On the macroscopic level, the addition of surfactant had the effect of softening the mucin gels for surfactant concentrations greater than the CAC, while microscopically this resulted in a systematic decrease in the measured heterogeneity of individual tracer particle trajectories. Both findings are consistent with the excess of small surfactant molecules outcompeting and disrupting the hydrophobic interactions responsible for maintaining the mucin-rich regions, thus gradually loosening the network in these domains and shrinking the mucin-poor regions.

Finally on the macroscopic scale, the addition of salt to the pH-neutral MUC5AC gels had the effect of increasing the viscoelastic moduli as was also observed by decreasing the pH. Mechanistically, however, this stiffening was shown to arise from a fundamentally different structural mechanism. On the microscopic scale, increasing the salt concentration had the effect of decreasing the anomalous diffusion exponent α while maintaining homogeneous particle trajectories and Gaussian step size distributions. These observations are consistent with the presence of stronger, longer lived interactions between mucin molecules due to reduced electrostatic repulsion between the sugar side chains in the presence of salt, as well as a homogeneous gel structure with a characteristic mesh size significantly smaller than the one-micron diameter probe particles.

Importantly, although analysis of microscopic thermal fluctuations in mucin gels using the standard analysis developed for homogeneous complex fluids¹⁸ was shown to not be predictive of their macroscopic linear viscoelastic response (particularly for the mucin gels prepared under acidic conditions), the analysis we have outlined clearly demonstrates that the combination of microscopic and macroscopic rheological measurements provides complementary information that aids in explaining the complex viscoelastic response observed in these physiologically-important hydrogels. Ultimately, while our understanding of this system is far from complete, we expect that improved insight into the structure of mucin networks and unraveling the principal interaction mechanisms at play will be particularly important for understanding how the rheo-mechanical properties of mucus hydrogels are altered by a number of environmental factors in the context of both regular physiologic function as well as by pathological and therapeutic agents.