BranchAnalysis2D/3D Automates Morphometry Analyses of Branching Structures

Abstract

Background

Morphometric analyses of biological features have become increasingly common in recent years with such analyses being subject to a large degree of observer bias, variability, and time consumption. While commercial software packages exist to perform these analyses, they are expensive, require extensive user training, and are usually dependent on the observer tracing the morphology.

New Method

To address these issues, we have developed a broadly applicable, no-cost ImageJ plugin we call ‘BranchAnalysis2D/3D’, to perform morphometric analyses of structures with branching morphologies, such as neuronal dendritic spines, vascular morphology, and primary cilia.

Results

Our BranchAnalysis2D/3D algorithm allows for rapid quantification of the length and thickness of branching morphologies, independent of user tracing, in both 2D and 3D data sets.

Comparison with Existing Methods

We validated the performance of BranchAnalysis2D/3D against pre-existing software packages using trained human observers and images from brain and retina. We found that the BranchAnalysis2D/3D algorithm outputs results similar to available software (i.e., Metamorph, AngioTool, Neurolucida), while allowing faster analysis times and unbiased quantification.

Conclusions

BranchAnalysis2D/3D allows inexperienced observers to output results like a trained observer but more efficiently, thereby increasing the consistency, speed, and reliability of morphometric analyses.

Introduction

Morphological features of biological surfaces are studied for data interpretation in several research fields. The process is generally performed by trained observers using stereological counting techniques, and thus is subject to intra- and inter-observer variability. Some commercial software packages exist to aid researchers in performing these analyses (e.g., Neurolucida, Imaris, Metamorph), but these packages are often expensive, require tracing of the contours of the surface being analyzed, and require extensive user training prior to use (Dickstein et al., 2001; Srivastava et al., 2011; Swanger et al., 2011). Open-source alternatives to commercial packages (i.e., AngioTool) are easier to use but only analyze one specific type of data (i.e., vasculature), often require user tracing of contours of the surfaces of interest, and only function in 2D images (Zudaire et al., 2011). Morphometric analyses are now often routinely performed on both 2D and 3D data sets, and the lack of 3D functionality severely limits the applicability of open-source software packages. As plugins have been developed previously for Fiji ImageJ (Schindelin et al., 2012), such as AnalyzeSkeleton 2D/3D and Local Thickness which function in both 2D and 3D data sets (Arganda-Carreras et al., 2010; Dougherty and Kunzelmann, 2007), we developed an open-source algorithm capable of performing morphometric analyses of both 2D and 3D images with minimal user interaction. We validated our algorithm using images of Golgi-Cox stained brain slices (for spine visualization) in 2D and 3D data images, maximum intensity projections of brain tissue immunolabeled for primary cilia, and images of retinal vasculature. Together, these analyses show both the precision and efficiency of the algorithm, as compared to semi-automated analyses, when utilizing multiple test models with branching morphologies.

Materials and Methods

All experimental protocols were performed with approval from the Institutional Animal Care and Use Committees of Albany Medical College, Harvard Medical School, and Beth Israel Deaconess Medical Center, and complied with the National Institutes of Health Guide for the Care and Use of Laboratory Animals.

Explanation of the Branch Measure Computations

ImageJ currently supports methods of calculating the medial axis transform, local thickness, and longest-shortest path, but does not combine all three processes. A user must manually correlate the output of the three processes in a time intensive and error prone process. We have adapted the underlying mathematics of the three currently existing algorithms and rewritten them to ensure their combined functionality in a new algorithm we call BranchAnalysis2D/3D.

Here, we provide a condensed explanation of the important mathematics utilized to write each of the steps of BranchAnalysis2D/3D. A brief explanation of the following steps is presented in Figure 1 and Tables 1 and 2 with explanations in the legend. A ‘thresholded’ image input is loaded into BranchAnalysis2D/3D and is first subjected to a medial axis transform giving a skeleton representation of the original input image (Lee et al., 1994). We have adapted the mathematics they present for use in ImageJ. The accuracy of this method depends on the resolution of the image acquisition system, and the derived transform will have a stochastic error corresponding to the dimension of one pixel. This medial axis transformed image (Fig. 1A, C) is then analyzed to determine branch points (defined as having more than two neighboring points) and end points (defined as having only one neighboring point).

Figure 1. Schematic of the Algorithm Workflow.

A simplified explanation of the algorithm workflow is presented above. The user manually pre-processes the input image into a ‘thresholded’ binary image. This binary image is then used as the input to BranchAnalysis2D/3D which then returns the results of the analysis (termed output). The output shows the original image (A) followed by the ‘thresholded’ binary image (B). The optimal skeleton is presented in white (C) and is overlaid on the original image (D). The local thickness is shown as a heat map with darker colors corresponding to smaller local thicknesses (E), and an overlay of the local thickness onto the original image (F). The tagged skeleton is also shown with branch points labeled in purple (G). The main dendritic shaft as calculated by the algorithm is shown in red (H), and all spines as calculated by the algorithm are shown in red (I). Overlaid images are not shown by the algorithm, but are presented here to allow for visual confirmation of the results.

Table 1. Example algorithm output of dendritic shaft analysis.

The sample output from the longest-shortest path calculation is presented below. Analysis was performed on the input image presented in Figure 1. (Spx, Spy, Spz) is the (x,y,z) position of the starting voxel of the longest-shortest path.

# Branches	# Junctions	# End-Points	# Junction Voxels	# Slab Voxels	Average Branch Length (μm)	# Triple Points
50	24	27	82	658	1.726	23
# Quadruple Points	Maximum Branch Length (μm)	Longest Shortest Path (μm)	Spx	Spy	Spz
1	5.258	48.423	16.679	1.627	0

Table 2. Example algorithm output of dendritic branch/spine analysis.

Calculations of maximum thickness, average thickness, and classification as a spine are not currently supported in ImageJ. Analysis was performed on the input image presented in Figure 1. (V1x, V1y, V1z) and (V2x, V2y, V2z) is the (x,y,z) position of the starting and ending voxel of each branch, respectively.

	Skeleton ID	Branch length (μm)	V1x	V1y	V1z	V2x	V2y	V2z	Euclidean distance (μm)	Running avg. length (μm)	Max. thickness (μm)	Avg. thickness (μm)	Spine	Avg. intensity
1	1	5.402	10.48	9.46	0	13.53	5.80	0	4.766	4.787	7.81	6.588	0	255
2	1	4.107	0.20	37.02	0	1.63	33.56	0	3.739	3.857	9.849	6.498	0	255
3	1	3.676	3.36	28.17	0	4.37	24.92	0	3.41	3.131	12.207	7.817	0	255
4	1	3.479	8.75	17.39	0	11.09	15.36	0	3.1	3.039	8.246	7.123	0	255
5	1	3.402	4.37	24.92	0	6.41	22.48	0	3.177	3.118	11.18	7.359	0	255
6	1	3.142	14.14	2.85	0	15.56	0.71	0	2.567	2.654	9.434	7.211	0	255
7	1	2.957	5.70	27.87	0	3.36	28.17	0	2.359	2.836	12.166	5.801	1	255
8	1	2.483	6.31	20.04	0	6.41	22.48	0	2.443	2.237	11.18	8.531	0	255
9	1	2.455	8.95	20.85	0	7.63	19.12	0	2.176	2.233	9	5.945	1	255
10	1	2.406	2.44	32.24	0	2.85	30.00	0	2.274	2.063	15.033	12.201	0	255
11	1	2.406	4.68	32.65	0	2.44	32.24	0	2.274	2.293	9	5.03	1	255
12	1	2.269	8.34	23.09	0	6.41	22.48	0	2.026	2.105	11.402	7.307	1	255
13	1	2.269	16.07	4.58	0	14.14	3.76	0	2.097	2.072	6.325	3.348	1	255
14	1	2.262	2.24	24.82	0	4.37	24.92	0	2.138	2.16	9.487	4.919	1	255
15	1	2.066	13.22	11.19	0	11.49	11.80	0	1.833	1.975	8.246	3.656	1	255
16	1	2.041	2.85	30.00	0	3.36	28.17	0	1.9	1.68	15.033	12.291	0	255
17	1	2.031	3.15	34.78	0	1.63	33.56	0	1.954	1.93	9.849	4.988	1	255
18	1	2.017	4.58	20.44	0	6.31	20.04	0	1.776	1.94	7.81	3.663	1	255
19	1	2.006	1.73	27.66	0	3.36	28.17	0	1.705	1.894	12	6.023	1	255
20	1	1.999	11.09	15.36	0	11.49	13.53	0	1.875	1.686	9.22	8.32	0	255
21	1	1.971	4.17	31.43	0	2.85	30.00	0	1.943	1.889	15.033	7.776	1	255
22	1	1.94	7.63	19.12	0	8.14	17.39	0	1.802	1.572	9.055	8.385	0	255
23	1	1.922	10.37	18.10	0	8.75	17.39	0	1.776	1.791	8.246	3.629	1	255
24	1	1.922	12.61	3.46	0	13.42	4.78	0	1.552	1.698	7.28	4.612	1	255
25	1	1.82	6.31	20.04	0	7.63	19.12	0	1.608	1.444	9	8.072	0	255
26	1	1.659	1.63	33.56	0	2.44	32.24	0	1.552	1.278	9.849	7.833	0	255
27	1	1.617	9.76	12.81	0	11.09	12.31	0	1.417	1.485	12	7.197	1	255
28	1	1.55	10.88	10.48	0	11.19	11.90	0	1.456	1.23	10.296	7.49	0	255
29	1	1.414	14.44	0	0	15.56	0.71	0	1.326	1.301	9.434	5.047	1	255
30	1	1.389	11.09	12.31	0	11.49	13.53	0	1.286	1.034	11.705	8.876	0	255
31	1	1.389	9.26	9.05	0	10.48	9.46	0	1.286	1.274	7.071	4.612	1	255
32	1	1.371	13.42	4.78	0	14.14	3.76	0	1.241	1.117	7.616	6.797	0	255
33	1	1.21	16.68	1.62	0	16.37	0.71	0	0.965	1.084	8	4.658	0	255
34	1	1.203	17.49	0.71	0	16.37	0.71	0	1.119	1.135	8.485	5.605	1	255
35	1	1.186	10.48	9.46	0	10.88	10.48	0	1.095	0.89	7.071	5.719	0	255
36	1	1.168	7.53	16.48	0	8.14	17.39	0	1.1	1.048	8	4.524	1	255
37	1	1.101	12.51	13.73	0	11.50	13.53	0	1.037	1.066	8.944	5.844	1	255
38	1	1	14.14	2.85	0	14.14	3.76	0	0.915	0.754	7.28	6.834	0	255
39	1	0.957	12.41	5.49	0	13.32	5.39	0	0.921	0.921	7.071	4.307	1	255
40	1	0.898	11.70	10.27	0	10.88	10.48	0	0.839	0.823	6.325	4.574	1	255
41	1	0.88	12.20	12.20	0	11.49	11.80	0	0.82	0.799	8.246	6.227	1	255
42	1	0.814	15.56	0.71	0	16.37	0.71	0	0.814	0.61	10	8.833	0	255
43	1	0.754	14.24	5.90	0	13.53	5.80	0	0.719	0.754	7.071	3.943	1	255
44	1	0.694	8.14	17.39	0	8.75	17.39	0	0.61	0.407	8.944	8.34	0	255
45	1	0.652	13.32	5.39	0	13.42	4.78	0	0.619	0.407	7.28	7.14	0	255
46	1	0.551	13.32	5.39	0	13.53	5.80	0	0.455	0.305	7.071	7.028	0	255
47	1	0.491	11.39	15.66	0	11.09	15.36	0	0.431	0.439	8.246	6.829	1	255
48	1	0.449	11.09	12.31	0	11.19	11.90	0	0.419	0.203	11.705	11.221	0	255
49	1	0.347	11.19	11.90	0	11.49	11.80	0	0.322	0.102	10.296	9.029	1	255
50	1	0.246	13.93	2.75	0	14.14	2.85	0	0.227	0.215	6	5.333	1	255

The longest-shortest path is then computed to determine the shortest continuous path that traverses the maximum number of branch and end points using the Floyd-Warshall algorithm (Skiena, 2008). We have again adapted the Floyd-Warshall algorithm for use in ImageJ to compute the branch positions from the medial axis transform previously described and present the salient mathematics used. The Floyd-Warshall algorithm computes the transitive closure of a set of a graph by defining the problem as the sum of the shortest paths between each pair of vertices or branch points. Transitive closure is defined as a matrix of all reachable paths wherein reachable implies existence of a direct path from vertex A to vertex B. Hence, for a k^th iteration of the algorithm, the path from vertex A to B can be determined using intermediate vertices within the range of [1,k] by a path directly through all points A to k−1:

$$R^{(\mathrm{k})}[\mathrm{A},\mathrm{B}]=R^{(\text{k-}1)}[\mathrm{A},\mathrm{B}]$$

and also by a path from A to k and from k to B by:

$$R^{(\mathrm{k})}[\mathrm{A},\mathrm{B}]=R^{(\text{k-}1)}[\mathrm{A},\mathrm{B}]\text{and}{R}^{(\text{k-}1)}[\mathrm{k},\mathrm{B}].$$

To generate a matrix for transitive closure, the recurrence relating the elements of R^(k) to R^(k−1) can be defined as:

$$R^{(\mathrm{k})}[\mathrm{A},\mathrm{B}]=R^{(\text{k-}1)}[\mathrm{A},\mathrm{B}]\text{or}(R^{(\text{k-}1)}[\mathrm{A},\mathrm{k}]\text{and}{R}^{(\text{k-}1)}[\mathrm{k},\mathrm{B}]).$$

The k^th iteration of the Floyd algorithm determines the shortest paths between every pair of vertices A,B that use only vertices among [1,k] as intermediates by:

$$D^{(\mathrm{k})}[\mathrm{A},\mathrm{B}]=min\{D^{(\text{k-}1)}[\mathrm{A},\mathrm{B}],D^{(\text{k-}1)}[\mathrm{A},\mathrm{k}]+D^{(\text{k-}1)}[\mathrm{k},\mathrm{B}])\}.$$

Once the longest-shortest path is determined by the method described above, all branches extending from a branch point to an end point, and not part of the longest shortest path, are subsequently called spines.

We then use a local thickness algorithm (Fig. 1A, E) to determine the thickness at each point along each of the branches (Hildebrand and Rüegsegger, 1997). We have adapted the mathematics they present for use in conjunction with the previously described medial axis transform and Floyd-Warshall algorithm. A summary of the relevant mathematics we employed is presented below. To achieve a manageable computation of local thickness, the process is done in two steps. The first step calculates the distance map by calculating the Euclidean distance from each point (q) in the structure to the nearest background point. This distance is equivalent to the radius of the largest sphere centered at the point and still completely self-contained within the structure. This transformation is defined as:

$${\mathrm{D}}_{\text{map}}(\mathrm{q})=max(\{\mathrm{r}>0\mid \text{sph}(\mathrm{q},\mathrm{r})\subseteq \mathrm{\Omega }\}),\mathrm{q}\in \mathrm{\Omega }.$$

where D_map(q) is the distance map of q, r is the radius of the sphere, and Ω all points within the structure. This defines the local thickness as:

$$\mathrm{\tau }(\mathrm{p})=2·\underset{q\in X(p)}{max}(D_{\mathit{map}}(\mathrm{q}))$$

where the set X(p) represents the set of center points of all circles with radii equal to their corresponding distance value including the point p:

$$\mathrm{X}(\mathrm{p})=\{\mathrm{x}\in \mathrm{\Omega }\mid \mathrm{p}\in \text{sph}(\mathrm{x},{\mathrm{D}}_{\text{map}}(\mathrm{x}))\}.$$

Using this definition of local thickness leads to a massive computational overhead, and instead it is easier to define the distance map as the set of center points of all non-redundant circles:

$${\mathrm{\Omega }}_{\mathrm{R}}=\{\mathrm{p}\in \mathrm{\Omega }\mid \text{sph}(\mathrm{p},{\mathrm{D}}_{\text{map}}(\mathrm{p}))\not\subset \text{sph}(\mathrm{x},{\mathrm{D}}_{\text{map}}(\mathrm{x})),\mathrm{p}\ne \mathrm{x},\mathrm{x}\in \mathrm{\Omega }\}$$

then it is only necessary to check for the corresponding circles in these points by redefining the set X(p) as:

$$\stackrel{\sim }{X}(\mathrm{p})=\{\mathrm{x}\in {\mathrm{\Omega }}_{\mathrm{R}}\mid \mathrm{p}\in \text{sph}(\mathrm{x},{\mathrm{D}}_{\text{map}}(\mathrm{x}))\}.$$

This necessary additional calculation of the distance ridge can be done efficiently on discrete data by making the inclusion test local for the neighbor pixels only. Like the method we used to calculate the medial axis transform, the accuracy of this method depends on the resolution of the image acquisition system, and the local thickness will have a stochastic error corresponding to the dimension of one pixel.

Algorithm Development

The algorithm was developed using the Integrated Design Environment Eclipse Neon v3.0 (The Eclipse Foundation) with Java version 1.8.0.11. Images were analyzed by two trained observers (Obs. A, B) to determine inter-observer variability, and one observer on separate days (Obs. A1, A2) to determine intra-observer variability.

Code Availability

Both the source code and compiled version of the algorithm are available at GitHub (https://github.com/ferlandlab/BranchAnalysis2D-3D.git).

Algorithm Workflow

A flowchart of this process and the interpretation of the output is provided in Figure 1 and in the sample data sets provided with the compiled version of BranchAnalysis2D/3D.

Golgi-Cox stained brain tissue and image acquisition

Brains from mice were removed and processed using the Golgi-Cox staining method (Ferland et al., 2005). All brains were immersed in a solution of 5% potassium dichromate, 5% mercuric chloride, and 4% potassium chromate for 5–6 weeks. The brains were then dehydrated, infiltrated, and embedded in nitrocellulose. The sections were cut under an 80% alcohol drip, transferred to water, blackened in a 5% solution of sodium carbonate, dehydrated in ethanol and cleared in trepineol. Sections were then rinsed in xylene, mounted and coverslipped.

Images of dendrites and spines were acquired using a Zeiss Imager.M2 microscope with a 40x or a 63x objective (Zeiss Plan-Achromat 40x/0.75 or 63x/1.4, respectively). Dendrites were chosen with no specific criterion to test the algorithm’s performance across a wide variety of conditions with variable noise.

Dendritic spine morphometry analysis

Dendritic spine length and head/neck diameter was measured using semi-automated methods present in ImageJ for calculating lengths and local thicknesses. The dendritic spines were grouped as either stubby, mushroom, or thin based on the descriptions below. The measurements below were adapted from multiple sources (Papa et al., 1995; Srivastava et al., 2011; Swanger et al., 2011).

• Stubby: Length ≤ 2 μm,

• Mushroom: 2 μm < Length ≤ 5 μm, Head/Neck Diameter ≥ 1.3 μm

• Thin: 2 μm < Length ≤ 5 μm, Head/Neck Diameter ≤ 1.3 μm

Length was calculated as an average running length of the spine, and head/neck diameter was defined as the maximum local thickness value. For 3D stacks, spine morphometry for all indicated spines was calculated and total density determined as the sum of thin, mushroom, and stubby spines. Statistical comparisons were performed using one-way ANOVA using Tukey’s HSD tests for post-hoc analysis.

Primary cilia immunolabeling in brain

Brains from mice were removed and processed for immunohistochemistry. Briefly, all animals were perfused transcardially with PBS followed by a 4% PFA solution, and the brains removed. Brains were incubated overnight in 4% PFA, washed with PBS, and cryoprotected in a 30% PBS-sucrose solution. Brains were then sectioned at 30 μm using a freezing microtome and processed for immunolabeling as free-floating sections. Tissue was permeabilized using 0.04% Triton X-PBS, blocked in 10% normal goat serum in PBS, and cilia immunolabeled using anti-adenylyl cyclase III (Santa Cruz, 1:1000). Sections were mounted and imaged with a confocal laser scanning microscope, Zeiss LSM TPMT. The resulting image stacks were converted to maximum intensity projections.

Primary cilia analysis

Primary cilia lengths were measured within Fiji ImageJ, and number of cilia determined from the number of measurements. The time of analysis was measured as previously described. Statistical comparisons were performed for time of analysis and number of cilia detected using Student Newman-Keul’s t-tests between the human consensus and algorithm. Statistical comparison for cilia length was performed using one-way ANOVA with Tukey’s HSD post-hoc tests.

Retina vasculature staining and analysis

Neonatal mice were euthanized at post-natal day 5. Whole eyes were harvested and then fixed overnight at 4°C with 3.7 % PFA. Flat mount retinas were prepared, immunostained with anti-CD31 (1:50, BD Pharminogen), and mounted, essentially as previously described (Pitulescu et al., 2010). Vasculature was analyzed using both AngioTool (Zudaire et al., 2011) and our algorithm to assess total vessel length, which was defined as the sums of the vessel length between each branch point. Student’s t-test was used to determine if there was a significant difference between estimated vessel lengths. Vessel diameter was analyzed by our algorithm and by two observers as previously described. A one-way ANOVA with Tukey’s HSD post-hoc analysis was used to determine if any significant differences existed in estimated vessel diameter.

Image Analysis

Observers determined spine sub-types using Neurolucida, primary cilia length using Fiji ImageJ, vasculature total length using AngioTool, and vasculature vessel diameter using Fiji ImageJ (sample images of each type shown in Figure 2). Two trained observers performed the analysis, referred to as Observer A (Obs. A) and Observer B (Obs. B). Obs. A performed the analysis on two separate days to account for intra-observer variability. The Observers’ results were each compared to the output of the algorithm using one-way ANOVA (Statistica) and AngioTool was compared against the algorithm using the Student Newman Keul’s t-test. The average time of analysis per image, including pre-processing steps, was measured by each observer performing the analysis using pre-existing software packages (Neurolucida for dendritic spines, Fiji ImageJ for primary cilia, and AngioTool and Fiji ImageJ for retinal vasculature) and using the algorithm. Analysis times were measured using a computer with an Intel Core i7-4500U, 1.80 GHz processor.

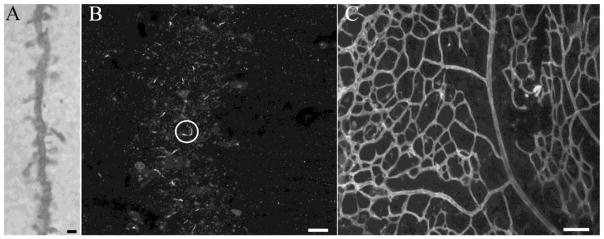
Figure 2. Sample Dataset Images.

Representative images used in the analyses of dendrite and spines (A), primary cilia (B), and retinal vasculature (C) are shown. One primary cilium is enclosed within the white circle in panel B. Scale bars = 2 μm (A),5 μm (B), and 80 μm (C).

Results

The algorithm’s performance was validated with four data sets: 1) 2D dendrite images, 2) 3D dendrite image stacks, 3) primary cilia in the CA1 hippocampal region, and 4) retinal vasculature (Table 3; Fig. 2). For spine analyses of 2D dendrites, BranchAnalysis2D/3D was found to output similar spine densities as observers using Neurolucida (F _3,14 = 0.03, p = 0.9929), as well as similar densities of stubby, thin, and mushroom spines (F_3,14 = 0.04, p = 0.9892; F_3,14 = 0.2, p = 0.8960; F_3,14 = 0.11, p = 0.9539, respectively). Observers using Neurolucida also outputted similar overall spine densities, stubby, thin, and mushroom spine densities as BranchAnalysis2D/3D for analyses of 3D dendrite image stacks (F_3,4 = 0.03, p = 0.9927; F_3,4 = 0.01, p = 0.9986; F_3,4 = 0, p = 1; F_3,4 = 0.2, p = 0.8948, respectively). The observers using Fiji ImageJ found similar primary cilia numbers and lengths as BranchAnalysis2D/3D in the hippocampal CA1 region (F_3,9 = 0.01, p = 0.9986; F_3,9 = 0.14, p = 0.9346, respectively). AngioTool and BranchAnalysis2D/3D outputted similar total vessel lengths (p = 0.3392), and observers using Fiji ImageJ determined similar vessel diameters as BranchAnalysis2D/3D (99.3% match between observer determined vessel diameter and BranchAnalysis2D/3D determined vessel diameter).

Table 3.

The algorithm outputs similar results to human observers, but requires less analysis time.

Image Type	Obs. A, Day 1	Obs. A, Day 2	Obs. B	Algorithm
2D Dendrite Spines/μm	0.196 ± 0.0289	0.203 ± 0.0282	0.196 ± 0.0289	0.206 ± 0.0180
2D Dendrite Stubby Spines/μm	5.4 ± 0.815	5.533 ± 0.848	5.267 ± 0.176	5.667 ± 0.500
2D Dendrite Thin Spines/μm	0.4 ± 0.227	0.533 ± 0.185	0.667 ± 0.293	0.533 ± 0.132
2D Dendrite Mushroom Spines/μm	0.4 ± 0.227	0.267 ± 0.199	0.267 ± 0.176	0.267 ± 0.101
2D Dendrite Analysis Time (min)	2.386 ± 0.0628	2.518 ± 0.501	2.518 ± 0.0329	1.236 ± 0.0265*
3D Dendrite Spines/μm	0.354 ± 0.0515	0.355 ± 0.0514	0.356 ± 0.0513	0.368 ± 0.0557
3D Dendrite Stubby Spines/μm	0.233 ± 0.0484	0.238 ± 0.0491	0.250 ± 0.0461	0.250 ± .0503
3D Dendrite Thin Spines/μm	0.0142 ± 0.0127	0.0142 ± 0.0127	0.0163 ± .0100	0.0163 ± .0100
3D Dendrite Mushroom Spines/μm	0.107 ± 0.163	0.102 ± 0.0188	0.0928 ± 0.0166	0.0926 ± 0.0161
3D Dendrite Analysis Time (min)	5.525 ± 0.0165	5.563 ± 0.246	5.498 ± 0.0599	3.593 ± 0.00783*
Primary Cilia Number	27.9 ± 3.553	28.2 ± 3.572	27.4 ± 3.197	27.4 ± 3.339
Primary Cilia Length (μm)	5.633 ± 0.195	5.691 ± 0.201	5.730 ± 0.201	6.005 ± 0.195
Primary Cilia Analysis Time (min)	4.363 ± 0.0438	4.334 ± 0.0468	4.353 ± 0.0520	2.794 ± 0.0327*
Retinal Vasculature Vessel Diameter (μm)	5.201 ± 0.0235	5.355 ± 0.0276	5.149 ± 0.024	5.196 ± 0.023
Retinal Vasculature Analysis Time (min)	59.061 ± 0.117	59.220 ± 0.063	59.191 ± 0.100	21.018 ± 0.479*
	AngioTool	Algorithm
Retinal Vasculature Total Length (mm)	20.575 ± 1.523	23.186 ± 1.936

Values represent average ± SEM.

^*Indicates significant differences (p < 0.01) from observers

BranchAnalysis2D/3D was significantly faster than observers using other analysis tools in all four test data sets (2D Dendrite – F_3,14 = 149.06, p < 0.0001, Tukey HSD p < 0.01 (algorithm vs. observers); 3D Dendrite – F_3,4 = 662.75, p < 0.0001, Tukey HSD p < 0.01 (algorithm vs. observers); Primary Cilia – F_3,9 = 251.49, p < 0.0001, Tukey HSD p < 0.01 (algorithm vs. observers); F_3,7 = 4956.18, p < 0.0001, Tukey HSD < 0.01 (algorithm vs. observers)).

Discussion

Although multiple software packages exist for morphometric analyses, we have developed a more broadly applicable and convenient analysis algorithm made available as an open-source ImageJ plugin. BranchAnalysis2D/3D is different from already existing software packages such as Metamorph (Srivastava et al., 2011) and AngioTool (Zudaire et al., 2011) as BranchAnalysis2D/3D is not specialized for one data type, and can handle 3D data sets. BranchAnalysis2D/3D also has advantages over commercial software packages such as Neurolucida and Imaris since it is an open source project, and requires minimal user training.

BranchAnalysis2D/3D performs its comparisons at the pixel/voxel level. As a pixel/voxel is a continuous function, it is possible to compute morphometric measures, such as thickness, at a sub-pixel/sub-voxel level by profiling the pixel/voxel curve intensity using methods such as the full-width half-maximum method. By using only pixel/voxel level comparisons, there may be small errors in our morphometry measures when regarding the pixel as a discrete quantity with fixed intensity. Most widely used commercial software packages, i.e. Neurolucida and Imaris, also do not determine morphometric measures at sub-pixel and sub-voxel accuracy (Peng et al., 2014; Yang et al., 2013). Consideration of sub-pixel and sub-voxel measures would be important for future algorithm development especially since it could provide biologically relevant information for image processing. However, given that observers using the industry standard software (Neurolucida) obtained similar results to our algorithm, the errors present within the algorithm are clearly not sufficient to bias the results with the sample images used here. Thus, our algorithm is as precise as other methodologies. Future work could introduce sub-pixel/sub-voxel calculation methods to improve the accuracy of BranchAnalysis2D/3D.

In addition, adding automated ‘thresholding’ processes to BranchAnalysis2D/3D will increase its future functionality by removing any user interaction with input images from the analysis process and significantly increase the speed of processing. Thus, BranchAnalysis2D/3D provides significant advantages to both trained and untrained observers performing morphometric analyses by providing a widely available, rapid, and consistent algorithm that outputs results equivalent to already existing software.

Highlights.

• An open-source algorithm for analysis of branching structures is presented

• Algorithm output matches output from human observers using existing analysis tools

• The algorithm is faster than human observers using other analysis tools

• BranchAnalysis2D/3D automation decreases investigator bias

• BranchAnalysis2D/3D can be used to measure any branching structure