A New Approach to Compressed Sensing for NMR

Abstract

Compressed sensing (CS) has attracted a great deal of recent interest as an approach for spectrum analysis of nonuniformly sampled NMR data. Although theoretical justification for the method is abundant, it suffers from several weaknesses, among them poor convergence of some algorithms, and it remains an open question whether NMR spectra satisfy the sparsity requirements of CS theorems. The versions of CS used in NMR involve minimizing the l₁ norm of the spectrum. They bear similarity to maximum entropy (MaxEnt) reconstruction, but critical comparison of the methods can be difficult. Here we describe a formalism that places CS and MaxEnt reconstruction on equal footing, enabling critical comparison of the two methods. We also describe a new algorithm for CS that restricts the computation of the l₁ norm to the real channel for complex spectra and ensures causality. Preliminary 1D results demonstrate that this approach ameliorates some artifacts that can occur when using the l₁ norm of the complex spectrum.

Spectrum analysis of time series data has captured the attention of mathematicians, scientists, and engineers for centuries. NMR spectroscopists are relative newcomers, compared with illustrious figures such as Gauss(1), Prony(2), Fourier(3), and Tukey(4). NMR spectroscopists continue to mine the rich literature on spectrum analysis for "novel" methods, a task sometimes made difficult because of terminology employed by different fields: identical or closely related methods are often described in very different terms that obscure relationships among the methods.

The approach known as compressed sensing (CS), frequently attributed to Candes(5), is finding widespread application for spectrum analysis of NMR data collected using nonuniform sampling (NUS)(6–11). CS methods typically work by minimizing the l₁ norm of the spectrum (i.e. the sum of its absolute values). Logan’s Theorem(12) states that perfect recovery of the spectrum is possible even from incomplete and noisy measurements by minimizing the l₁ norm of the spectrum while ensuring consistency with the measured data, provided that certain conditions on sparsity and noise level are met, and the spectrum is band-limited.

Common CS algorithms involve iteratively thresholding the spectrum(10, 13– 15). This approach has a long and rich prior history, including iterative thresholding image processing algorithms due to van Cittert(16), Jansson(17), and Papoulis(18). Iterative thresholding algorithms for NMR spectra involve two steps. In the thresholding step, values in the frequency spectrum are set to zero if they are below some threshold in absolute value. Then in the replacement step, the inverse Fourier transform of the thresholded spectrum is computed. Values corresponding to measured data are then replaced by the measured values, and the result is Fourier transformed to the frequency domain. These two steps are repeated alternately until convergence. The connection between the iterative thresholding algorithms and the theoretical work of Logan was made explicit by Stern et al.(15), who proved that the fixed-point of iterative soft thresholding (IST) has minimum l₁ norm. Iterative soft thresholding differs from iterative thresholding only in the thresholding step: values below the threshold are set to zero, and values above the threshold are reduced in absolute value by the threshold amount (keeping the same phase).

While iterative thresholding algorithms hold strong heuristic appeal and are trivial to code, as fixed-point methods they are sometimes subject to premature convergence(15), in which the step size becomes vanishingly small before the optimum (minimum l₁ norm) is reached. A potentially more fundamental limitation of CS is that NMR spectra may not meet the sparsity conditions of Logan’s Theorem or other CS theorems(19). The Lorentzian lineshapes that occur in NMR spectroscopy are not band-limited, and furthermore are not localized to single points in the frequency domain. A difference between NMR spectra and imaging applications of CS is that images are non-negative and real, whereas NMR spectra are complex (and even their absorptive components need not be non-negative). Finally, CS methods are not guaranteed to produce a unique spectrum.

CS has been proposed as an alternative to maximum entropy (MaxEnt) reconstruction for spectrum analysis of NUS NMR data(6–11). Critical comparison of the two methods is not straightforward, however, because most of the proposed algorithms constrain the inverse Fourier transform of the spectrum to exactly match the measured data(9, 10) (for example by stopping the iterative thresholding procedure following a replacement step). It is important to note that the proof of the equivalence between IST and l₁-norm minimization(15) holds only when the final step is thresholding, not replacement, and the results of these algorithms cannot accurately be said to minimize the l₁ norm. MaxEnt reconstruction as originally formulated by Wernecke and D’Addario(20), in contrast, merely ensures that the inverse transform of the spectrum is statistically consistent with the measured data to within a prior estimate of the noise. While other MaxEnt methods such as Forward Maximum Entropy (FM)(21) and Maximum Entropy Interpolation (MINT)(22) that exactly or closely match the measured data have been demonstrated and offer an advantage of being nearly linear, they “over-fit” the measured data.

Here we describe an approach to CS that constrains the spectrum to agree with the empirical data in a manner analogous to MaxEnt reconstruction. By ensuring a known level of agreement between the reconstructed spectra and the known (empirical) data, this enables fair comparisons of MaxEnt and minimum l₁ norm spectra that have the same level of agreement. The approach employs robust gradient search and a metric for measuring the degree of convergence that is more strict than relying on the step size. We restrict the computation of the l₁ norm to the real component of complex spectra. Provided that the phase of the spectrum can be determined and adjusted so that the real component is absorptive, this helps limit the support of Lorenztian peaks to relatively few frequency values, thus improving the overall sparsity compared to a computation that includes dispersive imaginary components, an idea explored by Mayzel et al.(23). In addition, we incorporate support for including a convolution kernel in the Fourier inversion between the spectral estimate and the time domain, enabling deconvolution to help narrow spectral peaks as an alternative method for improving the sparsity.

Theory

Our approach to l₁ norm regularization is based on a formalization similar to that of MaxEnt regularization(24), although there are a few differences in the details below. The desired spectrum f is one which minimizes a regularization functional S(f) subject to two constraints: f must be causal and f must be consistent with the measured data. S(f) is defined to be the l₁ norm computed for just the real component of f (or real-real quadrant for a two-dimensional spectrum, and so on):

$$S(\mathbf{f})=\sum _{\mathrm{n}=0}^{\mathrm{N}-1}|\text{real}(f_n)|,$$ (1)

where N is the number of points in the spectrum. The data constraint is defined in terms of the root-mean-square (RMS) difference between the inverse discrete Fourier transform (IDFT) of f and the measured data d:

$$C(\mathit{f},\mathit{d})=\sqrt{\sum _m{|\text{IDFT}{(\mathit{f})}_m-d_m|}^2/\mathit{\text{nc}}}$$ (2)

Here the sum runs over only the measured data points rather than all N points in IDFT(f), and nc is the total number of components included in the sum (real and imaginary parts of the data are counted as separate components). Eq. (2) can be generalized to support deconvolution of a known line shape from the measured data by factoring in a convolution kernel k:

$$C(\mathit{f},\mathit{d})=\sqrt{\sum _m{|k_m\text{IDFT}{(\mathit{f})}_m-d_m|}^2/\mathit{\text{nc}}}$$ (3)

Thus, we seek to find f such that S(f) is minimal subject to the constraints that f is causal and

$$C(\mathbf{f},\mathbf{d})\le \mathit{\text{aim}},$$ (4)

where aim is an estimate of the RMS noise level in d. Because the S and C functionals are both convex, the existence of a minimum is guaranteed, and the minimum will satisfy either C(f,d) = aim or else f = 0. However, because S is not strictly convex, the minimum need not be unique.

It is well known that for causal spectra, the imaginary part is determined by the real part via the Hilbert transform(25). Therefore there is no need to store the imaginary part of f during the computation, and indeed our algorithm stores only the real part, which we will call h:

$$h_n=\text{real}(f_n).$$ (5)

The problem of computing IDFT(f) from h is solved as follows. The real part of f_n is one-half the sum of f_n and its complex conjugate, and complex conjugation in the frequency domain corresponds to complex conjugation plus reversal in the time domain(24). Therefore

$$\text{IDFT}{(\mathbf{h})}_m=(1/2)[\text{IDFT}{(\mathbf{f})}_m+\text{conj}(\text{IDFT}{(\mathbf{f})}_{N-m})]$$ (6)

(where we take IDFT(f)_N to be the same as IDFT(f)₀). Causality says that in the time domain, the data points at negative times are all equal to 0; by the cyclic nature of the discrete Fourier transform this means that IDFT(f)_m is equal to 0 for all m > N/2. Hence from Eq. (6) it follows that:

$$\text{IDFT}{(\mathbf{h})}_m=\{\begin{array}{cc}\text{real}(\text{IDFT}{(\mathbf{f})}_m)\hfill & \text{if }m=0,\hfill \\ \text{IDFT}{(\mathbf{f})}_m/2\hfill & \text{if }1\le m<N/2.\hfill \end{array}$$ (7)

Although this leaves the imaginary part of IDFT(f)₀ undetermined, the rest of the terms appearing in Eqs. (2) or (3) can be gotten from IDFT(h):

$$\text{real}(\text{IDFT}{(\mathbf{f})}_0)=\text{IDFT}{(\mathbf{h})}_0,$$ (8)

$$\text{IDFT}{(\mathbf{f})}_m=2\text{ IDFT}{(\mathbf{h})}_m\text{ for }1\le m<N/2.$$ (9)

(We require that N be more than twice as large as the largest index m appearing in the measured data, so that the sums in Eqs. (2) and (3) run over values of m that are all less than N/2. This is tantamount to zero-filling the measured data by at least a factor of two.)

In addition, it is generally recognized that owing to the difference between the continuous and discrete Fourier transforms, in order to obtain an accurate base line it is necessary to divide the first point of the time-domain data by two prior to transformation(26). To put it another way, the m=0 term in the definition of C should be computed from the difference between 2×IDFT(f)₀ and d₀ rather than the difference between IDFT(f)₀ and d₀. Note: Since the imaginary part of IDFT(f)₀ is not determined by h, its component must be omitted from the sums in Eqs. (2) or (3).

Putting these ideas together, we reformulate the problem: We seek a real spectrum h such that S(h) is minimal subject to the constraint that C(h,d) = aim, where C(h,d) is now given by:

$$C(\mathit{h},\mathit{d})=\sqrt{\sum _m{|2k_m\text{IDFT}{(\mathit{h})}_m-d_m|}^2/\mathit{\text{nc}}}$$ (10)

(and the imaginary component is not included in the m=0 term of the sum).

This constrained minimization problem can be converted to an unconstrained minimization by introducing a Lagrange multiplier λ: Find h minimizing S(h) + λC(h,d), where λ is selected so that the minimum satisfies C(h,d) = aim. However, we choose instead to set τ equal to 1/λ and find h minimizing the objective functional

$$Q(\mathbf{h},\mathbf{d},\mathrm{\tau })=\mathrm{\tau }S(\mathbf{h})+C(\mathbf{h},\mathbf{d}).$$ (11)

Using τ rather than λ makes no difference to the final result, but it does permit a simple comparison with the IST algorithm because τ turns out to be equal to the threshold value(15).

(Our algorithm does not constrain the values of h to be non-negative, but such a constraint would be very easy to add. Note that a major difference between NMR and most imaging application of CS is the absence of a non-negativity constraint.)

The algorithm employs a slightly modified Conjugate Gradient (CG) minimization(27) to find h. The algorithm can be used in two different modes. In the first mode, the user specifies τ beforehand and the algorithm simply computes h so as to minimize Q(h,d,τ). This mode is analogous to the “constant-λ” algorithm we previously described for MaxEnt reconstruction (28) and thus can be called the “constant-τ“ mode. This is useful when computing 2D spectra for successive planes of a 3D data set (or 1D spectra from a 2D data set), as it ensures that nonlinearities are similar for different planes and thus simplifies calibration of the nonlinearities for quantitative applications. Applied to 3D data, a typical plane or set of planes would be selected and iteratively reconstructed using different values of τ, and the entire set of planes is then reconstructed using the value of τ that yields C(h,d) with the desired value of aim. In the second mode, the user specifies aim and the algorithm finds both τ and h so that h minimizes Q(h,d,τ) and C(h,d) = aim. This is the “constant-aim” mode. Applied to planes of a 3D data set, this mode typically yields different values for τ, which is an obstacle to quantitation.

CG minimization is quite efficient when the function to be minimized is quadratic. In our case C(h,d) is quadratic, and S(h) is linear provided the computation is restricted to a domain in which none of the h_n values change sign. Indeed, the absolute value function is not differentiable at the origin, which causes difficulties for gradient-based techniques. Our algorithm handles this situation by adopting the following conventions at indices n for which h_n = 0:

• If |∇C(h,d)_n| ≤ τ then ∇S(h)_n and ∇Q(h,d,τ)_n are both set to 0. Under these circumstances, any small change to h_n will result in an increase in Q; setting ∇Q(h,d,τ)_n to 0 prevents the algorithm from changing h_n.

• Otherwise ∇S(h)_n is set to either 1 or −1 according to whether ∇C(h,d)_n is negative or positive. Under these circumstances, Q can be decreased by changing h_n in the direction opposite ∇C(h,d)_n, and after such a change, ∇S(h)_n will be equal to the value adopted here (1 or −1).

During each step of the CG minimization, if the step would cause any element h_n to change sign, h_n is set to 0 instead. This prevents the quadratic extrapolation used by CG from being applied outside its domain of validity. In addition, the CG computation is reset (by forgetting the previous steps) whenever the support set of ∇S(h) (i.e., the set of indices n at which ∇S(h)_n is nonzero) changes; the next step will follow the gradient of Q rather than the conjugate gradient. It is expected that as the computation converges toward the final answer, these exceptional cases will arise relatively rarely.

The algorithm computes a test statistic before each step:

$$\mathit{\text{test}}={\tau }^{-1}\sqrt{\sum _{n=0}^{N-1}{(\nabla Q(\mathbf{h},\mathbf{d},\tau ))}^2/\mathit{\text{nsupp}}}$$ (12)

where nsupp is the size of the support set of ∇S(h) (∇Q(h)_n is necessarily equal to 0 at each n outside the support set). This statistic measures the degree of convergence. In the first mode of operation, the minimization ends when test < 0.0001.

The second mode is more complicated. The algorithm makes an initial overestimate of τ, which it decreases over time. As long as C(h,d) remains above aim, the algorithm decreases τ by 0.8 and restarts the CG minimization whenever test falls below 0.01. But once C(h,d) has fallen below aim, the algorithm changes strategy. Now whenever test is below 0.01 and is also below |C(h,d) − aim| / aim, the algorithm takes a single step along ∇C(h,d). The length of the step is chosen to make the new value of C(h,d) equal to aim, and following the step, τ is recalculated as:

$$\mathrm{\tau }=-\sum _{n=0}^{N-1}\nabla C{(\mathbf{h},\mathbf{d})}_n\nabla S{(\mathbf{h})}_n/\mathit{\text{nsupp}}$$ (13)

At all other iterations the algorithm uses CG minimization to decrease Q(h,d,τ) while holding τ fixed, as described above. The computation ends when test and |C(h,d) − aim| / aim are both smaller than 0.0001.

Results and Discussion

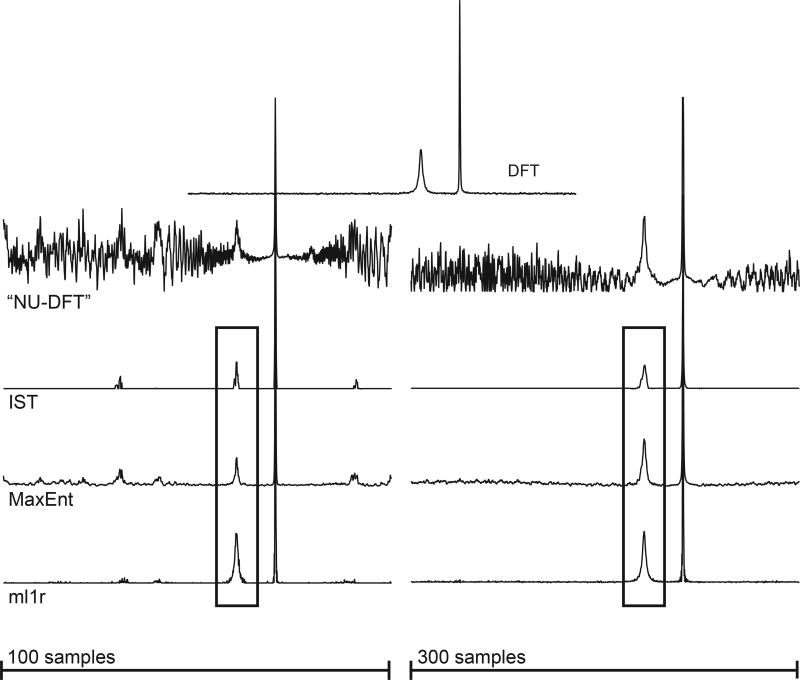
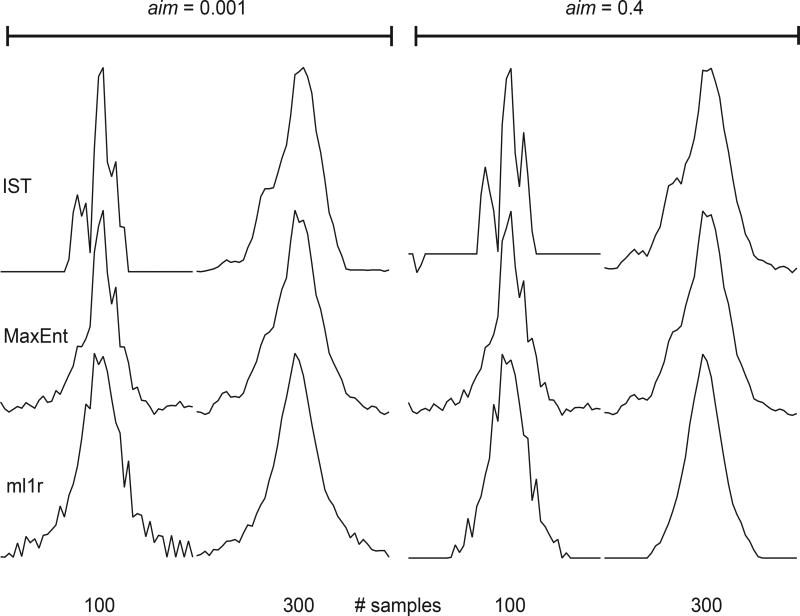
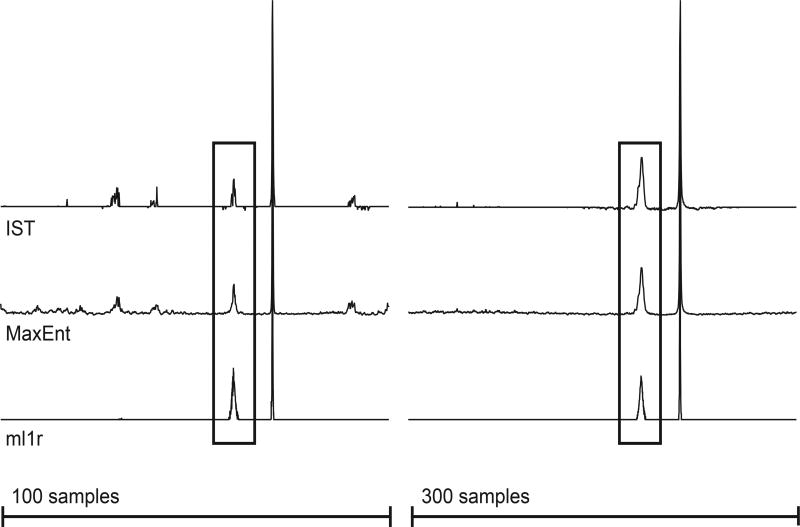
Preliminary results using synthetic signals plus random noise are shown in Figures 1–3, using the constant-aim mode. Our ml1r algorithm is comparable in speed to MaxEnt, on the order of 10 ms for the spectra shown here using a 3.7 GHz Intel Xeon processor. IST is considerably slower, on the order of 100 ms for the spectra shown. The synthetic data was nonuniformly sampled using an exponentially biased scheme selecting 100 or 300 samples from the uniform 1024-element data vector. The top trace of Fig. 1 shows the DFT of the uniformly sampled data; the second row of traces depict the results of “nonuniform DFT”, in which the samples not utilized are set to zero prior to Fourier transformation. Successive traces show the results for IST, MaxEnt, and our new algorithm (ml1r, for minimized l₁ norm, real), for 100 samples (left) and 300 samples (right) for IST and MaxEnt. For ml1r, because the algorithm necessarily applies one zero-fill to ensure causality of the spectrum, samples with indices larger than 512 were removed from the sampling schedule, so that the number of actual samples used for ml1r reconstructions were 83 and 250 respectively, instead of 100 and 300 samples, respectively. In Fig. 1 the MaxEnt and ml1r reconstructions were computed in the “MINT” limit, tightly constrained to match the sampled data, so that they can be compared with the IST results. While IST does much better at suppressing sampling artifacts than MaxEnt or ml1r, close examination of the broad peak reveals artifactual splitting of the single resonance for both 100 and 300 samples. ml1r attains comparable sampling artifact suppression without splitting the resonance. Fig. 2 shows results obtained with IST, MaxEnt, and ml1r in the Bayesian limit, where aim is set to a value comparable to the noise. Comparison with Fig. 1 shows that in the Bayesian limit minimizing the complex l₁ norm (IST) does worse at suppressing sampling artifacts than in the MINT limit, whereas ml1r suppresses sampling artifacts better in the Bayesian limit; changing the value of aim from the MINT to the Bayesian regime has relatively little impact on MaxEnt. Fig. 3 gives a clearer indication of the impact of the choice of aim on the structure of the weak peak.

Figure 1.

Top row: DFT of 1024-point synthetic data plus noise (noise RMS = 0.1). Successive rows: spectral estimates employing 100 (left) and 300 (right) samples according to an exponentially biased sampling scheme (see supplementary information). The value of aim was 10⁻³ for all IST, MaxEnt, and ml1r spectra. The peaks enclosed by rectangles are expanded in Figure 3.

Figure 3.

Expansion of the regions enclosed by rectangles in Figures 1 and 2. Spectra on the left half correspond to the MINT regime (small aim, 10⁻³); spectra on the right half correspond to the Bayesian regime (larger aim, 0.4).

Figure 2.

Spectral estimates in the Bayesian regime employing 100 (left) and 300 (right) samples according to an exponentially biased sampling scheme (see supplementary information). The value of aim was 0.4 for all IST, MaxEnt, and ml1r spectra. The peaks enclosed by rectangles are expanded in Figure 3.

Concluding remarks and future directions

Our algorithm readily extends to data of arbitrary dimension, by restricting the l₁ norm computation to the purely absorptive quadrant (real-real component for two dimensions) of the spectrum, and we are conducting critical comparisons of the approach with conventional MaxEnt reconstruction and MINT for two- and three-dimensional NUS data. The preliminary one-dimensional results shown here suggest a number of avenues for further investigation. If indeed the greater sparsity of the real component is responsible for the mitigation of artifacts compared to using the l₁ norm of the complex spectrum, then similar effects should be apparent when comparing reconstructions of broad spectral components with those for narrow spectral components, or comparing crowded spectra with simpler, more sparse spectra. Other issues that need further investigation are the multiplicity of solutions due to the non-strict convexity of the l₁ norm, its application to spectra that contain both positive and negative signals, and the use of deconvolution to reduce the support (increase the sparsity) of NMR spectra.

While our approach facilitates critical comparison of CS and MaxEnt approaches in NMR, there remain other obstacles to identifying best practices. One is the lack of consensus metrics for spectral quality, which also hampers the comparison of NUS strategies. Further advances in NUS and non-Fourier spectrum analysis could benefit from a “shared task”, or a competition similar to Critical Assessment of Structure Prediction (CASP)(29).