Electron carriers in microbial sulfate reduction inferred from experimental and environmental sulfur isotope fractionations

Abstract

Dissimilatory sulfate reduction (DSR) has been a key process influencing the global carbon cycle, atmospheric composition and climate for much of Earth’s history, yet the energy metabolism of sulfate-reducing microbes remains poorly understood. Many organisms, particularly sulfate reducers, live in low-energy environments and metabolize at very low rates, requiring specific physiological adaptations. We identify one such potential adaptation—the electron carriers selected for survival under energy-limited conditions. Employing a quantitative biochemical-isotopic model, we find that the large S isotope fractionations (>55‰) observed in a wide range of natural environments and culture experiments at low respiration rates are only possible when the standard-state Gibbs free energy (ΔG′°) of all steps during DSR is more positive than −10 kJ mol⁻¹. This implies that at low respiration rates, only electron carriers with modestly negative reduction potentials are involved, such as menaquinone, rubredoxin, rubrerythrin or some flavodoxins. Furthermore, the constraints from S isotope fractionation imply that ferredoxins with a strongly negative reduction potential cannot be the direct electron donor to S intermediates at low respiration rates. Although most sulfate reducers have the genetic potential to express a variety of electron carriers, our results suggest that a key physiological adaptation of sulfate reducers to low-energy environments is to use electron carriers with modestly negative reduction potentials.

Introduction

A large part of Earth’s microbiome exists under energy limitation (Whitman et al., 1998; Kallmeyer et al., 2012; Lever et al., 2015; Lau et al., 2016) and metabolizes at rates 10⁴ to 10⁶ times slower than organisms in culture (Hoehler and Jørgensen, 2013). As the subsurface continental and seabed environments in which these organisms persist are largely inaccessible to direct experimentation, their physiology and biochemistry in their natural habitats are unresolved. How do these organisms maintain basic cell functions, such as growth and division, under such extreme energy limitation?

Sulfate-reducing bacteria and archaea, which are responsible for about half of the organic matter respiration in marine sediments (Jørgensen, 1982), are among the keystone organisms in many low-energy environments (Edwards et al., 2005; Jørgensen and D'Hondt, 2006; Orsi et al., 2016). They metabolize at extremely low rates (Hoehler and Jørgensen, 2013; Bowles et al., 2014; Jørgensen and Marshall, 2016), which must require physiological adaptations such as increased efficiency of substrate uptake (Lever et al., 2015; Jørgensen and Marshall, 2016). The exact adaptive tactics that enable their strategy of persistence, however, remain unknown. In particular, it is unclear how the varied spectrum of electron carriers in sulfate-reducing organisms (SROs) might support energy conservation under energy-limited natural conditions.

Single-cell genomic studies show that most sulfate reducers have the genetic potential to express a variety of electron carriers, such as menaquinones, and all of them have genes encoding for ferredoxin (Pereira et al., 2011). High potential electron carriers like ferredoxins are often abundant in environmental metagenomes from subsurface environments that host SROs (Orsi et al., 2013; Keller et al., 2015; Lau et al., 2016; Oberding and Gieg, 2016; Wu et al., 2016), whereas metatranscriptome studies of S-driven deep subsurface microbial ecosystems have also identified gene transcripts encoding for small proteins with low redox potential like rubredoxin and rubrerythrin expressed by SROs (Lau et al., 2016; Orsi et al., 2016). The physiological role of those proteins remains unclear. However, the mere presence of rubredoxin- and rubrerythrin-encoding gene transcripts in these anoxic environments is puzzling, as both proteins are proposed to function as part of an oxidative stress response system in laboratory cultures of sulfate-reducing bacteria (Lumppio et al., 2001).

We investigated this apparent ecological inconsistency with a systems biochemical model of S isotope fractionation during dissimilatory sulfate reduction. We show that the reduction potential of the intracellular electron carriers for this metabolic pathway controls the magnitude of the S isotope fractionation that it produces. In turn, this allows us to connect S isotope fractionations and environmental electron donors observed in subsurface environments to the potential physiological roles of electron carriers in SROs. The widespread occurrence of large S isotope fractionations in many energy-limited environments suggests that the ability to use electron carriers with very modest reduction potentials is of general importance and a key adaptation of sulfate reducers living in energy-limited environments.

Electron carrier identity is a critical component of the energy metabolism of SROs

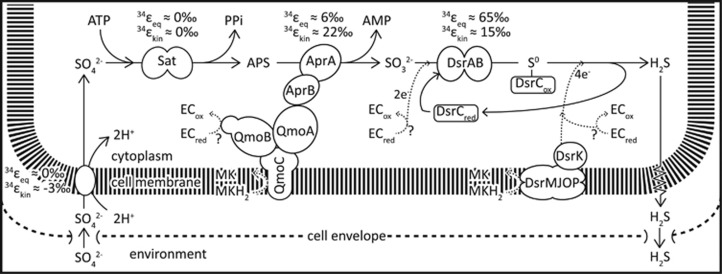
SROs use a respiratory mechanism with sulfate (SO₄²⁻) as the terminal electron acceptor. The dissimilatory reduction of SO₄²⁻ (DSR) is a multistep reaction (Figure 1), where SO₄²⁻ is first symported into the cell, activated with adenosine triphosphate (ATP) to form adenosine 5′phosphosulfate (APS), which is then reduced to sulfite (SO₃²⁻) and ultimately to sulfide (H₂S). A comparative genomic analysis shows conservation of genes encoding for the sulfur metabolic enzymes (sulfate transporters, sulfate adenylyl transferase, APS reductase and dissimilatory sulfite reductase (DsrAB)) for the membrane-bound Qmo and Dsr complexes, as well as for ferredoxin across 25 sequenced SROs (Figure 1) (Pereira et al., 2011).

Figure 1.

Simplified illustration of the dissimilatory sulfate reduction network and S isotope fractionation associated with each reaction step. Proposed modes of electron flow are indicated with dashed arrows. See text for a detailed description. ³⁴ε_eq, equilibrium S isotope fractionation; ³⁴ε_kin, kinetic S isotope fractionation; Apr, APS reductase; Dsr, dissimilatory sulfite reductase; EC_red, reduced electron carrier; EC_ox, oxidized electron carrier; MK, menaquinone; MKH₂, menaquinol; Sat, sulfate adenylyl transferase. The figure is adapted from Wing and Halevy (2014) and includes new insights into the DsrC cycle from Santos et al. (2015).

Although the physiological role of most of the conserved key enzymes in SROs has been resolved (Figure 1), their interaction with electron carriers remains uncertain. In addition to ferredoxin, menaquinone is present in most sulfate reducers (Collins and Widdel, 1986; Tindall et al., 1989). As menaquinones are membrane-bound, they can be directly involved in energy conservation by contributing to a transmembrane proton gradient. As a result, recent biochemical work has focused on finding a direct physiological role of menaquinone and the omnipresent ferredoxin in DSR (Ramos et al., 2012; Keller et al., 2014; Price et al., 2014a; Duarte et al., 2016).

APS reduction, for example, is catalyzed by APS reductase, which receives electrons through the membrane-bound quinone-interacting oxidoreductase (Qmo) complex (Fritz et al., 2002; Ramos et al., 2012; Duarte et al., 2016). Although it is generally assumed that menaquinone oxidation releases electrons to the membrane-bound QmoC subunit, this may be thermodynamically unfavorable because of the similar potentials of APS reduction (E′° APS/AMP+HSO₃⁻=−65 mV) and menaquinone reduction (E′° MK/MKH₂=−74 mV) at standard conditions (Ramos et al., 2012). Hence, ferredoxin, with a more negative standard-state reduction potential (−398 mV; Ramos et al., 2012), has been proposed to be involved in the reduction of APS through an electron confurcation scheme (Ramos et al., 2012; Keller et al., 2014; Price et al., 2014b; Rabus et al., 2015).

The direct electron donors during sulfite reduction are even less well known (Figure 1). Two electrons are transferred to the catalytic site of DsrAB through an unidentified electron carrier, reducing SO₃²⁻ to an enzyme-bound S^II intermediate (Santos et al., 2015). DsrC, a small soluble protein with a C-terminal arm containing two cysteines, then binds to the catalytic site, transfers two additional electrons to the S^II intermediate and eventually forms a DsrC-bound S⁰ trisulfide product, in which the S⁰ originates from SO₃²⁻ and forms a bridge between the two cysteines (Santos et al., 2015). In a next step, this DsrC-bound S⁰ trisulfide is reduced to H₂S and DsrC. The reaction requires a total of 4 electrons, 2 for the reduction of S⁰ to H₂S, and 2 to recycle DsrC. Although this reaction is partly catalyzed by a membrane-bound DsrMKJOP complex, implicating the oxidation of menaquinol, other electron carriers have been proposed (Oliveira et al., 2008; Venceslau et al., 2014; Santos et al., 2015).

In addition to ferredoxin and menaquinone, a number of other electron carriers—rubredoxin, flavodoxin, cytochrome c3 and rubrerythrin—have been identified in many SROs (Odom and Peck, 1984; Fauque et al., 1988; Kremer et al., 1988; Rabus et al., 2006; Ramos et al., 2012; Price et al., 2014b; Rabus et al., 2015; Dörries et al., 2016). Likewise, several transmembrane redox complexes, such as Hmc, Tmc, Ohc or Rnf are found in many SROs, although their function is only partly understood (Pereira et al., 2011). Most insights into the physiology of sulfate reducing organisms, as well as predictions and speculations about the physiological role of electron carriers, have been based on pure cultures grown under optimal conditions (high-energy availability, fast growth). How these findings relate to organisms living in natural low-energy environments is unclear. Investigation of the variability in isotope fractionation in natural low-energy environments as well as in pure cultures has the potential to shed new light on this fundamental question.

Large S isotope fractionation is common in natural energy-limited environments

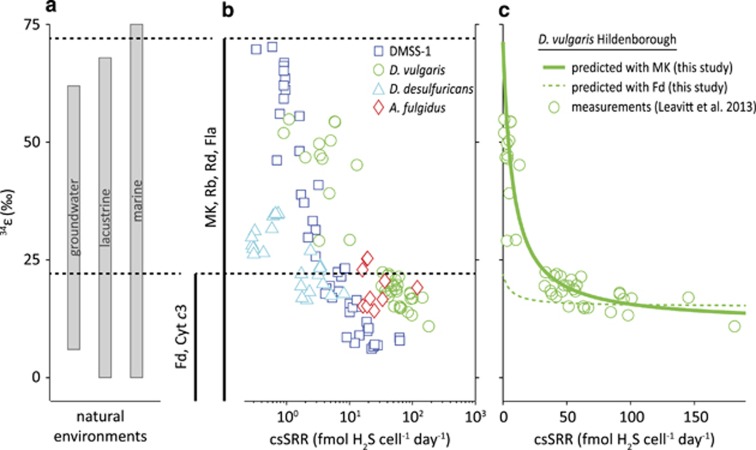
Sulfate-reducing microbes preferentially process S-bearing metabolites containing the light stable isotope of S, ³²S, leaving the residual sulfate enriched, and the product sulfide depleted, in ³⁴S. The degree of this fractionation during DSR is quantified as ³⁴ε=(³⁴α–1) × 1000 (in permil, ‰), where ³⁴α=(³⁴S/³²S)_sulfate/(³⁴S/³²S)_sulfide. In laboratory cultures, ³⁴ε ranges from −3‰ to 72‰ (Kaplan and Rittenberg, 1964; Chambers et al., 1975; Habicht and Canfield, 2001; Wortmann et al., 2001; Sim et al., 2011b, 2012; Leavitt et al., 2013). The upper end of this range is proposed to reflect near-thermodynamic equilibrium fractionation (Wing and Halevy, 2014) and is accessed in the laboratory only at the lowest growth rates and cell-specific sulfate reduction rates (csSRR) (Sim et al., 2012).

Large, near-thermodynamic S isotope fractionations associated with DSR are also observed in low-energy niches in many natural environments (Figure 2), including intertidal mudflats (Böttcher et al., 2000), lakes (Ivanov et al., 2001), coastal environments (Kaplan et al., 1963; Goldhaber and Kaplan, 1975), continental shelves (Wortmann et al., 2001), deep sea sediments (Böttcher et al., 2004; Orsi et al., 2016) and euxinic water columns (Werne et al., 2003). In the majority of these environments, the quality of the low-molecular weight organic compounds that support DSR is poor and, as a result, csSRR is low and the observed S isotope fractionations are large. Understanding the energetics that allows ubiquitously large fractionations thus has the potential to shed light on the physiology and metabolism of the majority of sulfate reducers in natural environments.

Figure 2.

Predicted (this study) and experimentally determined (previously reported) rate-fractionation relationships during DSR. (a) Reported range of S isotope fractionation from natural environments (data compiled in Sim et al., 2011a) and (b) rate-fractionation relationships determined in pure culture experiments with DMSS-1 (Sim et al., 2011a, 2011b, 2012), D. vulgaris Hildenborough (Leavitt et al., 2013), D. desulfuricans (Chambers et al., 1975) and A. fulgidus (Habicht et al., 2005) grown on organic substrates. The magnitude of S isotope fractionation increases with decreasing csSRR. The black vertical lines indicate the possible range of S isotope fraction allowed by the respective electron carriers (determined in this study). The full range of environmental and experimental fractionation is reproducible with electron carriers with modestly negative reduction potentials such as for example, menaquinone (MK). Ferredoxin (Fd) as a direct electron donor would limit the maximum fractionation to <22‰, which is inconsistent with reported experimental data at low csSRR. (c) Predicted rate-fractionation relationship with menaquinone (solid line) and ferredoxin (dashed line) as electron carrier vs. experimental data (markers) from experiments with D. vulgaris Hildenborough (Leavitt et al., 2013). Cyt c3, cytochrome c3; Fla, flavodoxin; Rb, rubredoxin; Rd, rubrerythrin.

Materials and methods

Below we outline our theoretical approach. A detailed description of the model, underlying experimental datasets, and sensitivity analyses can be found in the Supplementary Information and in Wing and Halevy (2014). All acronyms used are summarized in Table 1.

Table 1. Nomenclature.

Acronym	Description
DSR	Dissimilatory sulfate reduction
SRO	Sulfate-reducing organism
EC	Electron carrier
R r/o	Ratio of reduced to oxidized electron carrier concentrations
csSRR	Cell-specific sulfate reduction rate
ΔG′°	Standard Gibbs free energy
E′°	Standard reduction potential
K M	Michaelis–Menten half saturation concentrations
α eq	Equilibrium fractionation factor
α kin	Kinetic fractionation factor
34 ε	S isotope enrichment factor;34 ε=(α−1) × 1000
MK	Menaquinone
Rb	Rubredoxin
Rd	Rubrerythrin
Fla	Flavodoxin
Cyt c3	Cytochrome c3
Fd	Ferredoxin

Electron carrier identity impacts the maximal whole-organism S isotope fractionation

The magnitude of whole-organism S isotope fractionation during DSR varies with temperature, the carbon source, and sulfate availability (Bruchert et al., 2001; Canfield, 2001; Habicht and Canfield, 2001; Johnston et al., 2007; Sim et al., 2011b; Bradley et al., 2016). In addition, many studies have shown that the magnitude of S isotope fractionation correlates inversely with csSRR (Figure 2) (Harrison and Thode, 1958; Kaplan and Rittenberg, 1964; Chambers et al., 1975; Sim et al., 2011a, 2011b, 2012; Leavitt et al., 2013). This range of S isotope fractionation magnitude has been related to the reversibility of the individual steps in the sulfate reduction pathway (Rees, 1973; Brunner and Bernasconi, 2005; Bradley et al., 2011; Wing and Halevy, 2014).

Briefly, in DSR, SO₄²⁻ is transported into the cytoplasm, activated with ATP to form APS, which is then reduced to SO₃²⁻ and ultimately to H₂S:

where 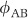, for example, is the flux from A (extracellular SO₄²⁻) to B (intracellular SO₄²⁻). The overall isotope fractionation, 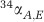, can be expressed as:

where 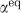are the equilibrium isotope fractionations (α^eq≡R_reactant/R_product, where R is ³⁴S/³²S, in a reactant or product in isotopic equilibrium) and α^kin are the kinetic isotope fractionations (α^kin≡³²k/³⁴k, where ³²k and ³⁴k refer to the enzymatic reaction rate constants of the light and heavy isotopologues) of each step. The net fractionation of each step varies between α^eq and α^kin depending on the value of f, the reversibility, which is defined as the ratio of the reverse to forward flux in the reaction (for example, 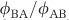in the leftmost reaction in reaction network 1) and varies from unity at equilibrium to zero for a completely unidirectional reaction.

For each step during DSR, α^eq can be calculated theoretically (Bigeleisen and Mayer, 1947; Urey, 1947; Otake et al., 2008; Eldridge et al., 2016) for a given temperature (here 25 °C if not stated differently, the experimental temperature of the rate-fractionation study with the model sulfate reducer Desulfovibrio vulgaris (Leavitt et al., 2013)). Constraints on α^kin are poorer. Sulfate uptake into the cell and its subsequent activation to APS seem to have a 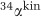close to unity (Harrison and Thode, 1958) (Figure 1). The following reduction steps, however, discriminate against ³⁴S leading to a measurable fractionation in the intermediate substrates (Harrison and Thode, 1958; Kemp and Thode, 1968; Leavitt et al., 2015). This ³⁴S depletion in the cell’s internal metabolite pools will only be expressed as a relative ³⁴S enrichment in the residual extracellular sulfate pool if all preceding steps are to some degree reversible (that is, if f in equations 2,3,4,5 is not close to zero; see Supplementary Information for a detailed discussion on the reversibility of enzymatic reactions).

The reversibility, f, is linked to the actual free energy of a reaction (ΔG_r) via the flux–force theorem (Beard and Qian, 2007):

where R is the gas constant and T the temperature. Importantly, ΔG_r depends on the standard-state Gibbs free energy (ΔG′^o) and on the concentrations of intracellular metabolites:

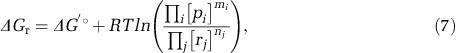where [p_i] and [r_j] are the concentrations, and m_i and n_j the stoichiometric coefficients, of the product i and reactant j, respectively. In combination with enzyme kinetic principles (Flamholz et al., 2013), this shows that net S isotope fractionations are under the proximate control of the energetics and kinetics of the S reactions, as they govern the relative levels of the S-bearing metabolites for a given csSRR.

The prescribed csSRR can be thought of as encompassing the effects of substrate availability and quality, and the partitioning of energy yield between cellular function and growth, albeit without an explicit account for the dependence of csSRR on these factors. We used the link between the expressed net fractionation at low csSRR and ΔG_r of the reactions in the DSR network to constrain the identity of the electron carriers used during APS and SO₃²⁻ reduction in their natural low-energy environment. As the standard reduction potential (E′°) of the electron carriers is a major component of ΔG_r, reproduction of the large isotopic fractionations at low csSRR place direct limits on the reduction potential of the electron carriers involved and, therefore, on their identity.

Results and discussion

We find that large S isotope fractionations, such as those observed in natural environments (Figure 2a) and in pure culture experiments at low respiration rates (Figure 2b), are only possible with electron carriers with modestly negative reduction potentials. Moreover, menaquinone, rubredoxin, rubrerythrin and some flavodoxins not only allow large S isotope fractionation at low csSRR, but also predict specific csSRR-fractionation relationships that have been observed in pure culture experiments (Figure 2c). Electron carriers with strongly negative reduction potentials (for example, ferredoxin) limit the maximum achievable fractionation to less than 22‰, which is inconsistent with laboratory and natural data at low csSRR (Figure 2).

Three parameters exert primary control on the magnitude of S isotope fractionation at a given csSRR: electron carrier identity (ΔG′°), R_r/o and K_M values

We identified two criteria that must be fulfilled by any proposed energy metabolism scheme for DSR (Supplementary Table S1). First, large S isotope fractionation (>55‰) must be achieved at prescribed low respiration rates (~0.1 fmol H₂S per cell per day). Second, intracellular metabolite concentrations, namely [SO₄²⁻]_in, [PPi], [APS] and [SO₃²⁻], must be within physiological limits (10⁻⁹ to 10⁻³ M).

Although the second criterion sets the physiological limits of our model, the first criterion constrains the energetics that allows DSR to operate in a net forward direction, but close enough to thermodynamic equilibrium that large isotopic fractionations are possible, as observed in natural environments. Large isotope fractionations are only possible when the reversibility terms, f, in equations 2,3,4,5 approach unity (Figure 1). To identify the parameters controlling reversibility, we combined equations 6 and 7 with expressions for the net rate of each reaction and solved for f (see Supplementary Information for a complete derivation). By doing so, three parameters emerged as possible controls on the reversibility of each reaction at a specific respiration rate: (i) the standard-state Gibbs free energies, ΔG′°, for each of the reactions, (ii) the ratio of reduced to oxidized electron carrier concentrations (R_r/o=[EC_red]/[EC_ox], where EC stands for electron carrier) for APS and SO₃²⁻ reduction, and (iii) the Michaelis–Menten half-saturation concentrations (K_M) of the sulfur-bearing metabolic substrates.

The first of these controls (ΔG′°) can be calculated directly from the reduction potential of the half-reactions for the respective electron carriers at standard-state conditions. After calculating ΔG′° for a wide range of electron carriers suggested to participate in APS and SO₃²⁻ reduction schemes, we varied the second and third controls, R_r/o and K_M, to extremal values and explored the dependence of the maximum achievable S isotope fractionation on these parameters. This exercise showed that the influence of R_r/o and K_M is co-dependent and critically affected by the values calculated for ΔG′°. Thus, we start with a discussion of the identity of the electron carriers and energy supply schemes that enable large fractionation at low csSRR. We then explore the interplay among R_r/o, K_M values, and electron carrier identity and use the second criterion—reasonable intracellular metabolite concentrations—to place physiological limits on R_r/o.

Large S isotope fractionation requires electron carriers with small-magnitude reduction potentials

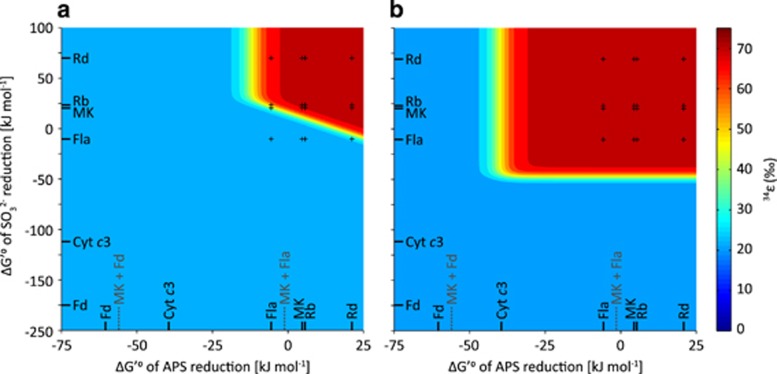
The observation of large fractionation (>55‰) at low respiration rates (~0.1 fmol H₂S per cell per day) requires nearly full reversibility of all steps during DSR (Figure 1; Equations 2,3,4,5). Assuming default values for R_r/o and K_M (Supplementary Tables S4 and S5), full reversibility of APS and SO₃²⁻ reduction is only possible when electron carriers with modestly negative reduction potentials are involved in DSR (Figures 3a and 4a). Specifically, the standard-state Gibbs free energy (ΔG′°) of APS and SO₃²⁻ reduction must each be less negative than approximately −10 kJ mol⁻¹. When electron carriers with strongly negative reduction potentials are involved, the ΔG′° of these reactions is more negative, and they operate far from equilibrium, leading to net S isotope fractionations that are much smaller than the thermodynamic limit. In principle, at a low enough csSRR, DSR should operate close to thermodynamic equilibrium and isotope fractionations should be large, irrespective of the electron carrier involved. However, the limitation of the maximal fractionation described above occurs even at csSRR as low as 10⁻⁴ fmol H₂S per cell per day, equivalent to the lowest rates observed in natural environments (Hoehler and Jørgensen, 2013).

Figure 3.

Maximum achievable S isotope fractionation at low csSRR for (a) reasonable, and (b) extreme conditions (see Supplementary Table S5, Supplementary Figure S1 and Supplementary Dataset S1). Even with extreme values for R_r/o and K_M large fractionation is only possible when ΔG′° of APS reduction >−40 kJ mol⁻¹ and ΔG′° of SO₃²⁻ reduction >−50 kJ mol⁻¹. The black ticks and text indicate the calculated ΔG′° of the reaction with the respective electron carrier; the dashed grey lines and text indicate the calculated ΔG′° of the reaction with the respective electron carriers in potential electron confurcation schemes. A confurcation scheme of ferredoxin and menaquinone for APS reduction, for example, limits the possible range of isotope fractionation to less than 22‰ and is therefore inconsistent with observations. csSRR=0.1 fmol H₂S per cell per day; R_r/o =20 (a) or 0.001 (b). Reasonable and extreme K_M values are listed in Supplementary Table S5. Standard redox potentials for the electron carriers are given in Supplementary Table S3. Cyt c3, cytochrome c3; Fd, ferredoxin; Fla, flavodoxin (with a modestly negative reduction potential); MK, menaquinone; Rb, rubredoxin; Rd, rubrerythrin.

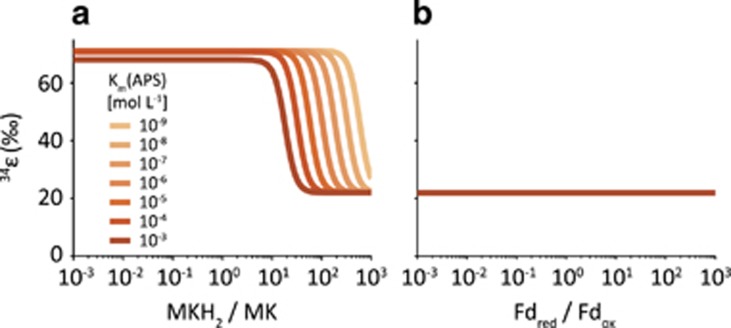
Figure 4.

Maximum achievable S isotope fractionation as a function of reduced to oxidized electron carrier concentration ratios at low csSRR (0.1 fmol H₂S per cell per day). The electron carrier involved in both APS and SO₃²⁻ reduction is (a) menaquinone and (b) ferredoxin. For menaquinone, fractionation at low R_r/o plateaus at ~72‰, the sulfate-sulfide equilibrium fractionation. For ferredoxin, APS (and SO₃²⁻ reduction) remain irreversible even at low R_r/o and the maximum fractionation reaches ~22‰, the sum of the sulfate-APS equilibrium fractionation and the kinetic fractionation of APS reduction.

Variation of R_r/o and K_M values may expand the range of possible electron carriers, but even when these parameters are varied to extremes (see Supplementary Information) the involvement of some electron carriers limits the possible range of fractionation to less than 22‰. Specifically, variation of R_r/o and K_M values permits a standard-state Gibbs free energy (ΔG′°) of APS reduction greater than −40 kJ mol⁻¹ and that of SO₃²⁻ reduction >−50 kJ mol⁻¹ (Figure 3b). Any potential electron transfer scheme must meet this requirement. Below we discuss first the constraints that this places on the involvement of any single physiological electron carrier, and then the implications for the existence of proposed electron supply schemes.

Most SROs have genes encoding for a wide range of electron carriers. Similarly, environmental metagenome analyses, as well as transcriptome studies from a variety of environments reveal a large range of metabolic potential of the respective communities (Keller and Wall, 2011; Zhou et al., 2011; Orsi et al., 2013; Lau et al., 2016; Orsi et al., 2016). The requirement for small-magnitude reduction potential described here means that some proposed electron carriers, such as ferredoxin, cannot be the direct electron donors for APS and SO₃²⁻ reduction, at least at low csSRR. Instead, menaquinone, rubredoxin, or rubrerythrin might be involved in DSR, because of their slightly negative to positive reduction potential. Membrane-associated menaquinones have been found in most SROs (Collins and Widdel, 1986; Tindall et al., 1989) and are essential for the reduction of APS at least in Desulfovibrio alaskensis (Keller et al., 2014). Menaquinol (MKH₂) oxidation during DSR is thought to be coupled to H⁺ release into the periplasm, contributing to the establishment of a proton gradient across the cytoplasmic membrane that can further be used for ATP generation (Pires et al., 2003; Venceslau et al., 2010; Keller et al., 2014). Although this proposed physiological function and the widespread occurrence of menaquinones across SROs suggests their involvement in DSR, their feeble reduction potential often results in their rejection as sole electron carriers in favor of more robust electron sources. Our results, however, show that isotope fractionation can reconcile the omnipresence and small reduction potential of menaquinones during DSR.

Rubredoxins are also present in most sulfate-reducing prokaryotes and are also possible components of the electron transport chain supplying DSR (Odom and Peck, 1984). They are small proteins, containing an iron center and four cysteine residues and have been purified from the cytoplasmic fractions of all known Desulfovibrio strains (Bell et al., 1974; Odom and Peck, 1984; LeGall and Peck, 1987; Moura et al., 1999). The identification of a NADH:rubredoxin oxidoreductase in Desulfovibrio gigas is a compelling argument for a role of rubredoxin in energy conservation in sulfate-reducing prokaryotes (LeGall, 1968; Odom et al., 1976; Kremer et al., 1988). Likewise, rubrerythrin has been purified from several sulfate-reducing bacteria (LeGall et al., 1988; deMaré et al., 1996; Moura et al., 1999) and its encoding genes are highly expressed during growth of Archaeoglobus fulgidus (Hocking et al., 2014). Its function during DSR is poorly understood, and rubrerythrin as well as rubredoxin are perhaps involved in oxidative stress mitigation rather than in electron transport to the S intermediates (Lumppio et al., 2001). The suggested physiological function of rubrerythrin and rubredoxin as part of an oxidative stress mitigation system, however, should be reconsidered given the high abundance of their gene transcripts expressed by SROs in anaerobic deep-subsurface environments (Lau et al., 2016; Orsi et al., 2016). In fact, in the same metatranscriptome datasets, genes that encode typical oxidative stress mitigation systems, such as superoxide reductase or glutathione peroxidase, were not upregulated (Lau et al., 2016; Orsi et al., 2016). This suggests that oxygen contamination during sampling did not significantly affect the results, and that a role for rubrerythrin and rubredoxin in SROs other than oxidative stress mitigation should be considered.

It is important to note that from a purely isotopic perspective, any electron carrier with a standard reduction potential greater than approximately −220 mV will result in modestly negative ΔG′° of the redox reactions and could therefore serve as the physiological electron donor to APS and SO₃²⁻ reductase at low csSRR (Figure 3, Supplementary Table S3). Flavodoxins, for example, have two oxidation states with reduction potentials of E′° F/FH ≈ −115 mV and E′° FH/FH₂ ≈ −371 mV, respectively (Thauer et al., 1977). It is hence possible that at low csSRR FH oxidation, but not FH₂ oxidation, drives the reduction of APS or SO₃²⁻. Similarly, several types of ferredoxins are known, for example, ferredoxin I and ferredoxin II in D. gigas, with reduction potentials of −398 mV and −130 mV, respectively (Odom and Peck, 1984). Ferredoxin II with a modestly negative reduction potential is expressed by some, but not all, SROs (Pereira et al., 2011). By contrast, ferredoxin I with a strongly negative reduction potential seems to be a conserved protein among all SROs (Pereira et al., 2011) and is hence ascribed an important role in the overall electron transport chain during DSR (Ramos et al., 2012; Grein et al., 2013; Hocking et al., 2014; Keller et al., 2014; Price et al., 2014b; Rabus et al., 2015). Moreover, several ferredoxin-reducing enzymes have been identified in sulfate reducers such as ferredoxin:NADH or pyruvate:ferredoxin oxidoreductases (Ogata and Yagi, 1986; Keller and Wall, 2011; Pereira et al., 2011; Rabus et al., 2013) and in experiments with D. alaskensis G20 the generation of reduced ferredoxin proved to be important for fitness (Price et al., 2014b). However, although ferredoxin I is ubiquitously present among sulfate reducers, its physiological function remains unclear. The strongly negative reduction potential of ferredoxin I means it cannot be the direct electron donor to APS and SO₃²⁻ reductase (with the exception of a specific electron transfer scheme to DsrAB as outlined below), at least at low respiration rates. Instead, it is possible that at least in some SROs, ferredoxin II could replace ferredoxin I in its function and drive APS or SO₃²⁻ reduction. In general, ferredoxins (I or II) may also be indirectly involved in DSR by acting as electron capacitors and regulating the redox poise of the direct electron donor to sulfate reduction intermediates. Such a potential indirect involvement of ferredoxin is not explicitly treated in our model and can thus not be excluded.

In summary, our findings are in line with recent observations from anoxic deep-subsurface environments, where relatively high abundance of electron carrier-encoding gene transcripts, which in laboratory experiments are associated with oxidative stress mitigation, have been found. Our predictions, although in agreement with observational data from low-energy environments, directly challenge energetic arguments that are often used to evaluate the role of various electron carriers involved in APS and SO₃²⁻ reduction. In general, it is assumed that if one intracellular redox reaction during DSR is more exergonic at standard state than another, then it is more likely to occur in living cells. However, cells do not live at standard state, and can have intracellular metabolite concentrations that are many orders-of-magnitude different than standard values. As long as a net metabolic reaction is energetically favorable, intracellular metabolite concentrations adjust within physiological limits to allow net forward fluxes (albeit close to thermodynamic equilibrium) for all intermediate reactions, even for those that are unfavorable at standard-state conditions (Milo and Phillips, 2015).

Moreover, from a thermodynamic perspective, bacterial growth is most efficient when the energetic requirements for biomass synthesis and maintenance of cellular functions are balanced by energy production from the respiring processes (von Stockar et al., 2006). In other words, at a small ΔG of the overall metabolic reactions, which is generally the case in the subsurface biosphere, higher respiration rates are possible when using electron carriers with modestly negative reduction potential (Supplementary Figure S2). This is because less of the available ΔG is dissipated in inefficient redox reactions. We suggest that as ATP production is proportional to the total respiration (here sulfate reduction) rate, electron carriers with modestly negative reduction potential allow production of enough ATP for survival at a smaller environmental ΔG (that is, under less favorable conditions) than do strongly negative reduction potential electron carriers (Supplementary Figure S2).

Large S isotope fractionation constrains possible electron supply schemes

The paradigm that more energetic standard-state reactions are more biologically relevant has led to the conclusion that, for example, rubredoxins are unlikely electron carriers during DSR because of their rather positive reduction potentials (Rabus et al., 2006). Similarly, it has been argued that menaquinone (E′°=−74 mV) cannot be the single electron donor to APS reduction, because of the apparently unfavorable energetics of the reaction at standard-state conditions (Ramos et al., 2012; Grein et al., 2013; Keller et al., 2014; Rabus et al., 2015). As a result, a second electron donor with a strongly negative reduction potential is invoked to drive the APS reduction reaction in a so-called electron confurcation scheme (Ramos et al., 2012; Grein et al., 2013; Keller et al., 2014). The most commonly assumed confurcation partner donating electrons to APS is ferredoxin (E′°=−398 mV), even though its direct involvement has yet to be demonstrated. We find that at least at low csSRR and in organisms that display large S isotope fractionations, ferredoxin with its strongly negative reduction potential cannot be the confurcation partner. A confurcation scheme of menaquinol and ferredoxin, each donating one electron to the reduction of APS, results in a ΔG′° of −56 kJ mol⁻¹ for this reaction (Figure 3). This leads to a kinetic control of APS reduction even at very low respiration rates and limits the achievable range of isotope fractionation to less than 22‰, which is inconsistent with observations. Our results support the inference that menaquinol oxidation can reduce APS through the QmoABC and AprAB complexes without the involvement of a third partner (Duarte et al., 2016). Our approach places firm limits on the electron confurcation schemes that are possible for APS reduction; a viable scheme must have ΔG′° >−40 kJ mol⁻¹ (for example, menaquinol + flavodoxin; Figure 3b), at least at low csSRR.

The electron budget during SO₃²⁻ reduction has recently been clarified (Santos et al., 2015). The first two electrons for SO₃²⁻ reduction are likely transferred from an unknown electron carrier, whereas the latter four ultimately originate from menaquinol oxidation (Figure 1; Santos et al., 2015). From the calculated ΔG′° of this specific scenario (Supplementary Table S2, Supplementary Table S3) and the requirement that ΔG′° >−10 kJ mol⁻¹, we conclude that only a few electron carriers, the ones with E′° >−220 mV, are potential candidates for transferring the first two electrons to DsrAB (menaquinone, rubredoxin, rubrerythrin and some flavodoxins; Figure 3a and Supplementary Table S3). Similarly, any proposed electron bi- or confurcation scheme involved in DsrC recycling must meet the requirement of ΔG′° >−10 kJ mol⁻¹ for the net reaction, or else it will result in small S isotope fractionations at low csSRR. With default R_r/o and K_M values, we find that no such scheme allows large fractionation at low csSRR. Allowing extreme ranges of K_M values and R_r/o significantly expands the list of possible electron carriers transferring the first two electrons to DsrAB. In this case, it appears that the requirement of ΔG′°>−50 kJ mol⁻¹ is met with all of the investigated electron carriers (Supplementary Table S3). For example, with ferredoxin transferring the first 2 electrons to the reduction of SO₃²⁻ and the remaining four ultimately originating from menaquinol oxidation, we calculate a ΔG′° of −41 kJ mol⁻¹ for the overall redox reaction. Although this value allows large fractionation at low csSRR, it requires R_r/o to be <0.05 and an extremely low affinity (K_M(H₂S) ⩾100 mM) of Dsr toward H₂S (Figure 3b and Supplementary Table S5). Importantly, if future experimental results show that R_r/o and K_M(H₂S) indeed take such values, our results suggest a direct physiological role for ferredoxin in SO₃²⁻ reduction, instead of, or in addition to, its proposed regulatory function as electron capacitor.

S isotope fractionation and physical limits constrain intracellular R_r/o values to a narrow range

We have shown that large S isotope fractionation at low csSRR is possible only if electron carriers with slightly negative to positive reduction potentials are involved in DSR, even when all other parameters in the bio-isotopic model were allowed to vary to extremes. Importantly, K_M values are relatively well constrained from independent biochemical analyses in several sulfate reducing bacteria and archaea (Supplementary Table S5 and Supplementary Dataset S1) and we adopted literature K_M values for most cases. In contrast to the relatively well-constrained K_M values, information on the ratio of reduced to oxidized electron carriers, R_r/o, is rare, and so we explored the influence of this parameter in more detail.

Only a relatively narrow range of R_r/o values affects the reversibility of the electron transfer reactions, and therefore the net S isotope fractionation (Figure 4). For a given electron carrier, S isotope fractionation transitions from a plateau to a floor across a narrow, approximately tenfold change in R_r/o values. The threshold values of R_r/o at which the fractionation transition occurs is weakly dependent on the K_M values for the enzymatic redox reactions in DSR (Figure 4). In the case of menaquinone as sole electron carrier in DSR, for example, maximum S isotope fractionation approaches 72‰ at low csSRR (~0.1 fmol H₂S per cell per day; Figure 4a). Above a certain threshold of R_r/o, however, the energetics of APS reduction become increasingly favorable and this reaction departs from equilibrium, resulting in a kinetically controlled net S isotope fractionation of only 22‰ (Figures 1 and 4a, and Equations 2,3,4). The same kinetic control of APS reduction is observed when ferredoxin is the sole electron carrier, resulting again in net S isotope fractionation of 22‰ (Figure 4b). In this case, however, the maximum fractionation remains at 22‰, independent of the value of R_r/o.

Importantly, in both of the above examples, the identity of the physiological electron carriers involved governs the S isotope fractionation achieved on the floor and plateau, but the R_r/o and K_M values determine the precise location of the transition in the fractionation landscape. Thus, the theoretical exercise of choosing extremely low values for R_r/o places the allowable fractionation on the plateau, and increases the range of electron carriers that allow large fractionation at low csSRR. However, extreme values of R_r/o may violate our second criterion—reasonable intracellular metabolite concentrations. A combination of large fractionation at low csSRR and plausible intracellular metabolite concentrations can, therefore, constrain the physiological values of R_r/o.

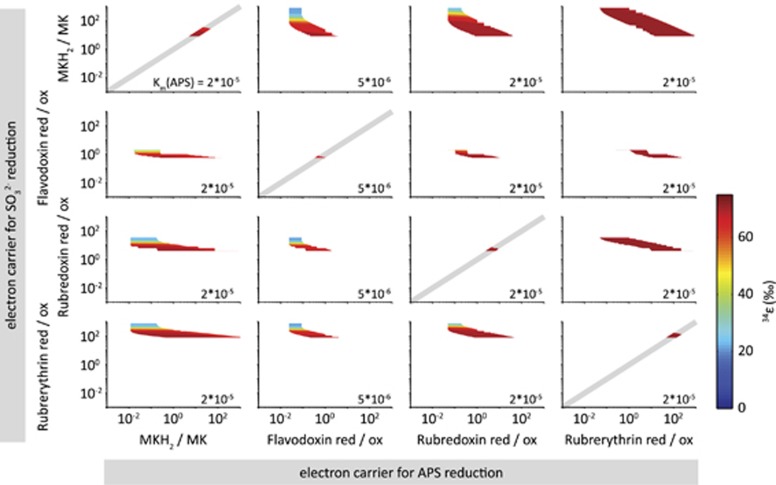
To restrict possible ranges of R_r/o, we require that all intracellular metabolite concentrations never drop below 1 nM, which for typical sulfate reducer volumes would mean less than a single molecule in the cell, and never exceed 1 mM. We further allow different electron carriers to be involved in APS and SO₃²⁻ reduction, resulting in different R_r/o values for these two reactions. For a given combination of electron carriers we vary each R_r/o from 10⁻³ to 10³ and calculate the net S isotope fractionation (³⁴ε) and intracellular metabolite concentrations, (that is, [SO₄²⁻]_in, [APS], [PPi] and [SO₃²⁻]). Figure 5 shows the calculated ³⁴ε at a csSRR of 0.1 fmol H₂S per cell per day for cases in which all metabolite concentrations fall in the range between 1 nM and 1 mM at csSRR between 0.1 and 125 fmol H₂S per cell per day. The white space indicates parameter combinations that lead to metabolite concentrations outside these boundaries. In all cases, we are left with a relatively narrow range of possible values for R_r/o. When the same electron carriers are involved in APS and SO₃²⁻ reduction, the possible values for R_r/o are even more tightly constrained (indicated by the grey 1:1 lines in Figure 5). For example, if menaquinone is the electron carrier involved in both APS and SO₃²⁻ reduction, then R_r/o (MKH₂/MK) must lie in the range between ~10 and ~30 for large isotope fractionation at low csSRR, with plausible metabolite concentrations (Figure 5 upper left panel).

Figure 5.

The range of R_r/o yielding reasonable (1 nM–1 mM) intracellular metabolite concentrations. Results are shown only for electron carriers that allow near-thermodynamic fractionations at low csSRR. Columns and rows show electron carriers for APS and SO₃²⁻ reduction, respectively. White space indicates combinations of R_r/o that produce unreasonable intracellular metabolite concentrations over some or all of the range of csSRR accessed in culture experiments (0.1 to 125 fmol H₂S per cell per day). Colored contours indicate the magnitude of net isotope fractionation at a csSRR of 0.1 fmol H₂S per cell per day and with values of K_M for APS at Apr shown in the lower right corner of each panel. Other K_M were at their default values (Supplementary Table S5). When the same electron carrier is involved in both APS and SO₃²⁻ reduction (on the diagonal), the possible range of R_r/o is further constrained to be on the solid grey line.

In summary, we have identified a set of low-potential electron carriers, R_r/o, and K_M values that permit large S isotope fractionation at low csSRR, and at reasonable intracellular metabolite concentrations. Importantly, this set of parameters allows not only large fractionation at low csSRR, but also reproduction of the full set of ³⁴ε values (−3‰ to 72‰) observed over the range of csSRR seen in nature and in culture (Figure 2) (Wing and Halevy, 2014). However, although the requirement for large fractionations at low csSRR constrains the electron carriers (and hence the metabolic pathway) under these conditions, it is possible that a shift in metabolic strategy occurs when favorable growth conditions allow a significant increase in csSRR. In fact, such a shift is consistent with the observed high csSRR in culture experiments and the correspondingly low S isotope fractionations. A switch in metabolic strategy could involve sulfur cycling through a separate enzymatic pathway, or a shift from strongly negative electron carriers in high-energy environments to modestly negative ones in low-energy environments. The latter switch could be implemented by different ratios of, for example, MK and Fd feeding into DSR, possibly through the involvement of separate transmembrane complexes (for example, Hmc or Tmc) that may be capable of receiving electrons from various donors.

Conclusions and implications

Living in low-energy environments is challenging. This is why the seemingly wasteful production of rubredoxin- and rubrerythrin-encoding gene transcripts in anoxic environments is puzzling (Lau et al., 2016; Orsi et al., 2016), given their assumed role as oxidative stress mitigators (Lumppio et al., 2001). Using a systems biochemical-isotopic approach to address this apparent ecological inconsistency, we found that DSR can occur at low csSRR in these environments only with electron carriers with modestly negative reduction potentials like rubredoxin and rubrerythrin. It may be that these low-energy environments are transiently oxygenated (Contreras et al., 2013), requiring constitutive maintenance of an oxygen defense system. In this case, low-potential proteins like rubredoxin and rubrerythrin may have been spandrelled into service as the electron carriers for DSR. Such functional co-option may be consistent with the view that evolution in energy-limited environments is essentially a sorting process rather than an adaptive one (Starnawski et al., 2017). However, from a thermodynamic perspective, bacterial growth is most efficient when the energetic requirements for biomass synthesis and maintenance of cellular functions are balanced by energy production from the respiring processes (von Stockar et al., 2006). This suggests that there may be a clear adaptive advantage to using electron carriers with modestly negative reduction potential in energy-limited environments.

In fact, when the net ΔG of the DSR pathway is compared among different electron carriers at the same csSRR (Supplementary Figure S2), our results show that electron carriers with modestly negative reduction potential require less available energy than high-potential carriers to maintain equivalent respiration rates. We suggest this is because less of the limited available energy is diverted toward inefficient redox reactions aimed at maintaining an available pool of high potential electron donors. In other words, as ATP production is proportional to the total rate of respiration (here sulfate reduction), electron carriers with modestly negative reduction potential allow production of enough ATP for survival at a smaller environmental ΔG (that is, more energy-limited conditions) than do strongly negative reduction potential electron carriers. As the difference in net ΔG is many orders of magnitude (Supplementary Figure S2), it seems possible that adoption of low-potential electron carriers may represent an adaptive solution to such a strong energetic selection pressure. Although here we specifically revealed physiological adaptations of SROs to energy-limited habitats, our approach can also be extended to study other metabolic pathways, such as sulfide oxidation, methanogenesis or anaerobic ammonium oxidation, through their natural variations in stable isotope fractionation.