Electroviscous Dissipation in Aqueous Electrolyte Films with Overlapping Electric Double Layers

Abstract

We use dynamic atomic force microscopy (AFM) to investigate the forces involved in squeezing out thin films of aqueous electrolyte between an AFM tip and silica substrates at variable pH and salt concentration. From amplitude and phase of the AFM signal we determine both conservative and dissipative components of the tip sample interaction forces. The measured dissipation is enhanced by up to a factor of 5 at tip–sample separations of ≈ one Debye length compared to the expectations based on classical hydrodynamic Reynolds damping with bulk viscosity. Calculating the surface charge density from the conservative forces using Derjaguin–Landau–Verwey–Overbeek (DLVO) theory in combination with a charge regulation boundary condition we find that the viscosity enhancement correlates with increasing surface charge density. We compare the observed viscosity enhancement with two competing continuum theory models: (i) electroviscous dissipation due to the electrophoretic flow driven by the streaming current that is generated upon squeezing out the counterions in the diffuse part of the electric double layer, and (ii) visco-electric enhancement of the local water viscosity caused by the strong electric fields within the electric double layer. While the visco-electric model correctly captures the qualitative trends observed in the experiments, a quantitative description of the data presumably requires more sophisticated simulations that include microscopic aspects of the distribution and mobility of ions in the Stern layer.

1. Introduction

The vast majority of solid surfaces, including mineral surfaces, semiconductors, polymers, and biological membranes, spontaneously assume a finite surface charge upon immersion into water. This charging is caused either by dissociation of surface groups or by adsorption of charged species dissolved in the water.¹⁻³ The resulting surface charge, which can reach densities up to the order of a few elementary charges per nanometer square is screened by the counterions in the electrolyte in a space charge layer with a typical thickness ranging from a fraction of a nanometer up to tens of nanometers, depending on the concentration of dissolved salts, see Figure 1a. The properties of the resulting ionic distribution, the electric double layer (EDL), are crucial for many disciplines of science and technology, including electrochemistry,⁴ colloid science⁵ and micro- and nanofluidics,^6,7 energy conversion and storage,⁸⁻¹⁰ membrane technology, and enhanced oil recovery.¹¹ Often, the relevance arises from the intrinsic coupling between fluid flow and electrical transport within the EDL. The traditional approach to model such electrokinetic phenomena is based on continuum physics. Fluid flow as well as electrical charge distribution are described in terms of flow fields and charge distributions that evolve according to the classical Navier–Stokes and Maxwell equations. In this context, the properties of the interfaces are casted into boundary conditions for charge, mass, and momentum transport. Classically, the EDL is decomposed into two parts, a diffuse layer, in which the distribution of electrical charge is described by the Poisson–Boltzmann theory and a compact part, the “Stern” layer, which comprises ions that are directly adsorbed to the solid surface. The ions in the Stern layer are usually assumed to be positioned about an ion radius away from the solid surface. In EDL models, there is a sharp boundary between ions in the Stern layer that are taken to be immobile and do not contribute to any electrical current and those in the diffuse part of the EDL, which move under the influence of electric fields and hydrodynamic drag. The solvent is also believed to be immobilized in the vicinity of the solid surface. Similar to the electric problem, there is a “slip plane”, from where onward continuum Navier–Stokes equations with bulk fluid properties are used to describe the flow. The Smoluchowski equation² that describes how tangential electric fields at solid–liquid interfaces give rise to an effective slip velocity in the presence of a finite ζ potential at the slip plane is one of the most widely used relations resulting from this classical EDL model. This approach has evolved into one of the most widely used pumping mechanisms in microfluidics, electro-osmotic pumping. Scientifically, casting all the details of microscopic molecular interactions into boundary conditions of macroscopic continuum models with sharp transitions between mobile and immobile parts of the system is not very satisfying. More importantly, it has also become clear throughout decades of research, and in particular within the past decade or so with the rise of various types nanoelectrofluidic applications, that important aspects of these phenomena cannot be captured in a continuum picture. Examples of such failures include the capacitance of electric double layers, the discrepancy between charge densities based on electrophoresis and titration, quantitative predictions of electro-osmotic flow, surface conduction, as well as simply the charge distribution and microscopic structure of the EDL. Various approaches have been introduced to account for these deficiencies. In particular, the so-called dynamic Stern layer concept allowed for ions in the Stern layer to respond to tangential electric fields while leaving them along the adjacent water unaffected by hydrodynamic drag (see refs (12,13)). More recent treatments involve both extensions of the Poisson–Boltzmann equation to account for the finite ion size.^7,14

Figure 1.

(a) A sketch of the electric double layer. Red dots represent positive charges, blue dots negative charges; ψ₀ and σ₀ are the potential and surface charge at the substrate, ψ_β and σ_β the potential and surface charge at the transition from the Stern to the diffuse layer. (b) Schematic presentation of the experimental setup. The blue laser ray indicates the photothermal driving of the cantilever, while its deflection is detected by reflecting the red laser onto a four quadrant detector. The flow in the electrolyte between the tip and the substrate has a pressure driven and an oppositely directed electro-osmotic component.

A frequently investigated generic situation is the hydraulic resistance experienced upon pumping an electrolyte solution through a nanochannel with charged walls. In this case, the hydrodynamic flow carries along the ions within the diffuse part of the EDL thereby generating a streaming current. This streaming current gives rise to a streaming potential, which, in turn drives a compensating Ohmic current of mobile ions in the center of the channel. Viscous drag between the fluid and the moving ions generates an additional flow that increases the hydraulic resistance of the channel that is frequently interpreted as an effective “electro-viscous” enhancement of the viscosity.¹⁵ It is maximum if the channel width is comparable to the thickness of the EDL. This electro-viscous effect is also believed to be the origin of the enhanced viscosity of suspensions of charged colloidal particles as compared to the well-known Einstein relation for hard spheres.^16,17 Notwithstanding the general qualitative acceptance of this scenario, substantial quantitative discrepancies between experiment and theory are rather common, in particular for nanochannels,^8,18−22 where the microscopic properties, e.g., of the internal surfaces, are difficult to characterize and frequently poorly known.²¹ A sound and quantitative picture of electro-viscous dissipation enhancement requires simultaneous characterization of (i) the surface charge (or potential), (ii) the hydrodynamic boundary conditions, (iii) the distribution of the ions in the vicinity of the interface, and (iv) their local mobility.

Force measurements in thin lubricant films provide another approach to study the same type of phenomena. The first experimental studies on friction enhancement in thin film flow date back to the pioneering work of Israelachvilli²³ who studied the dissipation near mica substrates using the surface force apparatus (SFA) technique, but they did not observe any significant increase of the dissipation for electrolytes. Later Raviv et al. reported no dissipation enhancement for aqueous electrolytes, also using an SFA, in contrast to nonpolar liquids for which the effective viscosity diverges at small mica–mica distances.^24,25 These measurements where all performed at neutral pH, in which case the diffuse layer charge of mica is rather low and hence little viscosity enhancement is expected. In the 2000s an extensive series of colloidal probe atomic force microscopy (AFM) studies on hydrodynamic squeeze out were performed in the context of hydrodynamic slip.²⁶⁻³¹ While addressing possible effects of enhanced surface charge in passing²⁶ the primary goal of these studies was to identify the role of hydrodynamic slip at hydrophilic and, in particular, at hydrophobic surfaces. Hence, like the SFA measurements, these studies did not systematically address fluid compositions that lead to high surface charges. In recent years, a wealth of novel experimental techniques have been developed that provide an increasingly detailed picture of the microscopic properties of solid–electrolyte interfaces. X-ray reflectivity³²⁻³⁴ and surface X-ray diffraction³⁵ have revealed the positions of ions and surrounding hydration water molecules with atomic precision. X-ray spectroscopy techniques have produced a detailed information about the binding configurations of interfacial water and ions.³⁶ Optical vibrational spectroscopy, in particular nonlinear sum frequency generation, has delivered valuable information about the ordering of molecules at interfaces, including in particular the average orientation of interfacial water.³⁷⁻⁴⁰ Atomic force microscopy and spectroscopy have provided simultaneous insight into the arrangement of adsorbed ions and water molecules in three dimensions⁴¹⁻⁴⁵ along with values of electrostatic and other forces that allow to quantify certain aspects of the interfacial charge distribution.^41,46 Increasingly, the techniques are being exploited to study kinetic and transport properties at solid–liquid interfaces.^34,38,47 At the same time, molecular simulations have advanced dramatically.⁴⁸⁻⁵³ They allow to trace the position of each individual atom in the system in time and thereby provide, within the limitations of the underlying molecular force fields and base functionals, the most detailed picture conceivable of ions and solvent molecules at solid–liquid interfaces. One of the key insights from both advanced experiments and molecular simulations has been that the description of solid–electrolyte interfaces requires more than solving an electrostatic problem for the distribution of charge. The solvent, water, plays a very important role in mediating interactions, solvating the ions, and screening electric fields. In many cases, ions can adsorb to interfaces in competing states of hydration that display different dynamics. Hydration water can thereby stabilize specific configurations of adsorbed ions.^41,42 At the same time, the properties of interfacial water itself are different from the bulk, e.g., regarding structure and dielectric response, which are affected by packing constraints, hydrogen bonding, and, given the large dipole moment of water molecules, the strong local electric fields within the EDL.

In the present work we use dynamic AFM measurements to determine the dissipation upon squeezing out thin aqueous solutions of NaCl at (primarily) elevated pH, see Figure 1b. The experiment makes use of a combination of analysis procedures that we have developed in recent years to quantify dissipation^54,55 and to analyze the conservative tip–sample interaction forces^41,46 to solve for the surface charge in the diffuse part of the EDL. Experiments are carried out using oxidized silicon wafers as samples and spherical tips with radius of approximately 1μm, equally made of oxidized silicon. Standard continuum models, Poisson–Boltzmann (PB) and DLVO theory in combination with specific surface speciation reactions as well as continuum hydrodynamics, are used as a reference frame to extract effective quantities of the surface charge density and the enhancement of effective viscosity. The article is organized as follows: in Section 2, we provide an overview of the materials and experimental methods to extract tip–sample interaction stiffness and damping from the measured signals using photothermal excitation amplitude modulation AFM. The first part of Section 3 is devoted to the analysis of the conservative part of the tip–sample interaction using PB and DLVO theory and presents the results for the surface densities. The second part of Section 3 addresses the analysis of the dissipative forces, in which we define a viscosity enhancement factor c_ev with respect to the dissipation based on the bulk viscosity. The results are compared to a simplified continuum approximation of the classical electroviscous effect and, more favorably, to a model ororiginally proposed by Lyklema and Overbeek based on an electric field-enhanced local viscosity. We end with a discussion of our results in the light of other recent work on ionic mobility within the EDL.

2. Methods

2.1. AFM Force Spectroscopy with Photothermal Excitation

Using amplitude modulation (AM) AFM we probe the amplitude and phase response of the cantilever tip, while we drive the bending of the cantilever by photothermal excitation, i.e., we locally heat the cantilever with a laser beam. Analyzing the motion of the cantilever tip in terms of a harmonic oscillator,^54,56−60 one can express the tip–substrate interaction force F_ts in the interaction stiffness k_int = −∂F_ts/∂h and interaction damping γ_int = −∂F_ts/∂ḣ as

1

where F_ts(h, 0) is the equilibrium force at distance h. Linearizing F_ts is justified because the oscillation amplitude is less than 1 nm, which is much smaller than the characteristic length of the interaction force. Solving the equation of motion of the harmonic oscillator, we derive in Appendix A:

2

3

where A and ϕ are the amplitude and phase of the cantilever deflection measured at a distance h from the substrate while A_∞ and ϕ_∞ are the amplitude and phase, measured at 140 nm from the substrate. Δγ_c is an offset that is added to account for the small but finite hydrodynamic coupling between tip and sample at the calibration distance, which we will calculate using continuum hydrodynamics, as discussed further below. (Alternatively, one could use the measured transfer function of the cantilever and continuum hydrodynamics to calculate the phase and amplitude offset at h = 140 nm.) Before we can calculate k_int and γ_int with eqs 2 and 3, we have to calibrate the cantilever parameters k_c, γ_c, and ω₀. The stiffness k_c is obtained from the thermal noise spectrum of the cantilever⁶¹ when it is not in contact with the substrate, i.e., h > 1 μm. The damping coefficient γ_c is obtained from the resonance frequency ω₀ and the quality factor Q of the oscillator under liquid. The hydrodynamic load on the cantilever beam varies with tip–substrate separation, but is constant for 130 nm < h < 1 μm.⁶² In this range h is much smaller than the height of the tip cone. Therefore, ω₀ and Q are determined from the thermal noise spectrum measured at a distance of 140 nm from the surface.⁶³ At this distance, the tip–substrate interaction is supposed to be negligible. Figure 2 shows the photothermal response function, measured at a distance of 140 nm. This response is compared with the response calculated from the thermal noise spectrum. The slight difference between both response functions is caused by the thermal driving coefficient A_T^* which is also frequency dependent, see Appendix A. Knowing k_int and γ_int one can calculate both the conservative part F_c of the interaction force (by integration of k_int) and the dissipative force F_d. However, we will use k_int = −∂F_c/∂h and γ_int = −F_d/ḣ themselves, because we calculate the excess pressure Π in the liquid film between tip and substrate. For a spherical colloidal probe with radius R_tip the relation between the measured k_int and the non dissipative part of the excess pressure Π_c = [Π–ḣ ∂Π/∂ḣ] between tip and substrate turns out to be quite simple. Because the local thickness of the liquid film can be approximated with h(r) = h₀+r²/(2R_tip), where h₀ is the distance between substrate and the apex of the tip, the conservative part of the force on the tip exerted by the liquid film is calculated as F_c(h₀) = ∫₀–Π_c(h) 2πrdr ≃ 2πR_tip∫_h0^∞–Π_c(h)dh. Differentiating left and right-hand side of last equation with respect to h₀ then results in

4

while the interaction damping is given by

5

Figure 2.

(a) Example of an amplitude- (black) and phase- (blue) distance curve, measured with a colloidal tip. The fluid is 100 mM NaCl solution at pH 5.7. The amplitude is normalized by A_∞, the phase is determined with respect to ϕ_∞, both measured at 140 nm. (b) Measured frequency response of the same cantilever (amplitude: black dots, phase: blue dots) under photothermal excitation in liquid. The red lines represent the calculated response using the cantilever parameters determined from its thermal noise spectrum: k_c = 0.66 N/m, γ_c = 2.17 μNs/m, ω₀/2π = 16.11 kHz, ω/2π = 11 kHz, and A_∞ ≈ 0.8 nm.

2.2. Materials

As a substrate we use a part of a silicon wafer covered with a thermally grown silica layer, 90 nm thick. The sample is firmly glued, using epoxy, to a stainless puck, which is magnetically clamped to the piezo stage of the AFM. The RMS roughness of the surface is approximately 0.2 nm for a 1 μm × 1 μm area. Prior to use, the substrate is rinsed with consecutively isopropanol, ethanol and ultra pure water (Milli-Q Inc.) in a sonication bath for 10 min. After drying with a jet of N₂, it is exposed to a plasma of residual air (Harrick Plasma) during 30 min. The cantilevers are cleaned in a similar manner without using a sonication bath. The electrolyte solutions are prepared by dissolving NaCl (Sigma-Aldrich) in ultra pure water. The pH of the solution is controlled by adding NaOH. The resulting pH value is measured using a HI 1053 probe (HANNA Instruments). For our measurements we used 3 solutions with a pH of 9.3 and 2 with pH 5.7. The sodium concentration ranged between 0.1 mM and 100 mM, see Table 1. To obtain the desired concentrations, first a stock solution of 1 M NaCl was prepared by weighing in the right amount of NaCl salt. From this 10 mL amounts of 100, 10, 1, and 0.1 mM NaCl were obtained by repeated dilution. These solutions have a pH of 5.7. To raise the pH to 9.3, 10 μL of 0.1 M NaOH is added to 10 mL of the NaCl solutions. As we will discuss later on, during the experiments the lowest concentration turns out to be 0.2 instead of 0.1 mM. This is most probably due to slight contamination of the sample during the nonperfect fluid exchange in the measuring cell.

Table 1. Best Fitting pK Values, Debye Length κ^–1, Surface Potential eψ_∞/k_BT, Surface Charge σ_∞, and Color Code Used in the Graphs, for the Electrolyte Solutions Used in This Study^a.

pH	[NaCl] [mM]	pKH	pKNa	κ–1 [nm]	eψ∞/kBT	σ∞ [e/nm2]	color
9.3	0.2	8.345	1.775	20.6	–5.65	–0.092	black
9.3	1.0	7.837	1.775	9.6	–4.84	–0.131	blue
9.3	10	8.345	1.775	3.1	–2.81	–0.141	red
5.7	1.0	5.950	1.750	9.7	–3.65	–0.070	cyan
5.7	100			1.0			green

^aSee also the remark below eq 13 about our definition of ψ_∞ and σ_∞.

2.3. Instrumentation and Experimental Procedures

The measurements are carried out on an Asylum ES AFM equipped with photothermal excitation (Blue drive), a sealed fluid cell and a temperature control unit. We use cantilevers with a colloidal probe as a tip. Such cantilever is a rectangular beam with a cone-shaped silicon tip (Team nanotec, LRCH, R_tip = 1080 nm). The beam is a bilayer of typically 1.5 μm thick silicon with a 50 nm thick coating of gold. Length and width of the beam are about 150 and 15 μm, respectively. The total tip cone height is typically 15 μm and the full-cone angle 45°. The AFM cantilever is completely immersed in a droplet of electrolyte that is sandwiched between the substrate and the top of the cell. The volume of the droplet is 0.2 mL. The electrolyte is injected and removed via a pair of plastic syringes (free of lubricants). To exchange the electrolytes, a new solution is injected via the inlet while at the same time the mixed solution is sucked out via the outlet of the fluid cell. Before we replace the fluid, the cantilever is withdrawn from the surface and repositioned afterward. During an exchange step in total 4 mL, i.e., 20× the drop volume, is injected, which is assumed to be sufficient to remove all the original liquid. After exchanging the electrolyte solutions, we wait approximately 10 min to equilibrate the system. The AFM scanner is placed in a chamber with temperature control. The temperature of the chamber has been set to 30 °C. During the actual measurement of the tip–sample interactions, the cantilever is driven at a frequency ω ≈ 0.7ω₀ by an intensity-modulated blue laser diode that is focused on the gold coated topside of the cantilever close to its base. This direct photothermal driving prevents the excitation of extra resonances (“forest of peaks”) usually observed with acoustic driving,⁵⁴ that complicates the analysis severely, as described in refs (55,64). Figure 2 shows a very smooth transfer function which is characteristic for photothermal excitation. The amplitude of the cantilever oscillation is set to approximately 0.8 nm by tuning the intensity of the blue laser. For each amplitude- or phase-distance curve, the distance between cantilever and surface is ramped from 140 to 0 nm at a ramp velocity of 75 nm/s. For each fluid composition we measure typically 10 to 30 approach curves. One of the most crucial steps for the reliability of our conclusions regarding the enhanced electroviscous damping is an accurate procedure to determine the tip–sample contact position. This procedure involves a combination of amplitude-phase-distance curves and the average static deflection of the cantilever, as described in Appendix F. For the present conditions of relatively stiff cantilevers (k_c = 0.66 N/m), small free oscillation amplitudes at large distance (<1 nm) and slow approach rates, the uncertainty amounts to δh₀ < 1 nm. It takes 20 to 30 min to measure one fluid composition. Judging from the amplitude- and phase-distance curves, the tip–sample interaction does not vary within this timespan. This implies that the pH level stays constant and the solution does not suffer from adsorption of, for instance, CO₂. The position of the driving laser and the detection laser is kept fixed with respect to the cantilever throughout all measurements.

3. Results

In this section we present our experimental results. First we discuss the conservative forces and how we determine the surface charges. These data are used as input for the analysis of the dissipation measurements, which will be discussed next in the context of electrolyte composition and charging behavior of tip and substrate.

3.1. Conservative Forces and Surface Charge

In Figure 3 the primary results of our measurements with the colloidal probe have been presented. The characteristic transition in the A(h) and the ϕ(h) curves, as given in Figure 3a and b, reflects the range of the electrostatic interactions which is given by the Debye length κ^–1. For a 1 mM salt solution it is approximately 10 nm. The resulting force gradient (interaction stiffness) in Figure 3c, shows this dependence on κ^–1 even better: the final exponential decays are 1/3.2, 1/10, and 1/18 nm^–1 for 10, 1, and 0.1 mM and pH = 9.3, respectively, see also Figure 4d. For 10 and 1 mM these values match with the estimated Debye lengths of 3 and 10 nm. For the lowest concentration we conclude from this observation that the intended concentration of 0.1 mM is in fact 0.2 mM. At these low concentrations the solutions are very sensitive to slight contamination of the sample for instance due to nonperfect fluid exchange in the measuring cell, which can explain the observed deviation. To relate the measured interaction stiffness with the electrostatic properties of the electrolyte film, tip, and substrate, we use DLVO theory incorporating charge regulation due to surface chemistry.

Figure 3.

Amplitude (a) and phase (b) response of the colloidal probe cantilever as a function of tip–substrate separation. The amplitude is normalized by A_∞, the phase is with respect to ϕ_∞ = 0. From these data the interaction stiffness k_int (c) and interaction damping γ_int (d) are determined.

Figure 4.

(a) The normalized merit function for the tested (pK_H, pK_Na) pairs for a solution with pH 9.3/1 mM. (b) The contour plot of the surface charge; the blue line matches the maximum merit curve in (a). (c) The normalized merit function for the tested (pK_H, pK_Na) pairs for all four solutions. (d) The electrostatic part of the measured interaction stiffness versus tip–substrate distance (dots) and the best fitting calculated curves (lines) for the four solutions: pH 5.7/1 mM (cyan), pH 9.3/0.2 mM (black), pH 9.3/1 mM (blue), and pH 9.3/10 mM (red).

DLVO Calculation

The conservative DLVO force per unit area or disjoining pressure Π between tip and substrate results from three contributions, i.e., the osmotic, electrostatic, and van der Waals pressure:

6

The first term represents the osmotic contribution:

7

with ψ being the electric potential, e the elementary charge, and k_BT the thermal energy. Z_i is the valency and n_i^∞ the bulk concentration of ions of species i. In our experiment four ionic species are present, as there are cations and anions from dissolved NaCl as well as hydroxide and hydrogen ions due to auto hydrolysis. The second term represents the electrostatic contribution:

8

with ε₀ the electric permittivity of vacuum and ε_r the relative dielectric constant of water. In the third term:

9

A_H represents the Hamaker constant. Note that Π_osm and Π_el depend on both the tip–substrate distance h and the local distance to both surfaces, but their sum depends only on h. Calculation of the osmotic and electrostatic contribution requires knowledge of the electric potential between the tip and the substrate. This potential is governed by the Poisson–Boltzmann equation, which is conventionally solved by assuming either constant charge or constant potential on tip and substrate. These assumptions are justified for large tip–substrate separations (where tip and substrate only weekly interact with each other), but usually fail in the regime of small tip–substrate distances. In this regime (κh < 10, where κ is the reciprocal Debye length) the local charge density and potential vary with separation distance h to compensate the confinement-induced modification of the surface chemistry. We consider two surface reactions, deprotonation of the silanol groups, ∼ SiOH ⇌ ∼ SiO^– + H⁺, and adsorption of Na⁺ ions on the deprotonated sites, ∼ SiONa ⇌ ∼ SiO^– + Na⁺, with equilibrium constants:

10

and

11

respectively. Here the index s indicates the surface itself and d the boundary between the Stern layer and the diffuse part of the double layer. Moreover, the total site density Γ is constant:

12

Note that the distribution of Na⁺ and H⁺ ions is governed by the Boltzmann relation, and their concentrations near the tip and substrate differ from the bulk. The surface potential ψ_s is related to the diffuse layer potential ψ_d via the Stern layer capacitance: C_s = εε₀/d_s = σ/(ψ_s–ψ_d). Combining eq 10 to 12 the surface charge σ = −e{SiO^–} can be expressed as

13

with d_s = 0.4 nm the thickness of the Stern layer. The procedure to calculate the electrostatic potential and the surface charge is explained in detail by Zhao et al.⁴⁶

It should be noted that in this study the surface charge is defined as the sum of the charge accumulated in the substrate or zero plane and the charge in the Stern or β plane, while the surface potential is defined as the potential at the β plane as defined in Figure 1.

Surface Charge Determination

Eq 13 provides the boundary conditions for the Poisson–Boltzmann equation. In this expression the bulk concentrations of the ions are known. The site density and the stern layer capacitance are more consistently reported in literature than the pK values of the considered reactions.⁴⁶ Therefore, we take pK_H and pK_Na as the parameters to fit. For each pair of pK values we can evaluate Π_calc numerically as a function of tip–substrate distance h and compare them with the experimentally found Π_exp. The fit quality is characterized by a merit function⁴⁶Q(pK_H, pK_Na) = 1/χ² where χ² = ∑_j {Π_calc(j) – Π_exp(j)}². Data at separations h < 5 nm are not used in the fitting procedure, because the DLVO theory, as it is continuous in nature, is inadequate to describe the interactions at these small distances.¹ Moreover, at these distances van der Waals forces and the oscillatory solvation forces due to ordering in the liquid become dominant. In Figure 4a, we show the merit function for the data measured at pH 9.3/1 mM. The function is normalized by its maximum. It is worthwhile to note that the best fitting pairs are not unique. This is because the excess pressure Π is governed by σ, which is a function of both pK_H and pK_Na, as shown in eq 13. The decrease of charge by promoting deprotonation, e.g., decreasing the pK_H, can be fully compensated by promoting at the same time cation adsorption, e.g., increasing the pK_Na. This explains the strong correlation between the optimal values of pK_H and pK_Na as observed in Figure 4a. The slight variation along the optimal merit curve is unphysical and caused by the resolution with which the pK values are probed. It can be suppressed by increasing the resolution, at the expense of considerably longer calculation times. In Figure 4b the merit functions for all relevant electrolyte solutions have been shown. Because the correlation between both pK values in the optimal merit curve depends on concentration and pH, we expect different optimal merit curves for different concentrations and pH values. However, provided that the pK values are invariant under pH or ionic strength variation (and that the experimental errors are negligible), we expect one unique (pK_Na, pK_H) pair for all conditions, and all the curves should cross this unique point. As we observe from Figure 4b the maximum merit curves for pH = 9.3 indeed cross each other almost in a single point near (pK_Na, pK_H) = (1.7 ± 0.1, 8.2 ± 0.2). However, the curve for pH = 5.7 strongly deviates, resulting in a quasi-triangular region near (pK_Na, pK_H) = (2.0 ± 0.4, 7 ± 1.4). This observation is in agreement with previous findings.^46,65,66 As the value of this optimum is considerably lower than the optimum for pH = 9.3 only, we conclude that our description of the charge regulation is too simplistic. An exact model of the charging behavior at variable pH would require a more complex reaction scheme. For our present purposes, however, the exact surface chemistry is not a major concern. Our primary goal is to determine the surface charge for a given fluid composition. In that respect, it is sufficient to realize that the combinations of pK values that fit the experimental force curves equally well, all correspond to constant surface charges. This is indeed the case, as illustrated in Figure 4b for the specific case of pH 9.3/1 mM NaCl. The corresponding surface charges (at infinite tip–sample separation) for the other fluid compositions are summarized in Table 1, along with the optimum pK values, surface potentials and Debye lengths. In Figure 4d, the best fitting interaction stiffness curves are compared with the experimental data in a semilog plot, showing in all cases a nice agreement between fit and experiment. The exponential decay of the curves confirms the expected Debye length. In Figure 5a, the resulting surface charge is shown as a function of the tip–surface separation. The magnitude of the surface charge decreases with decreasing separation. This is a consequence of the charge regulation: the concentration of both H⁺ and Na⁺ increases in the overlapping diffuse layer when it becomes thinner. Therefore, the chemical equilibrium shifts toward a higher H⁺ and Na⁺ adsorption, reducing the number of charged sites on the substrates. As expected, the surface charge dramatically increases when the pH changes from 5.7 to 9.3. A high pH favors the deprotonation of the silica substrate, so the surface becomes more negatively charged. At a Na⁺ concentration of 1 mM, it increases from −0.07 to −0.13 e/nm². The concentration dependence as observed in Figure 5b is less obvious. On the one hand due to the increasing bulk concentration of the sodium, [Na⁺]_∞, the equilibrium should shift toward a higher sodium adsorption. This is represented by the shift of the charge regulation curves (eq 13, the full lines in Figure 5) to the right with increasing concentration. But on the other hand the Debeye length (which is hardly affected by pH variation) decreases. This steepens the solution of the Grahame equation with increasing concentration, see the dotted lines in Figure 5. So the adsorption is reduced. The net effect is a gradual increase of the surface charge with concentration as can be observed from the downward shift in the crossing points of the full lines with the corresponding dashed lines.

Figure 5.

(a) The calculated surface charge as a function of separation distance. The color scheme is the same as in Figure 3. (b) The surface charge versus dimensionless potential as obtained from charge regulation (full lines) and from the PB equation (Grahame equation, dotted lines), for the four solutions. The crossing of corresponding curves indicate the actual surface charge at large tip–substrate separations.

3.2. Dissipation in the Electrolyte Film

Figure 3d shows the measured damping coefficient γ_int as a function of the tip–substrate distance h. As expected, γ_int is found to diverge as the tip approaches the surface. The curves also display a clear dependence on ionic strength and pH. As a reference, we calculate the hydrodynamic damping for a spherical tip approaching a flat substrate in a neutral liquid. Assuming no slip on tip and substrate, the hydrodynamic or Reynolds damping γ_ref(h) is for h/R_tip < 0.15 within 5% accuracy given by⁶⁷

14

where η_b is the bulk viscosity of the solution, 0.797 mPa s at T = 30 °C, R_tip = 1.08 μm the radius of the tip, and h the separation between the tip apex and the substrate.

Before comparing the experimental data to the reference case, we need to correct for the offset Δγ_c of the finite tip–sample damping at the cantilever calibration distance of 140 nm. For a colloidal probe with a radius of 1.08 μm the hydrodynamic damping is approximately Δγ_c = 0.09 μNs/m as we learn from eq 14, which is 4% of the value obtained from the calibration: γ_c ≈ 2.17 μNs/m. With this correction in place, all curves display the expected asymptotic scaling ∝ h^–1 for h > 100 nm, as shown in Figure 6.

Figure 6.

Damping coefficient, γ_int versus tip–substrate distance h from Figure 3d plotted on logarithmic scales. The reference case, pH 5.7/100 mM, has been plotted in green. Other curves are pH 9.3/0.2 mM (black), pH 9.3/1 mM (blue), pH 9.3/10 mM (red), and pH 5.7/1 mM (cyan). The dashed line represents the Reynolds damping, eq 14, using the value for bulk viscosity and has a slope −1.

We expect that the measured damping for the pH 5.7/100 mM solution behaves for h > 5 nm like the reference because in this case the surface charge is fully screened within the first few nanometers due to the Debye length of only 1 nm. The Reynolds damping as calculated with eq 14, the black dashed line in Figure 6, matches nicely with the green γ_int curve, measured for pH 5.7/100 mM, indeed. It also confirms the no slip assumption, which is in agreement with previous findings for hydrophilic surfaces.^27,28,68 In contrast to the data measured at pH 5.7/100 mM, the damping, γ_int(h), measured for the other four electrolyte solutions significantly deviates from the Reynolds damping. This implies that the dissipation, and so the friction, in the electrolyte film depends on the ionic charge distribution. Using the expectation based on Reynolds theory as a reference, we define the damping enhancement coefficient c_ev as

15

In Figure 7c_ev is plotted versus κh for 4 electrolyte solutions. When the tip approaches the substrate (decreasing separation), the enhancement increases monotonically until it reaches a maximum for κh ≲ 0.5. On further approach the enhancement decreases again, but here the tip is so close to the interface that nonelectric interactions like van der Waals forces and short-range solvation forces come into play. Therefore, we do not consider these short distances in our analysis. It should be noted that the absolute value of the dissipation enhancement curves depends crucially on the accuracy of the tip–sample contact position. Allowing for an uncertainty of ±1 nm, as discussed in the experimental section would lead to an increase or decrease of the maxima of the curves in Figure 7 by approximately a factor of 2. However, the qualitative shape and the relative order of the curves are not affected by this uncertainty. The maxima of the curves in Figure 7 correlate with the surface charge on the bounding surfaces, see Table 1. For larger distances this correlation persists for the pH 9.3 curves, but the behavior of the pH 5.7 curve (cyan) deviates from this trend. To understand the observed dissipation behavior at least qualitatively, we consider two effects. Due to the surface charge on tip and substrate counterions accumulate in the electrolyte film between them, where the ions get trapped in the local potential field. This causes an additional body force on the electrolyte film that hinders the squeeze-out of liquid in the thin film when the tip approaches the substrate and enhances the dissipation in the film.¹⁵ This is known as the classical electro-viscous effect. To estimate the enhancement we assume that the ion distribution relaxes fast to its equilibrium distribution at the momentary tip–substrate distance on a time scale much shorter than the squeeze-out time scale. Knowing the mobility of the ions and their distribution in the film, we can calculate the resulting radial electric field E_r and from that the body force ρ_eE_r on the liquid. This force is taken into account when we calculate the pressure needed to squeeze-out the liquid in the film. The second effect that we consider is the electric field dependence of the viscosity which also enhances the dissipation in regions with a high electric field i.e. near the charged substrates.⁶⁹ This is called the visco-electric effect:

16

We will calculate the modification of the flow profile in the gap due to these effects. Although we are aware of the restrictions, we use the standard mean field approach and solve the Poisson–Boltzmann equation assuming a Stern layer of adsorbed cations and a diffuse outer double layer to determine the ion distributions, as we did for our surface charge calculations. The governing equations for the flow field u are given by the continuity equation and the Navier–Stokes equation:

17

where ρ is the density of the electrolyte solution, η its viscosity, 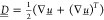is the rate of strain tensor and ρ_eE the body force acting on the liquid. Because the equilibration time of the ions is short compared to the characteristic time of the oscillating flow, ωh²/D_ion ≃ 5 × 10^–3 for ω/2π = 10 kHz, h = 10 nm, and D_ion ≃ 10^–9 m²/s, we consider the equilibrium ion distributions, instead of solving the Nernst–Planck equation for the ion densities and fluxes. Therefore, we model the body force in radial direction, see Appendix B for details, as

18

Here n^± = exp(∓eψ/k_BT) is the local cation and anion concentration while D_± is the cation/anion diffusion coefficient. Moreover, because h²ρ/μt₀ ≃ 10^–5, hρ U₀/μ ≃ 10^–6, and h/R_tip ≃ 10^–2, eq 17 reduces to

19

Because ψ(z,h) is known from the DLVO analysis, we can calculate ρ_eE_r using eq 18 and solve u_r(z) for given r from eq 19. Applying the boundary conditions u_r(0) = u_r(h) = 0, we get the flow profile, see Appendix C:

20

where w(z,h) is a dimensionless function, with w(0,h) = w(h,h) = 0, which has to be calculated numerically. To establish a relation between ∂_r p and U₀ we consider the continuity equation:

21

Here U₀ is the speed of the cantilever tip with respect to the substrate. Because ∂_r p does not depend on z we can rewrite last equation as

22

where w_av(h) = h^–1∫₀^hw(z,h) dz. Next, the dissipative force is calculated from the ∂_rp profile under the tip:

23

Eventually, we obtain for a spherical tip with radius R_tip and a flat substrate:

24

In Appendix C we explain in detail how the actual calculations are performed. Once γ_int is known, the electro-viscous coefficient is given by

25

In last expression we used 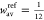. The results of these calculations are shown in Figure 8.

Figure 7.

Measured electro-viscous enhancement c_ev = γ_int/γ_ref – 1 versus dimensionless tip–substrate distance κh for pH 5.7/1 mM (cyan curve), pH 9.3/0.2 mM (black curve), pH 9.3/1 mM (blue curve), and pH 9.3/10 mM (red curve). The inset shows c_ev versus h.

Figure 8.

Measured c_ev = γ_int/γ_ref – 1 as a function of κh (a), compared with calculated curves for the electro-viscous case with κδ = 1 (b), the visco-electric case with f_ve = 2.4 × 10^–14(m/V)² (c) and the combined effect with f_ve = 1.2 × 10^–14(m/V)² and κδ = 0.5 (d). Color scheme as before. The inset of (a) shows the measured c_ev on logarithmic axes. The purple curve is the expectation for large κh.

Electro-Viscous Effect

In Figure 8b the results for the electro-viscous model are shown. The electric body force ρ_eE_r, and so the strength of the effect, is determined by the dimensionless number κδ, see Appendix C, which is defined as

26

δ can be considered as the effective thickness of the stagnant layer near substrate and tip due to the ion distribution. This thickness is under our experimental conditions close to the Debye length κ^–1. Comparing these curves with the experimental results in Figure 8a, we observe that the calculated coefficients are of the right order of magnitude, specially for the pH 9.3/10 mM case (black curves), but the width of the calculated curves is much larger than experimentally observed. Moreover, the observed dependence on substrate surface charge is opposite to the model calculations. In fact the maximum c_ev value scales with the surface potential ψ_∞ instead of the surface charge σ_∞ because the radial field E_r is a monotonic increasing function of ψ. Reducing the value for κδ, results in an enhancement of c_ev, but hardly reduces the width of the curves, nor does it change the order of the curves. So this model fails to predict the observed effect correctly.

Visco-Electric Effect

In Figure 8c the results for the visco-electric model are shown. In this case the dissipation enhancement is controlled by the coefficient f_ve. This coefficient has never been conclusively measured for water but it is estimated⁷⁰ to be of the order 10^–15(m/V)². This implies that the local viscosity will double in value for electric field strengths of the order 3 × 10⁷ V/m. When we solve the PB equation, we also obtain the local field strength E_z(z,h) in the electrolyte film for all tip–substrate separations and all fluid compositions. Close to the wall, the electric field is in the order of 10⁷ V/m. In the middle of the gap, the field strength decays to zero due to the symmetry of the equally charged tip and substrate. In our calculations we optimized the value for f_ve and found that for f_ve = 2.5 × 10^–14(m/V)² the maxima in the calculated curves match rather well with the experimental results. More importantly, the calculations predict the observed dependence on substrate charge density now correctly, i.e., the order black-blue-red for the pH 9.3 curves is nicely reproduced, because the local electric field increases monotonic with the surface charge σ_s ≃ σ_∞. Also the width of the calculated curves, although still a factor two off, matches much better with the experimental observations. While the electro-viscous calculations only reproduce the strength of the enhancement within an order of magnitude, the visco-electric calculations reproduce also the observed surface charge dependence quite well as well as the width of the experimental enhancement curves. To observe the combined effect we plot in Figure 8d the curves obtained for κδ = 0.5 and f_ve = 1.2 × 10^–14(m/V)².

4. Discussion

To understand the behavior as shown in Figure 8 we go back to Figure 1b and consider a simple picture in which the regions in the liquid film near both substrates have a flow resistance that is considerably higher than in the bulk due to either viscosity enhancement or opposing body forces. These layers of enhanced flow resistance have a typical thickness δ. For large separations h the flow will avoid these high resistance layers and the damping will behave like γ = 6πη₀R_tip²/(h – 2δ). This γ(h) dependence is indicated by the upward curving blue line in the inset of Figure 9. However, when tip and substrate come close together, h ≃ 2δ, the liquid is forced to flow through the high resistance layers. Supposing an effective viscosity η_eff > η₀, the damping behavior for h < δ will be given by γ = 6πη_effR_tip/h. This dependence is indicated by the upper black line with slope −1. With this limiting behavior for both h ≪ δ and h ≫ δ, the overall behavior will be given in good approximation by the red curve in the inset of Figure 9. This curve agrees qualitatively quite well with the experimental results in Figure 6. The lower black line with slope −1 represents the dissipation behavior in absence of any enhancement, and corresponds with the dashed black line in Figure 6. Translating the red curve into the enhancement curve c_ev(h) = γ/γ_ref – 1 we obtain the full red curve given in the main figure. Comparing this curve with the curves in Figure 7, we observe for h > 2 nm qualitatively the same decaying behavior with increasing separation with a typical decay length of about 5–10 nm. However, the behavior for h < 2 nm is different. In part, this is caused by the charge regulation. In our simple picture we assumed a constant effective viscosity in the high resistance layers. But in Figure 5a we observe that for h → 0 the surface charges decrease. Hence we expect that for small h values the flow resistance in this layer decreases, too. This will result in an h dependence of the viscosity enhancement as given by the dashed red line in Figure 9. With the discussion around Figure 9 in mind we consider again the results from Figure 8. In our qualitative picture the enhancement for large distances depends only on the effective width δ which will be proportional to the Debye length κ^–1. Indeed we see that the blue and cyan curves in Figure 8a, which have the same value for κ^–1 ≃ 10 nm, overlap for κh > 3. Looking at the inset of Figure 8a, the curves become very noisy at larger κh values but the trend confirms our expectation as indicated by the purple dotted curve, c_ev = (κh–1)⁻¹. Considering the other limit, κh < 2, the enhancement is now mainly determined by the resistance increase in the friction layers. This increase should depend primarily on the local potential (in case the friction is caused by the electric body forces, see Appendix B and C) or the local electric field strength (when the friction is caused by viscosity enhancement, see Appendix D). In the first case (Figure 8b) the friction enhancement scales monotonically with the local potential, while in the second case (Figure 8c), which agrees better with the experimental results (Figure 8a), the viscosity enhancement scales with the square of the surface charge on tip and substrate and thus with the square of the local field strength. Finally, for κh ≪ 1 the potential in the liquid film increases with decreasing h and becomes independent of the position in the film.⁷¹ This is called the zero field limit and implies that in both scenarios the friction enhancement will reduce to zero. Hence, for κh → 0 also the c_ev coefficient should reduce to zero. The onset of this trend indeed seems to be visible in the experimental c_ev(h) curves. Comparing both scenarios we may conclude that friction enhancement due to viscosity enhancement in the double layer describes our experimental findings fairly well. In this case the behavior can be explained in a simple picture taking into account both the effective layer thickness, that is close tot the Debye length, and the surface charge density on tip and substrate. However, the value obtained for the viscosity enhancement coefficient f_ve = 2.5 × 10^–14 is quite large compared to the value estimated in literature, 1 × 10^–15 (m/V)². In contrast, the electro-viscous model provides a much poorer description of the data. In particular, the model fails to predict the correct order of the damping enhancement as a function of the fluid composition (Figure 8b). Moreover, the range of the enhancement extends much farther from the surface than observed experimentally.

Figure 9.

Expected dissipation behavior in a simple “enhanced friction layer” picture.

Earlier Approaches

The hydrodynamic drag force for two charged surfaces that approach each other in an electrolyte solution has been investigated theoretically.⁷²⁻⁷⁴ In these studies the squeeze-out flow of the ions in the electrolyte film between two adjacent particles is opposed by an inward electro-osmotic flow to conserve the charge neutrality in the film. This osmotic flow is driven by a streaming potential, which is established by the initial outflow of ions. Chun and Ladd give a detailed analysis,⁷² including the case of two parallel surfaces in an NaCl environment. They consider the system to be quasi-static and use the narrow gap approximation, based on the same arguments as we have given above. They obtained a numerical estimation for c_ev, considering constant charge and constant potential as boundary conditions for the PB equation. Their results show for both boundary conditions that the electro-viscous coefficient increases gradually when the gap height decreases from κh = 10 to κh = 3 to c_ev = 0.4. It decreases sharply when the separation is further reduced from κh = 3, and it approaches zero when κh → 0. The maximum enhancement is much smaller than our experimental observation. If we consider a parabolic tip on a flat surface, the electro-viscous coefficient c_ev is expected to be smaller, as shown in ref (73) for the case of two spherical particles, resulting in an even larger deviation between prediction and measurement. Their findings thus support our conclusion that the observed enhanced damping is probably not caused the classical electro-viscous effect.

Microscopic Properties of the Stern Layer

Overall, our comparison of the experimental data to the two competing models is based on a number of simplifying assumptions. First, of all, we make use of Poisson–Boltzmann theory despite the fact that we observe the enhanced damping in a region of very high surface charge, where crowding effects may matter and affect the mobility of ions.⁷ Moreover, we assume a classical rigid Stern layer model with immobile ions and a no-slip boundary condition and constant dielectric permittivity for the water. Detailed numerical studies⁷⁴⁻⁷⁸ in recent years have demonstrated that many of these assumptions are violated to some extent. For instance, Bonthuis and Netz⁴⁸ show in a theoretical study that within a few Ångstrom from the substrate the viscosity strongly increases while the relative permittivity decreases from 81 in the bulk to 1 near the substrate. Aluru and co-workers^50,51 give, based on molecular dynamics calculations, an estimate for this viscosity enhancement, which is of the same order of magnitude as the estimation of Lyklema.⁶⁹ Moreover, their calculations show a decrease of the mobility of the counterions within the first nm from the substrate. Several experimental studies corroborate the conclusions from these theoretical investigations. More detailed numerical studies will be required to reach a quantitative understanding of the enhanced dissipation in confined electrolyte layers.

5. Conclusion

We have studied the hydrodynamic damping in thin electrolyte films with overlapping electric double layers, using AFM amplitude modulation force spectroscopy. The AFM technique has a unique advantage compared to conventional approaches. It enables the simultaneous determination of both the surface charge density and the hydrodynamic damping as a function of the tip–substrate distance by analyzing the conservative and dissipative part of the measured force–distance curves. Our analysis of the conservative part of the tip–substrate interaction shows that one can accurately measure the surface charge density on tip and substrate with AFM force spectroscopy. From the force–distance measurements in electrolyte solutions with varying ionic strength and pH, we observe that the viscous dissipation enhancement is correlated with the surface charge density on tip and substrate as well as the ionic strength (e.g., Debye length) in the electrolyte film. Using the measured surface charges, the enhancement in dissipation is calculated following two scenarios; (i) from the excess ion distribution and streaming current in the diffuse layer, (ii) from the viscosity enhancement due to the strong electric field in the double layer. The experimental data agree qualitatively with the calculations, the order of magnitude of the effect is correctly reproduced, but for case (i) the calculated surface charge dependence is not in agreement with the experimental observations, nor is the distance dependence. For case (ii) the surface charge dependence agrees quite well with the experimental observations and also the distance dependence is much better reproduced. However, the value obtained for the viscosity enhancement coefficient is approximately a factor 25 larger than the value estimated in literature. Our analysis shows that the description of an electric double layer using a mean field approach is not sufficient when it comes to the details of the electro-hydrodynamic dissipation near charged substrates. Moreover, the interfacial water layer at a charged surface, a few Ångstroms thick, can be superviscous while the conductance of the Stern layer may contribute substantially to viscous dissipation. However, the complex interplay between surface charge, structure of the interfacial water layer and surface conductance is far from resolved.

Appendices

A. Force Conversion with Photo-Thermal Excitation

The bending of the cantilever is driven by locally heating it with a laser beam. The laser intensity I varies harmonically as I = I₀+I_A exp(jωt) where ω is the driving frequency and I_A the amplitude of the oscillating intensity. Due to the oscillating temperature field over the cantilever, the relation between force F and tip displacement z is given by

27

where k_c is the effective stiffness of the cantilever and z_T the zero-load-deflection due to the temperature enhancement along the beam caused by the laser radiation with intensity I. According to linear response theory z_T can be written, for small thermal variations, as z_T(t) = ∫₀^∞A_T(t′) I(t–t′) dt′ or in the frequency domain as z_T(ω) = A_T(ω) I_A. The amplitude and phase of the tip displacement, z(ω) = Ae^jϕ, are measured as a function of the tip-substrate distance h, to probe the influence of the tip-substrate interaction on the oscillation behavior of the cantilever tip. We model the tip deflection as an harmonic oscillator:^59,60

28

where m*= k_c/ω₀² the effective mass of the cantilever including the added mass due to the surrounding liquid, ω₀ the resonance frequency, γ_c = k_c/(ω₀Q) its damping coefficient, Q the quality factor of the oscillator and F_ts the tip-sample interaction force given in eq 1. Substituting eq 1 into eq 28, we obtain

29

Writing z(ω) = Ae^jϕ and A_T^* = A_Te^jϕ_T the transfer function becomes

30

Because the thermal driving coefficient A_T^*(ω) is not known, we measure at a fixed frequency ω not only Ae^jϕ at a certain distance h but also A_∞e^jϕ_∞ at 140 nm from the substrate, where both k_int and γ_int are negligible small. Considering the ratio A/A_∞e^{j(ϕ–ϕ_∞)} we obtain with eq 30:

31

from which we obtain the force inversion formulas:

32

and

33

B. Estimate of the Body Force

We consider a parallel plate geometry with a distance h between the substrates. We assume, based on the fast equilibration time, that the ion distributions are in equilibrium, i.e.:

where ψ_# = eψ/k_BT. In this case the outward streaming current is balanced by an inward conduction current. The radial streaming current is given by

while the conduction current can be expressed as

Because in equilibrium j_str + j_cnd = 0 we can express E_r in u_r according:

while ρ_e = e(n⁺ – n^–). Therefore, we obtain for the body force:

34

C. Description of the Actual Dissipation Calculation

To perform the actual calculation we make eq 19 dimensionless:

where w = u_r/u₀ and ζ = z/h. Moreover, we write ρ_eE_r as

where 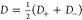and 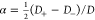. Defining:

we end up with

35

where

Appendix E describes how to solve this equation numerically with the boundary conditions w(0) = w(1) = 0. We can write the solution formally as w = f(ζ, h). Multiplying f(ζ, h) with u₀ results in the dimensional form of the flow profile:

with f_av(h) = ∫₀¹f(ζ, h) dζ

Note 1: Both δ and κ depend on the ionic strength n_∞, in such way that

Note 2: In case no surface charges are present, i.e., for ψ(z) = 0, the flow profile is just parabolic: ∂_ζ²w = −1. Hence, with f_av = 1/12 and we get the well known result:

For a sphere-plate geometry, characterized by 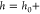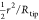, we indeed obtain the Reynolds damping force:

D. Calculation of the Visco-Electric Coefficient

According to Lyklema⁶⁹ the viscosity of water depends on the electric field strength according:

36

where f_ve ≈ 10^–15 m²/V² is the visco-electric coefficient. As the field strength varies with position we must consider the position dependence of the viscosity when solving the Navier-Stokes equation:

37

where is the rate of strain tensor. We investigate these relations in a parallel plate geometry in the limit h/R ≪ 1. Here h(r) is the gap height and R the characteristic radial distance. Neglecting inertia and the ∂_rψ term, eq 37 reduces to

38

while the continuity relation reads:

39

where U₀ is the velocity of the upper surface (i.e., the tip). To continue, we rewrite eq 38 in dimensionless form as

40

with ζ = z/h, η_r = η/η₀, and w = u_r/u₀. Because ∂_z∂_rp = 0 we can choose u₀ = −h²∂_rp/η₀ and write last equation as

41

The solution is again formally given by w = g(ζ, h) and w_av = ∫₀¹  g(ζ, h) dζ. Because ⟨u_r⟩ = −h²∂_rp/η₀w_av, we obtain for the pressure gradient:

42

which is, when one replaces g(ζ, h) with f(ζ, h), identical with eq 22. Hence, also the expression for γ_int is given again by

43

where g_av(h) = ∫₀¹ g(ζ, h) dζ.

To take into account both the electro-viscous and the visco-electric effect we can use the same approach and generalize our result by considering g(ζ, h) as the solution of:

44

where in this case δ² = η₀D/(2n_∞k_BT). Again, γ_int can be calculated with eq 43.

E. Solving Eq 44

Because eqs 35 and 41 are equal to eq 44, for η_r = 1 and δ^–1 = 0, respectively, we only need to describe how to solve the last equation. To do so, we define q(ζ) = η_r∂_ζw_r and rewrite the second order differential equation as two first order equations:

45

46

This set is solved using an iterative Runge Kutta integration scheme, with the boundary conditions w(0) = 0 and q(0) = q_guess. In the iteration process we optimize q_guess in such a way that eventually the second boundary condition for w, i.e., w(1) = 0, is fulfilled, too. This is achieved by taking an upper and lower limit for q_guess, take q_guess as the average of these two limits and calculate w(1) by applying the integration routine. If w(1) > 0 we replace the upper limit by q_guess, otherwise the lower limit by q_guess and repeat the process. In this way we restrict the possible values for q_guess to an interval that decreases every iteration by a factor two, until the difference between upper and lower limit is small enough.

F. Calibration of the Tip–Substrate Distance

To explain the calibration procedure we define in Figure 10 the substrate position z_s, the tip position z_t, and the base position z_b of the cantilever, such that the tip deflection u and the tip–substrate distance h are given by u = z_t – z_b and h = z_t – z_s, respectively. When the tip is in hard contact with the substrate, i.e., z_t = z_s, the local slope of the u vs z_b curve is −1 and the tip deflection is given by u′ = z_s–z_b′, so z_s is known from the extrapolation of the linear part of the curve to u = 0. When the tip interacts more weakly with the substrate, as indicated in the inset of the graph, we know that u = z_t – z_b by definition and from the geometry depicted in the inset that u = z_s – z₁. Hence, z_t = z_b+z_s–z₁ and the tip–substrate distance is given by h = z_t – z_s = z_b – z_s+u. So, once z_s has been determined properly on the z_b scale we can determine the tip-substrate distance h. The actual calibration is done by measuring for each tip-liquid-substrate configuration a few times but at least once the mean deflection curve u(z_b) up to hard contact (blue line in Figure 10) simultaneously with the amplitude curve A(z_b) (dashed blue line). From the first curve the value for z_s is determined. To prevent damage due to hard contact, most curves are measured with an amplitude set point of typically 80% of the amplitude at large distance. All these u(z_b) and A(z_b) curves (the red curves in Figure 10) are shifted along the z_b axis such that they optimally overlap with the blue curves. In this way we can determine the zero point of the u(h) curves within 0.5 nm. A real world example of the procedure has been shown in Figures S1 and S2 of ref (55).

Figure 10.

Full blue and red curve represents cartoons of typical mean displacement curves u = z_t – z_b versus z_b. The blue curve is measured up to the linear regime in hard contact, the red one only gently touches the substrate. Cartoons of the simultaneously measured amplitude vs distance curves (dashed lines) are also shown.

The authors declare no competing financial interest.