Significance
Topological mechanical metamaterials are a type of structure, which can be used to design and control softness. They have been proposed as components for many applications, including for cushioning mechanical shocks and isolation of mechanical deformations as well as controlling actuation and failure. We provide a realization of a specific type of topological structure—a gapped topological lattice in three dimensions. We then use this structure to localize soft deformations either on the surface of the material or in the bulk along line defects called dislocations.
Keywords: topological, metamaterials, dislocations, rigidity, isostatic
Abstract
Topological states can be used to control the mechanical properties of a material along an edge or around a localized defect. The rigidity of elastic networks is characterized by a topological invariant called the polarization; materials with a well-defined uniform polarization display a dramatic range of edge softness depending on the orientation of the polarization relative to the terminating surface. However, in all 3D mechanical metamaterials proposed to date, the topological modes are mixed with bulk soft modes, which organize themselves in Weyl loops. Here, we report the design of a 3D topological metamaterial without Weyl lines and with a uniform polarization that leads to an asymmetry between the number of soft modes on opposing surfaces. We then use this construction to localize topological soft modes in interior regions of the material by including defect lines—dislocation loops—that are unique to three dimensions. We derive a general formula that relates the difference in the number of soft modes and states of self-stress localized along the dislocation loop to the handedness of the vector triad formed by the lattice polarization, Burgers vector, and dislocation-line direction. Our findings suggest a strategy for preprogramming failure and softness localized along lines in 3D, while avoiding extended soft Weyl modes.
Mechanical metamaterials can control softness via a balance between the number of degrees of freedom (dfs) of their components or nodes and the number of constraints caused by connections or links (1–9). This balance, first noted by Maxwell (10) and later explored by Calladine (11), is termed isostaticity. In isostatic materials, softness can manifest itself via large-scale deformations [for example, as uniform Guest–Hutchinson modes (12, 13)] or via periodic soft deformations corresponding to so-called Weyl modes (14, 15). Uniform softness can be exploited to create extraordinary mechanical response (16), such as materials with a negative Poisson’s ratio (1, 2, 17). Alternatively, localized softness has been programmed into isostatic materials in one and two dimensions via a topological invariant called the polarization (3, 5) that controls mechanical response and stress localization (18) at an edge [including the edge of a disordered sample (19)], at an interface, or bound to a moving soliton (4). These mechanical (20–28) examples of topological metamaterials (29–31) exhibit a general feature of topological matter (32, 33): a correspondence between integer invariants in the bulk and response at a boundary. Large-scale and localized deformations are deeply intertwined, as can be seen in demonstrations in which topological soft modes are created or destroyed by applying large uniform strains (34). For many applications, such as cushioning (35), programmed assembly (36), or controlled failure (37), materials need to be designed with nonuniform yield behavior. Deformation or failure at a specified region can be programmed via a combination of topological polarization and localized defects (37, 38). Soft regions can selectively achieve large displacements [for example, in self-folding origami (36, 39, 40)] and isolate the rest of the material from strain (35).
Although there are a number of examples of isostatic periodic structures in one, two, and three dimensions, the 3D case is unique, because all prior realizations of 3D isostatic lattices include large-scale periodic deformations along continuous lines in momentum space (15, 35, 37). These Weyl lines define families of periodic soft modes in the material bulk and contain a number of modes that scales with the linear size of the structure. As ref. 35 explores, Weyl lines can be useful to create a metamaterial surface with anisotropic elasticity, but to create a material with a top surface that is much softer than the bottom, it proves necessary to collapse two Weyl lines on top of each other. An alternative would be to find a metamaterial without Weyl lines. However, these Weyl lines are generic and have a topological character, which ensures that they cannot be annihilated locally—a single Weyl loop can only be destroyed by shrinking it to a point. This presents a challenge in 3D isostatic metamaterial design: to achieve a “gapped” (i.e., allowing Goldstone modes but having no Weyl modes) topological material analogous to those in two dimensions (3, 5, 34), in which softness can be controlled and localized without modulating materials parameters. In contrast to traditionally used composite materials, such mechanical response can be designed to be topologically robust and independent from auxiliary properties, such as thermal or electrical conductivity.
In this work, we design gapped topological materials by exploring the parameter space of the generalized stacked kagome lattice and study the effect of defect lines in such 3D materials. Localizing topological states along these lines (i.e., codimension-2 manifolds) parallels recent interest in multipole topological insulators, which go beyond the usual case of bulk-boundary correspondence with a (codimension-1) hypersurface boundary (41, 42). Our strategy relies on the presence of a nonzero topological polarization oriented along the axis. This topological polarization P can be exploited to localize soft modes in the material bulk by introducing topological defects within the lattice structure called dislocation loops. These dislocations are characterized by a topological invariant called the Burgers vector b. Along the dislocation, we show that the topological charge characterizing the softness or rigidity of the lattice (with unit cell volume ) depends on the orientation of the dislocation line and is given by per unit length.
Gapping the Stacked Kagome Lattice
We examine the mechanics of metamaterial structures by using a lattice model for the displacements of nodes and strains of the links. We place a point mass at each vertex and connect the neighboring ones by linear springs. Such models capture the small-strain response of realistic structures that are either 3D-printed from soft polymers (35, 37) or assembled from construction sets (4) or laser-cut components (38). The mechanics of these ball–spring networks are captured via the linearized equation of motion , where is a N-dimensional vector containing the displacements of all particles in dimensions relative to their equilibrium positions. For a given lattice geometry, we calculate the dynamical matrix , which relates the forces exerted by springs to displacements of the particles. For simplicity, we work in units, in which all particle masses and spring constants are one. In the linear regime, we can find the dynamical matrix by first relating the -dimensional vector of spring extensions to the displacements via . The rigidity matrix contains entries determined by the equilibrium positions of the particles and the connectivity of the lattice. In combination with Hooke’s law, the matrix lets us calculate the dynamical matrix via the relation (2, 11). From the relation , we note that contains soft modes [i.e., collective displacements that (to lowest order) do not stretch or compress any of the springs]. However, the matrix relates forces on particles to spring strains via . From this relation, one notes that contains combinations of spring tensions that do not give rise to particle forces. These configurations are dubbed states of self-stress, because they define load-bearing states, which put the lattice under a static tension (11).
To calculate soft modes (states of self-stress), we need to numerically solve the configuration-dependent equation (). However, a mathematical result called the rank-nullity theorem lets us compute the difference between the number of zero modes and the number of states of self-stress (2, 5, 11). This difference, the softness charge , is given by the dimensionality of the matrix and can only change if balls or springs are either added or removed. We focus on the special case of isostatic, or Maxwell, lattices defined by when the system is considered under periodic boundary conditions. These lattices are marginally rigid and exhibit a symmetry between zero modes and states of self-stress.
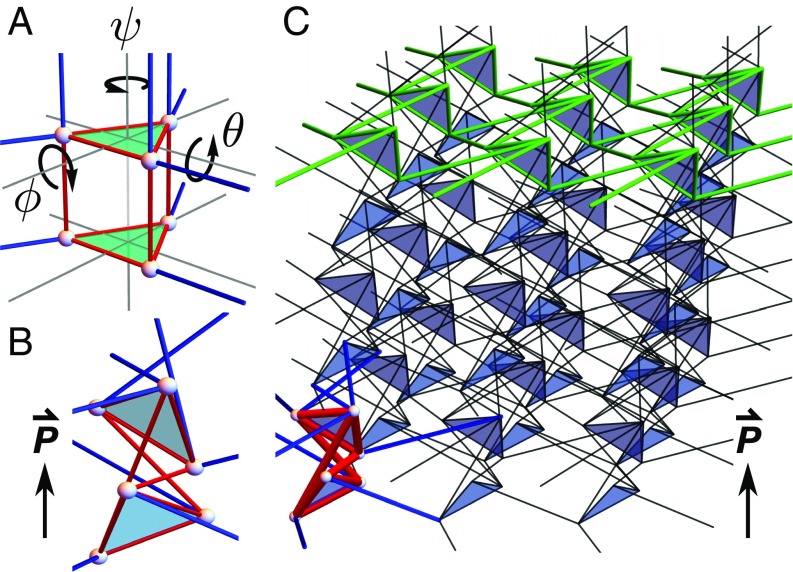
To design metamaterials based on simple, repeated patterns, we focus on periodic structures. Periodicity allows us to explicitly calculate zero modes and states of self-stress in a large sample. We begin with a highly symmetric, “undeformed” lattice and explore its configuration space by changing the positions (but not the connectivity) of the nodes. The specific geometry that we consider is illustrated in Fig. 1: this stacked kagome lattice has a coordination number and ; the lattice is isostatic. This lattice is based on the two-triangle unit cell shown in Fig. 1A, which corresponds to two unit cells of the kagome lattice stacked on top of each other. We deform the lattice via the orientations of the triangles, which are governed by the three angles of rotation around the axes, respectively. Within this structure, we explore a range for each of the three angles from to . In Fig. 1B, we show the deformed unit cell for a particular structure in this region, which corresponds to the choice . This unit cell builds the periodic geometry in Fig. 1C. We proceed to quantitatively show that this metamaterial has no Weyl lines.
Fig. 1.
Architecture of a 3D stacked kagome lattice. (A) We consider the doubled unit cell of a vertically stacked kagome lattice and rotate the top constituent triangle around three perpendicular axes by angles [the bottom triangle is rotated by ]. (B) For the choice of these parameters, we obtain a unit cell that corresponds to a (gapped) 3D lattice with a topological polarization P and without Weyl lines. (C) Architecture of the (gapped) metamaterial, with one unit cell emphasized in the lower left corner and a 2D kagome sublattice surface highlighted in green along the top.
We calculate the spectrum of normal modes by considering plane-wave solutions of the form , where the index refers to a particle within one unit cell and the lattice index enumerates different unit cells within a lattice. The three-component wave vector k is periodic in each component with . This collection of points forms the first Brillouin zone of the lattice. The Bloch representation of the rigidity matrix in this plane-wave basis is . A zero mode at wave number k is a vector of unit cell displacement that solves . Thus, within this setting, zero modes correspond to the zeros of the complex function . By examining this function, we find the zero modes for different configurations of the lattice.
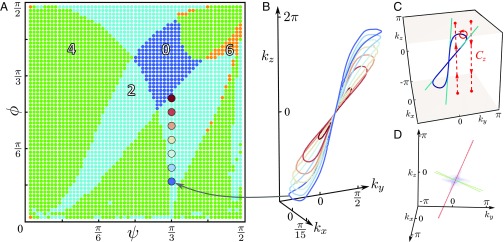
We numerically evaluate zero modes for the stacked kagome lattice (details are in Generalized Stacked Kagome Lattice and Soft Directions) and for most values of the angles , we find collections of zero modes along compact loops in k space (Fig. 2A). These Weyl loops, shown in Fig. 2 B and C, are analogous to 1D nodal lines (43–45) and experimentally observed 0D Weyl points (46, 47) in 3D electronic semimetals and photonic crystals. In isostatic lattices, the number of Weyl loops is always even, because the materials’ time-reversal symmetry maintains reflection symmetry in the Brillouin zone—each Weyl loop comes in a pair with its reflected partner (15). Furthermore, these loops attach to the origin of the Brillouin zone along soft directions (i.e., the lines tangent to the Weyl loops at the origin). We count the number of loops by looking at soft directions in the neighborhood of the origin, and in Fig. 2A, we plot this count in a slice of parameter space. In this phase diagram, we note regions with up to six different loops. Strikingly, the middle of the diagram displays a region in which no Weyl loops exist (Fig. 2 A and D).
Fig. 2.
Phase diagram of stacked kagome lattices. (A) The number of soft directions in – parameter space for (Fig. 1A). The region in dark blue corresponds to a gapped topological lattice, whereas the rest corresponds to lattices containing two (cyan), four (green), or six (orange) Weyl loops. (B) Weyl loops along the line corresponding to magnified points in A. As the gapped region is approached, we observe Weyl loops shrinking toward the origin until they disappear. (C) An example of the soft mode structure in reciprocal space for a lattice with a single two-Weyl loop structure (in blue), which corresponds to the cyan point in A. The integration of a phase around any contour (e.g., solid red circles) enclosing the Weyl loop gives an integer winding number that we use to check the topological nature of the Weyl loop. Note that this contour can be deformed into a pair of contours (; dashed red lines) traversed in opposite directions: this illustrates how the winding number across the Brillouin zone changes as the Weyl loop is traversed. Near the origin , the loop manifests itself via soft directions (teal). (D) The Brillouin zone of a lattice corresponding to the blue point in A. At the origin, the softest regions (blue region) align themselves with the soft directions of lattices with (red) or (green).
We conclude that, although Weyl loops are generic, the stacked kagome lattice also exhibits gapped configurations in the sense that they contain no Weyl loops (but do contain gapless Goldstone modes). In lattices with Weyl loops, the number of soft modes scales as the linear size of the system, whereas gapped lattices have only the three uniform Guest–Hutchinson modes (12, 13). We are not aware of any other realizations of a 3D isostatic lattice that is gapped in this sense. In the next section, we address the implications of the existence of a gap for the topological characterization of mechanical networks.
Topological Rigidity in Three Dimensions
For the gapped isostatic lattice, an integer topological invariant called the polarization can be computed from the bulk phonon spectrum (3). This winding number invariant is only well-defined in the gapped case: in Weyl lattices, the closure of the gap prevents a consistent definition. That is, when Weyl loops are present, the polarization changes depending on the choice of contour in the Brillouin zone. The mechanical consequences of polarization are found in the spectrum of the material’s soft surface waves. Polarization controls which surfaces have more soft modes: this is the mechanical version of the bulk-boundary correspondence principle.
For the polarized lattice, a polarization vector P can be computed via , where are the three lattice vectors and in our case, the unit cell dipole . This dipole is computed via the expression , where are the positions of the bond centers relative to the center of mass of the unit cell (3). The three coefficients are winding numbers computed by integrating the phase change of the complex function across a straight-line contour crossing the Brillouin zone:
| [1] |
where is a closed contour in the direction (3). This integral is well-defined for contours along which . The integers depend smoothly on the choice of contour and are constant. In gapped lattices, the determinant is nonzero everywhere except for the origin . As a consequence, the winding numbers are independent of the chosen contour, and the polarization is a topological invariant. However, Weyl loops partition the space of straight-line contours into lines going through the inside (outside) of the loop. Because along the loops, contours on either side of the loop can have different winding numbers . Note that the combination of any two such contours taken in opposite directions can be smoothly deformed (without intersecting the Weyl line) into a small circle enclosing the Weyl line as shown in Fig. 2C. The winding number around this small circle is an invariant and equal to the difference between for on two sides of the loop. This topological protection guarantees that a single Weyl loop cannot be destroyed, which explains why Weyl loops only vanish by shrinking to the origin within the phase diagram in Fig. 2A. In summary, Weyl lines are protected by a winding number, and gapped lattices can have a well-defined topological polarization.
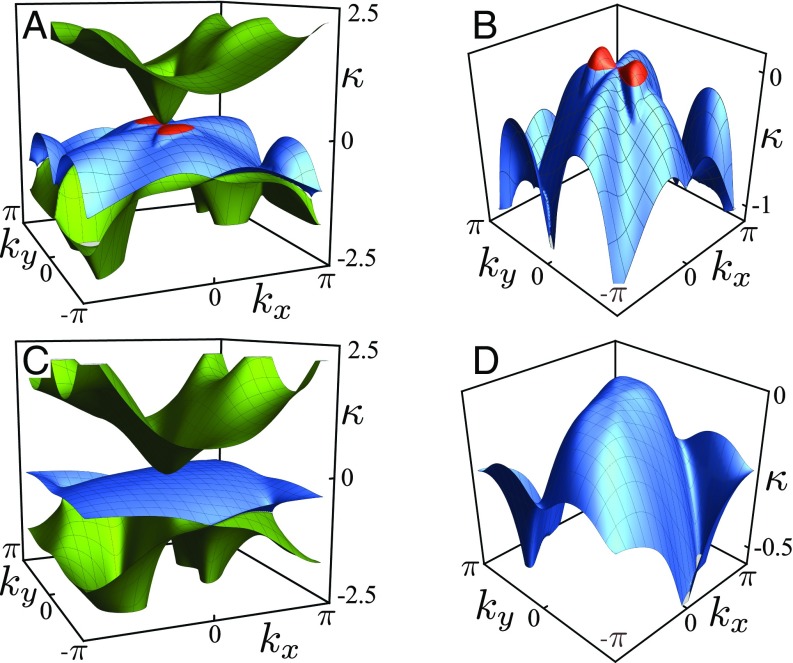
Bulk-boundary correspondence states that the topological invariants computed in the bulk can have significant effects on the mechanics of a sample with boundaries. We show this correspondence by computing the topological invariants and the spectrum of soft edge states in the stacked kagome lattice. In the bulk of the Weyl lattice corresponding to (compare Fig. 2 A and C), the winding number around the loop is . The for contours inside and outside of the loop differs by one. To see the boundary counterpart of the correspondence, we compute the spectrum of soft edge states for this lattice with a stress-free surface parallel to the plane (Fig. 1C). In Fig. 3 A and B, we show the (signed) inverse penetration depth for soft surface modes in the 3D Brillouin zone for wave vector . These plane-wave solutions of correspond to soft modes of the form . The middle mode of Fig. 3A (zoomed in view shown in Fig. 3B) changes sides: for (Fig. 3A, red region), the soft mode is attached to the bottom surface and decays upward into the bulk, whereas for (Fig. 3A, blue region), the mode is localized on the top surface. For the line corresponding to the projection of the Weyl loop onto the 2D Brillouin zone, the penetration depth is infinite, and , because the Weyl lines are soft modes in the bulk. The difference in between inside and outside of the Weyl loops is the bulk invariant , which corresponds to the difference between the number of soft surface modes across the projected Weyl loop. This connection follows from Cauchy’s argument principle for Eq. 1, which states that the third winding numbers count, up to a constant, the number of modes with zero energy () at a boundary. These observations confirm bulk-boundary correspondence.
Fig. 3.
Surface modes for a polarized lattice (C and D) compared with a lattice with Weyl lines (A and B). A surface mode in a plane perpendicular to the axis (e.g., Fig. 1C) decays exponentially into the material bulk with amplitude , where is the inverse penetration depth. Lattice with Weyl lines . (A) Inverse penetration depth for three soft surface modes over the entire surface Brillouin zone (sBZ). For small wave vectors , these modes correspond to the three acoustic phonons. (B) Zoomed in view of the middle mode in A: the part of wave vector space for which the mode lives on the bottom side is colored in red, whereas the part corresponding to the top side is in blue. The projection of the Weyl line from the bulk onto the sBZ corresponds to a line with infinite penetration depth () and separates the red and blue regions. Polarized lattice . (C) Inverse penetration depth for the same three modes as in A but for a different choice of parameters, corresponding to the blue region in Fig. 2A. (D) Zoomed in view of the middle mode in C, which (in contrast to the mode in B) is localized on the top of the lattice only: it is blue throughout. Significantly, the bulk () modes that correspond to the Weyl loop are absent for this lattice.
A similar correspondence exists in the polarized lattice. There, the invariant polarization pointing along the axis is given by , which we computed for parameters . To understand the effect of P on the boundary, note that, in analogy with electromagnetism, the softness charge in region is related to the flux of polarization P through the region’s boundary . In a nearly uniform, polarized lattice (3),
| [2] |
where is the boundary’s inward normal and is the volume of a unit cell. The difference between the softness charges at the top vs. the bottom is determined by P: for the stacked kagome, we expect one more band of soft modes along the top surface relative to the bottom. The total number of soft surface modes is three as a result of three bonds being cut per unit cell (3). We plot the inverse penetration depth for this extra band in Fig. 3 C and D within the 2D Brillouin zone. Unlike the Weyl lattice, the whole middle band in Fig. 3C is blue: the top surface has an extra band of soft modes. These modes have amplitudes that decay exponentially away from the top surface and can be alternatively interpreted as modes attached to the bottom surface and exponentially amplified into the bulk, similar to the modes studied in disordered systems in ref. 48.
Eq. 2 shows that topological polarization acts analogously to an electric polarization. Inside a homogeneous polarized material, the charge is zero. However, if homogeneity is broken by the presence of boundary or defects, charge can accumulate at these spots.
Local Rigidity and Softness at Dislocations
In topological mechanics, regions with positive softness charge contain mechanisms for soft elastic deformation, whereas regions with negative charge are prone to buckling (37). Eq. 2 suggests that regions of nonzero polarization flux can occur in a structurally inhomogeneous material without modulating the composition (i.e., as an alternative to composites). We choose dislocations to provide this inhomogeneity.
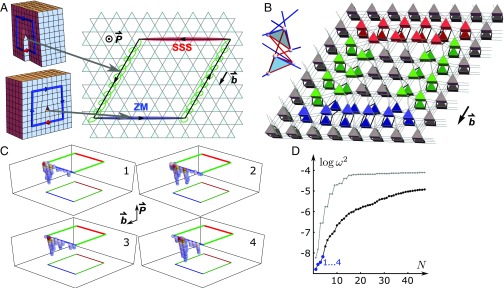
The natural defects in 3D crystals are line dislocations: displacements of unit cells along straight lines. In many crystalline solids, such defects control mechanical deformations and plasticity. These defect lines are topologically protected and must either terminate at the material boundaries or form a closed dislocation loop (Fig. 4 A and B). When the dislocations terminate at boundaries, they provide inhomogeneities extended along a channel (or curve) in 3D space. The topological invariant corresponding to a dislocation is the Burgers vector given by , where is the displacement of a particle at point x in the periodic lattice because of the presence of the dislocation and is any closed contour surrounding the dislocation line. The invariant b is contour-independent and therefore, constant along the dislocation. Together with dislocation line direction , the Burgers vector expresses how the dislocation affects the surrounding lattice.
Fig. 4.
Dislocation loops can act as dipoles of topological charge. (A) Architectures of a dislocation loop in a periodic lattice: in a screw dislocation, the Burgers vector b is parallel to the dislocation line, whereas in an edge dislocation, the Burgers vector and the dislocation line are perpendicular. A dislocation loop can combine edge and screw dislocations along its contour. In a polarized lattice (with polarization P), a dislocation line separates in space an edge dislocation segment that carries zero modes (ZMs; blue) from an edge dislocation segment that carries states of self-stress [SSS; red; for example, via screw dislocations (green), which carry no such charges]. The net topological charge, defined as the difference between ZM and SSS, is zero when summed over a dislocation loop contour. Nevertheless, the dislocation loop carries a topological charge dipole, which is, in this example, parallel to the Burgers vector b. (B) Geometry of the dislocation loop. Each prism represents a unit cell with triangles oriented according to as shown in Inset. (C) Numerical results for the four lowest-frequency phonons (excluding the trivial translations) in a large ( unit cells) polarized lattice that has a dislocation loop: warmer color signifies a larger displacement within that unit cell. Plotted are only those unit cells that have displacements above a cutoff of 20% of the maximum. Note the localization of the softest modes to the near side of the loop in accordance with A and the polarization P. (D) The common logarithm of lowest mode frequencies for the th lowest mode plotted vs. , comparing two large samples (same size as C). The mode frequencies are significantly lower for the dislocated lattice (black) than in the nondislocated case (gray). Without a dislocation, the lowest eigenmodes are the extended plane-wave acoustic phonons, whereas with the dislocation, these modes include both the acoustic phonons and the modes localized along the dislocation loop (in blue, four lowest modes with eigenvectors that are plotted in C).
Line dislocations come in two primary types called edge and screw dislocations (Fig. 4A). For edge dislocations, b and are orthogonal: the displacement u pushes unit cells apart to insert a half-plane of unit cells that extends from the dislocation line in the direction . In this way, edge dislocations are 3D generalizations of 2D point dislocations. By contrast, for screw dislocations, the b and vectors are parallel: the displacement u pushes neighboring cells apart along the loop. In this way, screw dislocations give rise to an inherently 3D spiral structure. Along a dislocation loop, the Burgers vector b is constant, but the line direction changes. As Fig. 4A shows, a dislocation loop can contain both edges and screws.
The interplay between line properties and topological polarization P of the lattice leads to a softness charge. On evaluating Eq. 2 in a deformed region (Rigidity Charge Bound to Line Dislocations), we obtain the total topological charge to be , where is the unit cell volume of the uniform lattice. Significantly, the charge density is nonzero when the partial derivatives fail to commute, which happens only at the dislocation line itself and only when are linearly independent. Then, the volume integral for the topological charge reduces to an integral along the dislocation line:
| [3] |
where parameterizes the dislocation line and is a family of contours enclosing this line at each . The integrand of Eq. 3 gives the charge line density at each , which using the definition of the Burgers vector, evaluates to
| [4] |
(Rigidity Charge Bound to Line Dislocations has a detailed derivation). Equivalently, we could write . In particular, screw dislocations do not carry charge—their Burgers vector points along the line direction. For edge dislocations, the inserted rows terminate at the dislocation line, creating a boundary within the material. If P points along (against) the half-plane direction , these rows carry extra polarization out (in). Note that, for any dislocation loop, the net charge is zero. However, dislocations loops do separate softness charges in space, resulting in a topological charge dipole, as shown in Fig. 4A. This dipole is oriented within the –P plane and can be quantified by a dipole moment, which captures the amount of charge separated and the distance of separation. The dipole’s b (P) component is the area of the dislocation loop after it is projected onto the plane formed by the two vectors b (P) and (Dislocation Loop Dipole Moment shows the derivation). For the loop in Fig. 4A composed of edge and screw dislocations, all of the charges are localized along the edge dislocations, and the dipole moment is along b.
A positive charge density corresponds to soft modes localized along part of the dislocation loop. We investigate this localized softness within a polarized lattice using the configuration shown schematically in Fig. 4A and plotted for a small sample in Fig. 4B. In Fig. 4C, we show that, for the softest (i.e., lowest-frequency nontranslational) modes of this lattice, the unit cells with the largest displacements are localized along the near side of the loop, in agreement with Eq. 4. This can be contrasted with the lowest-energy modes of a sample without a dislocation: in Fig. 4D, we show that the dislocated lattice has soft modes at lower frequencies. Whereas the lowest modes in the nondislocated sample are the largest-wavelength acoustic phonons that fit within the periodic box, the lowest modes of the dislocated lattice are a combination of these acoustic phonons and the many localized modes, such as the ones shown in Fig. 4C.
Our work suggests a design principle for materials that will localize either large strain or large stress along a boundary, line, or parts of a closed loop, leading to preprogrammed yielding and failure.
Supplementary Material
Acknowledgments
We thank Paul Baireuther, D. Zeb Rocklin, and Bryan G. Chen for fruitful discussions and T. C. Lubensky for a critical reading of the manuscript. We acknowledge funding from the Foundation for Fundamental Research on Matter (FOM), the Netherlands Organisation for Scientific Research (NWO), and Delta Institute for Theoretical Physics. V.V. was primarily supported by the University of Chicago Materials Research Science and Engineering Center, which is funded by National Science Foundation Grant DMR-1420709.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1713826115/-/DCSupplemental.
References
- 1.Bertoldi K, Reis PM, Willshaw S, Mullin T. Negative poisson’s ratio behavior induced by an elastic instability. Adv Mater. 2010;22:361–366. doi: 10.1002/adma.200901956. [DOI] [PubMed] [Google Scholar]
- 2.Sun K, Souslov A, Mao X, Lubensky TC. Surface phonons, elastic response, and conformal invariance in twisted kagome lattices. Proc Natl Acad Sci USA. 2012;109:12369–12374. doi: 10.1073/pnas.1119941109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kane CL, Lubensky TC. Topological boundary modes in isostatic lattices. Nat Phys. 2013;10:39–45. [Google Scholar]
- 4.BGg Chen, Upadhyaya N, Vitelli V. Nonlinear conduction via solitons in a topological mechanical insulator. Proc Natl Acad Sci USA. 2014;111:13004–13009. doi: 10.1073/pnas.1405969111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lubensky TC, Kane CL, Mao X, Souslov A, Sun K. Phonons and elasticity in critically coordinated lattices. Rep Prog Phys. 2015;78:073901. doi: 10.1088/0034-4885/78/7/073901. [DOI] [PubMed] [Google Scholar]
- 6.Meeussen AS, Paulose J, Vitelli V. Geared topological metamaterials with tunable mechanical stability. Phys Rev X. 2016;6:041029. [Google Scholar]
- 7.Rocks JW, et al. Designing allostery-inspired response in mechanical networks. Proc Natl Acad Sci USA. 2017;114:2520–2525. doi: 10.1073/pnas.1612139114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yan L, Ravasio R, Brito C, Wyart M. Architecture and coevolution of allosteric materials. Proc Natl Acad Sci USA. 2017;114:2526–2531. doi: 10.1073/pnas.1615536114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Coulais C, Sounas D, Alù A. Static non-reciprocity in mechanical metamaterials. Nature. 2017;542:461–464. doi: 10.1038/nature21044. [DOI] [PubMed] [Google Scholar]
- 10.Maxwell JC. On the calculation of the equilibrium and stiffness of frames. Philos Mag. 1864;27:294–299. [Google Scholar]
- 11.Calladine C. Buckminster fuller’s “tensegrity” structures and clerk maxwell’s rules for the construction of stiff frames. Int J Solids Struct. 1978;14:161–172. [Google Scholar]
- 12.Guest S, Hutchinson J. On the determinacy of repetitive structures. J Mech Phys Sol. 2003;51:383–391. [Google Scholar]
- 13.Kapko V, Treacy MMJ, Thorpe MF, Guest SD. On the collapse of locally isostatic networks. Proc R Soc A. 2009;465:3517–3530. [Google Scholar]
- 14.Rocklin DZ, Chen BG, Falk M, Vitelli V, Lubensky TC. Mechanical weyl modes in topological maxwell lattices. Phys Rev Lett. 2016;116:135503. doi: 10.1103/PhysRevLett.116.135503. [DOI] [PubMed] [Google Scholar]
- 15.Stenull O, Kane C, Lubensky T. Topological phonons and weyl lines in three dimensions. Phys Rev Lett. 2016;117:068001. doi: 10.1103/PhysRevLett.117.068001. [DOI] [PubMed] [Google Scholar]
- 16.Florijn B, Coulais C, van Hecke M. Programmable mechanical metamaterials. Phys Rev Lett. 2014;113:175503. doi: 10.1103/PhysRevLett.113.175503. [DOI] [PubMed] [Google Scholar]
- 17.Lakes R. Foam structures with a negative poisson’s ratio. Science. 1987;235:1038–1040. doi: 10.1126/science.235.4792.1038. [DOI] [PubMed] [Google Scholar]
- 18.Rocklin DZ. Directional mechanical response in the bulk of topological metamaterials. New J Phys. 2016;19:065004. [Google Scholar]
- 19.Sussman DM, Stenull O, Lubensky TC. Topological boundary modes in jammed matter. Soft Matter. 2016;12:6079–6087. doi: 10.1039/c6sm00875e. [DOI] [PubMed] [Google Scholar]
- 20.Nash LM, et al. Topological mechanics of gyroscopic metamaterials. Proc Natl Acad Sci USA. 2015;112:14495–500. doi: 10.1073/pnas.1507413112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Susstrunk R, Huber SD. Observation of phononic helical edge states in a mechanical topological insulator. Science. 2015;349:47–50. doi: 10.1126/science.aab0239. [DOI] [PubMed] [Google Scholar]
- 22.Kariyado T, Hatsugai Y. Manipulation of dirac cones in mechanical graphene. Scientific Rep. 2015;5:18107. doi: 10.1038/srep18107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Mousavi SH, Khanikaev AB, Wang Z. Topologically protected elastic waves in phononic metamaterials. Nat Commun. 2015;6:8682. doi: 10.1038/ncomms9682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Khanikaev AB, Fleury R, Mousavi SH, Alù A. Topologically robust sound propagation in an angular-momentum-biased graphene-like resonator lattice. Nat Commun. 2015;6:8260. doi: 10.1038/ncomms9260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Yang Z, et al. Topological acoustics. Phys Rev Lett. 2015;114:114301. doi: 10.1103/PhysRevLett.114.114301. [DOI] [PubMed] [Google Scholar]
- 26.Huber SD. Topological mechanics. Nat Phys. 2016;12:621–623. [Google Scholar]
- 27.Souslov A, van Zuiden BC, Bartolo D, Vitelli V. Topological sound in active-liquid metamaterials. Nat Phys. 2017;13:1091–1094. [Google Scholar]
- 28.Bertoldi K, Vitelli V, Christensen J, van Hecke M. Flexible mechanical metamaterials. Nat Rev Mater. 2017;2:17066. [Google Scholar]
- 29.Rechtsman MC, et al. Photonic Floquet topological insulators. Nature. 2013;496:196–200. doi: 10.1038/nature12066. [DOI] [PubMed] [Google Scholar]
- 30.Lu L, Joannopoulos JD, Soljačić M. Topological photonics. Nat Photon. 2014;8:821–829. [Google Scholar]
- 31.Wang P, Lu L, Bertoldi K. Topological phononic crystals with one-way elastic edge waves. Phys Rev Lett. 2015;115:104302. doi: 10.1103/PhysRevLett.115.104302. [DOI] [PubMed] [Google Scholar]
- 32.Hasan MZ, Kane CL. Colloquium: Topological insulators. Rev Mod Phys. 2010;82:3045–3067. [Google Scholar]
- 33.Bernevig BA, Hughes TL. Topological Insulators and Topological Superconductors. Princeton Univ Press; Princeton: 2013. [Google Scholar]
- 34.Rocklin DZ, Zhou S, Sun K, Mao X. Transformable topological mechanical metamaterials. Nat Commun. 2017;8:14201. doi: 10.1038/ncomms14201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Bilal OR, Süsstrunk R, Daraio C, Huber SD. Intrinsically polar elastic metamaterials. Adv Mater. May 3, 2017 doi: 10.1002/adma.201700540. [DOI] [PubMed] [Google Scholar]
- 36.Hawkes E, et al. Programmable matter by folding. Proc Natl Acad Sci USA. 2010;107:12441–12445. doi: 10.1073/pnas.0914069107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Paulose J, Meeussen AS, Vitelli V. Selective buckling via states of self-stress in topological metamaterials. Proc Natl Acad Sci USA. 2015;112:7639–7644. doi: 10.1073/pnas.1502939112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Paulose J, BGg Chen, Vitelli V. Topological modes bound to dislocations in mechanical metamaterials. Nat Phys. 2015;11:153–156. [Google Scholar]
- 39.Silverberg JL, et al. Using origami design principles to fold reprogrammable mechanical metamaterials. Science. 2014;345:647–650. doi: 10.1126/science.1252876. [DOI] [PubMed] [Google Scholar]
- 40.Chen BGG, et al. Topological mechanics of Origami and Kirigami. Phys Rev Lett. 2016;116:135501. doi: 10.1103/PhysRevLett.116.135501. [DOI] [PubMed] [Google Scholar]
- 41.Benalcazar WA, Bernevig BA, Hughes TL. Quantized electric multipole insulators. Science. 2017;357:61–66. doi: 10.1126/science.aah6442. [DOI] [PubMed] [Google Scholar]
- 42.Serra-Garcia M, et al. 2017. Observation of a phononic quadrupole topological insulator. arXiv:1708.05015.
- 43.Volovik GE. In: Quantum Phase Transitions from Topology in Momentum Space. Unruh WG, Schützhold R, editors. Springer; Berlin: 2007. pp. 31–73. [Google Scholar]
- 44.Burkov AA, Hook MD, Balents L. Topological nodal semimetals. Phys Rev B. 2011;84:235126. [Google Scholar]
- 45.Lu L, Fu L, Joannopoulos JD, Soljačić M. Weyl points and line nodes in gyroid photonic crystals. Nat Photon. 2013;7:294–299. [Google Scholar]
- 46.Xu SY, et al. Discovery of a weyl fermion semimetal and topological fermi arcs. Science. 2015;349:613–617. doi: 10.1126/science.aaa9297. [DOI] [PubMed] [Google Scholar]
- 47.Lu L, et al. Experimental observation of weyl points. Science. 2015;349:622–624. doi: 10.1126/science.aaa9273. [DOI] [PubMed] [Google Scholar]
- 48.Yan L, Bouchaud JP, Wyart M. Edge mode amplification in disordered elastic networks. Soft Matter. 2017;13:5795–5801. doi: 10.1039/c7sm00475c. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.