Slow domain reconfiguration causes power-law kinetics in a two-state enzyme

Significance

Dynamic disorder in enzyme catalysis due to conformational heterogeneity is widespread in nature. However, the structural origin for such conformational multiplicity is often elusive. Our results show that the opening and closing of two domains in the redox enzyme QSOX is hampered by a broad ensemble of slowly exchanging open conformations. This heterogeneity is a direct result of the disordered interdomain linker paired with interactions between the domains. Since the effective domain concentration in natural fusions of distinct modules such as in QSOX is very high, interdomain interactions can be persistent, thus resulting in slow sampling. We therefore expect that multidomain enzymes are particularly prone to catalytic disorder such as memory effects.

Abstract

Protein dynamics are typically captured well by rate equations that predict exponential decays for two-state reactions. Here, we describe a remarkable exception. The electron-transfer enzyme quiescin sulfhydryl oxidase (QSOX), a natural fusion of two functionally distinct domains, switches between open- and closed-domain arrangements with apparent power-law kinetics. Using single-molecule FRET experiments on time scales from nanoseconds to milliseconds, we show that the unusual open-close kinetics results from slow sampling of an ensemble of disordered domain orientations. While substrate accelerates the kinetics, thus suggesting a substrate-induced switch to an alternative free energy landscape of the enzyme, the power-law behavior is also preserved upon electron load. Our results show that the slow sampling of open conformers is caused by a variety of interdomain interactions that imply a rugged free energy landscape, thus providing a generic mechanism for dynamic disorder in multidomain enzymes.

The function of proteins is intimately linked to their structural plasticity (1–5), which is particularly prevalent in enzymes that require a coordination of conformational and chemical transitions. Support for a ligand-induced funneling of an enzyme through its conformational states (6), or for a preferred directionality of enzyme motions (7), suggests a coevolution of structure, function, and dynamics. Despite being optimized for catalysis, individual enzyme molecules display variations in turnover rates (8–15), implying that the catalytic efficiency can vary between different conformations. For conformational motions much slower than turnover, an enzyme may even “memorize” its catalytic rate between successive turnover cycles, which can lead to memory (8, 16) and hysteresis (17–19) effects. However, even in cases in which such heterogeneity does not lead to deviations from classical Michaelis-Menten behavior, parameters such as Michaelis constant and catalytic rate will then have different microscopic interpretations (20).

Compared with the increasing experimental evidence for dynamic disorder in enzyme kinetics, little is known about its structural origin. NMR-relaxation experiments were particularly successful in identifying correlations between turnover and conformational rates (5, 7, 21), and single-molecule experiments even identified deviations from classical reaction rate theory for local distance fluctuations in a flavin reductase (10). However, large-scale motions such as the opening and closing of domains often follow classical kinetics (7, 22–24). The description of protein motion as diffusion on a multidimensional free energy surface has frequently been used in the past to conceptualize biomolecular dynamics (25–27) and, for sufficiently high free energy barriers, the landscape picture converges to classical rate equations. Deviations are expected for barrier heights close to the room temperature energy (28, 29) or if the experimental coordinates cannot differentiate sufficiently between the microscopic states. Even though the latter is likely to be the rule rather than an exception, rate equations are still applicable if the internal exchange between “hidden” microstates is faster than transitions between experimentally distinguishable states (30, 31), thus partially explaining their stunning success in protein dynamics.

Here, we describe a remarkable exception that provides a potential mechanism for dynamic disorder in multidomain enzymes. Using single-molecule FRET (smFRET), we monitored the conformational dynamics of the electron-transfer enzyme TbQSOX (quiescin sulfhydryl oxidase from the parasite Trypanosoma brucei) from nanoseconds to milliseconds. TbQSOX is a natural fusion of two catalytic domains, a protein disulfide isomerase (PDI)-like oxidoreductase module composed of a thioredoxin (Trx) domain (32) and an Erv-family sulfhydryl oxidase domain (Erv) (33, 34) (Fig. 1A). QSOX is localized to the Golgi apparatus (35) and secreted to the extracellular environment (36) where it uses a thiol-based electron relay to generate disulfide bonds in proteins. Each domain contains a redox-active site formed by a di-cysteine (CXXC) motif (Fig. 1A). The domains are linked with a flexible linker to allow the alternate communication of the active sites with each other and with substrates, thus leading to an exchange between open- and closed-domain arrangements (Fig. 1A). In a first step, electrons from the substrate reduce the CXXC motif in the N-terminal Trx domain, a reaction that requires the enzyme to occupy a domain-open conformation in which the active sites face solution (Fig. 1A). The electrons are subsequently shuttled to the second cysteine pair in the Erv domain, which requires the association of both active sites (closed state) and the formation of an interdomain disulfide. Finally, the electrons are transferred to a bound FAD cofactor in the Erv domain, which is reoxidized by O₂ thereby generating H₂O₂.

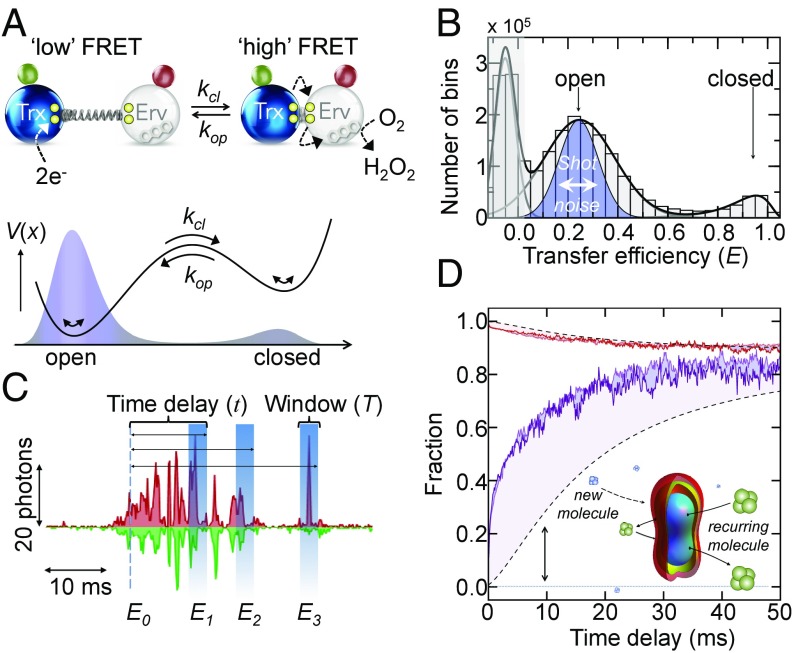
Fig. 1.

Two-state opening and closing measured with smFRET. (A) Trx domain (blue) and Erv domain (white) in the open and closed state are schematically depicted with the flexible linker (spring), CXXC motifs (yellow), the FAD cofactor (Erv domain), and the donor (green) and acceptor (red) fluorophores. A double-well free energy profile (black line) results in a bimodal distribution of open and closed states (shaded in blue). (B) Transfer efficiency histogram of doubly labeled TbQSOX in the absence of substrate (bin time: 100 μs). The peak close to E = 0 results from molecules without an active acceptor dye (gray shading). The blue-shaded region indicates the expected distribution of the open state based on photon noise. The black line is a fit with a superposition of two log-normal and a Gaussian function. (C) Time trace donor (green) and acceptor (red) signals. Transfer efficiencies (E₁, E₂, E₃) of bins that follow an originally selected bin with E₀ within a window T after a delay τ will be different due to conformational switching and the arrival of new molecules. (D) Time course of the fraction of open molecules after initial selection of closed molecules (purple) and open molecules (red) for two different laser intensities, 50 μW (lighter color) and 100 μW (darker color). Black dashed lines indicate the expected kinetics in the absence of conformation switching based on $p_{same}\left(t\right)$. (Inset) Confocal volume.

Results

Recombinant TbQSOX was labeled site-specifically with the FRET-donor AlexaFluor 488 at position 116 in the Trx domain and with the FRET-acceptor AlexaFluor 594 at position 243 in the Erv domain (37). We monitored single TbQSOX molecules while freely diffusing through the observation volume of a confocal microscope (SI Appendix). In the absence of substrate, we observed two peaks in the FRET histograms that correspond to open and closed conformations (37) (Fig. 1B). In equilibrium, the majority of molecules reside in the open state with low transfer efficiencies, while the closed conformation with a high transfer efficiency is only populated by 12% (Fig. 1B) (37). Thus, the enzyme visits two macroscopic open and closed conformations even in the absence of substrate. Since the CXXC motifs in both domains are oxidized under these conditions, the formation of a covalent interdomain disulfide bridge between the Trx and Erv domains, the key step for electron shuttling between the domains, is apparently not required for domain closure, in accord with previous observations (37). To extract information about the time scales of opening and closing, we took advantage of the fact that a diffusing molecule may enter and exit the confocal volume multiple times (Fig. 1C). Once a molecule leaves the observation volume, the chance of it returning to this volume within a short time interval is greater than the chance of detecting a new molecule. Analyzing this recurrence of molecules is well suited to study reaction dynamics in the important regime of microseconds and milliseconds (38, 39). To extract kinetics, we binned the photon traces in steps of 100 μs and identified all bins with the enzyme in the closed conformation (E ≥ 0.8). In a second step, we constructed FRET histograms for those bins that followed the originally identified set with a delay time t (Fig. 1C). With increasing delay, the relative population of open molecules increases while the population of closed molecules decayed (Fig. 1D and SI Appendix, Fig. S1). A complementary result was obtained when the open population (0.1 ≤ E ≤ 0.5) was selected for the analysis (Fig. 1D). At long delay times, the fractions of open molecules from the two types of analysis converged to the equilibrium value, as expected. Experiments at two different laser intensities gave similar results (Fig. 1D), implying that contributions from photo-bleaching or triplet dynamics of the dyes are negligible. Notably, the observed kinetics $p_{obs}\left(t\right)$ is a convolution of two contributions (Fig. 1D): conformational switching between open and closed states, which is characterized by $p_{conf}\left(t\right)$, and the time-dependent likelihood that two bins are from the same molecule, $p_{same}\left(t\right)$. However, both effects can be disentangled by directly determining $p_{same}\left(t\right)$ from the autocorrelation functions of bin-pairs within the same experiment (38) (SI Appendix, Fig. S1). The observed kinetics is then given by

$$p_{obs}\left(t\right)=p_{same}\left(t\right)\hspace{0.17em}{p}_{conf}\left(t\right)+\left[1-p_{same}\left(t\right)\right]\rho .$$ [1]

Here, $\rho$ is the equilibrium distribution of open molecules, which is accessible from the measured FRET histogram (Fig. 1B). Rearranging Eq. 1 finally provides the actual conformational kinetics, $p_{conf}\left(t\right)$.

Identifying Conformational Heterogeneity in TbQSOX.

Using the effect of molecular recurrence, the open-close kinetics are readily accessible from 100 μs to 20 ms, thus covering two orders of magnitude in time. However, despite the fact that TbQSOX switches between two well-separated conformational states (open and closed) (Fig. 1 A and B), which would suggest single exponential kinetics, the observed decays are highly nonexponential. Strikingly, a double-logarithmic plot shows a linear decrease with a slope of β = 0.11 (Fig. 2A), suggesting a power-law decay of the closed conformers (p_c) of the type $p_c\left(t\right)\propto t^{-\left|\beta \right|}$, which hints at multiple molecular processes that contribute to the kinetics. Since the fraction of closed molecules, p_c(τ) , is naturally bounded between 1 and the equilibrium fraction ρ, a reasonable description of the data are given by

$$p_c\left(t\right)=\rho {\left(1+t/t_0\right)}^{-\left|\beta \right|}+\left(1-\rho \right),$$ [2]

which only includes two fitting parameters (β, t₀) since the equilibrium fraction $\rho$ is independently determined from the FRET histograms. A fit with Eq. 2 provides an excellent description of the data (Fig. 2A). An alternative approach to describe highly nonexponential decays is based on Kohlrausch-Williams-Watt functions of the type

$$p_c\left(t\right)=\rho \text{exp}\left[-{\left(kt\right)}^{\beta }\right]+\left(1-\rho \right),$$ [3]

which have previously been used to model fast relaxation processes in protein-folding reactions (40). Here, k is the rate and β is the stretching exponent. However, fits with Eq. 3 do not describe the experimental kinetics, and significant deviations are found at short times (Fig. 2A), suggesting that the power law in Eq. 2 is more appropriate. Admittedly, however, the power law is purely empirical and does not contain information about the number and connectivity of the interconverting species. A mechanistic approach to describe the kinetics requires the assumption of hidden conformational states in the FRET histogram. The simplest motifs that can account for the nonexponential kinetics include either two indistinguishable open (O₁ and O₂) or closed (C₁ and C₂) states, thus leading to at least four possible mechanisms: $C\leftrightarrow O_1\leftrightarrow O_2$ (COO),$O_1\leftrightarrow C\leftrightarrow O_2$ (OCO), $C_1\leftrightarrow C_2\leftrightarrow O$ (CCO), and $C_1\leftrightarrow O\leftrightarrow C_2$ (COC). All four models are kinetically equivalent and require three independent fitting parameters, provided that one of the four rates is determined by the equilibrium fraction in the FRET histograms. A fit with any of the four models leads to a sufficient description of the experimental data. Notably, however, a fit with the empirical power law is still better (R² = 0.996 vs. R² = 0.989), despite the smaller number of fitting parameters (Fig. 2A). Unfortunately, the four models are kinetically indistinguishable and their cyclic versions or models with even more conformational states may also be possible. In fact, support for a broader ensemble of conformations comes from TbQSOX variants with different attachment positions of the donor fluorophore (37). While these variants exhibit different transfer efficiencies in the closed conformation, the transfer efficiencies of the open state are very similar to each other, suggesting that “open” TbQSOX samples an ensemble of different conformations (37). This is not surprising per se given the fact that both domains are connected by a linker that is only partially resolved in the X-ray structure of the enzyme (34), thus indicating its flexibility. In accord with a heterogeneous open ensemble, the donor fluorescence lifetime of the open state deviates from the expected value for a single donor-acceptor distance. This deviation suggests a distribution of distances that is essentially static at the nanosecond time scale of the fluorescence lifetime (Fig. 2B), implying that the fluorescence intensity decays contain information on the shape of this distribution (41). We therefore analyzed the fluorescence intensity decays of the open subpopulation using the empirical distance distribution (41):

$$P_O\left(r\right)=4\pi r^2\text{exp}\left[-{\left(r-r_0\right)}^2/2{\sigma }^2\right].$$ [4]

Here, r is the donor-acceptor distance, σ determines the width of the distribution, and r₀ is the offset from zero. A global fit of the donor and acceptor intensity decays results in σ = 3.2 nm and r₀ = 2.75 nm (Fig. 2C and SI Appendix), which corresponds to a broad distribution of open conformers with an average donor-acceptor distance of 6.5 nm compared with 2.2 nm as obtained from the X-ray structure of the closed state (34) (Fig. 2D).

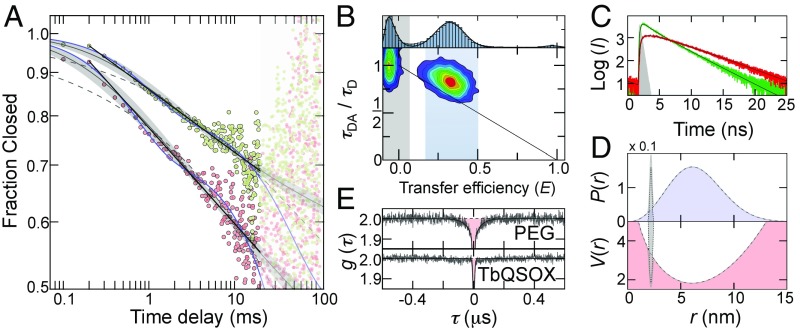
Fig. 2.

Power-law kinetics and heterogeneity detected with smFRET. (A) Time decay of the closed population corrected for the arrival of new molecules with (red circles) and without (green circles) 1 mM DTT. Weighted fits with a power law (black lines), Eq. 2 (gray lines) with a 95% CI (gray shading), a stretched exponential fit with Eq. 3 (gray dashed lines), and a double exponential fit with the COO-model (blue lines) are shown for comparison. Data points >20 ms were excluded from the fit. (B) FRET histogram (Top) and 2D correlation map between donor fluorescence lifetime and transfer efficiency in the absence of substrate. The solid line shows the dependence for a single donor-acceptor distance. The blue region indicates molecules selected for the fluorescence lifetime analysis shown in C. (C) Subpopulation-specific fluorescence intensity (I) decays for donor (green) and acceptor (red) of open TbQSOX. Black lines are global fits based on the distance distribution in Eq. 4 (SI Appendix). The instrumental response function is shown in gray. (D) Distance distribution (Top) and free energy potential in units of k_BT (Bottom) of open TbQSOX (black dashed line) resulting from the fits in C. An estimate of the closed distribution based on the X-ray structure of TbQSOX (34) is shown for comparison (dotted lines). (E) Normalized donor-acceptor cross-correlation functions for doubly labeled PEG 5000 (Top) and TbQSOX in the absence of substrate (Bottom). Black lines are fits with a product of exponential functions (SI Appendix).

To determine the time scales at which the open conformers are sampled, we used nanosecond fluorescence correlation spectroscopy (42). Fluctuations in the donor-acceptor distance cause an anticorrelation between the emission of donor and acceptor photons that leads to a rise in the donor-acceptor cross-correlation function. In fact, in a control experiment on doubly labeled PEG (PEG 5000), a flexible polymer with a mean transfer efficiency similar to that of “open” TbQSOX (SI Appendix, Fig. S2), we clearly find distance dynamics with a correlation time of τ_c = 40 ± 3 ns (Fig. 2E). In contrast, no signal is observed in the equivalent experiment with TbQSOX (Fig. 2E), suggesting that the internal dynamics within the open ensemble are slower than 1 ms.

Notably, transitions within an open ensemble on the binning time scales of 100 μs would effectively broaden the FRET distributions. Indeed, a comparison of the width of the low-FRET peak with that expected from photon noise shows a significant broadening (Fig. 1B). To check whether the excess width results from static or dynamic heterogeneity, we selected molecules from the “left” and “right” sides of the open FRET distribution and constructed recurrence histograms for all events that follow within the shortest delay time of 100 μs (Fig. 3A). As expected, the two sets of molecules chosen from either side of the low-FRET distribution show markedly different FRET distributions that we denote with O¹ and O². Surprisingly, however, a clear exchange from O² to O¹ becomes visible with increasing delay time (Fig. 3A) that is significantly faster than expected for the static heterogeneity resulting from the arrival of new molecules in the confocal volume given by $1-p_{same}\left(t\right)$ (Fig. 3B and SI Appendix), which suggests the presence of a dynamic ensemble of open conformations. Importantly, the time scale of these dynamics overlaps partially with the transitions between open and closed molecules (Fig. 3C). Hence, macroscopic transitions between open and closed conformations mix with internal transitions within the basin of open conformers and thus are likely to contribute to the nonexponential decay kinetics in TbQSOX.

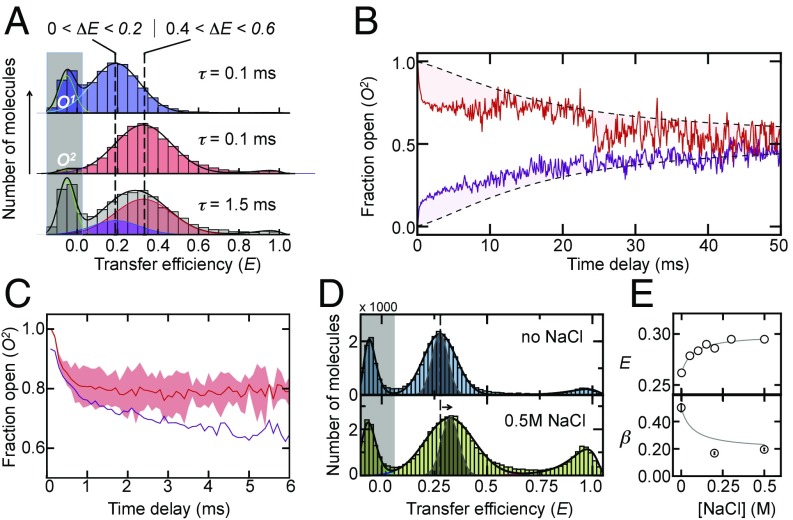
Fig. 3.

Slow exchange within the open state detected with RASP. (A) Single-molecule recurrence histograms of the open populations, O¹ (blue) and O² (red), at different delay times (indicated). The Bottom shows the amount of O¹ (blue) that is formed 1.5 ms after starting with 100% O² (red). The transfer efficiency ranges for the selection of O¹ (Left) and O² (Right) are indicated. Solid lines are fits to a sum of Gaussian functions. (B) Time course of the fraction of O² after initial selection of molecules from O¹ (purple) and O² (red). Black dashed lines indicate the kinetics in the absence of conformation switching due to the arrival of new molecules. (C) Time course of the fraction of O² corrected for the arrival of new molecules (red) in comparison with the decay of the closed population (purple). The red-shaded area is the error resulting from averaging the kinetics in B. (D) Transfer efficiency histograms in the absence (Top) and presence (Bottom) of NaCl. The gray-shaded distribution indicates the expected distribution based on photon noise. (E) Mean transfer efficiencies (Top) and β-exponents (Bottom) as a function of the salt concentration. The solid line is an empirical fit. RASP, recurrence analysis of single particles.

What is the molecular origin of the unusually slow domain rearrangements of TbQSOX in the open state? Do specific or nonspecific interdomain interactions transiently trap TbQSOX in a variety of free energy minima? In fact, one of the two existing X-ray structures of TbQSOX shows an arrangement in which the Trx domain is rotated by 165° relative to its position in the closed conformation (34), suggesting that domain interactions different from those of the closed form are possible. In case competing interdomain interactions cause the slow domain rearrangements, modulations of the interaction between both domains are expected to affect the open-close kinetics. For instance, both domains have a negative net charge, such that we would expect increasing electrostatic interdomain repulsions with decreasing salt concentrations (43). Indeed, in line with this idea, the mean transfer efficiency of the open ensemble shifts to lower values with decreasing concentrations of NaCl, indicating less association between the domains. Furthermore, the peak in the FRET histogram in the absence of NaCl narrowed (Fig. 3D), suggesting a faster exchange within the open ensemble or a reduced conformational heterogeneity. Importantly, the kinetics of opening and closing are qualitatively different at low and high salt concentrations (Fig. 3E). A pronounced increase in the β-exponents with decreasing concentrations of NaCl suggests a decreased contribution of the heterogeneous open ensemble to the kinetics (SI Appendix), which agrees well with the lower mean transfer efficiency and the reduced width of the distribution (Fig. 3 D and E). Notably, the fluorescence anisotropy of the donor remains unaltered by the addition of salt, showing that the rotational freedom of the dyes is not affected (SI Appendix, Fig. S3). Our results therefore suggest that nonspecific interdomain interactions impair the opening and closing of TbQSOX, suggesting a rugged multidimensional free energy landscape. How can these observations be rationalized in the one-dimensional picture given by our FRET coordinate?

Domain Interactions Cause Subdiffusive Dynamics.

The classical approach to tackle this question starts from a generalized Langevin equation that includes the dynamics along “hidden” coordinates as slowly fluctuating external forces (44). Alternative approaches include conventional rate equations with fluctuating rates (45) or fractional Brownian motion models with time-dependent diffusion coefficients (46). In the latter, the distribution of open and closed states, $p\left(r,t\right)$, is defined by the diffusion equation

$$\partial p\left(r,t\right)/\partial t=D\left(t\right)\partial /\partial r\left[V\prime \left(r\right)+\partial /\partial r\right]\hspace{0.17em}p\left(r,t\right)$$ [5]

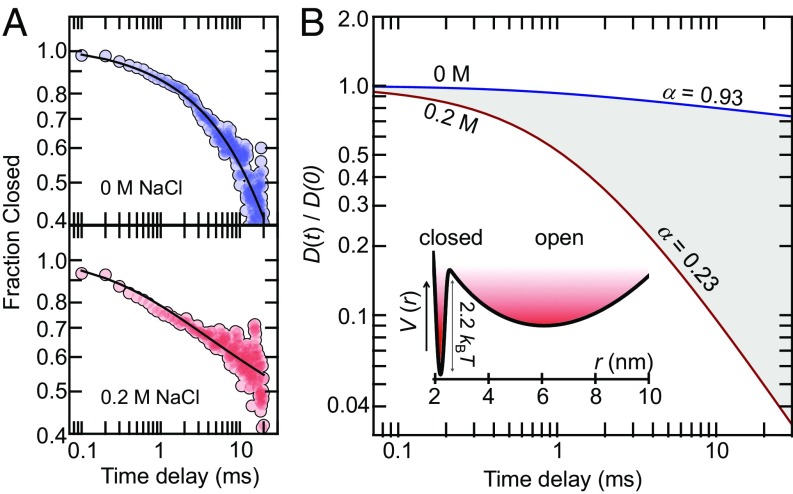
with a time-dependent diffusion coefficient $D\left(t\right)$ (46). Given a realistic potential $V\left(r\right)$, the time dependence of $D\left(t\right)$ can be estimated from our experimental data. However, since the potential for TbQSOX is not known in detail, approximations are unavoidable. As an estimate, we use the determined distance distribution, $P_O\left(r\right)$, of open molecules (Fig. 2D) together with a Gaussian distribution, $P_C\left(r\right)$, for the closed state that peaks at the Cα-distance between the labeling sites (Fig. 2D) (34). The resulting potential is then given by $V\left(r\right)=-lnP\left(r\right)$, where $P\left(r\right)$ is a properly weighted sum of $P_O\left(r\right)$ and $P_C\left(r\right)$. Using this estimate, we fit the data at low (0 M) and high (0.2 M) salt concentrations by numerically solving Eq. 5 with the empirical function $D\left(t\right)=D\left(0\right){\left(1+bt\right)}^c$ (SI Appendix), which results in an excellent fit of both datasets (Fig. 4A). However, the time dependence of $D\left(t\right)$ differs significantly between the conditions (Fig. 4B). [The absolute values of the diffusion coefficients (0.1–1 nm²/ms) depend sensitively on the precise shape of the potential and we do not discuss these values here.] While the diffusion coefficient only changes moderately at low-salt conditions, thus implying classical diffusion with nearly exponential kinetics, a pronounced decay is found at high salt concentrations (i.e., under conditions of stronger interdomain interactions). In fact, on millisecond time scales (1–20 ms), the diffusion coefficient behaves as $D\left(t\right)\propto t^{\alpha -1}$ with α = 0.23, which suggests that the dynamics of TbQSOX are subdiffusive (Fig. 4B). Importantly, subdiffusive dynamics directly hint at rugged or even fractal-like free energy landscapes (47), thus confirming our interpretation and raising the question of how these dynamics respond to an electron load caused by the model substrate DTT.

Fig. 4.

Estimate of the relative diffusion coefficients for opening and closing at low and high salt concentrations. (A) Experimental decays (circles) at 0 M NaCl (Top) and 0.2 M NaCl (Bottom) are shown in comparison with fits (black lines) using the numerical solution of the fractional Brownian motion model (Eq. 5) with the empirical relationship $D\left(t\right)=D\left(0\right){\left(1+bt\right)}^c$. The fit results in b = 1.52 ms⁻¹ and c = −0.08 at 0 M NaCl and b = 0.89 ms⁻¹ and c = −1.03 at 0.2 M NaCl. (B) Time dependence of the relative diffusion coefficients at 0 M NaCl (blue) and 0.2 M NaCl (red), obtained from the fits shown in A. The apparent power-law exponents α (in the text) in the region from 1 ms to 20 ms are indicated in the figure. (Inset) Estimated free energy potential along the experimental distance coordinate (SI Appendix).

Dynamics of TbQSOX During Substrate Turnover.

The substrate DTT binds predominantly to open conformers (34, 37) in which the active CXXC motif of the Trx domain faces the solution. The addition of DTT causes a clear redistribution of open and closed conformations in the transfer efficiency histograms (Fig. 5A). Up to 1 mM DTT, the high-FRET population increases, thus indicating a shift toward the closed conformation. At higher concentrations, however, the trend reverses and the open conformation dominates again (Fig. 5A). While the initial increase of closed conformers is explained by the formation of an interdomain disulfide and other closed species (37, 48), the decrease at high DTT concentrations is caused by the formation of an open species in which both domains are loaded with electrons (37).

Fig. 5.

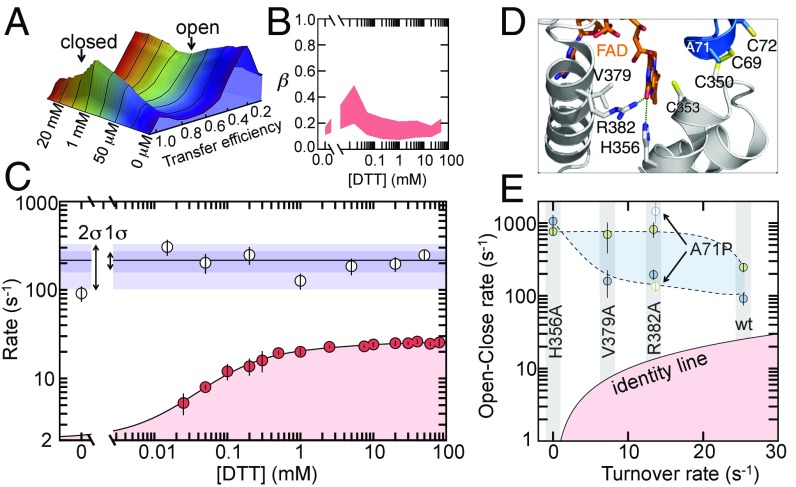
The effect of substrate and mutations on the conformational kinetics and activity of TbQSOX. (A) Transfer efficiency histograms measured under steady-state conditions at different concentrations of DTT. (B) β-Exponents obtained at varying DTT concentrations. The upper border results from weighted fits of the decays with Eq. 2 and the lower border comes from unbounded power law fits. (C) Rates (defined as the inverse half-life) for turnover (red circles) and open-closing reactions (white circles). Error bars are the SD for the turnover data (n = 3) and errors of the weighted fit for the open-close rates. Blue shaded areas indicate 1 and 2 SDs of all rates in the presence of DTT. The turnover rates were fitted with a previous model (37) (SI Appendix). (D) Structure of the active site of TbQSOX in the closed conformation (PDB ID: 3QD9). The Trx and Erv domains are indicated in gray and blue, respectively. The side chains of catalytically important residues are represented as sticks. (E) Comparison of open-close rates in the absence (blue circles) and presence (green circles) of 50 mM DTT with the turnover rate. Open symbols represent the variant A71P. The black solid line is the identity line.

Qualitatively, the main features of the open-close decays (Fig. 2A) remain unaffected by the presence of substrate. The decays are well described by a power law with β ≤ 1/2 over the full range of DTT concentrations, suggesting that the subdiffusive dynamics persist also in the presence of substrate. A moderate increase in β (Eq. 2) at very low concentrations of DTT is followed by a subsequent decrease at higher concentrations (Fig. 5B), which indicates a redistribution of the microscopic processes involved in the global opening and closing of the domains. Small but significant differences are also found in the rate of opening and closing. In the absence of substrate, we find an opening-closing rate of 91 ± 16 s⁻¹ (Fig. 5C). However, already at the lowest DTT concentration (15 μM), the rate is increased and, within the error of the experiment, remains constant at a value of 216 ± 57 s⁻¹ (Fig. 5C), in good agreement with the rate of electron shuttling between the domains (280 s⁻¹) (48). The substrate-induced increase in the opening-closing rate together with the change in the β-exponent indicates that the electron load changes the distribution of microstates and the barriers that separate them. A comparison with the turnover rates (Fig. 5C) shows that the open-close dynamics are an order of magnitude faster over the full range of substrate concentrations, such that the open-close motions of the enzyme are unlikely to be rate-limiting for catalysis. In fact, previous experiments identified the electron transfer to FAD to be rate-limiting in catalysis (48), a step that does not necessarily require global conformational changes. However, even though the opening and closing motions of TbQSOX are not rate-limiting, they are key for catalysis by shuttling electrons between both domains, thus raising the question of how mutations of catalytic residues alter these dynamics.

To address this question, we investigated variants of TbQSOX with altered catalytic turnover rates (Fig. 5D and SI Appendix, Fig. S5). For example, alanine substitutions of near active-site residues R382, V379, and H356 in the Erv domain have been shown to significantly lower the turnover rate (37). While the residue V379 is proposed to line the O₂ route toward the FAD cofactor, thus being responsible for an effective oxidation of FAD, the residues R382 and H356 form hydrogen bonds with FAD and orient the cofactor favorably to allow an efficient electron transfer to the FAD (49, 50) (Fig. 5E). In addition, we investigated a mutation in the CXXC motif of the Trx domain (A71P), which has previously been shown to significantly reduce the turnover rate of QSOX (37, 51).

We performed single-molecule recurrence experiments for all four variants of TbQSOX with and without saturating amounts of DTT (50 mM). We found the apparent power-law decays to be conserved throughout the set of variants with rates that were substantially faster than the turnover rate (Fig. 5E and SI Appendix, Fig. S5). However, differences are apparent on a quantitative level. While the variants R382A and V379A show a substrate-induced acceleration of the open-close motions similar to the WT enzyme, the variants H356A and A71P do not follow this trend (Fig. 5E). For example, the addition of substrate to the variant A71P leads to a decrease in the open-close rate, opposite to the behavior of the WT enzyme (Fig. 5E). Previous experiments indicated that A71P has a less oxidizing Trx active site with a prolonged lifetime of the “closed” interdomain disulfide (37), which likely causes the slower open-close equilibrium observed in the presence of substrate. Another unexpected result is found for the inactive variant H356A. Here, the substrate DTT has no effect on the open-close kinetics (Fig. 5E). Given the fact that a replacement of histidine 356 by alanine perturbs the local positioning of FAD but still enables substrate binding and electron shuttling between the domains (37), the result implies that the local electron transfer from the CXXC motif in the Erv domain to FAD also modulates the opening and closing of the domains, a result that demonstrates the delicate link between catalysis and dynamics. In total, two out of four active-site variants show substantial alterations of their conformational fluctuations, suggesting that enzyme dynamics can be more vulnerable than previously thought. Particularly in proteins with a broad ensemble of conformers, such as TbQSOX, mutational perturbations may propagate through the enzyme interaction network in unanticipated ways. A redistribution of free energies within the macroscopic open and closed states may only marginally affect the kinetics if the exchange within each basin is fast compared with global transitions between the basins. However, in TbQSOX, this exchange is comparatively slow and alterations in one of the macroscopic ensembles can have pronounced effects on the overall kinetics.

Conclusions

The link between conformational fluctuations and catalytic activity has become central to our view of enzymes as dynamic catalysts with evolved function. Here, we complement this view by taking conformational heterogeneity into account. Disorder in the sense of a coexisting spectrum of conformations has mainly been considered to be relevant for protein-folding reactions (52), and the behavior of intrinsically disordered proteins (53), while the structures of enzymes are typically thought to be structurally well defined and highly optimized for their biological function. This is not the case for TbQSOX, in which the relative domain orientation in the open state is disordered and slowly exchanging, which gives rise to complex kinetics, despite the apparent two-state behavior of the enzyme. In addition, local heterogeneity may also be associated with the closed state of TbQSOX but the insensitivity of FRET at short-length scales precludes any structural conclusion in this case. Notably, recent simulations of the domain reconfiguration in phosphoglycerate kinase also revealed power-law decays from picoseconds to microseconds in the autocorrelation function of the interdomain displacement, which was explained by a fractal topology of the underlying free energy landscape with self-similarity at different length scales (54). Our results on TbQSOX suggest that this behavior even extends to the biologically more relevant micro- to millisecond time scale. Notably, conformational multiplicity can also cause nonexponential dwell-time distributions of chemical states (e.g., FAD in its reduced and oxidized form), an effect known as enzymatic memory (8) or hysteresis (17). While being unlikely for TbQSOX due to the fast open-close motions of TbQSOX compared with catalysis (Fig. 5C), we expect that this effect will be pronounced for other multidomain enzymes with faster turnover rates.

However, is the conformational heterogeneity functionally relevant for TbQSOX? The biological function of TbQSOX and its homologs is to generate disulfide bonds in proteins (34). Typically, this task is carried out by dual-enzyme systems: one enzyme generates disulfide bonds in the substrate proteins and a partner transfers the electrons to a final acceptor (55, 56). The natural fusion of the two functional modules in QSOX has been shown to increase the efficiency of the enzyme by a factor of 2,500 for the human homolog (34). Given this tremendous rate enhancement, conformational heterogeneity may be irrelevant as long as unspecific domain interactions do not stably trap the enzyme in inactive conformations. However, the natural substrates of TbQSOX are proteins, which are dynamic themselves. Even if irrelevant for catalysis, the broad distribution of waiting times in the open ensemble may represent a significant advantage in binding a wide variety of complex substrates. A slow sampling of the domain configurations may also provide unorthodox options for the regulation of enzymatic and metabolic activity. This aspect has already been recognized in the early work on hysteretic enzymes (i.e., enzymes that slowly interconvert between differently active conformers and that provide unique capacities to buffer metabolic pathways against fast changes in ligand concentrations) (17).

In summary, our experiments demonstrate the presence of a rugged free energy landscape for the enzyme TbQSOX, a phenomenon that may be generic to multidomain enzymes with disordered linkers, and rate equations with a limited number of states may not be adequate to model this complexity.

Materials and Methods

TbQSOX and its variants were expressed, purified, and labeled as described previously (37). Unless stated otherwise, all experiments were performed in 20 mM sodium phosphate pH 7.5 with 200 mM NaCl, containing 0.01% Tween20 to prevent surface adhesion of the enzyme. Details of the single-molecule experiments and their analysis are described in detail in the SI Appendix.