Significance
This work identifies properties of a combinatorial face code that are conserved across all 2,000 faces tested. The same properties of a combinatorial olfactory code in insects has earlier been shown to be preserved across odors and odor mixtures. That the same features of combinatorial codes are conserved for two such different systems (primate vision and insect olfaction) raises the possibility that these conserved features of a code may be used for similar computations.
Keywords: face encoding, face recognition, combinatorial code
Abstract
A recent paper demonstrated that the pattern of firing rates across ∼100 neurons in the anterior medial face patch is closely related to which human face (of 2,000) had been presented to a monkey [Chang L, Tsao DY (2017) Cell 169:1013–1028]. In addition, the firing rates for these neurons can be predicted for a novel human face. Although it is clear from this work that the firing rates of these face patch neurons encode faces, the properties of the face code have not yet been fully described. Based on an analysis of 98 neurons responding to 2,000 faces, I conclude that the anterior medial face patch uses a combinatorial rate code, one with an exponential distribution of neuron rates that has a mean rate conserved across faces. Thus, the face code is maximally informative (technically, maximum entropy) and is very similar to the code used by the fruit fly olfactory system.
With a few exceptions, any of us can rapidly learn to recognize any of the 7 billion faces in the world, and we can identify a familiar face in a fraction of a second (1–3). Although our subjective experience is that our eyes “show” us a face, in fact, faces are represented by the firing rates of particular populations of neurons (4). An important question, then, is: What are the special features of the neural code used to represent faces?
A complete knowledge of the face code would require that we fully understand the neural circuitry responsible for face recognition and could predict, for any face, the firing rates of the face neurons on the basis of the circuit properties. This is a version of the approach adopted by Chang and Tsao (4). A partial understanding of the face code can, however, be achieved by identifying those features of the code that are conserved across all faces. This is the approach I take here. I will conclude that the population of face neurons I study has the same mean firing rate for every face and that the probability distribution for firing rates of the population is also conserved. Conservation principles like the one I describe for faces can have implications for how the face code is used by later circuitry, as I explain in Discussion.
The neurons we and other primates use for identifying faces are concentrated in specific, very small cortical regions, called “face patches” in monkeys (5, 6). These face patches contain neurons that respond specifically to faces or features of faces, and the patches are spread along the inferior temporal cortex. Going from posterior to anterior, face patches contain neurons whose response characteristics change from one face patch to the next. In the most posterior patches, neurons tend to fire in response to face features, but by the anterior medial (AM) patch, neurons (called “AM neurons” in the following) respond about equally to any view of an entire face (with the exception of the back of the head) (7).
A recent advance in our understanding of the neural representation of faces [Chang and Tsao, 2017 (4); hereafter referred to as just “Chang and Tsao”] came from presenting an awake monkey with 2,000 human face images and recording the responses of almost 100 AM neurons to the presentation of these faces. From the firing rates of this population of neurons in response to any specific one of the faces, Chang and Tsao could relate the response to which face had caused it. Furthermore, if a new face was presented to the monkey, the authors could predict the firing rates of the population of AM neurons. In summary, because the firing rates of the neurons could be related to which face caused the response, and because a novel face could be used to predict the firing rates in response to the face, it is clear that this population of AM neurons is using a neural code that links firing rates to the face presented. The specific goal of the present work is to identify properties of this neural face code by examining the database of firing rates produced by each of 98 AM neurons in response to each of the 2,000 faces. These data were supplied to me by Chang and Tsao.
Results
I start with a 98 by 2,000 matrix (data used by Le Chang and Doris Tsao in their paper). This matrix contains the average firing rate for each of the 98 AM neurons and each of the 2,000 faces. Each neuron and face is identified by its location in the matrix, so neurons are numbered 1 through 98, and faces by 1–2,000. To gather data on so many face stimuli in a reasonable period, Chang and Tsao presented each face three to five times, with each presentation lasting 150 ms, followed by a gray screen for another 150 ms. The rate data in the Chang and Tsao matrix are averages over presentations for each face stimulus and over time (see Chang and Tsao for details).
The Neural Face Code Is Combinatorial.
What is a combinatorial code? The idea of a neural combinatorial code was first proposed for the mouse olfactory system (8). Mouse odorant receptor genes constitute a large gene family with ∼1,000 members and, because each odorant receptor neuron expresses receptor proteins encoded by only a single family member, mice have ∼1,000 distinct odorant receptor neurons. Each odorant receptor neuron also responds with different firing rates to many different odors. A population of different types of odorant receptor neurons, then, generates a pattern of firing rates that is, in general, different for every odor. In this way, the vast number of odors mice may need to recognize can be encoded by ∼1,000 neurons. Because the mouse uses rates of 1,000 different neurons to encode each odor, every distinct odor is represented by a point in a high (here, 1,000-D) dimensional space. What I have just described is called a “combinatorial odor code,” and such a code is useful whenever a very large number of similar, but distinct, stimuli must be discriminated.
In the visual system, information about location of a stimulus is received from which neurons are responding to that particular stimulus. In the olfactory system, however, all of the sensory neurons respond to odors. The information about which odor is present is not specified by which neurons in the population of olfactory receptors are firing. Rather, odor identity is given by the pattern of firing rates across a population. This distinction between which neurons in a population are firing vs. the pattern of rates across the population is the hallmark of a combinatorial code.
Here, I describe the combinatorial code used by neurons in the AM face patch where only ∼100 neurons are needed to encode the 2,000 different faces. As Chang and Tsao have stressed, a combinatorial code for faces is much more efficient than encoding only one (or a few) faces per neuron.
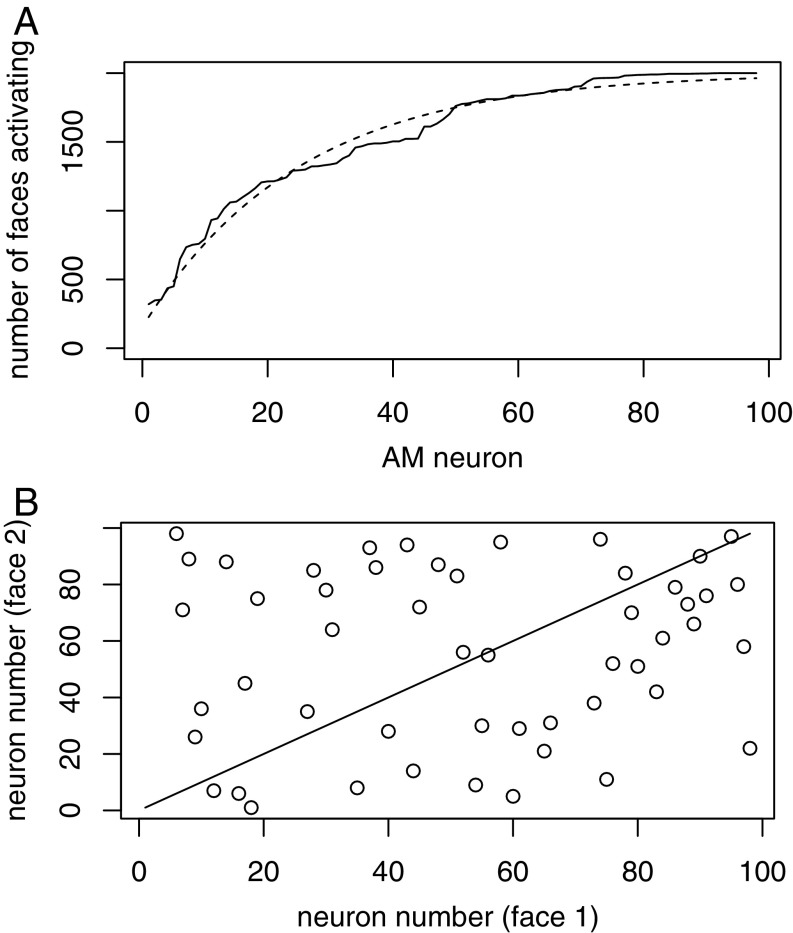
For the 98 neurons I study here, the number that failed to respond to a specific face stimulus—that is, had a firing rate of 0—ranged from 11 to 37, with an average number of ∼22 nonresponding neurons for each face. However, the identity of the nonresponding neurons varied from face to face, and every AM neuron responded, perhaps with a very low rate, to several hundred or more different face stimuli. The number of faces that evoked some nonzero response in a specific AM neuron ranged from 320 to all 2,000 faces, with an average number of 1,554 across all 98 AM neurons. Thus, most AM neurons responded (perhaps with very low rates) to most faces, but 12 AM neurons responded to less than half of the face stimuli presented. Seven of the 98 neurons responded to all 2,000 faces with rates that ranged from 1 to 75 Hz for different faces. Thus, different AM neurons responded to different numbers of faces, as illustrated in Fig. 1A.
Fig. 1.
Properties of the AM face code. (A) Number of faces (of 2,000) that evoke a response in each of the 98 AM neurons. Each face is specified by a number from 1 to 98, but here the neurons are rank-ordered according to the number of faces that evoke a response. On the abscissa, the rank-ordered faces is displayed, and on the ordinate, the number of faces that evoke a response in each neuron is presented. An exponential distribution with a mean of 25 AM neurons has been superimposed on the observed data in the figure. (B) Which neurons respond to each of two faces. On the abscissa is a vector of 50 numbers that give the index (a number from 1 to 98) for each neuron in order of increasing firing rates for face-response vector 1. The ordinate uses the face-response vector (50 long) for face 2.
We can ask which of the 98 neurons were used to encode each face, where neuron identity is specified by its number (from 1 to 98). If we rank-order the 50 neurons that are firing most rapidly for each face (all faces produce at least some firing in 61 neurons), we can produce 2,000 vectors, each with 50 numbers (each entry in the vector designates a neuron that fired for the face). Neuron numbers are listed in their order of increasing neuron firing rates, so that the first entry in the vector specifies the slowest firing of the 50 neurons, and the last entry specifies the neuron with the highest rate for that face. These vectors are called “face-response vectors,” and two such vectors, for faces 1 and 2, are presented in Fig. 1B to illustrate the idea. If the same neurons fired for both faces (if the same face were presented twice, for example), they would fall on the diagonal straight line in the figure. The fact that only one point (for AM neuron 90) fell on this line means that either the same neurons were firing at different rates for the two faces or that different neurons were firing. For the 50 AM neurons represented in face-response vector 1, 32 of the same neurons were used by face 2, and 18 neurons were different. Of the 32 neurons that were used by both faces, only 1 (AM neuron 90) was at the same location in both face-response vectors. To characterize plots like this for pairs of faces, I calculated a correlation coefficient for the two vectors. For this particular pair of faces, the correlation coefficient was 0.08, so the two face-response vectors were nearly uncorrelated.
I also calculated the correlation coefficients for the face-response vectors for all 1,999,000 face pairs. The correlation coefficients ranged from −0.62 to 0.74, and the average across the absolute value of the coefficients gave a mean correlation coefficient of 0.13. High positive correlations meant that the face stimuli must have been similar (same neurons with nearly the same rate). A mean close to zero (0.13) for the absolute value of correlation coefficients meant that most face pairs used the same neurons at different rates or different neurons, as would be expected for a combinatorial code. The extremes of the range of correlation coefficients (the largest correlation was 0.74) presumably arose because those particular face pairs were quite similar. I return to this point in Discussion.
Constraints on the Face Code.
We know from Chang and Tsao that the rates of the 98 AM neurons carry enough information to identify the faces. And we know from the above analysis that different faces produce nonzero firing rates for different numbers of neurons (61–88 of 98 AM neurons); that most faces activate, at least minimally, most AM neurons; and that all 98 neurons are activated by multiple face stimuli. Thus, it seems that the AM face patch neurons use a combinatorial code to identify faces. Here, I show two constraints on the combinatorial face code.
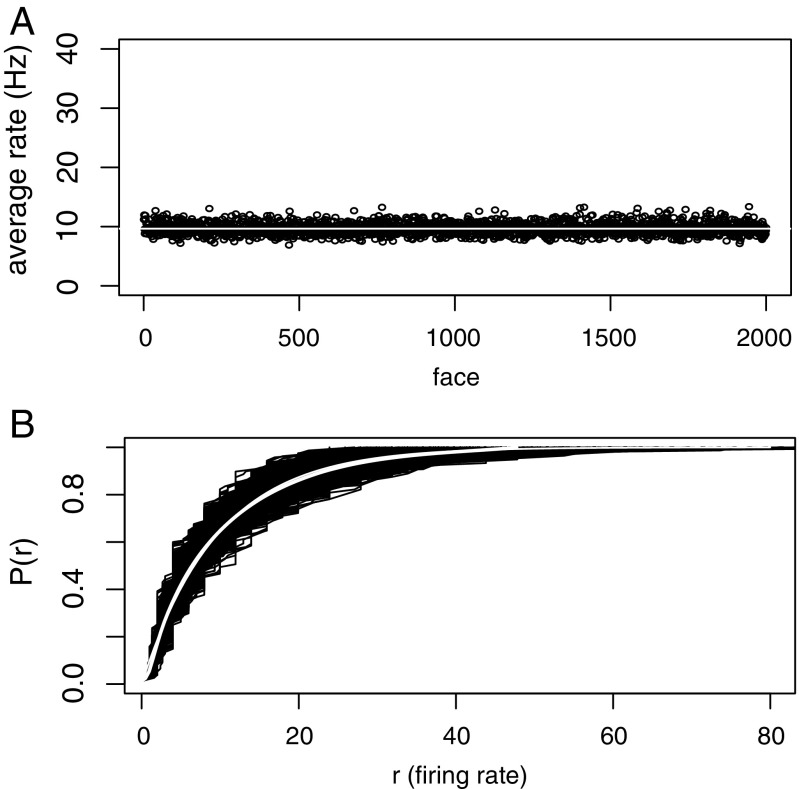
As noted above, which neurons are activated varied across the 2,000 faces. The mean firing rate (excluding neurons with a zero rate) across AM neurons was approximately the same across all faces, as is shown in Fig. 2A. The mean rate across the 2,000 face stimuli was 9.7 Hz (white line in Fig. 2A) with a SD of 0.97.
Fig. 2.
Constraints on the combinatorial face code. (A) The mean firing rate of active neurons (ordinate) as a function of face number (abscissa). The white line represents the grand mean firing rate of 9.7 Hz calculated across the 2,000 individual mean rates. (B) Cumulative probability distribution of AM neuron rates. The abscissa gives the firing rate for each AM neuron, and the ordinate is the cumulative probability. The distribution functions for 2,000 faces are superimposed (black band), and an exponential distribution with a mean of 9.7 Hz (thin white line) and the average across all 2,000 observed distribution functions (thicker white line) are superimposed.
The distributions of firing rates, then, have a mean that is close to the same across all faces. Codes, like the face code, are most informative (that is, they have maximum entropy according to information theory; ref. 9, chapter 14, Entropy) for only certain firing-rate distribution functions. If the mean for a code is constrained to be constant, the associated maximum entropy distribution for rates is an exponential (section 14-4, The Maximum Entropy Method, examples 14–18 of ref. 9). Maximum entropy codes are of interest because, roughly speaking, they are the ones that encode the most faces with the fewest neurons. Note that the notion of “face code” has two distinct aspects: (i) the rules that map face identity to the firing rates of neurons, and (ii) the rules that firing rates follow that are independent of which face is being encoded. Here, I consider only the second aspect of the face code.
I therefore compiled a cumulative firing rate distribution for each face and show all 2,000 distribution functions superimposed in Fig. 2B. Also, I superimposed on Fig. 2B a cumulative exponential distribution with a mean of 9.7 (thin white curve) and the cumulative distribution obtained by averaging across the 2,000 individual observed distributions (thicker white curve); in this figure, the two curves are indistinguishable. Note that no adjustable parameters were used in this superimposition. Although some scatter is seen in the observed distributions that are superimposed, the exponential distribution describes the data well and is very close to the average across the observed distributions.
How might the scatter in the observed rate distributions arise? Because the number of neurons that responded to each face ranged between 61 and 88, this relatively small sample size used to estimate an exponential rate distribution would be an unavoidable source of scatter. To evaluate this source for scatter, I generated 2,000 samples from a cumulative exponential distribution (mean = 9.7 Hz), each with the same ample size (number of AM neurons) as the observed distributions. Much of the scatter in the empirical distributions could be accounted for from what was expected from the sample sizes of the number of responding neurons for each face.
Discussion
My main conclusion was that the AM face patch uses a combinatorial rate code, one with an exponential distribution of AM neuron rates that has the same mean for all face stimuli. The interpretation of my conclusion depends on the Chang and Tsao result that the firing of a population of AM cells has all of the information necessary to faithfully distinguish the 2,000 faces studied.
Until the recent Chang and Tsao paper, many of the AM face cells were often thought to encode a single, specific face (10, 11). This idea was based on the observation that some AM cells appeared to respond to just one face out of many presented. An important conclusion, then, of the Chang and Tsao paper was that AM face cells are not selective for just one, or a few, faces, but rather responded to many faces. A conclusion of my work is that AM neurons use a combinatorial code and thus respond to many faces. This conclusion supports the Chang and Tsao result that each AM neuron responds to many faces, but is based on an alternative approach to their data that does not make use of principal components analysis or the special properties of the Chang and Tsao face space.
The Chang and Tsao database of face stimuli was generated in the following way: First, they started with a dataset with frontal views of 200 actual faces and then used a two-step procedure to find an average of these faces (12, 13). The first step was to find each face shape from landmarks defining specific features (location of mouth, eyes, etc.), and the second step was to determine the local facial textures. From the averages across face shape and spatial texture, the authors extracted 200 shape descriptors and 200 local texture descriptors that were used to find the 50 principal components describing the average face (25 for shapes and 25 for textures). Starting from the average face and morphing along each of the 50 principal components (basis vectors for their face space), the authors constructed a 50-dimensional face space with realistic face stimuli. The 2,000 face stimuli presented were a random sample of this face space. Any actual face could also be projected onto the set of 50 basis vectors (the principal components) to characterize it. And the firing rates of the AM neurons could be used to find the projection of any face stimulus onto the 50-dimensional face space. For a more complete description of the construction of the face stimuli, refer to Chang and Tsao.
The point of reviewing the construction of the Chang and Tsao face space was to note the distinctive characteristics of the face stimuli studied here. Because morphing was used to produce face stimuli along the 50 basis vectors, the faces in this database might have been more similar to each other than would be the case for a “random” sample of faces. By comparing the nearly 2 million face pairs in the Chang and Tsao database, the most similar faces should then have had a higher correlation coefficient, and some face pairs might have been more similar than usual because of the use of morphing in generating the face space. Of course, any database with a large number of faces will have some pairs that are similar. To decide whether generating a database by morphing along principal components would give more similar faces than a database of randomly selected faces would require a separate detailed study.
The data presented here highlight a problem relating to understanding how the face code is used for face recognition and learning and what role the properties of the combinatorial face code I describe here play in these processes. Perhaps unexpectedly, the combinatorial face code is quite similar to the odor code used by the fruit fly olfactory system (14). Flies have a gene family with ∼50 members, genes that encode the fly odorant receptors (15). Each odorant receptor neuron in the fly’s nose expresses a single member of this family, so there are 50 distinct types of odorant receptor neurons, each of which responds to most odors. Thus, every odor is represented as a point in a 50-dimensional space by a combinatorial code. Information from the fly’s nose is transmitted to the first olfactory brain structure, the antennal lobe. The antennal lobe has ∼50 types of projection neurons (16), one for each olfactory neuron type, that send information to another olfactory brain structure called the mushroom body (17, 18).
The combinatorial code used by the fly projection neurons has, for each odor, an exponential distribution of firing rates with the same mean for all odors (14), just like the AM neurons. Also, flies can learn to recognize any odor, a recognition they exhibit by approaching or avoiding the odor according to whether they have been rewarded or punished in the presence of that odor (19, 20). Once an odor has been learned, a fly can recognize it in a fraction of a second, just as we can learn to recognize any face and can identify a familiar face in a fraction of a second. Thus, the same problem—identifying an arbitrary point in a high-dimensional space—is solved by the fly for odor recognition and the monkey for face recognition.
The fly learns to identify an odor by generating a “tag” in the mushroom body calyx, a tag being a small population of neurons, ∼100, that substitutes for the combinatorial odor code for learning (14). This tag has two main properties: First, all of the odor information the fly has can be recovered from the tag (although the tag bears no obvious resemblance to the code for that odor), and, second, the tags for two odors selected at random use nonoverlapping populations of neurons. Having a tag that is as close to unique as possible for each odor is essential for learning (which occurs in lobes of the mushroom body) because only active synapses can have their synaptic strength modified by learning. If two tags overlap, then each tag would be modifying the strength of the same synapses, and confusion between the odors could result. Note that the combinatorial code itself could not be used for learning because the code for any specific odor would alter synaptic strengths for many other odors. For the fly, the mechanism through which disjoint tags are generated depends on having the exponential distribution of firing rates for every odor (see discussion in ref. 14).
As Quiroga pointed out (21), one of the important next steps for face cell research will be to go from perception-dominated face responses to face learning. If we could believe that the same general strategy works for fly olfaction and monkey face recognition, we can anticipate that the face code would be sent to the dentate gyrus, where a tag for each face would be generated. This tag would then be used for learning faces in the CA3 and CA1 regions of the hippocampus.
Possible parallels between the fly and monkey systems can suggest mechanisms, but only new experiments can establish how the face code is actually used.
Materials and Methods
Experimental Procedures.
All of the analysis presented here was based on a data file supplied by Chang and Tsao. Their original Matlab file was converted to a .csv text file for use with an R script running under RStudio.
Cumulative Histograms.
The original .csv data file was converted in R to a 98 × 2,000 data matrix (called ) for the 98 AM neurons and the 2,000 face stimuli. Each face was associated with 98 firing rates. Two additional matrices were then derived from . The first was a version of , called , in which all 2,000 columns were sorted in increasing order of firing rates, and the second version was , which resulted from applying the R function order( ) to each column of . This order( ) function gave the index for each neuron (the index identifies the AM neurons) in order of increasing firing rates. Having both and let me keep track of which neurons were associated with which rates in . The three matrices , , and were used throughout the rest of the analysis.
The Fig. 2 Graphs.
The next step in the analysis was to discover how many (and which) of the AM neurons failed to respond to each face (AM neurons that have a firing rate = 0 for a given face). Using the matrix, I constructed a 2,000-long vector with the number of zeros in each column of , and with I constructed a list of vectors with the AM neuron indices that corresponded to nonresponding AM neurons. Subtracting each entry in from 98 (total number of AM neurons in each column), I found the number of neurons that did respond to each face. Also, using and , I found a 2,000-long list (called ) of vectors with the responding AM neuron rates rank ordered. These vectors excluded AM neurons with a firing rate = 0.
Using probability distributions (represented by cumulative histograms) rather than the more familiar probability density functions had several advantages, one of which was that no binning was required. To estimate a probability distribution for a face that has neurons firing, the rank-ordered firing rates were placed on the abscissa of a graph and a vector with entries ()/ was put on the ordinate of the graph to provide a cumulative histogram that was a good approximation to the distribution function. That is, for each rate on the abscissa, the ordinate was stepped up by . Note that this procedure assigned the cumulative probability = 1 for the fastest-firing neuron for each face. As long as the number of firing neurons was large enough, the most rapidly firing AM neuron would have a probability distribution value that is close to . The plots in Fig. 2B are superimpositions like this for the 2,000 vectors in the list of cumulative histograms.
To make Fig. 2A, a 2,000-long vector with the mean of each of the elements in the list (the AM neuron firing rates for each face) was constructed, and the values in this list were plotted against the numbers () on the abscissa. The superimposed exponential distribution function just used the R function pexp(x,1/9.7), where the mean across all 2,000 means of individual distributions was Hz.
Because a different number of AM neurons responded to each face, the sample size varied from face to face, and calculating the mean across vectors of different lengths required care. The way I did this was to use the R function approx(x, y) that took unequally spaced vectors (like those in the list on the abscissa of the graphs for distribution functions) and linearity interpolated the corresponding ordinate values so that both were equally spaced. When this was done, the result was 100 abscissa values and 100 ordinate values, so the mean and SD of each across all 2,000 faces could be found. The estimates of the average were then plotted in Fig. 2 B and C, and 5 times the SD of the mean appears in Fig. 2C.
With fairly small sample sizes (like 61–88 responsive neurons for each face) of an exponential distribution function, the result was scatter of the sort shown for the estimates of the observed distribution functions for the 2,000 faces. To see if observed amount of scatter across 2,000 distribution functions could be accounted for by the sample sizes, I generated 2,000 random samples from an exponential distribution function (with the same sample sizes found for the 2,000 faces) using the R function rexp(), where is the length of the sample and is the mean of the exponential distribution. These simulated distribution functions are plotted in Fig. 2D in just the same way that the observed distribution functions were plotted in Fig. 2B.
Fig. 1 Graphs.
From the matrix —which gives the firing rate of AM neurons for each face (the columns of ) and the firing rate for all faces for each AM neuron (the rows of )—I constructed a vector of length 98 that contained the number of faces with nonzero firing rates for each AM neuron. This vector was sorted (entries are put in increasing order of faces). The sorted vector is on the abscissa of Fig. 1A, and the number of faces that produced nonzero responses is on the ordinate.
Fig. 1A establishes that all 98 AM neurons respond to a range of hundreds up to 2,000 faces, one of the hallmarks of a combinatorial code. For Fig. 1B, I noted that the other defining characteristic of a combinatorial code is that the same AM neuron fires at different rates for various faces. To examine this property, I used the matrix which has the identifying index (1–98) placed in order of firing rate for each face. For two faces (1 and 2), I plotted in Fig. 1B the 50 fastest firing neuron indices for face 1 on the abscissa and for face 2 on the ordinate. It is clear from this plot that the same AM neurons were firing at different rates (specifically, with a different rank order) for the two faces. To quantify this difference, I calculated the correlation coefficient for faces 1 and 2 and obtained value close to zero. Fig. 1B was just an illustration of the method. I also used the R function cor( ) to calculate the 2,000 by 2,000 correlation matrix for all pairs of faces and used the R function upper.tri( ) to replace entries in the matrix with zeros everywhere in the correlation matrix, except in the upper triangle (which contained correlation coefficients for all pairs of different faces). This modified correlation matrix was then used to find the mean, range, and absolute value of all correlation coefficients for face pairs. Note that the absolute value was necessary to prevent positive and negative correlation values (which are present in about equal numbers) from canceling in finding the mean value.
Supplementary Material
Acknowledgments
I thank the Aspen Center for Physics, where much of the work was carried out, for hospitality. This work was supported by National Science Foundation Grants PHY-1444237 (to C.F.S.) and PHY-1066393 (to Aspen Center for Physics).
Footnotes
The author declares no conflict of interest.
References
- 1.Barragan-Jason G, Cauchoix M, Barbeau E. The neural speed of familiar face recognition. Neuropsychologia. 2015;75:390–401. doi: 10.1016/j.neuropsychologia.2015.06.017. [DOI] [PubMed] [Google Scholar]
- 2.Sinha P, Balas B, Ostrovsky Y, Russell R. Face recognition by humans: Nineteen results all computer vision researchers should know about. Proc IEEE. 2006;94:1948–1962. [Google Scholar]
- 3.di Oleggio Castello MV, Gobbini MI. Familiar face detection in 180ms. PLoS One. 2015;10:e0136548. doi: 10.1371/journal.pone.0136548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chang L, Tsao DY. The code for facial identity in the primate brain. Cell. 2017;169:1013–1028. doi: 10.1016/j.cell.2017.05.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Tsao DY, Moeller S, Freiwald WA. Comparing face patch systems in macaques and humans. Proc Natl Acad Sci USA. 2008;105:19514–19519. doi: 10.1073/pnas.0809662105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hung CC, et al. Functional mapping of face-selective regions in the extrastriate visual cortex of the marmoset. J Neurosci. 2015;35:1160–1172. doi: 10.1523/JNEUROSCI.2659-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Freiwald W, Tsao D. Functional compartmentalization and viewpoint generalization within the macaque face-processing system. Science. 2010;330:845–851. doi: 10.1126/science.1194908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Malnic B, Hirono J, Sato T, Buck L. Combinatorial receptor codes for odors. Cell. 1999;96:713–723. doi: 10.1016/s0092-8674(00)80581-4. [DOI] [PubMed] [Google Scholar]
- 9.Papoulis A, Pillai SU. Probability, Random Variables and Stochastic Processes. McGraw Hill; Boston: 2002. [Google Scholar]
- 10.Riesenhuber M, Poggio T. Hierarchical models of object recognition in cortex. Nat Neurosci. 1999;2:1019–1025. doi: 10.1038/14819. [DOI] [PubMed] [Google Scholar]
- 11.Valentine T. A unified account of the effects of distinctiveness, inversion, and race in face recognition. Q J Exp Psychol. 1991;43:161–204. doi: 10.1080/14640749108400966. [DOI] [PubMed] [Google Scholar]
- 12.Cootes TF, Edwards GJ, Taylor CJ. Active appearance models. IEEE Trans Pattern Anal Mach Intell. 2001;23:681–685. [Google Scholar]
- 13.Edwards GJ, Taylor CJ, Cootes TF. Proceedings, Third IEEE International Conference on Automatic Face and Gesture Recognition 14–16 April, 1998. IEEE; New York: 1998. Interpreting face images using active appearance models; pp. 300–305. [Google Scholar]
- 14.Stevens C. What the fly’s nose tells the fly’s brain. Proc Natl Acad Sci USA. 2015;112:9460–9465. doi: 10.1073/pnas.1510103112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wilson R. Early olfactory processing in Drosophila; mechanisms and principles. Annu Rev Neurosci. 2013;36:217–241. doi: 10.1146/annurev-neuro-062111-150533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bhandawat V, Olsen S, Gouwens N, Schlief M, Wilson R. Sensory processing in the Drosophila antennal lobe increases reliability and separability of ensemble odor representations. Nat Neurosci. 2007;10:1474–1482. doi: 10.1038/nn1976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Aso Y, et al. The neuronal architecture of the mushroom body provides a logic for associative learning. eLife. 2014;3:e04577. doi: 10.7554/eLife.04577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tanaka N, Tanimoto H, Ito K. Neuronal assemblies of the Drosophila mushroom body. J Comp Neurol. 2008;508:711–755. doi: 10.1002/cne.21692. [DOI] [PubMed] [Google Scholar]
- 19.Aso Y, et al. Mushroom body output neurons encode valence and guide memory-based action selection in Drosophila. eLife. 2014;3:e04580. doi: 10.7554/eLife.04580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Waddell S. Reinforcement signalling in Drosophila; dopamine does it all after all. Curr Opin Neurobiol. 2013;23:324–329. doi: 10.1016/j.conb.2013.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Quiroga RQ. How do we recognize a face? Cell. 2017;169:975–977. doi: 10.1016/j.cell.2017.05.012. [DOI] [PubMed] [Google Scholar]