Atmospheric escape from the TRAPPIST-1 planets and implications for habitability

Significance

The search for exoplanets has rapidly emerged as one of the most important endeavors in astronomy. This field received a major impetus with the recent discovery of seven temperate Earth-sized exoplanets orbiting the nearby ultracool dwarf star TRAPPIST-1. One of the most crucial requirements for conventional (surface-based) planetary habitability is the presence of an atmosphere over long timescales. We determine the atmospheric escape rates numerically and analytically for the planets of the TRAPPIST-1 system and show that the outer planets are potentially likely to retain their atmospheres over billion-year timescales. Our work has far-reaching and profound implications for atmospheric escape and the habitability of terrestrial exoplanets around M dwarfs.

Abstract

The presence of an atmosphere over sufficiently long timescales is widely perceived as one of the most prominent criteria associated with planetary surface habitability. We address the crucial question of whether the seven Earth-sized planets transiting the recently discovered ultracool dwarf star TRAPPIST-1 are capable of retaining their atmospheres. To this effect, we carry out numerical simulations to characterize the stellar wind of TRAPPIST-1 and the atmospheric ion escape rates for all of the seven planets. We also estimate the escape rates analytically and demonstrate that they are in good agreement with the numerical results. We conclude that the outer planets of the TRAPPIST-1 system are capable of retaining their atmospheres over billion-year timescales. The consequences arising from our results are also explored in the context of abiogenesis, biodiversity, and searches for future exoplanets. In light of the many unknowns and assumptions involved, we recommend that these conclusions must be interpreted with due caution.

With the number of detected exoplanets now exceeding 3,600 (1), exoplanetary research has witnessed many remarkable advances recently. One of the most important areas in this field is the hunt for Earth-sized terrestrial planets residing in the habitable zone (HZ) of their host stars—the HZ represents the region within which a planet can support liquid water on its surface (2); a probabilistic version of the HZ, encompassing a wide range of planetary and stellar parameters, has also been formulated (3). The importance of this endeavor stems from the fact that such planets can be subjected to further scrutiny to potentially resolve the question of whether they may actually harbor life (4).

Most of the recent attention has focused on exoplanets in the HZ of M dwarfs, i.e., low-mass stars that are much longer lived than the Sun, for the following reasons. First, M dwarfs are the most common type of stars within the Milky Way (5), implying that $\sim {10}^{10}$ Earth-sized planets in the HZ of M dwarfs may exist in our Galaxy (6). Second, owing to the HZ being much closer to such stars, it is much easier to detect exoplanets and characterize their atmospheres, if they do exist (7). Finally, this field has witnessed two remarkable advances within the last year: the discovery of Proxima b (8) and the seven Earth-sized planets transiting the ultracool dwarf TRAPPIST-1 (9, 10). The significance of the former stems from the fact that it orbits the star closest to the Solar System, and the latter is important because there exist as many as three planets in the HZ with the possibility of life being seeded by panspermia (11).

In light of these discoveries, the question of whether terrestrial exoplanets in the HZ of M dwarfs are habitable is an important one (7). Among the many criteria identified for a planet to be habitable, the existence of an atmosphere has been posited as being crucial for surficial life as we know it (4, 12). It is therefore evident that the study of atmospheric losses from exoplanets constitutes a crucial line of enquiry. Empirical and theoretical evidence from our own Solar System suggests that the erosion of the atmosphere by the stellar wind plays a crucial role, especially for Earth-sized planets where such losses constitute the dominant mechanism (13, 14), and the same could also be true for exoplanets around M dwarfs (15, 16). Recent studies of atmospheric ion escape rates from Proxima b (and other M-dwarf exoplanets) also appear to indicate that the resulting ion losses are significant because of the extreme space weather conditions involved (17), potentially resulting in the atmosphere being depleted over a span ranging from tens to hundreds of millions of years (15, 18–20).

Hence, in this paper we focus primarily on the atmospheric ion escape rates of the seven TRAPPIST-1 planets by adapting a sophisticated multispecies magnetohydrodynamics (MHD) model which self-consistently includes ionospheric chemistry and physics and electromagnetic forces. In this work, we do not tackle the wide range of hydrodynamic escape mechanics that have been explored for terrestrial planets (16, 21) for the above reasons.

The Stellar Wind of TRAPPIST-1

To commence our analysis of stellar wind-induced atmospheric loss, the stellar wind parameters of TRAPPIST-1 are required. Since the space weather conditions at the TRAPPIST-1 planets are presently unknown from observations, we must rely upon simulating the stellar wind of TRAPPIST-1. The latter is implemented by means of the Alfvén Wave Solar Model (AWSoM), a data-driven global MHD model that was originally developed for simulating the solar corona and solar wind (22, 23). The AWSoM has been proved to be successful in reproducing high-fidelity solar corona conditions (23, 24) and can readily be adapted to self-consistently model stellar wind profiles for a wide range of stars (17, 25, 26). To adapt the AWSoM for modeling the TRAPPIST-1 stellar wind, we use the rotational period, radius, and mass of the star based on the latest estimates (27) and a mean magnetic field typical of similar late M dwarfs (28). Further details concerning our approach can be found in Modeling the Stellar Wind of TRAPPIST-1.

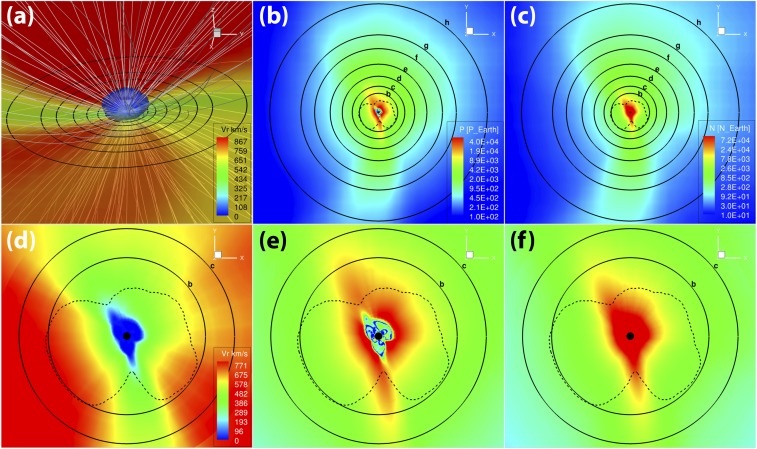
The steady-state stellar wind solution is illustrated in Fig. 1. Compared with the normal solar wind solution (29), the stellar wind of TRAPPIST-1 is much faster (approximately three times) when evaluated at the same stellar distance. The critical surface is defined as the region where $v_s=v_f$, with $v_s$ and $v_f$ representing the stellar wind and fast magnetosonic speeds, respectively. The surface occurs at distances of $\sim 30$ $R_{\ast }$ and $\sim 20$ $R_{\ast }$ for the fast and slow stellar winds; these winds originate at different regions on the star and have different speeds and densities (23). Hence, this leads to a very unique feature of the TRAPPIST-1 system, namely that part of the orbit of TRAPPIST-1b (the closest planet) lies within the critical surface, while all of the other planets are embedded in the supermagnetosonic stellar wind.

Fig. 1.

The steady-state stellar wind of TRAPPIST-1. (A) The 3D stellar wind configuration with selected magnetic field lines. The background contour shows stellar wind speed at the equatorial plane (z = 0). The blue isosurface represents the critical surface beyond which the stellar wind becomes supermagnetosonic. The black solid lines represent the orbits of seven planets, TRAPPIST-1b to TRAPPIST-1h. (B) The equatorial plane z = 0 showing the stellar wind dynamic pressure normalized by the solar wind dynamic pressure at 1 astronomical unit (AU). The dashed line shows the critical surface location. (C) The equatorial plane z = 0 showing the stellar wind density normalized by the solar wind density at 1 AU. (D–F) A zoom-in view of the equatorial plane at z = 0 near TRAPPIST-1 depicting the stellar wind velocity, normalized dynamic pressure, and density, respectively. Note that the color bar for E is the same as for B, and that for F is identical to that for C.

This striking scenario does not exist within our own Solar System primarily because of the proximity of TRAPPIST-1b to its host star (in conjunction with a strongly magnetized stellar wind). As TRAPPIST-1b orbits within the critical surface, the planet could magnetically interact with its host star directly. In turn, the star–planet interaction could perhaps (i) regulate the rotational rate (30), (ii) modify the properties of a local dynamo (31), and (iii) even give rise to a dynamo mechanism (32). In this context, we observe that variations in the magnetic field occur during the stellar cycle caused by the dynamo process. Thus, the distance of the critical surface is expected to also vary concomitantly, implying that TRAPPIST-1b could be subject to frequent transitions between submagnetosonic and supermagnetosonic stellar wind conditions along the lines of Proxima b (17).

Another distinguishing feature of the stellar wind from TRAPPIST-1 is its higher density. When combined with the higher wind speed, all of the planets are subjected to a much larger dynamic pressure compared with that experienced by the Earth. At the orbit of TRAPPIST-1b, the dynamic wind pressure is about ${10}^3$–${10}^4$ times greater than the solar wind dynamic pressure at Earth. Even when we consider the furthermost planet, TRAPPIST-1h, the dynamic pressure is about 100–300 times larger than the near-Earth environment. The existence of such an extreme wind pressure has already been documented for Proxima b (17), and its effects on the evolution of the planet’s magnetosphere have also been thoroughly investigated (15, 19). The ramifications of these extreme space weather conditions on the atmospheric ion escape rates of the TRAPPIST-1 planets are explored in Discussion and Conclusions.

We note that the mass-loss rate from TRAPPIST-1 is $\sim 2.6\times {10}^{11}$ g/s, which is about $10\%$ of the solar mass-loss rate. Although the density and velocity of the stellar wind are higher for TRAPPIST-1, the smaller size of the host star is responsible for yielding a value lower than that of the active young Sun (33). The mass-loss rate $\left(\sim 0.1{\dot{M}}_{\odot }\right)$ obtained for TRAPPIST-1 is broadly consistent with the upper bound of $\sim 0.2{\dot{M}}_{\odot }$ for the slightly larger star, Proxima Centauri (34).

Finally, the stellar wind parameters provided in this paper are useful in determining the radio auroral emission from the TRAPPIST-1 planets, which can be used to constrain their magnetic fields (35). In Deducing the Magnetic Fields of the Trappist-1 Planets, we show that the radio emission could potentially peak at $\mathcal{O}(0.1)$ MHz and result in a radio flux density of $\mathcal{O}(0.1)$ mJy; the latter could be enhanced by two to three orders of magnitude during a coronal mass ejection (CME) event.

Ion Escape Rates for the TRAPPIST-1 Planets

To simulate the ion escape rates for the seven planets of the TRAPPIST-1 system, we use the sophisticated 3D Block Adaptive Tree Solar-Wind Roe Up-Wind Scheme (BATS-R-US) multispecies MHD (MS-MHD) model that has been extensively tested and validated in the Solar System for Venus and Mars (36–39) and was recently used to study the atmospheric losses from Proxima b (15). The reader is referred to these papers and to Atmospheric Ion Escape Rates for the TRAPPIST-1 Planets for further details concerning the numerical implementation, the model equations, and the physical and chemical processes encoded within the model. Note that the neutral atmosphere is the source of the produced ions through, e.g., photoionization and charge exchange and that only a small fraction of them will escape into space. Hence, the atmosphere will, in addition to being eroded, also undergo changes in the chemical composition (15).

The Input Parameters of the Model.

For the most part, we concern ourselves with describing and motivating our choice of the different input parameters required for the BATS-R-US model. Before proceeding further, we caution the readers that many of the relevant planetary and stellar wind parameters of the TRAPPIST-1 system are unknown or poorly constrained. Hence, it is important to recognize that, because of the many uncertainties involved, the ensuing escape rates may not necessarily be representative of the TRAPPIST-1 system.

The BATS-R-US model relies upon an atmospheric composition akin to Venus and Mars, implying that the TRAPPIST-1 planets are also assumed to possess a similar composition. There are several factors that must be noted in this context. First, as seen from our Solar System, the ion escape rates for Venus, Mars, and Earth are similar despite their compositions, sizes, and magnetic-field strengths being wildly dissimilar (13, 14), thereby indicating that the ion escape rates may be relatively sensitive to stellar wind parameters compared with planetary properties (the difference in stellar wind parameters at Venus, Earth, and Mars is only up to a $\mathcal{O}(1)$ factor); this is also partly borne out by the atmospheric ion escape rate calculations for Proxima b (15, 19). In addition, it has been shown recently that the ion escape rates are only weakly dependent on the surface pressure (15). We observe that the inner planets of the TRAPPIST-1 system could have experienced significant losses of ${\text{H}}_2$ and water over fast timescales (40, 41), leaving behind other atmospheric components. Finally, a Venus-like atmosphere for the inner planets cannot be ruled out empirically, as noted in ref. 42. [In broader terms, gaining a thorough understanding of Venus-type exoplanets is highly relevant, because it allows us to compare and contrast their properties against those of exo-Earths (43).]

The next two input parameters to be specified are the surface pressure and the scale height for each of the planets. The former remains unknown at this stage, and we work with the fiducial value of 1 atm at this stage. We anticipate that the surface pressure does not significantly alter the escape rates, at least for extreme stellar wind conditions, as demonstrated in ref. 15. The scale height $H_x$ is defined as

$$H_x=\frac{kT}{m{g}_x},$$ [1]

where $g_x$ is the acceleration due to gravity for planet $X$. The latter quantity can be easily computed for all of the planets since their masses and radii are known (10, 27).

The stellar wind parameters are obtained from the model described in The Stellar Wind of TRAPPIST-1. We must also prescribe the extreme UV (EUV) fluxes received at each of these planets, since the EUV flux plays an important role in regulating the extent of photoionization and the resultant stellar heating. This is accomplished by using the values for the TRAPPIST-1 planets computed in refs. 40, 41, and 44.

The planetary magnetic field is a potentially important factor in regulating the ion escape rates. We consider the scenario where the planets are unmagnetized because this case yields an upper limit on the allowed escape rates (15). Hence, if a planet was characterized by “low” escape rates in the unmagnetized limit, it would also typically possess low escape rates in the presence of a magnetic field. It must also be borne in mind that the planets orbiting TRAPPIST-1 are likely to be tidally locked, and it has been argued that such planets are likely to possess weak magnetic fields (45). If a planet is weakly magnetized, it is likely that the total ion escape rate will be comparable to (but slightly lower than) the unmagnetized case (15).

Results from the Model.

For each planet, we consider two limiting cases. The first case corresponds to the scenario with maximum dynamic (and total) pressure over one orbit of the planet. The second case corresponds to the case with minimum total pressure, but with the maximum magnetic pressure. The corresponding stellar wind parameters are provided in Table S2, and the escape rates are in Table 1.

Table 1.

Ion escape rates in s⁻¹

Total pressure	O+	${\mathrm{O}}_2^{+}$	${\text{CO}}_2^{+}$	Total
Maximum total pressure
Trappist-1b	5.56 × 1027	2.09 × 1026	1.52 × 1026	5.92 × 1027
Trappist-1c	1.54 × 1027	1.38 × 1026	1.32 × 1026	1.81 × 1027
Trappist-1d	1.29 × 1027	3.80 × 1025	1.14 × 1025	1.34 × 1027
Trappist-1e	7.01 × 1026	2.83 × 1025	1.10 × 1025	7.40 × 1026
Trappist-1f	5.23 × 1026	3.37 × 1025	1.19 × 1025	5.68 × 1026
Trappist-1g	2.17 × 1026	2.71 × 1025	1.32 × 1025	2.58 × 1026
Trappist-1h	1.06 × 1026	1.65 × 1025	6.98 × 1024	1.29 × 1026
Minimum total pressure
Trappist-1b	9.33 × 1026	4.99 × 1025	2.92 × 1025	1.01 × 1027
Trappist-1c	4.23 × 1026	9.22 × 1025	2.76 × 1025	5.42 × 1026
Trappist-1d	2.81 × 1026	3.07 × 1025	1.04 × 1025	3.23 × 1026
Trappist-1e	2.20 × 1026	4.19 × 1025	1.25 × 1025	2.74 × 1026
Trappist-1f	1.88 × 1026	4.30 × 1025	1.10 × 1025	2.42 × 1026
Trappist-1g	9.33 × 1025	5.85 × 1025	1.38 × 1025	1.66 × 1026
Trappist-1h	4.52 × 1025	2.69 × 1025	4.39 × 1024	7.66 × 1025

For all seven planets, the case with maximum total pressure yields a total atmospheric ion escape rate that is a few times higher than that of the corresponding case with minimum total pressure. The innermost trio of planets (TRAPPIST-1b, -1c, and -1d) have escape rates higher than ${10}^{27}$ s⁻¹, while the outermost four have rates lower than this value when the case with maximum total pressure is considered. In comparison, the escape rates for Mars, Venus, and Earth are $\sim {10}^{24}-{10}^{25}$ s⁻¹ (13), while that of Proxima b is $\sim 2\times {10}^{27}$ (15). In our subsequent analysis, we focus on this case (maximum total pressure) since it leads us toward determining the upper bounds on the escape rates.

Using the mixing-length formalism of ref. 46 in conjunction with the definitions of the stellar and planetary mass-loss rates, it can be shown that

$$N_x\propto {\left(\frac{R_x}{a}\right)}^2{\dot{M}}_{\star },$$ [2]

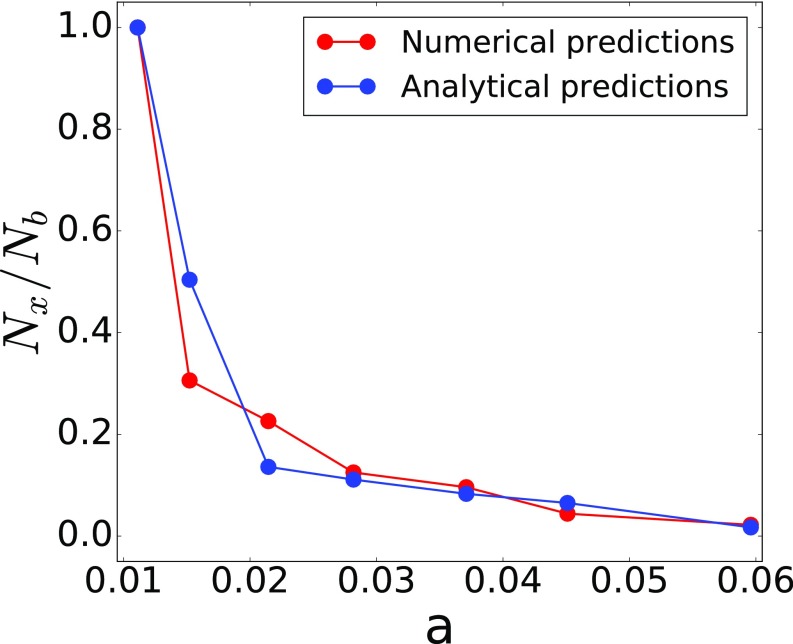
where $N_x$ is the atmospheric escape rate arising from stellar wind stripping, ${\dot{M}}_{\star }$ is the stellar mass-loss rate, and $R_x$ and $a$ are the radius and semimajor axis of the planet $X$, respectively (47, 48). We have normalized the escape rates for the TRAPPIST-1 planets in terms of the escape rate for TRAPPIST-1b and compare the numerical and analytical predictions in Fig. 2.

Fig. 2.

The plot of the normalized escape rate as a function of the semimajor axis for the case with maximum total pressure. The seven distinct points represent the seven planets of the TRAPPIST-1 system.

An inspection of Fig. 2 reveals that the analytical formula is in excellent agreement with the numerical simulations, especially for the outermost four planets (TRAPPIST-1e to -1h) which are regarded as being potentially capable of retaining atmospheres over gigayear timescales. Even for the inner planets, we find that the analytical results fall within the numerical values by a factor of $\lesssim 2$. Hence, Eq. 2 may facilitate a quick estimation of the atmospheric escape rates from unmagnetized planets. However, for both the simulations and the analytic results, it is important to note that the atmospheric escape rates were higher in the past, although quantitative estimates are difficult since the time-dependent stellar mass-loss rates are poorly constrained.

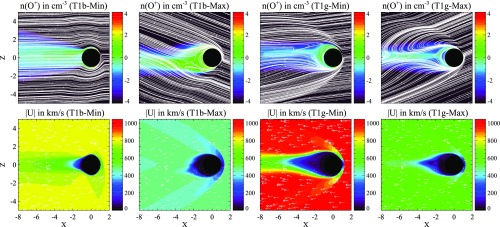
Fig. 3 depicts how the oxygen ions escape from two planets of the TRAPPIST-1 system (TRAPPIST-1b and -1g) along with the interplanetary magnetic-field lines. From the color contours, it is evident that the ion loss rate at TRAPPIST-1b is larger than that at TRAPPIST-1g. The solar wind magnetosonic Mach number of TRAPPIST-1b for the case with minimum total pressure ($P_{tot}$) equals 0.94, and therefore there is no shock formed in front of the planet (because of its submagnetosonic nature). This is particularly noteworthy since this condition is not prevalent in our Solar System for any of the eight planets. On the other hand, such a condition has been observed for moons located inside the planetary global magnetosphere (e.g., Ganymede and Titan). In contrast to the above case, the bow shock is present in all other cases and planets of the TRAPPIST-1 system.

Fig. 3.

The logarithmic-scale contour plots of the O⁺ ion density (Top row) with magnetic field lines (in white) and stellar wind speed (Bottom row) with stellar wind velocity vectors (in white) in the meridional plane. Left two columns correspond to TRAPPIST-1b (minimum and maximum $P_{tot}$) while Right two columns represent TRAPPIST-1g (minimum and maximum $P_{tot}$). The X and Z coordinates have been normalized in terms of the corresponding planetary radius.

Based on the background colors in Fig. 3, Bottom row, minimum $P_{tot}$ corresponds to the fast stellar wind and maximum $P_{tot}$ signifies the slow stellar wind, which is fully consistent with the classical solar/stellar wind picture. The high $P_{tot}$ manifested in the “slow” stellar wind is mostly a consequence of the high stellar wind density. Fig. 3, Bottom row also indicates that the stellar wind accelerates away from the star; the stellar wind velocity at TRAPPIST-1g is obviously larger than that at TRAPPIST-1b. These conclusions can also be verified through an inspection of Table S2.

From Fig. 3, we observe that the plasma boundaries are compressed because of the fact that the total pressure is much higher at these planets compared with that experienced by Venus. The escape of ions is primarily driven by the pressure gradient and $𝐉\times 𝐁$ forces in the momentum equation (38). Finally, we refer the reader to Fig. S1, which depicts the ionospheric profiles of TRAPPIST-1g for the cases with minimum and maximum total pressure.

Discussion and Conclusions

We have arrived at an upper bound on the ion escape rates by considering the scenario where the planets are unmagnetized and subject to the maximum total (or dynamic) pressure. It was concluded that the innermost planet TRAPPIST-1b has an upper bound of $5.92\times {10}^{27}$ s⁻¹ while the corresponding value for the outermost planet TRAPPIST-1h is $1.29\times {10}^{26}$ s⁻¹. As the planets are approximately Earth sized and assumed to have a surface pressure of 1 atm, we can estimate the timescales over which these planets can retain their atmospheres. The values range from $\mathcal{O}\left({10}^8\right)$ y for TRAPPIST-1b to $\mathcal{O}\left({10}^{10}\right)$ y for TRAPPIST-1h. Moreover, we also see from Fig. 2 that the overall escape rate declines monotonically as one moves outward, from TRAPPIST-1b to TRAPPIST-1h. Hence, taken collectively, this may suggest that TRAPPIST-1h is the most “stable” planet among them, when viewed purely from the perspective of atmospheric ion loss. Along the same lines, it seems likely that TRAPPIST-1g will represent the best chance for a planet in the HZ of this planetary system to support a stable atmosphere over long periods. [The 3D climate simulations appear to suggest that TRAPPIST-1f and TRAPPIST-1g may not be amenable to surficial life as they enter a snowball state (49), but the effects of tidal heating, which are expected to be considerable (27), were not included in the model.]

At this stage, we must reiterate the caveats discussed earlier. First, most of the planetary and stellar parameters are partly or wholly unknown since the appropriate observations are not currently existent. The presence of (i) a more massive atmosphere, (ii) a different atmospheric composition, and (iii) the planet’s magnetic field is likely to alter the extent of atmospheric loss to some degree. Nonetheless, it can be surmised that the unmagnetized cases (with maximum total pressure) considered herein do yield robust upper bounds on the atmospheric ion escape rates. Apart from atmospheric loss, it is possible that outgassing processes could very well replenish the atmosphere (50). Hence, resolving the existence of an atmosphere over gigayear timescales necessitates an in-depth understanding of the interplay between source and loss mechanisms. Finally, it is important to note that stellar properties evolve over time, implying that the escape rates are also likely to change accordingly. In the case of M dwarfs such as TRAPPIST-1, the pre–main-sequence phase is particularly long and intense and expected to have an adverse impact on atmospheric losses (7, 51). The ensuing effect of extreme ultraviolet radiation on hydrodynamic and ion escape rates during this phase has not been investigated in this paper.

Bearing these limitations in mind, we now turn to a discussion of the implications. We have argued that TRAPPIST-1h and TRAPPIST-1g represent the most promising candidates in terms of retaining atmospheres over gigayear timescales. Instead, if the atmosphere were to be depleted over $\mathcal{O}\left({10}^8\right)$ y, this could prove to be problematic for the origin of life (abiogenesis) on the planet although it must be acknowledged that the actual timescale for abiogenesis on Earth and other planets remains unknown (52). Abiogenesis has been argued to be accompanied by an increase in biological (e.g., genomic) complexity over time (53, 54), although this growth is not uniform and may be contingent on environmental fluctuations. Hence, ceteris paribus, a planet capable of sustaining a stable atmosphere over long time periods (along with retaining a stable climate) might have a greater chance of hosting complex surficial organisms. The outer planets of the TRAPPIST-1 system may therefore lead to more diverse biospheres eventually.

We have also shown that the ionospheric profiles for the TRAPPIST-1 planets in the HZ are not sensitive to the stellar wind conditions at altitudes $\lesssim 200$ km (Fig. S1). This is an important result in light of the considerable variability and intensity of the stellar wind, since it suggests that the lower regions (such as the planetary surface) may remain mostly unaffected under normal space weather conditions. [Stellar flares may have either a deleterious or a beneficial effect on prebiotic chemistry that is dependent on a complex and interconnected set of factors (55, 56).]

Let us turn our attention to Table 1 for the seven Earth-sized exoplanets of the TRAPPIST-1 system. It is seen that the ion escape rate reduces as one moves outward. Hence, for similar multiplanetary systems around low-mass stars, it may be more prudent to focus on the outward planet(s) in the HZ for detecting atmospheres since their escape rates could be lower. Similarly, when confronted with two planets with similar values of $R_x$ and $a$ (Eq. 2), we propose that searches should focus on stars with lower mass-loss rates and stellar magnetic activity. Finally, our results and implications are also broadly applicable to future planetary systems detected around M and K dwarfs endowed with similar features (11).

To summarize, we have studied the atmospheric ion escape rates from the seven planets of the TRAPPIST-1 system by assuming a Venus-like composition. This was done by using numerical models to compute the properties of the stellar wind and the escape rates, and the latter were shown to match the analytical predictions. We demonstrated that the outer planets of the TRAPPIST-1 system (most notably TRAPPIST-1h and TRAPPIST-1g) are capable of retaining their atmospheres over gigayear timescales. However, as many factors remain unresolved at this stage, future missions such as the James Webb Space Telescope will play a crucial role in constraining the atmospheres of the TRAPPIST-1 planets (57). In particular, a recent study concluded that spectral features for six of the seven TRAPPIST-1 planets could be detected with $<20$ transits with 5 $\sigma$ accuracy (58). Such observations would help constrain theoretical predictions, pave the way toward looking for biosignatures, and empirically estimate the putative habitability of these planets.