Role of the Axon Initial Segment in the Control of Spontaneous Frequency of Nigral Dopaminergic Neurons In Vivo

Abstract

The spontaneous tonic discharge activity of nigral dopamine neurons plays a fundamental role in dopaminergic signaling. To investigate the role of neuronal morphology and architecture with respect to spontaneous activity in this population, we visualized the 3D structure of the axon initial segment (AIS) along with the entire somatodendritic domain of adult male mouse dopaminergic neurons, previously recorded in vivo. We observed a positive correlation of the firing rate with both proximity and size of the AIS. Computational modeling showed that the size of the AIS, but not its position within the somatodendritic domain, is the major causal determinant of the tonic firing rate in the intact model, by virtue of the higher intrinsic frequency of the isolated AIS. Further mechanistic analysis of the relationship between neuronal morphology and firing rate showed that dopaminergic neurons function as a coupled oscillator whose frequency of discharge results from a compromise between AIS and somatodendritic oscillators. Thus, morphology plays a critical role in setting the basal tonic firing rate, which in turn could control striatal dopaminergic signaling that mediates motivation and movement.

SIGNIFICANCE STATEMENT The frequency at which nigral dopamine neurons discharge action potentials sets baseline dopamine levels in the brain, which enables activity in motor, cognitive, and motivational systems. Here, we demonstrate that the size of the axon initial segment, a subcellular compartment responsible for initiating action potentials, is a key determinant of the firing rate in these neurons. The axon initial segment and all the molecular components that underlie its critical function may provide a novel target for the regulation of dopamine levels in the brain.

Introduction

The electrical activity of midbrain dopaminergic (DA) neurons underlies the fundamental role that this population plays in motor control and motivation and related disorders (Fahn, 2008; Wise, 2009; Canavier et al., 2016). Their tonic, spontaneous firing activity is punctuated by phasic firing and pauses that encode behaviorally relevant stimuli (Schultz, 2007; Henny et al., 2012; Paladini and Roeper, 2014). On the other hand, tonic firing is responsible for setting baseline dopamine levels in the striatum (Sulzer et al., 2016), which enables activity in postsynaptic motor, cognitive, and motivational systems (Goto et al., 2007; Schultz, 2007). Moreover, it has been proposed (Grace, 2016) that the level of tonic firing in DA neurons sets the gain of the response of the system to stimuli that evoke phasic bursts; the higher the level of background tonic activity in a neuron, the more likely that a stimulus will elicit a burst. The stimulus sets the timing of the phasic response, but the background level of tonic firing determines the amplitude of the response. In addition, the dendritic Ca²⁺ signals that control synaptic plasticity have a supralinear dependence on the tonic firing rate (Hage and Khaliq, 2015). Therefore, the determinants of the spontaneous tonic firing rate in vivo are critical to the regulation of dopaminergic signaling and the motor and motivational circuits that receive these signals.

The spontaneous tonic firing rate of DA neurons depends on many factors, including the density of intrinsic ionic conductances (Ping and Shepard, 1996; Liss et al., 2001; Seutin et al., 2001; Hahn et al., 2006; Canavier et al., 2016), the expression of the calcium-binding protein calbindin (Brown et al., 2009), the level of synaptic input (Lobb et al., 2010; Canavier et al., 2016), the level of D₂ receptor activation (Pucak and Grace, 1994; Hahn et al., 2006), and (for ex vivo recorded neurons) somatodendritic compartment morphology (Jang et al., 2014). It is unclear, however, how the weight of any single parameter contributes to the observed variation (1–8 Hz) in the spontaneous tonic firing rate in vivo.

Since, in most neurons, action potentials are initiated at the axon initial segment (AIS) (Kole et al., 2008), it is important to assess the role of the AIS and its interaction with the somatodendritic domain from which it originates in regulating in vivo tonic firing in DA neurons. We showed previously that AIS size is considerably variable across the substantia nigra pars compacta (SNc) DA neuronal population (Gonzalez-Cabrera et al., 2017), a factor that has been shown to relate to firing rate in other neuronal types (Kuba et al., 2010; Evans et al., 2015; Gulledge and Bravo, 2016). Likewise, AIS distance to the soma, which in DA neurons should be considerably variable given the dendritic origin of the axon (Hausser et al., 1995; Gentet and Williams, 2007; Blythe et al., 2009), could also contribute to differences in rate or excitability in DA neurons, as also reported in other experimental models (Grubb and Burrone, 2010a; Thome et al., 2014; Gulledge and Bravo, 2016). In this work, we aim to clarify the role of the AIS and its interaction with the somatodendritic domain in the activity of DA neurons by providing a detailed morphological, electrophysiological and computational analysis of the size and position of the AIS in individual neurons, and propose a novel mechanism for determination of firing rate in this population.

Materials and Methods

Animals.

Experimental procedures were performed on adult male mice C57BL/6 strain obtained from the animal house at the Faculty of Biological Sciences, Pontificia Universidad Católica de Chile, and were approved by the Ethics Committees of the School of Medicine of the Pontificia Universidad Católica de Chile and of the Comisión Nacional de Investigación Científica y Tecnológica (CONICYT), both of which conform to the guidelines of the U.S. National Institutes of Health (NIH).

Extracellular recording and juxtacellular labeling.

Electrophysiological recordings were made in 22 mice (23–30 g). Anesthesia was initially induced with isoflurane (Isoflurano USP, Baxter Healthcare), followed by urethane (1.5 g per kg, i.p., ethyl carbamate, Sigma). Animals were placed in a rat stereotaxic frame adapted to mouse using a MA-6N head-holding adaptor (Narishige). Body temperature was maintained at 37°C using a homeothermic heating device (ATC 1000, World Precision Instruments). Anesthesia levels were assessed by examination of the electrocorticogram (ECoG) and by testing reflexes to a cutaneous pinch or gentle corneal stimulation. Topical benzocaine (20%, Mayon) and PBS solution, pH 7.4, were applied to all surgical incisions to prevent pain and dehydration, respectively. The ECoG was recorded from motor cortex (M2) to monitor spontaneous and driven brain states during electrophysiological sessions (coordinates, AP, +2.1 mm; ML, 1.2 mm in relation to bregma; Paxinos and Franklin, 2012; Schiemann et al., 2012). Extracellular recordings of single-unit activity were made using borosilicate glass electrodes (∼1–1.5 μm tip diameter, 10–15 MΩ; World Precision Instruments), obtained using a vertical puller (Narishige Scientific Instrument Laboratory PC-10 model). Pipettes were filled with a solution consisting of 0.5 M NaCl and 1.7% neurobiotin (w/v; Vector Laboratories). A single-axis in vivo micromanipulator (IVM-1000; Scientifica) connected to an ultralow noise IU controller rack was used to descend electrodes in the z-axis into the brain. Stereotaxic coordinates for substantia nigra single-unit recording were derived from Paxinos and Franklin (2012) and Schiemann et al. (2012) (AP, - 3.0 mm; ML, 1.4 mm).

For quantification, spontaneous firing was recorded for at least 15 min. Following the recordings, neurons were labeled by the juxtacellular method (Pinault, 1996). Briefly, the electrode was advanced slowly toward the neuron while a microiontophoretic square current was applied (2–10 nA positive current, 200 ms duration, 50% duty cycle). The optimal position of the electrode was identified when the firing of the neuron was robustly modulated by the positive current injection. Modulation was performed for at least 3 min to obtain reliable labeling. The neurobiotin was then left to transport along neuronal processes for 2–3 h. After the labeling sessions, the animals were perfuse-fixed with ∼25 ml of PBS, pH 7.4, followed by ∼50 ml 4% paraformaldehyde (w/v) in phosphate buffer, pH 7.4. Finally, the brains were postfixed in 4% paraformaldehyde in PBS overnight, maintained in 30% sucrose in distilled water for 48 h, and sectioned.

Neuronal and axon initial segment identification.

The brains were cut in the coronal plane on a freezing-stage microtome (Reichert–Jung Hn-40) at 25 μm. All sections containing the substantia nigra were incubated with Cy3-conjugated streptavidin (1:1000, Jackson ImmunoResearch) for 2 h to reveal the neurobiotin. After mounting, the sections were examined with an epifluorescent microscope (Nikon Eclipse Ci) to confirm that neurons were completely filled with tracer. The section containing the cell body and the two immediately adjacent sections were selected, blocked with 3% normal horse serum (NHS) in PBS (v/v; Jackson ImmunoResearch), and incubated with goat anti-Ankyrin-G (Ank-G) antibody (1:5000; Santa Cruz Biotechnology) in PBS and 1% NHS for 2–3 d at room temperature. After that, sections were incubated overnight with guinea pig-anti-tyrosine hydroxylase (TH) antibody (1:1000; Synaptic Systems) in PBS, 1% NHS, and 0.3% Triton-X. They were then incubated in Alexa Fluor 488-conjugated donkey anti-goat antibody (1:1000; Jackson ImmunoResearch) and Dylight-405-conjugated donkey anti guinea pig antibody (1:1000; Jackson ImmunoResearch). Three 10 min washes were performed in between and after incubation in streptavidin or antibodies. Labeling for neurobiotin and colocalization of neurobiotin-labeled processes with Ank-G and TH was assessed. Only those neurons that were neurochemically identified as substantia nigra DA neurons by immunoreactivity for TH were analyzed further.

Microscopy and imaging.

Fluorescence imaging for all neurobiotin-labeled profiles across sections was performed with a laser-scanning confocal microscope (Nikon Eclipse C2) using NIS-Elements C program (Nikon software) to acquire and export images. Low-magnification images were acquired with appropriate 10× and 20× objectives. High-magnification and z-stack images were acquired with a 60× oil-immersion objective (1.4 numerical aperture). Images taken for 3D neuronal reconstruction were 512 × 512 pixels in size with resolution of 0.41 μm/pixel and taken in z-stacks of 0.5 μm steps between images. For 3D reconstructions of the AIS, images were 2048 × 2048 pixels in size with resolution of 0.1 μm/pixel and taken in z-stacks of 0.25 μm steps. To show the extent of the AIS and for illustration purposes only, images from z-stack images were flattened into single maximum intensity projections using NIH ImageJ. To ensure the best signal-to-noise ratio in all stack images, maximum and minimum intensity pixels were established independently in each channel and for each z-stack acquired during the acquisition sessions using the NIS-Elements C program (Nikon software).

Neuronal reconstructions.

All neurons that were selected for digital reconstruction were completely filled and all of the dendrites extended to natural tapering ends. Axons were usually traced for long distances on their way to the forebrain. Neurons were reconstructed in three dimensions from all z-stack images taken with the confocal microscope using Neurolucida (MicroBrightField). Neuronal fragments from every section were traced onto a corresponding digital section using the Serial Section Manager in Neurolucida (Henny et al., 2012, 2014). The AIS identified by immunofluorescence for Ank-G was reconstructed from z-stack images. For the entire somatodendritic and AIS reconstruction, a correction factor in the z-axis was applied to account for the shrinkage that follows dehydration and histological processing, which in our hands is ∼40%. Quantitative data for anatomical parameters were obtained using the Neurolucida Explorer software.

To determine the location of each reconstructed neuron in the substantia nigra, we delimited the substantia nigra, ventral tegmental area, and retrorubral field (nuclei containing TH-positive neurons) in the section containing the soma of labeled neurons and compared them to those provided by Fu et al. (2012) and Paxinos and Franklin (2012).

Data acquisition and electrophysiological analysis.

Biopotentials were digitized on-line using a Power 1401 analog-to-digital converter (Cambridge Electronic Design) and Spike2 for acquisition and online analysis of data (version 5.15, Cambridge Electronic Design). Single-unit activity and the ECoG were sampled at 12.5 and 5.6 kHz, respectively. Recording from electrodes were amplified 10× through Neuro DATA IR283A (Cignus Technology) and 100× by DPA-2FS (Scientifica) and “wideband” filtering (0.3–5000 Hz; DPA-2FS; Scientifica). ECoG electrode was amplified 2000× through DPA-2FS (Scientifica) and filtering (0.3–1500 kHz; DPA-2FS; Scientifica).

Measurements of firing rate, coefficient of variation (CV) of the interspike interval (ISI), and percentage of spikes in bursts were taken from the last 3 min of a 15 min period of spontaneous activity recording, as performed before the labeling procedure. Firing rate and CV of the ISI were obtained directly from the Spike2 software. The percentage of spikes in bursts was obtained from a suitable open access script developed by Cambridge Electronic Design to interface with Spike2. The average waveform trace (Fig. 1A) was composed of 200 coincident spikes (Spike2 software) taken from the last 3 min of spontaneous activity recording, as indicated above.

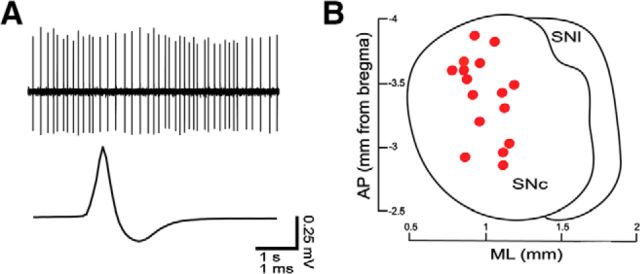
Figure 1.

In vivo electrophysiological recordings from identified nigral neurons. A, In vivo spontaneous firing and average spike waveform. B, Cell body location of recorded and neurobiotin-labeled neurons (red circles, dorsal view). SNl, Substantia nigra pars lateralis.

Bursts were composed of least three spikes, and the classical criteria outlined by Grace and Bunney (1984) were used, that is, a burst begins when two action potentials occur within 80 ms of each other and ends when an ISI >160 ms appears.

Statistical analysis.

To assess whether data sets were normally distributed, we performed the single-sample Kolmogorov–Smirnov test using GraphPad Prism 6. Because, in general, data sets were not normally distributed, we used nonparametric statistical testing throughout. Correlative (Spearman's correlation) statistics were performed using GraphPad Prism 6. Significance for all statistical tests was set at p < 0.05.

Dopamine neuron model.

The dynamics of the membrane potential V(t) in our dopamine neuron models are described by the equivalent circuit governed by a first-order differential equation: C_M(dV_i/dt) = −I_Na (V_i) − I_Ca(V) − I_{K, dr}(V_i) − I_{K, A} (V_i) − I_{K, SK}(V, [Ca²⁺]_i) − I_leak(V_i) − I_NaP − I_axial(V_i, V_j), where C_M is the membrane capacitance per unit area, I_Na is the fast sodium current, I_Ca is a composite Ca²⁺ current, I_{K, dr} is the delayed rectifier potassium current, I_{K, A} is the transient outward A-type potassium current, I_SK is the Ca²⁺-activated small conductance potassium current, I_leak is an ohmic leakage current, and I_NaP is the electrogenic sodium pump current. The subscripts i and j represent different compartments of the neuron. The axial current I_axial represents the axial flow of current between adjacent compartments and is calculated transparently by the NEURON simulation package (Hines and Carnevale, 1997). Each current I_x in the above equation that depends on membrane potential V has a maximal conductance g_x and a reversal potential E_X. The sodium current has both an activation variable m and an inactivation variable h, the delayed rectifier potassium current has only an activation variable n, and the A-type potassium current has an inactivation variable (q) and an activation variable (p). The SK potassium current does not have voltage-dependent gating variables, but instead is activated by an increase in intracellular calcium concentration [Ca]_i. Therefore, the model also includes a material balance on the Ca²⁺ ion, which enters via I_Ca and a component of the leak current carried by Ca²⁺ ions, and is removed by a nonelectrogenic Ca²⁺ pump. The Ca²⁺ current is activated in the subthreshold regime, so it most closely resembles the L-type current (Durante et al., 2004), which is an important source of subthreshold depolarization. However, it is a composite because the L-type current may not be the major source of calcium influx that activates the SK channel (Putzier et al., 2009; de Vrind et al., 2016). All parameters that are different between the published model of Kuznetsova et al. (2010) and the present study are listed in Table 1. The SK calcium-activated conductance was reduced by 20% to obtain a spontaneous firing rate consistent with experimental observations of the reconstructed neuron (∼4 Hz) used in our study; different morphologies require somewhat different parameter settings due to the variable surface area to volume ratios of the compartments between reconstructions.

Table 1.

Parameters changed from original model

Parameter	Value
Cm	0.75 μF/cm
Ra	100 Ωcm
INa, P, i	207.3 nA/cm2
gKA, d, a	226 μS/cm2
gSK, i	11.8 μS/cm2
sCaL	5.0

The table shows parameters changed from the original model of Kuznetsova et al. (2010). The original model had distinct values for the soma and proximal and distal dendrites in the adjustment of A-type current K⁺ conductance parameter g_KA. We used a single value for all dendrites and did not change the value for the soma. The value s_CaL for the steepness of the voltage dependence of I_Ca is not actually different between studies, but there was a typographical error in the original publication, so the correct value for s_CaL is here. We minimized the effect of a minor slow variable in the original model, the cytosolic Na⁺ concentration, by setting it to a small fixed value (0.81 mm), which effectively set the value of the Na⁺ pump to the constant value given above.

Kuznetsova et al. (2010) used both a schematic model implemented in C and a multicompartmental model implemented in the neural simulation package NEURON (Hines and Carnevale, 1997). The reconstruction used for their NEURON model came from a publicly available morphology contributed by Vetter et al. (2001) to the NeuroMorpho.org database (Ascoli, 2006). We used only models implemented in NEURON and used our own reconstructed neural morphology, which, in contrast to that in the previous study, includes an AIS and part of the axon. The model was calibrated so that the action potential during pacemaking initiates in the AIS, given the high density of voltage-gated Na⁺ channels (Na_v) present in this compartment (Zhou et al., 1998; Kole et al., 2008; Hu et al., 2009; Gonzalez-Cabrera et al., 2017). Therefore, some parameters of the AIS differ from those of the rest of the neuron, as shown in Table 2. Consistent with the literature (Kole et al., 2008; Hu et al., 2009; Bender and Trussell, 2012), the spike-generating conductances, g_Na and g_{K, dr}, are much larger in the AIS, and the half-activation and half-inactivation of the gating variables for I_Na are more negative than in the rest of the neuron. These changes also required an adjustment on the slope of activation gating variable. For experiments in which synaptic noise was added to the model, please refer to Canavier and Landry (2006).

Table 2.

Axon initial segment parameters that differ from the rest of the neuron

Parameter	Not AIS	AIS
Vhalf, m	−34.6 mV	−39.6 mV
Vhalf, h	−56.8 mV	−61.8 mV
Sm	6.0	10.0
gNa	550 μS/cm2	27500 μS/cm2
gKV	665 μS/cm2	19950 μS/cm2

Note that in addition to increasing g_Na, the voltage dependence of the Na⁺ channel in the AIS had to be shifted in a hyperpolarized direction to guarantee that the action potential originates in the AIS, and that the delayed rectifier conductance in the AIS must also be increased to repolarize the action potential.

Results

We systematically correlated the spontaneous firing rate in vivo with the position and size of the AIS for individual SNc DA neurons by running serial physiological, neurochemical, and anatomical analyses at the single-cell level. The spontaneous activity of neurons in anesthetized mice was recorded extracellularly (Fig. 1A) from neurons that were then juxtacellularly labeled with neurobiotin to determine their location within the SNc (Fig. 1B) and reveal their entire somatodendritic and proximal axonal domain (Fig. 2). Two examples of recorded and then neurobiotin-labeled neurons (Fig. 2A1,B1) that were identified as dopaminergic by immunoreactivity to TH are shown (Fig. 2A2,B2). We visualized the AIS in DA neurons using immunostaining for Ank-G (Gonzalez-Cabrera et al., 2017), a scaffolding protein that anchors Na_v (Zhou et al., 1998; Grubb and Burrone, 2010b), in the previously recorded, labeled, and neurochemically identified neurons. The arrows in Figure 2, A3, A4, and B1–B3, show examples of neurobiotin processes immunoreactive for Ank-G in these neurons, thus revealing their AISs. As evident in the flattened and merged stack images (arrowheads in Fig. 2A5,B4), we found that the AIS varied in location (distally in Fig. 2A5, proximally in B4) and size (short in Fig. 2A5, long in B4). We also found that most AIS (15 of 16) branched from a dendritic process. To obtain accurate and detailed information on AIS location and size, the entire somatodendritic domain and AIS, along with the proximal axonal compartments, were traced from high-magnification confocal image stacks and 3D reconstructed with an assistant software. Figure 2, A6 and B5, shows neurons with short and distal (A6) and long and proximal (B5) AISs, respectively. The range of the values obtained by quantifying the somatodendritic morphologies of reconstructed SNc dopaminergic neurons are given in Table 3 and by quantifying the morphology of the AIS in Table 4.

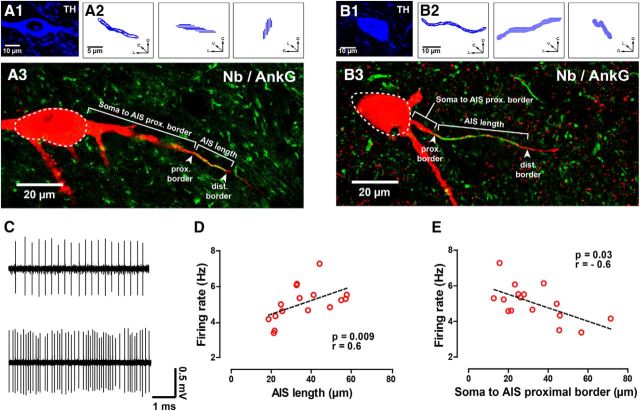
Figure 2.

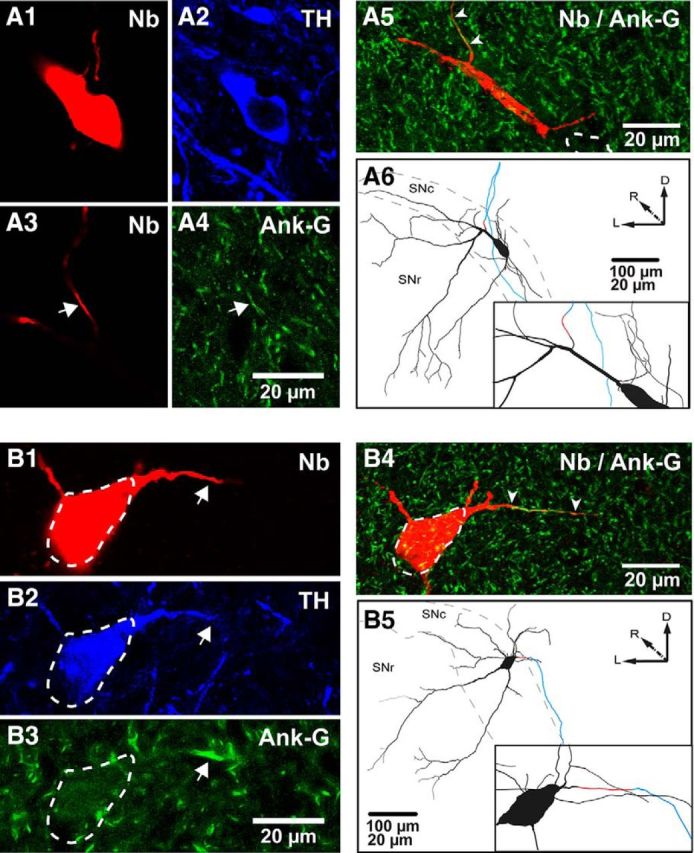
Identification and reconstruction of the AIS and somatodendritic domain of dopaminergic neurons. A1–A4, Neurobiotin (Nb)-labeled (A1) and TH-expressing (A2) soma. A distal Nb-labeled process from same neuron (A3, arrow) expresses Ank-G (A4, arrow). A5, As seen in the flattened z-stacked image, this AIS is short and distally located (arrowheads, soma in dashed lines). A6, A caudal view of the 3D reconstruction and inset (black, cell body and dendrites; red, AIS; blue, axon) for the same neuron. B1–B5, Nb-labeled (B1) and TH-expressing soma (B2, dashed lines). A proximal process is indicated (arrows in B1, B2), which expresses Ank-G (B3, arrow). In this case, the AIS is longer and proximally located, as shown in the flattened image (B4) and a caudal view of the 3D reconstruction and inset for the same neuron (B5), color coded as in A6. SNl, Substantia nigra pars lateralis; D, dorsal; R, rostral; L, lateral.

Table 3.

Somatodendritic morphology of reconstructed SNc DA neurons

Parameters (16 neurons)	Mean	SEM	Range
Dendritic length (μm)	6340	614	3130–11,622
Dendritic surface (μm2)	12,454	1380	6252–23,925
Somatic surface (μm2)	1340	128	621–2294
Somatodendritic surface (μm2)	13,794	1508	6873–25,143
Number of primary dendrites	4.3	0.4	2–7
Highest branch order	7.3	0.8	3–13

Table 4.

Axon initial segment morphology of reconstructed SNc DA neurons

Parameters (16 neurons)	Mean	SEM	Range
Length (μm)	36.1	3.4	18.7–57.8
Surface (μm2)	101.9	8.5	53.4–144.8
Soma to AIS proximal border (μm)	32.5	4.1	12.7–71.4
Soma to AIS midpoint (μm)	50.1	2.7	34.2–80.8
Soma to AIS distal border (μm)	68.1	2.1	56.1–90.1
Dendritic order origin	1.5	0.2	0–3

We measured AIS length and distance from soma to AIS proximal border in the identified neurons (Fig. 3A,B) and found that the spontaneous firing rate of the recorded neurons in vivo (Fig. 3C) increased with AIS length (Fig. 3D) and decreased with soma to AIS distance (Fig. 3E). Neither AIS length nor location correlated with regularity (as determined by the CV) or percentage of spikes fired in bursts (data not shown). The firing rates, CV, and percentage of spikes fired in bursts for all analyzed neurons are given in Table 5.

Figure 3.

Spontaneous rate is positively correlated with AIS length and negatively correlated with distance from the soma. A1–B3, TH expression (A1, B1) and orthogonal views of reconstructed AISs (A2, B2) of two neurobiotin (Nb)-labeled neurons shown in flattened z-stack images (red in A3, B3, soma in dashed lines). Costaining with Ank-G (green in A3, B3) revealed their AISs (arrowheads in A3, B3). For illustration purposes, indications of typical AIS measurements and hallmarks are provided in the figure. The neuron in A1–A3 shows a short and distal AIS, whereas the neuron in B1–B3 displays a long and proximal AIS. C, Extracellular recording of the neuron in Figure 2A, with a short and distally located AIS (top), and of the neuron in Figure 2B, with a long and proximally located AIS (bottom). D, E, Firing rate is positively correlated with AIS length (D) and negatively correlated with distance from soma to the proximal border of the AIS (E). r is Spearman's correlation coefficient. C, Caudal; D, dorsal; L, lateral; V, ventral.

Table 5.

Physiological data of identified and reconstructed SNc DA neurons

Parameters (16 neurons)	Mean	SEM	Range
Firing rate (Hz)	5.04	0.2	3.4–7.3
CV ISI	0.38	0.06	0.2–1.02
Spikes in bursts (% of total)	8.2	13.02	0–41.4

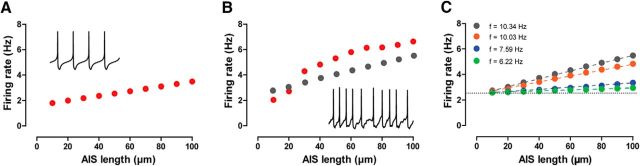
To determine whether position and/or size of the AIS controls the rate, as well as to identify the mechanisms that may account for the role of the AIS, we implemented a model of spontaneously firing DA neurons based on pacemaking mechanisms (Kuznetsova et al., 2010; Table 1) using the neuronal reconstructions described previously (Fig. 2; Tables 3, 4) and including high Na_v density in the AIS for action potential initiation (Bender and Trussell, 2012; Gonzalez-Cabrera et al., 2017; Table 2). The model allowed us to vary morphological parameters in a controlled manner, which is impossible to conduct in in vivo or even ex vivo experiments. Figure 4A systematically examined the effect of AIS length by replacing the original AIS with reconstructed AISs (of different lengths) from other neurons. The firing rate increased with increasing AIS length in a manner consistent with experimental observations (Fig. 3D). Figure 4B systematically examined the effect of proximity of the AIS to the soma by the simulated grafting of a neuron's own AIS (and axon) onto different positions within its own somatodendritic compartment. In contrast to experimental observations (Fig. 3E), position alone did not affect the rate. Figure 4C selectively and systematically examined the effect of the AIS length by artificially changing this length in the model. This manipulation, like the one in Figure 4A, also reproduced the positive correlation between firing rate and length observed experimentally (Fig. 3D). Figure 4D selectively and systematically examined the effect of distance between AIS and soma by artificially varying this distance in the model. This manipulation, like the one in Figure 4B, also failed to reproduce the negative correlation between firing rate and distance observed experimentally (Fig. 3E).

Figure 4.

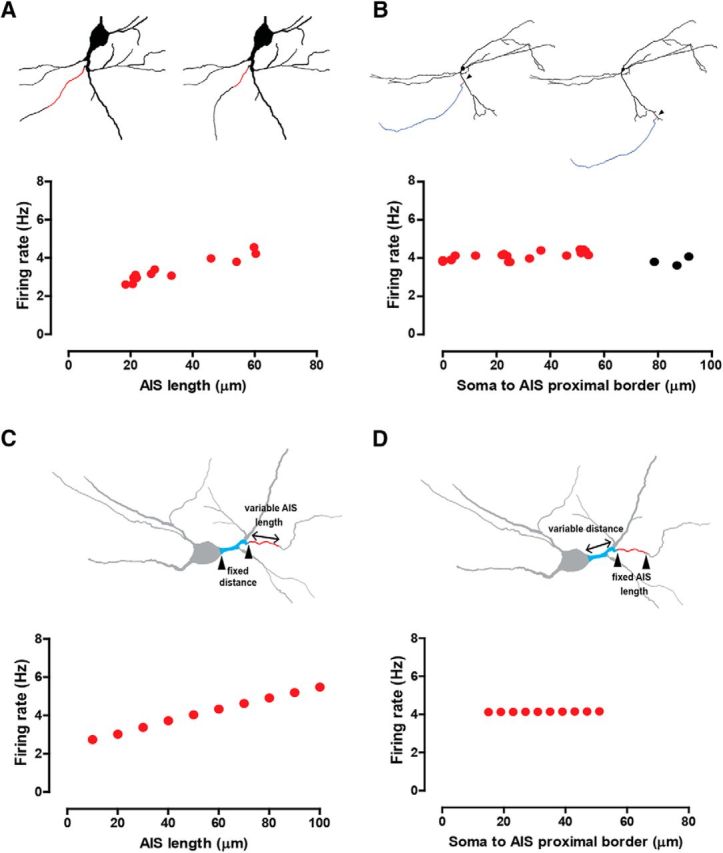
Computational modeling using morphological manipulations shows that AIS size (but not position) drives the firing rate. A, Firing rate observed when AISs from other reconstructed neurons replace the actual AIS (AIS in red, top diagrams), as a function of AIS length. B, Firing rate observed when a neuron's own AIS is grafted to random locations within the somatodendritic tree (arrowheads), as a function of AIS position. Black circles indicate presence of backpropagation failures (see Results and Fig. 9). C, Firing rate observed when artificially varying AIS length while keeping soma-to-AIS proximal border distance fixed. The top schematics show how lengths were varied. D, Firing rate observed when artificially varying soma-to-AIS proximal border distance while keeping AIS length fixed, as shown in the top schematics.

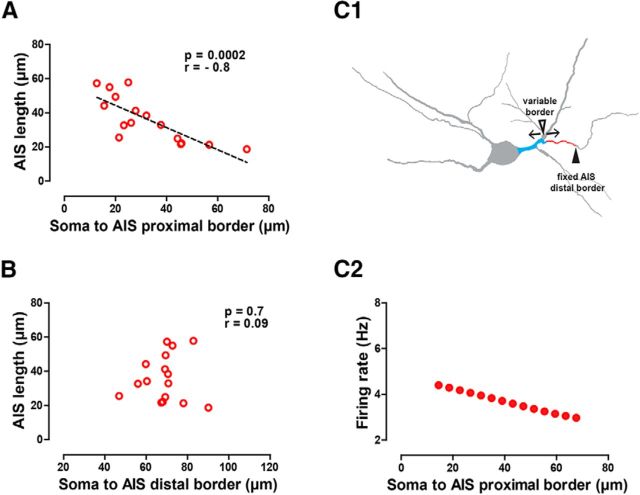
To resolve this conflict with experimental observations, we reexamined the relationship between size and position in the experimental morphological data. We found a negative correlation (Fig. 5A) between AIS size and the distance to the proximal border of the AIS. In general, the closer the AIS is to the soma (range, 12.7–71.4 μm), the longer the AIS (range, 57.8–18.7 μm; Fig. 5A). However, the distance of the AIS distal border to the soma was independent of AIS size and averaged ∼70 μm (Fig. 5B, Table 4). In fact, for longer AISs, the proximal border more closely approached the soma, as illustrated schematically in Figure 5C1. We constrained the model to honor the experimentally observed correlation between position and length by constraining the distal border of the AIS to a constant position (Fig. 5C1). We then increased the dendritic section length and reduced AIS length according to the equation L(d) = −0.6479d + 57.28, where L is the length of AIS, and d is the distance from soma to AIS. Honoring the correlation between size and position allowed us to reproduce the experimental result that the firing rate decreases with increasing distance of the AIS from the soma (Fig. 5C2) while still reproducing the result that firing rate increases with increasing length. Together, the results in Figures 4 and 5 indicate that the size of the AIS, but not its position, is a key determinant of the firing rate.

Figure 5.

AIS length is negatively correlated with proximity; honoring this constraint gives an apparent dependence on position. A, Experimental data show AIS length negatively correlates with the distance from the soma to the proximal border of the AIS. B, Experimental data show AIS length is not correlated with the distance from the soma to the distal border of the AIS. C1, C2, Lengths of the axon-bearing dendrite and AIS were artificially covaried in the model, keeping their total length constant by keeping the distal border of the AIS fixed (solid arrowhead) and reciprocally modifying AIS length and soma-to-AIS proximal border distance (open arrowhead) in the actual morphology (C1). This covariation reproduces the physiologically observed negative correlation of soma to AIS distance with firing rate (Fig. 3E). Spearman's correlation coefficient (r) is shown in A and B.

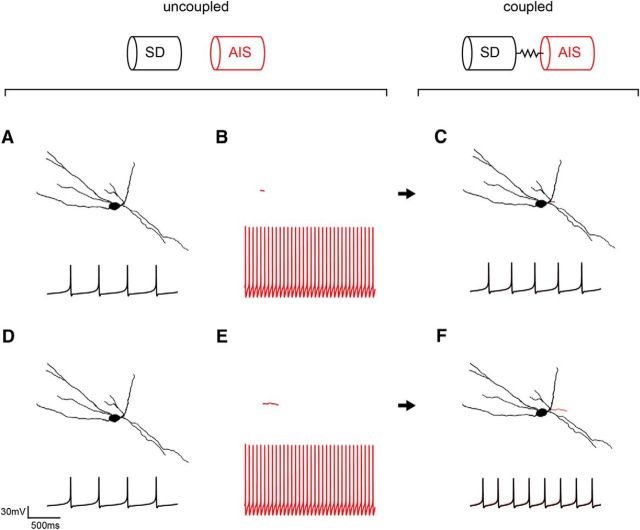
What mechanism could explain the relation between AIS size and firing rate in the intact neuron? We propose that the somatodendritic and AIS compartments function as spatially segregated coupled oscillators to set the firing rate in the intact neuron. To test this idea, we coupled a somatodendritic compartment that fired slowly in isolation (Fig. 6A,D) to faster-firing short (B) or long (E) isolated AIS. The AIS compartment fires more rapidly than the somatodendritic domain by virtue of its 50-fold larger Na⁺ channel density (Bender and Trussell, 2009; Table 2). We found that coupled somatodendritic–AIS compartments fired at frequencies in between those of the uncoupled somatodendritic domain and AIS; yet, the larger the AIS, the higher the compromise frequency reached by the coupled somatodendritic–AIS compartment (Fig. 6C,F).

Figure 6.

Coupled oscillator explanation of results using the computational model. In each panel, the morphology of the compartment is given above the firing rate. A, An isolated somatodendritic (SD) domain (black) fires at a slow frequency, as seen in the intracellular membrane potential trace recorded in the soma. B, The corresponding isolated AIS (red) fires more rapidly, as seen in the intracellular membrane potential trace recorded in the isolated AIS. C, When the two are electrotonically coupled using the NEURON software, a compromise frequency intermediate between the two is achieved, as seen in the intracellular traces recorded at the soma. D, The isolated somatodendritic domain (black) is repeated from A. E, The size of the AIS (red) was artificially increased, a change that does not affect its firing rate (see text). F, The same somatodendritic domain coupled to a larger AIS reaches a faster compromise frequency than when it was coupled to a smaller AIS in C.

As can be seen in Figure 6, B and E, changes in length do not affect the firing rate of an isolated AIS, since changes in length without changes in conductance density do not affect the current flow per unit area, which determines the time course of the membrane potential. However, since the AIS was modeled with Ca²⁺-dependent K⁺ currents, changing the surface-to-volume ratio of an isolated AIS could theoretically affect its firing frequency, as proposed for different surface to volume ratios of dendritic and somatic compartments in previous models of DA neurons (Wilson and Callaway, 2000), because the rate of accumulation and removal of Ca²⁺, unlike the membrane potential dynamics, depend on the surface to volume ratio. In an isolated AIS whose spontaneous frequency was ∼11 Hz, neither changes in length (from 10 to 100 μm, keeping diameter constant) nor diameter (from 0.5 to 6.0 μm with constant length, or from 0.5 to 6.0 μm with constant surface by concomitantly decreasing length) resulted in changes in frequency (data not shown). These data indicate that differences in firing rate result from the different compromise frequencies reached by long or short AIS when coupled to the somatodendritic domain.

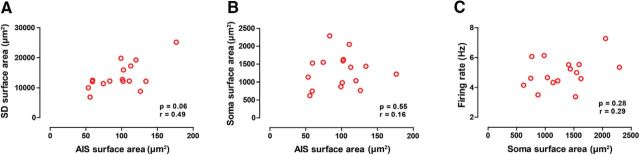
Because of the nonlinear differential equations that describe the model system, the coupling between the AIS and somatodendritic domain is highly nonlinear; therefore, we decided to investigate the dependence of the firing rate on the somatodendritic domain and AIS surface area. Somatodendritic surface area was artificially varied while keeping the AIS size constant by scaling the length for every dendritic and somatic compartment by a factor from 0.25 to 1.5 in steps of 0.25. In the observed range of somatodendritic sizes (Table 3), this variation produced a modest decrease in firing rate (Fig. 7A1). The experimental data (Fig. 7A2) over approximately fourfold variability in somatodendritic size (Table 3) show a weak negative trend that is consistent with the model prediction, but did not achieve significance. Increasing the AIS surface area while keeping the somatodendritic area constant, on the other hand, increased the spontaneous firing rate (Fig. 7B1; as we found with AIS length in Fig. 3D). We then plotted the spontaneous firing rate observed previously in vivo versus the AIS surface area to test this model prediction with the reconstructed neurons and found a similar positive correlation of firing rate with AIS surface area (Fig. 7B2). Clearly, the AIS surface area has more influence on the firing rate of the intact model neuron, likely due to its faster intrinsic firing rate when uncoupled, and the effect of the AIS surface area is much more pronounced in the data as well. Finally, we examined the dependence of firing rate on the AIS/somatodendritic surface area ratio in the model (Fig. 7C1). In the experimental data, which are by nature heterogeneous rather than smoothly varying, we found an even tighter positive correlation with AIS/somatodendritic surface area ratio (Fig. 7C2) than with AIS surface area (Fig. 7B2). This makes sense because the ratio contains the inverse of the somatodendritic surface area; hence, from Figure 6A we expect a weak positive correlation of the inverse with rate. Combining this weak positive correlation with inverse somatodendritic surface area with a strong positive correlation with the AIS surface area in the numerator, we expect an even stronger positive correlation of the ratio with rate, as observed. The validation of model predictions argues strongly for the coupled oscillator model.

Figure 7.

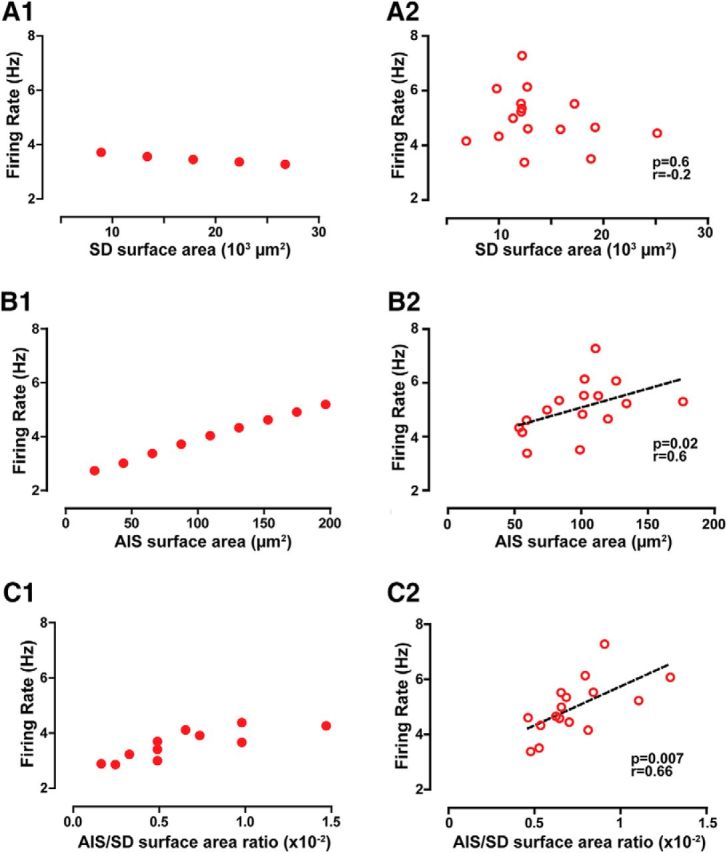
The model predicts and data confirm that AIS surface area is a more effective driver of firing rate than somatodendritic (SD) area. A1, A2, In the model (A1), firing rate decreases slightly with increased somatodendritic surface area, as tested within the physiologically observed range of somatodendritic surface areas. In the experimental data (A2), a negative trend in firing rate is observed as somatodendritic surface area increases, but it does not achieve significance. B1, B2, In the model (B1), firing rate increases with increasing AIS surface area. In the experimental data (B2), firing rate is positively correlated with AIS surface area. C1, C2, In the model (C1), firing rate increases as the AIS/somatodendritic surface area ratio is varied. In the experimental data (C2), there is a tight correlation between AIS/somatodendritic surface area ratio (see results). Spearman's correlation coefficient (r) is shown in A2, B2, and C2.

The result that AIS size drives tonic DA neuron activity is robust to the details of the model. For example, similar results (Fig. 8A) were obtained with a somatodendritic compartment that exhibits only a subthreshold oscillation (Ping and Shepard, 1996) when uncoupled from the axon (Fig. 8A). To get this result, we restored the SK conductance to the value in the original model (Kuznetsova et al., 2010). We also tested the influence of synaptic activity on the model. Tonic DA neuron activity in vivo is less regular (Table 5) than pacemaking activity as observed in vitro, largely due to the presence of synaptic activity impinging on the somatodendritic domain in the in vivo situation. Adding synaptic noise to the model (Canavier and Landry, 2006) to produce irregular firing (Fig. 8B) did not change the direction of the previously shown dependency of spontaneous firing rate on AIS length (Fig. 4C). We next addressed the mechanism that makes changes in AIS length more effective in changing the frequency of the intact neuron compared to changes in somatodendritic length. In Figure 8C, we decreased the intrinsic firing rate of the isolated AIS by decreasing the Na_V conductance. As the rate was decreased, the effect of changes in length of the AIS was markedly reduced, confirming that the higher rate was largely responsible for the disproportionate influence of the length of this compartment on the firing rate in the intact model neuron.

Figure 8.

The dependence of firing rate on AIS size is robust. A, The firing rate still increases with AIS length in the case of a somatodendritic compartment that only exhibits subthreshold oscillations (data not shown) and therefore only spikes when coupled to an AIS, as shown by the membrane potential traces in the inset. B, The firing rate also increases with AIS length (red symbols) in the case of added synaptic noise in the dendrites, which results in a less regular firing pattern, as seen in the membrane potential traces of the inset. Glutamatergic synapses that produce the AMPA and NMDA currents were symmetrically distributed on dendrites, and the interevent intervals for these events were generated using a simulated Poisson process. Also, a tonic GABAergic current was located on the soma and dendrites (see Results). The gray symbols show the tonic firing rates from Figure 4C for the same morphology in the absence of synaptic input and are for comparison purposes. C, Decreasing the intrinsic firing frequency of the AIS (see color-coded inset) by decreasing AIS Na_V conductance values results in a weaker influence of the AIS length in the resulting coupled frequency.

In the coupled oscillator results explained in Figure 6, the AIS and the soma synchronize, and fire action potentials in a one-to-one ratio (Fig. 6C,F). The action potential is always initiated in the AIS, with a very small delay between the action potential in the AIS and the action potential in the soma. However, with increasing distance from the soma (Fig. 9B), the action potentials in the AIS could lose their ability to backpropagate throughout the dendritic tree, and thus fail to trigger an action potential in a one-to-one ratio in the soma that is far from the AIS. Noticeably, the somatodendritic domain may not be capable of slowing the AIS down to match the somatic frequency in this case, likely because the entire somatodendritic tree would not be tightly synchronized at the compromise frequency exhibited in the soma, which is slower than the free-running frequency of the isolated AIS. Because branch order and distance are correlated (higher branch orders tend to be located at greater distances from the soma), failures of one-to-one locking could depend also on branching order, as shown in Figure 9C. The depolarizing current flowing axially from the AIS leaks out along each dendrite and would be also decremented at every branch point, exacerbating the effect of distance. Thus, parts of the somatodendritic domain that are too far away from the AIS, both in terms of distance and branch order, may fail to one-to-one phase lock with the AIS. However, the effect of AIS position on backpropagating action potentials remains an experimentally open question.

Figure 9.

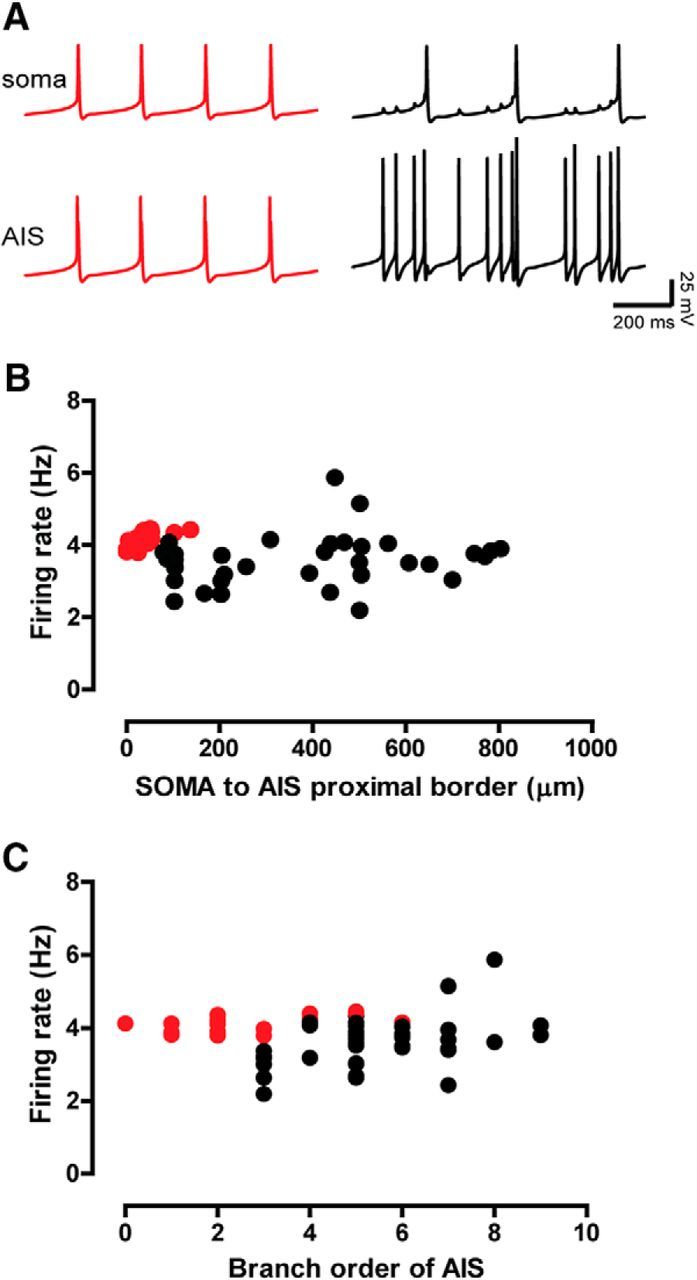
One-to-one locking between AIS and soma breaks down with distance and branch order. A, Examples of backpropagation success (red) and failure (black) evidenced by the intracellular membrane potential traces of both the soma and the AIS in modeling experiments of increasing soma-to-AIS distance. Success means that every AIS action potential successfully triggers a somatic action potential (one to one). In this example of backpropagation failure, only every fourth AIS action potential successfully triggers a somatic action potential (four to one). B, Spontaneous firing rate versus soma-to-AIS distances using the same morphology shown in Figure 4B and encompassing a wider range of distances, distinguishing between success (red circles) and failure backpropagation (black circles). C, Spontaneous firing rate versus the branch order in which AIS were artificially located, using the same morphology shown in Figure 4B.

Since we have demonstrated that AIS surface area, rather than somatodendritic surface area, is critical in regulating the basal tonic firing rate of SNc dopamine neurons, we next checked to see whether AIS surface area was correlated with somatodendritic surface area. We also checked whether soma size, which we have so far considered part of the somatodendritic domain, could relate to AIS size too. As seen in Figure 10A,B, we found that neither was related to AIS size, suggesting that AIS size is controlled independently of somatodendritic size. Finally, we controlled whether somatic size could relate to firing rate. As shown in Figure 10C, somatic surface area did not relate to firing rate.

Figure 10.

AIS size is independent of somatodendritic (SD) or somatic size; somatic size does not relate to firing rate. A, B, Somatodendritic surface area and somatic area are uncorrelated with AIS length. C, Somatic surface area does not predict firing rate. r is Spearman's correlation coefficient.

Discussion

In this work, we provide a systematic description of the size and location of the AIS in nigral dopaminergic neurons at the single-cell level. We further show how the size and position of the AIS, but not the size of the soma or the somatodendritic domain, are correlated with the spontaneous firing rate in vivo. Further computational modeling indicates that the size of the AIS, but not its position, is a causal determinant of the firing rate in these neurons.

A novel AIS–somatodendritic coupled oscillator mechanism

Our results propose a novel mechanism for regulating the spontaneous firing rate of DA neurons in vivo. A coupled oscillator model (Wilson and Callaway, 2000; Kuznetsov et al., 2006) was previously proposed to limit the maximum discharge frequency of DA cells. This model postulated coupling between somatic and distal dendritic components with distinct intrinsic time courses for the Ca²⁺ dynamics due to differing surface to volume ratios (Wilson and Callaway, 2000) and suggested a critical role for Ca²⁺ dynamics in regulating the frequency. A more recent study, on the other hand, proposed a dual oscillatory mechanism underlying discharge frequency including both Ca²⁺ and Na⁺ dynamics (Guzman et al., 2009). Based on experimental data (Guzman et al., 2009) and implemented in a single compartment, their model includes a Ca_v1 channel-dependent oscillator and an Na_v1 channel-dependent oscillator. Their study suggests that the Na_v1 channel-dependent oscillator entrains the Ca_v1 channel-dependent oscillator, thereby setting the frequency. Our model includes both Ca²⁺ channel-dependent and Na⁺ channel-dependent oscillatory mechanisms across the entire neuron, with the addition of a spatially segregated AIS with a high Na⁺ channel density, as proposed previously by Grace and Bunney (1983). Most importantly, in our model and its predecessors (Kuznetsova et al., 2010; Fellous et al., 2016), the Na_v1 channel-dependent oscillator entrains the Ca_v1 channel-dependent oscillation and thereby sets the frequency, as suggested by Guzman et al. (2009).

Our model proposes that the AIS and somatodendritic compartments are two independent and spatially segregated Na_v1 channel oscillators that synchronize their firing at a common frequency (Remme et al., 2010). Based on higher expression of Na_v channels in the AISs of DA neurons, we predict that isolated AISs of DA neurons fire faster than the intact neurons or the isolated somatodendritic compartments. We also predict that the AIS surface area has a greater influence on the compromise firing frequency than the somatodendritic surface area, largely because of the AIS higher frequency and its greater compactness, which keeps this compartment synchronized (Figs. 7A1,B1,C1, 8C). One experimental observation consistent with our prediction is that focal application of TTX near the soma and proximal dendrites (and likely near the AIS) of ex vivo DA neurons reduced the firing rate more effectively than focal application of TTX in the distal somatodendritic tree (Jang et al., 2014).

Previously, a multiple oscillator model (Hasselmo et al., 2007) was suggested to explain the firing pattern of entorhinal grid cells, in which different oscillators had distinct frequencies, with an output hypothesized to be a linear sum of these oscillations. In contrast, a different model (Remme et al., 2010) suggested that multiple oscillators within a somatodendritic tree tend to phase lock at a compromise common frequency, rather than oscillate independently, due to nonlinearity of neural oscillators. Our results (Fig. 9A, black trace) show that there are circumstances in which the neuron can, to some degree, report two independent oscillations.

Autonomous pacemaker neurons, that is, those that fire spontaneously in the absence of synaptic input, are critical components of neural circuits (Ramirez et al., 2004), especially in the basal ganglia (Surmeier et al., 2005). The role of the AIS in controlling the basal firing rate may generalize to other neurons whose spontaneous activity is also driven by pacemaking mechanisms (Ramirez et al., 2004; Surmeier et al., 2005).

The distance between the proximal border of the AIS and the soma is not relevant to the compromise firing frequency (Figs. 4B, 5B). However, the model predicts that larger distances or too many intervening branch points prevent the action potentials in the AIS from triggering action potentials on a one-to-one basis in the soma (Gulledge and Bravo, 2016; Figs. 4B, 9B,C, black circles). Assuming that action potentials are initiated in the distal AIS (Mainen et al., 1995; Gonzalez-Cabrera et al., 2017), the location for action potential initiation (AIS distal border) in our neurons was never found farther than 90 μm (Table 4, Fig. 5B) or a branching order more than three from the soma (Table 4), perhaps to insure effective backpropagation.

Model limitations

The higher expression of Na_v channels and Ank-G at the AIS has been confirmed experimentally in these neurons (Gonzalez-Cabrera et al., 2017; current study; Figs. 2, 3). However, there have been no studies on differential expression of Ca_v on the AIS in the DA neuron population, and evidence in other neuronal models is contradictory regarding higher Ca_v expression on the AIS (compare Bender and Trussell, 2009; Grubb and Burrone, 2010a). In our model, Ca²⁺ conductance was homogeneously distributed across the somatodendritic domain and AIS, but this is an issue that clearly calls for future experimental work. Additional work is also required to better constrain the spatial density distributions, conductances, and kinetic parameters of other channels expressed in these neurons as well.

Implications of AIS size and position in vulnerability and plasticity

Fast-firing dopaminergic neurons have larger and more proximal AISs. Given that firing rate facilitates Ca²⁺ influx (Guzman et al., 2009; Michel et al., 2016), that Ca²⁺ channels have been observed to locate at AISs of other neurons (Bender and Trussell, 2009), and that increased Ca²⁺ load is associated with increased vulnerability to neurodegeneration in SNc DA neurons (Michel et al., 2016), we propose that neurons with a large AIS comprise a particularly vulnerable DA neuron subpopulation (Gonzalez-Cabrera et al., 2017).

Mechanisms regulating dendritic and axonal growth, arborization, and maintenance are dependent on, among other things, activation of BDNF and the TrkB receptor pathway. We found that AIS size was independent of somatodendritic surface area or dendritic length, despite a greater than fourfold variability in the size/length of both the somatodendritic domain and AIS, suggesting that independent mechanisms regulate the size of these two domains. This is consistent with observations of cortical neurons, in which the terminal growth of dendrites and axon seem to be regulated by independent mechanisms (Guo et al., 2012; Gonzalez et al., 2016). Mechanisms regulating AIS size and position in other neuronal types are not entirely clear, but the evidence indicates that they must involve Ank-G present at the AIS (Jenkins and Bennett, 2001; Grubb and Burrone, 2010b), as well as the expression of Ank-B, αII-spectrin, and βII-spectrin in the distally adjacent axonal cytoskeleton (Galiano et al., 2012). That the size of the AIS must be regulated independently from overall size of the somatodendritic compartment is perhaps not surprising given the dynamism observed for this structure (Grubb and Burrone, 2010a; Kuba et al., 2010; Evans et al., 2015).

We also observed that the distance from soma to the distal border of AIS did not vary as much as the distance to the AIS proximal border. The observation of a more “rigid” distal border in contrast to a more “flexible” proximal border is reminiscent of the processes that define the AIS/distal axon boundary during development (Galiano et al., 2012), where the AIS distal border is fixed by the formation of distal axon cytoskeleton that restricts Ank-G and the AIS to move further along the axon. Yet, previously reported plastic changes in AIS length (Kuba et al., 2010) and position (Grubb and Burrone, 2010a) were both proposed to occur via displacement of the AIS distal border. If plastic changes in AIS length of DA neurons occur during adulthood, our results would suggest that changes in length would occur instead at the proximal border.

Since the baseline activity level of the DA neurons regulates the gain of phasic signaling (Hage and Khaliq, 2015; Grace, 2016), plasticity in the size of the AIS may be a novel mechanism for adjusting the gain of dopaminergic signaling. Moreover, the baseline activity of SNc DA neurons also sets the baseline level of dopaminergic tone in the striatum (Sulzer et al., 2016). These levels are thought to homeostatically regulated at an optimal basal level of dopamine by feedback mechanisms that sense dopamine and in turn regulate the activity of dopamine neurons and dopamine release (Grace, 1995). For example, dopaminergic functionality is maintained despite the extensive loss of DA neurons early in Parkinson's disease by increased synthesis and release of dopamine from those DA neurons that remain (Zigmond et al., 1990). Given the importance of the size of the AIS, plasticity in the size of the AIS might be used as a homeostatic mechanism to regulate the level of tonic dopamine in the target striatal areas.