Abstract
A general method is reported for improving the segmentation of abnormal cell nuclei in cervical cytology images. In automation-assisted reading of cervical cytology, one of the essential steps is the segmentation of nuclei. Despite some progress, there is a need to improve the sensitivity, particularly the segmentation of abnormal nuclei. Our method starts with pre-segmenting the nucleus to define the coarse center and size of nucleus, which is used to construct a graph by image unfolding that maps ellipse-like border in the Cartesian coordinate system to lines in the polar coordinate system. The cost function jointly reflects properties of nucleus border and nucleus region. The prior constraints regarding the context of nucleus-cytoplasm position are utilized to modify the local cost functions. The globally optimal path in the constructed graph is then identified by dynamic programming with an iterative approach ensuring an optimal closed contour. Validation of our method was performed on abnormal nuclei from two cervical cell image datasets, Herlev and H&E stained manual liquid-based cytology (HEMLBC). Compared with five state-of-the-art approaches, our graph-search based method shows superior performance.
Keywords: Image cytometry, Cervical cells, Abnormal nuclei, Segmentation, Graph-based segmentation
1. Introduction
Automation-assisted reading techniques have the potential to reduce errors and increase productivity in cervical cancer screening (Birdsong, 1996; Biscotti et al., 2005; Wilbur et al., 2009; Kitchener et al., 2011; Zhang et al., 2014a). The key function of these techniques is to automatically distinguish potentially abnormal cells from a large numbers of normal cells in cervical cytology slides for further manual reading by pathologists (Birdsong, 1996; Biscotti et al., 2005; Wilbur et al., 2009; Kitchener et al., 2011; Zhang et al., 2014a). Both the nuclear and cytoplasmic morphological features are useful in distinguishing between abnormal and normal cells (Solomon and Nayar, 2004; Marinakis et al., 2009). However, recent studies have demonstrated the important role of nuclei in cancer recognition (Zink et al., 2004; Plissiti and Nikou, 2012a, b). More specifically, in cervical cytology diagnosis, all the cell abnormalities including atypical squamous cells of undetermined significance (ASC-US), ASC-cannot exclude HSIL (ASC-H), low grade squamous intraepithelial lesion (LSIL), high SIL (HSIL), and squamous cell carcinoma, accompany nuclear abnormality (Solomon and Nayar, 2004). In order to accurately characterize nuclear abnormality, reliable automated detection/segmentation of abnormal nuclei in cervical cytology is a necessary step, and is of utmost importance in automation-assisted reading techniques (Zhang et al., 2014a).
Most of the previous studies were developed to segment cervical cytology images with normal nuclei. Active contour model (Bamford and Lovell, 1998), morphology reconstruction (Plissiti et al., 2011), and level set (Bergmeir et al., 2012) are the most commonly used techniques for the accurate detection of nucleus boundary. To date, the segmentation of normal cervical nuclei has already achieved high accuracy. Researchers have started to change their attention to other more challenging tasks such as overlapping nuclei (Plissiti and Nikou, 2012a,b) and cytoplasm splitting (Lu et al., 2015; Guan et al., 2014). Segmentation of abnormal nuclei is critical in real clinical setting and remains challenging due to their variations in size, irregular shape and non-uniform chromatin distributions.
Until now, only a few studies are related to the topic of abnormal nuclei segmentation in cervical cytology. The pioneer work was reported in Chang et al. (2009) but only very limited data were reported. Succeeding researchers usually evaluate their methods on the Herlev database (Jantzen et al., 2005) which consists of single abnormal cell images. Li et al. (2012) proposed a radiating gradient vector flow (RGVF) snake model, which detects nucleus boundary in a radiating manner over the GVF field, to refine the initial segmentation of nuclei. In Gençtav et al. (2012), a multi-scale watershed approach is proposed to over-segment the image, and a classifier is then trained to identify the nucleus from the candidates. In a most recent work, fuzzy C-means (FCM) (Chankong et al., 2014) is utilized to separate the image into patches which are then combined into three clusters based on thresholding operation.
A more practically-oriented segmentation method for detecting/segmenting abnormal nuclei within a field-of-view (FOV) had recently been reported and evaluated by our group (Zhang et al., 2014a,b). Specifically, a local adaptive graph cut (LAGC) approach (Zhang et al., 2014b), which models the nucleus and background as two Poisson distributions is proposed to refine the coarse segmentation of both normal and abnormal nuclei. Recently, a deep learning initialization and superpixels graph cut refinement method was proposed by our group with the aim of improving the segmentation of nuclei (Song et al., 2015). Our previous approaches work well in most situations although they may generate inaccurate boundaries when the nuclei exhibit poor staining and/or their boundary contrast is low.
In order to handle the challenges presented in abnormal nucleus segmentation, we move away from the usage of traditional cervical cell segmentation techniques (Bengtsson and Malm, 2014; Plissiti and Nikou, 2013), and rely on the usage of graph-search based segmentation (Li et al., 2006), because it is known to be globally optimal in finding object boundaries. Specifically, we employ a 2D dynamic programming approach. Similar approaches have been successfully used in the segmentation of ellipse-like objects in other types of biomedical images (Baggett et al., 2005; Chiu et al., 2012; Fu et al., 2014). Especially for the abnormal nucleus segmentation task, specific information involving nucleus shape information, expected nucleus border and regional properties and nucleus context prior constraints are incorporated in a global optimal solution. Following an initial segmentation of nuclei and cytoplasm, our method is general and yields improved cell nucleus segmentation. We show quantitative comparisons between the proposed method and the state-of-the-art approaches (Li et al., 2012; Gençtav et al., 2012; Chankong et al., 2014; Zhang et al., 2014b; Song et al., 2015) on two datasets with different types of cervical cytology images, Herlev (Jantzen et al., 2005) and H&E stained manual liquid-based cytology (HELBC) (Zhang et al., 2014b).
2. Methods
State-of-the-art cervical nucleus segmentation methods often work in a coarse-to-fine manner. In the coarse stage, general segmentation techniques (e.g., Hough transform (Bergmeir et al., 2012), K-means (Li et al., 2012), thresholding (Zhang et al., 2014b), deep learning (Song et al., 2015)), or others are used to generate coarse nucleus candidates. The fine stage operates on each of these candidates, aiming at providing more accurate segmentation. Our graph-search based segmentation focuses on the fine stage, and is specifically designed for the refinement of coarse/initial segmentation of nucleus, given the rough segmentation of nucleus and cytoplasm regions (as shown in Fig. 1).
Fig. 1.

The segmentation framework of the proposed graph-search based method. (For interpretation of the references to color in the text, the reader is referred to the web version of the article.)
The refinement framework consists of five steps: (1) a rectangle (sub-image) around each nucleus candidate is cropped according to an annotation protocol which relies on the coarsely (initially) segmented nucleus boundary; (2) image unfolding is performed on the cropped sub-image to construct a graph; (3) nucleus-specific costs are assigned to each node in the graph; (4) a globally optimal path (red curve in Fig. 1) with the lowest cost is determined; and (5) the path is mapped onto the original sub-image by reversing the initial unfolding transformation and the improved nucleus boundary is obtained.
2.1. Nucleus image cropping
Given the initial segmentation of nucleus, the annotation protocol which was used to crop early gestational sac in ultrasound images (Zhang et al., 2012) is utilized since such a protocol ensures involving the entire nucleus area and a sufficiently large cytoplasm/background region around the nucleus. Briefly, a nucleus sub-image is defined based on the coarse boundary of the nucleus, using which we can compute the length L of the major axis and the center x0 of the smallest upright bounding rectangle. Then a rectangle with sides of Len = L +ΔL centered at x0 is cropped and determined to be the sub-image for graph-search based segmentation.
2.2. Image unfolding (graph construction)
Given a cropped image, image unfolding is performed by transforming the image coordinates from Cartesian to polar with the center of the cropped bounding box used as the unfolding center, as shown in Fig. 2. As a result, the ellipse-like border of the nucleus becomes a curve which starts from the first column and ends at the last column in the unfolded image. With the unfolded image, a graph with Ng graph columns is constructed and searched for the optimal path, where Ng equals to the number of columns of the unfolded image. In this graph, each node (yellow points in Fig. 2(b)) corresponds to a pixel in the unfolded image. The successors of a node (pointed by green arrows in Fig. 2(b)) are defined as the three nodes on the subsequent column corresponding to three possible changes of edge direction.
Fig. 2.

Schema of the graph-search based nucleus segmentation approach. Based on (a) the original cropped Cartesian image, (b) the graph is constructed from the image center (green point) using a polar transform. Yellow points represent pixels/nodes. Green arrows point to the successors of a node. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.)
2.3. Cost function
The cost function used for the identification of nucleus boundary is of the primary importance for the success of the segmentation. In this work, the cost assigned to the graph node contains three specific information related to cervical (abnormal) nuclei, i.e., the expected nucleus border properties, nucleus regional homogeneity properties, and nucleus context prior constraints, as depicted in the example given in Fig. 3. By combining these information components and obtaining an optimal solution, the overall segmentation process is generally robust to address typical variation of cervical (abnormal) nuclei.
Fig. 3.
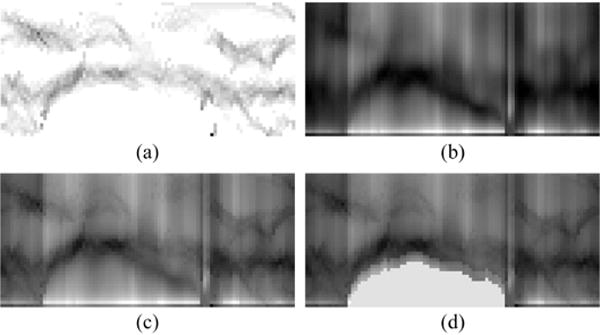
An example of cost components, corresponding to the case in Fig. 2. (a) The edge cost function image. (b) The region cost function image. (c) The combined cost function image. (d) The context prior constrained cost function image.
2.3.1. Nucleus border properties
Although non-ideal illumination, inconsistent staining, and artifacts tend to degrade the image quality, nucleus borders are still usually identifiable in most cell images. This observation motivates the design of an edge cost. In addition, since the boundary of nucleus is usually darker than the surrounding cytoplasm, gradient direction from dark to bright is considered. Specifically, the edge cost ce (Fig. 3(a)) is calculated based on the gradient magnitude gmag and gradient direction gdir of graph f as follows,
| (1) |
| (2) |
| (3) |
where and are the gradient in the x and y direction, respectively. For a specific node (i, j), its gradient in the x and y direction can be discretized as I(i + 1, j) − I(i − 1, j) and I(i, j + 1) − I(i, j − 1), respectively (Sonka et al., 2014), where I(i, j) represents the gray-scale intensity of node (i, j). Note that small deviations from this pattern are not critical because of the smoothness constraints of graph connections. Since the cytoplasm is also darker than the surrounding background, the values of ce between cytoplasm and background might even be stronger than that between the nucleus and cytoplasm. To remove such unwanted edges, the background pixels in each graph column are assigned low cost (marked as black color). Here, the background is determined by coarse segmentation.
2.3.2. Nucleus region properties
For images which are severely unfocused or where nucleus is surrounded by deep stained cytoplasm, the nucleus border gradients may be fuzzy. Furthermore, due to non-optimal autofocusing, different grades of abnormalities, inconsistent staining, and noise, the nuclear chromatin distribution (texture) may vary substantially. Nevertheless, most nucleus regions are still distinguishable from their surrounding background. Therefore, we add a region cost as a second component of our cost function to allow a segmentation to succeed even without the presence of gradients and without the assumption of a particular texture model. The region cost cr (Fig. 3(b)) is calculated using the Mumford-Shah functional as proposed by Chan and Vese (2001). This cost is minimized when nodes (i, j) coincide with the object boundary and best separate the object and background with respect to their mean intensities. For our constructed graph, this cost is assigned as the sum of the inside and outside variances computed in the graph column as follows:
| (4) |
where I is the gray-scale intensity, the two constants a1 and a2 are the mean intensities of pixels above (0≤j′ ≤ j) and below (j < j′ < J) the boundary, respectively, and J represents the last effective node on the graph column. Similar to the edge cost calculation, to alleviate the unwanted high values of cr between the cytoplasm and background, only pixels not in the background regions are considered in Eq. (4).
2.3.3. Combination of cost terms
The combination of edge and region information has proven successful in medical image segmentation tasks (Chakraborty et al., 1996). Therefore, the aforementioned edge and region cost terms are combined into a total cost function c (Fig. 3(c)) to allow more robust segmentation,
| (5) |
where α and β are the weights for the edge term and region term, respectively, satisfying α + β = 1. Each of the two terms is normalized to the range [0,1] before their combination.
2.3.4. Nucleus context prior constraints
Although the coarsely detected borders between cytoplasm and background are mostly excluded from the aforementioned cost calculations, relatively large image gradient near such borders can still exhibit low cost values. Because the nucleus/cytoplasm ratio is usually large for abnormal cervical cells, some abnormal nuclei might be located close to the border between cytoplasm and background. As a result, the graph search-based segmentation might incorrectly identify such borders (highlighted by green color in Fig. 4(a)) as nucleus boundaries since they might have lower costs than the nucleus boundaries. To solve this problem, specific prior constraints are designed inspired by the “Just-Enough-Interaction” (JEI) principle (Beichel et al., 2016). By modifying the graph local costs using interactively-provided clues, JEI is able to refine the initial automated segmentation. In this paper, we adapt the principle of JEI into nucleus segmentation by modifying the local cost functions based on the cytoplasm-nucleus context, consequently affecting the outcome of the graph-search segmentation.
Fig. 4.
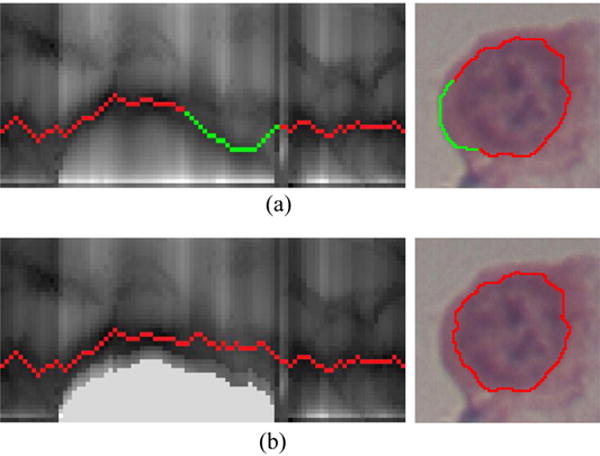
An example of context prior constraints, corresponding to the case in Fig. 3. (a) Incorrectly identified the cytoplasm-background border as the nucleus boundary, highlighted in green. (b) Correctly identified nucleus boundary after using context prior constraints. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.)
Given the coarsely segmented cytoplasm boundary represented by the point set in the polar coordinate system (dark blue points in Fig. 5(a)), where 0 ≤ bj ≤ Len with 0 indicating no cytoplasm on the current column, the affected nodes on graph column j are defined as those between the row bj −Δd (light blue points in Fig. 5(b)) and row bj +Δd (purple points in Fig. 5(b)). Let c (i, j) and c′(i, j) denote the costs of node n(i, j) before and after considering the proximity of cytoplasm, respectively, then two kinds of constraints including the hard context constraint and the context prior penalty are used to modify the costs of these affected nodes, and the costs of all other (unaffected) nodes remain unchanged,
| (6) |
The details for having these two constraints are as follows. First, for the context prior penalty, the costs of nodes on affected columns, which are immediately above the cytoplasm points need to become less “attractive” by utilizing an update function,
| (7) |
where d(.) denotes the distance (number of nodes).Δd controls the locality of the cost modification and corresponds to the affected range on the columns. Second, resulting from the hard context constraint, nodes on affected columns far away from coarsely segmented cytoplasm boundary points (below pj) become less attractive when modified according to the truncated L1 distance (Felzenszwalb and Zabih, 2011). K is set as 2 to make nodes that are outside the cytoplasm boundary less attractive to allow the segmented nucleus boundary to be outside of the cytoplasm boundary in case of inaccurate coarse detection of the cytoplasm. Illustrative examples of the refined cost function and its optimal path are shown in Figs. 3(d) and 4(b), respectively.
Fig. 5.
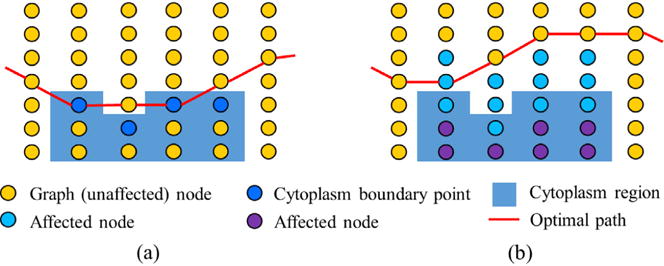
The illustration of the context prior constraints. (a) The optimal path passes through cytoplasm boundary points. (b) Incorporation of context prior constraints. Affected nodes above and below the cytoplasm boundary are modified by context prior penalties and hard context constraints, respectively. (For interpretation of the references to color in the text, the reader is referred to the web version of the article.)
2.4. Optimal path
After the graph is constructed, the optimal path is determined by dynamic programming (Sonka et al., 2014). However, the path found by standard dynamic programming does not guarantee a closed contour after reversely mapping onto the original image, since the starting node p1 and ending node on the path are not necessarily on the same row (Fig. 6(a)).
Fig. 6.
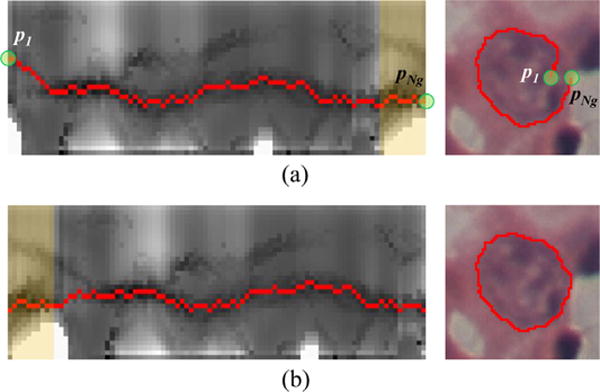
Connectivity constrained boundary detection. (a) Discontinuous boundary is detected. (b) Boundary detection results using the proposed connectivity constraints. (For interpretation of the references to color in the text, the reader is referred to the web version of the article.)
To solve this problem, an iterative approach is applied if a discontinuous boundary is detected, which is determined by , where t is the tolerance for distance discontinuity and is set as 3 pixels:
Set k = 1.
Cut the last k · C columns (overlaid with yellow color in Fig. 6) and concatenate them to the start of the graph.
Determine an optimal path and its starting node p1 and ending node of the newly formed graph by dynamic programming.
The process ends when, , otherwise, set k = k + 1, and repeat step 2–step 3.
The exact value of C has almost no impact on the method’s performance, and is simply set as 10.
2.5. Unfolding reversal
Finally, to get a closed contour of nucleus on the original image in Cartesian coordinate system, reversely mapped coordinates of adjacent nodes on the optimal path are directly connected.
3. Experimental methods
3.1. Data
The experiments were mainly carried out on abnormal nuclei from two types of cervical cytology images, which were acquired by different slide preparation, different staining methods, and also under different imaging conditions:
Herlev (Jantzen et al., 2005) – Pap-smear with Papanicolau (Pap) stained cervical cell images;
HEMLBC (Zhang et al., 2014b) – manual liquid-based cytology with H&E stained cervical cell images.
The Herlev dataset consists of 917 images of isolated cells collected at the Herlev University Hospital by a digital camera and microscope. Seven classes of cervical cells were manually classified by skilled cyto-technicians and physicians. Four types of abnormal cells were identified: mild dysplasia, moderate dysplasia, severe dysplasia, and carcinoma, with cell counts of 182, 146, 192, and 150, respectively. In addition, three types of normal cells were: superficial squamous, intermediate squamous, and columnar epithelial, with cell counts of 74, 70, and 98, respectively. The Herlev dataset also provides manual segmentation for all nuclei. Examples of some abnormal cells are shown in Fig. 7(a). Generally, the higher the abnormal degree, the darker and more irregular the nuclei, and the smaller the cytoplasm.
Fig. 7.
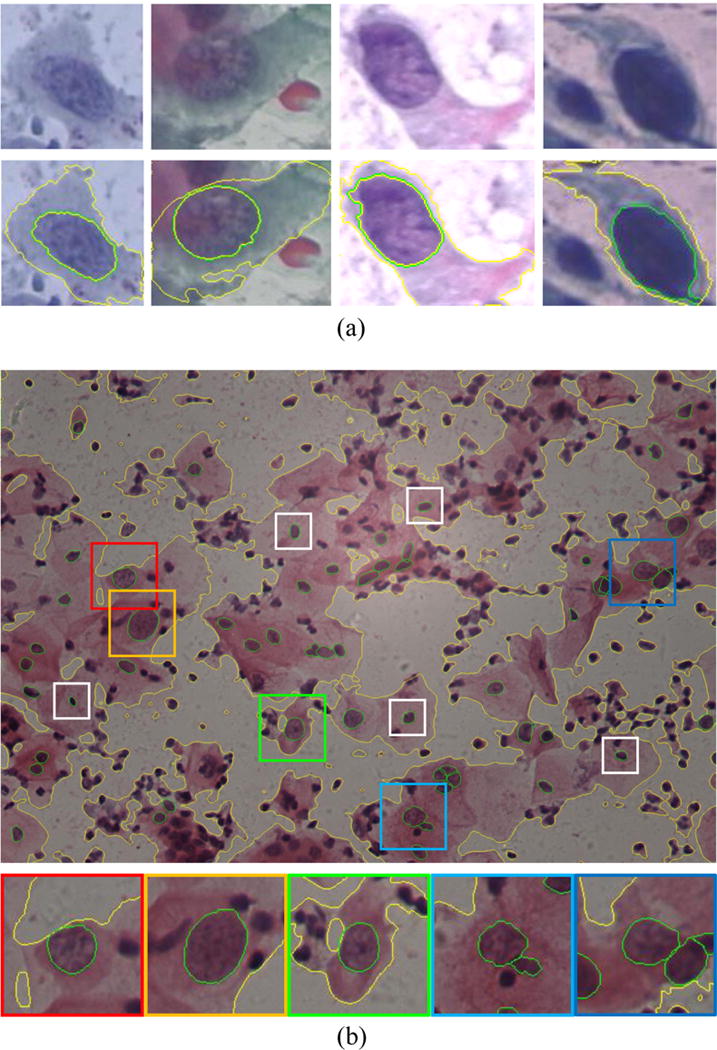
Examples of abnormal cervical cells from (a) the Herlev dataset and (b) HEMLBC dataset with boundaries of the cytoplasm and the nuclei marked as yellow and green, respectively. In (a), from left to right, the nuclei tend to be darker and more irregular and the cytoplasm smaller, corresponding to mild dysplasia, moderate dysplasia, severe dysplasia, and carcinoma cells. In (b), abnormal and normal nuclei are annotated by colored and white bounding boxes, respectively. Abnormal nuclei are generally larger and some are darker than normal nuclei. For more detail about distinguishing cervical cell abnormality, please refer to Solomon and Nayar (2004) and Jantzen et al. (2005). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.)
The HEMLBC dataset consists of 21 images within FOVs captured at the People’s Hospital of Nanshan District by using our previously developed autofocusing system (Olympus BX41 microscope with 20× objective, Jenoptik ProgRes CF Color 1.4 Megapixel Camera, and MS300 motorized stage) (Zhang et al., 2014a). Image resolution is 1360 × 1024, with each pixel 0.208 μm2 in size. There are 64 abnormal cells from 15 cervical cell images annotated by a pathologist, who also manually traced boundaries of all abnormal nuclei twice. The expert segmentations serve as the ground truth and are used to conduct inter-observer variability analysis. A representative image is shown in Fig. 7(b), where five abnormal and five normal nuclei are highlighted by (larger) colored and (smaller) white bounding boxes, respectively.
3.2. Abnormal nucleus segmentation on the Herlev data
To evaluate the performance of our method on the Herlev dataset, initial segmentation of nuclei and cytoplasm was the first step using Li et al.’s (2012) preprocessing approach, because this approach was specifically designed for the Herlev data. Briefly, the L* channel in the CIELAB color space is extracted and normalized to [0,255] linearly to form the grayscale image, and then a spatial K-means clustering algorithm is used to divide the image pixels into three classes of cytoplasm, nuclei and background. Then, geometric information is used to select the most likely nucleus candidates. After that, different from Li et al.’s (2012) method, we simply select the segmented component with the closest distance to the image centroid as the nucleus candidate, where our annotation protocol is applied to crop sub-image for graph-search based segmentation. The cropping parameter ΔL is experimentally set as 20 pixels (throughout this paper) considering a tradeoff between accuracy and computational burden. The segmentation accuracy is not sensitive to the variation of ΔL (refer to Section 4.1). The parameters for graph-search based segmentation in this experiment were set as Ng = 360, α = 1, β = 1 and Δd = 2.
3.3. Abnormal nucleus segmentation on HEMLBC data
The initial segmentation of nuclei and cytoplasm follows our previous approach (Zhang et al., 2014b): a multi-way graph cut is used to segment the cytoplasm, and adaptive thresholding is used to coarsely locate nucleus candidates. For each abnormal nucleus candidate, our annotation protocol is utilized to crop sub-image for further graph-search based refinement. Note that in accordance with Zhang et al. (2014b), the V channel in HSV color space of the cropped sub-image is stretched linearly and processed by a 5 × 5 median filter to serve as the input of graph-search based refinement. For more details, please refer to the work of Zhang et al. (2014b). The parameters in this experiment are also set as α = 1, β = 1 and Δd = 2, but with Ng = 90 since the nucleus image sizes in this dataset are smaller than that in the Herlev dataset due to a lower-amplification lens.
3.4. Normal nucleus segmentation
We further evaluate the proposed fine segmentation method on normal nuclei from the Herlev dataset. The same initial segmentation method (Li et al.’s, 2012, as specified in Section 3.2) is utilized. The parameters in this experiment were set as the same as in Section 3.2.
3.5. Quantitative evaluation methodologies
The evaluation of the proposed segmentation method is based on the comparison with five state-of-the-art methods including RGVF snake (Li et al., 2012), multi-scale watershed (Gençtav et al., 2012), FCM (Chankong et al., 2014), LAGC (Zhang et al., 2014b), and superpixels GC (Song et al., 2015) using pixel-based criterion. For the Herlev dataset, the precision and recall as in Li et al. (2012), Gençtav et al. (2012), and Chankong et al. (2014) are used; for the HEMLBC dataset, the precision, recall, F-measure and overlap as in Zhang et al. (2014b) and Song et al. (2015) are used. The precision and recall indicate the fraction of the amount of nucleus correctly identified in the segmented object, and in the reference ground truth, respectively. The F-measure gives the harmonic mean of precision and recall. These indices are defined as follows:
| (8) |
| (9) |
| (10) |
| (11) |
where TP denotes the number of correctly identified pixels of the nucleus, FP is the number of pixels in background which were incorrectly identified as nucleus, and FN is the number of nucleus pixels missed by segmentation. All results are reported as the mean ± standard deviation.
Furthermore, linear regression analysis (Cox and Hinkley, 1979) and Bland–Altman plots (Martin Bland and Altman, 1986), which used nuclear area as a quantitative measure, are used to evaluate the relationship between the manual and automatic segmentation of abnormal nuclei on HEMLBC dataset as in Zhang et al. (2014b). Note that nuclear area is used because it is one of the most important features to distinguish abnormal and normal cervical cells (Zhang et al., 2014a; Solomon and Nayar, 2004; Marinakis et al., 2009).
3.6. Computational resource
The proposed graph-search based method is implemented using Matlab and tested on HP Z400 workstation with 3.33 GHz Xeon W3680 CPU, 24 GB of RAM, running Windows 7 SP1 Enterprise. The mean execution times of graph-search per cell on each dataset are reported.
4. Results
4.1. Evaluation on the Herlev data
Fig. 8 shows examples of our segmentation results on the Herlev dataset. It can be seen that our method generates accurate nucleus boundaries across a variety of cells with abnormal nuclei (different size, irregular shape and non-uniform chromatin distributions). Table 1 shows the quantitative comparison of RGVF snake (Li et al., 2012), multi-scale watershed (Gençtav et al., 2012), FCM (Chankong et al., 2014), and our method in terms of average precision and recall of segmentation for all types of abnormal nuclei from the Herlev dataset. It can be seen that our new graph-search based method outperforms the state-of-the-art approaches (Li et al., 2012; Gençtav et al., 2012; Chankong et al., 2014) on most sub-datasets. However, statistic comparison with these approaches (Li et al., 2012; Gençtav et al., 2012; Chankong et al., 2014) is unavailable since their detailed results cannot be obtained. Note that results in method (Li et al., 2012) were obtained as described in Gençtav et al. (2012). In addition, a sensitivity analysis is performed for the parameter ΔL by varying its value as 10, 15, 20, 25. The resulting average precision/recall on all abnormal nuclei are 0.92/0.91, 0.92/0.92, 0.91/0.94, 0.91/0.94, respectively, indicating a very limited sensitivity to ΔL. The average execution time of graph-search is 0.08 ± 0.03 s per cell.
Fig. 8.
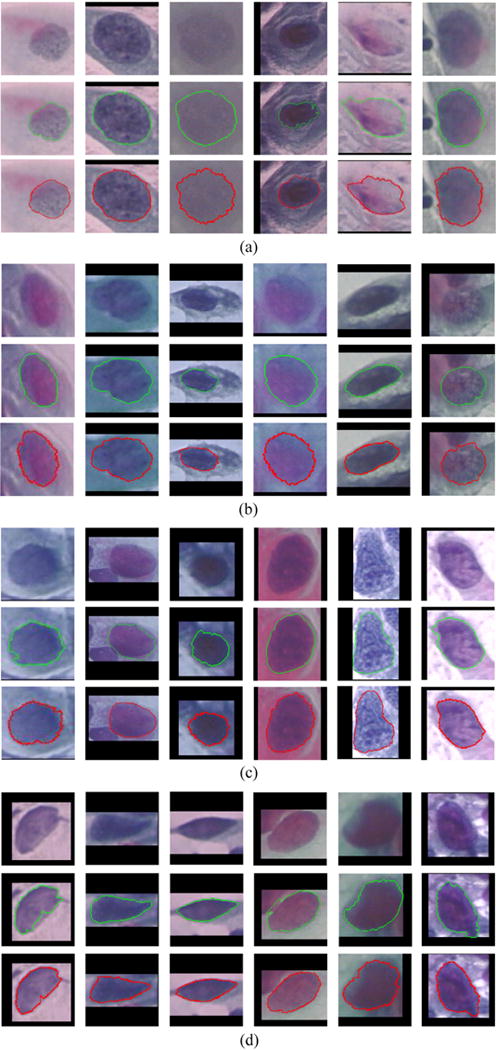
Examples of our graph-search based segmentations on (a) mild dysplasia, (b) moderate dysplasia, (c) severe dysplasia, and (d) carcinoma cervical nuclei from the Herlev dataset (Jantzen et al., 2005). In each sub-figure ((a)–(d)), from the first to the third rows are original image, ground truth (green boundaries), and our segmentation results (red boundaries), respectively. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.)
Table 1.
Comparison of average nucleus segmentation performance of RGVF snake (Li et al., 2012), multi-scale watershed (Gençtav et al., 2012), FCM (Chankong et al., 2014), and our graph-search based methods on the abnormal cervical cells from the Herlev data (Jantzen et al., 2005). Bold values indicate the best performance for each column.
| Methods | Mild dysplasia (182 cells)
|
Moderate dysplasia (146cells)
|
Severe dysplasia (197 cells)
|
Carcinoma (150 cells)
|
||||
|---|---|---|---|---|---|---|---|---|
| Precision | Recall | Precision | Recall | Precision | Recall | Precision | Recall | |
| Li et al. (2012) | 0.92 ±0.13 | 0.90±0.16 | 0.89 ±0.15 | 0.87 ±0.17 | 0.88 ±0.15 | 0.90 ±0.13 | 0.84 ±0.18 | 0.88 ±0.11 |
| Gençtav et al. (2012) | 0.88 ±0.17 | 0.86 ±0.16 | 0.91 ± 0.10 | 0.86 ±0.14 | 0.90 ± 0.12 | 0.89 ±0.11 | 0.89 ±0.15 | 0.90 ± 0.08 |
| Chankong et al. (2014) | 0.80 ±0.31 | 0.86 ±0.26 | 0.81 ±0.25 | 0.88 ±0.19 | 0.79 ±0.28 | 0.88 ±0.21 | 0.70 ±0.29 | 0.88 ±0.23 |
| Our method | 0.90 ±0.13 | 0.95 ±0.11 | 0.90 ±0.11 | 0.96 ± 0.07 | 0.91 ± 0.10 | 0.93 ± 0.12 | 0.93 ± 0.08 | 0.91 ± 0.13 |
4.2. Evaluation on HEMLBC data
Fig. 9 shows examples of our segmentation results on the HEMLBC dataset. Table 2 provides the comparison of LAGC (Zhang et al., 2014b), superpixels GC (Song et al., 2015), our new method, and intra-observer variability in terms of average precision, recall, F-measure, and overlap of segmentation for all analyzed abnormal nuclei. As can be seen, our new graph-search based method outperforms the previous approaches (Zhang et al., 2014b; Song et al., 2015) in all the comparisons.
Fig. 9.

Examples of graph-search based segmentation on abnormal cervical nuclei from the HEMLBC dataset (Zhang et al., 2014b). In each sub-figure, from the first to the third rows are original image, ground truth (green boundaries), and our segmentation results (red boundaries), respectively. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.)
Table 2.
Comparison of average nucleus segmentation performance of LAGC (Zhang et al., 2014b), superpixels GC (Song et al., 2015) and our graph-search based methods on abnormal cervical cells from HEMLBC dataset (Zhang et al., 2014b). Bold values indicate the highest performance for each automated method.
| Methods | Precision | Recall | F-measure | Overlap |
|---|---|---|---|---|
| Zhang et al. (2014b) | 0.88 ±0.14 | 0.91 ± 0.07 | 0.884 ±0.08 | 0.81 ±0.12 |
| Song et al. (2015) | 0.90 ± NA | 0.91 ± NA | 0.897 ± NA | 0.83 ± NA |
| Our method | 0.91 ± 0.04 | 0.96 ± 0.04 | 0.930 ± 0.03 | 0.87 ± 0.05 |
| Intra-observer | 0.94 ± 0.04 | 0.96 ± 0.03 | 0.953 ± 0.02 | 0.91 ± 0.03 |
Fig. 10 shows results of linear regression analysis and Bland–Altman plots when comparing nucleus areas. We compare with the LAGC method (Zhang et al., 2014b): (1) the LAGC method achieves r2 = 0.88 with Manual 1, our new method shows substantially improved correlation with Manual 1 segmentation (r2 = 0.97), which was virtually identical to the manual reproducibility (intra-observer variability) (r2 = 0.97); (2) the LAGC method achieves 95% limits of agreement of [−55,77] versus Manual 1, while the new method agrees much better with Manual 1 segmentation and ([−20,52]) was close to the agreement of manual reproducibility ([−22,36]). Similar observations are found between the new method and Manual 2 (Fig. 10(b)). The average execution time of graph-search is 0.02 ± 0.02 s per cell.
Fig. 10.
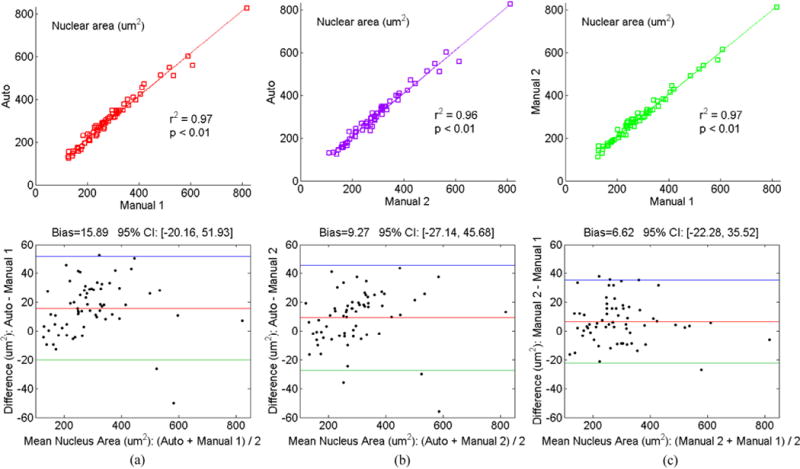
Statistical correlation analysis and Bland–Altman plots between (a) automated (our graph-search) method and Manual 1 segmentation, (b) automated (our graph-search) method and Manual 2 segmentation, and (c) Manual 2 and Manual 1 segmentation on abnormal cervical nuclei from HEMLBC dataset (Zhang et al., 2014b).
4.3. Evaluation on normal nuclei
The normal nuclei segmentation performance of our method on the Herlev dataset is listed in Table 3, where comparisons with RGVF snake (Li et al., 2012), multi-scale watershed (Gençtav et al., 2012), and FCM (Chankong et al., 2014) are also provided. Our method shows high recall but relatively low precision. This was mainly because the utilized initial segmentation method (Li et al., 2012) failed to extract some normal nuclei in squamous cells especially when the cytoplasm showed heavy or non-uniform staining. For example, in the 74 superficial and 70 intermediate squamous cells, 13 (18%) and 10 (14%) nuclei cannot be extracted (large cytoplasm regions were wrongly extracted as nuclei), respectively. Consequently, our fine segmentation method cannot be properly initialized. When removing these cells from the experiment, our method* (Table 3) shows promising precision.
Table 3.
Comparison of average nucleus segmentation performance of RGVF snake (Li et al., 2012), multi-scale watershed (Gençtav et al., 2012), FCM (Chankong et al., 2014), and our graph-search based methods on the normal cervical cells from the Herlev data (Jantzen et al., 2005). Our method*: remove outliers (23 squamous cells in which nuclei cannot be properly extracted by initial segmentation).
| Methods | Superficial squamous (74 cells)
|
Intermediate squamous (70 cells)
|
Columnar (98 cells)
|
|||
|---|---|---|---|---|---|---|
| Precision | Recall | Precision | Recall | Precision | Recall | |
| Li et al. (2012) | 0.92 ± 0.12 | 0.88 ± 0.14 | 0.95 ± 0.03 | 0.92 ± 0.06 | 0.83 ± 0.16 | 0.76 ± 0.20 |
| Gençtav et al. (2012) | 0.69 ± 0.37 | 0.63 ± 0.37 | 0.79 ± 0.29 | 0.73 ± 0.31 | 0.85 ± 0.15 | 0.77 ± 0.18 |
| Chankong et al. (2014) | 0.95 ± 0.12 | 0.75 ± 0.33 | 0.98 ± 0.03 | 0.82 ± 0.25 | 0.88 ± 0.20 | 0.78 ± 0.25 |
| Our method | 0.75 ± 0.34 | 0.98 ± 0.08 | 0.81 ± 0.29 | 0.99 ± 0.02 | 0.86 ± 0.16 | 0.93 ± 0.11 |
| Our method* | 0.90±0.10 | 0.98±0.03 | 0.93±0.06 | 0.99±0.02 | 0.86±0.16 | 0.93±0.11 |
5. Discussion
5.1. Comparison with state-of-the-art methods
For the task of abnormal nucleus segmentation in cervical cytology, previous approaches can be divided into three categories according to their utilized clues. The first category mainly relies on the nucleus gradient clue, and the nuclei are segmented using RGVF snakes (Li et al., 2012) or multi-scale watershed frameworks (Gençtav et al., 2012). As mentioned in Section 2.3.2, only using the gradient information may not be able to handle the challenges caused by severely unfocused images or low boundary contrast. As shown in Table 1, compared to the gradient-based RGVF snake approach (Li et al., 2012), our method achieves better accuracy when using the same initial segmentation. The second category directly uses image intensity clue in FCM-based segmentation (Chankong et al., 2014). Such an approach might not be robust enough in practice when the image quality suffers from non-ideal illumination, inconsistent staining, and noise. This can be reflected by the lowest performance of Chankong et al. (2014) in Table 1. The third category of methods models the distribution of nucleus intensity (Zhang et al., 2014b) or color information (Song et al., 2015) for the GC-based segmentation. However, any assumption regarding a distribution model might not be correct given that nuclear chromatin distribution may vary substantially (Zhang et al., 2014b). Moreover, relying on the color information limits the generalization ability of such approach (Song et al., 2015). As a result, the performance of methods in this category is lower than that of our new method (Table 2). Besides the above limitations, previous approaches ignore the nucleus shape prior and the specific characteristic of abnormal nuclei, which were included in our graph-search based segmentation in a globally optimal manner.
5.2. Advantages of the proposed method
The main advantage of our graph-search based approach for nucleus segmentation is its ability to embed shape information about nuclei in the graph construction, and its flexibility to incorporate problem-specific prior knowledge when designing the cost function. Subsequently, the specifically designed knowledge-based cost function is robust to the various challenges facing segmentation of abnormal cervical nuclei. In addition, our new method is well suited for practical use due to the fast optimization process of dynamic programming. Overall, the methodology is general as the parameters used in two totally different types of cervical cytology images are almost the same, with the only different parameter being Ng. The final segmentation is insensitive to the choice of Ng.
While the proposed method was only tested on cervical cell images, our ongoing study showed that it may be easily extended to other microscopy images (e.g., Drosophila cells (Quelhas et al., 2010)) and histopathology images (e.g., glioblastoma multiforme cells (Chang et al., 2013)) for improving the nucleus segmentation. This is likely to be fairly straightforward, provided there is similar nucleus-cytoplasm structure.
5.3. Limitations
Our method in part relies on the initial segmentation results. If the initial detected nucleus center is far away from the correct nucleus region, or if the initial extracted cytoplasm boundary is not correct, the final segmentation results may fail, as shown in Fig. 11(a) and (b), respectively. Fortunately, erroneous segmentation of cytoplasm-background boundaries rarely happen since most cervical cytoplasm can be reliably segmented by current approaches (accuracies ranging from 93% to 97% (Zhang et al., 2014b; Song et al., 2015; Li et al., 2012; Guan et al., 2014)). Nevertheless, more robust initial segmentation methods need to be exploited in future work.
Fig. 11.

Two examples of inaccurate nucleus segmentation due to erroneous initial segmentation of the (a) nucleus and (b) cytoplasm. In each sub-figure, from left to right are original image, initial segmentation, ground truth segmentation, ground truth nucleus, and our segmentation, respectively. The green point labels the initial detected nucleus center. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.)
6. Conclusion
A graph-search based method for improving the segmentation of abnormal cervical nuclei is proposed. The nuclear shape constraint is embedded in the construction of the segmentation graph. Globally optimal segmentation is guaranteed according to the cost function based on nucleus-specific edge- and region-information, and abnormal nucleus context prior information. The method is tested on abnormal nuclei from two cervical cell datasets with different specimen preparation and staining techniques. The experimental results demonstrate the high efficiency and superior performance of the proposed method by comparing with five state-of-the-art methods in terms of abnormal nucleus segmentation accuracy. Our method is therefore general, and can be incorporated into current automation-assisted cervical screening systems to improve the sensitivity of recognizing abnormal cells.
Assessment of segmentation performance on overlapping nuclei needs further evaluation in our future work, and we will exploit other state-of-the-art detection and initial segmentation techniques (e.g., shape and size estimation of blobs Kong et al., 2013, deep learning based semantic segmentation Shelhamer et al., 2017) to improve the performance of the current method.
Acknowledgments
This work was supported in part by the NIH Grant R01EB004640, the National Natural Science Foundation of China61427806 and 81501545, and the China Postdoctoral Science Foundation Grant 2014M552230.
Footnotes
Conflict of interest
There is no conflict of interest in this paper.
References
- Baggett D, Nakaya M, McAuliffe M, Yamaguchi TP, Lockett S. Whole cell segmentation in solid tissue sections. Cytometry A. 2005;67(2):137–143. doi: 10.1002/cyto.a.20162. [DOI] [PubMed] [Google Scholar]
- Bamford P, Lovell B. Unsupervised cell nucleus segmentation with active contours. Signal Process. 1998;71(2):203–213. [Google Scholar]
- Beichel RR, Van Tol M, Ulrich EJ, Bauer C, Chang T, Plichta KA, Smith BJ, Sunderland JJ, Graham MM, Sonka M, et al. Semiautomated segmentation of head and neck cancers in 18F-FDG PET scans: a just-enough-interaction approach. Med Phys. 2016;43(6):2948–2964. doi: 10.1118/1.4948679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bengtsson E, Malm P. Screening for cervical cancer using automated analysis of pap-smears. Comput Math Methods Med. 2014;2014:1–12. doi: 10.1155/2014/842037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergmeir C, Silvente MG, Benítez JM. Segmentation of cervical cell nuclei in high-resolution microscopic images: a new algorithm and a web-based software framework. Comput Methods Progr Biomed. 2012;107(3):497–512. doi: 10.1016/j.cmpb.2011.09.017. [DOI] [PubMed] [Google Scholar]
- Birdsong GG. Automated screening of cervical cytology specimens. Hum Pathol. 1996;27(5):468–481. doi: 10.1016/s0046-8177(96)90090-8. [DOI] [PubMed] [Google Scholar]
- Biscotti CV, Dawson AE, Dziura B, Galup L, Darragh T, Rahemtulla A, Wills-Frank L. Assisted primary screening using the automated ThinPrep imaging system. Am J Clin Pathol. 2005;123(2):281–287. [PubMed] [Google Scholar]
- Chakraborty A, Staib LH, Duncan JS. Deformable boundary finding in medical images by integrating gradient and region information. IEEE Trans Med Imaging. 1996;15(6):859–870. doi: 10.1109/42.544503. [DOI] [PubMed] [Google Scholar]
- Chan TF, Vese LA. Active contours without edges. IEEE Trans Image Process. 2001;10(2):266–277. doi: 10.1109/83.902291. [DOI] [PubMed] [Google Scholar]
- Chang CW, Lin MY, Harn HJ, Harn YC, Chen CH, Tsai KH, Hwang CH. Automatic segmentation of abnormal cell nuclei from microscopic image analysis for cervical cancer screening. IEEE International Conference on Nano/Molecular Medicine and Engineering (NANOMED) 2009:77–80. [Google Scholar]
- Chang H, Han J, Borowsky A, Loss L, Gray JW, Spellman PT, Parvin B. Invariant delineation of nuclear architecture in glioblastoma multiforme for clinical and molecular association. IEEE Trans Med Imaging. 2013;32(4):670–682. doi: 10.1109/TMI.2012.2231420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chankong T, Theera-Umpon N, Auephanwiriyakul S. Automatic cervical cell segmentation and classification in pap smears. Comput Methods Progr Biomed. 2014;113(2):539–556. doi: 10.1016/j.cmpb.2013.12.012. [DOI] [PubMed] [Google Scholar]
- Chiu SJ, Toth CA, Bowes Rickman C, Izatt JA, Farsiu S. Automatic segmentation of closed-contour features in ophthalmic images using graph theory and dynamic programming. Biomed Opt Express. 2012;3(5):1127–1140. doi: 10.1364/BOE.3.001127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox DR, Hinkley DV. Theoretical Statistics. CRC Press; 1979. [Google Scholar]
- Felzenszwalb PF, Zabih R. Dynamic programming and graph algorithms in computer vision. IEEE Trans Pattern Anal Mach Intell. 2011;33(4):721–740. doi: 10.1109/TPAMI.2010.135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu H, Qiu G, Shu J, Ilyas M. A novel polar space random field model for the detection of glandular structures. IEEE Trans Med Imaging. 2014;33(3):764–776. doi: 10.1109/TMI.2013.2296572. [DOI] [PubMed] [Google Scholar]
- Gençtav A, Aksoy S, Önder S. Unsupervised segmentation and classification of cervical cell images. Pattern Recognit. 2012;45(12):4151–4168. [Google Scholar]
- Guan T, Zhou D, Liu Y. Accurate segmentation of partially overlapping cervical cells based on dynamic sparse contour searching and GVF snake model. IEEE J Biomed Health Inform. 2014;19(4) doi: 10.1109/JBHI.2014.2346239. [DOI] [PubMed] [Google Scholar]
- Jantzen J, Norup J, Dounias G, Bjerregaard B. Nature inspired Smart Information Systems. Vol. 2005. NiSIS; 2005. Pap-smear benchmark data for pattern classification; pp. 1–9. [Google Scholar]
- Kitchener HC, Blanks R, Dunn G, Gunn L, Desai M, Albrow R, Mather J, Rana DN, Cubie H, Moore C, Legood R, Gray A, Moss S. Automation-assisted versus manual reading of cervical cytology (MAVARIC): a randomised controlled trial. Lancet Oncol. 2011;12(1):56–64. doi: 10.1016/S1470-2045(10)70264-3. [DOI] [PubMed] [Google Scholar]
- Kong H, Akakin HC, Sarma SE. A generalized Laplacian of Gaussian filter for blob detection and its applications. IEEE Trans Cybernet. 2013;43(6):1719–1733. doi: 10.1109/TSMCB.2012.2228639. [DOI] [PubMed] [Google Scholar]
- Li K, Wu X, Chen DZ, Sonka M. Optimal surface segmentation in volumetric images – a graph-theoretic approach. IEEE Trans Pattern Anal Mach Intell. 2006;28(1):119–134. doi: 10.1109/TPAMI.2006.19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li K, Lu Z, Liu W, Yin J. Cytoplasm and nucleus segmentation in cervical smear images using radiating GVF snake. Pattern Recognit. 2012;45(4):1255–1264. [Google Scholar]
- Lu Z, Carneiro G, Bradley A. An improved joint optimization of multiple level set functions for the segmentation of overlapping cervical cells. IEEE Trans Image Process. 2015;24(4):1261–1272. doi: 10.1109/TIP.2015.2389619. [DOI] [PubMed] [Google Scholar]
- Marinakis Y, Dounias G, Jantzen J. Pap smear diagnosis using a hybrid intelligent scheme focusing on genetic algorithm based feature selection and nearest neighbor classification. Comput Biol Med. 2009;39(1):69–78. doi: 10.1016/j.compbiomed.2008.11.006. [DOI] [PubMed] [Google Scholar]
- Martin Bland J, Altman D. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986;327(8476):307–310. [PubMed] [Google Scholar]
- Plissiti ME, Nikou C. Image Analysis and Recognition. Springer; 2012a. Cervical cell classification based exclusively on nucleus features; pp. 483–490. [Google Scholar]
- Plissiti ME, Nikou C. Overlapping cell nuclei segmentation using a spatially adaptive active physical model. IEEE Trans Image Process. 2012b;21(11):4568–4580. doi: 10.1109/TIP.2012.2206041. [DOI] [PubMed] [Google Scholar]
- Plissiti ME, Nikou C. Biomedical Imaging and Computational Modeling in Biomechanics. Springer; 2013. A review of automated techniques for cervical cell image analysis and classification; pp. 1–18. [Google Scholar]
- Plissiti ME, Nikou C, Charchanti A. Automated detection of cell nuclei in pap smear images using morphological reconstruction and clustering. IEEE Trans Inf Technol Biomed. 2011;15(2):233–241. doi: 10.1109/TITB.2010.2087030. [DOI] [PubMed] [Google Scholar]
- Quelhas P, Marcuzzo M, Mendonça AM, Campilho A. Cell nuclei and cytoplasm joint segmentation using the sliding band filter. IEEE Trans Med Imaging. 2010;29(8):1463–1473. doi: 10.1109/TMI.2010.2048253. [DOI] [PubMed] [Google Scholar]
- Shelhamer E, Long J, Darrell T. Fully convolutional networks for semantic segmentation. IEEE Trans Pattern Anal Mach Intell. 2017 doi: 10.1109/TPAMI.2016.2572683. (in press) [DOI] [PubMed] [Google Scholar]
- Solomon D, Nayar R. The Bethesda System for reporting cervical cytology: definitions, criteria, and explanatory notes. Springer Science & Business Media; 2004. [Google Scholar]
- Song Y, Zhang L, Chen S, Ni D, Lei B, Wang T. Accurate segmentation of cervical cytoplasm and nuclei based on multi-scale convolutional network and graph partitioning. IEEE Trans Biomed Eng. 2015;62(10):2421–2433. doi: 10.1109/TBME.2015.2430895. [DOI] [PubMed] [Google Scholar]
- Sonka M, Hlavac V, Boyle R. Image Processing, Analysis, and Machine Vision. Cengage Learning (4th) 2014 [Google Scholar]
- Wilbur DC, Black-Schaffer WS, Luff RD, Abraham KP, Kemper C, Molina JT, Tench WD. The Becton Dickinson FocalPoint GS imaging system clinical trials demonstrate significantly improved sensitivity for the detection of important cervical lesions. Am J Clin Pathol. 2009;132(5):767–775. doi: 10.1309/AJCP8VE7AWBZCVQT. [DOI] [PubMed] [Google Scholar]
- Zhang L, Chen S, Chin CT, Wang T, Li S. Intelligent scanning: automated standard plane selection and biometric measurement of early gestational sac in routine ultrasound examination. Med Phys. 2012;39(8):5015–5027. doi: 10.1118/1.4736415. [DOI] [PubMed] [Google Scholar]
- Zhang L, Kong H, Chin CT, Liu S, Fan X, Wang T, Chen S. Automation-assisted cervical cancer screening in manual liquid-based cytology with hematoxylin and eosin staining. Cytometry A. 2014a;85(3):214–230. doi: 10.1002/cyto.a.22407. [DOI] [PubMed] [Google Scholar]
- Zhang L, Kong H, Chin CT, Liu S, Chen Z, Wang T, Chen S. Segmentation of cytoplasm and nuclei of abnormal cells in cervical cytology using global and local graph cuts. Comput Med Imaging Graph. 2014b;38(5):369–380. doi: 10.1016/j.compmedimag.2014.02.001. [DOI] [PubMed] [Google Scholar]
- Zink D, Fischer AH, Nickerson JA. Nuclear structure in cancer cells. Nat Rev Cancer. 2004;4(9):677–687. doi: 10.1038/nrc1430. [DOI] [PubMed] [Google Scholar]


