Observation of structural universality in disordered systems using bulk diffusion measurement

Abstract

We report on the first experimental observation of classical diffusion distinguishing between structural universality classes of disordered systems in one dimension. Samples of hyperuniform and short-range disorder were designed, characterized by the statistics of the placement of μm-thin parallel permeable barriers, and the time-dependent diffusion coefficient was measured by NMR methods over three orders of magnitude in time. The relation between the structural exponent, characterizing disorder universality class, and the dynamical exponent of the diffusion coefficient is experimentally verified. The experimentally established relation between structure and transport exemplifies the hierarchical nature of structural complexity — dynamics are mainly determined by the universality class, whereas microscopic parameters effect the non-universal coefficients. These results open the way for non-invasive characterization of structural correlations in porous media, complex materials, and biological tissues via a bulk diffusion measurement.

How does a measurement of a macroscopic characteristic relate to microscopic structure? This ill-posed question has been repeatedly asked in many disciplines — famously, “Can one hear the shape of a drum?” [1] — and its answer depends on the kind of measurement. Naively, one could imagine that infinitely many parameters needed to specify sample’s structure would in one way or the other contribute to the outcome. Physical intuition, however, tells that only a few parameters profoundly affect the measurement; identifying these relevant parameters is generally nontrivial, especially for irregular, or disordered systems. For instance, even small irregularities in a periodic lattice can change perfectly conducting metallic bands into an insulator due to quantum localization [2].

Here we consider classical diffusion in structurally disordered systems, where the practical answer to the above question could help quantify the underlying microstructure of complex materials [3–8] and living tissues [9–13]. We experimentally demonstrate that the qualitative behavior of the time-dependent diffusion coefficient is tied to the long-range structural fluctuations. While systems may strongly differ in their microscopic parameters, there are only a few universality classes of such fluctuations—in essence, a system can be disordered in one of a few distinct ways—and each universality class yields a particular power-law behavior of the observed macroscopic diffusion coefficient.

Technically, we experimentally verify the recently derived relation [10]

$$\vartheta =\frac{p+d}{2}$$ (1)

between the structural exponent p, and the dynamical exponent ϑ of the Brownian motion x_t in structurally disordered stationary media in d spatial dimensions. The defining signature of structural complexity is reflected in the structural exponent p which takes discrete values according to the universality class, as illustrated in Fig. 1 for our d = 1-dimensional samples. Equation (1) relates p to the long-time tail in the bulk diffusion coefficient [10] (the mean-squared displacement rate)

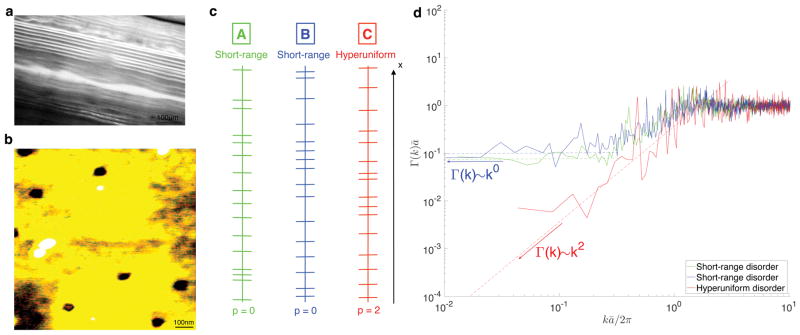
FIG. 1. Structure and universality classes of the samples.

a Representative optical microscopy image of the SR sample. b, AFM image of a single barrier. c, Digitized 1d cut-outs of the two SR samples (A–B) and HU sample C. d, Power spectrum (3) of the barrier density n(x) reveals qualitative differences between the disorder classes as k → 0: A plateau (p = 0) in Γ(k) for the SR samples (A–B), and k^p scaling with p = 2 for HU sample (C).

$$D_{\text{inst}}(t)\equiv \frac{\partial }{\partial t}\frac{\langle {(x_t-x_0)}^2\rangle }{2}\simeq D_{\infty }+c·t^{-\vartheta },t\to \infty .$$ (2)

The macroscopic diffusion coefficient D_∞ ≡ D_inst(t)|_t=∞ and the power-law amplitude c are non-universal, i.e. depend on the microstructural parameters. On the other hand, as we experimentally demonstrate in Fig. 2, the relation (1) is universal [10], akin to the relations between critical exponents [14] in statistical physics, where the notion of universality originates.

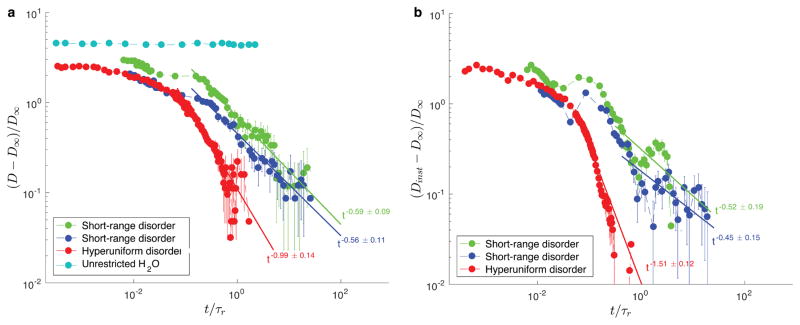
FIG. 2. Dynamical exponent (1) identifies the disorder classes.

a, The tail in the cumulative diffusion coefficient D(t) (see text) distinguishes between SR and HU disorder, via exponent ϑ̃ = min {ϑ, 1} (Table I). Note that ϑ̃ ≡ ϑ ≈ 1/2 for both SR samples (made of barriers with different permeability), while ϑ̃ ≈ 1 for the HU sample, indicating that the “true” ϑ > 1. D(t) = const for unrestricted water is shown for comparison. b, To access ϑ for HU disorder, we obtain the tail in D_inst(t), equation (2). While results are noisier due to numerical differentiation, the exponent values ϑ ≈ 1/2 for SR and ϑ ≈ 3/2 for HU, cf. Table I, are consistent with equation (1).

Formally, the structural universality class is defined [10] by the k → 0 scaling of the power spectrum

$$\mathrm{\Gamma }(k)\equiv {\int }_V\text{dr}{e}^{-i\mathbf{kr}}{\langle n({\mathbf{r}}_0+\mathbf{r})n({\mathbf{r}}_0)\rangle }_{{\mathbf{r}}_0}=\frac{{\mid n(\mathbf{k})\mid }^2}{V}~k^p$$ (3)

of the restrictions which embody the sample’s microscopic structure. The exponent p, taking a handful of discrete values such as in Fig. 1d, describes how fast the spatial correlations Γ(r) in the density of the restrictions n(r) decay at large distances r, and thereby characterizes the system’s heterogeneity. The values p > 0 correspond to hyperuniform media [15, 16] (sample C), where the fluctuations are suppressed relative to the short-range (e.g. Poissonian) disorder (p = 0, samples A and B); p < 0 correspond to strong disorder, where the fluctuations are enhanced [9, 10]. Qualitatively, the variance in the number of restrictions within a volume V grows ∝ V for short-range disorder (according to the central limit theorem), slower than V for hyperuniform disorder (such as in maximally random jammed packings [17]), and faster than V for strong disorder. The relation (1) relies on self-averaging [18], p +d > 0, ensuring the existence [10] of finite D_∞.

Two samples exhibiting short-range (SR) disorder were constructed by stacking flat, porous, permeable barriers in a layered geometry (as shown in Supplementary Fig. S1c [19]), and random positions, inside a glass tube filled with H₂O. One SR sample was constructed using the barriers with 15 nm pore diameter (A in Fig. 1c) and one SR sample using the barriers with 45 nm pore diameter (B in Fig. 1c). Fig. 1b reveals a pore density of 8 pores/μm² by AFM. These two different samples correspond to two different realizations of short-range disorder and the one-dimensional lines shown in Fig. 1c correspond to digitized cut-outs of the actual samples representing the barrier spacings of a part of the sample.

A representative optical microscopy image of SR sample A is shown in Fig. 1a and yields an average spacing ā ≈ 12.5 μm between the centers of the barriers. The short-range character of the arrangement is proven by the finite value of the plateau Γ(k)|_k→0 of the power spectrum, Fig. 1d, and is also consistent with the probability density function (PDF) of the successive barrier spacings (Supplementary Fig. S7 [19]) lacking a “fat tail”. The non-Possonian nature of barrier arrangement in both SR samples is shown by the value Γ(k)|_k→0 · ā which is different from unity (in contrast to the Poissonian, i.e. fully uncorrelated placement), and is consistent with non-exponential PDF of the barrier spacings.

On the other hand, the hyperuniform (HU) disordered sample C, shown in Fig. 1c (and Supplementary Fig. S1-a-b-d [19]), was achieved by placing identical rectangular copper plates, ~ (45 ± 4) μm thick, between the permeable barriers with pore diameter of 45 nm and is characterized by reduced long-range structural fluctuations. Ideally, the barriers would create a periodic lattice (with ā ≈ 51.0 μm) which would result in Bragg peaks in Γ(k) and Γ(k < π/ā) ≡ 0. However, experimental inaccuracies in the placement of the barriers and copper plates act as random displacements from ideal lattice positions, resulting in apparent hyperuniformity [15] of a “shuffled lattice” [20], for which the power spectrum Γ(k) ~ k² for kā ≪ 1. The spectrum in Fig. 1d is indeed consistent with the exponent value p = 2.

We underscore that it is practically impossible to discern the qualitative differences between the samples A, B and C — or to reveal the disorder universality class by the naked eye. Based on local sample cut-outs, shown in Fig. 1c, the three samples look very similar, when the dimensions are rescaled such that mean spacing between the barrier centers is the same for all of them. However the power spectrum Γ(k), shown in Fig. 1d, readily shows similarity between samples A and B, and their qualitative difference from sample C, as its low k scaling captures the universal features in the large-scale behavior of the density fluctuations. For the computation of Γ(k), the reader is referred to Supplementary section II as well as Fig. S8. [19] In what follows, we show how a bulk diffusion measurement distinguishes between the SR and HU classes, thereby yielding the form of Γ(k) for kā ≪ 1 (i.e. for distances exceeding ā), and experimentally validating the relation (1) in dimension d = 1.

The conventional cumulative D(t) ≡ 〈(x_t − x₀)²〉/2t of H₂O was measured using pulse-gradient diffusion NMR [3] over a broad range of diffusion times t, from 1.0 ms to 4.5 s, spanning over 3 orders of magnitude, and translating to mean square displacements 〈(x_t − x₀)²〉^1/2 ranging from 2 μm to 144 μm. Measuring such short mean square displacements requires fast switching and strong in magnitude gradient pulses. Therefore, a homemade gradient coil was constructed [21, 22] capable of delivering gradient pulses of approximately 90 G/cmA. However, such strong gradient pulses may introduce errors in the experimental data, such as those due to eddy currents. To mitigate such effects, two pulse sequences were used for the diffusion measurements (cf. Supplementary Materials [19]) which made use of bipolar gradient pulses for short times, and asymmetric pules for long times.

Figure 2a shows the time dependence of the cumulative diffusion coefficient D(t), of H₂O diffusing through the three samples, as well as for unrestricted H₂O (cyan). Note that the diffusion coefficient for unrestricted H₂O (cyan) was rescaled using D_∞ from sample A. While there is no time dependence in D(t) for unrestricted H₂O, a power-law exponent ϑ̃ = 0.59±0.09 in D(t) − D_∞ ~ t^−ϑ̃ was observed for H₂O diffusing through sample A and ϑ̃ = 0.56 ± 0.11 for sample B. Note that the exponent ϑ̃ is the same with ϑ of eq. (2) if ϑ < 1. The exponents are in remarkable agreement with equation (1) for p = 0 and d = 1, and with earlier prediction [23] for the tail in D(t). On the other hand D(t) − D_∞ for H₂O diffusing through the HU sample exhibits the 1/t tail with ϑ̃ = 0.99 ± 0.14. The range in which the least squares fit was performed was chosen such that the χ²/dof was minimized. The structural and dynamical exponents, as well as main characteristic of the samples such as residence and diffusion times τ_r and τ_D, are given in Table I.

TABLE I. Sample parameters and exponents for disorder classes.

Theoretical (eq. 1) and experimental (Fig. 2) power-law exponents ϑ̃ and ϑ in the tails of D(t) and D_inst(t). The (non-universal) macroscopic diffusion coefficient, D_∞, mean barrier spacing ā as computed from optical microscopy, pore diameter of the barriers, residence time τ_r ≡ ā/2κ, and time to diffuse in-between barriers, τ_D ≡ ā²/2D₀ are also shown.

Sample	Disorder class	p	ϑ̃th	ϑ̃	ϑth	ϑ	τr, ms	τD, ms	D∞, $\frac{\mu {\mathrm{m}}^2}{ms}$	ā, μm	Pore diam., nm
A (green)	SR	0	1/2	0.59 ± 0.09	1/	0.52 ± 0.19	157.2	34.2	0.42 ± 0.04	12.5	15
B (blue)	SR	0	1/2	0.56 ± 0.11	1/2	0.45 ± 0.15	117.2	43.0	0.58 ± 0.05	14.1	45
C (red)	HU	2	1	0.99 ± 0.14	3/2	1.51 ± 0.12	2949.0	754.9	0.63 ± 0.04	58.9	45

The 1/t tail in D(t) in the HU sample indicates that ϑ > 1. Indeed, the cumulative $D(t)\equiv \frac{1}{t}{\int }_0^t\mathrm{d}\tau D_{\text{inst}}(\tau )$ may be used to determine ϑ only in the case when the power-law tail in D_inst(t) is sufficiently slow [10], ϑ < 1. In this case, the instantaneous mean squared displacement rate (2) has similar behavior to the average rate 〈(x_t − x₀)²〉/2t over the whole interval t; formally, the above integral converges at the upper limit. However, when the underlying ϑ > 1, the tail $D(t)-D_{\infty }=\frac{1}{t}{\int }_0^t\mathrm{d}\tau [D_{\text{inst}}(\tau )-D_{\infty }]\simeq \frac{1}{t}{\int }_0^{\infty }\mathrm{d}\tau [D_{\text{inst}}(\tau )-D_{\infty }]$ is determined by the short τ, such that the 1/t factor overshadows the effect of ϑ. In other words, D(t) − D_∞ ~ t^−ϑ̃, where ϑ̃ = min{ϑ, 1}. Hence, if the tail in D(t) has ϑ̃ = 1, which is the case for the HU sample, one has to obtain D_inst(t) via numerical differentiation to uncover the true ϑ > 1, with the expense of amplifying the experimental noise.

Figure 2b shows the computed instantaneous D_inst(t) = ∂_t[tD(t)], using numerical differentiation with Savitzky-Golay (SG) regularization [24] (cf. Supplementary Materials [19]), along with the weighted least squares fit (solid line). The time window in which the fit was performed was chosen such that the χ²/dof was minimum. As expected, for both SR samples, D_inst(t) reaches its universal limit D_∞ according to equation (2) with ϑ = 0.52 ± 0.19 for sample A and ϑ = 0.45±0.15 for sample B (cf. Table I), consistent with the above results for ϑ̃ and equation (1) with p = 0 and d = 1. For the HU sample, the dynamical exponent ϑ = 1.51 ± 0.12, is notably different from that for SR samples, and in agreement with equation (1) for p = 2 and d = 1. The least squares fit was stable with respect to the SG filtering window and polynomial order producing reasonable values of χ²/dof (cf. Supplementary Materials for details, Fig. S4–S5 [19]). Note that the fit is mainly weighted by the first points which have good signal-to-noise ratio. An important observation of Figure 2b is that the molecules in the HU sample gets homogenized by the diffusion process qualitatively faster than in the SR samples A–B, so that the power law tail becomes pronounced already when t ~ τ_r. This is a general consequence of a more efficient coarse-graining in a qualitatively more ordered (hyperuniform) sample. As noted in ref. [10], in the “extreme” case of a fully periodic sample, diffusion exhibits coherence due to infinitely long spatial correlations, which makes the sample effectively homogenized already when t ~ τ_D.

Previous applications of bulk diffusion for characterizing microstructure below imaging resolution focussed on the short-time [25] initial decrease $D(t)\simeq D_0(1-\frac{4\sqrt{D_0}}{3d\sqrt{\pi }}\frac{S}{V}·t^{1/2})$ of the cumulative diffusion coefficient, as a result of the increasing fraction $~\sqrt{D_{0}t}S/V$ of random walkers restricted by walls. In this limit, it is the net amount of the restrictions that is relevant, irrespective of their positions in space—akin to the net drum surface area derived from the density of high frequency eigenmodes [1]. This technique has been used for quantifying the surface-to-volume ratio (S/V) of porous media [4] and biological samples such as red blood cell suspensions [26] and brain tumor cells in mice [27].

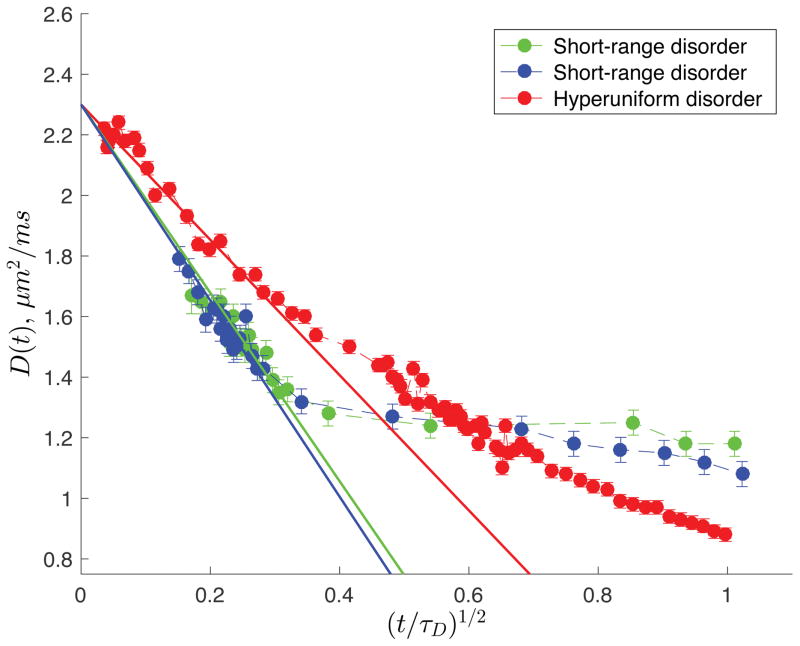
Experimentally, the short-time limit is highly demanding on the pulsed field gradients. However, for our samples, displacements as short as L(t) ≈ 2 μm are accessible with our homemade gradient coil. Fig. 3 highlights the initial t^1/2 decrease of D(t) for t/τ_D ≪ 1, when the short time limit is valid (cf. Table I for the values of τ_D). For sample A, the average spacing of the barriers was determined from S/V ≡ 2/ā, and found to be ā = 11.4 μm, deviating by ~ 9% from the value expected from the images acquired via optical microscopy. Simirarly, for sample B, ā = 12.0 μm deviating by ~ 15% from the value expected from the images acquired via optical microscopy and reported in Table I. For HU sample, ā = 61.5 μm deviated by approximately ~ 4%from the predicted value (Table I). In the least squares fits shown in Fig. 3, the free diffusion coefficient D₀ was fixed to the exact value at the corresponding temperature. Note that the maximum (t/τ_D)^1/2 used for the least squares fit (solid lines of Fig. 3) was 0.31 for sample A, 0.27 for sample B and 0.24 for sample C (see Supplementary Materials Fig. S6 for statistical analysis of the fit [19]). As mentioned earlier, the initial t^1/2 decrease, sensitive only to the net amount of restrictions, cannot reveal structural correlations. Therefore, the qualitative differences between the two disorder classes are not apparent in Fig. 3 — only the quantitative differences in S/V = 2/ā are seen in the slopes of the curves at small t.

FIG. 3. Short timet^1/2 decrease [25] of D(t).

Quantifying the net amount of restrictions, S/V = 2/ā; the difference in the large scale fluctuations is not revealed. The cumulative diffusion coefficient D(t) exhibits the t^1/2 decrease for t/τ_D ≪ 1.

To summarize, our experiments for the first time reveal the qualitative difference in the diffusive dynamics between samples with qualitatively different spatial statistics of structural fluctuations, justifying the application of the concept of universality to classical transport in disordered media, and validating the fundamental relation (1) between structural and dynamical exponents. The coefficients c and D_∞ of equation (2) for the two SR samples are non-universal, and reflect the density of the barriers and their permeability (cf. Supplementary Materials [19]). However, the dynamical exponent ϑ remains the same, because the statistics of large-scale fluctuations for both samples A and B are governed by the central limit theorem (finite correlation length, a plateau in Γ(k)|_k→0). On the other hand, based on the dynamical exponent ϑ, qualitative differences were revealed between the samples exhibiting short-range (A, B), and hyperuniform disorder (C) (where fluctuations are reduced [15, 16] relative to those governed by central limit theorem since Γ(k)|_k→0 → 0), verifying that diffusion can identify the structural universality class of the medium.

After the seminal 1991 observation of diffusion diffraction [28] yielding the structure factor of water-filled identical confining pores, the late Paul T. Callaghan insightfully referred to diffusion as microscopy [3]. This q-space technique has enabled determination of the shape of regular confining structures with impermeable walls, such as pores of any shape [29]. The present investigation suggests that the time-dependent diffusion coefficient (2) reveals the parameter that microscopy does not provide — the elusive to the naked eye statistics of structural correlations, which are able to distinguish and characterize randomly looking, or disordered, and permeable samples such as those in Fig. 1c, using a low-resolution bulk transport measurement. As most building blocks of living tissues, such as cells and organelles, are not fully confining (cells have permeable walls; water can move along the dendrites and axons), we believe this fundamental result can serve as a basis for quantitative investigations of μm-level structural correlations in complex materials [6] and in live biological tissues [9–12] with diffusion NMR and MRI.