Quantitative Susceptibility Mapping: Report from the 2016 Reconstruction Challenge

Abstract

Purpose

The aim of the 2016 quantitative susceptibility mapping (QSM) reconstruction challenge was to test the ability of various QSM algorithms to recover the underlying susceptibility from phase data faithfully.

Methods

Gradient-echo images of a healthy volunteer acquired at 3 Tesla in a single orientation with 1.06 mm isotropic resolution. A reference susceptibility map was provided, which was computed using the susceptibility tensor imaging algorithm on data acquired at 12 head orientations.

Susceptibility maps calculated from the single orientation data were compared against the reference susceptibility map. Deviations were quantified using the following metrics: root mean squared error (RMSE), structure similarity index (SSIM), high-frequency error norm (HFEN), and the error in selected white and grey matter regions.

Results

Twenty-seven submissions were evaluated. Most of the best scoring approaches estimated the spatial frequency content in the ill-conditioned domain of the dipole kernel using compressed sensing strategies. The top ten maps in each category had similar error metrics but substantially different visual appearance.

Conclusion

Because QSM algorithms were optimized to minimize error metrics, the resulting susceptibility maps suffered from over-smoothing and conspicuity loss in fine features such as vessels. As such, the challenge highlighted the need for better numerical image quality criteria.

INTRODUCTION

Quantitative susceptibility mapping (QSM) aims to determine a basic physical property (i.e. tissue magnetic susceptibility) in vivo that is highly sensitive to tissue molecular composition and disease-induced tissue damage (1–5). QSM solves an inverse field-to-source problem, calculating the underlying magnetic susceptibility distribution from gradient-echo (GRE) phase images. Early concepts for QSM have been introduced two decades ago (6–12) and more refined methods have been introduced recently to allow the calculation of susceptibility with reduced reconstruction artefacts from a single orientation in the clinical setting (13,14). The clinical value of QSM is currently being explored and holds great promise for vascular, inflammatory and neurodegenerative diseases of the brain (15–19). As such, the QSM field is rapidly developing, QSM is increasingly being used in clinical studies of neurological disorders, and applications outside the brain are being explored (20–24). The quantitative nature of the technique promises to provide biomarkers that allow the clinical monitoring of disease progression and treatment effects. However, especially considering the quantitative nature of QSM, clinical translation will require a thorough understanding of the reproducibility and accuracy of susceptibility measurements with QSM. Also, for a comparative assessment of QSM-based literature reports, it is important to understand how comparable susceptibility values are if they were reconstructed with different QSM algorithms.

A variety of algorithms has been developed for the numerical solution of the field-to-source inverse problem at the heart of QSM. However, although QSM is supposed to yield a physical tissue property, susceptibility maps calculated with different algorithms from the same dataset can show substantial differences, as illustrated in a recent review by Wang and Liu (1). To systematically compare and quantitatively assess the many available algorithms, we implemented the first QSM reconstruction challenge in the context of the 4^th International Workshop on MRI Phase Contrast and Quantitative Susceptibility Mapping, held from September 26^th to 28^th, 2016 at the Medical University of Graz, Austria (www.qsm2016.com). The primary goal of the challenge was to test the ability of various QSM algorithms to recover the underlying susceptibility distribution from a healthy volunteer’s phase data faithfully. The secondary goal was to provide a common reference dataset that would help benchmark not only existing QSM algorithms but also methods that would be developed in the future.

The challenge was announced at the Electro-Magnetic Tissue Properties (EMTP) (formerly SWI) study group meeting at the 2016 annual meeting of the International Society for Magnetic Resonance in Medicine (ISMRM) in Singapore on May 12^th, 2016. Data and instructions could be downloaded from the workshop website (qsm.neuroimaging.at) starting from May 12^th, 2016, and the deadline for a submission of reconstructed susceptibility maps was September 15^th, 2016. The results of the evaluation of submitted maps were presented and discussed at the QSM workshop in Graz on September 27^th, 2016. Additionally, the present report includes the input from the discussions in Graz and at the ISMRM EMTP study group meeting in Honolulu on April 26^th, 2017.

METHODS

General considerations on input and reference data

In the literature, evaluation of susceptibility mapping algorithms is frequently performed using numerical phantoms (25,26) or acquired phantom data (27–29). Most physical phantoms used have consisted of compartments filled with solutions or gels of different magnetic susceptibilities, i.e. regions of piece-wise constant magnetic susceptibility. Such geometries allow a near-perfect recovery of the underlying susceptibility distribution using regularization of the inverse problem with total (generalized) variation (TV/TGV) or morphological priors because the piece-wise constant constraints and priors exactly match the actual susceptibility distribution. Using a physical phantom would, therefore, put these types of algorithms at a competitive advantage compared to other algorithm types. Moreover, a piece-wise constant susceptibility distribution is not a realistic model of magnetic susceptibility in the brain.

A limitation of numerical models is that contributions from sources other than isotropic bulk magnetic susceptibility such as chemical exchange effects (30), anisotropic susceptibility (31,32) and microstructure (33–36) are difficult to model because the magnitude of these effects in vivo is not yet completely understood. Furthermore, physiological noise, flow, and partial volume effects are difficult to model realistically.

To address the shortcomings of physical phantoms and numerical models, in this challenge we decided to use a human susceptibility map measured in vivo as a reference. Attempting to take magnetic susceptibility anisotropy into account, we employed the susceptibility tensor imaging (STI) approach (37) to determine the reference map. STI reconstructs the susceptibility tensor distribution without any regularization or morphological priors. From the susceptibility tensor, it is possible to estimate the expected susceptibility distribution that would be measured with a single-angle susceptibility mapping technique. This effective susceptibility distribution was used as the reference susceptibility map in the challenge as described below.

We decided to provide the reference susceptibility map to the contestants to reduce the potentially negative impact of sub-optimal algorithm-specific parameter choices on the challenge outcome. The availability of the reference allowed the contestants to optimize algorithmic parameters properly and then submit the best scoring result they could achieve with their algorithm.

Selection of the reference

The candidates for gold standard susceptibility were either a COSMOS (27) susceptibility map, or χ₃₃ from the STI solution (37). The benefits of these two maps as reference susceptibility distributions include i) they are calculated without numerical regularization and, therefore, no spatial smoothing or incorporated prior information, and ii) high signal-to-noise ratio (SNR) since both maps are computed from joint processing of images acquired at 12 orientations of the head with respect to B₀.

COSMOS models susceptibility as a scalar, isotropic property, ignoring its orientation dependence. A COSMOS susceptibility map reflects the effective magnetic susceptibility averaged over all 12 orientations of the head. Therefore, we concluded that COSMOS susceptibility maps would not provide an accurate reference for single-angle susceptibility mapping with the head in the normal position, particularly in regions with anisotropic magnetic susceptibility, such as white matter. To mitigate this orientation bias, we chose χ₃₃ of the STI solution as the reference. Based on STI theory (37), the Fourier domain phase Θ(k), when the main field lies along H in the subject frame, is given by

$$\mathbf{\Theta }(\mathit{k})=\frac{1}{3}{\mathit{H}}^{\mathit{T}}·\mathit{X}·\mathit{H}-\mathit{H}·\mathit{k}\frac{{\mathit{k}}^{\mathit{T}}·\mathit{X}·\mathit{H}}{{\mathit{k}}^2}$$ [1]

where k is a vector of all Fourier domain coordinates and X is the susceptibility tensor in the subject frame and ()^T denotes matrix transposition. When the acquisition is performed in the transverse plane relative to the subject coordinates, i.e. H = [0,0,1]^T, the signal equation becomes

$$\mathbf{\Theta }(\mathit{k})=(\frac{1}{3}-\frac{k_z^2}{k^2}){\chi }_{33}-\frac{k_z}{k^2}(k_x{\chi }_{13}+k_y{\chi }_{23})$$ [2]

The relationship commonly used in single-orientation QSM assumes that the terms with the off-diagonal tensor elements, χ₁₃ and χ₂₃, are negligible:

$$\mathbf{\Theta }(\mathit{k})=(\frac{1}{3}-\frac{k_z^2}{k^2}){\chi }_{33},=\mathbf{D}{\chi }_{33},$$ [3]

where D is the dipole kernel in the Fourier domain. Equation [3] motivates the use of χ₃₃ as the reference susceptibility that gives rise to the observed phase signal.

Data and source code

MRI data were acquired in a healthy female volunteer (age 30) at a 3T system (Tim Trio, Siemens Healthcare GmbH, Erlangen, Germany) with Institutional Review Board approval from Massachusetts General Hospital.

The imaging data provided to the contestants as inputs for the susceptibility mapping included the following datasets:

• 3D gradient-echo magnitude and wrapped phase images acquired with axial slab orientation (and the head in the normal supine position).

• A magnetization-prepared rapid gradient-echo (MPRAGE) image (38) matching the GRE volume as it is routinely acquired in clinical brain imaging studies and certain QSM algorithms use this image as a prior information input.

• A background-field corrected tissue phase image. We used the Laplacian Boundary Value (LBV) method (39) after transmit phase removal by fitting and subtracting a 4^th-order 3D–polynomial. LBV was used because it outperformed all other proposed background-field correction methods in a recent comparison study (40). This image was provided in an attempt to eliminate a potential variability in submitted susceptibility maps due to differences in background field removal techniques. However, as single-step QSM methods are designed to solve background-field removal and inversion problems simultaneously, those algorithms could use the unprocessed wrapped phase GRE images.

• A brain mask obtained from Brain Extraction Tool (41) was also provided to reduce confounding effects resulting from the use of different masks.

• The reference susceptibility map χ₃₃ which was calculated using STI (37). The GRE phase images from each head orientation were affine-registered to the axial slab orientation (reference position), masked and the background fields removed as described for the single orientation case above. This local field information was then fed into an iterative LSQR solver (42) to estimate all components of the symmetric susceptibility tensor and provide the tensor element χ₃₃ as reference susceptibility map.

3D GRE with Wave-CAIPI acquisition (43) was used to acquire images of the head with 1.06 mm isotropic resolution in 12 different orientations with respect to B₀ (the head orientation table can be found in the downloadable dataset). Further sequence parameters were TE / TR = 25 / 35 ms, BW = 100 Hz/pixel and a 94-s acquisition time for each head orientation with 15-fold acceleration using a Siemens 32 channel head coil. Roemer/SENSE coil combination was employed (44,45), which used sensitivities estimated from reference acquisitions made with both, head and body coil reception. Wave-CAIPI is an accelerated acquisition/reconstruction technique that substantially reduces the scan time, which is especially useful for multi-orientation scans. Despite 15-fold acceleration, the average g-factor penalty due to parallel imaging reconstruction was only 9%. Thus, aliasing artifacts or noise amplification are not expected to impact the resulting susceptibilities (43).

MPRAGE acquisition employed the same resolution and matrix size as 3D-GRE, and sampled 4 echoes using TE1 = 2.05 ms, echo spacing = 1.84 ms, TR = 2510 ms, inversion time (TI) = 1200 ms, BW = 651 Hz/pixel and flip angle = 7°. The acquisition took 5 min 39 s using 2-fold GRAPPA acceleration (46). The magnitude images at all 4 echo times were combined by computing the root-sum-of-squares (47), and the combined magnitude image was provided to the participants.

In addition to the imaging data, MATLAB (The MathWorks, Natick, MA) source code was provided for the numerical evaluation of the data set according to the error metrics described in detail below. This code allowed the contestants to focus on optimizing their algorithmic parameters without spending time writing scripts for the calculation of error metrics. The source code also included the widely utilized fast QSM reconstructions, thresholded k-space division (TKD) (28) and a closed-form L2-regularized algorithm (48) to provide contestants with a direct performance comparison to these algorithms.

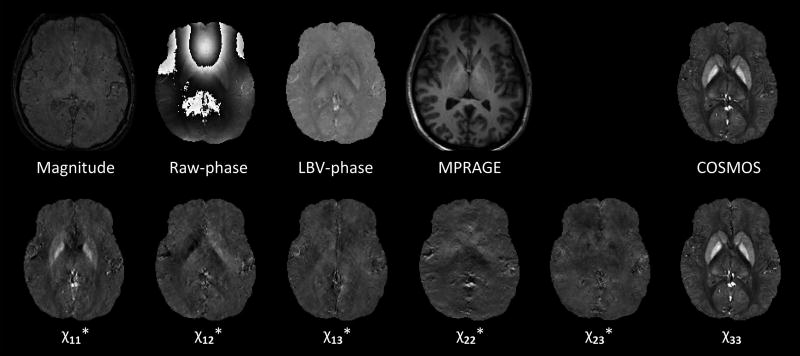
The images and the Matlab code for the QSM reconstruction challenge will remain available at http://qsm.neuroimaging.at. In addition to the data provided at the time of the challenge and described above, the archive currently also contains the GRE data magnitude and phase data acquired in all 12 orientations. The images provided are shown in Figure 1.

Figure 1.

Image data provided to the contestants. The susceptibility maps are scaled from −0.1 to 0.25 ppm, the raw phase is scaled between ±π radians and the LBV-phase image is scaled from −0.05 to 0.05 radians. With the exception of χ₃₃, the reconstructed susceptibility tensor component images were not provided for the reconstruction challenge, but are now included in the downloadable data set (marked here with asterisks).

Numerical measures of QSM reconstruction quality

We employed quantitative error metrics to evaluate the difference between the reference susceptibility map and the submitted susceptibility maps. As well as the root mean squared error (RMSE), which is commonly used in the literature, we employed three additional error measures, which are often utilized in the fields of computer vision and image reconstruction:

• The high-frequency error norm (HFEN) (49), which aims to measure the fidelity at high spatial frequencies. HFEN applies a Laplacian of a Gaussian (LoG) filter on the reference and input volumes and reports the L2 norm of their difference, normalized by the norm of the LoG-filtered reference.

• The structural similarity index (SSIM) (50), which is a combined measure obtained from three complementary components (luminance similarity, contrast similarity, and structural similarity). SSIM aims to provide a metric that better reflects the “visual” similarity to the reference.

• The absolute value of the mean error in selected anatomical structures (ROI error). To this end, we manually defined ROIs in white matter (genu and splenium of corpus callosum, frontal white matter, occipital white matter, capsula interna) and grey matter nuclei (globus pallidus, putamen, caudate nucleus, red nucleus, substantia nigra, and dentate nucleus) on the reference susceptibility map, χ₃₃.

These error metrics were calculated for each submitted map. For RMSE, HFEN and ROI error, smaller values denote better performance, whereas SSIM is normalized between 0 and 1, with 1 being the best possible result. The implementation of these error metrics was provided to the contestants as Matlab source code together with the downloadable image data set.

Our current challenge format did not include a comparison of the reconstruction speed of the different algorithms as the QSM images were processed on the individual computers of the respective research groups, using different development environments (e.g. Matlab, Python, C++, CUDA).

All susceptibility values are reported as ppm in the following.

RESULTS

Brief description of the algorithms used by the contestants

Overall, 27 susceptibility maps from 13 groups were evaluated. The algorithms either used the provided pre-processed (background removed) phase or the raw, wrapped phase. Several algorithms used the GRE magnitude for stabilization of the dipole inversion, and one approach (PHILIPS DTV) also utilized the MPRAGE images.

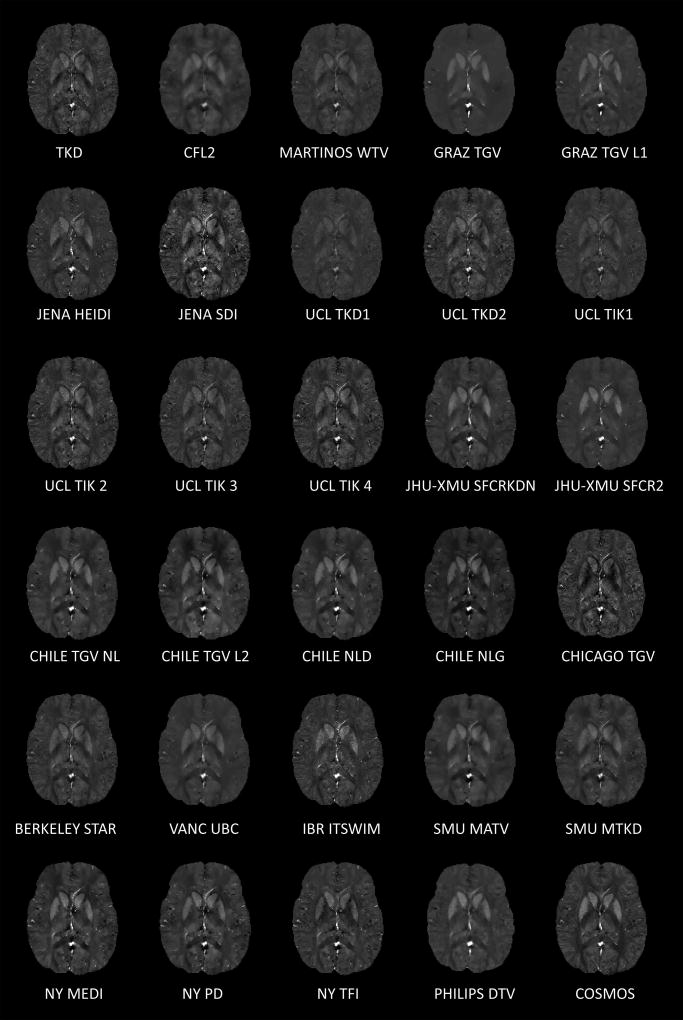
The algorithms are briefly described in table 1 and images of a single central transverse slice of all algorithms are shown in figure 2.

Table 1.

Brief description of all QSM algorithms participating in the reconstruction challenge

Name	Description	Input Phase RAW/LBV*
TKD (provided)	Truncated K-space Division (28) with zeroes at the ill-conditioned regions (cone) in k-space, threshold = 0.19.	LBV
CFL2 (provided)	Closed-form L2-regularized inversion (48).	LBV
MARTINOS WTV	Compressed Sensing compensated QSM (54), accelerated reconstruction using ADMM optimization.	LBV
GRAZ TGV	Total generalized variation (TGV) based method incorporating phase unwrapping, background field removal and dipole inversion in a single iteration (66).	RAW
GRAZ TGV L1	Total generalized variation (TGV) based method (66) with additional L1 magnitude stabilization.	RAW
JENA HEIDI	Hybrid algorithm that solves three sub-domains of k-space using different approaches, depending on the conditioning. The well-conditioned k-space was solved using unregularized LSQR, the critical part of the k-space was recovered by solving a weighted Total Variation Problem with priors derived from phase images, the transition area was derived from the LSQR solution using denoising (53). Parameters defining the three sub-domains were chosen to obtain optimal error measures relative to the gold standard.	LBV
JENA SDI	TKD algorithm with extreme thresholding of the dipole kernel and underestimation compensation based on the deconvolution point-spread function (67).	LBV
UCL TKD 1	TKD as in (14,67) i.e. without zeroes inside the k-space cone. A threshold of $\delta =\frac{2}{3}$ was used with no correction for χ underestimation.	LBV
UCL TIK	Closed-form Tikhonov inversion as alluded to in (68) and mentioned in (1) as a Tikhonov-regularized minimal norm solution. 1 had α = 0.0588 and no correction for χ underestimation. 2 had α = 0.0588 and correction for χ underestimation with a factor of 1.65. 4 had α =0.025 and correction for χ underestimation with a factor of 1.30.	LBV
JHU-XMU SFCRKDN	Based on the SFCR QSM paper in (58), simplified the L2 regularization terms in M-step and S-step, added de-noising operation, k-space based L1 solver and HEIDI like k-space combination.	LBV
JHU-XMU SFCR2	Based on the SFCR QSM paper in (58), L1 and L2 regularized two-step reconstruction with regularization a priori extracted from magnitude and interim susceptibility maps – see winning approach in categories HFEN and SSIM.	LBV
CHILE TGV L2	Magnitude weighted TGV. Uses an L2 data fidelity term, spatially weighted by the square of the magnitude. First order approximation of the non-linear term (69).	LBV
CHILE TGV NL	Non-linear TGV result. It uses a non-linear data fidelity term, similar to Liu's nonlinear MEDI but with a fast solver with alternating direction method of multipliers (ADMM) and a mixture of a global and local solvers to deal with the nonlinear equation.	LBV
CHILE NLD	Discretization of the dipole kernel based on (70). It uses finite differences and the DFT to achieve an analytical solution in the Fourier domain.	LBV
CHILE NLG	Dipole kernel defined in space by the Green’s function, integrating it for each voxel (71).	LBV
CHICAGO TGV	Algorithm based on the TGV QSM method (66), implemented on GPU-hardware (CUDA 7.5, NVIDIA GeForce GTX 980TI).	RAW
BERKELEY STAR	Streaking artifacts Reduction (STAR) via isolating and calculating strong susceptibility sources automatically, then large and small susceptibility values were reconstructed using a two-level TV regularization approach (72).	LBV
VANC UBC	LSMR solver (55) followed by weighted compressed sensing minimization – see winning approach in category RMSE.	LBV
IBR ITSWIM	Variable regularization threshold for inverse process / k-space improvement with a binary mask including the deep grey matter nuclei and veins used in the iterative algorithm (73).	LBV
SMU MATV	Morphology-Adaptive Total Variation (MATV) separates target susceptibility into smooth and non-smooth regions, where the latter are assigned smaller TV weights than smooth regions during dipole inversion (59) – see winning approach in the ROI accuracy category.	LBV
SMU MTKD	Truncated k-space division (TKD) with morphological priors (MTKD). The target susceptibility map is separated into smooth and non-smooth regions by exploiting morphological information. The gradient of the target susceptibility map is forced to be zero in the smooth regions, and to be the gradient of TKD-reconstructed susceptibility map in the non-smooth regions (74).	LBV
NY MEDI	Morphology Enabled Dipole Inversion (MEDI) method using a Bayesian regularization approach that adds spatial priors from the magnitude image (13,25).	LBV
NY PD	Solving the objective of MEDI using the Primal-Dual (PD) formulation of the total variation and a forward difference method for discretization (61).	LBV
NY TFI	The Total Field Inversion (TFI) method simultaneously estimates the background and local fields, preventing error propagation from background field removal to QSM (75).	RAW
PHILIPS DTV	Single-step QSM starting from wrapped raw phase using Directional Total-Variation with MPRAGE as a prior for estimating edges (76).	RAW

^*RAW = raw phase (for single step algorithms), LBV = LBV preprocessed phase.

Figure 2.

A single transverse slice from all QSM reconstructions submitted for the challenge. QSM images are scaled from −0.1 to 0.25 ppm.

Numerical results – “Winners”

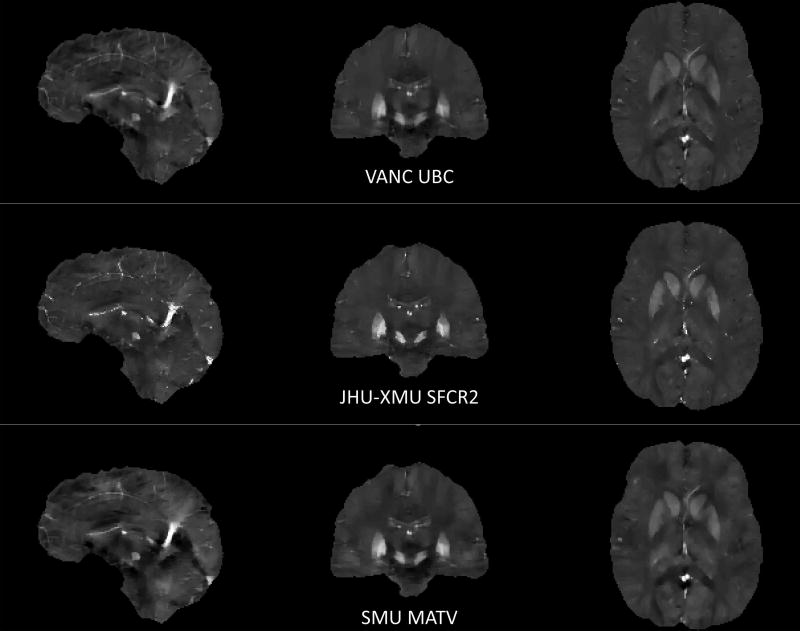
Table 2 shows the results of the top ranked algorithms in each evaluation category. When all submissions were evaluated, RMSE ranged from 69.0 to 140.9 (median = 83.9), HFEN from 63.5 to 127.3 (median = 75.9), SSIM from 0.94 to 0.63 (median = 0.82) and ROI ERROR from 0.016 to 0.039 ppm (median = 0.020).The winning QSM reconstructions are also depicted in detail in figure 3.

Table 2.

Top 10 algorithms with the best scores in each category evaluated for the QSM reconstruction challenge.

RMSE (%)		HFEN (%)		SSIM		ROI ERROR (ppm)
69.0	VANC UBC	63.5	JHU-XMU SFCR2	0.94	JHU-XMU SFCR2	0.016	SMU MATV
70.3	JHU-XMU SFCR2	68.8	GRAZ TGV L1		JHU-XMU SFCRKDN		NY PD
73.6	MARTINOS WTV	68.9	VANC UBC	0.93	NY MEDI	0.017	CHILE TGV NL
74.2	PHILIPS DTV	70.9	PHILIPS DTV		GRAZ TGV		CHILE NLD
74.6	GRAZ TGV L1	71.8	SMU MATV	0.87	GRAZ TGV L1		SMU MTKD
75.2	UCL TIK 1	73.1	UCL TIK 1	0.84	CHILE TGV L2	0.018	CFL2
76.6	UCL TKD 1	73.6	MARTINOS WTV		NY TFI		UCL TIK 2
77.5	GRAZ TGV	74.1	IBR ITSWIM	0.83	JENA HEIDI		UCL TIK 4
	BERKELEY STAR	74.2	JHU-XMU SFCRKDN		CHILE NLD		JHU-XMU SFCRKDN
79.1	SMU MATV		GRAZ TGV		CHILE TGV NL		CHILE TGV L2

Figure 3.

Sagittal, coronal and axial slices of QSM reconstructions of the winners in each category: RMSE (UBC), HFEN and SSIM respectively (SFCR2), and ROI error (MATV). QSM images are scaled from −0.1 to 0.25 ppm.

Winning Approach- RMSE

The winner in the RMSE category was the approach developed by Alexander Rauscher’s team at the University of British Columbia, Canada. This algorithm used a weighted variant of a two-step dipole inversion algorithm (51). It adopts an incremental dipole inversion strategy (52–54), dividing the Fourier domain into well-conditioned and ill-conditioned regions. In the first step, the well-conditioned region is reconstructed by solving ϕ = F⁻¹DF χ_well using an LSMR solver (55), where ϕ is the local field is spatial space, F is the forward Fourier transform and F⁻¹ is the inverse Fourier transform. In order to avoid streaking artifacts the implicit regularization properties of Krylov subspace methods (56) are used by terminating the iterative process after only 5 iterations.

To reconstruct the ill-conditioned region, a weighted total variation minimization problem was solved:

$${\chi }^{\ast }={\mathit{\text{argmin}}}_{\chi }{\Vert \chi \Vert }_{\text{WTV}}+\frac{\mu }{2}{\Vert \mathbf{M}\chi -{\chi }_{\mathit{\text{well}}}\Vert }_2^2$$ [4]

where M = F⁻¹ (|D| > δ)F is a sampling matrix taking the value 1 in the well-conditioned region and 0 in the ill-conditioned region according to a threshold δ applied to |D|, μ is the regularization parameter, ‖χ‖_WTV = Σ W |∇_χ| is the weighted anisotropic total variation, and W = 1/(|∇χ_well| + 10⁻⁶) is a weighting matrix derived from the gradient (∇) of the well-conditioned susceptibility map (χ_well) reconstructed in step 1. The minimization was solved using the alternating direction method of multipliers (ADMM) (57). The parameters used were μ = 6 · 10⁴ and δ = 0.197. The reconstruction time was 5.7 seconds.

Winning Approach- HFEN and SSIM

The SFCR2 algorithm developed by Xu Li’s team at Johns Hopkins University, Maryland, USA, was the winner in both HFEN and SSIM categories. The SFCR2 result was obtained by using a two-step structural feature based collaborative reconstruction (SFCR) algorithm (58). In the first step, an interim susceptibility map χ̂ was reconstructed by using a compressed sensing (CS) model in the Fourier domain with two regularization constraints:

$$\widehat{\chi }=\underset{\chi }{\text{argmin}}{\lambda }_1{\Vert \mathit{\text{diag}}(\mathbf{M}){\chi }_k(\mathbf{k})-\mathit{\text{diag}}(\mathbf{M})\mathbf{F}\chi \Vert }_2^2+{\Vert P_{\mathit{\text{mag}}}\nabla \chi \Vert }_1+{\lambda }_2{\Vert \mathbf{R}\chi \Vert }_2^2$$ [5]

where the structural prior P_mag was derived by thresholding the gradient amplitude of the magnitude image with 30% voxels considered as edges for L1 regularization (in P_mag edges were set to 0 and regions with no edges to 1). The fidelity mask R for the L2 regularization was generated by combining masks obtained via thresholding a preliminary QSM map χ_k(k) calculated with TKD and its gradient (similar to Fig. 4 in (58), with thresholds of 0.04 ppm for QSM and 0.1 for its gradient norm square). M is a binary mask indicating the well-conditioned region in the Fourier domain, i.e. M = |D| > δ where δ is a threshold on the dipole kernel in the Fourier domain. Parameters chosen for this step were δ = 0.19, λ₁ = 50 and λ₂ and processing was terminated after three iterations. The final susceptibility map was then fitted in the spatial domain using weighted minimization:

$$\chi =\underset{\chi }{\text{argmin}}{\gamma }_1{\Vert W(\varphi -{\mathbf{F}}^{-1}\mathbf{\text{DF}}\chi )\Vert }_2^2+{\Vert P_{\widehat{\chi }}\nabla \chi \Vert }_1+{\gamma }_2{\Vert \mathbf{R}\chi \Vert }_2^2$$ [6]

where the structural prior P_χ̂ was extracted from the interim susceptibility map _χ̂ (the solution of Eq. 5) with similar 30% edge voxels, W = 1/|ϕ|^1/3 is a weighting matrix calculated from the local field ϕ and the same fidelity mask R as in the first step was used. Regularization parameters chosen for this step were γ₁ = 50 and γ₂ = 1, and iterative processes were terminated after 2 iterations.

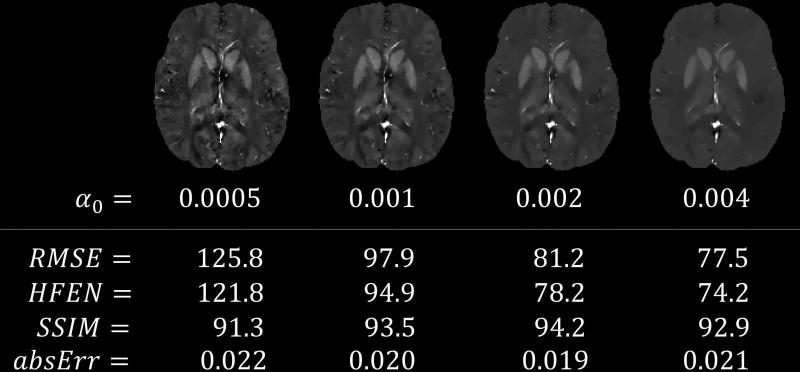
Figure 4.

QSM algorithms were optimized to minimize error metrics in this challenge. This figure shows results of the GRAZ TGV algorithm with varying regularization parameter α₀. While the QSM image with α₀ = 0.004 (right) suffered from over-smoothing and conspicuity loss in fine features such as vessels and the cortex, the RMSE was better than for the normally utilized α₀ = 0.0005 (left). QSM images are scaled from −0.1 to 0.25 ppm.

Winning Approach- ROI accuracy

The winner in this category was the morphology-adaptive total variation (MATV) algorithm developed by Yanqiu Feng’s team from Southern Medical University, Guangzhou, China. This algorithm first classifies the imaging target into smooth and non-smooth regions by thresholding the magnitude gradient map (59). In the dipole inversion, the regularization weights are adapted according to local morphological information: voxels in smooth regions are assigned larger TV regularization weights than in non-smooth regions. The QSM reconstruction via the MATV algorithm can be formulated as follows:

$$\chi =\underset{\chi }{\text{argmin}}{\Vert \mathrm{W}(\varphi -{\mathbf{F}}^{-1}\mathbf{\text{DF}}\chi )\Vert }_2^2+\alpha {\Vert P_{\mathit{\text{mag}}}\nabla \chi \Vert }_1+\beta {\Vert (1-P_{\mathit{\text{mag}}})\nabla \chi \Vert }_1$$ [7]

where W is a data weighting matrix to compensate the measured field noise (60) and α and β are the regularization parameters. The regularization parameters used were α = 0.003, β = 0.0009.

Given only a marginal difference to the above described approach, we would like to acknowledge also the Primal-Dual and Forward Gradient Implementation (PD) algorithm developed by Yi Wang’s team from Cornell University, New York, USA (61).

DISCUSSION

The QSM 2016 reconstruction challenge established a framework for the numerical comparison of QSM algorithms. We limited the challenge to a single data set that matched conventional clinical acquisitions closely with respect to the resolution, readout bandwidth, echo time and coverage. In the following, we summarize the results, discuss the limitations of the design of the challenge, and highlight the lessons learned.

Summary of results

The SFCR2 algorithm won in two categories, SSIM and HFEN, and finished second in the RMSE ranking. The other winners, regarding RMSE and ROI accuracy, were the algorithms from UBC and SMU. The top three algorithms in the RMSE ranking relied on reconstruction approaches known from compressed sensing (CS) MRI. As opposed to regularized inversion, where the entire Fourier domain is affected by regularization, in CS-approaches only the ill-conditioned Fourier sub-domain of the susceptibility map is estimated by minimizing a sparsity enforcing metric. This limitation to only a sub-space of the Fourier domain was probably the key for allowing these top-ranking approaches to produce the best reconstruction accuracies. However, also these winning maps were not ideal from a visual or radiological point of view, suffering from over-smoothing, and conspicuity loss in fine structures (Figures 2 and 3). CS techniques employed in accelerated MR data acquisition exploit incoherent aliasing artifacts arising from pseudo-random under-sampling of the k-space (62). The dipole artifacts in QSM reconstruction, however, appear more structured due to under-sampling only near the magic angle in the Fourier domain. Although the incoherent aliasing prerequisite for CS was fully not met, we think that these strategies performed well due to two main reasons:

1. Since the missing content in the ill-conditioned region is a relatively small portion (e.g. 20–30%) of the Fourier domain, its estimation is easier, and potential blurring artifacts mainly impact this conical region, while the majority of the Fourier spectrum of the susceptibility cannot be altered to minimize the employed sparsity or smoothness metric (54).

2. CS methods involving wavelet penalties do enjoy partial incoherence since the undersampling artifacts are distributed across the wavelet scales. The incoherence in both Total Variation and wavelet domains can be further improved by randomly under-sampling the ill-conditioned region (54).

Despite these points, CS methods are not necessarily immune to over-smoothing if they allow a reduction of the data consistency with a large regularization parameter. In this case, the data consistency becomes less important than the prior information, i.e. well-conditioned frequency content is no longer kept intact in favor of matching the CS constraint.

TKD and CFL2 solutions were provided as benchmark algorithms. The performance metrics RMSE / HFEN / SSIM for these algorithms were: 86.5 / 82.0 / 0.77 for TKD and 81.2 / 75.5 / 0.81 for CFL2. The winning algorithms had metrics: 69.0 / 63.5 / 0.94, corresponding to an improvement of 18% in RMSE, 19% in HFEN and 16% in SSIM over CFL2. The improvement in ROI accuracy was smaller, CFL2 ranked seventh in this category. We conclude that if the average susceptibilities inside specific grey and white matter ROIs are desired, a method as simple as CFL2 may provide sufficient accuracy. The submitted algorithms, however, provided a marked improvement in artifact mitigation and retention of high frequency features relative to the CFL2 benchmark.

In the last few years, several research groups have proposed single-step QSM algorithms, which estimate the underlying susceptibility directly from the raw phase without separate interim phase processing. Despite the fact that a very specific phase filtering pipeline (LBV + polynomial fitting) was applied to create the reference susceptibility maps, the single-step algorithms were capable of providing competitive results despite the processing pipeline bias for multi-step approaches in this challenge.

Among the submissions, one approach employed parallel computing on GPU hardware for rapid dipole inversion (CHICAGO TGV). Despite solving the same underlying mathematical problem as other TGV based methods, this has yielded different performance metrics due to (i) using different regularization parameters and a different number of iterations, (ii) different implementations of the mathematical libraries and (iii) double precision (CPU) versus single precision (GPU) computation also has a substantial impact on iterative methods as any numerical differences accumulate.

However, the main discussion points of this reconstruction challenge were the identification of performance metrics that would be representative of susceptibility image quality and the selection of reference susceptibility maps.

How representative are RMSE, HFEN, and SSIM of susceptibility map quality?

All three measures are global error metrics aiming to summarize the mismatch against a reference image in a single number. We intentionally allowed the contestants to optimize for low RMSE by extensive parameter search. Although the algorithm applied for the post-challenge experiments shown in Figure 4 yielded highly over-regularized smooth QSM images, the resulting RMSE was only approximately 10% higher than that of the winning algorithm. RMSE is a simple global error metric and is usually not a reliable indicator of visual quality or over-smoothing by itself. Recognizing this, we added HFEN and SSIM to create a multi-dimensional performance vector that would allow us to probe differences between image features. However, the limited visual quality of the submitted susceptibility maps leads us to the conclusion that it will be important to find better metrics for the evaluation of susceptibility map quality.

The reason why we provided the reference susceptibility map was to ensure that each algorithm produced the best scoring susceptibility map for the given metrics. However, a major outcome of this challenge turned out to be that the chosen numerical metrics, which are intensively applied in computer vision research, were problematic because they favored over-smoothing of the reconstructed susceptibility maps. Over-regularization was consistently observed as a strategy to improve all error metrics, leading to an unexpected visual appearance of the susceptibility maps that differs from the typical appearance of the maps known from the literature.

Further insights on this issue could be gained by comparing the three fidelity metrics (RMSE, HFEN, and SSIM) and quantitative accuracy inside regions of interest (ROI error). The simple CFL2 method ranked 3^rd in ROI accuracy, while not making it into the top 10 in any of the fidelity metrics. Despite performing well when average values were considered inside ROIs, its image quality suffered from streaking and blurring artifacts, which were better captured by RMSE, HFEN, and SSIM metrics. However, it is more difficult to gain insights from a comparison between the three fidelity metrics. RMSE, HFEN, and SSIM aimed to capture overall error, high-frequency deviation, and “visual” fidelity, respectively.

In future evaluations, some limitations of the metrics could be mitigated by incorporating experts’ visual rating of the submitted susceptibility maps. A potential way to amend the RMSE metric could be to compare the gradients of the susceptibility map against those in the reference map via $\nabla \text{RMSE}=100·{\Vert \nabla ({\chi }_{33}-{\chi }_{\mathit{\text{recon}}})\Vert }_2^2/{\Vert \nabla {\chi }_{33}\Vert }_2^2$. The metric ∇RMSE may provide a more direct measure of the fidelity of high frequency components, and could complement the existing metrics and the visual rating.

However, while optimization in respect to certain quality measures will require further systematic investigations, the degree of regularization should be also chosen according to the subsequent usage of the QSM images depending whether this is anatomical ROI evaluation, voxel-based analysis or visual inspection by radiologists.

Selection of the reference susceptibility map

We selected χ₃₃ instead of the COSMOS solution as standard reference to eliminate the potential orientation bias in the latter susceptibility map. However, this required the assumption that phase contributions from the off-diagonal tensor terms χ₁₃ and χ₂₃ in the transverse plane are negligible. As demonstrated in Figure 1, these contributions are non-negligible because the tensor elements can have about 70% amplitude relative to χ₃₃.

One potential way to combine the strengths of both reference map candidates in future challenges would be to mask out the anisotropic regions in the COSMOS map. Such an anisotropy mask could be obtained by thresholding the STI anisotropy defined as χ_msa = λ₁ − (λ₂ + λ₃)/2 where λ_i are the susceptibility tensor eigenvalues. This mask could be refined using a white matter segmentation.

Also related to limitations of the employed reference, there is clear evidence that the microstructural compartmentalization of magnetic susceptibility in white matter and its water distribution has a significant impact on the observed phase images (33–36). These effects are not accounted for by either COSMOS, STI or any of the single orientation reconstruction methods, yielding an error in susceptibility values in fiber bundles (33) that is difficult to estimate. As white matter represents a relatively large brain volume fraction, both WM measurements and whole brain metrics will be affected by these microstructural effects, and a particular regularization might inadvertently improve the metrics without resulting in a more accurate or precise reconstruction.

In summary, the existence of phase contrast related to off-diagonal tensor elements poses the question of what is the perfect susceptibility map reconstructed from a single-angle phase image? The presence of non-susceptibility contrast mechanisms including chemical exchange-induced frequency shifts (30), which are currently not accounted for by multi-orientation QSM algorithms poses the question of how we can measure the gold standard in-vivo susceptibility map. Both seem to be open questions in our field.

Lessons learned from the first QSM reconstruction challenge

We are fully determined to push forward, improve and extend this research endeavor based on lessons learned from this initial challenge. In particular, the feedback from members of the QSM community who attended the Graz Workshop and the EMTP study group meeting at the ISMRM 2017 was encouraging to proceed with an evaluation of the various algorithmic approaches to better understand the potential and limitations of QSM. The main suggestions and recommendations addressed the limitations of the performance metrics for evaluation of the submitted susceptibility maps and the choice of the reference map. We list the conclusions from the various discussions in the following:

1. Instead of relying entirely on error metrics, it would be informative for experienced radiologists and QSM experts to perform a visual assessment of submitted susceptibility maps.

2. The challenge could be divided into two parts, where the first part would assess the quantitative accuracy with respect to a known ground truth. To this end, the challenge could comprise phase data obtained using the forward model (11) on a realistic numerical brain phantom derived from STI or COSMOS susceptibility maps. The data could be made more realistic by adding noise, partial volume artifacts and contributions from anisotropic susceptibility sources. The second part would involve in-vivo patient data and aim to assess the robustness of the methods in a clinical scenario, in the potential presence of motion, blooming and signal dropout artifacts. For parameter tuning, a COSMOS reference from a healthy control could be provided.

3. Reference and submitted susceptibility maps could be compared on a per-voxel basis by assessing one-dimensional profiles or correlation coefficients.

4. A better in-vivo reference map could be created by incorporating the contribution of χ₁₃ and χ₂₃ into the field map provided to the contestants (transverse orientation). A potential way of implementing this could be by rearranging the STI relation in the transverse plane as follows:

   $$\mathbf{\Theta }(\mathit{k})=\mathbf{D}{\chi }_{33}-\frac{k_z}{k^2}(k_x{\chi }_{13}+k_y{\chi }_{23})=\mathbf{D}{\chi }_{33}-\frac{k_z^2}{k^2}(\frac{k_x}{k_z}{\chi }_{13}+\frac{k_y}{k_z}{\chi }_{23})$$ [8]

   now defining $\tilde{\chi }\triangleq \frac{k_x}{k_z}{\chi }_{13}+\frac{k_y}{k_z}{\chi }_{23}$,

   $$\mathbf{\Theta }(\mathit{k})=\mathbf{D}{\chi }_{33}-\frac{k_z^2}{k^2}\tilde{\chi }+\frac{1}{3}\tilde{\chi }-\frac{1}{3}\tilde{\chi }$$ [9]

   $$\mathbf{\Theta }(\mathit{k})+\frac{1}{3}\tilde{\chi }=\mathbf{D}({\chi }_{33}+\tilde{\chi })$$ [10]

   Equation 10 suggests that a new ground truth susceptibility could be created by χ_new ≜ χ₃₃ + χ̃ and that the input local field data could be amended by ${\mathbf{\Theta }}_{\mathit{\text{new}}}\triangleq \mathbf{\Theta }+\frac{1}{3}\tilde{\chi }$. A numerical challenge in computing χ̃ would be the division by k_z for the plane of frequencies where k_z = 0. To address this, we can interpret division by k_z as integration along z in image-space, and multiplication by k_x (or k_y) as differentiation along x (or y) axes (1). In a discrete implementation, integration would correspond to summation over z indices and differentiation would be the difference between neighboring voxels along x (or y) axes.

5. Include the computational efficiency as additional information or a separate category, which would require access to a single evaluation computer for all contestants on which the processing time of all algorithms could be accurately determined and compared.

6. The data consistency could be used as an additional metric. To this end, one could use the submitted susceptibility maps in a forward field simulation (11) and compare the resulting phase against the measured phase.

7. Susceptibility maps should be compensated for the known systematic underestimation before quality metrics are calculated. This approach would avoid underestimation resulting in poor metrics despite the reconstruction being of otherwise high quality.

8. The susceptibility could be evaluated exclusively in deep grey matter structures where QSM is more likely to be correct given the absence of highly anisotropic fiber bundles.

9. The mutual information, cross correlation and ∇RMSE between the reference and submitted maps could be included as additional quality metrics.

10. Multi-echo phase data could be provided to allow field maps to be derived by fitting the phase over echo times (63–65).

Most of these suggestions are feasible but may require additional data processing and acquisition. We have already updated the downloadable data set to include the magnitude and phase data from all 12 directions. This dataset could facilitate extensions such as an STI challenge, or future research towards computation of a better reference map. Since this dataset includes χ₃₃ and χ_COSMOS as well as all components of the susceptibility tensor, future publications on new algorithms may report performance metrics relative to any of these.

Another interesting avenue to explore could be issuing sub-challenges with clinical data from populations with different diseases. Such a challenge would be an excellent opportunity to test the robustness of the algorithms in the clinical setting, and performance evaluation would benefit from the experience of neuro-radiologists. However, the lack of a true gold standard reference renders the quantitative assessment of susceptibility maps beyond the description of apparent artifacts difficult.

In conclusion, the substantive differences between the various submitted susceptibility maps highlight a critical limitation of current regularized QSM techniques: the appearance of the resulting susceptibility maps depends strongly on the algorithm used and the associated parameter choices. Hence, a direct comparison of results from studies employing different QSM algorithms and parameters is challenging. Consequently, in the EMTP study group meeting at the ISMRM 2017 it was decided consensually, that another challenge will be designed based on the lessons learned from the present challenge.