Abstract
Effective inferential statistical analysis is essential for high quality studies in neuroscience. However, recently, neuroscience has been criticised for the poor use of experimental design and statistical analysis. Many of the statistical issues confronting neuroscience are similar to other areas of biology; however, there are some that occur more regularly in neuroscience studies. This review attempts to provide a succinct overview of some of the major issues that arise commonly in the analyses of neuroscience data. These include: the non-normal distribution of the data; inequality of variance between groups; extensive correlation in data for repeated measurements across time or space; excessive multiple testing; inadequate statistical power due to small sample sizes; pseudo-replication; and an over-emphasis on binary conclusions about statistical significance as opposed to effect sizes. Statistical analysis should be viewed as just another neuroscience tool, which is critical to the final outcome of the study. Therefore, it needs to be done well and it is a good idea to be proactive and seek help early, preferably before the study even begins.
Keywords: neuroscience, statistical analysis, experimental design
Few neuroscientists would deny the importance of inferential statistical analysis for the subject of neuroscience, either for the analysis and interpretation of one’s own data or simply to understand the neuroscience literature. Much of neuroscience is dominated by univariate statistical methods, especially those that are part of the general linear model (GLM), such as Student’s t tests and analyses of variance (ANOVAs). Gradually, multivariate statistical approaches are becoming more common, especially with the appreciation that most dependent variables in neuroscience are affected by many independent variables which interact in complex ways. In addition, Bayesian statistical approaches are increasingly being employed (Lesaffre and Lawson, 2012). However, a barrier to the use of such methods is a lack of understanding of basic classical, univariate statistical techniques, and in the last several years neuroscience has been criticised severely for the poor use of statistical procedures, particularly in relation to low statistical power (e.g., Button et al., 2013a; Smaldino and McElreath, 2016), the use of pseudo-replication (e.g., Lazic, 2010) and invalid analyses of interactions (Nieuwenhuis et al., 2011).
One problem with improving statistical understanding is that many researchers find the concept of null hypothesis significance testing (NHST) difficult to accept, because it leads to a simple dichotomous decision as to whether there is a statistically significant effect, rather than any judgement about the size or scientific meaning of any effect (see Gigerenzer, 2004; Lew, 2012; Perezgonzalez, 2015; Szucs and Ioannidis, 2017a, for critical analyses of this issue). NHST is part of traditional, frequentist statistical analysis and is not the only approach available; for example, Bayesian statistical analyses have become increasingly popular in biostatistics in general (Lesaffre and Lawson, 2012). Nonetheless, data analysis in neuroscience is still dominated by NHST, despite the fact that the American Statistical Association (ASA) has made it clear that scientific conclusions should not be based solely on whether a p value crosses a specific threshold and that this value alone does not afford an effective evaluation of evidence relating to a hypothesis (Wasserstein and Lazar, 2016). Szucs and Ionnidis (2017a) have even suggested that NHST should be used only in specific situations.
As Perezgonzalez (2015) describes, the NHST is really an amalgamation of Ronald Fisher’s approach to testing data, which determines the probability of the observed data under the null hypothesis, and Neyman-Pearson’s approach, which allows testing of the null hypothesis against an alternative hypothesis and involves consideration of the sample size necessary to obtain adequate statistical power and effect sizes. Perezgonzalez (2015) suggests that this fusion of the two forms of hypothesis testing actually negates the advantages of each and that it would be preferable to revert to their original formulations when and where they are appropriate.
Although many of the problems faced by neuroscientists when performing statistical analysis are similar to other areas of biology, there are some that are particularly difficult and frequent in neuroscience. Probably the most common example of this is the tendency to use small sample sizes in experimental neuroscience. Sometimes this is a result of the cost of animals, expensive experimental resources such as antibodies, and of course the desire and pressure to minimise the number of animals used. However, sometimes it is simply due to tradition. For example, there has been a tendency to use n = 3 replicates in biochemical experiments, often with no justification at all other than that previous studies have done the same (e.g., Verbitsky, 2013; Fosang and Colbran, 2015).
The main objective of this review is to provide a succinct overview of some of the most common problems in statistical analyses in the neurosciences, as a guide to focusing on the statistical issues that are most likely to be encountered. The content is based on over a decade of teaching statistics to undergraduate and postgraduate neuroscience and neuropharmacology students, as well as providing consultation on statistical analyses to neuroscience researchers. Since most neuroscience students I have encountered have limited understanding of the mathematical basis of statistics, this review will be delivered with minimal formal mathematical notation or equations.
THE IMPORTANCE OF EXPERIMENTAL DESIGN
Before any experiment begins, attention needs to be paid to some basic attributes of good experimental design: control groups, random allocation of subjects to conditions, blinding and replication. These concepts should be self-evident but they are often overlooked in the haste to begin and complete experiments in neuroscience (e.g., Kilkenny et al., 2009). The validity and reliability of measurements is paramount in obtaining high quality data (Loken and Gelman, 2017).
Adequate control groups are essential to determining whether an intervention has any real effect on a dependent variable. A classic example of lack of an adequate control group is a situation in which the effects of an intervention are measured over time but the control group is measured at one time point only, for example, the shortest one, resulting in the possibility that any effects observed in the treatment group are simply a result of the passage of time rather than the treatment itself.
Random allocation of subjects to experimental conditions is critical to avoiding bias in the way that subjects are used to represent a population. Probability sampling is based on the idea that each subject has a known probability of being selected for a condition. If the allocation of subjects to conditions is not truly random, then there is a possibility that the samples are biased. For example, in the study of the effects of 3,4-methylenedioxymethamphetamine (MDMA, ‘Ecstasy’) on the brain, if only people who present to major hospital neurology clinics are sampled, then there is the potential for bias to affect the study. Such people are more likely to suffer from more severe adverse side effects and live near a major University hospital, which may give them a particular socioeconomic profile. In fact, in many neuroscience publications, random allocation of subjects to conditions is not mentioned, although it is assumed to be the case (Kilkenny et al., 2009).
Blind measurement, in which the researcher does not know which animals or samples received the experimental treatment, and which received the control treatment, is often preferable. It may be especially important in studies in which subjective bias could interfere with accurate measurements. However, even apparently ‘objective’ measurements can be influenced by observer bias (Lilford et al., 2003). In human studies, ‘double blind’ designs are common, so that neither the subjects nor the experimenters are aware of who is assigned to the different experimental and control conditions.
Finally, replication is of paramount importance in experimental design. It is entirely possible for patterns to be apparent in the data from small samples even if they are due to chance alone. The idea that random occurrences are ‘balanced’ is known as the ‘Gambler’s Fallacy’ or the ‘Monte Carlo Fallacy.’ The importance of replication will be discussed below in relation to sample sizes and statistical power.
It is very important for a neuroscience researcher to be conscious of the kind of data he or she is collecting. For example, is it data from a continuous variable (‘interval’ or ‘ratio’ data), whose values are essentially uncountable and where probabilities can only be assigned on a continuum, or is it discrete data (‘nominal’ or ‘ordinal’ data) whose values are finite or countably infinite? In the former case, the numbers assigned to data have complete mathematical integrity, for example, the amplitude of a neuronal excitatory post-synaptic potential. Probabilities can only be assigned on a continuum for this sort of variable because, theoretically, no matter how small a change in it may be, a smaller one could be measured (provided that there is adequate measurement resolution). In this case, mathematically, 10 is literally twice 5. By contrast, for a discrete variable such as ratings on a Hamilton Depression Rating Scale, only whole numbers can be used and although these numbers represent an order, i.e., 4 is greater than 2, it is not necessarily the case that 4 is twice 2 in a mathematical sense, or at least it is difficult to prove this because it represents a subjective judgement. Neuroscientists tend to be preoccupied with the statistical analysis of continuous variables. However, other kinds of data are important as well. The frequency of adverse events in clinical trials of new neurologically important drugs is an important end point in determining whether a drug is safe. However, even recent clinical trials of cannabinoid drug treatments for childhood epilepsy have included no formal statistical analysis of such data using the Chi Squared or Fisher’s Exact Test (e.g., Devinsky et al., 2017).
In neuroscience the terms ‘parametric’ and ‘non-parametric’ are often used in relation to continuous and discrete variables, and variables that follow a normal or non-normal distribution, respectively. However, this is an over-simplification. ‘Parametric’ statistical procedures refer to those that assume that a random variable follows a known distribution, and although most statistical procedures used in neuroscience assume a normal distribution, it is possible to use parametric statistical tests that assume other kinds of distributions, for example, a Poisson distribution. Non-parametric statistical tests refer to those that do not assume a known distribution, although they often do involve some assumptions as well. In general, neuroscientists tend to consider non-parametric statistical tests, such as Mann-Whitney U tests and Kruskal Wallis tests, in cases where ordinal data such as ranks have been collected, for example a rating scale for seizure severity. Such data are often assumed not to follow a normal distribution, although this can depend on sample size. If the data are demonstrated not to follow a normal distribution, an alternative to non-parametric statistical analysis is to use bootstrapping to determine the sampling distribution of the mean. Since it is the normality of the sampling distribution of the mean that is actually important for GLM statistical procedures, by using resampling from the data for a particular sample size (e.g., n = 5), it is possible to determine whether the sampling distribution of the mean would be likely to be normal. Sometimes even if the parent distribution appears to be non-normal, the sampling distribution of the mean may in fact be normal, which is all that is necessary.
NON-NORMAL DISTRIBUTION OF DATA AND WHAT TO DO ABOUT IT
All statistical procedures that are part of the GLM, such as Student’s t tests, ANOVAs and linear regression, make similar assumptions (Rutherford, 2001; Doncaster and Davey, 2007; Kirk, 2013):
The experimental subjects (e.g., animals) are sampled randomly from a population or from within groups.
The measurements within each sample are independent and have uncorrelated model errors.
The variances between the samples are approximately equal or ‘homogeneous.’
The model errors are normally distributed (Rutherford, 2001; Doncaster and Davey, 2007; Smith, 2012; Kirk, 2013).
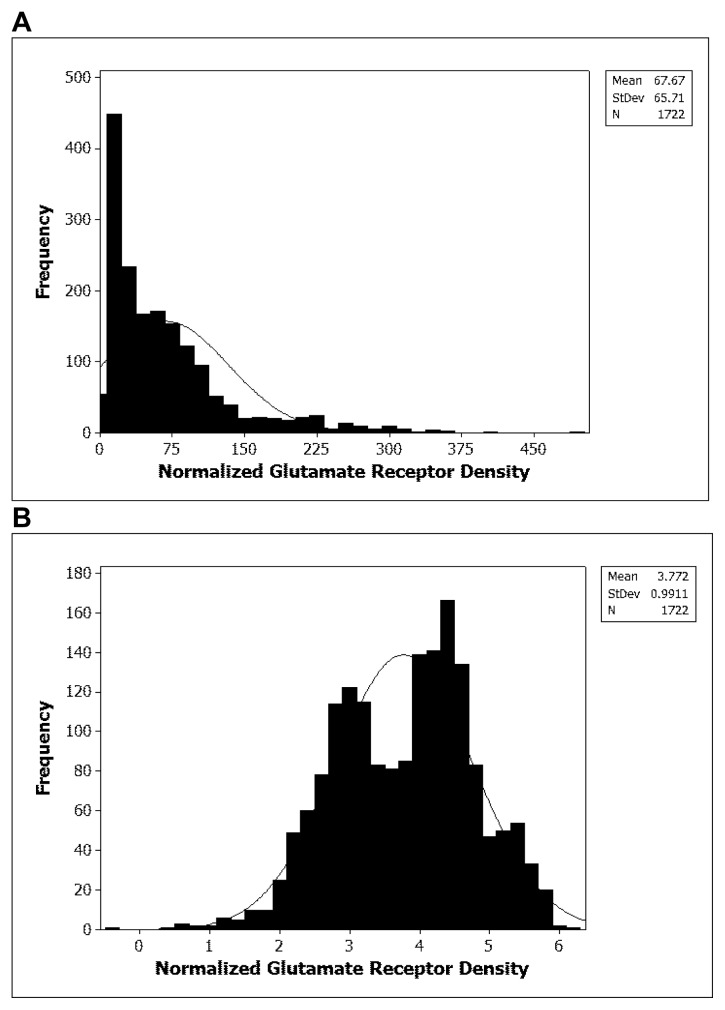
It is very common in neuroscience research to assume that the normality assumption for GLM Student’s t tests and ANOVAs is fulfilled without formally testing it using some form of goodness of fit test such as the Kolmogorov-Smirnov, Shapiro-Wilk or Anderson-Darling tests (Rutherford, 2001; Gamst et al., 2008). This is presumably due to the view that the central limit theorem will protect t tests and ANOVAs against the moderate violation of the assumption of normality “when samples sizes are reasonably large and are equal” (Winer et al., 1991, p.101). Unfortunately, the interpretation of “reasonably large” is problematic. Snedecor and Cochran (1989) suggest that while for some populations the sampling distribution of the mean may be normal with sample sizes of 4 or 5, in other cases it may need to be more than 100. The distributions of some variables are inherently non-normal. For example, frequency data have positive integer values in which random variation increases as the mean increases (Doncaster and Davey, 2007). On the other hand, Keppel and Wickens (2004) have argued that the normality assumption can be ignored once the sample sizes reach approximately 12 (see also, Rutherford, 2001). However, the symmetry of the distribution is also very important (Winer et al., 1991; Kirk, 2013). Obviously, if the normality assumption is not tested, then solutions to the violation of the normality assumption, such as natural log or square root data transformations, cannot be undertaken (Gamst et al., 2008; Fig. 1). One issue is that, if the sample size is small, for example, less than or equal to 5, there may not be sufficient information in order to judge whether the data are normally distributed or not. In this case, some researchers will choose to use a non-parametric statistical analysis, such as Mann-Whitney U tests (as an alternative to Student’s t tests) or Kruskal Wallis tests (as an alternative to a 1-way ANOVA). However, this can be difficult for designs that are not amenable to one factor analyses, since most commercial programs do not offer 2-way Kruskal Wallis tests as an alternative to 2-way ANOVAs (see Conover and Iman, 1981 for a review). What are the potential consequences of using ANOVA if the normality assumption is violated? Rutherford (2001) suggests that it will affect both the type I error rate and the power of the ANOVA F test.
Figure 1.
(A) Example of the non-normal distribution of glutamate receptor density in the rat hippocampus and (B) the effects of natural log transformation on that distribution. It can be seen that the transformation substantially improves the normality of the distribution. Modified from Zheng et al. (2013).
UNEQUAL VARIANCES AND WHAT TO DO ABOUT THEM
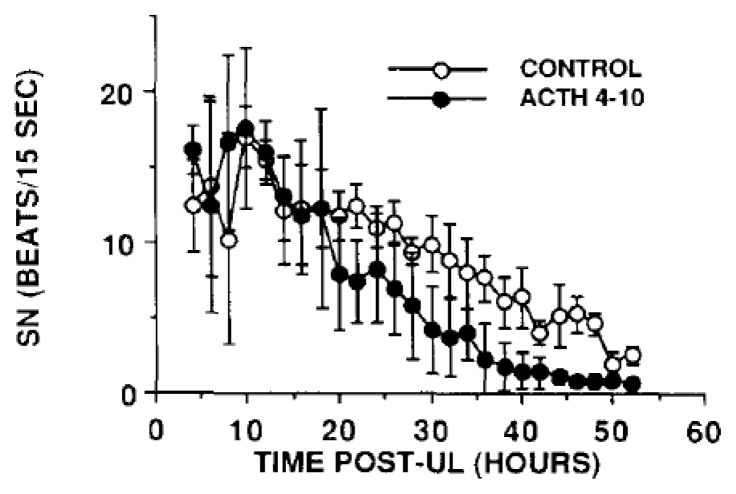
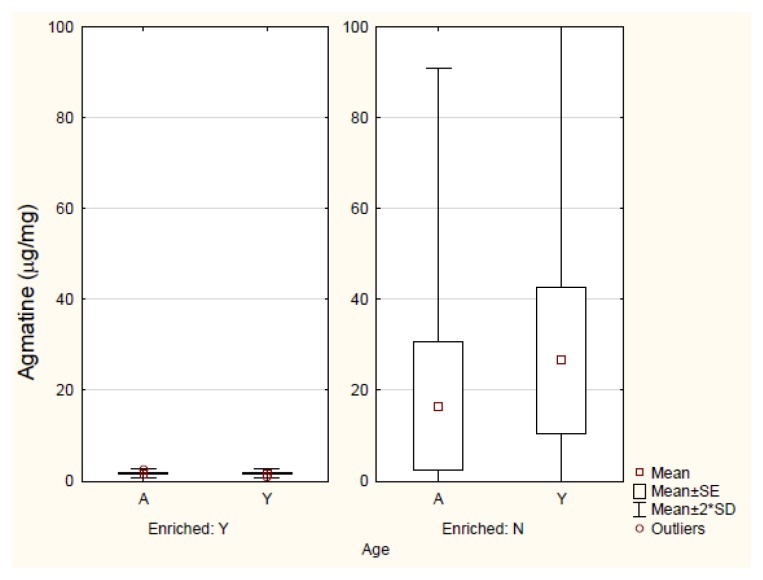
Another assumption of the GLM is that the variances associated with experimental error in the treatment populations to be compared, are approximately equal or ‘homogeneous’ (the ‘homogeneity of variance’ or ‘homoscedasticity’ assumption) (Winer et al., 1991). Many intervention studies in neuroscience are actually designed to reduce both the means and the variances of the dependent variable over time. For example, in studies of the recovery from neurological deficits following a neural lesion, the objective of a drug treatment may be to both reduce the mean value of a neurological deficit as well its variance, so that all of the drug-treated group exhibit a similar recovery (e.g., Gilchrist et al., 1990). An example of this is shown in Figure 2 but the principle applies to many rehabilitation studies. Box (1954a; Box, 1954b) demonstrated that the ANOVA F test is robust against ‘moderate’ violations of the homogeneity of variance assumption, provided that the sample sizes are equal. However, Box (1954a) showed that small changes in the ratio of the variances between treatment groups can alter the significance level of the F test, in some cases increasing the type I error rate. Wilcox (1987) has suggested that when the homogeneity of variance assumption is violated, the conventional F test should never be used. For this reason, some authors recommend using a more conservative type I error rate (Keppel and Wickens, 2004; Gamst et al., 2008). Winer et al. (1991) suggest that the solution is for experimenters to aim to use large and equal sample sizes and then to use the Box approximation to the F test in situations where this is not possible. The same data transformations that can be used to achieve normality of the data distribution, for example, natural log or square root transformations, often also result in homogeneity of variance (Winer et al., 1991; Gamst et al., 2008). However, as with the normality assumption, many studies in neuroscience do not report testing the homogeneity of variance assumption using tests such as Levene’s or Bartlett’s tests, before proceeding with an ANOVA. Such assumption tests are available in programs such as SPSS, SAS and Minitab, while other programs such as Prism provide the option of not making the assumptions or test the assumptions at the same time as conducting the statistical test. Figure 3 shows an example of extremely unequal variances where analysis using ANOVA would have been invalid without transformation.
Figure 2.
The compensation of spontaneous nystagmus (SN) for a saline control group and an ACTH-(4–10)-treated group following unilateral labyrinthectomy (UL). Bars represent means ± 1 SD. Note that as the means decrease, so do the SDs. Reproduced from Gilchrist et al. (1990) with permission.
Figure 3.
Levels of agmatine in the vestibular nuclei of aged (A) and young (Y) rats in enriched (Y) or non-enriched (N) environments. Note the large difference in variability between the enriched and non-enriched groups. Modified from Smith (2016).
CORRELATIONS OVER TIME OR SPACE AND WHAT TO DO ABOUT THEM FIXED VERSUS RANDOM EFFECTS
In the formulations of the ANOVA, the GLM has the form: data = model + error. Fixed effects involve only fixed levels of factors in the model, which are referred to as ‘fixed’ because the experimenter has chosen them specifically as the factors of interest and any conclusions drawn from the analysis do not extend beyond them (Rutherford, 2001; Kirk, 2013). In the case of studies in neuroscience, one obvious example of a fixed effect is drug treatment, surgery, or electrical stimulation, where there may be 2 levels or values: treatment versus a sham intervention. Animals are randomly allocated to each condition and the researcher has specifically chosen these conditions because of the nature of the research question. By contrast, random effects involve only random factors in the model, which are referred to as ‘random’ because they are believed to be only a random sample from a population of experimental conditions. Therefore, conclusions based on their investigation are extrapolated to a wider population of experimental conditions (Rutherford, 2001; Kirk, 2013). Common examples of random effects in the context of this area are the animals themselves, which are a random sample from a population of animals.
Since factorial repeated measures ANOVAs are so commonly used in neuroscience, it is common to have a ‘mixed’ design which contains both fixed and random factors (Rutherford, 2001). The fixed factor is often the treatment and the random factor, animals, over which several repeated measures are made. A 2-factor factorial model is often used where the objective is to investigate the effects of 2 independent factors on the dependent variable, for example, drug and time (Small et al., 2011). Sometimes, if the change in the dependent variable over a period of time is of interest, and repeated measurements can be made in the same animals (i.e., one observation per animal per time point), a repeated measures design with a single factor may be used. One of the most commonly used designs is a factorial design including one fixed, between group, measure, for example drug, and one repeated measure, over time, a so-called ‘mixed’ or ‘split-plot’ design (Festing, 2003).
COMPOUND SYMMETRY OR SPHERICITY
Another assumption of the ANOVA F test is that the variance-covariance matrices for the dependent variable are equal and symmetrical across the different treatment groups. Known as the ‘compound symmetry’ assumption, it is a special case of ‘circularity’ (Winer et al., 1991). ‘Sphericity’ is a less restrictive assumption, that the variances of the differences between the values of the dependent variable are approximately equal for all pairs of treatments (Quinn and Keough, 2002). This means that the covariances for all pairs of treatments will be zero and the variances will be equal. In violation of these assumptions, it is quite common in neuroscience studies for the data from individual subjects to be correlated over time or space (e.g., if samples are taken from different areas of the brain in each subject). In these cases the variance for the dependent variable may change systematically with repeated measures over time or space, and correlate with specific changes in the means for the repeated measure. One frequent example are recovery phenomena in which the average value for some neurological symptom is initially very high with a large variance, but as a recovery or compensation process takes place, the severity of the symptom decreases over time, but the variance systematically decreases as well (for an example, see Fig. 2). The strength of the correlation between observations may decrease as the distance (in time or space) between the measurements increases. These correlative or covariance relationships across the repeated measures can be characterized using various models, for example, an autoregressive order 1 (AR(1)) covariance structure, in which the current value of the dependent variable is related to the immediately preceding value (Brammer, 2003). It is possible to use mathematical transformations such as log and square root transformations to try to stabilize the variances (Quinn and Keough, 2002).
The systematic change in the variances of the repeated measure violates the assumption of sphericity, which can potentially inflate the type I error rate for an ANOVA (Winer et al., 1991). Mauchly’s test of sphericity can be used to evaluate the degree to which the assumption is violated; however, its use has been criticised because it assumes that the data are normally distributed and its sensitivity is related to the sample size (Winer et al., 1991; Quinn and Keough, 2002). Consequently, it is not recommended for routine use and Quinn and Keough (2002) suggest that it is safer to assume that the sphericity assumption is violated in repeated measures situations, which they usually are in neuroscience. One solution to this problem is to employ some form of correction, such as the Greenhouse-Geisser or Huynh-Feldt corrections, which make the type I error rate for the F test more conservative and reduce the statistical power for the repeated measure (Winer et al., 1991). However, it is rare for neuroscience researchers to use such corrections.
REPEATED MEASURES ANOVAS WITH UNBALANCED REPEATED MEASURES DESIGNS AND MISSING DATA
Unequal sample sizes increase the effects of the violation of the assumptions of normality and homogeneity of variance (Box, 1954a; Box, 1954b; Winer et al., 1991). Nonetheless, GLM ANOVAs can accommodate unequal sample sizes for different treatments (Quinn and Keough, 2002). By contrast, missing data are problematic for repeated measures ANOVAs. Missing data are common in neuroscience as a result of subjects dying or tissue deteriorating during an experiment or sometimes due to a measurement becoming technically impossible (Quinn and Keough, 2002). In this case, because the sums of squares for the treatment (SST) have to be weighted in relation to the number of observations for the treatment, and the sum of squares for the error (SSE) have to be weighted in relation to the number of samples for the experimental subjects, no two mean squares can have equal expected values under the null hypothesis (Kuehl, 2000; Kirk, 2013). Consequently, the F test of the null hypothesis cannot be exact (Kuehl, 2000).
Many statistical programs (e.g., SPSS) which offer repeated measures ANOVAs delete experimental subjects if they have missing data (Gamst et al., 2008; Field, 2011). Many studies in neuroscience already have small and unequal sample sizes; therefore, simply deleting data in the case of missing values is difficult to accept (Clark et al., 2012; Smith, 2012). The reduction in sample size will be likely to result in lower statistical power. It is also ethically objectionable to use of animals for research and then not include their data unless the data are technically flawed in some way (Smith, 2012). Some form of imputation procedure may be employed in order to estimate the missing values (‘Missing Values Analysis or MVA’) (Quinn and Keough, 2002; Gamst et al., 2008). A maximum likelihood (ML) and expectation-maximization (EM) approach (a combination of imputation and ML) can also be used (Quinn and Keough, 2002). However, only some programs (e.g., SPSS) offer the EM algorithm and for the ML and EM methods to be used, the missing data must be ‘missing at random’ (MAR, i.e., the probability that an observation is missing must not depend on the unobserved missing value but may depend on the group to which it would have belonged) or ‘missing completely at random’ (MCAR, i.e., the probability that an observation is missing must not depend on the observed or missing values) (Quinn and Keough, 2002; Smith, 2012). In other words, there can be no bias to the way that data are missing, a condition that is sometimes difficult to satisfy.
ALTERNATIVES TO REPEATED MEASURES ANOVAS: LINEAR MIXED MODEL ANALYSIS (LMM)
Since repeated measures data in neuroscience are usually correlated and therefore violate the ANOVA assumption of sphericity, one alternative approach is to use a linear mixed model (LMM) analysis in which the correlation in the data is modelled. Here the term ‘mixed’ refers to the fact that there is a mixture of ‘fixed’ and ‘random’ effects that have to be estimated (Gurka and Edwards, 2011). The development of LMM analyses was stimulated by epidemiological and clinical trial studies in which longitudinal data are often collected. In these cases, it is common for studies to have missing data. LMM analysis can accommodate this problem and also has fewer assumptions than ANOVAs (see below) (Fitzmaurice et al., 2004; Kutner et al., 2005; Vittinghoff et al., 2005; Brown and Prescott, 2006; West et al., 2007; Rao et al., 2011; Gurka and Edwards, 2011; Smith, 2012). In LMM analysis, an iterative maximum likelihood estimation procedure (MLE or restricted maximum likelihood estimation (REML)) is used to estimate parameters. This is an optimization procedure that uses calculus to choose as the parameter estimates, the values that result in the observed data having maximal probability (Miller and Miller, 2004; Fitzmaurice et al., 2004; West et al., 2007; Gurka and Edwards, 2011; Smith, 2012). The process is repeated over and over until it converges on the optimal solution. MLEs of the parameters are biased, however REMLs are not (Fitzmaurice et al., 2004; Brown and Prescott, 2006; West et al., 2007). Rather than the ANOVA approach of assuming that the repeated measures data are independent, or employing a correction procedure such as the Greenhouse-Geisser or Huynh-Feldt corrections if they are not, the correlational structure of the repeated measures data is modelled using various covariance matrix structures (14 are available in SPSS), for example: an unstructured covariance structure, autoregressive (AR, order 1) or autoregressive-moving average (ARMA) covariance structures (Little et al., 2000; Brammer et al., 2003; Clark et al., 2012; Smith, 2012). In SPSS, using an LMM analysis is not much different from performing an ordinary ANOVA, except that the best covariance matrix structure must be chosen. Although this seems complicated and laborious at first, in practice it only involves determining the model which is the best fit, which can be done using various information criteria (see below). Once demonstrated, students learn this procedure very quickly.
Other than the statistical package R (Crawley, 2007; Field et al., 2012; Davies, 2016), which requires programming, there are other freely downloadable programs that offer the LMM analysis option. For example, the InVivoStat program offers compound symmetry, AR1 and unstructured covariance structures as options (Clark et al., 2012; Smith, 2012). The default covariance structure in InVivoStat is compound symmetry, which means that all of the observations within subjects are correlated equally irrespective of their distance from each other. The AR1 structure is recommended for data with equally spaced time points and the unstructured covariance structure is for large sample sizes (Smith, 2012). LMM analyses have been employed in neuroscience studies as an alternative to using repeated measures ANOVAs (e.g., Brammer, 2003; Stiles et al., 2012; Zheng et al., 2012a,b; Zheng et al., 2014; Zheng et al., 2015). For small sample sizes it may be difficult to evaluate the best covariance structure and the use of the unstructured covariance matrix structure may result in a loss of statistical power. Modifications such as the Kenwood Rogers adjustment for small sample sizes have been proposed (Skene and Kenwood, 2010a) and a bias-adjusted empirical sandwich estimator and a modified Box correction for use with very small sample sizes have been investigated (Skene and Kenwood 2010a,b). Skene and Kenwood (2010a,b) have reported that the modified Box correction has an acceptable level of power (Skene and Kenwood 2010a,b).
In order to choose the optimal covariance matrix structure model, the goodness-of-fit is usually evaluated using an information criterion such as the Akaike’s Information Criterion (AIC, which indicates how well the covariance matrix structure describes the data), where the smallest value is the best (Fitzmaurice et al., 2004; Brown and Prescott, 2006; West et al., 2007). Other information criteria are available in programs such as SPSS, such as the Bayesian Information Criterion (BIC); however, some authors suggest that the BIC results in a higher probability of selecting a model that is too simple for the data because it employs greater penalties for models with a large number of parameters (e.g., Fitzmaurice et al., 2004; West et al., 2007; Gurka and Edwards, 2011).
Once the optimal covariance matrix structure model is found, the interpretation of the LMM analysis is really as straightforward as an ANOVA. For example, if there are two factors, the program output will display an F value for each one as well as for the interaction between the two, in addition to the usual degrees of freedom and p values. Post-hoc tests such as Bonferroni tests can be selected as they would for an ANOVA.
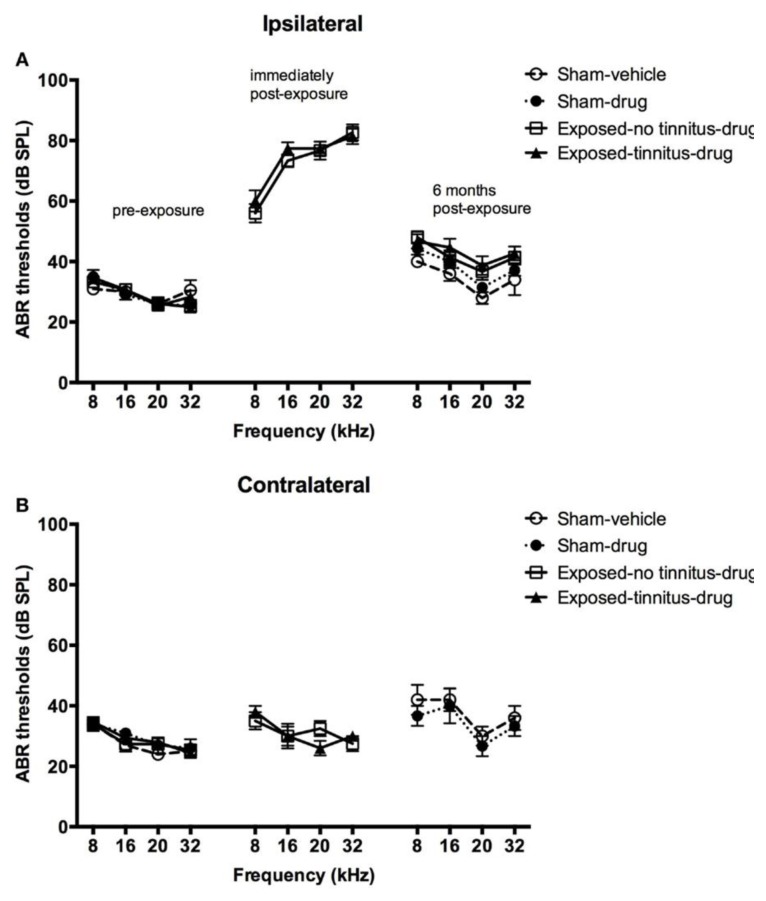
LMM analyses do not assume a balanced design, sphericity or homogeneity of variance; however, the sampling must still be random and the residuals (i.e., errors) normally distributed (Brown and Prescott, 2006). Compared to repeated measures ANOVAs, LMM analyses using a REML offer considerable advantages in situations in which there are multiple repeated measures and missing data, and we use them routinely (e.g., Zheng et al., 2012a,b; Zheng et al., 2014; Zheng et al., 2015; Fig. 4). It is convenient that LMM analyses are available not only in programs such as SPSS, SAS and R, but in the freely downloadable program, InVivoStat, which means that the option is available to everyone (Clark et al., 2012; Smith, 2012). Field has published books on the use of SPSS and R that are very easy to follow and include practical sections on LMM analyses with minimal mathematical detail (Field, 2011; Field et al., 2012).
Figure 4.
Auditory brainstem response (ABR) thresholds for the ipsilateral (A) and contralateral (B) ears of sham-vehicle, sham-acoustic trauma, exposed-no tinnitus-drug (delta-9-THC + cannabidiol) and exposed-tinnitus-drug animals pre-exposure, immediately post-exposure and 6 months post-exposure, as a function of stimulus intensity in dB SPL and frequency in kHz. Data are presented as means ± 1 SE. The design includes 2 between-group factors (i.e., drug and tinnitus) as well as frequency and time re exposure as repeated measures. These data were analysed using a 4 factor or 4-way LMM analysis. Reproduced from Zheng et al. (2015) with permission.
MULTIPLE TESTING AND HOW TO AVOID IT
Another perennial source of controversy in statistical analysis in neuroscience is the use of multiple testing, either using multiple Student’s t tests to examine every conceivable pairwise comparison or even the excessive use of multiple post-hoc tests following a significant ANOVA (Darlington, 2005). For a single Student’s t test, the type I error (α) rate is usually set at 5%. However, if there are many treatment groups, there are (p(p-1))/(2) possible pairwise comparisons among p treatment means, e.g., for 3 groups, = (3(3-1))/(2) = 3 comparisons; for 6 groups, = (6(6-1))/(2) = 15 comparisons (Darlington, 2005). Therefore, the risk of a type I error increases rapidly as the number of comparisons increases, i.e., the ‘experiment-wise’ type I error rate is no longer 5%. Although the increase in the type I error rate in relation to the number of comparisons is not simply linear, it increases with a steep curve and even for 7 comparisons, the actual type I error rate can be as high as 65% rather than 5%, which means that a false rejection of the null hypothesis can occur 65% of the time. Post-hoc tests, such Bonferroni t tests, control the type I error rate for the entire experiment so that it is divided amongst the number of comparisons made (Keselman et al., 2005; Darlington, 2005). Therefore, for 5 comparisons the real type I error rate will be 1% per comparison. This will reduce the power of each test and therefore may simply result in non-significant comparisons if too many are used. This can result in a situation that often baffles undergraduate students, where an ANOVA is significant but none of the pairwise comparisons is. Of course, the ANOVA and the post-hoc tests are asking different questions: the ANOVA is asking whether there is a significant difference amongst p means, whereas the post-hoc tests are asking whether there is a significant difference between any two means. The other problem that arises with multiple post-hoc tests is that they may not be ‘orthogonal’ or mathematically independent of one another and this may yield apparently contradictory results. If A is compared with B, B with C, and A with C, the comparisons of A with B and A with C are not independent.
The solution to this problem is in the design of the experiments themselves, in the use of planned comparisons (Quinn and Keough, 2002; Ruxton and Beauchamp, 2008) as well as the careful use of tests such as ANOVAs and post-hoc comparisons (Festing, 2003). First, multi-level designs in which means representing different factors and factor levels are of interest are best analysed using ANOVAs or LMM-type procedures, so that the type I error rate is fixed at 5% initially. If the design is a 2 × 2 factorial design, with 2 levels in each factor, for example the effects of amphetamine or saline on dopamine levels in the brains of male and female rats (therefore, factor 1 = drug treatment with 2 levels, drug versus vehicle; factor 2 = sex, with 2 levels, male versus female), then post-hoc tests will be unnecessary, because the ANOVA main effect result for the drug will indicate whether there is an effect of amphetamine independently of sex, the main effect result for sex will indicate whether there is an effect of sex independently of amphetamine, and the ANOVA interaction term will indicate whether the effect of amphetamine varies as a function of sex. This is a complete analysis and because there are only 2 levels of each factor, further post-hoc testing is unnecessary. A critical part of this kind of analysis is the information that the interaction provides, which is an important advantage of multi-level designs and ANOVA-style analyses and yet interactions are often ignored or not used properly (Nieuwenhuis et al., 2011). If post-hoc tests are necessary because there are more than two groups and specific information is needed about exactly where any pairwise differences lie, then as few tests as possible are best planned in advance or all comparisons performed using strict correction procedures. Choosing the pairwise comparisons to be made based on inspection of the data alters the probability of a type I error in major ways. However, in many cases post-hoc tests are not necessary if the interaction terms are used properly (Festing, 2003). However, Cramer et al. (2016) have made the important point that the ‘multiplicity problem’ does exist in multiway ANOVAs as well, in that as more factors and interactions are included, the actual type I error rate increases. In cases such as the effects of drug dose on a dependent variable, some form of non-linear regression analysis is often more appropriate than ANOVAs and multiple testing may not be necessary (Motulsky, 1995). In one analysis this will indicate the pattern of change in the dependent variable as a function of dose, whether it is statistically significant, and perhaps, more importantly, how large the effect is in terms of the coefficient of determination (i.e., the R2).
SAMPLE SIZE, STATISTICAL POWER AND PSEUDOREPLICATION
Perhaps no statistical topic has evoked more controversy in neuroscience in recent years than that of small sample sizes and under-powered studies. Statistical power (‘1 – β‘) is the probability that a statistical test will detect a significant difference if one exists. It is determined by a combination of the difference to be detected (i.e., ‘Δ’), the type I error rate (‘α’, usually 5%), the variability around the mean estimates (i.e., the standard deviations) and the sample sizes (‘n’). Since a difference of minimal interest may be fixed, the type I error rate is usually 5% (split between two tails), and a power of at least 80% is usually desired, the critical variables influencing power are usually variability and sample size (Eng, 2003; Norman et al., 2012; see Fig. 5). Beyond certain limits to do with experimental control, the variability may also be relatively fixed; therefore, only the sample size can be varied to increase power. Many neuroscientists wish to minimize the number of animals being used in their experiments, both because of the financial costs involved in expensive studies and also for ethical reasons. On the other hand, if the sample size is too small relative to the difference to be detected and the variability, then statistical power may be low, for example, 60%, which would mean that a significant difference would be missed 40% of the time.
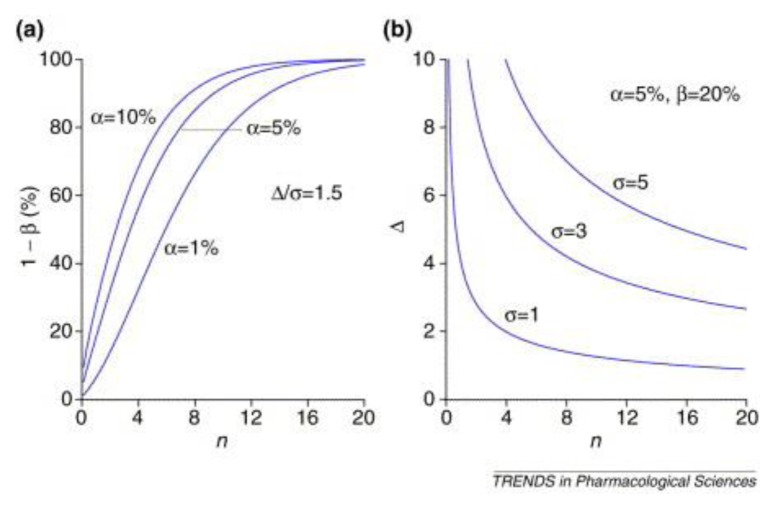
Figure 5.
The interdependence of type I error (α), type II error (β), variability (σ), the expected effect (Δ) and the sample size (n) in the statistical analysis of a given study. (a) The power of the two-tailed Student test as a function of sample size per group for a given standardized difference (i.e., Δ/σ = 1.5) and for α varying from 1% to 10% is shown. When Δ, σ and α (a false positive rate) are fixed, the power of the test (1 - β) can only be improved by increasing the sample size. (b) The difference that could be detected using a two-tailed Student test as a function of the sample size per group for given risks and for σ varying from 1 to 5 is shown. When σ, α and β (a false negative rate) are fixed, the required sample size becomes larger as the value of Δ decreases. When α, β and Δ are fixed, the estimated sample size is smaller as the variability decreases. Reproduced from Groupe Biopharmacie et Sante de la Societe Francaise de Statistique (2002), with permission.
Button et al. (2013) reported the results of 49 meta-analyses of neuroscience studies in which the median power was only 21%. The publication of this paper was followed by considerable debate about the circumstances in which small sample sizes can be justified (e.g., Quinlan, 2013; Ashton, 2013; Bacchetti, 2013, and rebuttal by Button et al., 2013b), and the issues merge with that of pseudoreplication discussed below. Smaldino and McElreath (2016) analysed the average power from 44 papers published in the social and behavioural sciences between 1960 and 2011 and found that it was 24%, with no increase over that period of time despite consistent calls for increasing statistical power in such studies. Dumas-Mallet et al. (2017) performed a meta-analysis of studies investigating the impact of biological, environmental and cognitive variables on neurological and psychiatric disorders and reported that the median statistical power for all of the studies considered together (n = 660) was between 8.5% and 29.9%. The studies of Alzheimer’s Disease had the lowest power of all (median = 8.5%) compared to the highest for major depressive disorder (median = 29.9%). Studies of somatic disease were compared and did not have more favourable power distributions, with median power values between 10.7% and 19.6%.
A great deal has been written about the problem of ‘p hacking’ in science in general and the problem exists in neuroscience as well. This term refers to a situation in which researchers intentionally collect data until they reach the point of statistical significance or select the statistical analyses that provide that result (Head et al., 2015). This results in the phenomenon of ‘publication bias,’ in which most of the published results in a field are actually false positive results (Head et al., 2015). Ioannidis et al. have also pointed out that even low power studies can result in a high rate of studies reporting false positives (Ioannidis, 2005; Ioannidis, 2015; see also Button et al., 2013a). The belief that if a difference is significant at p ≤ 0.05 then the study must be adequately powered reflects a fundamental misconception of the nature of probability and statistical power (Button et al., 2013a).
The problem of adequate sample sizes in neuroscience research is a perennial one, especially where it concerns animal-based research. Although sample size formulae can be used to determine the optimal n for a certain Δ, statistical power and variability, it can be very difficult to estimate these variables if a study is being conducted for the first time. If estimates of Δ and variability are not available from the published literature or the researcher’s previous studies, then simply guessing values can lead to very large sample sizes that are completely impractical (Bacchetti, 2013). Therefore, it is best to conduct some form of pilot study in order to estimate the information necessary to obtain reliable sample size values. Nonetheless, many researchers do not want to conduct pilot studies because of the increase in expense.
Provided reliable estimates of Δ and variability are available, the n can be estimated for a two sample Student’s t test by simple equations such as:
where zα = the type I error rate for a 2-sided test (= 1.96), z1-β = the desired power (e.g., 80% or 0.8), σ = the estimate of the standard deviation (e.g., 0.7), and Δ = the effect size of interest (15% or 0.15).
However, the sample size calculations rapidly become more complex as the design becomes more complex. Some commercial programs such as Minitab offer sample size calculations for different kinds of designs, while many such as SPSS do not offer them in the core program. There are specialized programs for calculating power and sample sizes such as nQuery; however, these are more complicated and many researchers cannot afford them. There are, however, free basic sample size calculators available on the internet such as Russ Lenth’s: http://homepage.stat.uiowa.edu/~rlenth/Power/(Lenth, 2001). Also, some introductory statistics books offer simple nomograms which allow sample sizes to be estimated visually (e.g., Pezzullo, 2013). There is no simple solution to the problem of determining optimal sample sizes in neuroscience research. Probably a major advance in addressing the problem is to be aware of it and concerned about the impact it can have on the results of the study. Increasing sample size is not the only solution to the problem. Because reducing variability increases statistical power, all other things being equal, planning to make measurements more precise by controlling sources of variability can be a very important step to increasing power (Cumming and Calin-Jageman, 2017).
The issue of sample size and statistical power is related to the problem of pseudo-replication in neuroscience (Lazic, 2010). ‘Pseudoreplication’ is a situation in which the number of ‘experimental units’, which is what a statistical test uses as the sample size, is confused with the number of observations per experimental unit. In these cases the sample size is inflated by confounding the relatively independent information, e.g., from different rats, with correlated information, e.g., from the same rat. As a result, statistical power will be artificially inflated (Lazic, 2010; see Fig. 6). A simple example of this is the scenario in which several hippocampal slices are removed from a sample of different rats, but the sample size is regarded as the number of slices rather than the number of rats. Whereas the different rats represent relatively statistically independent sources of information, the slices from the same rat do not, and when these are combined the result is a confounding of independent and correlated information. Worse still, if more slices are used from one rat than another, the total sample size will be biased towards certain individual rats, so that they will have a greater influence on the results. This can be a particular problem in single neuron recording, where, due to the technical difficulty in obtaining viable recordings from single neurons either extracellularly, intracellularly or using patch clamping, different numbers of neurons may be added together from different animals and preparations, so, for example, 20 neurons might be recorded from one rat but only 5 from another, and the sample size is regarded as 25 rather than 2 for the purposes of statistical analysis. The problem becomes even greater in the context of alert recordings in animals such as monkeys, where it is very difficult to use more than 2 or 3, and therefore, the n is regarded as the total number of neurons from the group of animals, with the possibility that one monkey is represented more than the others in the data (Fiorillo, 2010). One solution to this problem is to avoid conflating the data from different animals with data from the same animals, by either analysing them separately or building the ‘animal’ factor into a hierarchical or multi-level analysis so that it is taken into consideration (Fiorillo, 2010; Aarts et al., 2014). This relates to the fact that experiments that are better designed, by, for example, using nested split-split plot designs, can often provide greater statistical power with small sample sizes (Festing, 2003; Small et al., 2011; Aarts et al., 2014). In fact, in a recent paper by Nord et al. (2017), they suggest that the distibution of statistical power across the neuroscience studies reviewed by Button et al. (2013a), is more complex than it first appears, and that it varies substantially across different areas of neuroscience and may be related to whether a null result was obtained. However, many statisticians regard post-hoc power calculations as flawed (e.g., Hoenig and Heisey, 2001).
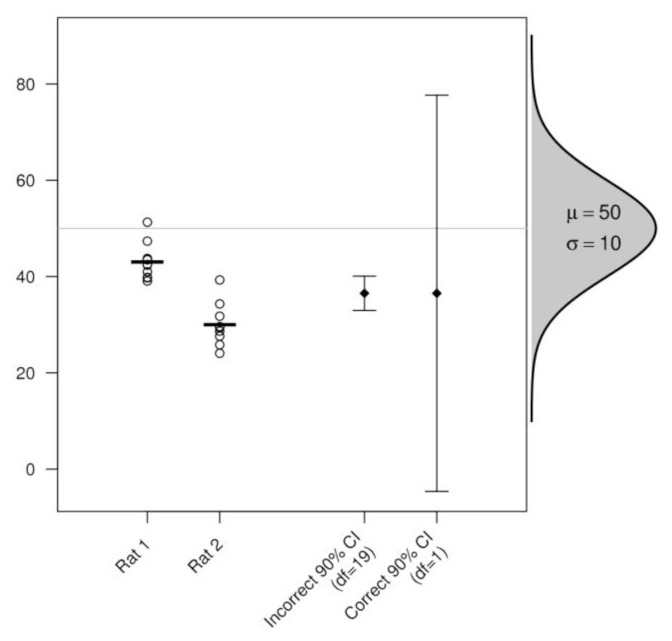
Figure 6.
An example of pseudo-replication. Two rats are sampled from a population with a mean (μ) of 50 and a standard deviation (σ) of 10, and ten measurements of an arbitrary outcome variable are made on each rat. The first (incorrect) 90% confidence interval (CI) uses all 20 data points and does not account for the hierarchical nature of the data. For the second 90% CI, the mean of the ten values for each rat is calculated first, and then only these two averaged values are used for the calculation of the CI. The error bar on the left is incorrect because each of the 20 data points is not a random sample from the whole population, but rather samples within two rats. This is evident from the fact that the 10 points are normally distributed around the mean of their respective rats, but not normally distributed around the population mean (horizontal grey line), as would be expected when independent samples are randomly drawn from a population. Increasing the number of observations on each rat does not lead to a more precise estimate of μ, which requires more rats. Note that the 90% CIs are plotted for clarity because the graph needs to be greatly compressed to display the 95% CIs. Reproduced from Lazic (2010) with permission.
THE IMPORTANCE OF EFFECT SIZES
One issue that concerns many neuroscientists, which is related to that of sample sizes and statistical power, is what some interpret to be an obsession with whether there is a significant difference, according to some arbitrary p = 0.05 criterion, as opposed to the magnitude and scientific meaning of any difference (Button et al., 2013a; Quinlan, 2013; Ashton, 2013; Bacchetti, 2013, and rebuttal by Button et al., 2013b). Quite obviously the nature of sample size calculation formulae means that for a given variability, smaller and smaller mean differences can be detected as the sample size is increased. However, the reliable detection of minute differences that have no scientific relevance is not in the interests of effective neuroscience research (Quinlan, 2013; Ashton, 2013; Bacchetti, 2013, and rebuttal by Button et al., 2013b). In the context of the Neyman-Pearson approach to NHST, there needs to be an emphasis on effect sizes rather than simply significant differences, so that information about the likely impact of the difference is provided in order to interpret its meaning (Lew, 2012; Cumming, 2012; Szucs and Ioannidis, 2017b). In subjects such as psychology, the magnitude of effects is often reported by using measures such as Cohen’s d or Eta2 values (Cumming, 2012; Szucs and Ioannidis, 2017). Partly in response to this issue, Benjamin et al. (2017, in press) have recently suggested that the significance level be changed from 0.05 to 0.005 in order to reduce the number of false positive statistical tests. Information about effects sizes is important beyond avoiding false positives, because they can be used in meta-analyses to contibute to the accumulation of evidence in a particular area (Borenstein et al., 2009). Button et al. (2013a) has pointed out, however, that an over-estimation of effect sizes can be worse for small, low-powered studies, because they can only detect large differences. This phenomenon has been referred to as the ‘winner’s curse’ (Button et al. (2013a).
CONCLUDING REMARKS
Statistical analysis is essential for effective neuroscience studies; however, in the last several years neuroscience has come under criticism for poor statistical analysis and design (e.g., Lazic, 2010; Kilkenny et al., 2009; Nieuwenhuis et al., 2011; Button et al., 2013; Curtis et al., 2015). Although many of the statistical issues that arise in neuroscience are similar to other areas of experimental biology, there are some that occur more regularly and this review has attempted to provide a guide to them. The first step to effective design and statistical analysis should always be to determine the nature of the data (e.g., discrete versus continuous variables), plan random allocation of subjects to the treatment and control groups, to consider the need for blind measurement, and how much replication is necessary. If parametric statistical tests are planned, then assumption tests should be run before using the intended analyses. Attention should be paid to evidence that the data are not normally distributed and may violate the homogeneity of variance assumption and mathematical transformations that might address these issues should be considered (see Fig. 1). An important consideration is whether the data will be likely to be correlated across time or space, i.e., repeated measurements over time or within animals or humans, and how this will impact on assumptions such as compound symmetry. Here it is worth considering using LMM analyses rather than repeated measures ANOVAs, especially if there are likely to be missing data. In programs such as SPSS and InVivoStat, running LMMs which model the correlation in repeated measures is not much more difficult than performing repeated measures ANOVAs.
It is essential that neuroscience studies are adequately powered to be capable of detecting differences of interest and, although it may not be easy, some effort to estimate effective sample sizes is necessary. With available data from previous studies this can be done using basic sample size calculators available on the internet (e.g., Lenth, 2001) or using those offered in programs such as Minitab. If such data are not available, it may be necessary to conduct a preliminary study in order to obtain that information. The actual number of independent experimental subjects should be clearly identified in order to avoid pseudo-replication (Lazic, 2010). In this case good experimental design can help to control for the influence of individual experimental subjects, e.g., animals, and also increase statistical power while reducing the number of subjects required (Festing, 2003). Finally, at least in the context of the Neyman-Pearson approach to NHST, attention needs to be shifted from mere significant differences to effect sizes as a way of gauging how meaningful the differences detected may be.
In the end, it is critical to view statistical analysis as another neuroscience tool, just like electron microscopy, immunohistochemistry or patch clamping, since it is critical to the end result of the study. It is also a way of obtaining the most out of the data, the work put into obtaining it, and the resources that have been used in the process (especially animal life). It is a good idea to be pro-active and ask for help early, preferably before the study even begins.
REFERENCES
- Aarts E, Verhage M, Veenvliet JV, Dolan CV, van der Sluis S. A solution to dependency: using multilevel analysis to accommodate nested data. Nat Neurosci. 2014;17(4):491–496. doi: 10.1038/nn.3648. [DOI] [PubMed] [Google Scholar]
- Ashton JC. Experimental power comes from powerful theories - the real problem in null hypothesis testing. Nat Rev Neurosci. 2013;14(8):585. doi: 10.1038/nrn3475-c2. [DOI] [PubMed] [Google Scholar]
- Bacchetti P. Small sample sizes are not the real problem. Nat Rev Neurosci. 2013;14(8):585. doi: 10.1038/nrn3475-c3. [DOI] [PubMed] [Google Scholar]
- Benjamin DJ, Berger JO, Johannesson M, Nosek B, Wagenmakers EJ, Berk R, et al. Redefine statistical significance. PsyArXiv Preprints. 2017 doi: 10.1038/s41562-017-0189-z. in press. [DOI] [PubMed] [Google Scholar]
- Borenstein M, Hedges LV, Higgins JPT, Rothstein HR. Introduction to meta-analysis. Chichester, UK: Wiley; 2009. [Google Scholar]
- Box GEP. Some theorems on quadratic forms applied in the study of analysis of variance problems: I: Effect of inequality of variance in the one-way classification. Ann Math Stat. 1954a;25:90–302. [Google Scholar]
- Box GEP. Some theorems on quadratic forms applied in the study of analysis of variance problems: II: Effects of inequality of variance and of correlation between errors in a two-way classification. Ann Math Stat. 1954b;25:484–498. [Google Scholar]
- Brammer RJ. Modelling covariance structure in ascending dose studies of isolated tissues and organs. Pharm Stat. 2003;2:103–112. [Google Scholar]
- Brown H, Prescott R. Applied mixed models in medicine. 2nd Edition. Chichester, England: Wiley; 2006. [Google Scholar]
- Button KS, Ioannidis JP, Mokrysz C, Nosek BA, Flint J, Robinson ES, Munafò MR. Power failure: why small sample size undermines the reliability of neuroscience. Nat Rev Neurosci. 2013a;14(5):365–376. doi: 10.1038/nrn3475. [DOI] [PubMed] [Google Scholar]
- Button KS, Ioannidis JP, Mokrysz C, Nosek BA, Flint J, Robinson ES, Munafò MR. Confidence and precision increase with high statistical power. Nat Rev Neurosci. 2013b;14(8):585–586. doi: 10.1038/nrn3475-c4. [DOI] [PubMed] [Google Scholar]
- Clark RA, Shoaib M, Hewitt KN, Stanford SC. A comparison of InVivoStat with other statistical software packages for analysis of data generated from animal experiments. J Psychopharmacol. 2012;26(8):1136–1142. doi: 10.1177/0269881111420313. [DOI] [PubMed] [Google Scholar]
- Conover WJ, Iman RL. Rank transformations as a bridge between parametric and non-parametric statistics. Am Stat. 1981;35:124–129. [Google Scholar]
- Cramer AOJ, van Ravenzwaaij D, Matzke D, Steingroever H, Wetzels R, Grasman RPPP, Waldorp LJ, Wagenmakers EJ. Hidden multiplicity in exploratory multiway ANOVA: Prevalence and remedies. Psychon Bull Rev. 2016;23:640–647. doi: 10.3758/s13423-015-0913-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crawley MJ. The R Book. Chichester, UK: Wiley; 2007. [Google Scholar]
- Cumming G. Understanding the new statistics Effect sizes, confidence intervals and meta-analysis. New York: Routledge; 2012. [Google Scholar]
- Cumming G, Calin-Jageman R. Introduction to the new statistics. Oxford, UK: Routledge; 2017. [Google Scholar]
- Curtis MJ, Bond RA, Spina D, Ahluwalia A, Alexander SP, Giembycz MA, Gilchrist A, Hoyer D, Insel PA, Izzo AA, Lawrence AJ, MacEwan DJ, Moon LD, Wonnacott S, Weston AH, McGrath JC. Experimental design and analysis and their reporting: new guidance for publication in BJP. Brit J Pharmacol. 2015;172(14):3461–3471. doi: 10.1111/bph.12856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darlington RB. Multiple testing. In: Everitt BS, Howell DC, editors. In encyclopedia of statistics in behavioral science. Chichester, UK: John Wiley and Sons; 2005. pp. 1338–1343. [Google Scholar]
- Davies TM. The book of R. San Francisco, CA: No Starch Press; 2016. [Google Scholar]
- Devinsky O, Cross JH, Laux L, Marsh E, Miller I, Nabbout R, Scheffer IE, Thiele EA, Wright S Cannabidiol in Dravet Syndrome Study Group. Trial of cannabidiol for drug-resistant seizures in the Dravet Syndrome. N Engl J Med. 2017;376(21):2011–2020. doi: 10.1056/NEJMoa1611618. [DOI] [PubMed] [Google Scholar]
- Doncaster CP, Davey AJH. Analysis of variance and covariance. Cambridge: Cambridge University Press; 2007. [Google Scholar]
- Dumas-Mallet E, Button KS, Boraud T, Gonon F, Munafò MR. Low statistical power in biomedical science: a review of three human research domains. R Soc Open Sci. 2017;4(2):160254. doi: 10.1098/rsos.160254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eng J. Sample size estimation: How many individuals should be studied? Radiol. 2003;227:309–313. doi: 10.1148/radiol.2272012051. [DOI] [PubMed] [Google Scholar]
- Field A. Discovering statistics using SPSS. Los Angeles, CA: Sage; 2011. [Google Scholar]
- Field A, Miles J, Field Z. Discovering statistics using R. Los Angeles, CA: Sage; 2012. [Google Scholar]
- Festing MFW. Principles: The need for better experimental design. Trends Pharmacol Sci. 2003;24:341–345. doi: 10.1016/S0165-6147(03)00159-7. [DOI] [PubMed] [Google Scholar]
- Fiorillo CD. Response to Lazic. BMC Neurosci. 2010;11:5. [Google Scholar]
- Fitzmaurice GM, Laird NM, Ware JH. Applied longitudinal analysis. Hoboken, NJ: Wiley; 2004. [Google Scholar]
- Fosang AJ, Colbran RJ. Transparency is the key to quality. J Biol Chem. 2015;290:29692–29694. doi: 10.1074/jbc.E115.000002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gamst G, Meyers LS, Guarino AJ. A conceptual and computational approach with SPSS and SAS. New York: Cambridge University Press; 2008. Analysis of variance designs. [Google Scholar]
- Gigerenzer G. Mindless statistics. J Soc Econom. 2004;33:587–606. [Google Scholar]
- Gilchrist DPD, Smith PF, Darlington CL. ACTH (4–10) accelerates ocular motor recovery in the guinea pig following vestibular deafferentation. Neurosci Letts. 1990;118:14–16. doi: 10.1016/0304-3940(90)90237-4. [DOI] [PubMed] [Google Scholar]
- Groupe Biopharmacie et Sante de la Societe Francaise de Statistique. How much for a star? Elements for a rational choice of sample size in preclinical trials. Trends Pharmacol Sci. 2002;23(5):221–224. doi: 10.1016/s0165-6147(02)01995-8. [DOI] [PubMed] [Google Scholar]
- Gurka MJ, Edwards LJ. Mixed models. In: Rao CR, Miller JP, Rao DC, editors. Essential statistical methods for medical statistics. Amsterdam: Elsevier; 2011. pp. 146–173. [Google Scholar]
- Head ML, Holman L, Lanfear R, Kahn AT, Jennions MD. The extent and consequences of p-hacking in science. PLoS Biol. 2015;13(3):e1002106. doi: 10.1371/journal.pbio.1002106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoenig JM, Heisey DM. The abuse of power: the pervasive fallacy of power calculations for data analysis. Am Stat. 2001;55(1):19–24. [Google Scholar]
- Ioannidis JPA. Why most published research findings are false. PLoS Med. 2005;2(8):e124. doi: 10.1371/journal.pmed.0020124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ioannidis JPA. Contradicted and initially stronger effect in highly cited clinical research. JAMA. 2015;294:218–228. doi: 10.1001/jama.294.2.218. [DOI] [PubMed] [Google Scholar]
- Keppel G, Wickens TD. Design and analysis: a researcher’s handbook. 4th Edition. Saddle River, NJ: Pearson Prentice Hall; 2004. [Google Scholar]
- Keselman HJ, Holland B, Cribbie RA. Multiple comparison procedures. In: Everitt BS, Howell DC, editors. In encyclopedia of statistics in behavioral science. Chichester, UK: John Wiley and Sons; 2005. pp. 1309–1325. [Google Scholar]
- Kilkenny C, Parsons N, Kadyszewski E, Festing MF, Cuthill IC, Fry D, Hutton J, Altman DG. Survey of the quality of experimental design, statistical analysis and reporting of research using animals. PLoS One. 2009;4(11):e7824. doi: 10.1371/journal.pone.0007824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirk RE. Experimental design Procedures for the behavioral sciences. 4th Edition. Los Angeles, CA: Sage; 2013. [Google Scholar]
- Kuehl RO. Design of experiments: statistical principles of research design and analysis. 2nd Edition. Pacific Grove, CA: Duxbury Press; 2000. [Google Scholar]
- Kutner MH, Nachtsheimm CJ, Neter J, Li W. Applied linear statistical models. Boston, MA: McGraw-Hill Irwin; 2005. [Google Scholar]
- Lazic SE. The problem of pseudoreplication in neuroscientific studies: is it affecting your research? BMC Neurosci. 2010;11:5. doi: 10.1186/1471-2202-11-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenth RV. Some practical guidelines for effective sample size determination. Am Stat. 2001;55:87–193. [Google Scholar]
- Lesaffre E, Lawson AB. Bayesian biostatistics. Chichester, UK: Wiley; 2012. [Google Scholar]
- Lew MJ. Bad statistical practice in pharmacology (and other basic biomedical disciplines): you probably don’t know P. Brit J Pharmacol. 2012;166:1559–1567. doi: 10.1111/j.1476-5381.2012.01931.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lilford RJ, Mohammed MA, Braunholtz D, Hofer TP. The measurement of active errors: methodological issues. Qual Saf Health Care. 2003;12(Suppl II):ii8–ii12. doi: 10.1136/qhc.12.suppl_2.ii8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Little RC, Pendergast J, Natarajan R. Modelling covariance structure in the analysis of repeated measures data. Stats Med. 2000;19:1793–1819. doi: 10.1002/1097-0258(20000715)19:13<1793::aid-sim482>3.0.co;2-q. [DOI] [PubMed] [Google Scholar]
- Loken E, Gelman A. Measurement error and the replication crisis. Science. 2017;355:584–585. doi: 10.1126/science.aal3618. [DOI] [PubMed] [Google Scholar]
- Miller I, Miller M. John E. Freund’s mathematical statistics with applications. NJ: Pearson Prentice Hall; 2004. [Google Scholar]
- Motulsky H. Intuitive biostatistics. New York: Oxford University Press; 1995. [Google Scholar]
- Nieuwenhuis S, Forstmann BU, Wagenmakers EJ. Erroneous analyses of interactions in neuroscience: a problem of significance. Nat Neurosci. 2011;14(9):1105–1107. doi: 10.1038/nn.2886. [DOI] [PubMed] [Google Scholar]
- Nord CL, Valton V, Wood J, Roiser JP. Power up: a re-analysis of ‘power failure’ in neuroscience using mixture modelling. J Neurosci. 2017;37(34):8051–8061. doi: 10.1523/JNEUROSCI.3592-16.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norman G, Monteiro S, Salama S. Sample size calculations: Should the emperor’s clothes be off the peg or made to measure? Brit Med J. 2012;345:19–21. doi: 10.1136/bmj.e5278. [DOI] [PubMed] [Google Scholar]
- Perezgonzalez DD. Fisher, Neyman-Pearson or NHST? A tutorial for teaching data testing. Front Psychol. 2015;6:223. doi: 10.3389/fpsyg.2015.00223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pezzullo JC. Biostatistics for dummies. Hoboken, NJ: Wiley Press; 2013. [Google Scholar]
- Quinlan PT. Misuse of power: In defense of small-scale science. Nat Rev Neurosci. 2013;14(8):585. doi: 10.1038/nrn3475-c1. [DOI] [PubMed] [Google Scholar]
- Quinn GP, Keough MJ. Experimental design and data analysis for biologists. Cambridge: Cambridge University Press; 2002. [Google Scholar]
- Rao CR, Miller JP, Rao DC. Essential statistical methods for medical statistics. Amsterdam: Elsevier; 2011. [Google Scholar]
- Rutherford A. Introducing ANOVA and ANCOVA A GLM approach. London, UK: Sage Publications; 2001. [Google Scholar]
- Ruxto GD, Beauchamp G. Time for some a prior thinking about post-hoc testing. Behav Ecol. 2008;19(3):690–693. [Google Scholar]
- Skene SS, Kenward MG. The analysis of very small samples of repeated measurements I: an adjusted sandwich estimator. Stats Med. 2010a;29:2825–2837. doi: 10.1002/sim.4073. [DOI] [PubMed] [Google Scholar]
- Skene SS, Kenward MG. The analysis of very small samples of repeated measurements II: a modified Box correction. Stats Med. 2010b;29:2838–2856. doi: 10.1002/sim.4072. [DOI] [PubMed] [Google Scholar]
- Small DS, Volp KG, Rosenbaum PR. Structured testing of 2 × 2 factorial effects: An analytic plan requiring fewer observations. Am Stat. 2011;65(1):11–15. [Google Scholar]
- Smaldino PE, McElreath R. The natural selection of bad science. Royal Soc Open Sci. 2016;3:160384. doi: 10.1098/rsos.160384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith PF. A note on the advantages of using linear mixed model analysis with maximal likelihood estimation over repeated measures ANOVAs in psychopharmacology: Comment on Clark et al. (2012) J Psychopharmacol. 2012;26(12):1605–1607. doi: 10.1177/0269881112463471. [DOI] [PubMed] [Google Scholar]
- Smith PF. Age-related neurochemical changes in the vestibular nuclei. Front Neurol. 2016;7:20. doi: 10.3389/fneur.2016.00020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snedecor GW, Cochran WG. Statistical methods. 8th Edition. Ames, IA: Iowa State University Press; 1989. [Google Scholar]
- Stiles L, Zheng Y, Darlington CL, Smith PF. The D2 dopamine receptor and locomotor hyperactivity following bilateral vestibular deafferentation in the rat. Behav Brain Res. 2012;227:150–158. doi: 10.1016/j.bbr.2011.11.006. [DOI] [PubMed] [Google Scholar]
- Szucs D, Ioannidis JPA. When null hypothesis significance testing is unsuitable for research: a reassessment. Front Hum Neurosci. 2017a;11:390. doi: 10.3389/fnhum.2017.00390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szucs D, Ioannidis JPA. Empirical assessment of published effect sizes and power in the recent cognitive neuroscience and psychology literature. PLoS Biol. 2017b;15(3):e2000797. doi: 10.1371/journal.pbio.2000797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verbitsky O. Experimental versus evaluation unit and multiplicity problem in cell biology study. Cell Biochem Biophys. 2013;66:157–159. doi: 10.1007/s12013-012-9464-9. [DOI] [PubMed] [Google Scholar]
- Vittinghoff E, Glidden DV, Shiboski SC, McCulloch CE. Regression methods in statistics: linear, logistic, survival and repeated measures models. New York, NY: Springer; 2005. [Google Scholar]
- Wasserstein RL, Lazar NA. The ASA’s statement on p-values: Context, process, and purpose. Am Stat. 2016;70(2):129–133. [Google Scholar]
- West BT, Welch KB, Galecki AT. A practical guide using statistical software. Boca Raton, FL: Chapman and Hall/CRC; 2007. Linear mixed models. [Google Scholar]
- Wilcox RR. New designs in analysis of variance. In: Rosenweig MR, Porter LW, editors. Ann Rev Psychol. Palo Alto, CA: Annual Reviews Inc; 1987. pp. 29–60. [Google Scholar]
- Winer BJ, Brown DR, Michels KM. Statistical principles in experimental design. 3rd Edition. New York: McGraw-Hill; 1991. [Google Scholar]
- Zheng Y, Cheung I, Smith PF. Performance in anxiety and spatial memory tests following bilateral vestibular loss in the rat and effects of anxiolytic and anxiogenic drugs. Behav Brain Res. 2012a;235:21–29. doi: 10.1016/j.bbr.2012.07.025. [DOI] [PubMed] [Google Scholar]
- Zheng Y, McNamara E, Stiles L, Darlington CL, Smith PF. Evidence that memantine reduces chronic tinnitus caused by acoustic-trauma in rats. Front Neuro-Otol. 2012b;127:1–10. doi: 10.3389/fneur.2012.00127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng Y, McPherson K, Smith PF. Effects of early and late treatment with L-baclofen on the development and maintenance of tinnitus caused by acoustic trauma in rats. Neurosci. 2014;258:410–421. doi: 10.1016/j.neuroscience.2013.11.032. [DOI] [PubMed] [Google Scholar]
- Zheng Y, Reid P, Smith PF. Cannabinoid CB1 receptor agonists do not decrease, but may increase, acoustic trauma-induced tinnitus in rats. Front Neuro-Otol. 2015;6:60. doi: 10.3389/fneur.2015.00060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng Y, Wilson G, Stiles L, Smith PF. Glutamate receptor subunit and calmodulin kinase II expression in the rat hippocampus, with and without T maze experience, following bilateral vestibular deafferentation. PLoS ONE. 2013;8(2):e54527. doi: 10.1371/journal.pone.0054527. [DOI] [PMC free article] [PubMed] [Google Scholar]