DNA knots occur in intracellular chromatin

Abstract

In vivo DNA molecules are narrowly folded within chromatin fibers and self-interacting chromatin domains. Therefore, intra-molecular DNA entanglements (knots) might occur via DNA strand passage activity of topoisomerase II. Here, we assessed the presence of such DNA knots in a variety of yeast circular minichromosomes. We found that small steady state fractions of DNA knots are common in intracellular chromatin. These knots occur irrespective of DNA replication and cell proliferation, though their abundance is reduced during DNA transcription. We found also that in vivo DNA knotting probability does not scale proportionately with chromatin length: it reaches a value of ∼0.025 in domains of ∼20 nucleosomes but tends to level off in longer chromatin fibers. These figures suggest that, while high flexibility of nucleosomal fibers and clustering of nearby nucleosomes facilitate DNA knotting locally, some mechanism minimizes the scaling of DNA knot formation throughout intracellular chromatin. We postulate that regulation of topoisomerase II activity and the fractal architecture of chromatin might be crucial to prevent a potentially massive and harmful self-entanglement of DNA molecules in vivo.

INTRODUCTION

DNA topoisomerases are nature's solution for removing the DNA entanglements that occur during the genome transactions. In particular, the type-2A topoisomerases bacterial topo IV and eukaryotic topo II use ATP to catalyze the passage of one segment of duplex DNA through an enzyme-mediated transient double-strand break in another (1). By this mechanism, inter-molecular passage of DNA segments leads to the catenation or decatenation of different DNA molecules, whereas intra-molecular DNA passage leads to change the number of DNA supercoils within a topological domain (1). The activity of topo IV and topo II is essential for chromosome replication and segregation, during which they remove the intertwines between the newly replicated DNA molecules (2,3). Type-2A enzymes are also necessary for the normal progression of DNA replication and transcription, during which they relax the positive DNA supercoils generated ahead of the DNA and RNA polymerases (2,3).

Another possible outcome of the type-2A topoisomerase activity is that intra-molecular DNA passage can lead to the formation or removal of DNA knots (4). In vitro studies had shown that type-2A enzymes produce abundant and complex DNA knots when juxtaposition of intra-molecular DNA segments is enhanced by DNA supercoiling, protein–DNA interactions or other DNA condensing agents (5–7). In turn, when knotted DNA molecules are naked in free solution, topo IV and topo II unknot them efficiently and are able to reduce the fractions of knotted molecules to values below than those corresponding to the thermodynamic equilibrium (8).

Whereas the implication of type-2A topoisomerases in the modulation of DNA supercoiling and in the resolution of intertwines between the newly replicated DNA molecules has been widely studied, little is known about their DNA knotting-unknotting activity in vivo. Indeed, the occurrence of DNA knots has been scarcely documented in living cells. In the context of bacteria, DNA knots have been found to accumulate in plasmids hosted in Escherichia coli strains that harbor mutations in topoisomerase genes (9,10). DNA knot formation has also been observed in replication bubbles of bacterial plasmids when replication forks are stalled (11,12). These knots are produced and eventually removed by the activity of topo IV (13,14). In the case of eukaryotes, to the best of our knowledge the occurrence of DNA knots has not been reported to date. In this regard, in vitro experiments had shown that DNA knots interfere with chromatin assembly and DNA transcription (15,16). Thus, a general assumption is that eukaryotic DNA is virtually knot-free. Consistent with this view, genome-wide analyses of chromosome architecture show little topological complexity (knotting or inter-linking) between the self-interacting domains (TADs) of eukaryotic chromatin (17,18). However, these experimental approaches have a resolution of tens to hundreds of DNA kilobases and are unable to discern whether intracellular DNA is entangled in shorter length scales. In that respect, computer simulations of polymer physics predict a high knotting probability when DNA molecules are condensed or confined in reduced volumes (19–21). Consequently, the occurrence of knots in chromatinized DNA could be significant within short length scales given the high concentration of DNA segments packaged within chromatin fibers and the abundant topo II activity that can pass such DNA segments through each other.

Here, we present the first evidence and analysis of the occurrence of DNA knots in eukaryotic chromatin. To this end, we used high resolution two-dimensional electrophoresis to assess the presence of DNA knots in yeast circular minichromosomes of distinct size and genetic configuration. We examined the relation of knot formation with DNA replication and transcription, and measured the dependence of DNA knotting probability on the size of the minichromosomes. We show that steady-state fractions of DNA knots are common in eukaryotic chromatin. This experimental finding sheds new light on the configuration and dynamics of nucleosomal fibers in vivo. We show also that the occurrence of DNA knots does not scale proportionally to the length of the nucleosomal fibers. This observation denotes the existence of a crucial mechanism that prevents the massive entanglement of intracellular DNA.

MATERIALS AND METHODS

Yeast strains, circular minichromosomes and knotted plasmids

Experiments were conducted with the Saccharomyces cerevisiae strain FY251 (S288C genetic background MATa his3-D200 leu2-D1 trp1-D63 ura3–52)) and its derivatives. The Δtop1 deletion mutant and the thermo-sensitive top2–4 mutant were obtained as described previously (22). Minichromosomes YRp3, YRp4, YRp401, YEp24, YCp50, YEp13 and YRp21 (Supplementary Figure S1) were amplified and purified as bacterial plasmids from Escherichia coli. Minichromosomes YRp1 and YRp2, which lack bacterial sequences, were constructed by circularization of linear DNA fragments. Monomeric forms of plasmids and DNA circles were gel-purified to transform yeast following standard procedures. Production of DNA knots in vitro was done by reacting purified bacterial plasmids with molar excess of topo II as described in Supplementary Figure S2.

Yeast culture and DNA extraction

Yeast cells were grown at 26°C in yeast synthetic media containing adequate dropout supplements and 2% glucose. Liquid cultures were monitored by optical density and flow cytometry for DNA content. pGAL1 promoter was activated or repressed by transferring sedimented cells into YP Broth media containing 2% galactose or 2% glucose, respectively. Before harvesting yeast cells, the DNA topology of circular minichromosomes was fixed in vivo as described previously (23) by quickly mixing the liquid cultures with one cold volume (–20°C) of ETol solution (ethanol 95%, 28 mM Toluene, 20 mM Tris–HCl pH 8.8, 5 mM EDTA). Fixed cells from a 25 ml culture were sedimented, washed twice with water, resuspended in 400 μl of TE (10 mM Tris HCl pH 8.8, 1 mM EDTA) and transferred to a 1.5-ml microfuge tube containing 400μl of phenol and 400μl of acid-washed glass beads (425–600 μm, Sigma). Mechanic lysis of >80% cells was achieved by shaking the tubes in a FastPrep^® apparatus for 10 s at power 5. The aqueous phase of the cell lysates was collected, extracted with chloroform, precipitated with ethanol, and dissolved in 100 μl of TE containing RNAse-A. Following 10 min incubation at 37°C, ammonium acetate was added to 0.5 M and DNA was precipitated with ethanol. Each DNA sample was dissolved in 50 μl of TE.

DNA electrophoresis

To observe the Lk distribution of the minichromosomes, 10 μl of each DNA sample was electrophoresed in a two-dimensional agarose gel in TBE buffer (89 mM Tris-borate, 2m M EDTA) containing 0.6 μg/ml chloroquine in the first dimension and 3 μg/ml chloroquine in the second dimension. To observe the knot species present in the minichromosomes, 40 μl of each DNA sample was reacted with nicking endonuclease BstNB1 (NEB). Serial dilutions of the nicked DNA samples were electrophoresed in two-dimensional agarose gel in TBE buffer and run at low and high voltage as described previously (24). Electrophoresis settings (agarose concentration, voltage and running time) were adjusted to the size of each minichromosome and are specified in Supplementary Table S1. Gels were blot-transferred to a nylon membrane and probed with minichromosome-specific DNA sequences labeled with AlkPhos Direct (GE Healthcare^®) or radio-labeled with ³²P. Probe signals of increasing exposure periods were recorded on X-ray films and by phosphorimaging.

DNA topology and numerical analyses

Lk distributions were analyzed as described previously (23). ΔLk was calculated by counting the number of Lk topoisomers spanning from the center of the interrogated Lk distribution to the center of the Lk distribution of relaxed DNA. Individual knot populations were quantified by using the ImageJ software on non-saturated signals obtained with serial dilutions (1, 0.1, 0.01, 0.001) of DNA samples loaded in the 2D gels. The relative abundancy of individual knot populations was calculated with respect to total amount of unknotted and knotted DNA circles. The graph that correlates knot complexity and the persistence length (P_L) of a thin chain was generated with the data of Frank-Kamenetskii et al. (25). Using these data, the relative abundancy of knots of more than three crossings (Kn > 3) was plotted as a function of the P_L (nm) of a chain of contour length 380 nm. The graph that correlates knot probability with the P_L and effective diameter d_E of a simulated chain was generated with the data of Rybenkov et al. (26), which described that the probability K^P of a knot of n statistical Kuhn lengths (Kuhn length = 2.P_L) and diameter d is given by the empirical equation K^P(n,d) = K^P(n, d zero)exp(-r.d/b), where b is the Kuhn length and r depends on the knot type and equals 22 for knot 3₁. Corresponding P_L and d_E values were determined for a chain of contour length 380 nm that produced the 3₁ knot with a probability of 0.017 (like minichromosome YRp4).

RESULTS

Electrophoretic characterization of knotted DNA

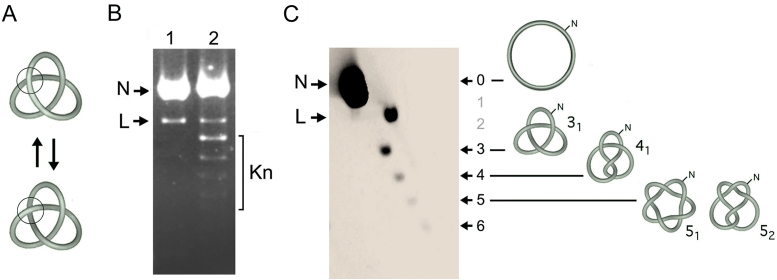
The DNA passage activity of topo II in a circular molecule of double-stranded DNA can result in the inversion of supercoil crossings but also in the formation or removal of DNA knots (Figure 1A). When the resulting DNA molecules are nicked, their helical tension (supercoiling) dissipates because the duplex can swivel around the uncleaved strand. However, the knots remain entrapped in the circular molecule. Since nicked DNA rings containing a knot are more compacted than the unknotted nicked circles, these forms have different velocities during agarose gel electrophoresis (Figure 1B). However, identification of knotted nicked DNA circles in one-dimensional gels can be ambiguous because they overlap with linear DNA fragments. This overlying can completely mask knotted molecules in DNA samples that contain abundant fragments of genomic DNA (i.e. whole cell extracts). This problem is solved by running a high resolution two-dimensional (2D) gel electrophoresis (Figure 1C). In the first gel-dimension, which is done at low voltage, knotted molecules have a gel velocity that correlates about linearly to knot complexity (i.e. the irreducible number of DNA crossings in a knot, Kn) (27). Accordingly, relative to the position of the unknotted circle that has zero crossings (trivial knot), positions corresponding to one and two crossings are empty because the simplest knot that has three crossings (trefoil knot or 3₁) (Figure 1C). Knot populations of increasing complexity form then a ladder that begins with 3₁ followed by the knot with four crossing (4₁), two knots with five crossings (5₁ and 5₂), and so on (Figure 1C). In the second gel-dimension, the gel is turned in orthogonal direction and electrophoresis is done at high voltage. In these conditions, the ladder of knotted molecules is retarded relative to the diagonal of linear DNA fragments (L) (24), thereby allowing unambiguous identification and quantification of individual knot populations (Figure 1C).

Figure 1.

Identification of DNA knot species by 2D gel electrophoresis. (A) Interconversion of the unknotted (top) and knotted (bottom) forms of a double-stranded DNA circle by the DNA passage activity of topo II (ball). (B) The agarose gel shows a 4.4 kb DNA plasmid before (lane 1) and after incubation with an excess of topo II to favor knot formation (lane 2). Before loading the gel, plasmid samples were nicked with a site-specific endonuclease to eliminate DNA supercoils. N, unknotted nicked circles. L, linearized DNA. Kn, knotted nicked circles. (C) The previous sample of lane 2 was examined in a 2D agarose gel electrophoresis. The first gel dimension (top to bottom at low voltage) separated knot species by their irreducible number DNA crossings, Kn, indicated as 3, 4, 5, 6. The position corresponding to 0 crossings (un-knotted ring or trivial knot) and the two empty slots corresponding to 1 and 2 crossings are indicated. The second gel dimension (left to right at high voltage) segregated the ladder of knot forms from the linear DNA molecules (L), which acquired higher gel velocity. Illustrations depict ideal shapes of the un-knotted nicked ring, the knot of three crossings (trefoil knot or 3₁), four crossing (4₁), and the two knots of five crossings (5₁ and 5₂). The 2D-gel electrophoresis was conducted, blotted and probed as described in the methods and Supplementary Table S1.

DNA knots occur in eukaryotic chromatin

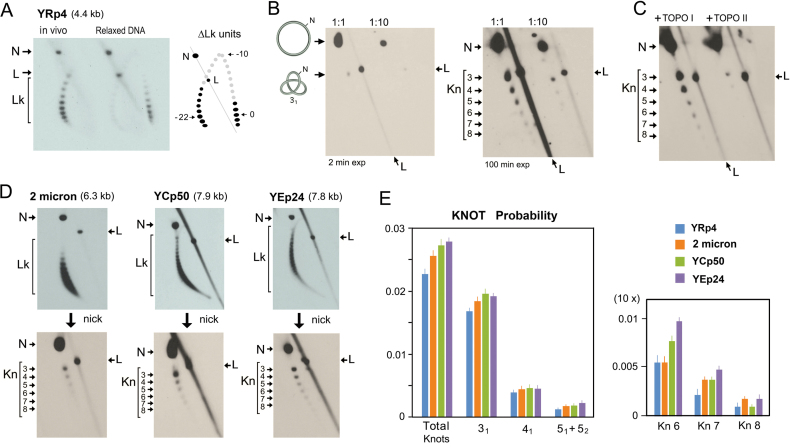
In order to examine the occurrence of DNA knots in vivo, we used yeast cells that hosted a variety of circular minichromosomes (Supplementary Figure S1). We grew the cells to exponential phase and fixed them quickly with a cold ethanol-toluene solution. As described in previous studies (23), this fixation step inactivates the cellular topoisomerases and precludes plausible alterations of the DNA topology of the minichromosomes during DNA extraction and subsequent manipulations. We loaded one part of the DNA sample in a 2D gel containing chloroquine in order to examine the DNA linking number (Lk) of the minichromosomes. We enzymatically nicked the remaining DNA sample and loaded it in a 2D gel of low-high voltage to test the presence of DNA knots. Figure 2 shows the results obtained with cells containing the replicative minichromosome YRp4 (4.4 kb). This minichromosome presented a Gaussian distribution of Lk values in vivo, which denoted the absence of subpopulations with unconstrained positive or negative DNA supercoiling. Comparison of the Lk distribution of YRp4 in vivo with that of the relaxed DNA in vitro indicated that the minichromosome has a Lk difference (ΔLk) of about –22 (Figure 2A). As indicated in previous studies (28), this ΔLk value was consistent with the stabilization of about one negative supercoil (ΔLk ≈ –1) per nucleosome (29) and the presence of 22 nucleosomes since the nucleosomal density of yeast chromatin is about 1 nucleosome/200 base pairs (30). Upon nicking the YRp4 DNA, all the supercoils were eliminated and the presence of knots was revealed (Figure 2B). A prominent knot 3₁ was followed by a monotonic ladder of knot species of increasing complexity. Knots with more than eight DNA crossings were discernible after long-exposure of the 2D gel-blots (Figure 2B). We corroborated that this ladder was formed by knotted double-stranded DNA circles because it was reduced when we reacted the DNA sample with topo II (Figure 2C). However, no change was produced when we treated the sample with topo I (Figure 2 C). We conducted analogous experiments to that of YRp4 with other yeast minichromosomes (Supplementary Figure S1), such as the yeast endogenous 2-micron plasmid (6.3 kb), the episomal plasmid YEp24 (7.8 kb) and the centromeric plasmid YCp50 (7.9 kb) (Figure 2D). We found that all these minichromosomes had a DNA knotting probability (k^P_CHR) comparable to that of YRp4 (k^P_CHR between 0.02 and 0.03) and presented similar patterns of knot complexity (Figure 2E).

Figure 2.

Yeast minichromosomes contain complex DNA knots. (A) Typical 2D gel electrophoresis of covalently closed DNA in presence of chloroquine, which displays the DNA linking number (Lk) distribution of the YRp4 minichromosome in vivo and of the YRp4 DNA relaxed in vitro. The Lk difference was calculated as the distance (ΔLk units) between the center of both Lk distributions across the arch of individual Lk topoisomers. (B) The in vivo DNA sample of YRp4 was enzymatically nicked and loaded in a 2D gel for analysis of DNA knotting. Gel lanes show 1:1 and 1:10 dilutions of the sample. Left and right panels show, respectively, short (2 min) and long exposures (100 min) of the gel-blot. (C) Result of the incubation of the nicked DNA sample of YRp4 with yeast topoisomerase I (TOPO I) and yeast topoisomerase II (TOPO II). (D) Lk distributions and knots species of the yeast 2-micron plasmid, YCp50 and Yep24 minichromosomes. The 2D gels in A-D were conducted, blotted and probed as described in the methods and Supplementary Table S1. The signals of nicked unknotted circles (N), linear DNA (L), Lk distributions (Lk) and knot populations with different irreducible number DNA crossings, Kn, (3–8) are indicated. (E) Total DNA knot probability and of knots 3₁, 4₁, 5₁+5₂, and knot species of 6 to 8 crossings (Kn6, Kn7, Kn8) in the indicated yeast minichromosomes. The plots show the mean and ±SD of three experiments.

Chromatin knots are not a byproduct of DNA replication

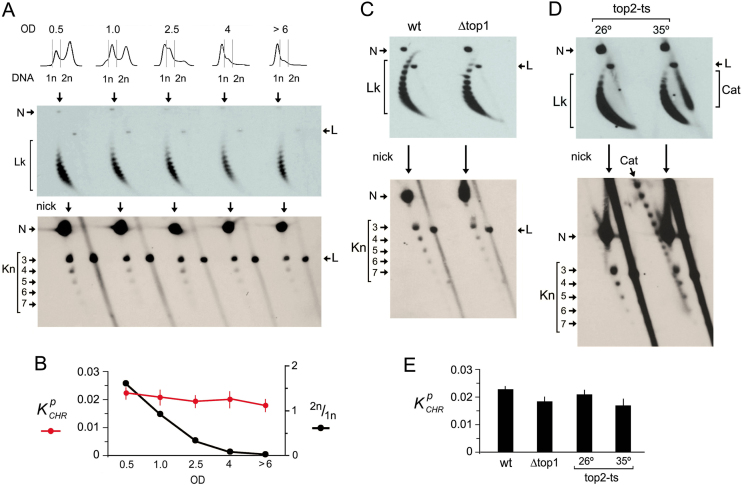
Minichromosomes YRp4, YEp24, YCp50 and the endogenous 2-micron plasmid differ in copy number and have distinct DNA replication origins and DNA transcription units (Supplementary Figure S1). The observation that they all presented similar DNA knotting probability and complexity suggested that knot formation was not related to DNA transactions (i.e. replication and transcription) or the presence of specific chromatin elements (i.e. centromeres). Consistent with this, we found that the k^P_CHR values were not meaningfully altered when yeast cultures passed from exponential growth to stationary phase and quiescence (Figure 3A). Accordingly, k^P_CHR values did not correlate with the relative abundance of DNA replicating cells (Figure 3B). We next examined knot formation in yeast topoisomerase mutants. Knotted fractions did not present significant changes in cells lacking topo I (Δtop1) or in cells with reduced topo II activity (top2-ts) (Figure 3C and D). Upon thermal inactivation of topo II, dimeric catenanes of newly replicated minichromosomes accumulated. These replication catenanes migrated as compacted structures in the 2D gels used for Lk analysis (Figure 3D). After nicking the DNA, these catenanes produced a ladder of species that differed in the number of catenation links (Figure 3D). Even in this condition, the fraction of knotted molecules was not significantly altered, thereby corroborating that the knots observed were not a byproduct of DNA replication (Figure 3E).

Figure 3.

Chromatin knots occur irrespective of cell proliferation and DNA replication. (A) Cells containing the YRp4 minichromosome were sampled during exponential growth (OD 0.5 and 1.0), during the shift to stationary phase (OD 2.5 and 4) and during the quiescent stage (OD > 6). The cellular DNA content (1n, 2n), the Lk distribution and the knot species of YRp4 present in each sample are shown. (B) Comparison of k^P_CHR values and the abundance of replicating cells (2n/1n) (mean and ±SD of three experiments). (C and D) Lk distribution and knot species of YRp4 present in wt cells, Δtop1 mutants and top2-ts mutants before (26°C) and after thermal inactivation of topoisomerase II (35°C during 2 h). The 2D-gel electrophoreses in A, C and D were run, blotted and probed as described in the methods and Supplementary Table S1. Gel signals are annotated as described in Figure 2. Position of un-nicked and nicked replication catenanes (Cat) are indicated in the gels for Lk analysis and knot analysis, respectively. (E) k^P_CHR values (mean and ±SD of three experiments) in wt cells, Δtop1 mutants and top2-ts mutants.

Steady state fractions of knots are maintained by topoisomerase II

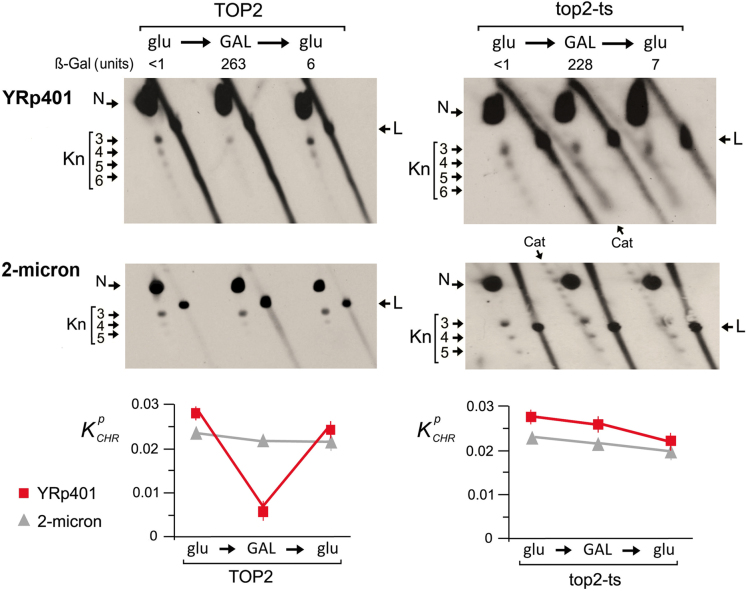
The above results suggested that the DNA knotting probability of yeast minichromosomes reflected a general property of the in vivo chromatin structure. We envisaged that the occurrence of knots could be then altered by enforcing a structural change in a whole population of minichromosomes. To test this notion, we used the minichromosome YRp401 (8.1 kb), which carries the sugar-regulatable pGAL1 promoter on a reporter LacZ gene (Supplementary Figure S1). We examined knot formation in YRp401 before and after the induction of high rates of DNA transcription (Figure 4). When pGAL1 was repressed in glucose-containing media, YRp401 had a k^P_CHR of 0.027, a knotting probability comparable to that of the endogenous 2-micron circle present in the same cells. However, when the pGAL1 promoter was activated in galactose-containing media, the k^P_CHR of YRp401 was reduced about four-fold, and when transcription was repressed again in glucose-containing media, the initial k^P_CHR value of this minichromosome was recovered. We next questioned whether this unknotting and re-knotting process was mediated by topo II activity. We therefore repeated the same experiment in the top2-ts mutant strain, in which we inhibited topo II before activating pGAL1 (Figure 4). In this condition, transcription of the LacZ gene was similarly induced and repressed, as denoted by ß-galactosidase activity. However, the unknotting and re-knotting process did not occur. These observations indicated that the formation and resolution of the DNA knots is a dynamic process that relies on the DNA-strand passage activity of topo II and that steady-state fractions of knots reflect a general trait of chromatin conformation in vivo.

Figure 4.

Chromatin knots are removed and reformed by topoisomerase II. The 2D gels compare knot formation in the YRp401 minichromosome, which carries pGAL1:LacZ. Experiments were conducted in TOP2 and in top2-ts yeast cells, and the knots produced in YRp401 were contrasted with the knots produced in the endogenous 2-micron plasmid. Yeast cultures were sampled during exponential growth at 26°C in glucose-containing media (glu), after shifting them 3 h at 35°C in galactose-containing media (GAL), and after 3 h back in glucose-containing media (glu). Lac Z transcription was monitored by the ß-galactosidase activity of cell lysates. The 2D-gel electrophoreses were run, blotted and probed as described in the methods and Supplementary Table S1. Gel signals are annotated as described in Figures 2 and 3. The plots show mean mean and ±SD of k^P_CHR of the YRp401 minichromosome and the 2-micron plasmid in two experiments.

DNA knot formation does not increase proportionally to chromatin length

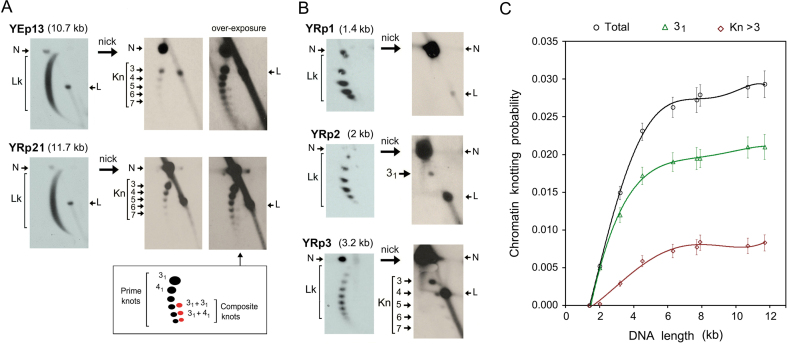
Computer simulations had predicted that the knotting probability of a random chain increases proportionally to the chain length (25). Subsequent in vitro experiments corroborated that the knotting probability of DNA during the circularization of linear DNA molecules in free solution increases proportionally to their length (26,31). We have observed that a similar length dependence appears also when DNA plasmids of different sizes are knotted by treating them with a molar excess of topo II in vitro (Supplementary Figure S2). In this regard, we noticed that such length dependence did not occur in vivo with the minichromosomes between 4.4 and 7.9 kb, since they all presented similar k^P_CHR values (Figure 2E). Thus, we measured k^P_CHR in a broader range of minichromosome sizes (Supplementary Figure S1). On the one hand, the episomal YEp13 (10.7 kb) and the replicative YRp21 (11.7 kb) presented a k^P_CHR of ∼0.028 (Figure 5A). This value was still comparable to that of minichromosomes of half their length. Regarding knot complexity, YEp13 and YRp21 showed a monotonic ladder of prime knots (i.e. indecomposable knots) alike the minichromosomes between 4.4 to 7.9 kb. However, YEp13 and YRp21 presented additional composite knots (i.e. 3₁+3₁ and 3₁+4₁), which we could not detect in shorter constructs. These composite knots migrated according to their minimal number of crossings in the first dimension, but moved faster than prime knots in the second dimension (Figure 5A). On the other hand, the k^P_CHR values dropped sharply in minichromosomes of size <4 kb (Figure 5B). Minichromosomes YRp3 (3.2 kb) and YRp2 (2 kb) had a k^P_CHR of 0.015 and 0.005, respectively. Their knot complexity was also reduced. We distinguished knot species of up to seven crossings in YRp3, but we detected just the knot 3₁ in YRp2. Finally, we did not find any trace of knot formation in YRp1 (1.4 kb), a well characterized minichromosome that results from the circularization of the genomic TRP1ARS1 segment of yeast and contains only seven nucleosomes (32). Therefore, k^P_CHR appeared to scale quickly in the minichromosomes of length up to about 4 kb. However, above this length, the slope of k^P_CHR was reduced ∼5-fold such that knot formation barely increased from 4 to 12 kb (Figure 5C). The probability of individual knot species analyzed is specified in Supplementary Table S2.

Figure 5.

Dependence of DNA knotting probability on chromatin length. (A) Lk distributions and knotted forms of the minichromosomes YEp13 (10.7 kb) and YRp21 (11.7 kb). Over-exposure of the gel-blots shows composite knots of six nodes (3₁ + 3₁) and of seven nodes (3₁ + 4₁). (B) Lk distributions and knotted forms of the minichromosomes YRp1 (1.4 kb), YRp2 (2 kb) and YRp3 (3.2 kb). The 2D-gel electrophoreses in A and B were run, blotted and probed as described in the methods and Supplementary Table S1. Gel signals are annotated as described in Figure 2. (C) DNA knotting probability of yeast minichromosomes in the size range 1.4–11.7 kb. The plot shows the probability (mean and ±SD of three experiments) of all knot species (Total), the trefoil knot (3₁) and knots with more than three irreducible nodes (Kn >3).

DISCUSSION

Our study provides the first evidence of the formation of DNA knots in eukaryotic cells. The results revealed that small amounts of DNA knots are present in vivo regardless of structural and functional elements of chromatin. These knots happen irrespective of DNA replication and cell proliferation, though their abundance is transiently reduced during DNA transcription in a topo II dependent manner. All together, these observations strongly suggest that steady state fractions of DNA knots produced by topo II are common in eukaryotic chromatin. This finding is not surprising when considering the high concentration of DNA segments within chromatin fibers and the abundant topo II activity that can potentially pass these segments through each other. Alternatively, DNA knots could be generated via intra-molecular DNA recombination. However, recombination events occur usually within specific DNA sequences, produce DNA insertions or deletions, and create distinctive populations of knot types (33–35). If the DNA knots uncovered here are consequent to random DNA passage activity of topo II, they should reflect biophysical and conformational properties of chromatin in vivo, as we discuss below.

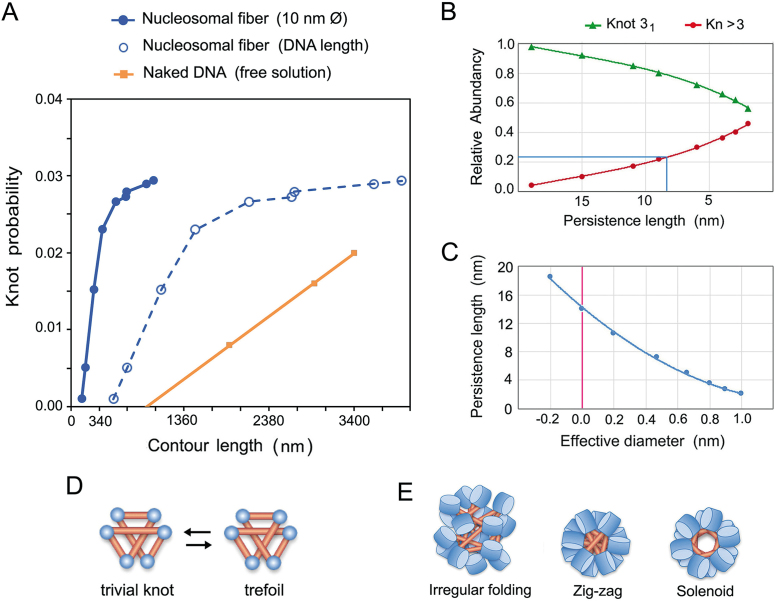
The probability of DNA knot formation in eukaryotic chromatin (k^P_CHR) reported here contrasts markedly with the knotting probability of DNA during the circularization of linear DNA molecules in free solution (k^P_DNA) (Figure 6A). The value of k^P_DNA increases proportionally to the DNA length and has a slope that depends on the duplex flexibility and its effective diameter (26,31). The DNA flexibility is denoted by its persistence length (P_L), which is about 50 nm (36). The DNA effective diameter (d_E) depends on the ionic environment and it was calculated to be about 5 nm in physiological salt concentrations (26,31). Our study shows that, up to a minichromosome size of about 4 kb, k^P_CHR increases with a slope higher than that of k^P_DNA and that, above this size, the slope of k^P_CHRis abruptly reduced. These differences were more noteworthy when we plotted k^P_CHR against the actual contour length of the minichromosomes, which equals to the sum of inter-nucleosomal DNA segments (Figure 6A).

Figure 6.

Properties of nucleosomal fibers deduced from DNA knot analysis. (A) Comparison of knotting probability of naked DNA in free solution (orange) with that of nucleosomal fibers (blue) as a function of their contour length (nm). Values of naked DNA are from previous studies (26,31). Values of chromatin are plotted against the total DNA length (dashed line) and against the length of a stretched 10 nm nucleosomal fiber (solid line). (B) Relative abundance of knot 3₁ and knots of more than three crossings (Kn > 3) as a function of P_L of a thin chain that has contour length 380 nm (as minichromosome YRp4). (C) P_L and d_E values of a simulated chain with a contour length of 380 nm that would produce the knot 3₁ with a probability of 0.017 (as the minichromosome YRp4). (D) At least six self-avoiding sticks are required to conform the trefoil knot. (E) Juxtaposition of DNA linker segments in solenoid, zig-zag and irregular folding models of nucleosomal fibers.

The simplest interpretation of the sharp slope of k^P_CHR values is that juxtaposition of intramolecular DNA segments in vivo is much higher than in DNA in free solution and, consequently, the probability of knot formation upon topo II-mediated DNA passage. Since juxtaposition of intramolecular DNA segments can be promoted by DNA supercoiling, some studies have already tackled the effects of supercoiling on knot formation and resolution. On the one side, several in vitro experiments with bacterial plasmids had revealed that DNA supercoils enhance DNA knotting by type-2 topoisomerases (5–7). On the other side, computer simulations had led to the proposal that DNA supercoiling could tighten existing DNA knots and facilitate their removal (37). However, the Lk distributions of the minichromosomes analyzed in our study showed no evidence of unconstrained supercoils that could promote DNA knot formation or resolution in vivo. Therefore, we excluded a significant role of DNA supercoiling to explain the observed k^P_CHR values. A more plausible explanation is that juxtaposition of DNA segments is due to the high flexibility of nucleosomal fibers in comparison to naked DNA. In this respect, in vivo analyses of DNA looping (38) and single particle tracking (39) evidenced the high flexibility of nucleosomal fibers, its P_L being qualitatively estimated to be shorter than the DNA linker length (10–20 nm). Here, we determined the apparent P_L and d_E values of the nucleosomal fibers in vivo by comparing our k^P_CHR data with previous simulations of knot formation in random polymer chains (25,26,40). To this end, we had to assume that the minichromosome knots were produced by topo II-mediated random passage of DNA segments. By considering the knot complexity (Figure 6B) and the probability of the 3₁ knot (Figure 6C), we calculated that nucleosomal fibers in vivo have knotting probability similar to that of a thin random polymer chain with a P_L of 8 and 14 nm, respectively. Larger P_L values would imply a negative d_E value, as if DNA linker segments were strongly attracted instead of repelled by electrostatic potential. Conversely, d_E values approaching the physical thickness of DNA (2 nm) would imply extremely low P_Lvalues (<3 nm), less than one turn of the double helix.

The high flexibility of nucleosomal fibers is mainly due to the adaptable angle between the entry and exit segments of the nucleosomal DNA, (41). In this respect, if DNA linker segments were to behave as nearly rigid sticks, another way to qualitatively interpret our k^P_CHR data is based on the minimum stick number to form a knot (42). This theory stablishes that at least six self-avoiding sticks are required to conform the knot 3₁ (Figure 6D). This view could explain why we did not detect knots in the YRp1 minichromosome (1.4 kb), which has only seven nucleosomes, a stick number close to the theoretical minimum. However, the 3₁ knot was readily formed in the slightly larger YRp2 minichromosome (2 kb) and knots of up to seven crossings were produced in YRp3 (3.2 kb). Then, in terms of chromatin architecture, our k^P_CHR data support zig-zag or intricate folding models of the nucleosomal fiber (43,44), in which DNA linker segments cross each other with higher frequency than in solenoid packaging models (45) (Figure 6E). Finally, another indication that DNA knot formation might be facilitated by intricate clustering of nearby nucleosomes was the decrease of knot abundance induced by DNA transcription (Figure 4). During DNA transcription, chromatin locally unfolds and thereby the juxtaposition of intra-molecular DNA segments is reduced (46) (Figure 7 A). Other processes, such as DNA supercoiling waves and topoisomerase activities associated to DNA transcribing complexes, could also alter steady state fractions of DNA knots. Future research might determine in more detail the interplay between chromatin dynamics and DNA knot turnover.

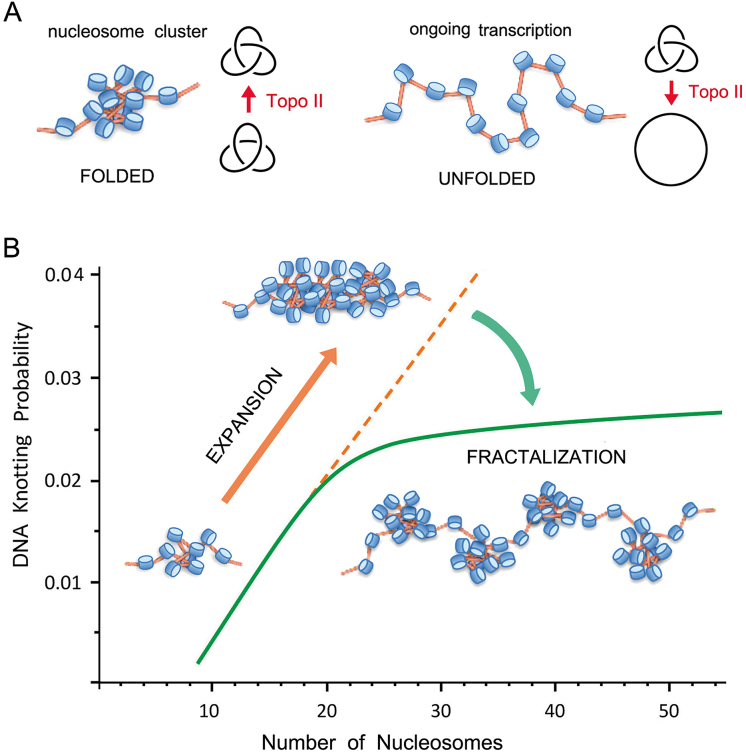
Figure 7.

Model of chromatin architecture inferred from DNA knotting probability. (A) Intricate folding of nucleosome arrays favors topo II-mediated knotting of intracellular DNA. Knotted fractions are reduced when nucleosomal clusters unfold during DNA transcription. (B) Uninterrupted expansion of nucleosomal fibers would produce proportional scaling of DNA knot formation (orange dashed line). Fractalization of the chromatin architecture minimizes instead the potentially harmful scaling of DNA entanglements (green line). The k^P_CHR data supports a fractal model, in which the ‘beads on a string’ architecture of the 10 nm nucleosomal fiber reiterates in its next level of organization by forming clusters of about 20 nucleosomes.

The abrupt reduction of the k^P_CHR slope when the size of the minichromosomes surpassed 4 kb (about 20 nucleosomes) was striking but likely to have a strong biological relevance. Computer simulations (25), circularization of linear DNA molecules in free solution (26,31), and topo II-mediated knotting of DNA plasmids in vitro (Supplementary Figure S2) indicated that DNA knotting probability increases proportionally to the DNA length. Therefore, some mechanism prevents the high knotting probability of nucleosomal fibers to keep climbing as their length increases, which would produce a massive entanglement of intracellular DNA. One possibility is that this inflection is achieved via the topo II ability to simplify the equilibrium DNA topology (8). In this regard, previous in vitro studies indicated that topo II is less efficient in simplifying thermal supercoils when the contour length of DNA decreases (47). A similar length dependence could explain why intracellular topo II unknots more efficiently the large than the small minichromosomes. Other mechanisms might direct also the activity of topo II to prevent the scaling of DNA knot formation. In this respect, recent studies indicated that the torsional state of chromatinized DNA (48) and the activity of condensins (49,50) can regulate DNA passage preferences of topo II in vivo.

A different feature that could explain the inflection of the k^P_CHR slope is a length-dependent transition in the packaging mode of the nucleosomal fiber. The folding architecture of chromatin fibers has been hotly debated (51–53). In addition to regular packing models (43–45), irregular folding models that incorporate variability in the nucleosome repeat length and other heteromorphic structures have been proposed in recent years (54–56). We envision two models that might explain the leveling of DNA knotting when a chromatin fiber reaches a length of about 20 nucleosomes. Both models invoke the transition from a globular to a fibrillary architecture. One possibility is that, below this length, strings of nucleosomes fold into intricate disordered structures that can be entangled by topo II. Above this length, nucleosomal fibers adopt a highly ordered or compacted configuration, which hampers the access of topo II to entangle the embedded DNA. However, no experimental evidence supports such abrupt length-dependent transition during the folding of nucleosome arrays (41,56). A more plausible mechanism through which the scaling of knot formation could be minimized is the fractalization of chromatin architecture. In this regard, our results support a model in which ‘beads on a string’ organization of the 10-nm nucleosome fiber reiterates in the next level of organization, in which the ‘bead’ unit is a cluster of about 20 nucleosomes (Figure 7B). As a result, DNA knot abundancy and complexity do not scale as would occur in an uninterrupted mesh of nucleosomes. According to this fractal organization, the small minichromosomes (<4 kb) examined in our study configured a single cluster of nucleosomes, whereas the larger ones configured two or more clusters. This architecture could explain the presence of composite knots in the larger minichromosomes, where prime knots might concur in separate nucleosome clusters. Remarkably, this fractal configuration is in line with most recent observations of intracellular chromatin. Mapping chromosome folding at nucleosome resolution indicated that yeast chromatin folds into clusters of 10–50 nucleosomes (57). Super-resolution nanoscopy showed that chromatin fibers are formed by heterogeneous clutches of nucleosomes (54). EM tomography revealed that intracellular chromatin is a disordered 5- to 24-nm-diameter granular chain (58). Minimization of DNA knot complexity might be therefore a fundamental outcome of the fractal architecture of intracellular chromatin.

In this discussion, we have assumed that the small fractions of DNA knots present in eukaryotic chromatin are merely a side effect of the ubiquitous DNA passage activity of topo II. However, it cannot be discarded that DNA knot formation in vivo might have regulatory and structural roles in other instances. Future research might clarify whether topo II activity and chromatin structure are modulated not only to lessen the potentially harmful entanglement of intracellular DNA but also to promote DNA knotting at specific sites. In this respect, earlier studies had been able to infer the spatial path of DNA in macromolecular ensembles from the characterization of DNA knots produced in vitro (59,60). Similar analyses with DNA knots formed in vivo might constitute a unique non-invasive approach to disclose the spatial trajectory of DNA during genome transactions.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR online.

FUNDING

Plan Estatal de Investigación Científica y Técnica of Spain [BFU2015-67007-P and MDM-2014-0435-02 to J.R., BES-2015-071597 to. A.V.]. Funding for open access charge: Plan Estatal de Investigación Científica y Técnica of Spain.

Conflict of interest statement. None declared.