Rolling circle amplification shows a sinusoidal template length-dependent amplification bias

Abstract

Biophysical properties of DNA such as its longitudinal and torsional persistence length govern many processes and phenomena in biology, DNA nanotechnology and biotechnology. It has, for example, long been known that the circularization efficiency of short DNA fragments shows a periodic pattern where fragments with integer helical turns circularize much more efficiently than those with odd helical half turns due to stronger stacking of duplex ends. Small DNA circles can serve as templates for rolling circle amplification (RCA), which is a common and extremely robust amplification mechanism for nucleic acids. We discovered a strong template length-dependent amplification efficiency bias of RCA with the same periodicity as B-DNA. However, stacking cannot explain the mechanism behind this bias as the presence of the polymerase in the bifurcation fork inhibits base stacking of ends. Instead, coarse-grained molecular dynamics simulations imply that different amplification efficiencies come from a varying fraying probability of the last two downstream base pairs. We conclude that an increased strain-promoted fraying probability can increase the polymerization rate compared to a relaxed template.

INTRODUCTION

Bending DNA is essential for many processes and phenomena in biology, DNA nanotechnology and biotechnology. For example, DNA–protein interactions can be modulated by the curvatures of DNA influencing both gene regulation, and replication and DNA is sharply bent in viral capsids or the chromosomes of eukaryotes. A common way to describe the biophysical properties of polymers including DNA is the worm-like chain model. In this model, the flexibility is expressed by its persistence length, which is the length up to which the polymer can be considered stiff. In physiologically relevant conditions, DNA exhibits a longitudinal persistence length of 50 nm or 150 base pairs (bp) and a torsional persistence length of 180 bp or 60 nm (1).

One phenomenon, that is strongly influenced by the persistence length of a polymer is the intramolecular circularization probability (or j-factor) (2). In general, circularization is inefficient for polymers around or below their persistence length. The same trend can be observed for the circularization of short DNA fragments. An additional strong influence of the twist on the circularization efficiency has also long been known (3). Double-stranded DNA fragments of similar length circularize with a significantly greater efficiency if their length is an integer multiple of the pitch (∼10.5 bp/turn), as stacking at the nicks in the resulting double-stranded circles is then least disrupted by torsional stress (4). For DNA fragments well below the persistence length, local distortions, nicks or kinks (5,6), or intrinsically bent sequences such as A-tracts (7) may, however, lead to much more efficient circularization than predicted by the worm-like chain model.

Such small circularized nucleic acids are interesting as model systems to study sharply bent DNA; as building elements for structural DNA nanotechnology (8–12); or can serve as templates for rolling circle amplification (RCA; sometimes also called rolling circle replication) (13–15).

RCA is a naturally occurring amplification technique utilized by bacteriophages, eukaryotic viruses and bacterial plasmids (16). During the process, a DNA circle is used as a template by a strand displacement polymerase such as Phi29 polymerase, Bst large fragment or T7 RNA polymerase that produces a long single strand containing many concatenated copies complementary to the template, which can be up to tens of thousands of nucleotides (nt) long (14). This isothermal process can be carried out at mild temperatures, is scalable and less prone than polymerase chain reaction (PCR) to certain errors such as sequence-dependent amplification bias (17), the propagation of mutations (18) or non-specific priming (19). Because of these benefits, RCA is used for the production of nanostructures (20–26), fabrication of new hydrogels (27,28) or applied for the development of drug delivery systems (29–31). Finally, it enables ultrasensitive biosensors and point of care diagnostic assays (32–34). For some applications, RCA is a better alternative to the PCR (see ‘Discussion’ section).

We discovered that the amplification efficiency in RCA shows a periodicity that corresponds to the helical repeat of B-form DNA resembling the length dependent periodicity known for the circularization of DNA fragments. However, we hypothesize that the mechanism here is a different one, as the presence of the polymerase prevents π-stacking across the replication fork. Coarse-grained molecular dynamics simulations of the circular DNA and the amplification fork suggest that differences in the fraying probability of the last two base pairs between the template strand and the displaced product strand cause this effect.

MATERIALS AND METHODS

Materials

Enzymes and respective buffers were purchased from New England Biolabs (NEB) or Thermo Fisher Scientific, dNTPs were purchased from New England Biolabs (NEB). Denaturing polyacrylamide gel electrophoresis (PAGE) gels (15% TBE urea gels, Thermo Fisher Scientific) were run at ∼55°C. Gels were post-stained with SYBR Safe (Thermo Fisher Scientific) or with other dyes (Supplementary Figure S2). Chemicals were purchased from Sigma-Aldrich. Primers were purchased from Eurofins Genomics (HPSF grade). Oligonucleotides for the pools were purchased from Invitrogen. All oligonucleotides were used without further purification.

Detailed amplification protocol

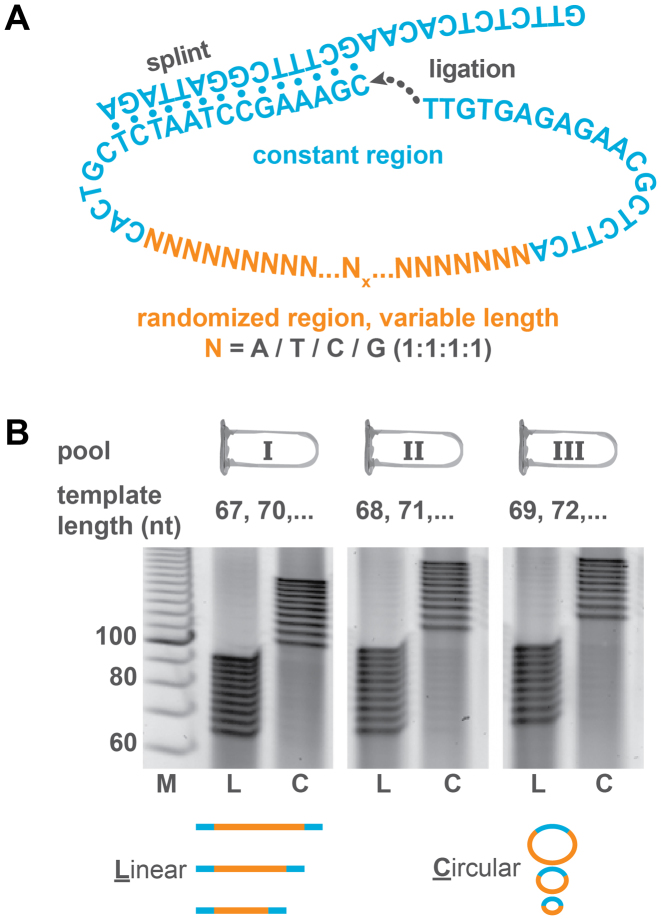
A pool of 29 oligonucleotides with a total size of 67–95 nt was designed. A randomized region (Poly‐N) ranging from 27 to 55 nt was extended to both sides with a constant region to serve as a template for the investigation of the length‐dependent amplification bias. The constant region was in total 40 nt long and consisted of two nicking sites (italic), a HindIII restriction site (bold) and two orthogonal barcodes of 10 nt each (TTGTGAGAGAACGCTCTTCANN…NNCACTGCTCTAATCCGAAAGC). As a result, the size of templates ranged from 67 to 95 nt. Templates were distributed into three or four distinct pools, with an increase of 3 or 4 nt within a pool, respectively.

All reactions and master mixes were prepared at room temperature (RT). For circularization, templates in each pool were diluted to a final concentration of 0.25 μM (per strand) in 1.5 ml DNA low‐binding polypropylene vial with ultrapure water. Phosphorylation of the pools was performed prior to ligation. For this, 25 μl of the pools were mixed in a 50 μl-reaction with: a master mix of 5 μl 10× T4 DNA ligase buffer, 19 μl water and 1 μl of T4 polynucleotide kinase (PNK, 10 U μl⁻¹) per reaction. Samples were incubated at 37°C for 30 min, heat inactivated at 65°C for 20 min. Prior to circularization, the ligation primers were annealed to the phosphorylated templates as follows: 50 μl of the phosphorylation reaction, a master mix of 0.5 μl of the primer (100 μM), 1 μl 10× T4 DNA ligase buffer and 8.5 μl water. Samples were incubated at 65°C for 2 min and cooled to RT at a rate of −2°C min⁻¹. A master mix of 1.5 μl 10× T4 DNA ligase buffer, 1.5 μl T4 DNA ligase (5 U μl⁻¹) and 12 μl of water were added to the annealing reaction, resulting in a final volume of 75 μl. Reactions were incubated at RT for 30 min and heat inactivated at 65°C for 10 min.

One round of RCA was performed with different DNA polymerases. After the desired incubation time, Nt.BspQI nicking endonuclease digest and a 15% urea denaturing PAGE were carried out to investigate the length‐dependent amplification bias qualitatively and quantitatively.

For RCA with Phi29 DNA polymerase, 1 μl of circularization reaction was mixed in a 25 μl-reaction with: a master mix of 2.5 μl 10× Phi29 DNA polymerase buffer, 0.25 μl 100× Bovine Serum Albumin (BSA, 10 mg ml⁻¹), 1 μl dNTP mix (10 mM each), 0.5 μl 4 mM DTT, 19.25 μl water and 0.5 μl Phi29 DNA polymerase (10 U μl⁻¹) per reaction. Reactions were incubated at 30°C for 20 min, 2 h or 14 h and heat inactivated at 65°C for 10 min. For RCA with Bst. 2.0 DNA polymerase, 1 μl of circularization reaction were mixed in a 25-μl reaction with: a master mix of 2.5 μl 10× Isothermal amplification buffer, 1.5 μl MgSO₄ 1 μl dNTP mix (10 mM each), 18 μl water and 1 μl Bst. 2.0 DNA polymerase (8 U μl⁻¹) per reaction. Reactions were incubated at 65°C for 20 min, 2 h or 14 h and heat inactivated at 80°C for 20 min.

For the nicking digest, nicking primers were added and the RCA products were digested into monomers with Nt. BspQI. For this, 2 μl of a nicking primer (sequence: TGAAGAGCGTTCTCTCACAA; 100 μM) were annealed to RCA product. Reactions were incubated at 95°C for 2 min and cooled to 70°C at a rate of −0.1°C s⁻¹, 70–60°C at a rate of −1°C min s⁻¹ and to RT at a rate of −0.1°C s⁻¹. The annealing reaction was prepared in a 50 μl-reaction with: a master mix of 2.3 μl 10× NEBuffer 3.1, 19.7 μl water and 1 μl of Nt.BspQI nicking enzyme (10 U μl⁻¹). Reactions were incubated at 50°C for 1.5 h and heat inactivated at 80°C for 20 min.

Following the digest, denaturing PAGE (15% acrylamide/bisacrylamide; 8.3 M urea) was carried out at a constant voltage of 220 V for ∼30 min at ∼55°C. A 10-bp molecular marker (0.1 μg μl⁻¹) was included in a separate lane as a size indicator. Gels were post‐stained for 10 min at 60 rpm in a staining solution of: 5 μl SYBR Gold, 45 ml of 1× TBE buffer and 5 ml ethanol. Gels were imaged (Typhoon FLA 9500 imager, GE) and image processing and quantification was performed by ImageJ. Data for the intensity profile were extracted with the ‘Plot Profile’ tool. A python script was written to fit Gaussian curves to the profile and to integrate over the area of each curve. The script is available upon request. The strongest band in each lane was normalized to 100% amplification efficiency. The normalized amplification efficiencies of all pools were plotted against the oligonucleotide size.

Molecular simulation

Simulations were performed with oxDNA, a model of DNA coarse-grained at the nucleotide level. Rigid nucleotides interact through base-stacking within and between DNA strands, hydrogen bonding between Watson–Crick-complementary bases, backbone connectivity and excluded volume, with electrostatic interactions represented by a Debye–Hückel potential. The forms of the potential are detailed elsewhere (35,36), and the simulation code is available online (https://dna.physics.ox.ac.uk.). Molecular dynamics simulations with an Andersen-like thermostat (37) were performed in order to measure the fraying probability of the terminal base pairs of the downstream duplex.

Fraying was detected using an established energy criterion for oxDNA: any pair of nucleotides with a hydrogen-bonding energy <15% of the maximum hydrogen-bonding energy is deemed to not be base paired (38). The base-pairing state of relevant nucleotides was checked every 100 MD steps. Three-dimensional harmonic traps were applied to 7 nt at the end of the upstream section of the minicircle to act as a proxy for the geometric constraints imposed on the minicircle by the enzyme. Nucleotides in the overhang were also disallowed from binding to any other nucleotides to avoid strand displacement or binding in areas where the excluded volume of the enzyme would normally prevent it from binding.

RESULTS

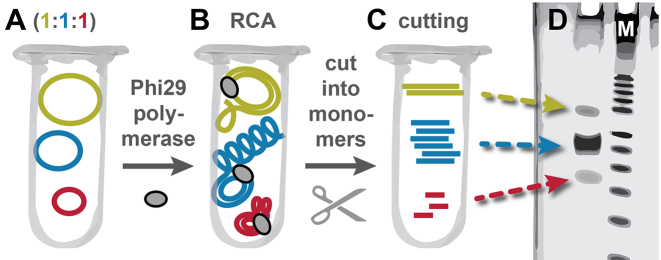
During our efforts to improve our RCA-based amplification method for the production of single-stranded oligonucleotides (20), we amplified different sequences (AT rich, CG rich, sequences with secondary structures, etc.) of different length in the same reaction. Before amplification, all sequences were present in equimolar ratios. After amplification, strong band intensity differences were observed by denaturing polyacrylamide gel electrophoresis (PAGE, Figure 1) that could not be correlated to the sequence design of the respective template. This confirms the low sequence-dependent amplification bias of RCA (17). Instead, the results suggested a length-dependent amplification bias.

Figure 1.

Workflow to study length-dependent amplification bias of RCA. (A) Equimolar ratios of single-stranded circular DNA templates of different length were pooled in one reaction tube. (B) These template mixes were amplified in the same tube by RCA by a strand displacement polymerase (e.g. Phi29 polymerase). (C) A restriction digest with nicking enzymes yielded monomeric copies of the circular templates of different length. (D) The relative length-dependent amplification efficiency was determined by denaturing PAGE (schematic).

Experimental design

To systematically investigate this effect, we decided to amplify templates ranging from 67 to 95 nt in parallel. In order to prevent a potential residual sequence-dependent amplification bias dominating the length-dependent amplification efficiency, all templates were designed to contain a common constant primer region (Figure 2A, blue) and a randomized region of varying length (orange). The common sequence contained a recognition site for a nicking enzyme that was used to cut the concatemer after the amplification. For combinatorial reasons, most oligonucleotide molecules with large randomized regions would have unique sequences. Therefore, a potential sequence-dependent amplification bias of some of these sequences would be averaged out or dominated by the majority of those sequences not displaying a strong sequence-dependent amplification bias.

Figure 2.

Preparation and circularization of template pools. (A) Each template contained the same constant region and a randomized region (poly-N) of varying length. The constant regions included a restriction site. The linear templates were circularized by splint ligation. (B) To be able to distinguish individual bands in PAGE, templates ranging from 67 to 95 nt were split into three pools (I, II, III) containing each template length at equimolar ratios. The linear pools (L) and circularized pools (C) were analyzed by PAGE.

Experimental implementation

As standard polyacrylamide gels do not provide single-nucleotide resolution, oligonucleotides of different lengths were distributed to three (or in some cases four) pools in an alternating way as described in Figure 2B. The relative concentrations of all oligonucleotides with a certain length were analyzed by denaturing PAGE before and after circularizing the template strand in order to exclude a bias during circularization (Figure 2B). The circularization was initiated by hybridizing the template strands with a common splint (Figure 2A) that is complementary to the common primer sequence. For entropic reasons, the splint induces an intramolecular circularization rather than an intermolecular polymerization at common oligonucleotide concentrations (nanomolar or micromolar range). The ends of the template strands were then enzymatically ligated into circular templates and analyzed by denaturing PAGE. The circular templates had a lower electrophoretic mobility than their linear equivalents such that they can easily be distinguished from linear templates. The circularization occurred with near-quantitative yields, and as expected, without a detectable length-dependent circularization bias.

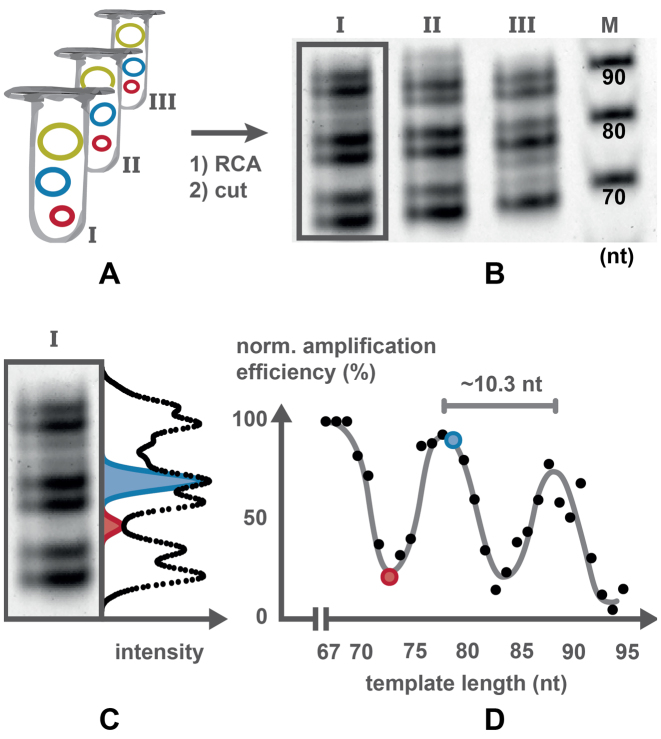
These circularized templates were then diluted (Figure 3A) and different strand displacement polymerases and dNTPs (deoxinucleotidetriphosphates) were added. After amplification, the long concatemers were cut into monomeric units. For this, a primer complementary to the constant region of the concatemer was annealed and enzymatically cut with a nicking enzyme as demonstrated previously (20). The resulting monomers were then separated by PAGE and the PAGE gels were stained with a DNA-specific fluorescent dye. The stained gels were imaged (Figure 3B), band intensities were digitally extracted from the images (Figure 3C) and plotted against the template size (Figure 3D). These resulting graphs show a periodic behavior with maxima in amplification efficiency at ∼68, 79 and 89 nt and minima at ∼73, 84 and 94 nt. The difference in efficiency between minima and maxima reached factors of up to about five (Figure 3D) for amplification times of several hours. For shorter amplification times, less material is produced and the bias was not as pronounced (Supplementary Figure S1).

Figure 3.

Determination of amplification efficiency. (A) The pools containing DNA templates of different length were amplified separately by RCA. The resulting concatemers were cut by nicking enzymes into linear monomers (B) which were separated by denaturing PAGE. (C) Intensity profile of an individual lane. Each point in the intensity profile corresponds to the sum of gray values of the pixels in one row. Gaussian curves were fitted to the profile to determine band intensities. Two example fits are shown. (D) The amplification efficiencies were normalized and plotted against the template length.

To allow for an exact quantification of the gel bands, we obtained the mass-fluorescence response curve of several gel staining dyes. We found that some of the most sensitive dyes such as SYBR Gold do not show a linear response over a large dynamic range, but produced a saturation curve (Supplementary Figure S2) and are therefore ill-suited for quantification. SYBR Safe revealed a linear response over a much wider dynamic range and was therefore used for most measurements.

Enzyme dependency

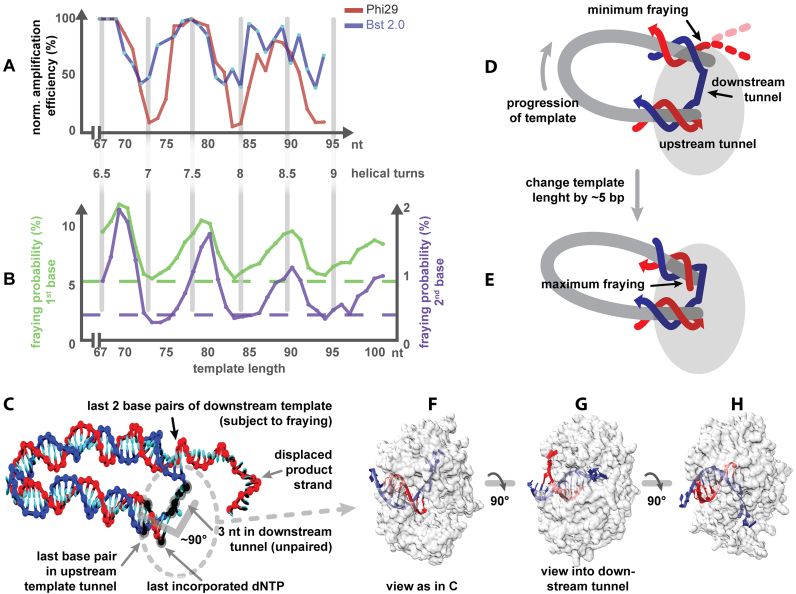
It is known that the sequence-dependent amplification bias in PCR is not only sequence, but also enzyme dependent (39,40). To test whether the template length-dependent amplification bias in RCA is an effect caused by the polymerase (Phi29), we investigated different strand displacement polymerases from different families and organisms including Phi29 polymerase, Bst 2.0, Vent (exo-), Klenow fragment and Phusion polymerase as a typical PCR polymerase. Several different enzymes are in principle capable of performing RCA (41,42), but only Phi29 polymerase and Bst 2.0 produced enough material in our experiments that allowed quantification by PAGE. The amplification with Bst 2.0 also revealed a sinusoidal template length-dependent amplification bias (Figure 4A). The amplitude was, however, smaller and the data was noisier due to a much lower overall amplification yield compared to Phi29. The period of the fitted sine curves is 10.3 (±0.2) nt being close to the 10.44 bp/turn reported for B-DNA (43). As the amplification was only successful with two enzymes, the enzyme dependency of the observed bias cannot be conclusively ruled out. However, two enzymes showed a length-dependent amplification bias that corresponded to the helical repeat of B-DNA and the minima/maxima were roughly in phase. Small differences of 1–2 nt between different polymerases may stem from different steric demands of the polymerases. We therefore hypothesized that the bias may be caused by the repeating helical structure of DNA template and intrinsic properties of these templates.

Figure 4.

Different conformations of the minicircle polymerase complex and the resulting effects. (A) The bias for Bst 2.0 and Phi29 pol (independent dataset from Figure 3D). The pitch length is 10.4 nt. (B) Fraying probability of the first and second base of the downstream template (for clarity not drawn to the same scale). The baseline of fraying (dashed) is with a linear DNA strand in the polymerase configuration. (C) A model of a simulated fraying experiment with minimal fraying. The relative conformation of the last base pair in the template tunnel, the last incorporated dNTP and the 3 nt in the downstream tunnel (highlighted in black) were fixed in the simulations. The location of the polymerase is indicated by the dotted oval. (D and E) Sketch of two minicircles differing in half a helical turn highlighting the location of the last base pairs subject to fraying. Further examples can be found in Supplementary Figure S5. D is depicted roughly as in C. (F–H) Models of the crystal structure of Phi29 polymerase in different orientations (PDB crystal structure: 2PZS) (47).

Modeling

As the polymerase amplifies the template strand, it exerts a torque on the product duplex. This torque could lead the DNA to rotate relative to the polymerase in two possible ways: (i) the whole circle could rotate around the polymerase or (ii) the DNA could rotate about its helical axis. We would argue that the latter mechanism is much more likely for templates of the size considered here. The crystal structure of Phi29 polymerase reveals that the product duplex tunnel and the downstream template tunnel are not straight but are bent (44) as indicated in Figure 4C. Due to this angle, configurations where the angle bisector points toward the center of the circular template will be significantly more favorable for templates less than the persistence length of DNA (150 bp) due to the lower bending energy. Furthermore, the outer part of the polymerase (left in Figure 4H upper half) is sterically more demanding than the inner part and may be difficult to accommodate in the narrow center of the circular template (45,46). We therefore expect that the orientation of the polymerase with respect to the center of the circular template remains as depicted in Figure 4C–E during the amplification. In other words, the entrance for the incoming dNTPs would always face outward. During amplification, a nucleotide incorporated in the product strand would be pushed in a helical fashion around the central axis of the product duplex toward the bifurcation point and then further into the single-stranded product. The progression of template in respect to the polymerase is indicated in Figure 4D.

Earlier simulations with oxDNA, a nucleotide-level coarse-grained model of DNA (35), suggested that the fraying (temporary melting of the terminal base pair) at nicks of tightly bent double-stranded DNA minicircles depends strongly on the ring size (4) in a similar periodic manner to that we observed here for the amplification or that of the length-dependent circularization efficiency (j factor) of short DNA fragments (3). Those earlier results can, however, not be directly related to RCA as the mechanism must be different for the amplification bias. First, templates with integer helical repeats are amplified up to 6-fold worse than templates with an odd number of helical half turns, whereas templates with integer helical repeats circularize best. Second, the downstream template tunnel of the Phi29 polymerase forces 3–4 nt to remain single stranded (Figure 4C) (47). The steric demand of the polymerase does therefore not allow π-stacking of the terminal base pair of the downstream template and the upstream template in the upstream template tunnel (Figure 4C–H).

We therefore performed new oxDNA simulations where we constrained the DNA to approximate the conformation in the polymerase complex (PDB crystal structure: 2PZS) (47). Specifically, we fixed the position of the first five base pairs of the product duplex to prevent rotation as well as the three unpaired nucleotides in the downstream template tunnel (Figure 4C). These latter nucleotides were defined as non-pairing bases to ensure that they would remain single stranded during the simulations. Additional steric constraints arising from the polymerase (Figure 4F–H) were not accounted for.

From the simulations, the fraying probability for the first and second base pairs of the downstream template next to the bifurcation point was measured for different template sizes ranging from 67–105 nt and is shown in Figure 4B. Although the fraying probabilities are modest—the base pairs are intact usually more than 90% of the time—they exhibit a clear periodicity. The strongest fraying was observed at odd helical half turns of DNA (69, 79, 90, 100 nt) (Figure 4E) and the least fraying at even helical half turns (Figure 4D). The first base frays with a probability between 5.5 and 11.7%, the second one between 0.3 and 2.0%. These values correspond to a roughly 1–2 k_BT difference in the free-energy cost for breaking these base pairs. In both cases, the fraying probability for circles with an even number of half turns is very similar to the fraying levels of a ‘cut’, unstrained linear reference template, which were 5.3% for the first and 0.4% for the second base. Furthermore, there is an overall decrease of the fraying probabilities toward these values with increasing template size.

DISCUSSION

The simulated template length-dependent fraying probability of the last two bases is strongly correlated to the experimentally observed amplification bias (Figure 4). All these results are consistent with a mechanism where there is greater stress in the DNA when there is a mismatch between the template length and integer multiples of the natural helical repeat of DNA (Figure 4E). It seems plausible that the polymerase can proceed with a decreased resistance (and therefore faster) in a configuration where the last bases are frayed, as opposed to a non-frayed configuration where these base pairs have to be broken. Similarly, Morin et al. (44) observed an increase in the velocity of the Phi29 polymerase when an external force was applied to the (non-circular) downstream template. They concluded that a mechanical stress which destabilizes the last two bases of the downstream template leads to an increased polymerase velocity. Our data suggests that the conformational stress of tightly bent DNA may also be responsible for the length-dependent fraying probability. In our simulations, the amplitude of the effect was strongest for the second base (up to 6-fold differences). The fraying probability further depended on the presence or absence of the product strand (Supplementary Figure S3). This difference would only be relevant on the first circuit of the template and can therefore not explain the time dependency of the bias of this highly processive polymerase. Perhaps the growing steric demand of the product random coil is the reason for an increase of the experimentally observed bias over time.

Our molecular simulations do not consider the steric demand of the polymerase or any forces applied by the polymerase to the downstream duplex (assuming a passive polymerase). For active polymerases, exerting a torque on the downstream template, the model also implies that smaller forces are required to break the terminal downstream duplex base pairs in circles with half-integer pitch length, thus accelerating the amplification velocity.

The simulated and experimentally observed sinusoidal trend is overlaid with an overall decreasing amplification efficiency of the maxima toward larger template sizes. For templates longer than the longitudinal (150 bp) and torsional (180 bp) persistence length of dsDNA (1), the stress at the bifurcation point is reduced. Thus, the template length-dependent amplification bias only plays a major role for templates around or below the persistence length of DNA. We therefore conclude that an increased intrinsic template strain-promoted fraying probability can increase the polymerization rate compared to the reaction rate in a relaxed (e.g. linear) template.

Implications for RCA-based applications

Our discovery is not only fundamentally interesting but has implications for many applications. The capacity of the PCR to rapidly amplify small amounts of template DNA has made it the most widespread amplification technique. However, PCR has some major drawbacks. For some applications that require high yields or single-stranded DNA (20); or for bioassays and sensors that require bias free, precise quantification (17), isothermal amplification methods such as RCA can be better alternatives to PCR. For these applications, a constant amplification efficiency under various conditions of for various template lengths is important as biased amplification could impede the reproducibility and robustness of experiments. For example, a 5-fold bias could decrease the sensitivity of a sensor or an assay by five times for linear (LRCA), 25 times for exponential (HRCA) and 625 times for quadratic (NRCA) amplification (48).

Similarly, for therapeutic applications, a bias might cause an inconsistent drug loading capacity. As an example, a DNA-based drug carrier might be five times bigger under certain conditions, and consequently could take up five times more active agent and deliver five times the dosage to the patient. For these reasons, the periodic length-dependent amplification bias of RCA should be taken into consideration when designing experiments. Changing the template size of an RCA template by as little as 5 nt or bp can influence the obtained results dramatically. When aiming for maximal amplification rates, circular templates should be chosen in the size range of the periodic maxima and shorter rings are generally amplified better than longer ones. It should be further noted that every additional round of RCA like in circle-to-circle amplification with two or more nested rounds of RCA (17,20) intensifies the bias (Supplementary Figure S4); the same effect can be expected for netlike RCA (48). Knowledge of the bias we reported here can therefore not only help to prevent or solve bias-related problems, but also improve RCA yields.

CONCLUSION

In conclusion, we described a previously unknown template length-dependent amplification bias of several 100% in RCA of small circular templates resembling the length-dependent circularization efficiency of DNA fragments. The proposed molecular mechanism behind the RCA bias is a varying fraying probability dependent on the conformation of the minicircle–polymerase complex. Our discovery helps to better understand the biophysical mechanisms behind RCA and may even be generalized for the action of other passive polymerases on geometrically constrained templates. In any case, the effect needs to be considered for many established and emerging methods using RCA in medicine, biotechnology, nanotechnology and material sciences.

DATA AVAILABILITY

The simulation code is available online (https://dna.physics.ox.ac.uk.). Data associated with the simulations is available at the Oxford University Research Archive (DOI: 10.5287/bodleian:VJJYJXOrg)

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Center for Advancing Electronics Dresden (cfaed) [starting grant to T.L.S.; DFG Center for Regenerative Therapies Dresden (CRTD), [Seed Grant 043_2615A6 to T.L.S.]; Engineering and Physical Sciences Research Council [EP/L015722/1 to D.P.]; Dresden International Graduate School for Biomedicine and Bioengineering (DIGS-BB) (to B.J., T.L.S.). Funding for open access charge: DIGS-BB.

Conflict of interest statement. None declared.