Abstract
Soil microorganisms mineralize lignin-derived aromatic carbon sources using oxidative catabolic pathways, such as the β-ketoadipate pathway. Although this aromatic pathway is one of the best-studied pathways in biochemistry, the complete pathway, including its regulation by aromatic carbon sources, has not been integrated into the metabolic network. In particular, information about the in vivo operation (e.g., kinetics and flux capacity) of the pathway is lacking. In this contribution, we use kinetic modeling and thermodynamic analysis to evaluate the in vivo operation of this key aromatic multi-step pathway. The resulting ab initio deterministic model of benzoate degradation via the β-ketoadipate (ortho-cleavage) pathway in Pseudomonas putida KT2440 is presented. The kinetic model includes mechanistic rate expressions for the enzymes and transport processes. The design and experimental validation of the model are driven by data generated from short-term perturbation experiments in a benzoate-limited continuous culture. The results of rigorous modeling of the in vivo dynamics provide strong support for flux regulation by the benzoate transporter and the enzymes forming and cleaving catechol. Revisiting the β-ketoadipate pathway might be valuable for applications in different fields, such as biochemistry and metabolic engineering, that use lignin monomers as a carbon source.
Keywords: Metabolic modeling, Pseudomonas putida, Aromatic metabolism, Transient response, Intracellular metabolites
Highlights
-
•
We describe a kinetic model for the β-ketoadipate pathway.
-
•
Short term metabolic responses were tracked on metabolite level by rapid sampling.
-
•
The model captures steady state and dynamic conditions of the β-ketoadipate pathway.
-
•
Thermodynamic analysis revealed regulation points of the pathway.
-
•
The results are discussed in the context of metabolic network operation.
1. Introduction
In nature, the metabolic conversion of lignin to aromatic monomers occurs via a series of cometabolic and secondary metabolic events that involve both fungi and bacteria (Bugg et al., 2011). Understanding the innate metabolism of microbes while they utilize complex aromatic compounds as their sole source of carbon and energy may provide clues for decoding the possible links among lignin degradation, aromatic monomers, central carbon metabolism and bio-product formation. Soil microorganisms (e.g., the Pseudomonads) are known to exhibit a common procession that is termed the ‘metabolic funnel’ to mineralize structurally diverse aromatic molecules into a few central aromatic intermediates through peripheral catabolic pathways. Those aromatic intermediates are further processed via the central aromatic pathways to the core metabolism of the cell (Díaz, 2004). The genomic analysis of a well-characterized member of the metabolically versatile bacterial species Pseudomonas putida revealed the existence of at least six major aromatic pathways for degrading central aromatic intermediates (i.e., protocatechuate, catechol, homogentisate, phenylacetate, nicotinic acid and gallic acid) (Jiménez et al., 2008, Jiménez et al., 2002, Nogales et al., 2011). Of these major pathways, the pathway involved in catechol degradation (i.e., the β-ketoadipate pathway) is the most prevalent and extensively studied. In addition to having a wide taxonomic distribution among both the prokaryotic and eukaryotic groups, the β-ketoadipate pathway provides a mechanism for the dissimilation of aromatic and hydroaromatic compounds (Parke et al., 2000). The pathway follows a two-step strategy: a ring cleavage by ring modification reactions is followed by ring fission and subsequent reactions that lead to the generation of TCA cycle intermediates (Harwood and Parales, 1996). This versatile metabolism of aromatic compounds has now sparked interest in renewable resource-based chemistry, and the possible impacts were reviewed previously (Fuchs et al., 2011, Wells and Ragauskas, 2012). One example is the microbial synthesis of cis,cis-muconic acid from benzoate. This route is explored as an alternative to chemical synthesis for the production of adipic acid, which is a commodity chemical for the production of nylon-6,6 (Mizuno et al., 1988, van Duuren et al., 2011, Vardon et al., 2015). The potential to apply these catabolic pathways for aromatic compounds in lignin-enriched streams and lignin-derived aromatic monomers can be further explored by examining the formation of medium-chain (C6–C14) polyhydroxyalkanoates by the versatile soil bacterium P. putida KT2440 (Linger et al., 2014).
In P. putida KT2440, the β-ketoadipate pathway is native, encoded on the chromosome, and lacks the meta-cleavage route that is localized on a mega plasmid (Nelson et al., 2002). Previous studies have shown direct evidence for the activation of the ortho-cleavage route of the β-ketoadipate pathway during the growth of P. putida on benzoate as the sole source of carbon and energy (Cao and Loh, 2008, Ornston and Stanier, 1966). Although numerous biochemical studies of the in vitro properties of the corresponding enzymes are available, the in vivo kinetics of this pathway remains poorly understood.
The central goal of this study is to quantify the in vivo metabolic response during benzoate degradation via the β-ketoadipate (ortho-cleavage) pathway in P. putida KT2440 (Sudarsan et al., 2014). Consequently, we analyze the enzyme kinetics in vivo using a mathematical model based on deterministic rate equations. The analysis is data-driven, and the response of the metabolome to dynamic system excitation (Theobald et al., 1997) is used to identify the kinetics of multistep enzyme reactions and to estimate the kinetic parameters using a bottom-up approach (Bruggeman and Westerhoff, 2007). The identified model is then used to predict system dynamics (i.e., changes in the intra- and extracellular concentrations of metabolites both at steady state and after a benzoate pulse). In the second part of this study, we draw on quantitative metabolome analysis and apply network-embedded thermodynamic (NET) analysis (Zamboni et al., 2008) as a tool to provide novel insights about the active regulatory sites of the β-ketoadipate (ortho-cleavage) pathway coupled to central carbon metabolism. The systematic incorporation of insights from the identified dynamic model and thermodynamic analysis will be useful in the future as a framework for formulating large-scale kinetic models.
2. Material and methods
2.1. Strain, medium, and pre-culture conditions
P. putida strain KT2440, which is a plasmid-free derivative of P. putida mt-2 (Bagdasarian et al., 1981), was used throughout this study. Cells from glycerol stocks were recovered on LB agar plates. Liquid cultures were started on LB medium, followed by two subsequent cultivations on modified M9 minimal medium supplemented with benzoate. Erlenmeyer flasks (1 L) were used in a rotary shaker at 30 °C and 150 rpm, ensuring fully aerated growth conditions.
The composition of the modified M9 medium supplemented with benzoate for chemostat cultivations was determined based on elemental balancing for the production of 5 g dry weight biomass per liter, with the following composition per liter: 15 g of Na-Benzoate; 2 g of Na2SO4·10h2O; 2.68 g of (NH4)2SO4; 1 g of NH4Cl; 1.46 g of K2HPO4; 0.4 g of NaH2PO4·2h2O; 0.25 g of MgSO4·7h2O; 22 mg of CaCl2·2h2O; 0.27 mg of ZnSO4·7h2O; 0.15 mg of MnSO4·H2O; 30.2 mg of Na−EDTA; 0.24 mg of CuSO4·5h2O; 24.1 mg of FeCl3·6h2O and 0.27 mg of CoCl2·6h2O. The final pH of the medium was 7.1.
2.2. Start-up of continuous cultivation and criteria for steady state
Cultivation was initiated in batch mode at 30 °C in a stirred tank bioreactor with a working volume of 1.5 L the airflow was maintained at 2 L min−1, and the pH was maintained at 7.0 by the addition of 20% (v/v) H3PO4. Batch cultivation was monitored continuously through changes in the dissolved oxygen (DO) concentration and increases in the OD450. Fed-batch operation was initiated with exponential feeding of benzoate solution (100 g L−1) after the complete consumption of benzoate in the growth medium (marked by a steep increase in the DO concentration). Exponential feeding was performed at a growth rate of 0.65 h−1 and was controlled by computer-aided feed-forward control. After the desired biomass concentration of approximately 5 gCDW L−1 (corresponding to an OD450 of 30) was reached, the continuous mode of operation was started with a dilution rate of 0.1 h−1, which was increased to 0.2 h−1. Steady-state conditions were confirmed when the biomass concentration and the exhaust analysis remained constant over a period of five mean residence times.
For the determination of the biomass concentration, 10 mL of the cell suspension was centrifuged (Heraeus Megafuge 1.0R, rotor 8030, 15 min, 3220g, 4 °C) in pre-weighed glass tubes. The biomass pellet was washed twice with a 0.9% NaCl solution, dried at 105 °C until reaching a constant weight and then weighed.
2.3. Benzoate pulse experiments
To avoid the adaptation of P. putida KT2440 to benzoate-limited conditions, stimulus-response experiments were performed for a low and defined number of generations. The steady-state conditions at a dilution rate of 0.2±0.003 h−1 were perturbed by increasing the residual concentrations of benzoate with a defined pulse of benzoate (introduced manually with a syringe) to generate a bulk concentration of 1.3 g L−1. Samples were withdrawn rapidly from the bioreactor at regular intervals. The opening times of the valves were synchronized and controlled via a computer-aided automated sampling system. During sampling, the feeding rate was corrected with a computer-aided peristaltic pump to compensate for the loss of reactor volume and to maintain a constant dilution rate of 0.2 h−1 throughout the sampling period.
2.4. Sampling procedure
Intracellular metabolites were quantified using a differential method of calculation (Taymaz-Nikerel et al., 2009, Theobald et al., 1997), in which the intracellular metabolite concentrations were calculated from the difference between the metabolite concentrations obtained in the total broth extracts and cell-free extracellular samples. The specific cell volume was determined to be 3.8 mL gCDW−1 for P. putida KT2440 under the above-mentioned culture conditions.
For the measurement of the total metabolite concentrations, 4 mL of sample broth was withdrawn, quenched rapidly in 1 mL of HClO4 (−25 °C, 35% w/v) and extracted for 15 min by end-over-end mixing at 4 °C. The compounds benzoate cis-diol and cis,cis-muconate were found to be acid labile, whereas benzoate and catechol were stable under acidic conditions. Consequently, the pH of the sample was adjusted to either pH 7 (for analyzing benzoate, benzoate cis-diol and cis,cis-muconate) or an acidic pH of 2 (for analyzing catechol). After centrifugation (Heraeus Megafuge 1.0R, rotor 8030, 15 min, 3220g, 4 °C), the supernatant was collected and stored at −20 °C until further analysis using HPLC.
Four milliliters of sample broth was sampled and filtered manually at room temperature to determine extracellular concentrations. The cells were separated rapidly using glass microfiber filters (Whatman, GD/X 25 syringe filter, 0.45 µm), and the obtained filtrate was stored at −20 °C until further analysis. The obtained filtrate was immediately mixed with 1 mL of HClO4 to prevent the auto-oxidation of catechol in the culture filtrates. The exact volumes of sample processed were quantified gravimetrically by weighing the tubes at every individual step of sample processing.
2.5. Metabolite analysis
Metabolites, such as benzoate, benzoate cis-diol, cis,cis-muconate, catechol and β-ketoadipate, were analyzed and quantified using reverse phase HPLC. Except for β-ketoadipate, all other metabolites were separated on a CC Nucleosil C-18 HD column (100 Å pore size, 5 µm particle size, 25 cm×4 mm inner diameter; Macharey-Nagel, Oensingen, Switzerland) and detected via an HPLC diode array detector (Elite LaChrom, Merck-Hitachi, Germany), with wavelengths ranging from 200 to 400 nm. The conditions used to separate the above-mentioned metabolites are described below. Solvent A was 100 mM ortho-phosphoric acid (pH 2), and solvent B was methanol. The starting concentration was 10% B in A. After 5 min, a gradient was established by increasing the concentration of B by 3% per min at a flow rate of 1 mL min−1. A sample volume of 10 μL was injected, and the column temperature was kept constant at 25 °C. The maximum wavelengths were 230 nm for benzoate, 262 nm for benzoate cis-diol, cis,cis-muconate and its isomers, and 276 nm for catechol. Under acidic conditions, benzoate cis-diol was found to decompose into salicylate and phenol; however, this phenomenon was not observed at neutral pH. Irrespective of handling conditions, cis,cis-muconate was found to mostly degrade spontaneously into its cis-trans isomer. Hence, the degradation kinetics of cis,cis-muconate was assessed, and the exact amount of cis,cis-muconate was quantified by combining the peak areas of cis,cis- and cis-trans-muconate, with a conversion factor of 0.855 for the cis-trans isomer.
The compound β-ketoadipate was separated on a Luna C8 (2) column (100 Å pore size, 5 µm particle size, 150 mm×4 mm inner diameter; Phenomenex, Torrance, USA) and detected via an HPLC Corona charged aerosol detector (Dionex Softtronic GmbH, Germering, Germany). Separation was achieved using mobile phase A, which consisted of 1% acetonitrile and 0.4% tri-fluoroacetic acid in distilled H2O, and acetonitrile as mobile phase B. The following elution profile was employed: elution started with 2% B for the first 8 min, followed by a sharp gradient of 98%, and elution was maintained until 14 min at a flow rate of 0.8 mL min−1. To equilibrate the column back to its initial conditions, the gradient was decreased to 2% B after 14 min. To quantify β-ketoadipate, 20 μL of the sample was injected, and the column temperature was kept constant at 40 °C.
3. Mathematical model
3.1. Stoichiometric model of benzoate metabolism
A stoichiometric metabolic network that included the reactions of the β-ketoadipate (ortho-cleavage) pathway, the TCA cycle, gluconeogenesis and the pentose phosphate pathway was compiled from the biochemical knowledge generated by the genome-scale metabolic model of P. putida (Nogales et al., 2008). These pathways can be regarded as four different modules that were aggregated to describe the steady-state behavior of benzoate metabolism. Although P. putida differs from Escherichia coli in terms of hexose utilization, the percent carbon content in the dry cells of both strains is approximately 47%, and the values do not differ significantly (Bratbak and Dundas, 1984). Van Duuren et al. (2013) also showed that the differences in the biomass composition of the two strains are negligible. Hence, the precursor requirements for biomass formation in P. putida were assumed to be similar to those of E. coli (Emmerling et al., 2002) in this study. In this model, we used a P/O ratio of 1, according to the work of Blank et al. (2008). In the simulation run with an alternative P/O ratio of 2, only the ATP production rate changed, while the fluxes in the benzoate pathway remained unchanged. To estimate the net fluxes, the NETTO module of the FiatFlux software (Zamboni et al., 2005) was used, and the absolute in vivo (net) fluxes were estimated using global material balances that were derived using (a) the stoichiometric reaction matrix, (b) physiological data (substrate uptake rates, product formation rates, and growth rates), and (c) the precursor requirements for biomass synthesis. Fischer et al. has described the appropriate statistical data treatment for flux estimation (Fischer et al., 2004), in which the residuals were weighted by division with the experimental variances σ2 from extracellular measurements. For each metabolite that was used as a precursor for biomass synthesis, a proportional error of 5% was assigned. The fluxes were then estimated by minimizing the sum of the weighted square residuals from both the metabolite balances and flux ratios using the MATLAB function fmincon starting from a randomly generated flux distribution.
The benzoate metabolic network is well determined without the use of flux ratios. The steady-state substrate uptake and product formation rates were calculated from the mass balance equations of the respective metabolites. The specific benzoate uptake rate at steady state () was then calculated using the following equation:
| (1) |
is the measured benzoate concentration at steady state; is the concentration of benzoate in the feed medium; is the biomass concentration, and is the dilution rate during continuous cultivation.
3.2. Kinetic model structure
To develop a dynamic model of the β-ketoadipate (ortho-cleavage) pathway, mass balance equations for the extracellular and intracellular metabolites were formulated. The derived equations were of the following form:
| (2) |
denotes the concentration of metabolite , and is the specific growth rate or dilution rate during continuous cultivation. is the stoichiometric coefficient for the metabolite in reaction , and is the rate of the reaction . The structure of the metabolic model is outlined in Fig. 1, and the complete set of mass balance equations is listed in Table 1. The concentrations of the metabolites were expressed in mM, and the rates were expressed in mM min−1.
Fig. 1.
Structure of the metabolic model of the β-ketoadipate (ortho-cleavage) pathway in P. putida KT2440. Metabolites: BEN, benzoate; DIOL, benzoate 1,2 cis-diol; CAT, catechol; MUC, cis,cis-muconate; ML, muconolactone; KAEL, β-ketoadipate enol-lactone; and KA, β-ketoadipate. Enzymes: BZT, benzoate permease; BDO, benzoate 1,2-dioxygenase; DIOLDH, benzoate cis-diol dehydrogenase; DIOLT, benzoate cis-diol transport; CDO, catechol 1,2-dioxygenase; CT, catechol transport; MISO, muconate and muconolactone isomerase (lumped); MUCT, cis,cis-muconate transport; LH, β-ketoadipate enol lactone hydrolase; KAT, β-ketoadipate transport; and KACOAT, β-ketoadipate succinyl-CoA transferase. The superscripts ‘ex’ and ‘in’ denote the extracellular and intracellular localizations, respectively, of the metabolites. The enzymes framed in red lines are sensitive to additional regulation phenomena (predictions from the thermodynamic analysis and manifested in the kinetic equations in Table 2).
Table 1.
Mass balance equations.a
| ||
| ||
| ||
| ||
| ||
| ||
| ||
| ||
| ||
| ||
| ||
| ||
| ||
| ||
| ||
|
a Culture parameters.
; ; ;
and are the liquid volume and the gas hold-up, respectively, in the fermenter; and are the volumetric medium and gas flow rates, respectively; is the concentration of O2 in the liquid phase; is the oxygen concentration in the dissolved oxygen sensor, where is the parameter for the first-order model of the dissolved oxygen sensor; , where P, T and R are the fermenter's pressure (bar), the cultivation temperature (K) and universal gas constant (bar L mol−1 K−1), respectively; is the partition coefficient of O2 between gas and liquid (Bloemen et al., 2003); and is the gas-liquid transfer coefficient for O2.
3.3. Kinetic rate expressions
The sequence of enzyme-catalyzed reactions involved in the breakdown and cleavage of benzoate is described by mechanistic rate expressions (Table 2). The rate expressions were chosen based on published in vitro investigations of the respective enzymes. For cases for which published information was scarce, several kinetic expressions were tested with appropriate assumptions, and those that represented the in vivo experimental data reasonably well were chosen. The selection of appropriate kinetic equations is described first for transport systems and then for benzoate catabolism.
Table 2.
Kinetic rate expressions.
| Benzoate transport: | ||
| ||
| Benzoate 1,2-dioxygenase: | ||
| ||
| Benzoate cis-diol dehydrogenase: | ||
| ||
| Benzoate cis-diol transport: | ||
| ||
| Catechol 1,2-dioxygenase: | ||
| ||
| Catechol transport: | ||
| ||
| Muconate isomerase: | ||
| ||
| β-Ketoadipate enol-lactone hydrolase: | ||
| ||
| β-Ketoadipate succinyl-Co-A transferase: | ||
| ||
| cis,cis-Muconate transporta: | ||
| ||
| β-Ketoadipate transporta: | ||
|
For cis,cis-muconate and β-ketoadipate transport, ; .
3.3.1. Transport systems
According to Thayer and Wheelis (1982), the transport of benzoate in P. putida is mediated by a permease, which is driven by the membrane potential. Assuming that this membrane potential remains constant, we used a kinetic rate expression for reversible influx-efflux kinetics, as suggested by Rizzi et al. (1996) for glucose transport in Saccharomyces cerevisiae (Rizzi et al., 1996). The kinetic rate expression is represented by Eq. (19) in Table 2. The rate equation is similar to the equation described for glucose permease in yeast (Rizzi et al., 1996), except for the inhibition by intracellular benzoate cis-diol rather than glucose-6-phosphate. Although no direct evidence exists for benzoate uptake inhibition by benzoate cis-diol, most phenols and other hydroxyl-substituted benzoates were found to be among the competing substrates that result in significant inhibition of benzoate uptake (Huang et al., 2005, Wang et al., 2011). The compounds benzaldehyde and benzonitrile were tested and reported as alternative substrates for benzoate permease (encoded by benK) and porin (encoded by benF) (Huang et al., 2005), thus elucidating the observed non-specificity towards benzoate.
The secretion processes of intracellular metabolites, such as benzoate cis-diol, catechol, cis,cis-muconate and β-ketoadipate, were modeled by considering the transport processes that are mediated by passive diffusion or active transport. For benzoate cis-diol and catechol transport, the structural property of the model is based on the assumption of reversible influx-efflux kinetics of catechol, with a Hill coefficient to describe the extracellular concentrations of benzoate cis-diol and catechol [Eqs. (22) and (24)]. The use of a Hill coefficient of 1 (i.e., c=1 in Eq. (24)) failed to successfully describe the experimental observations (i.e., the transport of catechol). However, introducing an empirical Hill coefficient (i.e., c>1) made it possible to mimic the active transport of toxic catechol through the cell membrane to the external medium; in addition, an increase in the Hill coefficient led to an apparent reduction in the effective influx of catechol. Catechols are also known to damage the integrity of the membrane due to their redox cycling activity (Schweigert et al., 2001). Although catechol is less lipophilic (with a log Po/w of 1.5), it is water soluble and can partition well into the cell membrane, causing a change in membrane fluidity (de Bont, 1998).
Functional analysis of the genes mucK (Williams and Shaw, 1997) and pcaT (Parke et al., 2000) revealed that their gene products are involved in the transport of cis,cis-muconate and β-ketoadipate. The diffusion of charged compounds across the cell is described by the constant field equation (Goldman, 1943, Keifer and Roos, 1981). The ionic charges of the compounds cis,cis-muconate and β-ketoadipate are −2. For the membrane potential, a constant value of −50 mV was assumed. With the assumption that the translocation of charged compounds through a carrier was symmetrical (according to previous studies (Lancaster and Hinkle, 1977, Michels et al., 1979)), the equation was modified to include the effect of the complex formed by the diffusion ion and the carrier. The concentration of the complex (ion: carrier protein) has been reported to be similar to that for the enzyme-substrate complex of Michaelis-Menten kinetics. Under the assumption of constant pH, the effect of protons was found to be negligible; thus, we modified the proposed equations to consider the effects of cis,cis-muconate and β-ketoadipate alone [Eqs. (28), (29)]. Depending on the extracellular pH and the transport conditions, the membrane potential might vary; hence, our assumption of a constant membrane potential of −50 mV must be verified in future experiments. The rate expressions used for the transport of cis,cis-muconate and β-ketoadipate can be extended to include the effects of proton concentrations (Andersen et al., 2009) and the membrane potential change (Page, 1987); however, this topic is outside the scope of investigation of this study.
3.3.2. Benzoate catabolism
The foremost reaction catalyzed by benzoate 1,2-dioxygenase (encoded by benABC) involves ring hydroxylation and the incorporation of dioxygen into the product. This reaction was modeled as an irreversible double substrate kinetic (Ge and Eltis, 2003) [Eq. (20)]. For the subsequent reaction (benzoate 1,2-cis-dihydrodiol dehydrogenase (encoded by benD)), we tested several rate expressions that describe the rapid increase and decrease in the intracellular benzoate cis-diol concentrations. The in vivo behavior of benzoate cis-diol could be satisfactorily explained by assuming Ping-Pong kinetics with dead-end inhibition by catechol [Eq. (21)] (Segel, 1975, Simpson et al., 1987). The formation and consumption of the cofactor NAD+ by the above two reactions is assumed to be stoichiometrically balanced; hence, the influences of these factors on the enzyme kinetics were not investigated in this study. The catA gene is known to encode the enzyme catechol 1,2-dioxygenase, which is a key enzyme responsible for the intra-diol cleavage of the aromatic ring and the conversion of catechol to cis,cis-muconate (Nakai et al., 1988). Jiménez and colleagues previously reported the presence of a second copy of the gene catA (named catA2) within the ben cluster for benzoate degradation in P. putida KT2440 (Jiménez et al., 2002) and also recently elucidated the biological role of the gene product of catA2 (CatA2) as a metabolic safety valve that reduces the intracellular levels of toxic catechol (Jimenez et al., 2014). In this study, the roles of the gene products of catA and catA2 (i.e., in catalyzing the conversion of catechol to cis,cis-muconate) were represented by a combined kinetic rate expression [Eq. (23)], which was described by a double substrate equation with allosteric activation, where oxygen acted as both the substrate and an effector (Broderick, 1999, Bugg and Winfield, 1998). Because oxygen was a second substrate for both dioxygenases, the oxygen balance was included as a state variable [Eq. (16)], and the oxygen demands of both dioxygenases were considered to describe the rate of oxygen transfer into the cells.
Further, the two isomerase reactions performed by cis,cis-muconate cycloisomerase and muconolactone isomerase were lumped into one single rate expression (i.e., muconate isomerase ()) (Fig. 1) due to their similar kinetic properties (Ornston, 1966). The resulting rate expression [Eq. (25)] was then described by reversible Michaelis-Menten kinetics (Smith, 1992), with an equilibrium constant () calculated from the reported values of the individual isomerase reactions (Ornston and Stanier, 1966). The consecutive enzyme β-ketoadipate enol-lactone hydrolase () is known to be inhibited by its product β-ketoadipate at high concentrations (10 mM) (Yeh and Ornston, 1984). However, because of the observed low concentrations (less than 1 mM), we assumed no inhibition by β-ketoadipate, and a rate expression with Michaelis-Menten type kinetics was used [Eq. (26)]. The penultimate enzyme of the β-ketoadipate pathway (i.e., β-ketoadipate: succinyl-coenzyme A transferase) was modeled with Michaelis-Menten kinetics (Parales and Harwood, 1992).
3.4. Estimation of maximal rates
At steady state, the deterministic form of the rate equations can be envisaged as follows:
| (30) |
Here, estimates of the maximal rates of the enzymatic reactions () were obtained from the steady-state fluxes () and steady-state concentrations (), and an appropriate estimate of the corresponding parameter vector () was obtained from the in vitro measurements. Subsequently, with an assumption that the enzyme concentrations remained frozen at their steady-state values after a substrate pulse (Rizzi et al., 1997), the unknown maximal rates were then given by the equation:
| (31) |
3.5. Model implementation and analysis
The Matlab-based software packages SBtoolbox2 and SBPD toolbox were applied to integrate the system of non-linear differential equations and to estimate the model parameters (Schmidt and Jirstrand, 2006). Parameter estimation was performed using an enhanced Scatter Search algorithm integrated into the SBPD toolbox (Rodriguez-Fernandez et al., 2006). The optimization routine integrates and minimizes the difference between the measured concentrations () and the model-predicted concentrations (), represented as the minimization of a weighted distance measure,
| (32) |
where is the number of data points for each experiment, and is the number of state variables. Here, corresponds to the different weights taken to normalize the contributions of each term, i.e., . The set of model parameters identified from the above-mentioned procedure was subjected to parameter fit analysis, in which repeated estimations were performed from randomly perturbed initial conditions. The parameters were perturbed randomly between the low and high bounds around the identified values. The results of parameter fit analysis were then used to gain statistical insights into the estimated parameters.
3.6. Network embedded thermodynamic (NET) analysis
Thermodynamic analyses of benzoate metabolism were performed using the Matlab-based software ‘anNET’ (Zamboni et al., 2008), in which the optimization problems were solved using the LINDO API library (LINDO Systems Inc., Illinois, USA). The genome-scale metabolic model of P. putida (Nogales et al., 2008) was used to predict the minimum set of flux directions for benzoate. The comprehensive summary of the thermodynamic information that was reported by Zamboni et al. (2008) was extended with additional information regarding the metabolites involved in benzoate degradation, which was obtained from group contribution methods (Finley et al., 2009). Beyond the actual measurements from benzoate-limited cultivations, the concentrations of non-measured metabolites were allowed to vary between 0.001 and 10 mM in the NET analysis. The optimization procedures for determining the feasible range of metabolic network operation using the Gibbs energies of reactions and the flux balance algorithm applied to constrain the metabolic network were summarized by Kümmel et al. (2006a) (Kümmel et al., 2006a; Kümmel et al., 2006b).
4. Results
4.1. Metabolic response of P. putida to benzoate
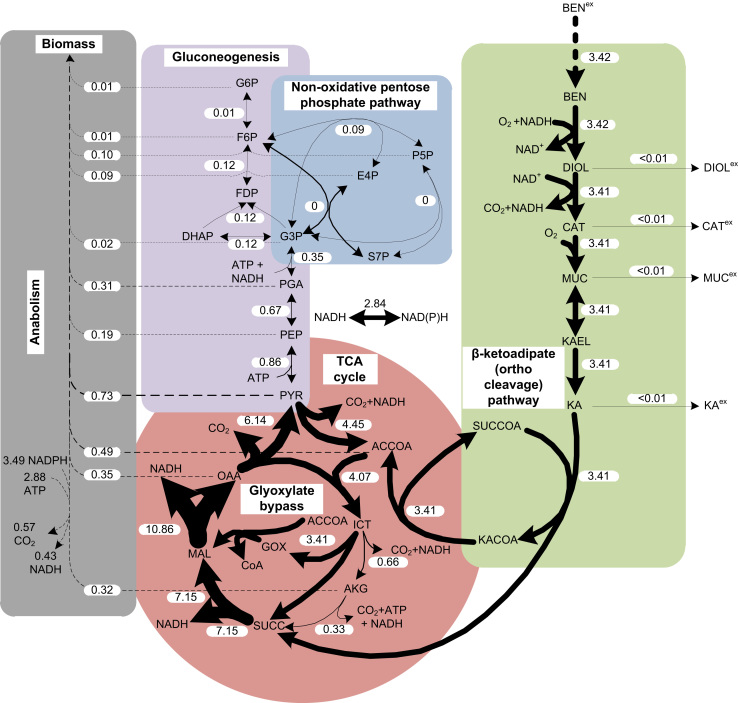
Benzoate uptake in P. putida is driven by an active transport system (Thayer and Wheelis, 1982), which has a specific uptake rate of 3.4 mmolbenzoate gCDW−1 h−1 (or 0.5 gbenzoate gCDW−1 h−1). Benzoate degradation via the β-ketoadipate (ortho-cleavage) pathway leads to equimolar quantities of CO2, succinate, and acetyl-CoA (Fig. 2) (Ampe and Lindley, 1996). Succinate and acetyl-CoA serve as fuels for anabolic reactions. The carbon skeletons that form glucose-6-phosphate originate from gluconeogenesis. The enzyme oxaloacetate decarboxylase (encoded by oadA) was considered as the first enzyme unique to gluconeogenesis. Pyruvate enters a series of predominantly gluconeogenic reactions that lead to the formation of fructose-6-phosphate and glucose-6-phosphate by fructose 1,6-bisphosphatase and phosphoglucoisomerase, respectively. A prominent flux via malate dehydrogenase was evident from the high flux through the glyoxylate cycle, which could be attributed to the post-translational modification of isocitrate dehydrogenase on acetogenic carbon sources (Walsh and Koshland, 1985).
Fig. 2.
In vivo flux distribution of P. putida KT2440 during growth on benzoate. Molar net fluxes (mmol gCDW−1 h−1) were obtained from the best fit (using the software FiatFlux) of substrate utilization rates on the respective substrates at a growth rate of 0.2 h−1. The arrows are drawn in proportion to the flux. The broken lines indicate flux towards biomass synthesis. Metabolites: BEN, benzoate; DIOL, benzoate 1,2 cis-diol; CAT, catechol; MUC, cis,cis-muconate; KAEL, β-ketoadipate enol-lactone; KA, β-ketoadipate; SUCCOA, succinyl CoA; KACOA, β-ketoadipyl coenzyme A; ACCOA, acetyl CoA; ICT, isocitrate; AKG, α-ketoglutarate; SUCC, succinate; MAL, malate; OAA, oxaloacetate; PYR, pyruvate; PEP, phosphoenolpyruvate; PGA, phosphoglyceric acid; G3P, glyceraldehyde 3-phosphate; DHAP, dihydroxyacetone phosphate; FDP, fructose di-phosphate; F6P fructose 6-phosphate; G6P glucose 6-phosphate; P5P pentose 5-phosphate; E4P erythrose 4-phosphate; and S7P sedoheptulose 7-phosphate. The superscript ‘ex’ denotes the extracellular localization of the metabolite.
Dynamic changes in the extracellular and intracellular metabolites of benzoate degradation were quantified after the residual concentrations of benzoate was increased using a defined pulse of benzoate. The extracellular metabolite fraction (i.e., the ratio of the extracellular concentration (EX) of a metabolite in the filtrate to the total concentration (T) of the same metabolite measured in PCA extracts) of the benzoate pathway metabolites was high. From this analysis, it is not possible to derive any reasonable values for intracellular concentrations due to the exponential increase in the standard deviations (Vielhauer et al., 2011). In our study, this problem applied to the compounds benzoate, cis,cis-muconate and β-ketoadipate. However, in dynamic conditions, calculations of the intracellular concentrations of benzoate cis-diol, catechol, and cis,cis-muconate were feasible. A step change in benzoate availability resulted in dynamic changes in the intracellular benzoate cis-diol and catechol concentrations, while the cis,cis-muconate concentrations increased steadily. The changes that propagated in the intracellular metabolites were on the order of seconds to minutes. For the steady-state conditions, the secretion of metabolites was as follows: β-ketoadipate>benzoate cis-diol>cis,cis-muconate>catechol; the extracellular β-ketoadipate concentrations approached a maximum concentration of 2 mM. These observations stimulate discussions about a metabolic overflow caused by the limited capacity of some of the enzymatic steps of the β-ketoadipate (ortho-cleavage) pathway in P. putida KT2440.
4.2. Evaluation of the kinetic model in predicting the benzoate metabolism response
To elucidate the complex interactions of the individual metabolites with enzymes of the pathway, a data-driven iterative modeling approach was applied. In this cycle, an abstract model of the β-ketoadipate (ortho-cleavage) pathway was refined until the measured data were described mathematically. The most appropriate model resulting from this iterative model-building cycle is outlined in Fig. 1, with the corresponding mass-balance and kinetic rate expressions. In total, the model comprises 27 time-dependent variables, of which 16 are states expressed as ordinary differential equations (Table 1), and 11 are reactions involved in either the transformation or transport of metabolites (Table 2). Multiple assumptions were essential to reduce the model complexity, especially in the case of insufficient in vitro or in vivo information regarding the enzymatic reactions. Some cardinal assumptions that were made to model the steady-state and transient behavior of the system are as follows: (a) the biomass, growth rate, and cell volume do not change during the transience after perturbation, (b) the mixing in the reactor is homogenous, and (c) a constant external pH of 7 and a membrane potential of −50 mV are maintained. Although the pulsed benzoate was consumed completely in an overall time span of ~25 min, the pulse response methodology applied for model validation was restricted to 12 min after perturbation. Within this time window, we assumed that the changes were primarily caused by metabolic regulation and by changes in biosynthetic reactions (e.g., protein biosynthesis was regarded as remaining in a “frozen” state) (Theobald et al., 1997). Consequently, the maximal enzyme capacities were assumed to remain at a steady-state value (for calculation of values, see Section 3.4). Apart from these intrinsic assumptions, the biochemical assumptions made to describe the kinetic properties of the enzymes are detailed in Section 3.3.
The time-series metabolome data generated from benzoate-pulse experiments were integrated into the model to identify the kinetic parameters using a stepwise internalization approach that was proposed previously (Rizzi et al., 1997). For this purpose, the measured concentrations of intracellular benzoate cis-diol ( and intracellular catechol () and the extracellular concentrations of benzoate (), catechol (), cis,cis-muconate () and β-ketoadipate () were included in the model identification procedure. Additionally, for metabolites with high extracellular concentrations, mass-balance equations were derived to introduce their total concentrations () into the model structure. The measurements were then numerically integrated with simulated concentrations from the mass-balance equations, and through minimization of the squared error, the unknown parameters were estimated (Table 3). For the model that resulted from this identification procedure, the predictions were in satisfactory agreement with the experimental observations. The identified model was able to predict both the steady-state and transient conditions introduced by a benzoate pulse (Fig. 3). To further validate the predictions of the constructed kinetic model, oxygen balance equations for the liquid and gas phases were included. The model fit the observed trend in the measured values of oxygen in the gas and liquid phases without additional parameter estimation (Fig. 4).
Table 3.
Kinetic parameters (initial and optimized values). Explanations for the enzyme abbreviations are provided in the legend of Fig. 1.
| Enzyme activities | Parameters | Initial values | Optimized values |
|---|---|---|---|
| BZT | KmBENT | 0.02 mM a | 0.0127 mM |
| KiBENT | 1⁎ | 5.06 mM | |
| BDO | KmBDO | 0.026 mMb | 0.026 mM |
| KmbO2 | 0.053 mMb | 0.053 mM | |
| KdBEN | 6.46 e−05 | 6.46 e−05 | |
| DIOLDH | KmDIOLDH | 0.2 mMc | 0.0387 mM |
| KmCATDH | 1⁎ | 0.0294 mM | |
| KiDIOLDH | 1⁎ | 12.72 mM | |
| DIOLT | KmDIOLTin | 1⁎ | 2.53 mM |
| KmDIOLTex | 1⁎ | 12.11 mM | |
| d | 1⁎ | 1.97 | |
| CDO | KmCDO | 0.002 mMd | 0.027 mM |
| KmcO2 | 0.06 mMd | 0.073 mM | |
| ncO2 | 1⁎ | 0.082 | |
| CT | KmCTin | 1⁎ | 9.28 mM |
| KmCTex | 1⁎ | 2.76 mM | |
| c | 1⁎ | 5.37 | |
| MISO | KmMISO | 0.09 mMe | 0.09 mM |
| KmLISO | 0.424 mMe | 0.424 mM | |
| KeqMISO | 1.03e | 10.80 | |
| MUCT | KmMUCT | 1⁎ | 0.025 mM |
| LH | KmKAEL | 0.012 mMf | (3.81 e−04 mM)⁎⁎ |
| KAT | KmKAT | 1⁎ | 1.42 mM |
| KACOAT | KmKACOAT | 0.40 mMg | (2.29 e−04 mM)⁎⁎ |
Arbitrary values.
Extremely low value indicates that the rate can be approximated by a zero-order reaction.
(Reiner, 1972).
Fig. 3.
Comparison between measurements (filled circles) and model simulations (continuous lines) after a pulse of benzoate (at time zero) in a steady-state benzoate-limited culture. The subscripts ‘RV’ and ‘CV’ on the y-axis represent the reactor volume and the cell volume, respectively. The superscripts ‘ex’, ‘in’, and ‘tot’ represent the extracellular, intracellular, and total concentrations, respectively, of the metabolite. Explanations for the metabolite abbreviations are provided in the legend of Fig. 1.
Fig. 4.
Comparison between measurements (filled circles) and model predictions (continuous lines) for oxygen in the liquid (top) and gas phases (bottom) during the benzoate pulse (at time zero) response experiment in a steady-state benzoate-limited culture. The subscript ‘RV’ on the y-axis represents the reactor volume. The solid lines are the results predicted using the dynamic model without additional parameter adaptation. Thus, these lines serve to validate the dynamic model.
4.3. Thermodynamic feasibilities of benzoate metabolism reactions
Due to the limited information regarding the regulatory interactions of the benzoate metabolic network, we examined the feasible ranges of benzoate metabolic network operation via thermodynamic analysis. According to the second law of thermodynamics, a reaction proceeds in the direction of negative .
NET analysis (Zamboni et al., 2008) was performed to elucidate the active regulatory sites of benzoate metabolism. NET analysis couples metabolite concentrations to an operating metabolic network and checks for thermodynamic feasibility based on the second law of thermodynamics (i.e., to allow for negative Gibbs energy for each preset flux). The steady-state intracellular concentrations of benzoate cis-diol and catechol and the extracellular concentrations of catechol and β-ketoadipate were used for NET analysis. From a flux balance analysis tool that is integrated into the anNET software, an operating benzoate metabolic network with 154 reactions and 183 metabolites was deduced from the P. putida genome-scale metabolic model iJN746 (Nogales et al., 2008). Thermodynamic consistency was demonstrated for the operation of the benzoate metabolic network with the given metabolite measurements, and the concentration ranges of the unmeasured metabolites were calculated for the feasible ranges of the estimated Gibbs energy of reactions. Of the 154 reactions of the benzoate metabolic network, the reactions of the β-ketoadipate (ortho-cleavage) pathway, the tricarboxylic acid cycle, gluconeogenesis, and the non-oxidative pentose phosphate pathway were analyzed in detail (Fig. 5).
Fig. 5.
Estimated ranges of the Gibbs energy of reaction () for the reactions of benzoate metabolism in P. putida KT2440. The reactions presented in boxes are far from equilibrium with large negative and are candidates for active regulation. Broken arrows indicate that the metabolites were excreted. Metabolites: ben, benzoate; bendiol, benzoate 1,2 cis-diol; cat, catechol; muc, cis,cis-muconate; mucl, muconolactone; 3oxael, β-ketoadipate enol-lactone; 3oxa, β-ketoadipate; succoa, succinyl CoA; 3oxacoa, β-ketoadipyl coenzyme A; accoa, acetyl CoA; icit, isocitrate; akg, α-ketoglutarate; succ, succinate; mal, malate; oaa, oxaloacetate; pyr, pyruvate; pep, phosphoenolpyruvate; 13dpg, 1,3-diphosphoglycerate; 2pg, 2-phosphoglycerate; 3pg, 3-phosphoglycerate; g3p, glyceraldehyde 3-phosphate; dhap, dihydroxyacetone phosphate; f16p, fructose di-phosphate; f6p, fructose 6-phosphate; g6p, glucose 6-phosphate; r5p, ribose 5-phosphate; e4p, erythrose 4-phosphate; x5p, xylulose 5-phosphate and S7P, sedoheptulose 7-phosphate. Enzymatic reactions: BZt1, benzoate permease; BZt3, benzoate transport porin; BZ12DOX, benzoate 1,2-dioxygenase; BZDIOLDH, benzoate cis-diol dehydrogenase; CATDOX, catechol 1,2-dioxygenase; MUCCYCI, muconate cycloisomerase; MUCLI, muconolactone isomerase; OXOAEL, β-ketoadipate enol lactone hydrolase; 3OADPCOAT, β-ketoadipate succinyl-CoA transferase; 3OXCOAT, β-ketoadipyl-CoA thiolase; ACONT, aconitase; ICDHyr, isocitrate dehydrogenase; AKGDH, α-ketoglutarate dehydrogenase; SUCD1, succinate dehydrogenase; SUCOAS, succinyl-CoA synthetase; FUM, fumarase; MDH, malate dehydrogenase; CS, citrate synthase; ICL, isocitrate lyase; MALS, malate synthase; OAADC, oxaloacetate decarboxylase; PDH, pyruvate dehydrogenase; PYK, pyruvate kinase; ENO, enolase; PGM, phosphoglycerate mutase; PGK, phosphoglycerate kinase; GAPD, glyceraldehyde-3-phosphate dehydrogenase; TPI, triose-phosphate isomerase; FBA, fructose-bisphosphate aldolase; FBP, fructose-bisphosphatase; PGI, glucose-6-phosphate isomerase; TKT1 and TKT2, transketolase; and TALA, transaldolase.
Active gluconeogenic reactions, such as pyruvate kinase (PYK), enolase (ENO), glyceraldehyde 3-phosphate dehydrogenase (GAPD), fructose bisphosphate aldolase (FBA), glucose 6-phosphate isomerase (PGI), and transketolase (TKT1 and TKT2) of the non-oxidative pentose phosphate pathway, exhibited a positive value for the Gibbs energy of reaction to direct the flow of carbon towards the synthesis of biomass precursors. All other reactions resulted in negative Gibbs energies of reaction, either close to or far from equilibrium. Notably, the ranges of the estimated Gibbs energies of reaction for the β-ketoadipate (ortho-cleavage) pathway enzymes benzoate cis-diol dehydrogenase (BZDIOLDH), catechol 1,2-dioxygenase (CATDOX), muconate cycloisomerase (MUCCYCI), 3-oxoadipyl/β-ketoadipyl CoA thiolase (3OXCOAT), and 3-oxoadipate/β-ketoadipate succinyl-CoA transferase (3OADPCOAT) were found to be highly negative. These reactions are strong candidates for active regulation, for example by changes in the rate of transcription and subsequent changes in enzyme activity. Interestingly, the Gibbs energies of reaction for the enzymes involved in other parts of the benzoate metabolic network were negative and had values close to equilibrium. The rates of these reactions depend only on the substrate concentrations and hence likely have limited control over the flux (Nielsen, 1997, Visser et al., 2004).
Further, in order to extend the link between thermodynamic analysis and parameter sensitivities, additional analysis has been performed by calculating the flux control coefficients with the software SBtoolbox2. The matrix of flux control coefficients is shown in (Fig. 6). The flux control coefficients can be linked to the free energy via the elasticities. Westerhoff et al. (Westerhoff et al., 1987) have shown the relationship between and elasticity coefficient in Eqs. (28)–(30) of their paper. The conclusions of the discussion of Westerhoff et al. indicate that reactions with low have high elasticity and have low flux control coefficients; and the opposite case i.e. the reactions with high have low elasticity and have high flux control coefficient for the corresponding reactions. From our analysis, the kinetic parameters of the corresponding reactions with large i.e. the reaction catalyzed by benzoate cis-diol dehydrogenase (KmDIOLDH, KmCATDH, KiDIOLDH), catechol 1,2-dioxygenase (KmCDO, ncO2), and β-ketoadipate succinyl-CoA transferase (KmKACOAT) were found to exert significant flux control over the pathway and the kinetic parameters of the reactions with low have no flux control over the pathway.
Fig. 6.
Flux control coefficients. The colors in row i and column j indicate the control that the parameter j exerts over the reaction rate i. The colors denote positive and negative control, respectively. A small increase in the Km value of catechol (i.e. KmCDO) or the hill coefficient (ncO2) exerts a negative control over all the fluxes of the pathway, and a positive control over the transport flux of benzoate cis-diol (). With respect to the enzyme benzoate cis-diol dehydrogenase, a small increase in the values of kinetic parameters KmDIOLDH, and KmCATDH exerts a negative control over the transport flux of benzoate cis-diol () and a positive control over the transport flux of β-ketoadipate (). A small increase in the value of KiDIOLDH exerts a negative control over all the fluxes of the pathway and a positive control over the transport flux of benzoate cis-diol (). With respect to the enzyme β-ketoadipate succinyl-CoA transferase, a small increase in the Km value of this enzyme (KmKACOAT) exerts a significant negative control over the transport flux of β-ketoadipate (). Also, a small increase in the kinetic parameter of cis-cis muconate (KmMUCT) and β-ketoadipate (KmKAT) transporters were found to exert a positive control over the transport rate of cis-cis muconate () and β-ketoadipate ().
5. Discussion
We investigated the well-known but poorly understood in vivo regulatory interactions of the β-ketoadipate (ortho-cleavage) pathway in P. putida KT2440 using an iterative model building process. Critical assumptions were necessary to describe the in vivo behavior of metabolites with appropriate reaction kinetics. In addition to metabolic regulation, there must be an additional regulation phenomenon at the enzyme level; this phenomenon was observed during the entire course of our pulse response experiments. The changes in metabolic regulation is known to occur on the time scale of seconds (Theobald et al., 1997). The hypothesis that an additional regulation phenomenon is superimposed on metabolic regulation was supported by the increasing degradation rate of benzoate with time (Fig. 7A). This observation is the main reason for restricting the metabolic response to 12 min after perturbation and not to a longer scale (12–23 min). The importance of additional regulation at the enzyme level was further illustrated in an experiment with sequential pulse experiments (Fig. 7B and C), in which the uptake rate of benzoate increased as the number of generations increased in a continuous culture kept at a constant dilution rate. Although the linear increase in the substrate uptake rate is a characteristic feature of continuous cultivation, whether the entire pathway or only the benzoate transport enzyme is optimized for carbon uptake is unknown and must be investigated thoroughly. A previous study showed that when the yeast S. cerevisiae is confronted with multiple glucose stimuli, the specific uptake rate of glucose is increased by a factor of seven compared with its steady-state value; this change accompanies altered expression of glucose transport proteins (Buziol et al., 2008). Moreover, prolonged glucose limitation of S. cerevisiae in a chemostat causes multiple steady states with different metabolite and enzyme levels (Wu et al., 2006). The observed deviations between the model predictions and the measurements (Fig. 3, Fig. 4) also indicate the presence of an additional regulation phenomenon in P. putida that cannot be compensated by parameter fitting with the existing model structure.
Fig. 7.
Changes in benzoate concentration and benzoate uptake rate in a benzoate-limited chemostat. (A) Change in benzoate concentration after a pulse of benzoate. The broken lines represent the time point of the benzoate pulse. (B) Specific rate of benzoate uptake during benzoate-limited cultivation of P. putida KT2440 at a dilution rate of 0.2 h−1. The data points represent the benzoate uptake rates calculated after the steady-state conditions were disturbed with identical benzoate pulses. The data points presented with filled circles represent one prolonged benzoate-limited chemostat (filled circles), and the data points presented with open squares, open diamonds, and open triangles represent individual chemostat experiments. (C) Changes in extracellular benzoate from three identical benzoate pulses performed in one prolonged chemostat at different time points. The broken lines represent the time point of the benzoate pulse. The data points presented with open circles, open squares and crosses represent the three different pulse experiments that were performed at 10.9, 17.8 and 27.3 generations, respectively. These figures represent the presence of an additional regulation phenomenon that cannot be described by the present model.
Major assumptions were made with respect to the feedback inhibition of benzoate transport and benzoate cis-diol dehydrogenase. Although no evidence to support a molecular basis for this phenomenon was reported in Pseudomonas for the former case of benzoate transport inhibition by benzoate cis-idol, a study with Corynebacterium glutamicum has shown that hydroxyl-substituted benzoates inhibit benzoate uptake significantly (Wang et al., 2011). In the latter case, feedback inhibition of benzoate cis-diol dehydrogenase by catechol was used purely to describe the in vivo dynamics of benzoate cis-diol and catechol concentrations. In addition, the reason for the low in vivo concentration of catechol compared with benzoate cis-diol might be the existence of two dedicated catechol dioxygenases, of which CatA2 was recently described as a safety valve that protects against toxic concentrations of catechol (Jimenez et al., 2014). Consequently, all of these factors might result in significant control of the total pathway flux by the benzoate cis-diol dehydrogenase.
The thermodynamic analysis indicated that the estimated Gibbs energy values of some reactions () were largely negative and that these reactions were operating far from equilibrium (Fig. 5). These reactions are catalyzed by benzoate cis-diol dehydrogenase (BZDIOLDH), catechol 1,2-dioxygenase (CATDOX), muconate cycloisomerase (MUCCYCI), β-ketoadipyl CoA thiolase (3OXCOAT), and β-ketoadipate CoA transferase (3OADPCOAT). These five reactions were classified as non-equilibrium reactions because at large −, the thermodynamic driving force is significant, and the rate of the reaction is regulated predominantly by changes in the enzyme capacity (for example, via transcription or the binding of effectors). These indications for sensitivity to additional regulation phenomena are partially manifested in the corresponding kinetic expressions. In our benzoate-pulse experiments, the substrates of these reactions were also found to be extracellular; this observation was true to a greater extent for some metabolites, such as β-ketoadipate, benzoate cis-diol, and cis,cis-muconate. The excretion or the overflow of the individual metabolites is most likely a result of the adaptation of the culture to the steady-state conditions of the continuous culture. Some of these excreted metabolites are extremely toxic (e.g., catechol), and other metabolites may be excreted due to simple metabolic overflow. The scenario can be changed by using different dilution rates, which may result in different concentrations of the enzymes. However, these phenomena were not studied in this project.
Bacterial mineralization of aromatics is well known to be critical e.g. on the level of benzene ring cleavage (Dagley, 1971, Evans, 1963). We initially hypothesized that catechol accumulation in shake flasks experiments are regulated by ring cleavage enzymes. The model and especially the quantitative description of all the rates allowed us to verify this hypothesis. In addition, catechol formation and especially benzoate uptake were identified as key and previously not recognized regulation points. For benzoate uptake, this new hypothesis was experimentally verified by sequential pulses. Amazingly cells reacted via aging/adaptation to the bottleneck benzoate uptake by increasing the benzoate uptake rate (Fig. 7B and C). This now can be taken as starting point again for defining new objectives, e.g. substrate uptake, product formation, etc. to run the systems biology iterative process (experiment-model-hypothesis-experiment…) a second time. In addition, model building is a purpose-driven-process. In other words: first define the purpose before starting to build the model. The purpose for the presented dynamic model is the application of re-designing the enzymatic makeup for the process/product of interest. In our specific case, objectives for follow up biotechnology research might be rate improvements for benzoate uptake and catechol formation and cleavage – the major flux bottlenecks identified by in vivo dynamic modeling (Fig. 1) on whatever level appropriate (metabolic engineering, reaction engineering, process engineering).
In summary, a data-driven modeling approach increased our understanding of the complex interactions of the β-ketoadipate (ortho-cleavage) pathway. The proposed model can capture the stationary and dynamic behavior of intracellular and extracellular metabolites. The systematic integration of quantitative metabolite data with thermodynamic information was pivotal for demonstrating that only a few reactions of benzoate metabolism are candidates for active regulation (e.g., transcriptional and/or allosteric regulation), whereas the rates of most reactions depend only on substrate concentrations that are close to equilibrium. Although the critical assumptions that were made regarding the regulation of the benzoate transport rate and benzoate cis-diol dehydrogenase activity are supported by in vivo dynamic modeling, they do invite future confirmation by in vitro investigations of these proteins. These findings highlight the necessity of quantifying metabolic rates of well known metabolic pathways in vivo. The biochemistry of pathway enzymes in the cytoplasm has to be described both theoretically in (dynamic) models as well as verified experimentally, e.g. in chemostat experiments. In this respect, direct translations of genomic sequence data/ annotations into metabolic flux networks are necessary, but not sufficient.
Acknowledgements
Laboratory and infrastructure support by the department of biochemical and chemical engineering, TU Dortmund University is gratefully acknowledged. We thank Stefan Kaschabek and Michael Schlömann for valuable discussions and for their support in providing benzoate cis-diol for analysis. We also thank Naruemol Noisommit-Rizzi, Andreas Freund, and Salaheddine Laghrami for their skillful assistance in rapid-sampling procedures and analytics. This project was supported by the International Max Planck Research School in Chemical Biology (IMPRS-CB) and was partially supported by the German Ministry of Science and Education (BMBF, Project ERA-NET SysMO, no. 0313980A) (VAPMdS) and by the Ministry of Innovation, Science, Research and Technology of North Rhine-Westphalia (Bio. NRW, Technology Platform Biocatalysis, RedoxCell).
References
- Ampe F., Lindley N.D. Flux limitations in the ortho pathway of benzoate degradation of Alcaligenes eutrophus: metabolite overflow and induction of the meta pathway at high substrate concentrations. Microbiology. 1996;142:1807–1817. doi: 10.1099/13500872-142-7-1807. [DOI] [PubMed] [Google Scholar]
- Andersen A.Z., Carvalho A.L., Neves A.R., Santos H., Kummer U., Olsen L.F. The metabolic pH response in Lactococcus lactis: an integrative experimental and modelling approach. Comput. Biol. Chem. 2009;33:71–83. doi: 10.1016/j.compbiolchem.2008.08.001. [DOI] [PubMed] [Google Scholar]
- Bagdasarian M., Lurz R., Riickert B., Bagdasarian M.M., Frey J., Timmis K.N. Specific-purpose plasmid cloning vectors II. Broad host range, high copy number, RSFlOlO-derived, and a host-vector system for gene cloning in Pseudomonas. Gene. 1981;16:237–247. doi: 10.1016/0378-1119(81)90080-9. [DOI] [PubMed] [Google Scholar]
- Blank L.M., Ionidis G., Ebert B.E., Bühler B., Schmid A. Metabolic response of Pseudomonas putida during redox biocatalysis in the presence of a second octanol phase. FEBS J. 2008;275:5173–5190. doi: 10.1111/j.1742-4658.2008.06648.x. [DOI] [PubMed] [Google Scholar]
- Bloemen H.H.J., Wu L., van Gulik W.M., Heijnen J.J., Verhaegen M.H.G. Reconstruction of the O2 uptake rate and CO2 evolution rate on a time scale of seconds. AIChE J. 2003;49:1895–1908. [Google Scholar]
- Bratbak G., Dundas I. Bacterial dry matter content and biomass estimations. Appl. Environ. Microbiol. 1984;48:755–757. doi: 10.1128/aem.48.4.755-757.1984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Broderick J.B. Catechol dioxygenases. Essays Biochem. 1999;34:173–189. doi: 10.1042/bse0340173. [DOI] [PubMed] [Google Scholar]
- Bruggeman F.J., Westerhoff H.V. The nature of systems biology. Trends Microbiol. 2007;15(1):45–50. doi: 10.1016/j.tim.2006.11.003. [DOI] [PubMed] [Google Scholar]
- Bugg T.D.H., Ahmad M., Hardiman E.M., Rahmanpour R. Pathways for degradation of lignin in bacteria and fungi. Nat. Prod. Rep. 2011;28:1871–1960. doi: 10.1039/c1np00042j. [DOI] [PubMed] [Google Scholar]
- Bugg T.D.H., Winfield C.J. Enzymatic cleavage of aromatic rings: mechanistic aspects of the catechol dioxygenases and later enzymes of bacterial oxidative cleavage pathways. Nat. Prod. Rep. 1998;15:513–530. [Google Scholar]
- Buziol S., Warth L., Magario I., Freund A., Siemann-Herzberg M., Reuss M. Dynamic response of the expression of hxt1, hxt5 and hxt7 transport proteins in Saccharomyces cerevisiae to perturbations in the extracellular glucose concentration. J. Biotechnol. 2008;134:203–210. doi: 10.1016/j.jbiotec.2008.02.002. [DOI] [PubMed] [Google Scholar]
- Cao B., Loh K.-C. Catabolic pathways and cellular responses of Pseudomonas putida P8 during growth on benzoate with a proteomics approach. Biotechnol. Bioeng. 2008;101:1297–1312. doi: 10.1002/bit.21997. [DOI] [PubMed] [Google Scholar]
- Dagley S. Catabolism of aromatic compounds by microorganisms. Adv. Microb. Physiol. 1971;6:1–46. doi: 10.1016/s0065-2911(08)60066-1. [DOI] [PubMed] [Google Scholar]
- de Bont J.A.M. Solvent-tolerant bacteria in biocatalysis. Trends Biotechnol. 1998;16:493–499. [Google Scholar]
- Díaz E. Bacterial degradation of aromatic pollutants: a paradigm of metabolic versatility. Int. Microbiol. 2004;7:173–180. [PubMed] [Google Scholar]
- Emmerling M., Dauner M., Ponti A., Fiaux J., Hochuli M., Szyperski T., Wu K., Bailey J.E., Sauer U. Metabolic flux responses to pyruvate kinase knockout in Escherichia coli. J. Bacteriol. 2002;184:152–164. doi: 10.1128/JB.184.1.152-164.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans W.C. The microbiological degradation of aromatic compounds. J. Gen. Microbiol. 1963;32:177–184. doi: 10.1099/00221287-32-2-177. [DOI] [PubMed] [Google Scholar]
- Finley S.D., Broadbelt L.J., Hatzimanikatis V. Thermodynamic analysis of biodegradation pathways. Biotechnol. Bioeng. 2009;103:532–541. doi: 10.1002/bit.22285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischer E., Zamboni N., Sauer U. High-throughput metabolic flux analysis based on gas chromatography–mass spectrometry derived 13C constraints. Anal. Biochem. 2004;325(2):308–316. doi: 10.1016/j.ab.2003.10.036. [DOI] [PubMed] [Google Scholar]
- Fuchs G., Boll M., Heider J. Microbial degradation of aromatic compounds – from one strategy to four. Nat. Rev. Microbiol. 2011;9:803–816. doi: 10.1038/nrmicro2652. [DOI] [PubMed] [Google Scholar]
- Ge Y., Eltis L.D. Characterization of hybrid toluate and benzoate dioxygenases. J. Bacteriol. 2003;185:5333–5341. doi: 10.1128/JB.185.18.5333-5341.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman D.E. Potential, impedance, and rectification in membranes. J. Gen. Physiol. 1943;27:37–60. doi: 10.1085/jgp.27.1.37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harwood C.S., Parales R.E. The β-ketoadipate pathway and the biology of self-identity. Annu. Rev. Microbiol. 1996;50:553–590. doi: 10.1146/annurev.micro.50.1.553. [DOI] [PubMed] [Google Scholar]
- Huang D.S., Whang T.J., Cheng F.C., Wu Y.P., Wand Y.T., Luo W.I., Wang Y.S. Toxicity assessment of mono-substituted benzenes and phenols using a Pseudomonas initial oxygen uptake assay. Environ. Toxicol. Chem. 2005;24:253–260. doi: 10.1897/04-212r.1. [DOI] [PubMed] [Google Scholar]
- Jiménez J.I., Canales A., Jimenez-Barbero J., Ginalski K., Rychlewski L., Garcia J.L., Diaz E. Deciphering the genetic determinants for aerobic nicotinic acid degradation: the nic cluster from Pseudomonas putida KT2440. Proc. Natl. Acad. Sci. USA. 2008;105:11329–11334. doi: 10.1073/pnas.0802273105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiménez J.I., Miñambres B., Luis J., Díaz E. Genomic analysis of the aromatic catabolic pathways from Pseudomonas putida KT2440. Environ. Microbiol. 2002;4:824–841. doi: 10.1046/j.1462-2920.2002.00370.x. [DOI] [PubMed] [Google Scholar]
- Jimenez J.I., Perez-Pantoja D., Chavarria M., Diaz E., de Lorenzo V. A second chromosomal copy of the catA gene endows Pseudomonas putida mt-2 with an enzymatic safety valve for excess of catechol. Environ. Microbiol. 2014;16:1767–1778. doi: 10.1111/1462-2920.12361. [DOI] [PubMed] [Google Scholar]
- Kaschabek S.R., Kuhn B., Mu D., Schmidt E., Reineke W. Degradation of aromatics and chloroaromatics by Pseudomonas sp.strain B13: purification and characterization of 3-oxoadipate: succinyl-coenzyme A (CoA) transferase and 3-oxoadipyl-CoA thiolase. J. Bacteriol. 2002;184:207–215. doi: 10.1128/JB.184.1.207-215.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keifer D., Roos A. Membrane permeability to the molecular forms of DMO in barnacle muscle and ionic forms of DMO in barnacle muscle. Am. J. Physiol. 1981;240:C73–C79. doi: 10.1152/ajpcell.1981.240.1.C73. [DOI] [PubMed] [Google Scholar]
- Kümmel A., Panke S., Heinemann M. Putative regulatory sites unraveled by network-embedded thermodynamic analysis of metabolome data. Mol. Syst. Biol. 2006;2:0034. doi: 10.1038/msb4100074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kümmel A., Panke S., Heinemann M. Systematic assignement of thermodynamic constraints in metabolic network models. BMC Bioinform. 2006;7:512. doi: 10.1186/1471-2105-7-512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lancaster J.R., Jr., Hinkle P.C. Studies of the beta-galactoside transporter in inverted membrane vesicles of Escherichia coli. I. Symmetrical facilitated diffusion and proton gradient-coupled transport. J. Biol. Chem. 1977;252:7657–7661. [PubMed] [Google Scholar]
- Linger J.G., Vardon D.R., Guarnieri M.T., Karp E.M., Hunsinger G.B., Franden M.A., Johnson C.W., Chupka G., Strathmann T.J., Pienkos P.T., Beckham G.T. Lignin valorization through integrated biological funneling and chemical catalysis. Proc. Natl. Acad. Sci. USA. 2014;111:12013–12018. doi: 10.1073/pnas.1410657111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michels P.A.M., Michels J.P.J., Boonstra J., Konings W.N. Generation of an electrochemical proton gradient in bacteria by the excretion of metabolic end products. Fems Microbiol. Lett. 1979;5:357–364. [Google Scholar]
- Mizuno S., Yoshikawa N., Seki M., Mikawa T., Imada Y. Microbial production of cis,cis-muconic acid from benzoic acid. Appl. Microbiol. Biotechnol. 1988;28:20–25. [Google Scholar]
- Nakai C., Nakazawa T., Nozaki M. Purification and properties of catechol 1,2-dioxygenase (pyrocatechase) from Pseudomonas putida mt-2 in comparison with that from Pseudomonas arvilla C-1. Arch. Biochem. Biophys. 1988;267:701–713. doi: 10.1016/0003-9861(88)90079-3. [DOI] [PubMed] [Google Scholar]
- Nelson K.E., Weinel C., Paulsen I.T., Dodson R.J., Hilbert H., dos Santos V.A., Fouts D.E., Gill S.R., Pop M., Holmes M., Brinkac L., Beanan M., Deboy R.T., Daugherty S., Kolonay J., Madupu R., Nelson W., White O., Peterson J., Khouri H., Hance I., Lee P.C., Holtzapple E., Scanlan D., Tran K., Moazzez A., Utterback T., Rizzo M., Lee K., Kosack D., Moestl D., Wedler H., Lauber J., Stjepandic D., Hoheisel J., Straetz M., Heim S., Kiewitz C., Eisen J., Timmis K.N., Düsterhöft A., Tümmler B., Fraser C.M. Complete genome sequence and comparative analysis of the metabolically versatile Pseudomonas putida KT2440. Environ. Microbiol. 2002;4:799–808. doi: 10.1046/j.1462-2920.2002.00366.x. [DOI] [PubMed] [Google Scholar]
- Nielsen J. Metabolic control analysis of biochemical pathways based on a thermokinetic description of reaction rates. Biochem J. 1997;321(1):133–138. doi: 10.1042/bj3210133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nogales J., Canales A., Jimenez-Barbero J., Serra B., Pingarron J.M., Garcia J.L., Diaz E. Unravelling the gallic acid degradation pathway in bacteria: the gal cluster from Pseudomonas putida. Mol. Microbiol. 2011;79:359–374. doi: 10.1111/j.1365-2958.2010.07448.x. [DOI] [PubMed] [Google Scholar]
- Nogales J., Palsson B.Ø., Thiele I. A genome-scale metabolic reconstruction of Pseudomonas putida KT2440: iJN746 as a cell factory. BMC Syst. Biol. 2008;2:79. doi: 10.1186/1752-0509-2-79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ornston L.N. The conversion of catechol and protocatechuate to β-ketoadipate by Pseudomonas putida. II. Enzymes of the protocatechuate pathway. J. Biol. Chem. 1966;241:3787–3794. [PubMed] [Google Scholar]
- Ornston L.N. Conversion of catechol and protocatechuate to β-ketoadipate (Pseudomonas putida) Methods Enzymol. 1970;17:529–549. [Google Scholar]
- Ornston L.N., Stanier R.Y. The conversion of catechol and protocatechuate to β-Ketoadipate by Pseudomonas putida I. Biochemistry. J. Biol. Chem. 1966;241:3776–3786. [PubMed] [Google Scholar]
- Page M.G.P. The role of protons in the mechanism of galactoside transport via the lactose permease of Escherichia coli. Biochim. Biophys. Acta. 1987;897:112–126. doi: 10.1016/0005-2736(87)90319-1. [DOI] [PubMed] [Google Scholar]
- Parales R.E., Harwood C.S. Characterization of the genes encoding β-Ketoadipate: succinyl-coenzyme A transferase in Pseudomonas putida. J. Bacteriol. 1992;174:4657–4666. doi: 10.1128/jb.174.14.4657-4666.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parke D., Argenio D.A.D., Ornston L.N. Bacteria are not what they eat: that is why they are so diverse. J. Bacteriol. 2000;182:257–263. doi: 10.1128/jb.182.2.257-263.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reiner A.M. Metabolism of aromatic compounds in bacteria. J. Biol. Chem. 1972;247:4960–4965. [PubMed] [Google Scholar]
- Rizzi M., Baltes M., Theobald U., Reuss M. In vivo analysis of metabolic dynamics in Saccharomyces cerevisiae: II. Mathematical model. Biotechnol. Bioeng. 1997;55:592–608. doi: 10.1002/(SICI)1097-0290(19970820)55:4<592::AID-BIT2>3.0.CO;2-C. [DOI] [PubMed] [Google Scholar]
- Rizzi M., Theobald U., Querfurth E., Rohrhirsch T., Reuss M. In vivo investigations of glucose transport in Saccharomyces cerevisiae. Biotechnol. Bioeng. 1996;49:316–327. doi: 10.1002/(SICI)1097-0290(19960205)49:3<316::AID-BIT10>3.0.CO;2-C. [DOI] [PubMed] [Google Scholar]
- Rodriguez-Fernandez M., Egea J.A., Banga J.R. Novel metaheuristic for parameter estimation in nonlinear dynamic biological systems. BMC Bioinform. 2006;7:483. doi: 10.1186/1471-2105-7-483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidt H., Jirstrand M. Systems biology toolbox for MATLAB: a computational platform for research in systems biology. Bioinformatics. 2006;22:514–515. doi: 10.1093/bioinformatics/bti799. [DOI] [PubMed] [Google Scholar]
- Schweigert N., Zehnder A.J.B., Eggen R.I.L. Chemical properties of catechols and their molecular modes of toxic action in cells, from microorganisms to mammals. Environ. Microbiol. 2001;3:81–91. doi: 10.1046/j.1462-2920.2001.00176.x. [DOI] [PubMed] [Google Scholar]
- Segel I.H. Enzyme Kinetics: Behavior and Analysis of Rapid Equilibrium and Steady-state Enzyme Systems. Wiley; New York: 1975. pp. 534–541. [Google Scholar]
- Simpson H.D., Green J., Dalton H. Purification and some properties of a novel heat-stable cis-toluene dihydrodiol dehydrogenase. Biochem. J. 1987;244:585–590. doi: 10.1042/bj2440585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith W.G. In vivo kinetics and the reversible Michaelis-Menten model. J. Chem. Educ. 1992;69:981. [Google Scholar]
- Sudarsan S., Dethlefsen S., Blank L.M., Siemann-Herzberg M., Schmid A. The functional structure of central carbon metabolism in Pseudomonas putida KT2440. Appl. Environ. Microbiol. 2014;80:5292–5303. doi: 10.1128/AEM.01643-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taymaz-Nikerel H., de Mey M., Ras C., Ten Pierick A., Seifar R.M., van Dam J.C., Heijnen J.J., van Gulik W.M. Development and application of a differential method for reliable metabolome analysis in Escherichia coli. Anal. Biochem. 2009;386:9–19. doi: 10.1016/j.ab.2008.11.018. [DOI] [PubMed] [Google Scholar]
- Thayer J.R., Wheelis M.L. Active transport of benzoate in Pseudomonas putida. J. Gen. Microbiol. 1982;128:1749–1753. doi: 10.1099/00221287-128-8-1749. [DOI] [PubMed] [Google Scholar]
- Theobald U., Mailinger W., Baltes M., Rizzi M. In vivo analysis of metabolic dynamics in Saccharomyces cerevisiae: I. Experimental observations. Biotechnol. Bioeng. 1997;55:305–316. doi: 10.1002/(SICI)1097-0290(19970720)55:2<305::AID-BIT8>3.0.CO;2-M. [DOI] [PubMed] [Google Scholar]
- van Duuren J.B., Puchalka J., Mars A.E., Bucker R., Eggink G., Wittmann C., Dos Santos V.A. Reconciling in vivo and in silico key biological parameters of Pseudomonas putida KT2440 during growth on glucose under carbon-limited condition. BMC Biotechnol. 2013;13:93. doi: 10.1186/1472-6750-13-93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Duuren J.B.J.H., Brehmer B., Mars A.E., Eggink G., Dos Santos V.A.P.M., Sanders J.P.M. A limited LCA of bio-adipic acid: manufacturing the nylon-6,6 precursor adipic acid using the benzoic acid degradation pathway from different feedstocks. Biotechnol. Bioeng. 2011;108:1298–1306. doi: 10.1002/bit.23074. [DOI] [PubMed] [Google Scholar]
- Vardon D.R., Franden M.A., Johnson C.W., Karp E.M., Guarnieri M.T., Linger J.G., Salm M.J., Strathmann T.J., Beckham G.T. Adipic acid production from lignin. Energy Environ. Sci. 2015;8:617–628. [Google Scholar]
- Vielhauer O., Zakhartsev M., Horn T., Takors R., Reuss M. Simplified absolute metabolite quantification by gas chromatography-isotope dilution mass spectrometry on the basis of commercially available source material. J. Chromatogr. B. 2011;879:3859–3870. doi: 10.1016/j.jchromb.2011.10.036. [DOI] [PubMed] [Google Scholar]
- Visser D., Schmid J.W., Mauch K., Reuss M., Heijnen J.J. Optimal re-design of primary metabolism in Escherichia coli using linlog kinetics. Metab. Eng. 2004;6:378–390. doi: 10.1016/j.ymben.2004.07.001. [DOI] [PubMed] [Google Scholar]
- Walsh K., Koshland D.E. Branch point control by the phosphorylation state of isocitrate dehydrogenase. A quantitative examination of fluxes during a regulatory transition. J. Biol. Chem. 1985;260:8430–8437. [PubMed] [Google Scholar]
- Wang S., Xu Y., Liu S., Zhou N. Conserved residues in the aromatic acid/H+ symporter family are important for benzoate uptake by NCgl2325 in Corynebacterium glutamicum. Int. Biodeterior. Biodegrad. 2011;65:527–532. [Google Scholar]
- Wells T., Ragauskas A.J. Biotechnological opportunities with the β-ketoadipate pathway. Trends Biotechnol. 2012;30:627–637. doi: 10.1016/j.tibtech.2012.09.008. [DOI] [PubMed] [Google Scholar]
- Westerhoff H.V., Plomp P.J., Groen A.K., Wanders R.J. Thermodynamics of the control of metabolism. Cell Biophys. 1987;11:239–267. doi: 10.1007/BF02797123. [DOI] [PubMed] [Google Scholar]
- Williams P.A., Shaw L.E. mucK, a gene in Acinetobacter calcoaceticus ADP1 (BD413), encodes the ability to grow on exogenous cis,cis-muconate as the sole carbon source. J. Bacteriol. 1997;179:5935–5942. doi: 10.1128/jb.179.18.5935-5942.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu L., Mashego M.R., Proell A.M., Vinke J.L., Ras C., van Dam J., van Winden W.A., van Gulik W.M., Heijnen J.J. In vivo kinetics of primary metabolism in Saccharomyces cerevisiae studied through prolonged chemostat cultivation. Metab. Eng. 2006;8:160–171. doi: 10.1016/j.ymben.2005.09.005. [DOI] [PubMed] [Google Scholar]
- Yeh W., Ornston L.N. p-Chloromercuribenzoate specifically modifies thiols associated with the active sites of β-ketoadipate enol-lactone hydrolase and succinyl CoA:β-ketoadipate CoA transferase. Arch. Microbiol. 1984;138:102–105. doi: 10.1007/BF00413008. [DOI] [PubMed] [Google Scholar]
- Zamboni N., Fischer E., Sauer U. FiatFlux-a software for metabolic flux analysis from 13C-glucose experiments. BMC Bioinform. 2005;6:209. doi: 10.1186/1471-2105-6-209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zamboni N., Kümmel A., Heinemann M. anNET: a tool for network-embedded thermodynamic analysis of quantitative metabolome data. BMC Bioinform. 2008;9:199. doi: 10.1186/1471-2105-9-199. [DOI] [PMC free article] [PubMed] [Google Scholar]