A Semiparametric Model for vQTL Mapping

Summary

Quantitative trait locus analysis has been used as an important tool to identify markers where the phenotype or quantitative trait is linked with the genotype. Most existing tests for single locus association with quantitative traits aim at the detection of the mean differences across genotypic groups. However, recent research has revealed functional genetic loci that affect the variance of traits, known as variability-controlling quantitative trait locus. In addition, it has been suggested that many genotypes have both mean and variance effects, while the mean effects or variance effects alone may not be strong enough to be detected. The existing methods accounting for unequal variances include the Levene’s test, the Lepage test and the D-test, but suffer from their limitations of lack of robustness or lack of power. We propose a semiparametric model and a novel pairwise conditional likelihood ratio test. Specifically, the semiparametric model is designed to identify the combined differences in higher moments among genotypic groups. The pairwise likelihood is constructed based on conditioning procedure, where the unknown reference distribution is eliminated. We show that the proposed pairwise likelihood ratio test has a simple asymptotic chi-square distribution, which does not require permutation or bootstrap procedures. Simulation studies show that the proposed test performs well in controlling Type I errors and having competitive power in identifying the differences across genotypic groups. In addition, the proposed test has certain robustness to model mis-specifications. The proposed test is illustrated by an example of identifying both mean and variances effects in body mass index using the Framingham Heart Study data.

1. Introduction

In the last two decades, quantitative trait locus (QTL) analysis has been used as an important tool to identify markers where the phenotype or quantitative trait is linked with the genotype (Falconer et al., 1996). Most of the existing tests for single locus association with quantitative traits aim at detecting the mean differences across genotypic groups. Recently, it has been suggested that there may be heterogeneity in variance across genotypes for functional loci as well, and this type of functional loci is named as variability-controlling quantitative trait loci (vQTL) (Rönnegård and Valdar, 2012). The variance heterogeneity can be explained by gene-by-gene (G×G) or gene-by-environment (G×E) interactions. For example, a genotypic effect at one locus may be affected by the genotype at an adjunct locus. Hence the genotypic effect at that locus is a composite of multiple distributions with different means, resulting in an inflated variance for that genotype (Struchalin et al., 2010; Deng and Paré, 2011). In addition, it has been shown that vQTL can be induced by linkage disequilibrium with nearby functional locus with mean effects only (Cao et al., 2014).

To capture the differences in variances, the Levene’s test has been used to prioritize loci to identify potential G×E interactions (Paré et al., 2010; Struchalin et al., 2010; Shen et al., 2012). This test is calculated similarly as the ANOVA F-test, except it is based on the absolute differences between each observation and its group mean. The Levene’s test is a powerful and robust test, when the genetic loci have only variance effects on the quantitative traits. However, it has been suggested that many loci have both mean and variance effects, while some of the mean or variance effects alone would not be strong enough to be detected (Shen et al., 2012; Cao et al., 2014). For example, Yang et al. (2012) founded several loci in the FTO (fat mass and obesity-associated) gene that have both mean and variance effects on body mass index (BMI). The Lepage test is a rank-based non-parametric test for either mean or variance difference, which combines the Kruskal-Wallis test statistic for mean difference and the Fligner-Killeen test statistics for variance difference, and has been shown to be powerful and robust when the locus has both mean and variance effects (Lepage, 1971; Hollander and Wolfe, 1999). Aschard et al. (2013) introduced a general distribution-based test or D-test, which can be thought as an extension of the classical Kolmogorov–Smirnov test (Brittain, 1987). There are two versions of D-test, namely, the constrained D-test (D_c) and the unconstrained D-test (D_u). The D_c test is designed for the situation when the effect of the variant is monotonic, while the D_u test has the ability to detect genetic effects in a broader range of situations (Aschard et al., 2013). Cao et al. (2014) recently proposed a likelihood ratio test based on a parametric model that can test the joint effects of mean and variance or either alone. However, the test by Cao et al. (2014) has inflated Type I error in the presence of non-normally distributed phenotypes. A parametric bootstrap procedure was suggested to overcome this drawback, which, similar to the D-test, can be computationally intensive.

In this article, we propose a semiparametric model and a novel pairwise likelihood ratio test, which aims to identify the combined differences in higher moments (e.g., mean, variance, skewness and kurtosis) among genotypic groups, and to offer more flexibility in distributions than parametric model based tests. Specifically, the proposed test combines the differences among three genotypic groups: the major allele homozygous group (denoted as group AA), the heterozygous group (denoted as group Aa), and the minor allele homozygous group (denoted as group aa). The distribution of quantitative trait in group Aa is used as a reference distribution and is completely left unspecified. To model the differences in distributions among genotypic groups, we impose a multi-parameter exponential tilt model (ETM) where multivariate parameters are allowed to capture the differences in higher moments. We note that different loci lead to different partition of genotypic groups. The reference distribution, i.e., the distribution of the quantitative trait in the heterozygous group, can vary substantially across loci. It is not easy to find a parametric model which can fit well at all of these loci. Fitting marker-specific parametric model may not be feasible for large number of loci, and leads to difficulty in model interpretations. Given the semiparametric ETM, a commonly used inference procedure can be empirical likelihood ratio method (Owen, 1988), which estimates the reference distribution by a profiling procedure (Anderson, 1979; Qin, 1998; Fokianos and Kaimi, 2006). However, the test based on the empirical likelihood may have inflated Type I errors (Qin and Liang, 2011). Permutation based methods, which can properly adjust for the Type I errors, can be used but subject to more computational cost. In this paper, we propose an alternative pairwise likelihood ratio test where the reference distribution is eliminated by a conditioning procedure such that the impact of the unknown reference distribution is minimized (Kalbfleisch and Sprott, 1970). Such a pairwise likelihood ratio test is found to have well controlled Type I errors and improved power over existing tests including the ANOVA test, the Levene’s test, the Lepage test and the D-test. In addition, we found that the proposed test has some degree of robustness to model mis-specifications.

This paper is organized as follows. In Section 2, we describe the proposed pairwise conditional likelihood ratio test, its null distribution and local asymptotic power. In Section 3, we conduct simulation studies to compare the Type I errors with nominal levels and powers of the proposed test with that of current tests. We apply our test to a study of genetic association between genotype and BMI, a quantitative trait, using the Framingham Heart Study (FHS) data in Section 4. Finally, we provide a discussion in Section 5.

2. Method

2.1 A semiparametric model for vQTL mapping

At the lth marker, let {u_l1, … , u_ln1} be independent and identically distributed (i.i.d.) quantitative traits (such as BMI, gene expression levels or blood pressure) for n₁ individuals with major allele homozygote genotype AA, {v_l1, … , v_ln2} be i.i.d. quantitative traits for n₂ individuals with heterozygous genotype Aa, and {w_l1, … , w_ln3} be i.i.d. quantitative traits for n₃ individuals with minor allele homozygote genotype aa. Denote f_l(·), h_l(·) and g_l(·) as the distributions of the quantitative traits in groups AA, Aa and aa, respectively. We propose the following parsimonious semiparametric model. Specifically, at the lth marker, we assume that the distributions of the quantitative trait for individuals with homozygote genotypes (i.e., AA or aa) are related to that for individuals with heterozygous genotype Aa by exponential tilting functions,

$$\log \frac{f_l\left(x\right)}{h_l\left(x\right)}={\alpha }_{l,\mathit{AA}}+{\beta }_{l,\mathit{AA}}^T\mathit{K}\left(x\right),\text{and}\log \frac{g_l\left(x\right)}{h_l\left(x\right)}={\alpha }_{l,\mathit{aa}}+{\beta }_{l,\mathit{aa}}^T\mathit{K}\left(x\right),$$ (1)

where the density function of the quantitative traits for individuals with heterozygous genotype Aa at the lth marker, h_l(·), is considered as a reference distribution, whose parametric form is completely unspecified. Here β_l,AA = (β_l,AA,1, …, β_lAA,d), and β_l,aa = (β_l,aa,1, …, β_l,aa,d) are d-dimensional vectors of unknown, K(x) = {K₁(x), … , K_d(x)} is a vector of pre-specified functions. The parameter β_l,AA measures the differences in higher moments in the quantitative trait between groups AA and Aa, and β_l,aa measures the differences between groups aa and Aa. The parameter α_l,AA (or α_l,aa) is the normalizing constant for density function f_l(·) (or g_l(·)), and is defined as ${\alpha }_{l,\mathit{AA}}=-\log \left[\exp \right\{{\beta }_{l,\mathit{AA}}^T\mathit{K}\left(x\right)\left\}{h}_l\left(x\right)\mathit{dx}\right]$ (or ${\alpha }_{l,\mathit{aa}}=-\log \left[\exp \right\{{\beta }_{l,\mathit{aa}}^T\mathit{K}\left(x\right)\left\}{h}_l\left(x\right)\mathit{dx}\right]$). It is easy to see that β_l,AA = 0 implies α_l,AA = 0, and similar relationship holds for β_l,aa and α_l,aa. For notational simplicity, we hereafter suppress the index l. It is easy to verify that normal, log-normal and beta distributions with unequal means and variances belong to the exponential tilt model (1). On the other hand, unlike any particular parametric model for these three groups, model (1) allows an unspecified marker-specific density function h(·), which is an important and desirable feature to model quantitative trait data due to heterogeneous distributions across different markers.

It has been suggested that there may be heterogeneity in both means and variances across genotypes for functional loci (Struchalin et al., 2010; Deng and Paré, 2011). It has also been shown in Paré et al. (2010) that the variance of a quantitative trait conditioning on the genotype is a function of the interaction between genotype and covariates. The formula from Paré et al. (2010) is restated in Web Appendix A for readers of interest. For simplicity of illustration and without loss of generality, we consider the ETM with four parameters that capture the differences in mean and variance. The extension to capture differences in higher order moments (such as skewness and kurtosis) is straightforward. Specifically, we let K(x) = (x; x²), β_AA = (β₁, β₂), β_aa = (β₃, β₄). At each marker, under model (1), the task of vQTL mapping can be formulated as testing for H₀ : β₁ = β₂ = β₃ = β₄ = 0. We note that H₀ is testing for any types of differences among the three genotypic groups, hence can capture the signal of differences in means and variances.

2.2 A novel pairwise conditional likelihood ratio test in a semiparametric model for vQTL mapping

We first construct a pairwise conditional likelihood. The key idea is to eliminate the reference distribution h(·) by conditioning on order statistics. Specifically, consider three types of pairs of observations extracted from different groups, namely pairs of observations from the group j and the group k for (j, k) = (AA, Aa), (Aa, aa) and (AA, aa). We denote these three possible pairs by type-1, type-2 and type-3 pairs, and calculate the following conditional densities.

For the type-1 pair, i.e., u_i from the group AA and v_j from the group Aa. The conditional density of (u_i, v_j), given their order statistics (t⁽¹⁾, t⁽²⁾), can be calculated as

$$\text{Pr}(u_i,v_j\mid t^{\left(1\right)},t^{\left(2\right)})=\frac{f\left(u_i\right)h\left(v_j\right)}{f\left(u_i\right)h\left(v_j\right)+f\left(v_j\right)h\left(u_i\right)}={\{1+R_{12}^{\mathit{ij}}\left(u_i,v_j;{\beta }_1,{\beta }_2\right)\}}^{-1},$$

where $R_{12}^{\mathit{ij}}\left(u_i,v_j;{\beta }_1,{\beta }_2\right)=R_{12}^{\mathit{ij}}=\exp \{{\beta }_1\left(v_j-u_i\right)+{\beta }_2(v_j^2-u_i^2\left)\right\}$. We note that the reference distribution h(·) is eliminated by such a conditioning procedure. A similar approach is adopted by Kalbfleisch (1978) in the setting of nonparametric tests and by Liang and Qin (2000) in the setting of regression analysis. Similarly, for the type-2 pair,

$$\text{Pr}(w_k,v_j\mid t^{\left(1\right)},t^{\left(2\right)})={\left\{1+R_{23}^{\mathit{kj}}\left(w_k,v_j;{\beta }_3,{\beta }_4\right)\right\}}^{-1},$$

where $R_{23}^{\mathit{kj}}\left(w_k,v_j;{\beta }_3,{\beta }_4\right)=R_{23}^{\mathit{kj}}=\exp \{{\beta }_3\left(v_j-w_k\right)+{\beta }_4(v_j^2-w_k^2\left)\right\}$. For the type-3 pair,

$$\text{Pr}(u_i,w_k\mid t^{\left(1\right)},t^{\left(2\right)})={\{1+R_{13}^{\mathit{ik}}\left(u_i,w_k;{\beta }_1,{\beta }_2,{\beta }_3,{\beta }_4\right)\}}^{-1},$$

where $R_{13}^{\mathit{ik}}\left(u_i,w_k;{\beta }_1,{\beta }_2,{\beta }_3,{\beta }_4\right)=R_{13}^{\mathit{ik}}=\exp \{\left({\beta }_1-{\beta }_3\right)\left(w_k-u_i\right)+\left({\beta }_2-{\beta }_4\right)(w_k^2-u_i^2\left)\right\}$.

For each possible pair, we can calculate the conditional density. Multiplying these densities together, we obtain the following pairwise log likelihood function for all observations,

$$l_p\left(\beta \right)=\frac{2}{N}\left[\sum _{i=1}^{n_1}\sum _{j=1}^{n_2}\{-\log (1+R_{12}^{\mathit{ij}})\}+\sum _{j=1}^{n_2}\sum _{k=1}^{n_3}\left\{-\log (1+R_{23}^{\mathit{kj}})\right\}+\sum _{i=1}^{n_1}\sum _{k=1}^{n_3}\{-\log (1+R_{13}^{\mathit{ik}})\}\right],$$

where β = (β₁, β₂, β₃, β₄), N = n₁ + n₂ + n₃. We note that the sum of log conditional densities of each type is standardized by the total number of individuals of the three groups. This is owing to the projection theory in U-statistics (Lehmann and Dabrera, 1975). Such modification of log likelihood is necessary so that the corresponding pairwise likelihood ratio test has a simple ${\chi }_4^2$ distribution. In addition, the constructed pairwise log likelihood l_p(β) is not a true likelihood function because the conditional densities are multiplied together as if they are independent. In fact, it belongs to the family of composite likelihoods (Besag, 1974; Lindsay, 1988). For more discussion on the composite likelihoods, please see the excellent review paper by Varin et al. (2011) and the references therein. The major motivation of using composite likelihood in many applications is to reduce the computational complexity such as substituting high-dimensional integration involved in full likelihoods with lower-dimensional integrals (Fieuws and Verbeke, 2006). However, in our proposed test, the major motivation is to reduce the impact of unknown reference distribution h(·) (Kalbfleisch and Sprott, 1970).

We propose to use the pairwise conditional likelihood ratio test for H₀ for two reasons. First, the likelihood-ratio based inference is generally preferred over Wald type inference, especially for small sample size (Murphy and Van der Vaart, 1997). In vQTL mapping, the number of individuals in the minor allele homozygous group aa may be rather small. In addition, the score test, although is computationally simple, may suffer from numerical instability (Pace et al., 2011). Second, the pairwise conditional likelihood ratio test, unlike the Wald test, does not require the estimation of covariance matrix. Estimation of the covariance matrix involves triple summations and can be computationally demanding.

Denote the maximum pairwise conditional likelihood estimator by $\widehat{\beta }=\mathrm{argmax}\left\{l_p\left(\beta \right)\right\}$. The pairwise conditional likelihood ratio test for H₀ is calculated as

$$\text{PLRT}=-2\{l_p\left(0\right)-l_p(\widehat{\beta }\left)\right\},$$

where l_p(0) = −{2 (n₁n₂ + n₂n₃ + n₁n₃) /N} log 2. Under general regularity conditions, the PLRT for H₀ converges weakly to ${\chi }_4^2$. The regularity conditions and the proof are provided in Web Appendices B and C.

It is worth mentioning that when choosing Aa as the reference group, the parameters (β₁, β₂, β₃, β₄) characterize the differences in distribution between homozygous genotypes and heterozygous genotype. The interpretation of the parameters β’s depends on the underlying distributions (Luo and Tsai, 2012). For example, in the normal model, parameters β₁ and β₂ characterize the differences in means and variances between major allele homozygous genotype and heterozygous genotype, while parameters β₃ and β₄ characterize the differences in means and variances between minor allele homozygous genotype and heterozygous genotype. In this paper, we choose Aa as the reference group for simplicity of interpretation. In fact, other choices (e.g. AA or aa) can be used as well and lead to the same test statistic. A proof of such invariance to the choice of reference group is provided in Web Appendix D.

2.3 Local asymptotic power and its implications

The power of different tests in finite samples will be investigated in Section 3. Here we provide a useful result on the asymptotic power of the PLRT test under a sequence of local alternatives. Specifically, consider a sequence of alternatives:

$$H_a:h(\cdot )=h_0(\cdot ),\beta =N^{-1∕2}{\tau }_0,$$

where τ₀ is a vector of constants. Note that under H_a, we do not explicitly specify the local alternative for α_AA and α_aa, because α_AA and α_aa are functions of β and h₀(·). Let n₁/N → ρ₁, n₂/N → ρ₂, and n₃/N → ρ₃ as n → ∞. With LeCam’s third lemma (Van der Vaart, 2000), we can show that under the alternatives H_a, the limiting distributions of PLRT is ${\chi }_4^2\left({\tau }_0^T{\Sigma }_A^o{\tau }_0\right)$, where

$${\Sigma }_A^o=\left(\begin{array}{cc}\hfill {\rho }_1\left(1-{\rho }_1\right)\hfill & \hfill {\rho }_1{\rho }_3\hfill \\ \hfill {\rho }_1{\rho }_3\hfill & \hfill {\rho }_3\left(1-{\rho }_3\right)\hfill \end{array}\right)\otimes \left(\begin{array}{cc}\hfill \mathrm{var}\left(v_j\right)\hfill & \hfill \mathrm{cov}(v_j,v_j^2)\hfill \\ \hfill \mathrm{cov}(v_j,v_j^2)\hfill & \hfill \mathrm{var}\left(v_j^2\right)\hfill \end{array}\right),$$

v_j is the quantitative trait for the jth subject in the reference group Aa, and ⊗ denotes the tensor product of two matrices. This result on the local asymptotic power provides an analytical procedure for power calculation. In addition, it can be shown that the power is maximized when the minor allele frequency (MAF) is close to 0.5. See Web Appendix E for detailed derivation and discussion.

3. Simulation study

We conduct simulation studies to evaluate the finite sample performance of the proposed test and compare to that of the existing tests. The following eight tests are considered: the proposed PLRT test, the Lepage test, the ANOVA test, the Levene’s test, the constrained D-test (D_c), the unconstrained D-test (D_u), the parametric test (LRT) and the test with parametric bootstrap (LRT(PB)) by Cao et al. (2014). We simulate SNPs with MAFs from 0.05 ~ 0.4 to mimic the functional SNPs, and the sample size N is set to be 1000, 2000 and 5000 to represent the relatively small to large sample cases. We consider three different parametric models which may or may not belong to ETM. Specifically, normal distributions (Model 1), t-distributions (Model 2) and χ² distributions (Model 3) are considered. Note that Model 1 satisfies the ETM assumption, while Models 2 and 3 do not, which are used to evaluate the robustness of the PLRT test to model mis-specifications with heavy-tailed or skewed distributions.

We evaluate the Type I errors and powers of the eight tests by considering four scenarios: 1. Type I error scenario (genotype has no effect on quantitative trait); 2. Power scenario I (genotype affects means of quantitative trait); 3. Power scenario II (genotype affects variances of quantitative trait); and 4. Power scenario III (genotype affects both mean and variances of quantitative trait). For Type I error scenario, the quantitative traits in the three genotypic groups are generated from the same distribution. For power scenarios I, II and III, we let the quantitative traits in three genotypic groups to be different in means only, in variances only and in both means and variances, respectively. We conduct 5000 simulations for the Type I error scenario, and 1000 simulations for the Power scenarios I, II and III. Due to space limitation, we only present the results for Type I error scenario and Power scenario III when sample size N = 2000 and MAF= 0.1 ~ 0.4. The results for other settings can be found in Web Tables 1 – 8 of Web Appendix F. The parameter settings of the power scenarios are provided at the end of each table.

Table 1 summarizes results when the quantitative traits are generated from normal distributions (Model 1). All tests control the Type I errors well at all nominal levels. When genotypes have both mean and variance effects, the proposed PLRT test and the LRT test proposed by Cao et al. (2014) are the most powerful tests, and have up to 40% more power than the other five tests. If we compare the performance of the tests under different MAFs varying from 0.1 to 0.4, we find that the power of the PLRT test increases when MAF becomes larger, which implies that the PLRT test has higher power in detecting common variant effect than rare variant effect. This agrees with the results on local asymptotic power and our intuition.

Table 1.

The Type I errors (×100) and power (×100) for the seven tests considered at 5%, 1%, 0.5% and 0.1% significance levels when quantitative trait were generated from the normal distributions (model 1). Power: mean and variance scenario. The sample size is 2000. The number of replicates is 5000 for Type I error comparison, and 1000 for power comparison.

Scenario	Level	PLRT	Lepage	ANOVA	Levene	Dc	Du	LRT	PLRT	Lepage	ANOVA	Levene	Dc	Du	LRT
	MAF=0.1								MAF=0.2
Type I error	5.0	5.0	4.9	5.0	4.8	4.5	4.6	5.6	5.0	4.3	4.8	4.4	5.0	5.4	4.9
	1.0	1.4	0.9	1.0	0.8	0.9	0.9	1.3	1.0	1.0	1.0	0.7	0.9	1.0	1.0
	0.5	0.8	0.6	0.5	0.3	0.5	0.4	0.6	0.5	0.5	0.5	0.3	0.5	0.5	0.5
	0.1	0.2	0.1	0.2	0.0	0.1	0.1	0.1	0.1	0.1	0.1	0.0	0.1	0.1	0.1
Power*	5.0	85.9	71.7	38.3	80.6	51.5	62.4	86.6	98.1	92.2	58.9	94.3	79.7	91.4	98.3
	1.0	68.7	49.6	19.6	61.7	28.1	32.9	72.8	93.5	77.9	34.8	83.4	58.0	74.0	94.4
	0.5	59.1	39.7	14.2	52.8	18.8	22.5	64.9	89.9	70.5	26.9	77.7	49.1	62.0	91.3
	0.1	39.7	22.1	6.3	33.8	6.5	7.8	48.2	77.8	51.8	14.0	61.2	28.6	35.2	81.2
	MAF=0.3								MAF=0.4
Type I error	5.0	4.9	4.6	4.6	4.6	4.8	5.1	5.1	5.0	4.6	4.8	4.8	5.1	4.7	5.1
	1.0	0.8	0.9	1.0	0.8	1.0	0.9	0.8	0.9	0.9	0.8	1.1	1.1	0.8	0.9
	0.5	0.4	0.4	0.5	0.5	0.4	0.4	0.3	0.5	0.5	0.5	0.5	0.5	0.4	0.5
	0.1	0.1	0.0	0.1	0.0	0.0	0.1	0.1	0.1	0.0	0.0	0.1	0.0	0.1	0.1
Power	5.0	99.0	95.9	67.7	96.6	88.9	97.9	99.1	99.4	95.4	73.0	95.6	91.7	97.4	99.5
	1.0	96.8	86.3	44.8	87.7	74.3	88.5	97.0	98.1	87.5	48.7	87.3	79.6	89.7	98.0
	0.5	94.4	80.3	35.3	83.3	66.5	80.1	94.9	95.7	82.1	38.5	81.6	74.0	85.8	95.7
	0.1	86.7	63.1	18.7	70.4	45.4	57.8	87.8	89.0	64.9	21.7	66.2	53.8	67.9	89.4

^*Differences in both means and variances: f(·) = N(0, 1), h(·) = N(0.1, 1.3), g(·) = N(0.2, 1.4)

Table 2 and Table 3 representatively demonstrate the performances of the eight tests when the data are generated from t distributions (Model 2) and χ² distributions (Model 3), where the assumption of the ETM does not hold. We can see the LRT test produces substantially inflated Type I errors. This observation is consistent with the conclusion in Cao et al. (2014) that the LRT test is sensitive to the normality assumption. The problem of inflated Type I error for the LRT test can be resolved by using parametric bootstrap, denoted by LRT(PB). All tests except for the LRT test control the Type I errors well at all nominal levels, suggesting a certain degree of model robustness to heavy-tailed distributions or skewed distributions. In Table 2, similar patterns for powers are observed as in Table 1, in that the PLRT test is the most powerful test. In Table 3, the proposed PLRT the D_c test, the D_u test and the LRT(PB) test are equally powerful, because the proposed test may lose some power due to skewness.

Table 2.

The Type I errors (×100) and power (×100) for the eight tests considered at 5%, 1%, 0.5% and 0.1% significance levels when quantitative trait were generated from the t distributions (model 2). Power: mean and variance scenario. The sample size is 2000. The number of replicates is 5000 for Type I error comparison, and 1000 for power comparison.

Scenario	Level	PLRT	Lepage	ANOVA	Levene	Dc	Du	LRT	LRT(PB)	PLRT	Lepage	ANOVA	Levene	Dc	Du	LRT	LRT(PB)
	MAF=0.1									MAF=0.2
Type I error	5.0	5.3	5.2	5.3	4.8	4.7	4.8	37.5	5.0	5.3	5.1	5.6	5.2	4.9	4.9	43.5	5.1
	1.0	1.2	1.1	1.4	1.3	1.0	1.0	24.2	0.9	1.5	1.1	1.0	1.1	0.9	0.7	29.4	0.8
	0.5	0.8	0.6	0.7	0.9	0.4	0.5	20.2	0.4	0.8	0.5	0.5	0.6	0.4	0.3	25.0	0.4
	0.1	0.2	0.1	0.3	0.4	0.1	0.1	13.7	0.1	0.1	0.1	0.1	0.1	0.1	0.1	17.6	0.1
Power*	5.0	66.0	51.8	60.6	37.9	59.4	65.9	86.5	68.7	91.3	75.5	79.6	52.2	75.7	84.8	98.2	83.2
	1.0	39.9	29.5	36.6	20.2	37.9	42.7	76.4	37.6	74.2	52.3	61.1	31.5	57.4	67.1	95.3	61.8
	0.5	31.8	20.5	28.6	16.3	30.0	33.6	71.9	28.4	66.0	44.0	52.5	24.0	49.8	57.7	93.3	50.4
	0.1	18.7	10.1	16.0	9.0	14.2	15.1	61.3	13.6	48.2	27.0	35.3	12.2	27.4	31.9	87.9	28.3
	MAF=0.3									MAF=0.4
Type I error	5.0	4.8	5.1	5.0	5.0	5.1	4.8	45.8	5.2	5.1	5.2	5.1	4.6	5.1	5.1	45.6	3.8
	1.0	0.9	0.9	1.3	1.0	0.8	0.8	31.9	0.7	1.0	0.8	1.0	1.0	1.0	0.9	32.2	0.9
	0.5	0.5	0.5	0.6	0.4	0.4	0.4	27.5	0.4	0.6	0.4	0.4	0.6	0.4	0.5	27.4	0.4
	0.1	0.1	0.1	0.1	0.1	0.1	0.1	19.9	0.1	0.1	0.1	0.0	0.1	0.1	0.1	19.9	0.0
Power	5.0	95.6	86.1	86.4	59.7	79.6	91.1	99.3	87.9	97.6	88.2	90.2	62.6	82.9	91.0	99.8	88.3
	1.0	86.6	66.6	71.2	36.1	65.6	77.9	97.8	66.7	90.9	73.0	73.7	38.2	66.2	78.7	98.7	65.5
	0.5	81.2	59.2	63.5	28.1	58.7	70.1	96.2	55.1	86.8	63.0	66.7	30.9	57.6	70.4	98.4	55.1
	0.1	66.5	39.2	48.0	16.0	38.3	49.4	93.9	32.9	71.8	46.1	49.9	17.8	40.6	49.9	96.1	29.5

^*Differences in both means and variances: f(·) = t(0, 6), h(·) = t(0.13, 4), g(·) = t(0.24, 3.2)

Table 3.

The Type I errors (×100) and power (×100) for the eight tests considered at 5%, 1%, 0.5% and 0.1% significance levels when quantitative trait were generated based on the χ² distributions (model 3). Power: mean and variance scenario. The sample size is 2000. The number of replicates is 5000 for Type I error comparison, and 1000 for power comparison.

Scenario	Level	PLRT	Lepage	ANOVA	Levene	Dc	Du	LRT	LRT(PB)	PLRT	Lepage	ANOVA	Levene	Dc	Du	LRT	LRT(PB)
	MAF=0.1									MAF=0.2
Type I error	5	5.3	5.0	5.0	4.6	5.0	4.8	9.5	5.0	4.9	4.4	5.0	4.5	4.8	4.8	9.0	5.1
	1	1.4	1.0	1.0	0.8	1.1	1.0	2.9	1.1	1.0	1.1	1.0	0.7	0.9	0.9	2.8	1.3
	0.5	0.9	0.5	0.5	0.4	0.5	0.6	1.9	0.5	0.5	0.5	0.6	0.3	0.4	0.6	1.6	0.6
	0.1	0.2	0.1	0.1	0.1	0.1	0.1	0.7	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.5	0.1
Power*	5	55.9	52.7	59.9	53.5	56.7	55.6	75.5	66.1	88.8	81.8	81.1	83.2	88.8	86.9	95.7	92.6
	1	32.4	31.9	38.3	32.7	36.1	32.6	61.0	43.2	69.0	62.2	61.5	65.1	76.3	72.1	89.4	80.8
	0.5	24.0	24.7	30.7	26.4	27.2	23.6	55.4	34.8	60.9	53.6	54.2	59.1	67.3	63.3	86.7	73.4
	0.1	12.3	13.0	17.2	15.6	12.1	10.2	40.3	20.8	42.6	35.6	36.9	41.4	46.8	40.4	75.7	56.2
	MAF=0.3									MAF=0.4
Type I error	5	4.8	4.8	4.8	4.4	5.1	5.3	8.9	4.6	5.1	4.9	4.7	4.9	5.0	5.1	9.2	4.9
	1	0.9	1.1	0.9	0.9	1.0	1.0	2.4	0.9	1.0	1.0	0.9	1.1	0.9	0.9	2.9	1.1
	0.5	0.4	0.5	0.4	0.5	0.5	0.6	1.5	0.3	0.5	0.6	0.5	0.5	0.3	0.4	1.7	0.5
	0.1	0.1	0.1	0.1	0.2	0.1	0.2	0.5	0.1	0.1	0.1	0.2	0.1	0.1	0.1	0.6	0.0
Power	5	95.4	91.3	88.8	94.0	96.9	97.3	98.4	97.9	98.1	95.3	90.8	97.7	97.9	98.4	99.4	99.3
	1	87.9	79.3	71.7	85.3	90.6	89.6	95.8	92.2	94.6	87.0	78.6	92.6	93.6	94.3	98.4	97.1
	0.5	82.3	71.8	63.3	81.0	85.0	83.1	94.6	89.0	91.6	82.3	70.0	90.1	91.4	92.1	97.5	95.1
	0.1	67.9	55.3	47.8	66.6	69.4	67.3	89.8	78.5	81.9	68.5	53.5	80.7	77.9	78.5	95.6	88.3

^*Differences in both means and variances: f(·) = χ²(0.2, 20), h(·) = χ²(3.5, 18), g(·) = χ²(10.8, 11)

The results for Power scenarios I and II when sample size N = 2000 are summarized in Web Tables 1, 2 and 3 of Web Appendix F. Under Power scenario 1 (mean effects only), the ANOVA test has slightly more power than the PLRT test, because the ANOVA test has only two degrees of freedom. The Levene’s test has essentially no power beyond Type I errors in this scenario because it can only detect differences in variances, not in means. Under Power scenario II (variance effects only), the PLRT test and the Levene’s test are the most powerful tests. Similar findings are obtained when sample size N is 1000 and 5000, which are summarized in Web Tables 4, 5, 6 and 7 of Web Appendix F.

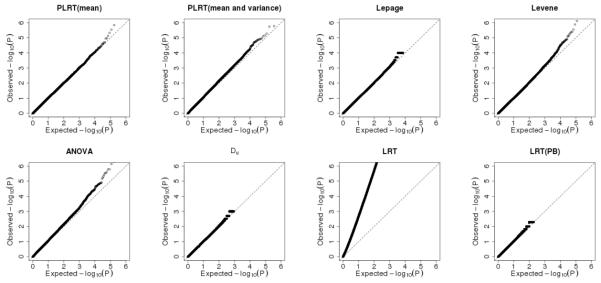
The major advantage of the proposed test over the LRT(PB) test is the computational efficiency. The LRT(PB) test requires large number of bootstraps for low Type I errors. For example, at the Type I error of 1%, the number of bootstraps required is ⩾ 10⁴, which takes 1091.06 seconds when sample size is 2000 for only one simulation (on a computer cluster node HP DL165-G6 with AMD 2.2 GHz CPU and 16GB memory). In practice, genome-wide association studies often have millions of SNPs to be tested. The number of bootstraps to reach genome-wide significance levels (e.g., 10⁻⁷) is computationally intractable. As a consequence, the p-values for affordable number of bootstraps for the genome-wide association study in Section 4 are truncated (see Figure 2), and cannot reach the genome-wide significance level. In contrast, the computational time for the proposed PLRT test under the aforementioned setting is only 8.92 seconds.

Figure 2.

Q-Q plots of observed p-values vs. expected p-values in the – log₁₀ scale from the genome-wide analysis.

In summary, our simulation studies suggest that the proposed PLRT test can correctly control the Type I errors, and is powerful to detect differences in both means and variances. In addition, the proposed PLRT test is robust under model mis-specifications and computationally effcient. We recommend the use of the PLRT test as a useful alternative to the existing methods.

4. Application to the Framingham Heart Study (FHS) data

The FHS data include individuals from three generations, original cohort, offspring cohort, and the third generation cohort (Splansky et al., 2007). To make the average ages comparable across the three generations, we extract the body weight and height information from the fourth clinic exam for the original cohort conducted during 1954–1958, the third clinic exam for the offspring cohort conducted during 1983 – 1987, and the first clinic exam for the third generation cohort conducted during 2002 – 2005. The quantitative phenotype of interest, BMI, is calculated as weight in kilograms divided by body height in meters squared, i.e., kg/m². Two thousand three hundred and eighty unrelated individuals (no paternal, maternal, or sibling relationships) with both phenotype information and genotype information are identified and included in our analysis.

We perform quality control for the genome-wide association study, including Hardy-Weinberg equilibrium, call rate for SNP/individual, and MAF greater than or equal to 5%. The reason we do not include SNPs with MAF less than 5% is that for all existing methods in vQTL analysis, the rule of thumb is to have at least 10 subjects per genotypic group to retain well controlled Type I errors. A total sample size greater than 10⁵ is required for MAF= 1% to guarantee there are at least 10 counts in the smallest group (i.e., N ⩾ 10/0.01²). However, in the FHS data, the sample size is only 2361 (19 subjects were removed due to low call rate). Therefore, in our analysis, we focus on 348,470 out of the 550,000 SNPs that have MAF greater than or equal to 5%.

We present the histograms of estimated skewness and kurtosis of BMI residuals after adjusting for covariates and population structure across genotypic groups based on 4290 SNPs from Chromosome 22 in Figure 1. Specifically, at each SNP, we calculate the skewness (or kurtosis) of BMI residuals within each genotypic groups (i.e., AA, Aa and aa groups), and then plot the histograms of these calculated skewness (or kurtosis). The histograms suggest there are some signals contained in skewness and kurtosis of the quantitative trait BMI in this Framingham Heart Study data. Thus, the proposed test has the potential in combining such signals in higher order moments, if the same size were sufficiently large.

Figure 1.

Histograms of skewness and kurtosis of BMI residuals after adjusting for covariates and population structure across genotypic groups. The results are based on 4290 SNPs from Chromosome 22.

The sample size of the data from the Framingham Heart Study is moderate (N = 2361), and the three genotypic groups are typically extremely unbalanced at SNPs with small allele frequencies. For this particular data analysis, we only consider differences in the first two moments. The proposed method with higher order moments is applicable to studies with larger sample sizes.

We first conduct the genome-wide association study to compare the results from the test for differences in mean, denoted by PLRT(mean), and the results from the test for differences in mean and variance, denoted by PLRT(mean and variance). The results are summarized in Web Table 9 of Web Appendix G. At the significance level of 1.45E-07 after Bonferroni correction for 348,470 tests, we find that none of the PLRT tests have identified significant SNP. This is because the sample size of the FHS study is only moderate (N = 2361), which leads to the relatively low power at stringent significance levels. To facilitate comparisons, we consider higher thresholds. As shown in Web Table 9, there is a substantial number of SNPs identified by PLRT(mean and variance) in addition to those identified by PLRT (mean).

We then compare the results from the proposed PLRT test with those from the existing tests (i.e., the Lepage test, the ANOVA test, the Levene test, the unconstrained D_u test, the LRT test and the LRT(PB) test). We consider two types of quantitative traits, namely BMI residuals after adjusting for covariates (age and sex) and population structure, and BMI residuals after adjusting for covariates, population structure and genotypic mean effect. We adjust for covariates by simply using the estimated residuals from the regression of BMI values on the covariates and principal components. The reason of considering the BMI residuals as quantitative trait is to compare the proposed test with the Levene’s test that detects variance differences only.

Figure 2 displays the Q-Q plots of observed p-values vs. expected p-values from tests under comparison in the – log₁₀ scale. The Q-Q plots suggest that Type I errors for the proposed PLRT test are well controlled and Type I errors for the LRT test proposed by Cao et al. (2014) are inflated, which is consistent with the observation from the simulation studies. QQ plot of p-values from LRT(PB) suggests the Type I errors are well controlled. The truncation of points in the plot is due to the limited precision from computationally affordable number of bootstraps (i.e., number of bootstrap was 200).

Table 4 presents the summary information of the top 10 SNPs identified by the proposed PLRT test among all 348,470 SNPs based on BMI residuals after adjusting for covariates (upper panel) and BMI residuals after adjusting for both covariates and genotypic group means (lower panel). Since the LRT test proposed by Cao et al. (2014) has inflated Type I errors, we did not include it in the comparison. In general, we find that the p-values from the proposed PLRT test are similar to those from the LRT(PB) test. On the other hand, the results from the other four test (the ANOVA test, the Levene’s test, the Lepage test and the D_u test) are different with those from the PLRT test in that all of them have p-values greater than 0.05 at least at one SNP. This is expected because the ANOVA test or the Levene’s test can only capture the mean or variance effects. The Lepage test and the D_u test are generally less powerful than the proposed PLRT test, although they are able to capture both mean and variance differences. The results in the lower panel in Table 4 suggest that the p-values from the proposed PLRT test are similar to those from the Levene’s test and the LRT(PB) test. As expected, the p-values from ANOVA test are 1 because it has no power in detecting differences other than means.

Table 4.

Summary results based on BMI (kg/m²) values after adjusting for covariates and population structure and after adjusting for covariates, population structure and genotypic mean effects for top 10 SNPs. The rank of p-values are based on the results from the PLRT test.

					P-value						Mean			SD
rs#	Chr	Position	Gene	MAF	PLRT	Lepage	ANOVA	Levene	Du	LRT(PB)	AA	Aa	aa	AA	Aa	aa
Results based on BMI value adjusting for covariates and population structure
rs2219576	4	52912589	SGCB	0.472	0.000	0.097	0.004	0.001	0.000	0.000	−0.30	0.33	−0.37	4.04	5.11	4.10
rs4898829	14	54602456	ATP5C1P1	0.344	0.000	0.018	0.423	0.009	0.007	0.005	0.05	0.04	−0.36	4.18	5.03	4.54
rs6049433	20	24127023	FLJ33581	0.439	0.000	0.000	0.000	0.028	0.003	0.015	0.23	−0.42	0.65	4.73	4.45	4.81
rs10968711	9	28676295	LINGO2	0.102	0.000	0.003	0.130	0.206	0.214	0.085	−0.10	0.39	0.72	4.67	4.48	2.42
rs12953383	18	41244911	IBTKP1	0.238	0.000	0.009	0.322	0.000	0.001	0.000	0.02	−0.12	0.49	4.82	4.03	5.80
rs10502817	18	41249142	IBTKP1	0.238	0.000	0.009	0.322	0.000	0.001	0.000	0.02	−0.12	0.49	4.82	4.03	5.80
rs1460242	8	106000000	RPL23P9	0.296	0.000	0.027	0.006	0.006	0.000	0.000	0.23	−0.06	−1.05	4.82	4.59	3.29
rs11646660	16	11648180	LITAF	0.111	0.000	0.002	0.014	0.004	0.010	0.010	−0.15	0.58	0.22	4.56	4.99	2.67
rs9504897	6	724502	EXOC2	0.083	0.000	0.003	0.158	0.017	0.137	0.005	−0.03	0.24	−1.20	4.62	4.69	1.26
rs17067163	8	3583092	CSMD1	0.074	0.000	0.257	0.026	0.004	0.002	0.000	0.10	−0.64	−0.35	4.78	3.50	4.33
Results based on BMI value adjusting for covariates, population structure and genotypic mean effect
rs756928	17	67877344	LINC01483	0.295	0.000	0.005	1.000	0.003	0.002	0.000	0.00	0.00	0.00	4.22	5.05	4.09
rs1519586	4	52846029	RPL37AP2	0.280	0.000	0.003	1.000	0.001	0.001	0.000	0.00	0.00	0.00	4.31	5.12	3.98
rs9359331	6	63886188	LOC442225	0.444	0.000	0.001	1.000	0.001	0.005	0.000	0.00	0.00	0.00	4.33	5.04	4.01
rs11745703	5	38755640	OSMR-AS1	0.416	0.000	0.006	1.000	0.004	0.009	0.000	0.00	0.00	0.00	4.03	4.92	4.83
rs7987211	13	42966734	FABP3P2	0.054	0.000	0.007	1.000	0.002	0.007	0.000	0.00	0.00	0.00	4.68	3.76	9.60
rs8177429	5	150403098	GPX3	0.080	0.000	0.002	1.000	0.003	0.020	0.000	0.00	0.00	0.00	4.74	3.73	6.53
rs768731	10	106834450	SORCS3	0.314	0.000	0.088	1.000	0.008	0.025	0.000	0.00	0.00	0.00	4.66	4.79	3.51
rs6491611	13	102089668	ITGBL1	0.119	0.000	0.004	1.000	0.006	0.017	0.000	0.00	0.00	0.00	4.84	4.03	2.92
rs26899	5	80360612	RASGRF2	0.252	0.000	0.007	1.000	0.004	0.045	0.000	0.00	0.00	0.00	4.67	4.75	3.25
rs6930903	6	28981244	ZNF311	0.264	0.000	0.004	1.000	0.004	0.005	0.000	0.00	0.00	0.00	4.38	5.06	3.69

Previous large-scale meta-analysis studies of mean or variance effects have identified 50 SNPs that are significantly associated with BMI (Willer et al., 2009; Speliotes et al., 2010; Yang et al., 2012; Berndt et al., 2013). From approximately 550,000 genotyped SNPs for FHS SHARe (SNP Health Association Resource) genome-wide association study, we extract 6724 SNPs within +/− 500,000 base pairs (i.e. 500Kb) of BMI associated SNPs. The results based on 4722 (positive controls) out of the 6724 SNPs that have MAF greater than 5% are summarized in Web Table 10 of Web Appendix G. The findings are similar to that from Table 4 in that the results from the LRT(PB) test agree well with those from the PLRT test. Due to the low power at stringent significance levels, we did not compare the results from this genome-wide association study and those from the established meta-analyses. This comparison will be possible for studies with larger sample sizes.

In summary, the proposed PLRT test can capture both mean and variance signals. Hence the proposed test can serve as a useful complement to the existing methods, and can potentially lead to new identification of SNPs that are associated with BMI.

5. Discussion

In this paper, we proposed a novel pairwise conditional likelihood ratio test to identify the differences in higher moments among three genotypic groups. The proposed PLRT test is derived by a conditioning technique, which eliminates the impact of an infinite dimensional nuisance parameter. Through simulation studies we demonstrated the feasibility and power of the proposed test. The proposed test has well controlled Type I errors, improved power and/or better computational efficiency over existing tests including the ANOVA test, the Levene’s test, the Lepage test, the D-test and the LRT tests by Cao et al. (2014). Thus, the proposed test is a useful alternative to the existing tests. A general form of exponential tilt model is formulated in equation (1), which can be used to detect for any order of moments among distributions. In this paper we have focused our attention on differences in means and variances because of the moderate sample size and the unbalanced genotypic groups. As shown in histograms of estimated skewness and kurtosis of BMI residuals after adjusting for covariates across genotypic groups based on 4290 SNPs from Chromosome 22 in Figure 1, there are some signals contained in skewness and kurtosis of the quantitative trait BMI in this Framingham Heart Study data. Tests for differences in higher order moments can be conducted by including higher dimensional functions in K(x). On the other hand, a relatively large sample size is needed to ensure that the higher order moments can be well estimated to be useful. One limitation of the proposed test is that the Type I errors may be inflated when the sample size in the minor allele homozygous group (aa) is small. To properly control Type I errors, a rule of thumb for all methods is to have at least 10 subjects in the minor allele homozygous group (aa), that is, the MAFs should be greater than 0.1 when sample size is 1000.

In this paper, we use K(x) = (x, x²) as the kernel function in the method development. Other kernels can be considered as well (Qin, 1998; Fokianos and Kaimi, 2006). However, these kernel functions need to be pre-specified. Mis-specifications may lead to invalid Type I errors. Alternatively, our test can be extended to accommodate transformations with unknown parameters K(x; φ), where φ is a finite dimensional parameter. One such example is the Box-Cox type transformation. This is a topic of future research.

Recently, Sun (2012) developed a new statistical framework for expression quantitative trait locus (eQTL) mapping using RNA-seq data by associating each gene with each SNP. Specifically, the RNA-seq measures were modeled by distributions for discrete variables, such as negative binomial distributions, rather than continuous variables in conventional methods. In addition, the allele specific expression information was incorporated in the eQTL mapping method. Sun (2012) showed that the proposed eQTL mapping methods were more powerful than the traditional eQTL methods, such as linear regression. However, parametric model assumptions have to be made, and violation of such assumptions may lead to biased inference. Extension of our semiparametric test to the eQTL mapping is of interest and is currently under investigation.

As suggested by referees, there are a few other directions for future research. First direction is to extend the proposed method to incorporate covariates. One potential limitation of the Levene’s test, the Lepage’s test and the D-test is that, as non-parametric tests, they are not easy to incorporate covariates. One ad hoc solution is to first regress on covariates and then apply the tests to the estimated residuals. It is worth mentioning that regressing the outcome on covariates and using residuals versus gene is a standard practice in many software. However, this process will become biased when genes are correlated with the covariates. In addition, using estimated residuals after adjusting covariates as the quantitative traits is not equivalent to adjusting covariates in a joint model, because the uncertainty in estimated residuals is ignored. This may lead to some inflation of Type I errors if such an uncertainty is substantial. In contrast, the proposed test under the ETM framework can be extended to incorporate covariates. Specifically, Rathouz and Gao (2009) introduced the exponential tilt regression model and discussed the case when the responses are arbitrary and the covariates are categorical. Luo and Tsai (2012) generalized the exponential tilt regression model by allowing arbitrary responses and covariates. A joint method that simultaneously tests differences across genotypic groups and adjusts for covariates is currently under investigation and will be reported in the future. The second direction is to propose a generalized score test. In this paper, we propose a pairwise likelihood ratio test to identify differences in higher moments among three genotypic groups. A generalized score test starting from the proposed pairwise likelihood, or from the parametric model of Cao et al. (2014), equipped with robust variance estimators, can also lead to valid and robust tests. The performance of these tests, compared to the existing ones, will be investigated and reported in the future.