Optimizing the presentation of bleeding and thrombosis data: Responding to censored data using Kaplan-Meier curves

We write to highlight inaccurate statistical analysis and graphical representation utilized in many thrombosis and bleeding time studies. Box-plots are widely used to report data obtained from thrombosis time and bleeding time assays. However, this representation is statistically inaccurate in trials where the endpoint of occlusion or bleeding cessation does not occur over the experimental time course. We propose herein that a shift from the limited box-plot representation to portrayal as a survival curve improves data reduction and statistical generalizability. To demonstrate this alternative, we reanalyzed previously published data from our laboratory [1].

In this study, we conducted thrombosis experiments with an inhibitory antibody (CAN12) to protease activated receptor 4 (PAR4), which dose-dependently delayed thrombosis in the Rose-Bengal model [1]. In the published figure, we depicted the data as a box-plot since that was the standard for showing thrombosis data, see Fig. 1A (Fig. 6 of the original publication). The experiment was monitored until complete occlusion or 90 min. Mice that did not fully occlude are accurately described in the text, saying “the thrombosis time was delayed to > 90 min”. However, the that is equal to 90 min. Upon reflection, this is not an accurate depiction of the data. The two Student’s t-tests that were used are inappropriate statistical analyses. In surveying numerous examples of thrombosis and bleeding time studies, we took note of bleeding time data published by Modjeski et al. using Kaplan-Meier survival curves in place of a two-tailed Student’s t-test with box-plots [2]. Survival curves are used for time-to-event data even when the endpoint or event is not death. We have revised our original published data using Kaplan-Meier survival curves (Fig. 1B).

Fig. 1.

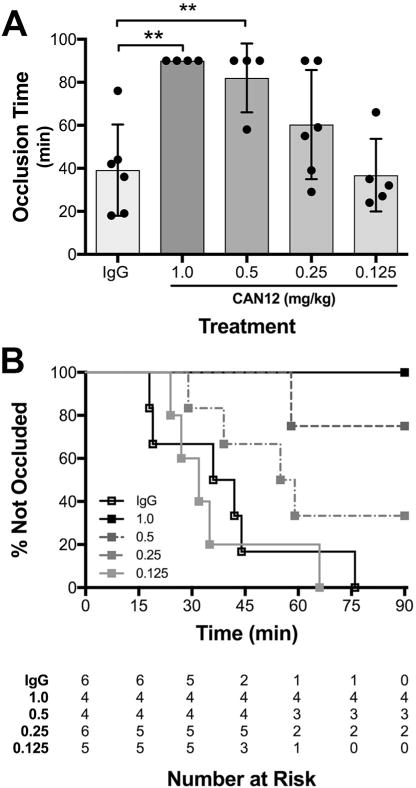
Comparison of censored thrombosis data represented as a box-plot to Kaplan-Meier curve using previously published data from our laboratory [1]. (A) C57BL/6 mice were pretreated with goat IgG (2 mg/kg), or CAN12 (1, 0.5, 0.25 or 0.125 mg/kg) for 10 min, and then subjected to the Rose Bengal carotid artery thrombosis model. Time to complete occlusion is indicated, or the experiment was terminated at 90 min. (B) The same data, represented as a survival curve. Benjamini–Hochberg (BH) corrected p < 0.05 vs. IgG for 1 and 0.5 mg/kg CAN12 treatments, all other treatments were not significantly different from controls.

The most immediate improvement provided by this representation is the accurate incorporation of censored data, which is not possible using the box-plot. In these hemostasis and thrombosis assays, observation continues until cessation of bleeding or complete occlusion, respectively. If the event of interest does not occur during the observation time, the data are described as right censored or fixed type I censored [3]. We only know that the event did not occur, however we do not know if or when the event will occur at some future time. Thrombosis and bleeding studies often include right censored data, pertaining to mice that never experience the terminal event. For example, a data point at 90 min could represent a mouse that experienced occlusion at 91 min, 120 min or not at all. Statistical methods such as a t-test or linear regression cannot adequately handle the uncertainty in censored data. It is also not correct to simply eliminate these points from the data as they still can offer valuable information. In Fig. 1A, the censored points are treated as the time of event, rather than the end of observation. A mouse that reaches full occlusion at 90 min is indistinguishable from a mouse that never forms a clot. Fig. 1B offers the advantage of identifying those censored points in a more meaningful way. This representation allows a distinction between censored data and event data at the conclusion of the experiment.

Not only does Fig. 1B incorporate the censored data visually, it also allows statistical analyses incorporating the censored data. The Kaplan-Meier survival curve represents the probability of surviving, or remaining event free, in a given time period while identifying changes in probability at intervals. In generating the Kaplan-Meier curve we utilized the Kaplan-Meier estimate to measure the fraction of mice with continued bleeding for a certain amount of time after treatment. Often, the survival curve is represented as a staircase and an event (e.g. time to occlusion) is indicated as a step down on the curve (Fig. 1B). This decreases the probability of survival, or event free time, for the remaining mice. Since the data contain censored points, we used the Log-rank (Mantel-Cox) Test to compare the differences in survival curves [3]. This analysis produced a p-value that evaluates the overall significance that at least one of the curves is different from the others. In order to compare the t-test and log-rank analyses, we examined the difference in the calculated p-values. Therefore, we used a Benjamini-Hochberg (BH) correction for multiple comparisons to generate p-values between specific curves and the control group (IgG). The corrected p-values for both 1 and 0.5 mg/kg CAN12 treatments were 0.036 vs the IgG control (Fig. 1B). These levels of significance are lower than the original published values (P < 0.01) with the same data in Fig. 1A. In this example, accurately identifying and including censoring in the analysis did not change the overall trend or conclusions that were originally made but other circumstances with different sample and effect sizes could be impacted [3].

An additional benefit gained from this portrayal is freedom from the assumptions required by the t-test. Comparing the proportion of events in groups using risk/odds ratios or logistic regression ignores the time dimension that impacts survival or time to the event. The Kaplan-Meier estimator used to generate time-to-event curves is a non-parametric statistic and therefore not bound to assumptions of normality. Overall significance can be determined, as we did, with the corrected log-rank test. The visualizations of the time point differences between different survival curves if they are non-normal and/or censored are achieved with the representation in Fig. 1B. Time point confidence intervals or confidence bands can be useful in eliciting temporal differences that are not clear in box-plot portrayals of time-to-event data as well, although not shown in Fig. 1B due to the number of curves. In addition, differences in the cumulative incidences can be readily determined. If the data are parametric and do not included censored points, either representation is appropriate.

Accurate graphical representation of data is essential for generalizability and clinical interpolation. In Fig. 1A, both the time to occlusion and the total amount of study time in which occlusion did not occur are used as endpoints that contribute to the statistical analysis of the data. This mixed definition of endpoints will lead to obstruction of analysis between groups of data. Even if the statistics are sound and modified to include the censoring, it is more accurate and useful to show this graphically as well. The endpoint needs to be defined consistently. To ensure that we are communicating clearly in our data, we propose that we as a scientific community shift from the inaccurate box-plot to the more revealing and inclusive Kaplan-Meier survival curve when documenting results from thrombosis and bleeding time assays.