The neural basis of value accumulation in intertemporal choice

Abstract

Making intertemporal choices (choosing between rewards available at different points in time) requires determining and comparing the subjective values of available rewards. Several studies have found converging evidence identifying the neural systems that encode subjective value in intertemporal choice. However, the neural mechanisms responsible for the process that produces intertemporal decisions on the basis of subjective values have not been investigated. Using model-based and connectivity analyses of functional magnetic resonance imaging data, we investigated the neural mechanisms underlying the value-accumulation process by which subjective value guides intertemporal decisions. Our results show that the dorsomedial frontal cortex, bilateral posterior parietal cortex, and bilateral lateral prefrontal cortex are all involved in the accumulation of subjective value for the purpose of action selection. Our findings establish a mechanistic framework for understanding frontoparietal contributions to intertemporal choice and suggest that value-accumulation processes in the frontoparietal cortex may be a general mechanism for value-based choice.

Introduction

Decisions involving tradeoffs between the magnitude of rewards and the delays at which they can be obtained are ubiquitous and often important in determining long-term well-being. For example, our long-term financial stability is largely dependent on our ability to forgo the satisfaction of immediate consumption for the sake of accumulating greater wealth for the future in the form of savings. These decisions are known as intertemporal choices and have long been the focus of economic (Thaler & Shefrin, 1981; Hoch & Loewenstein, 1991) and psychological (Mischel et al.,1989; Ainslie, 2001) theories of self-control. Recent neuroimaging studies have progressed toward a neurobiological understanding of intertemporal choice by identifying the neural systems that encode the subjective value of delayed rewards (McClure et al., 2004, 2007; Kable & Glimcher, 2007; Peters & Büchel, 2009). It is now generally agreed that the ventromedial prefrontal cortex (vmPFC) and ventral striatum play a key role in the valuation of future rewards (Kable & Glimcher, 2009; Peters & Büchel, 2011; van den Bos & McClure, 2013). However, the neural mechanisms that ultimately produce intertemporal decisions on the basis of subjective value remain poorly understood.

A proposal based on findings from the perceptual decision-making literature (Kable & Glimcher, 2009) and recent imaging studies dealing with simple value-based scenarios (Basten et al., 2010; Hare et al., 2011) suggests that frontoparietal regions, like the dorsomedial frontal (dmFC), posterior parietal (pPC) and lateral prefrontal (lPFC) cortex, guide intertemporal choice behavior by accumulating subjective value information encoded in the vmPFC and striatum (Kable & Glimcher, 2009). Recent computational modeling studies have shown that the mechanisms implied by this hypothesis can explain many features of intertemporal choice behavior (Dai & Busemeyer, 2014; Rodriguez et al., 2014), but the prediction that these mechanisms are localized in the frontoparietal cortex has not been tested.

We tested the hypothesis that frontoparietal regions accumulate subjective value information in intertemporal choice, using a combination of model-based and connectivity analyses of functional magnetic resonance imaging (fMRI) data. To this end, we designed an intertemporal choice task that systematically manipulated the value-accumulation process on an individual subject basis. The resulting neural activity was analysed to identify value-related responses in the vmPFC and to test for functional connectivity related to the action selection process. We also developed a model of value accumulation to account for behavior at the level of individual trials and leveraged the model to generate predictions of trial-to-trial variability in neural activity associated with value-accumulation mechanisms. Finally, we conducted additional tests of neural activity and functional connectivity within frontoparietal regions to test predictions derived from our value-accumulation model. Our findings suggest differential involvement of the dmFC, pPC and lPFC with value accumulation, revealing a mechanism by which frontoparietal regions guide intertemporal decisions.

Materials and methods

Based on prior literature from studies of evidence accumulation in other decision domains (Gold & Shadlen, 2007; Heekeren et al., 2008; Kable & Glimcher, 2009; Basten et al., 2010; Hare et al., 2011), we established four criteria for determining whether neural activity in the dmFC, pPC and lPFC may be interpreted as reflecting the accumulation of subjective value information for the purpose of action selection during intertemporal choice.

Criterion I

Regions implementing value accumulation during intertemporal choice must receive input from regions that encode the subjective value of delayed rewards. To test this criterion, we must identify brain regions associated with encoding subjective value and show evidence of functional connectivity between value-encoding and value-accumulation regions.

Criterion II

Activity in value-accumulation regions should correlate with trial-to-trial variability in value accumulation. Specifically, this criterion requires that we predict trial-to-trial variability in the amplitude of blood oxygen level-dependent (BOLD) responses from brain regions that receive encoded value input. We can derive predictions of trial-to-trial variability in value-accumulation activity using a computational model whose parameters have been estimated by fits to intertemporal choice behavior (Rodriguez et al., 2014).

Criterion III

Neural activity from value-accumulation regions should vary as a function of value input strength and as a function of response time (RT). These two features are critical signatures of evidence accumulation activity in single-neuron recordings during perceptual decision-making (Gold & Shadlen, 2007).

Criterion IV

Value-accumulation regions must influence motor responses. To test this criterion, we should find evidence of functional connectivity between value-accumulation and motor regions expressing the outcome of a decision.

Subjects

Twenty-five healthy adults participated in this study (16 females, age 19–46 years, mean 24.44 years). All participants gave written informed consent before completing the experiment. All procedures were approved by Stanford University’s Institutional Review Board and were in compliance with the 2013 World Medical Association Declaration of Helsinki for ethical research practices involving human subjects. One participant was excluded because the behavior did not allow us to estimate reliable temporal discounting parameters. Another participant was excluded because of data collection problems. Data from a total of 23 subjects were analysed (15 females, age 19–46 years, mean 24.52 years).

Discounting model and task design

Participants completed two intertemporal choice tasks. The first task used a staircase procedure to measure each individual’s discount rate k, assuming a hyperbolic discounting function

$$V_{\mathrm{D}}=\frac{r}{1+kt},$$ (1)

where V_D is the subjective value of the delayed reward, r is the monetary amount offered, and t is the delay. Using a maximum likelihood procedure, parameters were estimated from the first task and used to generate stimuli for the second task that varied systematically in V_D, which therefore also manipulated the relative value evidence (|V_D−V_I|) and the value-accumulation process in a predictable manner.

The staircase procedure used during the first task required participants to select between a delayed reward (of r dollars available at delay t) and a fixed immediate reward of $10 (V_I). For any choice, indifference between the immediate and delayed options implies a discount rate of k = (r−V_I)(V_I t)⁻¹. We refer to this implied equivalence point as k_eq; our procedure amounted to varying k_eq systematically until indifference was reached. Specifically, we began with k_eq = 0.02. If the subject chose the delayed reward, k_eq decreased by a step size of 0.01 for the next trial. Otherwise, k_eq increased by the same amount. Every time the subject chose both a delayed and an immediate offer within five consecutive trials, the step size was reduced by 5%. Participants completed 60 trials of this procedure. We placed no limits on the RT, and presented both offers on the screen, as ‘$10 now’ on the left side, and ‘$r in t days’ on the right.

After completing the first task, we fit a softmax decision function to participants’ choices. We assumed that the likelihood of choosing the delayed reward was given by

$$P_{\mathrm{D}}=\frac{1}{1+e^{-m(V_{\mathrm{D}}-V_{\mathrm{I}})}},$$ (2)

where m accounts for sensitivity to changes in discounted value.

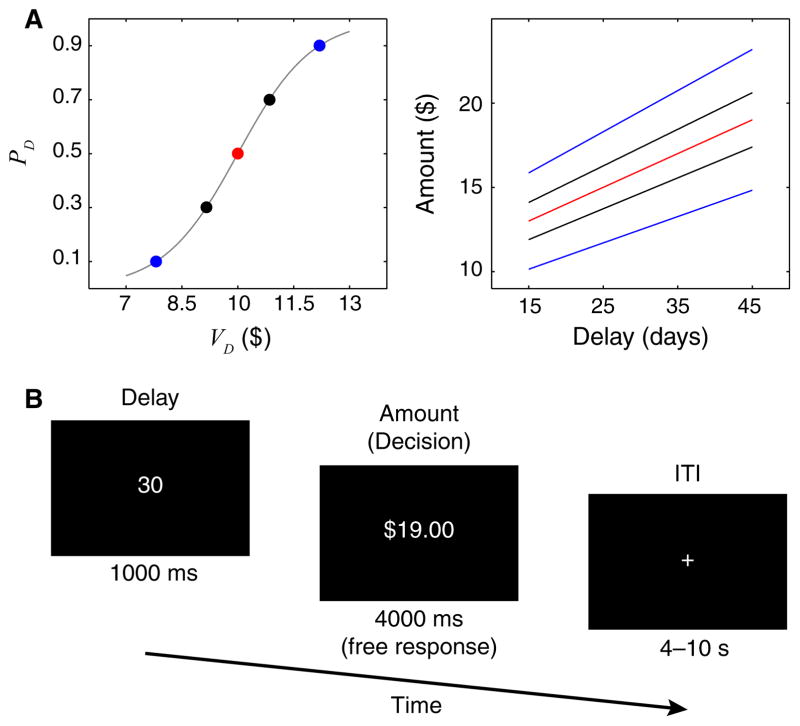
We collected fMRI data during the second task. In every trial, a delay t was randomly selected from a range of 15–45 days. We then calculated and offered an amount r that would give a P_D of 0.1, 0.3, 0.5, 0.7, or 0.9 (Fig. 1A). Delays were presented first for 1000 ms. The amount information (r) was then shown and kept on screen for a maximum of 4000 ms. A fixed immediate option of $10 was always available but was never visually presented (Fig. 1B).

Fig. 1.

Experimental design. (A) Discounted values of the delayed reward (V_D) corresponded to one of five controlled choice probabilities for each subject. Delays of between 15 and 45 days were combined with one of five different reward amounts to map varying delayed rewards to choice probabilities. (B) Within-trial sequential presentation of delay and amount information. ITI, intertrial interval.

We specifically selected a 1000 ms separation between the presentation of delay and amount information in order to maintain the experiment design as close as possible to the design that we used for another experiment where we collected electroencephalography data during the same task. In the context of the current dataset, the 1000 ms separation prevents us from distinguishing neural responses to delay and amount presentations. However, our sequential design allowed us to minimize the amount of time that subjects need to spend reading the screen before engaging in the decision process, eliminating a potential confound from our estimation of decision times. Moreover, our primary interest was on brain activity associated with the decision process, which was unaffected by this short interstimulus interval.

We measured the RT relative to the onset of the decision period. The duration of the decision period was fixed at 4000 ms. When subjects made choices in less than 4000 ms the amount information disappeared and the screen remained blank until 4000 ms elapsed. We discarded any trial in which a response was made in less than 200 ms or fell outside the decision period. We introduced an inter-trial interval of between 4 and 10 s to facilitate separability of the BOLD response between trials. In exchange for participation subjects received $40 cash and an additional amount, determined by their choice in a randomly selected trial, taken from the second task.

Participants completed 40 trials at every P_D level except at P_D = 0.5, for which they completed 80 trials. This permitted us to study the effects of relative value evidence, |V_D−V_I|, on fMRI measures with the same number of trials at each level. Trial types were randomized and counterbalanced over four blocks. We also counterbalanced the mapping between choices and button presses for every subject. During the first half of the second session, approximately half of the subjects (n = 11) indicated delayed reward choices by pressing a button with their left index finger and immediate choices by pressing a different button with their right index finger. The other subjects indicated their choices by the inverse left–right mapping. All subjects switched the initial response mapping during the second half of the session.

Analysis of behavioral data

Our first analyses of the data from this experiment were aimed at confirming that the task used during the second session manipulated behavior as intended. We first tested whether P_D varied as a function of V_D as predicted by Eqn 2. To test this, we ran a logistic mixed-effects regression on choice probabilities (observed during the second intertemporal choice task) as a function of V_D, calculated from the parameters observed during the first intertemporal choice task. We also tested if RT varied as a function of |V_D−V_I|. To test for RT effects, we ran a linear mixed-effects regression on median RT, using |V_D−V_I| as the regressor. Both behavioral analyses were conducted using R (R Core Team, 2013) and the Linear Mixed-Effects Models package (Pinheiro et al., 2013), and specified subjects as random effects.

To ensure that our behaviorally derived variables of interest for fMRI analyses reflected subjects’ preference during the fMRI session, we derived |V_D−V_I| and linear ballistic accumulator (LBA)-dependent measures based on the behavior observed during the second task, during which fMRI data was collected. We compared choice parameters obtained from both sessions beforehand and confirmed that these measures were not significantly different. However, using estimates derived from the fMRI session minimized measurement error as much as possible.

Single-trial linear ballistic accumulator parameters and value accumulation

In previous work, we evaluated the relative fits of several variants of the LBA model (Rodriguez et al., 2014). Here we used the previously found best-fitting LBA model variant to derive quantitative predictions of trial-to-trial variability in neural responses associated with value accumulation. Estimates for single-trial LBA parameters have been derived before (van Maanen et al., 2011), but our approach is slightly different because we estimates all parameters simultaneously, and we are interested in a total value of accumulation measure.

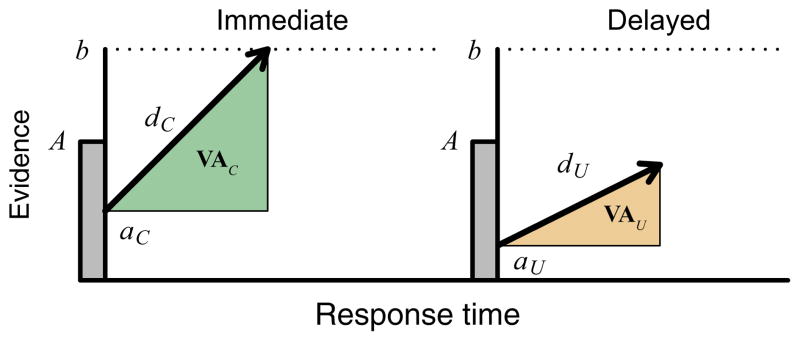
Our LBA model explains intertemporal decisions based on the accumulation of temporally discounted value. There are two accumulators in the model, one for immediate rewards and one for delayed rewards (Fig. 2). Trial-to-trial variability in choice and RT arises from independent variability in the rate of value accumulation (i.e. drift rate) and the starting point of each accumulator. A decision is made when the evidence in either the immediate or delayed reward accumulator reaches a threshold.

Fig. 2.

LBA model of intertemporal choice. The choice and RT on a given trial depend on which of two accumulators, representing the immediate and delayed options, reaches an accumulation bound (b) first. Trial-to-trial variability in behavior depends on the drift rate (d) and starting point (a) on each accumulator. Trial-specific measures of value accumulation (VA_C, VA_U) depend on single-trial estimates of drift rates and starting points for the chosen (C) and unchosen (U) options.

For each trial, we determined the drift rate and starting point that most likely produced the observed choice and RT using a hierarchical Bayesian inference procedure (Turner et al., 2013b) conditional on the previously established condition-specific and subject-specific parameters from Rodriguez et al. (2014).

The model had a total of four single-trial parameters that explain the choice and RT observed in a given trial, consisting of starting point (a) and drift rate (d) pairs for the chosen ({a_C,_i, d_C,i}) and unchosen ({a_U,_i, d_U,i}) alternatives. We use the capitalized subscripts C and U to indicate that the corresponding parameters are taken from the chosen and unchosen rewards, respectively; i refers to the trial number. In addition to the single-trial parameters, our LBA model had other subject-specific parameters constrained across trials: the response threshold b, the upper bound of the starting point A, the standard deviation of the between-trial variability in the drift rates, and the non-decision time τ, which also varied across conditions. The procedure that we used to find subject-specific parameters is described in detail elsewhere (Rodriguez et al., 2014).

Given a choice observed on trial i, the response time RT_i in the LBA model is a deterministic function of the parameters corresponding to the chosen alternative. The likelihood of {a_C,_i, d_C,i} is given by

$$L(a_{\mathrm{C},i},d_{\mathrm{C},i}\mid {\text{RT}}_i)=I\left({\text{RT}}_i=\frac{b-a_{\mathrm{C},i}}{d_{\mathrm{C},i}}+\mathrm{\tau }\right),$$ (3)

where I(·) denotes an indicator function equaling 1 when the specified identity is satisfied and 0 otherwise. Importantly, because this likelihood function contains two unknown parameters and only one observed data point, there are an infinite number of pairs {a_C,i, d_C,i} that could satisfy Eqn 3. To find an unique solution, we first found a drift rate d_C,i that satisfied the constraints in the data, and then determined the starting point a_C,i, through the deterministic relationship implied by Eqn 3.

To estimate d_C,i, we took 40 000 samples from the marginal distribution of d_C,i, which is given by

$$d_{\mathrm{C},i}\mid {\text{RT}}_i\propto \varphi \left(\frac{d_{\mathrm{C},i}-v_{\mathrm{C}}}{\mathrm{\sigma }}\right)I\left(d_{\mathrm{C},i}\in \left(\frac{b-A}{{\text{RT}}_i-\mathrm{\tau }},\frac{b}{{\text{RT}}_i-\mathrm{\tau }}\right)\right),$$

where ϕ(·) denotes the standard normal density function. Given d_C,i and RT_i, a_C,i is explicitly given by

$$a_{\mathrm{C},i}=b-({\text{RT}}_i-\mathrm{\tau })d_{\mathrm{C},i},$$

For the unchosen alternative, we imposed a lower bound constraint, namely, the pair {a_U,i, d_U,i} must produce an accumulation that reaches the threshold b after the observed RT_i (i.e. RT^* ∈ (RT_i, ∞)). This restriction allowed us to derive the marginal distributions of {a_U,i, d_U,i} and produce 40 000 samples of a_U,i and d_U,i to obtain single-trial estimates through evaluation of the Metropolis–Hastings ratio (Gelman et al., 2004; Robert & Casella, 2004). The posterior distribution of a_U,i given RT_i, is given by

$$a_{U,i}\mid {\text{RT}}_i\propto \mathrm{\Phi }\left(\frac{a_{U,i}/({\text{RT}}_i-\mathrm{\tau })-v_U}{\mathrm{\sigma }}\right)I\left(a_{U,i}\in (b-A,b)\right),$$

where Φ(·) is the standard normal cumulative density function of the drift rate for the unchosen alternative. Similarly, the posterior distribution for d_U,i, conditioned on RT_i, is given by

$$d_{U,i}\mid R{T}_i\propto A\mathrm{\varphi }\left(\frac{d_{U,i}-v_U}{\mathrm{\sigma }}\right)I\left(d_{U,i}\in \left(-\infty ,\frac{b-A}{R{T}_i-\mathrm{\tau }}\right)\right)+\left(b-d_{U,i}(R{T}_i-\mathrm{\tau })\right)\mathrm{\varphi }\left(\frac{d_{U,i}-v_U}{\mathrm{\sigma }}\right)\times I\left(d_{U,i}\in \left(\frac{b-A}{R{T}_i-\mathrm{\tau }},\frac{b}{R{T}_i-\mathrm{\tau }}\right)\right).$$

This procedure produced single-trial estimates that respect all of the assumptions of our best-fitting LBA model, in the sense that it recovers the normal and uniform distributions that the LBA model uses to account for data at the condition level.

To predict neural activity using our model, we obtained a measure of total value accumulation (TVA) in individual trials (Fig. 2; Eqn 4). TVA depends on three quantities: the decision time, the distance from the starting point to the accumulation threshold in the accumulator of the chosen alternative, and the drift rate of the unchosen alternative. Because the unchosen alternative does not reach its threshold, the value accumulation of the unchosen alternative does not depend on the distance from the starting point to the decision threshold. Instead, the accumulation contributed by the unchosen alternative is defined in terms of the total decision time, determined by the chosen alternative, and its projection onto the accumulation axis, determined by the drift rate of the unchosen alternative. Explicitly, TVA is defined as

$$\text{TVA}={\text{VA}}_{\mathrm{C}}+{\text{VA}}_U=\frac{{(b-a_{\mathrm{C},i})}^2}{2d_{\mathrm{C},i}}+\frac{d_{U,i}}{2}{\left[\frac{(b-a_{\mathrm{C},i})}{d_{\mathrm{C},i}}\right]}^2,$$ (4)

where (b–a_C,i)/d_C,i is the decision time, (b–a_C,i) is the distance from the starting point to the accumulation threshold and d_u,i is the drift rate for the unchosen alternative. Figure 2 shows the TVA for a hypothetical trial in which the immediate reward was chosen.

Linear ballistic accumulator and drift diffusion model total value accumulation comparisons

To demonstrate the generalizability of our accumulation hypothesis, we compared TVA predictions derived from our LBA model with TVA predictions derived from an analogous drift diffusion model (DDM) (Ratcliff, 1978) of intertemporal choice. Although Donkin et al. (2011) have shown that the DDM and LBA models provide strikingly similar interpretations of data, because our results rely on our newly-developed TVA measure, we felt that an evaluation of model differences would be useful in corroborating our results. To this end, we first fit a DDM model that had an equivalent number of free parameters to our LBA model. Specifically, we fixed the accumulation bound, upper range of starting point distribution and standard deviation of drift rate distribution across conditions for every subject. Only the mean of the drift rate distribution and the non-decision time were allowed to vary by condition for each subject. Once we had obtained the best-fitting model parameters using the same fitting procedures that we used to fit the LBA (Turner et al., 2013b; Rodriguez et al., 2014), we derived TVA predictions for each condition and every subject using a slightly simplified version of Eqn 4 for the DDM model. We then analysed the correlation between the LBA and DDM models.

Functional magnetic resonance imaging data collection and pre-processing

We collected fMRI data using a Discovery MR750 scanner (GE Healthcare). The fMRI analyses were conducted on gradient echo T2*-weighted echoplanar functional images with BOLD-sensitive contrast (42 transverse slices; TR, 2000 ms; TE, 30 ms; 2.9 mm isotropic voxels). Slices had no gap between them and were acquired in interleaved order. The slice plane was manually aligned to the anterior–posterior commissure line. The total number of volumes collected per subject varied depending on random intertrial intervals. The first 8 s (four volumes) of data contained no stimuli and were discarded to allow for T1 equilibration. In addition to functional data, we collected whole-brain, high-resolution T1-weighted anatomical structural scans (0.9 mm isotropic voxels). Image analyses were performed using SPM8 (http://www.fil.ion.ucl.ac.uk/spm/). During pre-processing, we first performed slice-timing correction and realigned functional volumes to the first volume. We then co-registered the anatomical volume to the realigned functional scans and performed a segmentation of gray and white matter on the anatomical scan. Segmented images were then used to estimate non-linear Montreal Neurological Institute normalization parameters for each subject’s brain. Normalization parameters estimated from segmented images were used to normalize functional images into Montreal Neurological Institute space. Finally, normalized functional images were smoothed using a Gaussian kernel of 8 mm full-width at half-maximum.

Functional magnetic resonance imaging analyses

Our first goal was to test for regions encoding the subjective value driving the dynamics of our decision model. To this end, we built a general linear model (GLM) that predicted BOLD responses on the basis of |V_D−V_I|. For this and all other fMRI analyses based on | V_D−V_I|, we relied on parameter estimates derived from the behavior observed during the fMRI part of the experiment. This allowed us to minimize any potential measurement error introduced by behavioral changes between the first and second intertemporal choice tasks. This GLM specified the onsets of the delay presentation and decision periods, as well as the onsets of the subjects’ response in every trial. Events in all three onset regressors were modeled as impulse delta functions and convolved with the canonical hemodynamic response function. The model also included the |V_D−V_I| measure as a parametric modulator of (BOLD) responses during the decision period. In addition, the model also included six regressors corresponding to the motion parameters estimated during data preprocessing and constants to account for the mean activity within each of the four sessions over which the data were collected. All other GLM models that we ran also included six motion regressors and session constants as regressors of no interest. Only the |V_D−V_I| modulated regressor was treated as a regressor of interest in the first-level contrast of our first GLM.

The group-level contrast was calculated as a one-sample t-test on the beta coefficients obtained from the subject-specific |V_D−V_I| modulated regressor. To determine the appropriate whole-brain family-wise error (FWE) rate correction at the cluster level, we used the AlphaSim function in AFNI (http://afni.nimh.nih.gov/). The Alpha-Sim function determines the cluster size that would result in less than 5% cluster-level false positives by performing a Monte Carlo simulation of contiguous voxels exceeding a specified uncorrected P-value under the null hypothesis, given a specified smoothness level in the data. We used an uncorrected voxel-wise threshold of P < 0.005 and an empirical estimate of the smoothness of the data to perform the Monte Carlo simulation. The resulting cluster size for our data was 290 voxels.

To test if the vmPFC region that we identified with the |V_D−V_I| GLM corresponded with the value-encoding region previously identified in the literature, we masked our group-level results with the vmPFC mask published in a previous meta-analysis of value-encoding studies (Bartra et al., 2013) and performed a small volume correction test of the overlapping cluster within the larger vmPFC region of interest (ROI).

In order to rule out the possibility that vmPFC activity could be best explained by chosen value, we performed two additional GLM analyses. The first GLM was identical to our original |V_D−V_I| GLM, but replaced |V_D−V_I| with the value of the chosen reward as the regressor of interest. The results of this GLM were tested at the whole-brain level. The second GLM included two regressors, the value of the chosen reward and |V_D−V_I| orthogonalized with respect to the value of the chosen reward. The orthogonalization procedure assigned shared variance between the relative and chosen value to chosen value. Results from this analysis therefore provide an upper bound of the degree to which chosen value explains BOLD signals, and a lower bound of the degree to which relative value explains BOLD signals. To evaluate the results of this GLM, we performed t-tests on the average beta coefficients within the ROI initially identified by the |V_D−V_I| regressor from our original GLM analysis.

We performed a psychophysiological interaction (PPI) analysis to test for functional connectivity with the vmPFC. We first extracted the time course of activity from the vmPFC region identified by our | V_D−V_I| GLM. Only voxels that fell inside the mask vmPFC region from the published meta-analysis (Bartra et al., 2013) were used as seed. We removed all of the variance in the vmPFC time series that was explained by the delay, response onset, motion regressors and session constants. Thus, the resulting time series only contained variance explained by the decision period onsets regressor. We then computed a spatial summary of the entire seed region by extracting the first eigenvariate from the ROI time series. Next, we constructed an interaction term by deconvolving the resulting eigenvariate with the canonical hemodynamic response function and multiplying the result by a delta function identifying the onsets of the decision period. Finally, we convolved the interaction term with the hemodynamic response function and included it in a GLM as our regressor of interest. The PPI GLM also included the convolved decision period onset regressor, the first vmPFC eigenvariate (without deconvolution) and an eigenvariate of the lateral ventricle (also without deconvolution) as regressors of no interest. The lateral ventricle eigenvariate was obtained using the same procedures used to obtain the vmPFC eigen-variate and was included in the model to control for an artifactual activation within the ventricles observed in a simpler GLM and to discard the possibility that the results observed within the cortex could also be explained by artifacts. The resulting effects from a contrast on the interaction term of the full PPI GLM just described represent a strengthening of the correlation with the vmPFC at around the time of the decision, over and above any inherent correlation with the vmPFC and any correlation due to the main effect of the decision period onset. Group-level inferences on this GLM were performed using the beta coefficients from the interaction term regressor.

To identify neural activity showing trial-to-trial variability associated with value accumulation, we ran a GLM that predicted BOLD responses on the basis of the TVA measure obtained from our LBA model. Again, we used the behavior observed during the fMRI task to estimate the LBA parameters from which we derived TVA. This GLM also included delay presentation, decision period and response onsets as regressors of no interest. The TVA measure was included as a parametric modulator of BOLD responses during the decision period. Group-level inferences were performed using the beta coefficients from the TVA parametric modulator.

We tested whether any frontoparietal regions showed joint effects in the vmPFC seeded PPI and the TVA GLMs. The test was performed by identifying regions in the conjunction of significant effects on both GLMs (P < 0.05, FWE corrected). All of our subsequent tests of frontoparietal activity and connectivity were performed by analysing average beta coefficients in the dmFC, pPC and lPFC ROIs identified in this conjunction. We tested for differences in beta coefficients between the dmFC, pPC and lPFC by performing repeated-measures ANOVAsand post-hoc one-sample and paired-sample t-tests on all subsequent GLM results. We performed correlation tests of mean signal amplitudes and beta coefficients across regions to test whether any of the reported differences could be explained by overall signal differences across regions. There were no significant correlations for any of the reported cross-regional beta coefficient differences that we report.

We also tested whether activity in the dmFC, pPC and lPFC varied as a function of |V_D−V_I| and RT. To test for |V_D−V_I| effects, we extracted beta coefficients from our ROIs, using the results of the |V_D−V_I| GLM that we had already estimated to identify value-encoding responses in the vmPFC. To test RT effects, we ran another GLM with all of the same regressors of no interest, but including RT as a parametric modulator of BOLD responses on the response onsets.

Finally, we ran two GLM analyses to test functional connectivity between our dmFC, pPC and lPFC ROIs and the motor cortex. We first identified left and right motor cortex regions by running a GLM that included separate response onset regressors for right and left responses in addition to delay and decision period onset regressors, and the other regressors of no interest. The contrast of interest on this GLM compared regions that were more active during left than right responses. We then defined two spherical ROIs inside the left and right motor cortex regions that were identified by this contrast. Subsequently, we constructed regressors from our motor cortex ROIs following the same procedure described above for the vmPFC PPI analysis. Finally, we ran separate GLMs that included motor cortex activity as the regressor of interest and the response onsets of the contralateral hand as a regressor of no interest, along with the motion regressors and session constants. Repeated-measures ANOVAs and t-tests were then used to analyse beta coefficients extracted from our dmFC, pPC and lPFC ROIs.

Results

Intertemporal choice behavior

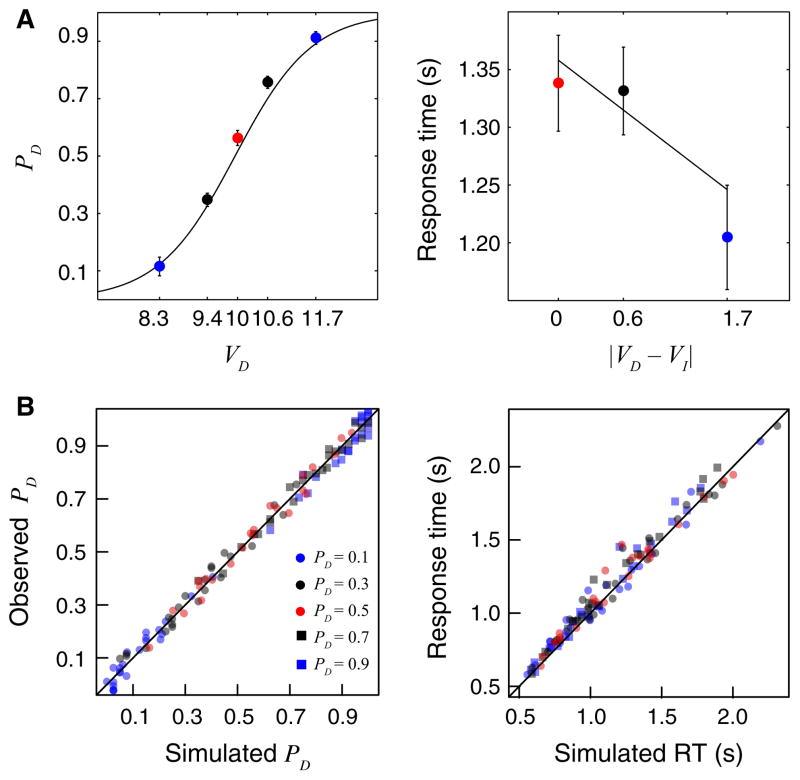
We first determined whether our task manipulated behavior in a way that allowed us to test our four criteria (see Materials and methods). Discount rate (k) estimates derived from the first session were highly correlated with (r = 0.98, t₂₁ = 23.83, P < 2 × 10⁻¹⁶) and did not differ significantly from (paired t-test: t₂₂ = 0.97, P = 0.34) estimates derived from the behavior observed during the fMRI session. To confirm that our manipulation controlled for choice probabilities, we ran a mixed-effects logistic regression to predict choices, using V_D as the predictor. V_D was highly predictive of choices (β = 1.39, z = 29.71, P < 1 × 10⁻¹⁶), with observed choice probabilities closely matching the targeted probabilities (Fig. 3A). We also tested whether |V_D−V_I| had a systematic effect on RT. Based on model simulations, we expected that |V_D−V_I| would have a negative effect on RT because |V_D−V_I| is negatively correlated with drift rates and low drift rates result in longer decision times (Rodriguez et al., 2014). To test this prediction, we ran a mixed-effects linear regression on median RT, using an ordinal regressor based on |V_D−V_I|. This regression analysis showed increased RT with decreased differences in value (Fig. 3A; β = −66.74, t₂₂ = −4.46, P = 1 × 10⁻⁴), confirming that our task systematically manipulated choice probabilities and RT as intended.

Fig. 3.

Behavioral results. (A) Left: observed choice probabilities closely matched the targeted choice probabilities. Right: RTs were slowest at indifference and decreased as a function of relative value evidence (|V_D−V_I|). Both plots show the data as solid dots that are color-coded by levels of relative value evidence. The solid lines correspond to the best-fitting mixed-effects regressions reported in the text. (B) Single-trial model parameters recover choice probabilities and median RT. Left: simulated and observed choice probabilities of the delayed reward for each of the five task conditions, labeled by their expected P_D and color-coded by |V_D−V_I| levels. Jitter was added to the plotted data to better reflect the total number of observations. Right: medians of the simulated and observed RTs, using the same color labels as on the left panel.

Single-trial linear ballistic accumulator model of value accumulation

Next, we confirmed that our parameter estimation procedure for the single-trial LBA model provided valid fits to behavior. To validate single-trial parameter estimates of value accumulation obtained from our LBA model, we simulated intertemporal choice data based on estimated drift rates and starting points, and compared the simulated and observed datasets. We ran two mixed-effects linear regressions: the first compared the logit transforms of simulated and observed choice probabilities, and the second compared simulated and observed median RT. Both regressions confirmed that our procedure for estimating single-trial parameters accurately recovered choice probabilities (β = 1.00, t₂₂ = 636.27, P = 1 × 10⁻¹⁶) and median RT (β = 0.95, t₂₂ = 45.42, P = 1 × 10⁻¹⁶; Fig. 3B).

Criterion I: Functional connectivity with value-encoding regions

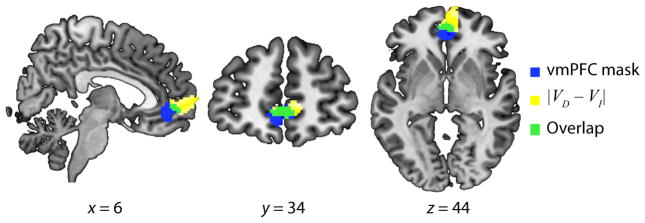
Our first goal in analysing fMRI data was to test for regions encoding subjective value and to identify regions that may receive value-encoding outputs through functional connectivity. To localize brain regions potentially encoding the input to the accumulation process, we ran a whole-brain GLM using |V_D−V_I| as a parametric regressor of BOLD responses. We refer to this quantity, |V_D−V_I|, as relative value evidence, the primary input to the LBA value-accumulation process (Rodriguez et al., 2014). The relative value evidence GLM identified a single significant region in the vmPFC (Fig. 4; P < 0.05 whole-brain FWE corrected at the cluster level). This vmPFC region remained significant when conjoined with the vmPFC value-encoding region identified in a recent meta-analysis (Bartra et al., 2013) (k = 67, P < 0.05, small-volume FWE within ROI).

Fig. 4.

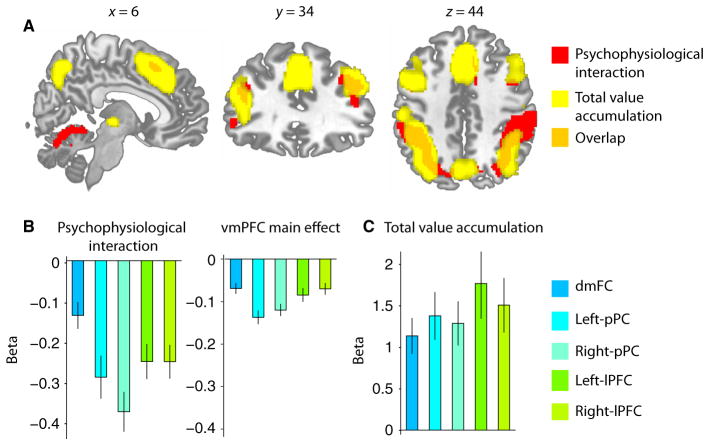
Value encoding in the vmPFC. Yellow, vmPFC region ([6, 62, 0], k = 356 voxels) in which neural activity correlated with |V_D−V_I| during the decision period; blue, vmPFC mask from a published meta-analysis of value-encoding studies (k = 448 voxels); green, overlap between vmPFC regions shown in yellow and blue (k = 67 voxels). The |V_D−V_I| contrast was thresholded at P < 0.005 at the voxel level (k > 290 voxels) and overlaid on the CH2 Montreal Neurological Institute anatomical image, shown in neurological convention with the right hemisphere on the right side.

One limitation from the previous analysis is that the chosen value (i.e. the discounted value of the chosen option) is correlated with relative value in the experiment (r = 0.47; mean across subjects). To test whether the chosen value could provide an alternative explanation for our results, we performed two additional GLMs, one in which we tested for any effects of the chosen value at the whole-brain level and another in which the chosen and relative value were included as separate regressors (see Materials and methods for details). The whole-brain GLM based on chosen value revealed no significant voxels in the vmPFC, even at the liberal threshold of P < 0.05 (uncorrected). The second GLM analysis revealed a significant effect within the vmPFC for relative value evidence (t₂₂ = 2.32, P = 0.03) but not for the chosen value (t₂₂ = 1.58, P = 0.12).

To examine functional connectivity with the vmPFC, we performed a PPI analysis that used activity from the vmPFC to predict neural activity in putative value-accumulation regions during intertemporal decision-making. We expected that activity in the vmPFC and frontoparietal regions involved in value accumulation would be negatively correlated. This inverse relationship was expected from model simulations. In the model, easier decisions have larger drift rates, requiring less time for evidence accumulation to reach a constant decision threshold; therefore, greater relative value evidence correlates with less total neural activity during value accumulation. Consequently, our PPI analysis tested whether the magnitude of the expected negative correlation between the vmPFC and putative value-accumulation regions increased at around the time when subjects could make a decision compared with other task time periods. Consistent with the hypothesis that frontoparietal regions integrate value in intertemporal choice, this analysis revealed statistically significant effects within the dmFC (superior frontal gyrus/supplementary motor area; [26, 6, 54]), bilateral pPC (inferior parietal lobule: left, [−12, −34, 26]; right, [48, −42, 52]) and bilateral lPFC (middle frontal gyrus: left, [−44, 44, 10]; right, [34, 42, 18]) (Fig. 5A; P < 0.05, FWE corrected at cluster level).

Fig. 5.

Functional connectivity with the vmPFC and value accumulation. (A) Red, regions showing evidence of increased connectivity with the vmPFC during the decision period; yellow, regions whose activity correlates with trial-to-trial variability in the TVA regressor derived from the LBA model; orange, overlap of regions shown in red and yellow. In particular, frontoparietal regions including the dmFC (k = 146 voxels), bilateral pPC (left, k = 1259 voxels; right, k = 987 voxels) and bilateral lPFC (left, k = 539 voxels; right, k = 790 voxels) show considerable overlap between the two contrasts. These five overlapping regions were used as ROIs for all remaining analyses. (B) Average beta coefficients from the TVA GLM. No differences between frontoparietal regions are evident in the strength of the TVA effect. (C) Average beta coefficients from the PPI GLM analysis seeded in the vmPFC. Left: beta coefficients for the interaction term. Right: beta coefficients from the vmPFC ROI main effect term. There are significant negative correlations between the vmPFC and all frontoparietal regions (right), and an increase in the strength of the correlation during the decision period (left). Bilateral pPC regions show the strongest evidence of functional connectivity with the vmPFC. Error bars represent the SEM in (B) and (C).

For illustrative purposes and to confirm that our PPI results reflect an increased negative correlation, which is independent of an expected negative correlation with the vmPFC, we analysed the average beta coefficients from frontoparietal regions that corresponded to the vmPFC main effect and interaction terms in the PPI GLM. As expected, frontoparietal regions showed a negative correlation with the vmPFC (all P < 0.01, one-sample t-tests; Fig. 5B); however, the beta coefficients from the interaction term, which are computed after taking into account the variance due to the vmPFC main effect, still identify significant negative effects in the dmFC, pPC and lPFC (Fig. 5A and B). Our beta coefficient analyses revealed inter-region differences in the strength of the main effect correlation with the vmPFC (F_4,88 = 11.44, P = 1 × 10⁻⁶) and the increase in correlation strength (F_4,88 = 7.58, P = 2.69 × 10⁻⁵). In particular, bilateral pPC regions showed more negative beta coefficients than the dmFC and bilateral lPFC regions (all P < 0.05, post-hoc paired sample t-tests; Fig. 5A and B).

Criterion II: Trial-to-trial variability in value accumulation

Having identified the vmPFC as a value-encoding region and regions that may receive value input through functional connectivity with the vmPFC, we next tested for regions where activity correlated with trial-to-trial variability in value accumulation. To this end, we ran a whole-brain GLM using TVA (Eqn 4) as a modulator of BOLD responses. In support of our primary hypothesis, this analysis identified overlapping effects with the vmPFC seeded PPI in the dmFC (k = 146), bilateral pPC (left, k = 1259; right, k = 987) and bilateral lPFC (left, k = 539; right, k = 790; Fig. 5A; P < 0.05, FWE corrected at cluster level). Analysis of the average beta coefficients for the TVA effect revealed no inter-regional differences (F_4,88 = 2.23, P = 0.07).

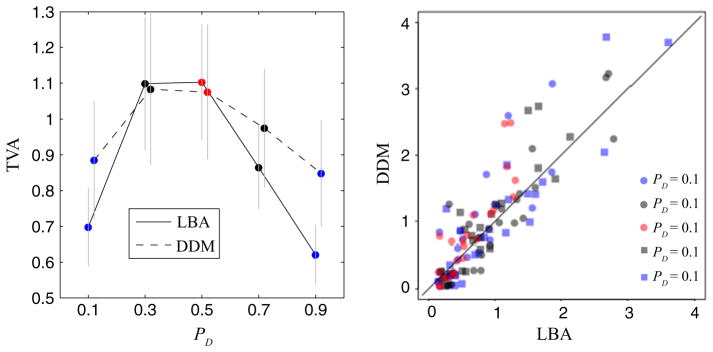
To test for the generalizability of the above results, we also evaluated the TVA predictions derived from a DDM (Ratcliff, 1978) with an equivalent number of parameters to our LBA model (Rodriguez et al., 2014). Specifically, we fit a DDM model allowing drift rates and non-decision time to vary across P_D conditions and derived TVA from the resulting best-fitting parameters, relying on a slightly modified version of Eqn 4 for the DDM. We then compared LBA and DDM TVA predictions across conditions. This analysis revealed strong correlations across subjects within all of the P_D conditions (min r = 0.84, t₂₁ = 7.08, P < 5.5 × 10⁻⁷; Fig. 6), showing that our value-accumulation results generalize beyond the specifics of the LBA model (also see Donkin et al., 2011).

Fig. 6.

Cross-model comparison of accumulation predictions. Left: mean TVAs across P_D conditions for the LBA and DDM show no systematic differences. Right: total value-accumulation predictions for the LBA and DDM models are highly correlated.

Criterion III: Drift rate and response time variability

Our third criterion requires that we identify significant variability as a function of input strength and RT. Both forms of variability in neural activity have been identified in single-cell recordings of perceptual evidence accumulation in monkeys (Gold & Shadlen, 2007), and can be inferred from model simulations. Systematic variability in the strength of the inputs received leads to differences in drift rates and this variability should be measurable as differences in neural activity. Moreover, because high input strength results in less overall accumulation activity, we expect a negative correlation between input strength and frontoparietal activity. Noise also accumulates as the accumulation process continues so that differential activity is also predicted by RT. Because RT is positively correlated with TVA, our model predicts a positive correlation between RT and neural activity in the dmFC, pPC and lPFC. We tested both of these predictions with analyses of average beta coefficients.

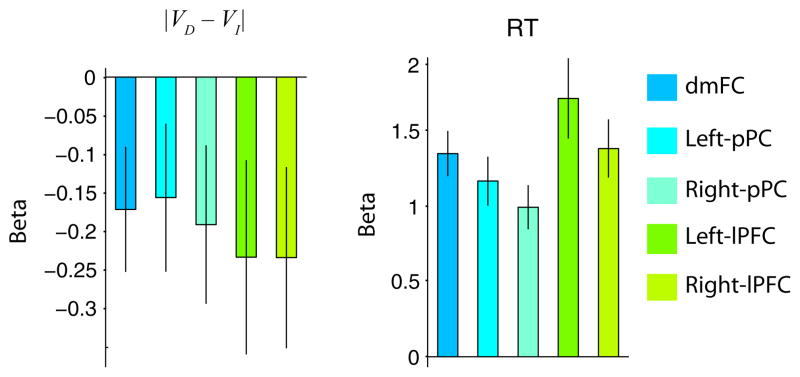
To test for input strength effects, we analysed average beta coefficients within our frontoparietal ROIs. Beta coefficients for this analysis were obtained from the same |V_D−V_I| whole-brain GLM that we used to identify value-encoding regions. Consistent with our prediction, we found negative relative value evidence effects within the dmFC (t₂₂ = −2.12, P = 0.02), pPC (left, t₂₂ = −1.62, P = 0.06; right, t₂₂ = −1.86, P = 0.04), and lPFC (left, t₂₂ = −1.86, P = 0.04; right, t₂₂ = −1.99, P = 0.03; one-sample t-tests, Fig. 7). There were no inter-regional differences in the strength of the negative correlation between |V_D−V_I| and frontoparietal BOLD responses (F_4,88 = 0.32, P = 0.86).

Fig. 7.

Relative value evidence and RT effects. Left: beta coefficients for the |V_D−V_I| GLM in all frontoparietal ROIs during the decision period. There are no differences in the strength of the |V_D−V_I| effect across regions. Right: beta coefficients from the RT GLM during the response. A stronger RT effect is evident in the dmFC and bilateral lPFC, relative to the effects in bilateral pPC. Error bars represent the SEM.

To test for RT effects, we first ran a GLM using RT as a modulator of BOLD responses locked to response onsets and then analysed average beta coefficients within our frontoparietal ROIs. Confirming our predictions, we found a significant positive effect within the dmFC, bilateral pPC, and bilateral lPFC (all P < 0.01; Fig. 7). The RT analysis revealed inter-regional differences (F_4,88 = 7.53, P = 1 × 10⁻⁴). The right pPC region showed a weaker correlation with RT than the dmFC and bilateral lPFC regions (all P < 0.01, post-hoc paired samples t-tests), whereas the left pPC showed a weaker correlation with RT than the dmFC (t₂₂ = −1.8, P = 0.04) and left lPFC (t₂₂ = −3.37, P < 0.01).

Criterion IV: Functional connectivity with the motor cortex

Finally, we tested for functional connectivity between frontoparietal regions implicated in value accumulation and the motor cortex. This analysis was based on the prediction that value-accumulation regions ought to influence the motor cortex if they are responsible for making decisions expressed through motor output. To test for response-related functional connectivity, we ran two GLMs that included motor cortex activity as regressors of interest and controlled for effects due to co-activation during responses (see Materials and methods).

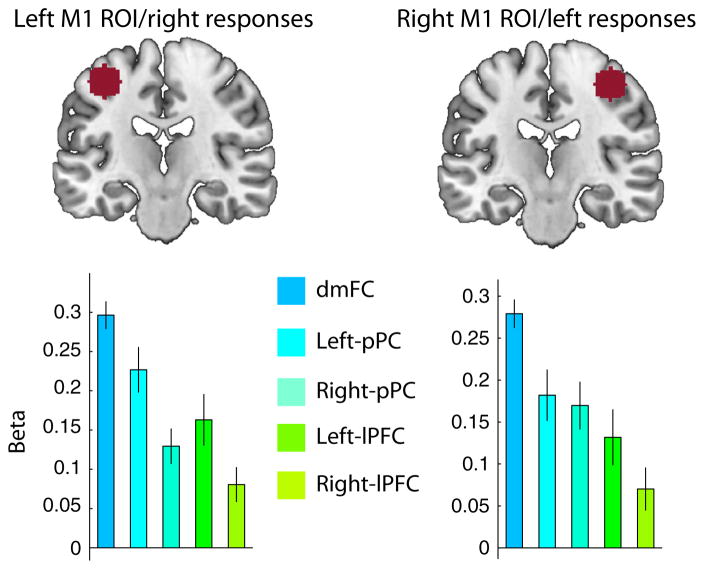
We found strong positive effects in the dmFC, bilateral pPC and bilateral lPFC (all P < 0.04, one-sample t-tests; Fig. 8), indicating that all five frontoparietal regions satisfy our last criterion. There were inter-regional differences in the strength of the correlations with the motor cortex (left ROI, F_4,88 = 14.28, P = 1 × 10⁻⁸; right ROI, F_4,88 = 8.87, P = 1 × 10⁻⁵; Fig. 8). The dmFC showed greater connectivity with the motor cortex than any other region (all P < 0.02, post-hoc paired-samples t-tests).

Fig. 8.

Functional connectivity with the motor cortex (M1). Top row: selected ROIs in the M1 to analyse functional connectivity with frontoparietal regions. Bottom row: beta coefficients for the left and right M1 GLMs. All frontoparietal regions showed evidence of a positive correlation with the M1 after controlling for co-activation effects due to the response. In particular, the dmFC shows the strongest correlation.

Discussion

Our findings are consistent with the hypothesis that frontoparietal regions, including the dmFC, bilateral pPC, and bilateral lPFC, may accumulate encoded value evidence during intertemporal choice. Neural activity in these frontoparietal regions showed evidence of functional connectivity with the vmPFC, displayed a correlation with trial-to-trial variability in relative value-evidence accumulation, varied as a function of input strength and RT, and showed evidence of functional connectivity with the motor cortex. These findings are generally consistent with previous studies looking at value accumulation in domains other than intertemporal choice (Basten et al., 2010; Hare et al., 2011), and suggest that value accumulation in the frontoparietal cortex may be a general mechanism for value-based choice.

Our findings contribute to at least three important problems in cognitive neuroscience. First, intertemporal choice has long been an important area of study in psychology and neuroscience, particularly in relation to concepts such as willpower and self-control. Our study establishes for the first time a mechanism by which value signals in the vmPFC are converted to actions in this important choice domain. This mechanism may be an important component of the self-control system in the brain. Previous studies suggest that the left lPFC serves as a self-control function via an indirect modulation of vmPFC value signals (Hare et al., 2009). Our findings suggest that a more direct route for left lPFC involvement in self-control may be via action selection though value accumulation.

Second, several decision-making studies have suggested different encoding schemes for value signals (Padoa-Schioppa & Assad, 2006, 2007; Lim et al., 2011; Bartra et al., 2013). In particular, previous studies have argued that the vmPFC encodes the total value of the options under consideration (Bartra et al., 2013). This encoding scheme is inconsistent with our finding that vmPFC activity correlates with relative value evidence (|V_D−V_I|). Instead, our results support the existence of a relative value signal in the vmPFC. The existence of this relative value-encoding scheme in the vmPFC has led some authors to suggest that the vmPFC is not only encoding value, but also making value-based decisions (Padoa-Schioppa, 2011). Such an interpretation is also at odds with our model, which suggests that decisions occur at a later stage of evidence accumulation in the frontoparietal cortex. In support of our model, we showed that the same sources of variability that explain choice probability and RT distributions also correlate with neural activity levels in the dmFC, pPC and lPFC.

Finally, there is a large amount of literature on and active debates about the computations mediated by the dmFC (including the anterior cingulate cortex). Alternative explanations for dmFC function include conflict detection (Botvinick et al., 2004), signaling error likelihood (Brown & Braver, 2005), or reflecting time on task (Grinband et al., 2011). Our results are consistent with the notion that the correlation between neural activity and RT reflects an accumulation process that coincides with some of these hypotheses but not others. In particular, our accumulation hypothesis is consistent with increases in dMFC activity co-varying with decision difficulty but is also able to account for the fact that RT should provide a better proxy for dMFC activity than several other task-defined measures. Given that the dmFC seems to be involved in evidence accumulation, its activity is not only driven by task demands but also by the endogenous stochasticity in the evidence accumulation mechanism. The RT is the closest observable proxy for the total amount of evidence accumulation in a given trial.

The findings from our beta coefficient analyses suggest that the dmFC, pPC and lPFC may contribute to value accumulation through different activity dynamics. The pPC showed the strongest functional connectivity with the vmPFC, and the weakest correlation with RT at the response onset. Both of these findings suggest that the pPC might be differentially involved with the initiation of the decision. The dmFC and lPFC may become more important later on in the value-accumulation process. Consistent with this hypothesis, the dmFC showed the strongest correlation with the motor cortex. However, the temporal resolution afforded by fMRI does not allow us to make a conclusive interpretation of the differences that we found between frontoparietal regions. Future studies using high temporal resolution methods, such as electroencephalography or magnetoencephalography, can play an important role in testing our predictions and further clarifying any differential contributions from the pPC, dmFC, and lPFC to intertemporal decision-making.

We used a computational model of behavior to construct a proxy for evidence accumulation. We chose the LBA because of its computational tractability (Rodriguez et al., 2014), which we exploited to derive predictions for neural activity on individual trials. Although alternative methods exist for linking model parameters to neural data (Turner et al., 2013a, 2015), our findings illustrate a theoretically complete and novel approach to the prediction of trial-to-trial variability of neural activity, based on an evidence accumulation model. In comparison with previously utilized methods for predicting neural activity related to evidence accumulation (Basten et al., 2010; Hare et al., 2011), our approach allows us to exploit trial-to-trial variance while preserving all of the distributional assumptions of the LBA model. Previous methods (van Maanen et al., 2011) attempt to exploit the trial-to-trial variance in analyses of perceptual decision-making behavior, but do not obey the specific constraints on the single-trial parameters provided by the model’s architecture.

The LBA model is one of several evidence accumulation models with the ability to explain behavior and neural activity (cf. Ratcliff & Smith, 2004). It shares key features with many other evidence accumulation models, including noise terms to account for trial-to-trial variations in RT and choice. Consistent with the generality of the accumulation mechanism that we tested, we showed that the predictions derived from our LBA model are not systematically different from the predictions that can be derived from a DDM. Nonetheless, there are subtle differences between the LBA and other evidence accumulation models that have been used to study neural activity in value-based decision-making (cf. Basten et al., 2010; Hare et al., 2011; Hunt et al., 2012; De Martino et al., 2013). We do not make any claims about the relative merits of the LBA over other value-accumulation models. Our analyses only aimed to test the hypothesis that frontoparietal regions may be involved in value accumulation in intertermporal choice. Model comparisons may be informative about which models may provide the best explanation for intertemporal choice data, but such conclusions are beyond our present scope.

In summary, our results support a quantitatively precise mechanism by which value drives intertemporal choices. Regions of the frontal and parietal cortex are critical in this action selection process. Our findings support a novel function for these cortical regions in intertemporal choice and could eventually provide a scaffold for understanding how these regions implement self-control during intertemporal decision-making.

Abbreviations

BOLD

blood oxygen level-dependent

DDM

drift diffusion model

dmFC

dorsomedial frontal cortex

fMRI

functional magnetic resonance imaging

FWE

family-wise error

GLM

general linear model

LBA

linear ballistic accumulator

lPFC

lateral prefrontal cortex

pPC

posterior parietal

PPI

psychophysiological interaction

ROI

region of interest

RT

response time

TVA

total value accumulation

vmPFC

ventromedial prefrontal cortex