Abstract
There has been an increasing interest in learning low-dimensional vector representations of medical concepts from electronic health records (EHRs). While EHRs contain structured data such as diagnostic codes and laboratory tests, they also contain unstructured clinical notes, which provide more nuanced details on a patient’s health status. In this work, we propose a method that jointly learns medical concept and word representations. In particular, we focus on capturing the relationship between medical codes and words by using a novel learning scheme for word2vec model. Our method exploits relationships between different parts of EHRs in the same visit and embeds both codes and words in the same continuous vector space. In the end, we are able to derive clusters which reflect distinct disease and treatment patterns. In our experiments, we qualitatively show how our methods of grouping words for given diagnostic codes compares with a topic modeling approach. We also test how well our representations can be used to predict disease patterns of the next visit. The results show that our approach outperforms several common methods.
I. Introduction
Electronic health record (EHR) data are widely used in healthcare research for exploratory and predictive analytics [1]–[3]. While EHR data contain structured information such as medical codes (e.g., ICD-9, ICD-10), they also contain unstructured information such as clinical notes which create challenges for designing effective algorithms to transform data into meaningful representations that can be efficiently interpreted and used in health care applications [4].
The success of extracting knowledge from clinical notes often requires the application of natural language processing (NLP) techniques. Learning distributed representations of words using neural network based models has been shown to be very useful in many NLP tasks. These models represent words as vectors and place vectors of words that occur in similar contexts in a neighborhood of each other. Among the existing models, Mikolov’s word2vec model [5] is among the most popular due to its simplicity and effectiveness in learning word representations from a large amount of data. Several studies applied word2vec on clinical notes data to produce effective clinical word representations for various applications [6]–[10].
While word2vec was initially designed for handling text, recent studies demonstrate that word2vec could learn representations of other types of data, including medical codes from EHR data [11]–[14]. Choi et al. used word2vec to learn the vector representations of medical codes using longitudinal medical records and show that the related codes indeed have similar vector representations [11]. Choi et al. designed a multi-layer perceptron to learn representations of medical codes for predicting future clinical events and clinical risk groups [12]. Gligorijevic et al. used code representation learned by word2vec to predict indicators of healthcare quality [14]. Choi et al. fed code representation learned by word2vec into a recurrent neural network to predict heart failure [13]. The limitation of those studies is that they focused only on representation of medical codes and did not utilize other sources of information from EHR data.
In this paper, we propose JointSkip-gram model: a novel joint learning scheme for word2vec model which embeds both diagnosis medical codes and words from clinical notes in the same continuous vector space. The resulting representations capture not only similarity between codes or words themselves, but also similarity between codes and words. Applications such as phenotyping [15], [16] and predictive modeling [12], [13] could benefit from these representations. As a clinical example, phenotypes for given disease concepts could be derived by retrieving their related words. To achieve this, directly applying word2vec and related algorithms may not be appropriate since codes and words are located in different parts of EHR and have different forms and properties. Our model is designed to tackle the heterogeneous nature of EHR data and builds a connection between medical codes and words in clinical notes.
In our experiments, we first qualitatively test if our representations are able to capture words related to given medical concepts. We compare our proposed model with Labeled LDA [17], a supervised counterpart of Latent Dirichlet Allocation (LDA) [18], which has been applied previously to clinical data analysis [19]–[21]. The results show that our representations indeed capture the relationship between words and codes. We also test the predictive power of our representations on the task of predicting patient diagnosis of the next visit given information from the current visit. The results show that representations learned by our approach outperform several common methods.
In the next section, we describe our method JointSkip-gram. In section 3 we explain experiment design and show results of our model and baselines. Finally in section 4 we make conclusion and discuss future research directions.
II. Method
In this section, we first formulate our problem setup. Then we overview Skip-gram [5], the architecture contained in word2vec toolkit designed for learning representations of natural language words which is also the basis of our method. Finally, we explain the proposed JointSkip-gram model.
A. Basic Problem Setup
Assume our dataset is a collection of patient visits. Each visit S is a pair (D, N) where D consists of an unordered set of medical codes {c1, c2, c3…, cn} summarizing patient’s health conditions during the visit, and N consists of an ordered sequence of words from clinical notes recorded during the visit (w1, w2, w3…, wm). We denote the size of the code vocabulary C as ∣C∣ and the size of the word vocabulary W as |W|.
B. Preliminary: Skip-gram
Fig. 1 illustrates the framework of Skip-gram. Given a word sequence (w1, w2, w3…, wm), Skip-gram relies on scanning it sequentially. For every scanned word wi, the log-likelihood of the words within its context window of a predefined size q is calculated as
| (1) |
where p(wj∣wi) is the conditional probability of seeing word wj within the context of word wi. It is defined as a softmax function
| (2) |
where is a T-dimensional vector providing the input representation of word wi and is a T-dimensional vector providing the context representation of word wj. After training, skip-gram provides two matrices: the input word matrix V ∈ ℝ|W|×T and the context word matrix V ∈ ℝ|W|×T word representation is typically assumed to be a desired representation of word wi to be used in subsequent predictive or descriptive tasks.
Fig. 1.
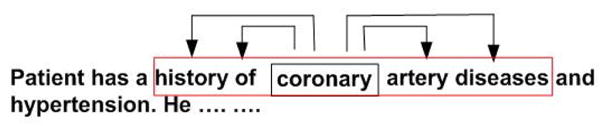
The framework of Skip-gram. Each word is used to predict its neighbours in a small context window. In this example the size of context window is 2.
To find the input and context vector representations of the words from the vocabulary, a stochastic gradient algorithm could be used to maximize the objective function (1).
Maximizing (1) is computationally expensive since the denominator in (2) sums over all words wk ∈ W. Instead of maximizing (1), Mikolov et al. proposed the skip-gram with negative sampling (SGNS) [5], which replaces log p(wj∣wi) in (1) with the sum of two logarithmic probabilities as follows. For each scanned word wi, the objective function is rewritten as
| (3) |
where probability p(wi, wj) is defined as sigmoid function :
| (4) |
and is the set of “negative words” that are sampled from a frequency distribution Pw over the word vocabulary W, where K is the number of randomly generated words for each context word. By maximizing (3), the dot product between frequently co-occurring words will become large and the dot product between rarely co-occurring words will become small.
The objective of Skip-gram is to find vector representations of words. In the resulting T-dimensional vector space, related words will be placed in the vicinity of each other, so their cosine similarity will be high.
C. Proposed model: JointSkip-gram
In the Skip-gram model, each scanned word is used to predict its neighbor words in the sequence. However, unlike the sequence of words in clinical notes N = (w1, w2, w3…, wm), medical diagnoses D = {c1, c2, c3…, cn} are an unordered set of medical codes. Therefore, context of code ci should include all other codes in the same visit: {cj|1 ≤ j ≤ n, j ≠ i}. Medical diagnosis can be viewed as a “bag” of patient’s health conditions during a visit. The semantics of a medical code can be inferred from other codes in the same bag. Furthermore, since both medical codes and clinical notes reflect a patient’s condition, there is also a relationship between them. For example, if a patient is assigned ICD-9 code “174” (female breast neoplasm), the clinical notes are likely to mention the patient’s surgery (e.g., mastectomy or lumpectomy) and the shape and size of a tumor.
To learn a relationship between medical codes and words in clinical notes, as shown in Fig. 2a, in JointSkip-gram, every code in D is scanned and each scanned code ci is used to predict not only other codes in D, but also all words in N. The log-likelihood of code ci can be expressed as
| (5) |
Similarly to Skip-gram, the probabilities p(cj|ci) and p(wj|ci) are defined as softmax functions
| (6) |
Fig. 2.
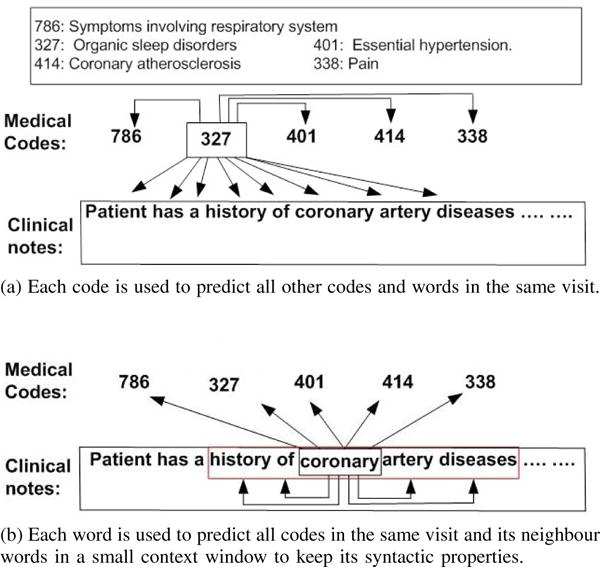
The framework of JointSkip-gram.
(a) Each code is used to predict all other codes and words in the same visit.
(b) Each word is used to predict all codes in the same visit and its neighbour words in a small context window to keep its syntactic properties.
Since we jointly learn vector representations of codes and words, matrices V ∈ ℝ(|W|+|C|)×T and U ∈ ℝ(|W|+|C|)×T include representations of both words and codes.
After scanning every code in D, JointSkip-gram proceeds by scanning the word sequence N. As shown in Fig. 2b, each scanned word wi in N is used to predict words within its context window of a predefined size q. Each scanned word wi is also used to predict all codes in D. The resulting log-likelihood of word wi can be expressed as
| (7) |
in which
| (8) |
Maximizing the sum of objective functions (5) and (7) over the whole set of visits in the dataset is computationally expensive since in (6) and (8), the denominators sum over all words in W and all codes in C. Like SGSN [5], we propose negative sampling version of JointSkip-gram. Instead of calculating softmax function, negative sampling method use computationally inexpensive sigmoid function to represent the probability that two words or codes are observed co-occurring in the dataset. For each scanned code ci, the negative sampling objective function becomes
| (9) |
where
| (10) |
Cneg = {ck ~ Pc|k=1, …, K} is the set of “negative codes” that are sampled from a frequency distribution Pc over the code vocabulary C and Wneg = {wk ~ Pw|k=1, …, K} is the set of “negative words” that are sampled from a frequency distribution Pw over the word vocabulary W, where K is the number of randomly generated negative samples. By maximizing (9), the objective is to increase the probabilities of co-occurring pairs p(ci, cj) and p(ci, wj) while decreasing the probabilities of random pairs p(ci, cN) and p(ci, wN).
Similarly, for each scanned word wi, the negative sampling objective criterion becomes:
| (11) |
where
| (12) |
Cneg and Wneg are the same as in (9). By maximizing (11), the probabilities of co-occurring pairs p(wi, wj) and p(wi, cj) will be large and the probabilities of random pairs p(wi, wN) and p(wi, cN) will be small.
Similarly to Skip-gram, stochastic gradient descent algorithm is applied to find vector representations of codes and words which maximize (9) and (11). Since JointSkip-gram represents codes and words in the same vector space, the words related to a given diagnostic code should be placed in its vicinity in the resulting vector space.
III. Experiments
A. Dataset description
MIMIC-III Dataset
The MIMIC-III Critical Care Database [22] is a publicly-available database which contains de-identified health records of 46, 518 patients who stayed in the Beth Israel Deaconess Medical Center’s Intensive Units from 2001 to 2012. The dataset contains both structured health records data and unstructured clinical notes data.
We used EHR data from all patients in the dataset. On average, each patient has 1.26 visits. For each visit, the average number of the recorded ICD-9 diagnosis codes is 11 and the average number of words in clinical notes is 7, 898. For each patient visit, we aggregated all diagnosis codes and clinical notes.
Preprocessing
For clinical notes, all digits and stop words are removed. The typos are filtered using PyEnchant, a Python library for spell checking. All words whose frequency is less than 50 are removed. The resulting number of unique words is 14, 302. Furthermore, the total number of unique ICD-9 diagnosis codes in the dataset is 6, 984. Codes whose frequency is less than 5 are removed. Since some codes are still relatively rare, we exploited the hierarchical tree structure of ICD-9 codes and grouped them by their first three digits. The size of final codes vocabulary is 752.
Training and Test Patients
We split the patients into training and test sets. All 38, 991 patients with a single visit are placed in the training set. Of the 7, 527 patients with 2 or more visits, we randomly assign 80% of them (6, 015 patients) to the training set and 20% of them (1, 512 patients) to the test set. Whole training set is used for learning representations.
JointSkip-gram training details
For each visit we created a (D, N) pair, as explained in II-A. The size T of vectors representing codes and words is set to 200. Stochastic gradient algorithm with negative sampling maximizing (9) and (11) is set to loop through all the training data 40 times. The number of negative samples is set to 5 and the size of the window for word context in the clinical notes is set to 5. Before applying JointSkip-gram model, we used a small portion (~10%) of clinical notes to pretrain word representations as we observed this improves our final representations.
To evaluate the quality of vector representations, we performed two types of experiments: (1) a qualitative evaluation of associations between codes and words in the vector space, (2) testing the predictive power of the vector representations on the task of predicting medical codes of the next visit. The following two subsections explain these experiments in detail.
B. Qualitative Evaluation
To evaluate how well JointSkip-gram represents words and medical codes in the joint vector space, we designed the following experiment. For a given ICD-9 diagnosis code, we retrieve 15 words which are its nearest neighbors in the vector space. The retrieved words are expected to be related to the ICD-9 code.
As an alternative to JointSkip-gram, we use labeled latent Dirichlet allocation (LLDA) [17], a supervised version of LDA [18]. In LLDA, there is a one-to-one correspondence between topics and labels. LLDA assumes there are multiple labels associated with each document and assigns each word a probability that it corresponds to each label. LLDA can be naturally adapted to our case by treating medical codes as labels and clinical notes as documents. For a given ICD-9 diagnosis code we retrieve 15 words with the highest probabilities and compare those words with the 15 words obtained by JointSkip-gram.
First, we selected 6 diverse ICD-9 codes in the EHR data that cover both acute and chronic diseases as well as common and less common diseases. Then, for each of the 6 ICD-9 codes, we found the most similar 15 words using JointSkip-gram and LLDA approaches. Table I shows the list of 15 selected words by both methods for the 6 ICD-9 codes. For each ICD-9 diagnosis code, we presented the two lists in a random order to a medical expert and asked two questions: (1) which list is a better representative of the diagnosis code, and (2) which words in each list are not highly related to the given diagnosis code. We recruited four physicians from the Fox Chase Cancer Center as medical experts for the evaluation.
TABLE I.
Most important 15 words (ranked by importance) for ICD-9 codes “570”, “174”, “295”, “348”, “311”, “042”. Disease description and frequency are listed in the brackets.
| 570 (Acute liver failure, 1067) | 174 (Female breast cancer, 139) | ||
|---|---|---|---|
|
| |||
| JointSkip-gram | LLDA | JointSkip-gram | LLDA |
|
| |||
| liver | arrest | metastatic | breast |
| hepatic | pea | mets | pres |
| cirrhosis | cooling | cancer | mastectomy |
| rising | sun | breast | flap |
| markedly | arctic | metastases | mets |
| shock | rewarmed | malignant | ca |
| lactate | cooled | metastasis | cancer |
| encephalopathy | atrophine | oncologist | metastatic |
| amps | dopamine | oncology | chemotherapy |
| picture | rewarming | chemotherapy | malignant |
| rise | cardiac | infiltrating | oncologist |
| elevated | coded | palliative | polumoprhic |
| cirrhotic | continue | tumor | reversible |
| bicarb | prognosis | melanoma | mastectomies |
| alcoholic | ems | mastectomy | crisis |
| 295 (Schizophrenic disorders, 691) | 348 (conditons of brain, 3781) | ||
|---|---|---|---|
|
| |||
| JointSkip-gram | LLDA | JointSkip-gram | LLDA |
|
| |||
| schizophrenia | schizophrenia | hemorrhagic | arrest |
| psych | paranoid | herniation | herniation |
| bipolar | psych | temporal | unresponsive |
| suicide | psychiatric | cerebral | corneal |
| psychiatry | disorders | brain | pupils |
| kill | personality | hemorrhage | brain |
| paranoid | hiss | parietal | cooling |
| ideation | guardian | ganglia | posturing |
| psychiatrist | psychiatry | occipital | head |
| hallucinations | hypothyroidism | extension | hemorrhage |
| psychosis | home | surrounding | noxious |
| personality | aloe | head | family |
| sitter | arrest | effacement | prognosis |
| disorder | pt | ataxia | pea |
| abuse | unresponsive | burr | gag |
| 311 (Depressive disorder, 3431) | 042 (HIV, 538) | ||
|---|---|---|---|
|
| |||
| JointSkip-gram | LLDA | JointSkip-gram | LLDA |
|
| |||
| patient | depression | aids | aids |
| abuse | tablet | viral | immunodeficiency |
| hallucinations | blood | fungal | virus |
| withdrawal | daily | opportunistic | human |
| ingestion | campus | bacterial | viral |
| questionable | mg | disseminated | load |
| thiamine | garage | immunodeficiency | cooling |
| remote | capsule | tuberculosis | partner |
| alcohol | building | organisms | acyclovir |
| significant | parking | herpes | thrush |
| overdose | one | undetectable | fevers |
| prior | discharge | acyclovir | induced |
| apparent | normal | detectable | antigen |
| depression | east | chlamydia | pneumonia |
| although | coherent | syphilis | blanket |
The evaluation results are summarized in Table II. As could be seen, all 4 experts agreed that JointSkip-gram words are a better representative for ICD-9 codes 570, 348, and 311. For the remaining 3 codes (174, 295, 042), the experts were split, but on none of them the majority went with the LLDA words. Looking at the average number of unrelated words identified by the experts, we can observe that the experts found much less unrelated words in the JointSkip-gram groups than in the LLDA groups for all 6 ICD-9 diagnosis codes. For ICD-9 code “570” (acute liver failure), JointSkip-gram finds “liver”, “hepatic”, “cirrhosis”, which are directly related to acute liver failure. Most other words in the JointSkip-gram list are indirectly related to liver failure, such as “alcoholic”, which explains one of the primary reasons for liver damage. On the other hand, LLDA can hardly capture related words, as evidenced by an average of 9.25 words that experts found unrelated. For ICD-9 code “174” (female breast cancer), “295” (Schizopherenic disorders) and “042” (HIV), both Joint-Skipgram and LLDA find highly representative words, although LLDA captures more unrelated words.
TABLE II.
Evaluation results by clinical experts.
| # of experts who think the method is better than the other | ||||||
|---|---|---|---|---|---|---|
|
| ||||||
| ICD-9 codes | 570 | 174 | 295 | 348 | 311 | 042 |
|
| ||||||
| JointSkip-gram | 4 | 2 | 3 | 4 | 4 | 2 |
| LLDA | 0 | 2 | 1 | 0 | 0 | 2 |
|
| ||||||
| Average # of unrelated words across experts | ||||||
|
| ||||||
| ICD-9 codes | 570 | 174 | 295 | 348 | 311 | 042 |
|
| ||||||
| JointSkip-gram | 2.25 | 0.75 | 0.75 | 1.25 | 3.25 | 0.75 |
| LLDA | 9.25 | 1.75 | 3 | 3.75 | 6.5 | 2.75 |
For code “311” (depressive disorder), both JointSkip-gram and LLDA have difficulties in finding related words. According to the feedback from one of our experts, only “abuse”, “hallucinations”, “alcohol”, “overdose”, “depression” and “thiamine” found by JointSkip-gram are related to the disease while only “depression”, “tablet”, “capsule” found by LLDA are recognizably related to depression. We hypothesize that for common diseases (e.g., “depression” and “hypertension”), which are not the primary diagnosis or relevant to treating the main reason for the ER visit, physicians are not likely to discuss them in clinical notes. Thus, it is difficult for any algorithm to discover words from clinical notes related to such diagnoses.
C. Predictive Evaluation
Another way to evaluate the quality of the vector representations of words and medical codes is through predictive modeling. We adopt the evaluation approach used in [23], which predicts medical codes of the next visit given the information from the current visit. In the previous work on this topic, the authors of [12], [23] used medical codes as features for prediction. In our evaluation, we use both medical codes and clinical notes to create predictive features. To generate a feature vector for the current visit, we find the average JointSkip-gram vector representation of the diagnosis codes in the current visit and the average JointSkip-gram vector representation of the words used in clinical notes. Then, we concatenate those two averaged vectors. We call this method Concatenation-JointSG, we compare it with the following five baselines:
Concatenation-One
We concatenate the one-hot vector of medical codes and the one-hot vector of clinical notes for each visit.
SVD
We apply singular vector decomposition (SVD) to Concatenation-One representations to generate dense representations of visits.
LDA
Using latent Dirichlet allocation (LDA) [18], each document is represented as a topic probability vector. This vector is used as the visit representation. To apply LDA, for each visit we create a document that consists of concatenation of a list of medical diagnosis codes and clinical notes. We note that LLDA is not suitable for this task since its topic only contains words.
Codes-JointSG
To evaluate the predictive power of medical codes, we create the features of the current visit as the average JointSkip-gram vector representation of the diagnosis codes.
Words-JoinSG
To evaluate the predictive power of clinical notes, we create the features of the current visit as the average JointSkip-gram vector representation of the words in clinical notes.
To test if JointSkip-gram vector representation have advantage over those of Skip-gram, in addition to the above five baselines, we trained Skip-gram on clinical notes and on medical codes separately. The resulting vector representations are not in the same vector space. We use Skip-gram representations to construct 3 more groups of features:
Codes-SG
The features of the current visit are the average Skip-gram vector representation of the diagnosis codes.
Words-SG
The features of the current visit are the average Skip-gram vector representation of the words in clinical notes.
Concatenation-SG
We concatenate the features from Codes-SG and Words-SG.
Given a set of features describing the current visit, we use softmax to predict medical codes of the next visit. We use Top-k recall [23] to measure the predictive performance. In the experiment, we test Top-k recall when k = 20, k = 30, and k = 40.
Training details
To create features for all proposed models (Skip-gram, JointSkip-gram, LDA, SVD), we use the training set. To train the Skip-gram model, we use 40 iterations, use 5 negative samples and the window size 5, the same as for JointSkip-gram. For SVD and LDA, we set the maximum number of iterations to 1000 to guarantee convergence. For JointSkip-gram, Skip-gram, SVD and LDA, we set the dimensionality of feature vectors to 200. To train the softmax model for next visit prediction, we use only patients with 2 or more visits in our training set. The softmax model are trained for 100 epochs using a stochastic gradient algorithm to minimize the categorical cross entropy loss function.
Table III shows the performance of softmax models that use different sets of features. A model using Concatenation-JointSG features outperforms other baselines in all three Top-k measures. The results also demonstrate that both medical codes and clinical notes in Concatenation-JointSG contribute to the prediction of future visit, since using the concatenation of word representations and code representations outperforms both Codes-JointSG and Words-JointSG.
TABLE III.
Performance of predicting medical codes of the next visit. The average and standard error of Top-k recall (k=20, 30, 40) are provided.
| Model | Top-20 recall | Top-30 recall | Top-40 recall |
|---|---|---|---|
|
| |||
| Concatenation-One | 0.489±0.004 | 0.590±0.004 | 0.661±0.004 |
| SVD | 0.478±0.004 | 0.588±0.004 | 0.652±0.004 |
| LDA | 0.431±0.004 | 0.530±0.004 | 0.605±0.004 |
| Codes-JointSG | 0.499±0.003 | 0.592±0.003 | 0.662±0.003 |
| Words-JointSG | 0.437±0.004 | 0.536±0.004 | 0.609±0.004 |
| Concatenation-JointSG | 0.506±0.003 | 0.599±0.003 | 0.670±0.003 |
Table IV shows a comparison between JointSkip-gram and Skip-gram features. In the table, features generated by JointSkip-gram outperforms their counterparts generated by Skip-gram. While the differences between Words-JointSG and Words-SG are not very large, Codes-JointSG and Concatenation-JointSG significantly outperform Codes-SG and Concatenation-SG, respectively. This indicates that JointSkip-gram not only captures the relationship between medical codes and words, but also learns improved word and code representations.
TABLE IV.
Top-k recall (k=20, 30 and 40) for JointSkip-gram and Skip-gram. The average and standard error are provided.
| Model | Top-20 recall | Top-30 recall | Top-40 recall |
|---|---|---|---|
|
| |||
| Codes-SG | 0.472±0.003 | 0.565±0.003 | 0.636±0.003 |
| Codes-JointSG | 0.499±0.003 | 0.592±0.003 | 0.662±0.003 |
|
| |||
| Words-SG | 0.432±0.004 | 0.532±0.004 | 0.605 ±0.004 |
| Words-JointSG | 0.437±0.004 | 0.536±0.004 | 0.609±0.004 |
|
| |||
| Concatenation-SG | 0.484±0.003 | 0.579±0.003 | 0.649±0.003 |
| Concatenation-JointSG | 0.506±0.003 | 0.599±0.003 | 0.670±0.003 |
IV. Conclusion
In this paper, we proposed JointSkip-gram algorithm to jointly learn representation of words from clinical notes and diagnosis codes in EHR. JointSkip-gram exploits the relationship between diagnosis codes and clinical notes in the same visit and represents them in the same vector space. The experimental results demonstrate that the resulting code and word representation places medical codes and words related to those codes in the vicinity of each other. They also show that the representations learned by the joint model are useful for construction of visit features. The future work should consider applying joint representations to a broader range of tasks, such as cohort identification. It will be worthwhile to explore more advanced prediction models such as deep neural networks.
Acknowledgments
This work was supported by the National Institutes of Health grants R21CA202130 and P30CA006927.
References
- 1.Ross MK, Wei W, Ohno-Machado L. “Big data” and the electronic health record. Yearbook of medical informatics. 2014;9(1):97. doi: 10.15265/IY-2014-0003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wu J, Roy J, Stewart WF. Prediction modeling using EHR data: challenges, strategies, and a comparison of machine learning approaches. Medical care. 2010;48(6):S106–S113. doi: 10.1097/MLR.0b013e3181de9e17. [DOI] [PubMed] [Google Scholar]
- 3.Jensen PB, Jensen LJ, Brunak S. Mining electronic health records: towards better research applications and clinical care. Nature reviews Genetics. 2012;13(6):395. doi: 10.1038/nrg3208. [DOI] [PubMed] [Google Scholar]
- 4.Yadav P, Steinbach M, Kumar V, Simon G. Mining Electronic Health Records: A Survey. ACM Computing Surveys. 2017 [Google Scholar]
- 5.Mikolov T, Sutskever I, Chen K, Corrado G, Dean J. Distributed representations of words and phrases and their compositionality. Proceedings of the 26th International Conference on Neural Information Processing Systems, NIPS13. 2013:31113119. [Google Scholar]
- 6.Moen H, Ginter F, Marsi E, Peltonen LM, Salakoski T, Salanter S. Care episode retrieval: distributional semantic models for information retrieval in the clinical domain. BMC medical informatics and decision making. 2015;15(2):S2. doi: 10.1186/1472-6947-15-S2-S2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wu Y, Xu J, Jiang M, Zhang Y, Xu H. AMIA Annual Symposium Proceedings. Vol. 2015. American Medical Informatics Association; 2015. A study of neural word embeddings for named entity recognition in clinical text; p. 1326. [PMC free article] [PubMed] [Google Scholar]
- 8.De Vine L, Zuccon G, Koopman B, Sitbon L, Bruza P. Proceedings of the 23rd ACM International Conference on Conference on Information and Knowledge Management. ACM; 2014. Medical semantic similarity with a neural language model; pp. 1819–1822. [Google Scholar]
- 9.Ghassemi MM, Mark RG, Nemati S. Computing in Cardiology Conference (CinC) Vol. 2015. IEEE; 2015. A visualization of evolving clinical sentiment using vector representations of clinical notes; pp. 629–632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Henriksson A. Representing clinical notes for adverse drug event detection. Association for Computational Linguistics. 2015 [Google Scholar]
- 11.Choi Y, Chiu CY, Sontag D. Learning low-dimensional representations of medical concepts. AMIA Summits on Translational Science Proceedings. 2016:123345. [PMC free article] [PubMed] [Google Scholar]
- 12.Choi E, Bahadori MT, Searles E, Coffey C, Sun J. Multi-layer representation learning for medical concepts. KDD. 2016 [Google Scholar]
- 13.Choi E, Schuetz A, Stewart WF, Sun J. Using recurrent neural network models for early detection of heart failure onset. Journal of the American Medical Informatics Association. 2017;24(2):361. doi: 10.1093/jamia/ocw112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gligorijevic DJ, Stojanovic J, Obradovic Z. Modeling healthcare quality via compact representations of electronic health records. Transactions on Computational Biology and Bioinformatics. 2016 doi: 10.1109/TCBB.2016.2591523. [DOI] [PubMed] [Google Scholar]
- 15.Pivovarov R, Perotte AJ, Grave E, Angiolillo J, Wiggins CH, Elhadad N. Learning probabilistic phenotypes from heterogeneous EHR data. Journal of biomedical informatics. 2015;58:156–165. doi: 10.1016/j.jbi.2015.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Joshi S, Gunasekar S, Sontag D, Joydeep G. Identifiable Phenotyping using Constrained Non-Negative Matrix Factorization. Machine Learning for Healthcare Conference. 2016:17–41. [Google Scholar]
- 17.Ramage D, Hall D, Nallapati R, Manning CD. Proceedings of the 2009 Conference on Empirical Methods in Natural Language Processing: Volume 1-Volume 1. Association for Computational Linguistics; 2009. Labeled LDA: A supervised topic model for credit attribution in multi-labeled corpora; pp. 248–256. [Google Scholar]
- 18.Blei DM, Ng AY, Jordan MI. Latent dirichlet allocation. Journal of machine Learning research. 2003 Jan;3:993–1022. [Google Scholar]
- 19.Chan KR, Lou X, Karaletsos T, Crosbie C, Gardos S, Artz D, Ratsch G. Data Mining Workshops (ICDMW), 2013 IEEE 13th International Conference on. IEEE; 2013. An empirical analysis of topic modeling for mining cancer clinical notes; pp. 56–63. [Google Scholar]
- 20.Arnold CW, El-Saden SM, Bui AA, Taira R. AMIA annual symposium proceedings. Vol. 2010. American Medical Informatics Association; 2010. Clinical case-based retrieval using latent topic analysis; p. 26. [PMC free article] [PubMed] [Google Scholar]
- 21.Ghassemi M, Naumann T, Doshi-Velez F, Brimmer N, Joshi R, Rumshisky A, Szolovits P. Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining. ACM; 2014. Unfolding physiological state: Mortality modelling in intensive care units; pp. 75–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Johnson AE, Pollard TJ, Shen L, Lehman LH, Feng M, Ghassemi M, Moody B, Szolovits P, Celi LA, Mark RG. MIMIC-III, a freely accessible critical care database. Scientific data. 2016;3 doi: 10.1038/sdata.2016.35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Choi E, Bahadori MT, Schuetz A, Stewart WF, Sun J. Doctor ai: Predicting clinical events via recurrent neural networks. Machine Learning for Healthcare Conference. 2016:301–318. [PMC free article] [PubMed] [Google Scholar]


