Abstract
Background:
Multiple methods are employed for modeling adaptation when projecting the impact of climate change on heat-related mortality. The sensitivity of impacts to each is unknown because they have never been systematically compared. In addition, little is known about the relative sensitivity of impacts to “adaptation uncertainty” (i.e., the inclusion/exclusion of adaptation modeling) relative to using multiple climate models and emissions scenarios.
Objectives:
This study had three aims: a) Compare the range in projected impacts that arises from using different adaptation modeling methods; b) compare the range in impacts that arises from adaptation uncertainty with ranges from using multiple climate models and emissions scenarios; c) recommend modeling method(s) to use in future impact assessments.
Methods:
We estimated impacts for 2070–2099 for 14 European cities, applying six different methods for modeling adaptation; we also estimated impacts with five climate models run under two emissions scenarios to explore the relative effects of climate modeling and emissions uncertainty.
Results:
The range of the difference (percent) in impacts between including and excluding adaptation, irrespective of climate modeling and emissions uncertainty, can be as low as 28% with one method and up to 103% with another (mean across 14 cities). In 13 of 14 cities, the ranges in projected impacts due to adaptation uncertainty are larger than those associated with climate modeling and emissions uncertainty.
Conclusions:
Researchers should carefully consider how to model adaptation because it is a source of uncertainty that can be greater than the uncertainty in emissions and climate modeling. We recommend absolute threshold shifts and reductions in slope. https://doi.org/10.1289/EHP634
Introduction
One of the direct public health risks posed by climate change is increased heat-related mortality and morbidity (Gosling et al. 2012; Hajat et al. 2014; Hales et al. 2014; Kingsley et al. 2016; Peng et al. 2011; Petkova et al. 2013, 2016; Sheridan et al. 2012; Vardoulakis et al. 2014; Wu et al. 2014) owing to increased occurrences of cardiovascular and chronic respiratory causes (Huynen and Martens 2015; Martens 1998; McMichael et al. 2006). Governments and community organizations around the world are increasingly allocating resources to prepare for a warmer future climate (Boeckmann and Rohn 2014). Central questions that should guide the decision-making process when making such investments include a) what are the likely health impacts of possible changes, and b) what are the interventions and programs, and the scale thereof, that offer the highest probability of reducing the magnitude of any adverse impacts? Answers to these questions depend in part on the extent to which populations may adapt to future climate change.
Adaptation mechanisms may occur through autonomous adaptation, such as physiological acclimatization and a range of behavioral adaptations such as dressing appropriately during hot weather. They may also occur through planned adaptation, such as the introduction of government subsidies to increase air conditioning installations or the introduction of heat health warning systems, or through public responses via health services such as changing prescription patterns and arranging home visits. Attempts to combine both autonomous and planned adaptation to represent the whole range of adaptation mechanisms and then to factor them into quantitative assessments of the impact of climate change on heat-related mortality by statistical modeling are largely based on liberal assumptions on the extent to which populations will adapt (Hayhoe et al. 2004; Honda et al. 2014b; Jenkins et al. 2014; Knowlton et al. 2007; Mills et al. 2014; Zacharias et al. 2015).
The potential to adapt is supported by a growing body of evidence that shows populations throughout the world are becoming less sensitive to high temperatures; for example, see reviews by Boeckmann and Rohn (2014) and Hondula et al. (2015). However, there is variation in the magnitude of the declines in sensitivity that have been observed between studies (e.g., Bobb et al. 2014; Schwartz et al. 2015; Todd and Valleron 2015), across locations (Gasparrini et al. 2015a), and over time (Åström et al. 2016). There are also overall limits to adaptation (Smith et al. 2014; Woodward et al. 2014) as, for example, air conditioning penetration reaches 100% or as physiological tolerance reaches biological limits. In addition, many studies neglect to unpick the factors that have driven declines in sensitivity to heat and whether the declines are due to autonomous or planned adaptation (Petkova et al. 2014b). Such omissions preclude an understanding of the policies that could help foster the most efficient adaptation practices. Multiple data sets on factors such as air conditioning penetration, human behavior, activation of heat health warnings, and changes in health care provision are needed to address this issue, but such data sets are rarely available at a sufficient temporal resolution (several decades) to elucidate the effects. The research needed to reveal these important insights will require an interdisciplinary approach that combines quantitative and qualitative methods.
Variation in the magnitude of observed declines in sensitivity to heat has limited the ability of researchers to investigate the effects of adaptation assumptions on projections of the impact of climate change. Thus, some researchers have not considered adaptation effects at all (e.g., Baccini et al. 2011; Hajat et al. 2014; Kingsley et al. 2016; Peng et al. 2011; Vardoulakis et al. 2014; Wu et al. 2014). Such an approach, however, which ignores what we refer to here as “adaptation uncertainty” (i.e., the sensitivity of impacts to including and excluding adaptation modeling respectively), is acknowledged to likely overestimate impacts (Huang et al. 2011; Martin et al. 2012; Petkova et al. 2013).
Within this context, a number of impact assessments have accounted for adaptation uncertainty by representing adaptation statistically in the modeling process, suggesting that impacts could be up to 30–80% (Jenkins et al. 2014; Sheridan et al. 2012) lower or more (Honda et al. 2014a) in the future with adaptation than without. Although the inclusion of adaptation may be considered an advantage over excluding it because it accounts for likely autonomous and planned adaptation, it is important that the modeling methods are justified robustly with reference to empirical evidence. An arbitrary assumption that populations might adapt by 100% (Honda et al. 2014a), for instance, could lead to underestimation of climate change impacts.
Statistical Methods for Modeling Adaptation
A variety of different statistical methods have been used to model adaptation. Six main methods can be employed (Table 1). In all but one study, where three of the methods were applied in the Netherlands (Huynen and Martens 2015), the six methods have been applied independently and have never been compared quantitatively, although an interesting discussion of the methods is presented by Kinney et al. (2008). Our study is distinct from all previous work because we compare all six methods across multiple European cities and because we consider multiple assumptions in the magnitudes of potential adaptation systematically for each method. We describe the six methods here and discuss their strengths and limitations.
Table 1.
Summary of statistical methods used to model adaptation in climate change impact assessments for heat-related mortality.
| Method | Summary | Strengths | Limitations | Studies that use the method |
|---|---|---|---|---|
| Absolute threshold shift | The absolute threshold temperature is shifted to a higher value under climate change, between and | Straightforward to apply | Magnitude of shift is arbitrarily defined without reference to epidemiological evidence | Dessai (2003) Gosling et al. (2009) Huynen and Martens (2015) Jenkins et al. (2014) |
| Relative threshold shift | The threshold, when defined as a percentile of the temperature distribution, is the same percentile under climate change as it is in the present (100% adaptation) | Straightforward to apply and supported by some (limited) empirical evidence | Informed by evidence from only a single empirical study (Honda et al. 2006) | Honda et al. (2014a) Honda et al. (2014b) Zacharias et al. (2015) |
| Reduction in slope of the exposure response function (ERF) | The slope of the ERF is reduced under climate change by up to 10% | Straightforward to apply | Magnitude of slope reduction is arbitrary and not straightforward to apply to nonlinear ERFs. | Huynen and Martens (2015) |
| Combined absolute threshold shift with reduction in slope of the ERF | The absolute threshold temperature is shifted to a higher value under climate and at the same time the slope of the ERF is reduced | Intuitive because it assumes that both the threshold and sensitivity to increasing heat will change under climate change | Magnitude of shift and slope reduction is arbitrary and not straightforward to apply to nonlinear ERFs | Huynen and Martens (2015) |
| Combined relative threshold shift with reduction in slope of the ERF | The relative threshold temperature is shifted to a higher value under climate, and at the same time, the slope of the ERF is reduced | Intuitive because it assumes that both the threshold and sensitivity to increasing heat will change under climate change | Magnitude of shift and slope reduction is arbitrary and not straightforward to apply to non-linear ERFs | Recommended by Huang et al. (2011) but not yet used in a climate change impact assessment. |
| Analog ERFs | Uses ERFs for locations with present temperatures similar to those projected to occur in the location of interest under climate change | Qualitatively informed by epidemiological evidence that populations in warmer/colder regions tend to be less/more sensitive to relatively higher temperatures (Davis et al. 2003) | Assumes that the underlying confounding factors that contribute to the ERF can be transferred to a different location | Hayhoe et al. (2004) Knowlton et al. (2007) Mills et al. (2014) |
Two methods are based on shifting the threshold temperature of an epidemiological exposure–response function (ERF). Many different conceptualizations of threshold temperatures are presented in the literature, including minimum mortality temperatures, optimum temperatures, and other derivations related to statistical differences in relative risk between baseline and extreme conditions (see Åström et al. 2016; Honda et al. 2014b; Petitti et al. 2016). Regardless of the specific statistical definition of the threshold, in general, the risks of heat-related mortality are lowest (or lower) at the threshold, whereas for temperatures higher than the threshold there is a proportionally higher risk (e.g., Baccini et al. 2008).
The “absolute threshold shift” method first defines the present-day threshold temperature in absolute terms () and then increases it in the future. Assessments have assumed shifts of the ERF in the future by up to (Jenkins et al. 2014), (Huynen and Martens 2015), (Dessai 2003) and (Gosling et al. 2009). This is perhaps the most straightforward method, which is why it has been used most frequently in previous studies. The magnitude of the shift tends to be selected arbitrarily and to be justified with no reference to empirical evidence from epidemiological studies.
The “relative threshold shift” method assumes “0% adaptation” when the threshold temperature in absolute terms (which is calculated originally as a percentile of the present-day daily temperature time series) is also used with the future time series. In contrast, “100% adaptation” is assumed when the threshold temperature for the future is at the same percentile value as that of the present day (the absolute value will therefore be higher in a warmer climate). The midpoint of the threshold temperatures between 0% and 100% adaptation is “50% adaptation.” Previous assessments have assumed 50% (Zacharias et al. 2015) and 100% adaptation (Honda et al. 2014a, 2014b). A caveat of this method is that the magnitude of shifts employed in the studies that use this method are based only upon changes in the threshold temperature observed in Tokyo between 1972 and 1994 (Honda et al. 2006).
Temperature-mortality ERFs are typically described by linear or nonlinear slopes that start from a threshold temperature. Accordingly, the third adaptation modeling method reduces the slope of the ERF in the future. Huynen and Martens (2015) assumed a 10% reduction in linear slope using this method. This method is intuitive because it is plausible that populations may become less sensitive to high temperatures under climate change, which would manifest as a reduction in the slope of the ERF. However, Huynen and Martens (2015) acknowledge that the 10% decline in slope that they applied is hypothetical, and they do not provide empirical evidence to support it. The method is straightforward to apply to a linear ERF but considerably more complicated for a nonlinear ERF.
The fourth and fifth methods combine shifts in the threshold with reductions in the slope. Huynen and Martens (2015) assumed a reduction in the slope of the ERF by 10% and combined this with absolute threshold shifts. No studies have yet combined a relative threshold shift with a reduction in slope despite encouragement that studies should combine shifts with reductions in slope (Huang et al. 2011).
The sixth method uses “analog ERFs,” that is to say, ERFs derived for locations with temperatures similar to those projected to occur in the future in the location of interest. Although the method has been criticized (Kinney et al. 2008), and although it assumes that the underlying confounding factors that contribute to the ERF can be transferred to a different location, it is popular (Hayhoe et al. 2004; Knowlton et al. 2007; Mills et al. 2014) because it draws upon epidemiological evidence that populations in warmer/colder regions tend to be less/more sensitive to relatively higher temperatures (Davis et al. 2003).
A caveat that runs through all the methods employed in previous work is that they are not supported with reference to specific empirical evidence that confirms the magnitudes of adaptation assumed. The only exception is that the relative threshold shift method has been justified with reference to the observation that threshold temperatures can generally be estimated using the 80–th percentile of the daily maximum temperature in multiple locations in Japan (Honda et al. 2007, 2014b). It would of course be preferable to replicate this observation across other locations. A novel opportunity exists to develop adaptation modeling methods based upon empirical evidence of historical adaptation because a growing body of evidence shows that in some cities and countries, populations are becoming less sensitive to extremes of heat (Arbuthnott et al. 2016; Åström et al. 2013, 2016; Bobb et al. 2014; Gasparrini et al. 2015b; Honda et al. 2006; Schwartz et al. 2015). The mechanisms associated with and driving this decline are a matter of debate, but it is clear from these studies that population sensitivity to heat can and does vary over time. Therefore, it is somewhat surprising that there has been no significant advancement in the statistical methods used to model adaptation over the past decade; the methods used ago are still being used now (Table 1).
Current Research Gaps
The application of multiple adaptation modeling methods across different climate change impact studies means that there is no clear understanding of the relative effects that each method can have on the impacts. Nor is there a recommendation of what method is most appropriate for application (Huang et al. 2011). This problem is compounded by the general lack of rationale for the adaptation methods chosen in past studies. Some methods have been used more frequently than others: for example, absolute threshold shifts (Table 1), perhaps because they are more straightforward to apply than some of the other methods.
The use of different Global Climate Models (also known as General Circulation Models; GCMs) and emissions scenarios in climate change impact assessments enables an evaluation of the sensitivity of the impacts to both “climate model uncertainty” and “emissions uncertainty” (Gosling et al. 2012; Hajat et al. 2014; Peng et al. 2011; Zacharias et al. 2015). Although a limited number of impact studies have included multiple GCMs, emissions scenarios, and adaptation assumptions together in the modeling exercise to account for these three key uncertainties (Gosling et al. 2009; Petkova et al. 2016; Sheridan et al. 2012), such a holistic approach is uncommon (Huang et al. 2011). To this end, little is known about the relative contributions of these three sources of uncertainty to ranges in projections of heat-related mortality impacts.
To address these important research gaps, our study had three main objectives. Firstly, we conducted the first systematic comparison of the range in projected impacts that arises from using different adaptation modeling methods employed in previous studies; secondly, we compared the range in impacts that arises from adaptation uncertainty (i.e., impacts with the inclusion/exclusion of adaptation) to the respective ranges from climate modeling and emissions uncertainty; and thirdly, we aimed to provide the first recommendation of one or several adaptation modeling methods to use in future impact assessments.
Methods
Experimental Design
We estimated the mean annual warm season (1 April to 30 September) heat-related mortality rate attributable to climate change () across 14 European cities (see Table 2) under the assumption that populations will not adapt in the future, that is, “no adaptation.” We then estimated the impacts using six different methods for modeling adaptation. In all cases, the impacts were estimated using climate projections from one GCM (HadGEM2-ES) that was run under a single emissions scenario [Representative Concentration Pathway (RCP) 8.5] to control for the effects of climate modeling and emissions uncertainty. We chose RCP8.5 because it is the highest of the four RCP emissions scenarios commonly used in climate modeling (Riahi et al. 2011), meaning that it should enhance elucidation of the effects of modeling adaptation with different methods under a plausible emissions scenario. This approach enabled calculation of the range in impacts that arises from estimating them with adaptation and with no adaptation.
Table 2.
Components of the Exposure Response Functions (ERFs) applied in this study, which are based on model estimates derived by Baccini et al. (2008).
| City | Threshold temperature () | Total population | Baseline daily mortality rate (per 100,000) | Relative risk (RR) | Concentration response factor (CRF) |
|---|---|---|---|---|---|
| Athens | 32.7 | 3188305 | 2.12 | 1.0554 | 0.054 |
| Barcelona | 22.4 | 1512971 | 2.37 | 1.0156 | 0.015 |
| Budapest | 22.8 | 1797222 | 3.95 | 1.0174 | 0.017 |
| Helsinki | 23.6 | 955143 | 1.79 | 1.0372 | 0.037 |
| Ljubljana | 21.5 | 263290 | 2.39 | 1.0134 | 0.013 |
| London | 23.9 | 6796900 | 2.19 | 1.0154 | 0.015 |
| Milan | 31.8 | 1304942 | 2.02 | 1.0429 | 0.042 |
| Paris | 24.1 | 6161393 | 1.88 | 1.0244 | 0.024 |
| Prague | 22 | 1183900 | 2.95 | 1.0191 | 0.019 |
| Rome | 30.3 | 2812573 | 1.88 | 1.0525 | 0.051 |
| Stockholm | 21.7 | 1173183 | 2.38 | 1.0117 | 0.012 |
| Turin | 27 | 901010 | 2.12 | 1.0332 | 0.033 |
| Valencia | 28.2 | 739004 | 1.98 | 1.0056 | 0.006 |
| Zurich | 21.8 | 990000 | 1.17 | 1.0137 | 0.014 |
We also estimated impacts with no adaptation using climate projections from five GCMs run under RCP8.5 to explore the effect of climate modeling uncertainty while controlling for adaptation and emissions uncertainty. Furthermore, we estimated impacts with HadGEM2-ES run under low (RCP2.6) and high (RCP8.5) emissions scenarios to explore the effect of emissions uncertainty while controlling for adaptation and climate modeling uncertainty. The experimental design is summarized in Table 3.
Table 3.
Summary of the experimental design, showing the adaptation modeling methods compared and the Global Climate Models (GCMs) and emissions scenarios used.
| Rationale | Range in impacts from adaptation uncertainty, controlling for climate modeling and emissions uncertainty | Range in impacts from climate modeling uncertainty, controlling for adaptation and emissions uncertainty | Range in impacts from emissions uncertainty, controlling for adaptation and climate modeling uncertainty | ||||||
|---|---|---|---|---|---|---|---|---|---|
| GCMs | HadGEM2-ES | HadGEM2-ES, IPSL-CM5A-LR, MIROC-ESM-CHEM, GFDL-ESM2, NorESM1-M | HadGEM2-ES | ||||||
| Emissions scenarios | RCP8.5 | RCP8.5 | RCP2.6, RCP8.5 | ||||||
| Number of climate model simulations | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 5 | 2 |
| Adaptation modeling method | No adaptation | Absolute threshold shift (“Thresh ”) | Relative threshold shift (“Thresh %”) | Reduction in slope of the ERF (“Slope”) | Combined absolute threshold shift with reduction in ERF slope () | Combined relative threshold shift with reduction in ERF slope () | Analog ERFs (“Analog”) | No adaptation | No adaptation |
| Magnitude of adaptation investigated | None | 25% | 5% | All 20 possible combinations | All 20 possible combinations | Use ERF from analog city | None | None | |
| 50% | 10% | ||||||||
| 75% | 15% | ||||||||
| 100% | 20% | ||||||||
| 25% | |||||||||
Note: ERF, Exposure Response Function; RCP, Representative Concentration Pathway; Sens, sensitivity; Thresh, threshold.
The 14 cities were chosen because ERFs that were developed using the same methodology for each city were available (Baccini et al. 2008). Thus, we had a consistent set of ERFs upon which to test the sensitivity of climate change impacts to adaptation assumptions.
Climate Change Projections
Time series of daily maximum temperature (), mean temperature (), and mean relative humidity (RH) were extracted for the grid cells located closest to each city for the present day (1981–2010) and for the future (2070–2099) from five GCM simulations (HadGEM2-ES GCM, IPSL-CM5A-LR, MIROC-ESM-CHEM, GFDL-ESM2, and NorESM1-M). This set of GCMs has been used in numerous impact assessments to demonstrate the range in impacts that can arise from climate modeling uncertainty (Warszawski et al. 2014).
Each GCM was run under RCP8.5 (high emissions) and RCP2.6 (low emissions) because these are the highest and lowest emissions scenarios, respectively, commonly used in climate modeling that are available from the four RCP emissions scenarios (Riahi et al. 2011). By using the highest and lowest emissions scenarios, we were able to investigate the maximum extent to which emissions scenario choice contributes to the uncertainty in projected heat-related mortality impacts.
The climate variables were bias-corrected towards an observation-based data set (Weedon et al. 2011) using an established method (Hempel et al. 2013) specifically designed to preserve long-term trends in temperature projections in order to facilitate climate change impact assessments. The GCM data could therefore be used for the present-day and future time periods in the impact assessment.
The ERFs we used (Baccini et al. 2008) required daily maximum apparent temperature (), which was computed as follows:
| [1] |
where is the daily mean dew point computed from and following the method described by Tetens (1930). For Barcelona, the daily mean apparent temperature () had to be calculated because the ERF for Barcelona required this instead of . Therefore, we calculated daily by replacing with in Equation 1.
Heat-Related Mortality Estimation
We applied city-specific linear ERFs derived from Baccini et al. (2008) for each of the 14 cities. The ERFs describe linear relationships between daily ( for Barcelona) and daily heat-related mortality in terms of relative risk (RR). RRs were reported by Baccini et al. (2008) as a percentage change in mortality per above the city-specific threshold temperature. We converted the RRs to RR ratios from
| [2] |
, the concentration-response factor [CRF, the estimated slope of the linear relationship between ( for Barcelona) and daily heat-related mortality] was derived from the following:
| [3] |
where is a change in daily ( for Barcelona) above the threshold temperature. The RRs, CRFs and threshold temperatures for each city are displayed in Table 2.
Daily heat-related mortality for each city was then calculated from the city-specific ERFs for the present day (1981–2010) and for the future (2070–2099). For both the present day and the future, we first calculated the daily attributable fraction, AF, which is the fraction of the mortality burden attributable to the risk factor [daily ( for Barcelona) above the threshold temperature], for the exposed population. Following the methods described in previous studies, it was assumed that the whole population at the threshold temperature is exposed (Huynen and Martens 2015; Knowlton et al. 2007; Schwartz et al. 2015; Vardoulakis et al. 2014):
| [4] |
Following an established method, the AF was multiplied by the baseline daily mortality rate (, Table 2) and the exposed population (Pop; Table 2) to yield the absolute number of daily heat-related deaths (Mort) for both the present day and the future (Hajat et al. 2014; Huynen and Martens 2015; Knowlton et al. 2007; Peng et al. 2011; Petkova et al. 2013; Schwartz et al. 2015; Vardoulakis et al. 2014; Wu et al. 2014), as follows:
| [5] |
Mort was calculated only for the warm season () because the ERFs were derived for these months only (Baccini et al. 2008). was then calculated by converting Mort into a mortality rate (per 100,000, using Pop) and then subtracting it for the present-day time period from the estimate for the future time period.
We did not change and Pop between time periods, in line with previous studies (e.g., Gosling et al. 2012; Petkova et al. 2013; Wu et al. 2014), because estimation of as a rate instead of as absolute deaths facilitates comparisons across GCMs, emissions scenarios, different cities, and different methods for modeling adaptation. Application of population projection scenarios [e.g., the shared socioeconomic pathways (SSPs), O’Neill et al. (2014)] would yield different absolute numbers of deaths between population scenarios but not different estimates of .
Modeling Adaptation
We investigated the sensitivity of to the six main adaptation modeling methods that we discussed earlier. was estimated for each of the 14 cities for each method separately (Table 3).
Absolute threshold shifts in the ERF of 1, 2, 3, and were investigated to cover the range of shifts employed in past studies using this method (Dessai 2003; Gosling et al. 2009; Huynen and Martens 2015; Jenkins et al. 2014).
For relative threshold shifts, we shifted the ERFs by 25, 50, 75, and 100% because these values cover the range of values used in past studies (Honda et al. 2014a, 2014b; Zacharias et al. 2015).
We reduced the slope of the ERF by 5, 10, 15, 20, and 25%. The 10% value was chosen in line with Huynen and Martens (2015), but because no other study has used this method, we also considered reductions of to provide an indication of what might result from other assumed selected reductions in slope.
Absolute threshold shifts (1, 2, 3, and ) and relative threshold shifts (25, 50, 75, and 100%) were each combined with reductions in the slope of the ERF (5, 10, 15, 20, and 25%).
Previous studies have paired locations for the analog ERF method by comparing mean annual temperatures (Knowlton et al. 2007), mean summer temperatures (Hayhoe et al. 2004), or maximum summer temperatures (Mills et al. 2014) between present-day and future time periods for multiple locations, but these approaches do not account for the whole statistical distribution of temperatures. This is a significant limitation because it is the extremes of temperature, as well as the mean, that are important for heat-related mortality.
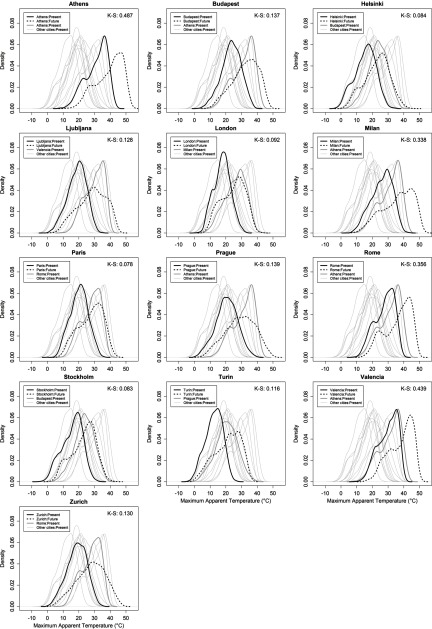
Therefore, we developed a more advanced approach that better accounts for the shapes of the temperature distributions between two cities. We created analog city pairs based on the projected probability distribution functions (PDFs) of warm-season daily . The best “match” for each city’s future climate was determined by performing a comparison of the nonparametric Kolmogorov–Smirnov (K-S) test statistic (Massey 1951) between present-day and future temperature distributions. The K-S test statistic is a measure of the maximum distance between two continuous distribution functions. For 13 cities (Barcelona was excluded here because it was the only city not to use in its ERF), the city whose present-day distribution that had the lowest test statistic when compared with an individual city’s future distribution was selected as a match. For example, the projected climate of London was found to be most similar to that of present-day Milan (out of the 12 possible options) (Figure 1; see also Table S1); thus, for London was computed using the London climate change projections as input to the Milan ERF.
Figure 1.
PDFs of present-day distributions for each city (solid black line); the future distribution under climate change as simulated by Global Climate Model HadGEM2-ES under Representative Concentration Pathway (RCP) 8.5 for the same city (dashed black line) and all other cities (solid thin gray lines); and for the same city, the distribution for the city that under climate change is best matched to it (solid thick gray line) according to the Kolomorgorov–Smirnov (K-S) statistic (displayed in the top right of each panel; K-S statistics for all possible matches are displayed in Table S1).
Results
Comparison of Impacts between Adaptation Modeling Methods
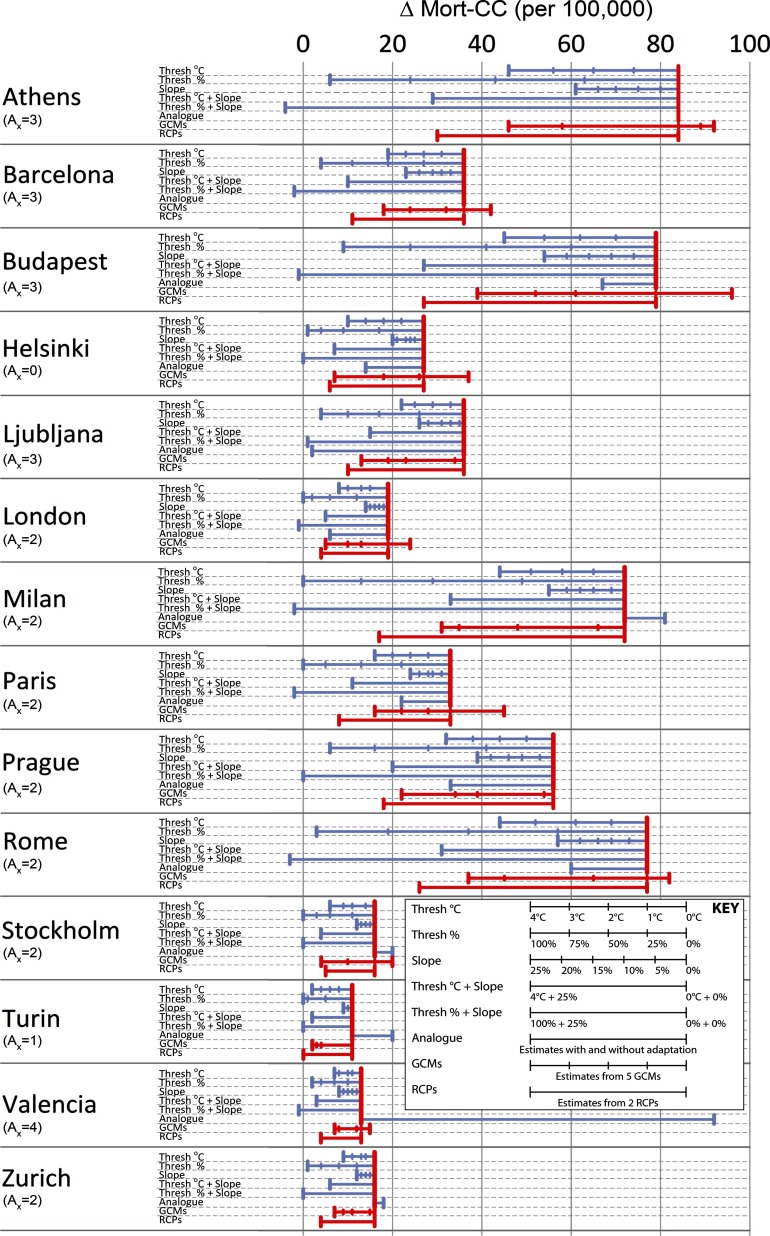
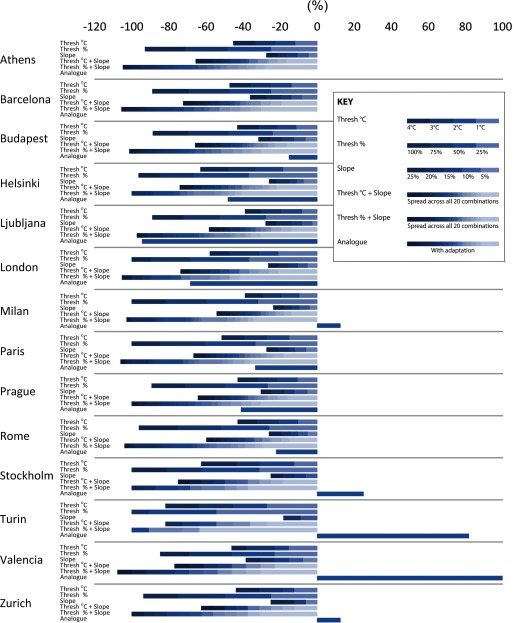
Figure 2 shows the range in impacts (per 100,000) for each city that result from including and excluding adaptation, and Figure 3 shows the difference (percent) in impacts between including and excluding adaptation for each adaptation modeling method. These two figures show that there are large contrasts in the ranges of impacts between the different adaptation modeling methods.
Figure 2.
Mean annual warm season heat-related mortality rates (per 100,000) attributable to climate change () for 2070–2099 using climate change projections from Global Climate Model (GCM) HadGEM2-ES run under Representative Concentration Pathway (RCP) 8.5, when different adaptation modeling methods are applied. Also displayed is with climate change projections from five GCMs run under RCP8.5 with no adaptation (“GCMs”), and with climate change projections from HadGEM2-ES run under two emissions scenarios (RCP2.6 and RCP8.5) with no adaptation (“RCPs”). Blue lines and whiskers denote where impacts have been estimated with adaptation modeling methods employed and red lines and whiskers denote where impacts have been estimated with no adaptation. denotes the number of adaptation modeling methods that have a range that is greater than or equal to the range for GCMs and/or RCPs. The ranges are quantitatively summarized in Table 4.
Figure 3.
Differences (percent) between estimating with each adaptation modeling method and with no adaptation. All estimates are for 2070–2099 with climate change projections from the Global Climate Model (GCM) HadGEM2-ES run under Representative Concentration Pathway (RCP) 8.5. The axis labels are the same as in Figure 2. This is not a stacked bar graph: The values should be read from the left (right) of each box if they are left (right) of zero. No analog projection is available for Athens because the city was its own match in the comparison of current and future temperature distributions; no analog projection is available for Barcelona because a different exposure variable was used for projections for Barcelona than for the other study cities.
The contrasts are highlighted in Table 4, which shows, as a mean across all 14 cities, the range of the difference (percent) in impacts between including and excluding adaptation. The ranges are 49% (absolute threshold shift), 94% (relative threshold shift), 28% (reduction in slope of the ERF), 68% (absolute threshold shift combined with a reduction in slope of the ERF), 103% (relative threshold shift combined with a reduction in slope of the ERF), and 76% (analog ERF).
Table 4.
Statistical ranges (maximum minus minimum values of the distribution) of the differences (%) between estimating with the upper limit of each adaptation modeling method (shown in parentheses) and with no adaptation.
| City | Absolute threshold shift () | Relative threshold shift () | Reduction in the slope of the ERF () | Absolute threshold shift combined with reduction in slope of ERF () | Relative threshold shift combined with reduction in slope of ERF () | Analog ERF (Analog) |
|---|---|---|---|---|---|---|
| Athens | 44 | 93 | 27 | 66 | 105 | 0 |
| Barcelona | 48 | 89 | 36 | 72 | 106 | 0 |
| Budapest | 42 | 89 | 32 | 66 | 101 | 15 |
| Helsinki | 61 | 96 | 26 | 74 | 100 | 48 |
| Ljubljana | 40 | 89 | 28 | 58 | 97 | 94 |
| London | 58 | 100 | 26 | 74 | 105 | 68 |
| Milan | 37 | 100 | 24 | 54 | 103 | 13 |
| Paris | 51 | 100 | 27 | 67 | 106 | 33 |
| Prague | 43 | 89 | 30 | 64 | 100 | 41 |
| Rome | 42 | 96 | 26 | 60 | 104 | 22 |
| Stockholm | 62 | 100 | 25 | 75 | 100 | 25 |
| Turin | 79 | 100 | 18 | 82 | 100 | 82 |
| Valencia | 45 | 85 | 38 | 77 | 108 | 608 |
| Zurich | 40 | 94 | 25 | 63 | 100 | 13 |
| Mean | 49 | 94 | 28 | 68 | 103 | 76a |
Note: The values describe the width of each bar in Figure 3. , heat-related mortality rate attributable to climate change; ERF, Exposure Response Function; Thresh, threshold.
if the result for Valencia (608) is removed.
Combining a relative threshold shift with a reduction in the ERF was associated with the largest ranges in impacts across all the methods for all cities except Valencia. Relative threshold shifts were associated with the second-largest ranges in impacts. For example, with relative threshold shifts of 50% (100%), declined from 84, 79, 72, and 77 deaths per 100,000 under no adaptation to 43 (6), 41 (9), 29 (0) and 37 (3) deaths per 100,000 with adaptation for Athens, Budapest, Milan, and Rome, respectively (Figure 2). In terms of the difference (percent) in impacts between including and excluding adaptation (Figure 3), these are equivalent to 49% (93%), 48% (89%), 60% (100%), and 52% (96%) respectively (Figure 3). In five cities, a relative threshold shift of 100% resulted in reaching zero (London, Milan, Paris, Stockholm, Turin); that is to say, climate change had no effect on heat-related mortality with adaptation.
Across the methods we considered, the smallest ranges in impacts occurred with reducing the slope of the ERF. For all cities, the differences in impacts between adaptation and no adaptation were when the slope was reduced by the maximum amount we considered (25% reduction in slope; see Figure 3).
The methods we investigated generally had similar effects on across cities; in other words, increasing the thresholds in the increments we considered from to and from 0% to 100% and reducing the slope by 0–25% were all associated with broadly linear declines in as the magnitude of assumed adaptation increased (Figure 2). The analog ERF method, however, resulted in more disparate estimates of . There were large differences between adaptation and no adaptation for some cities. For Ljubljana and London, was 36 and 19 deaths per 100,000, respectively, with no adaptation and 2 and 6 deaths per 100,000, respectively, with adaptation (Figure 2). This is equivalent to differences of 94% (Ljubljana) and 68% (London) between adaptation and no adaptation (Figure 3). However, for other cities, the use of analog ERFs resulted in greater with adaptation than without: for example, for Stockholm, Turin, and Valencia, where was 16, 11, and 13 deaths per 100,000, respectively, without adaptation and 20, 20, and 92 deaths per 100,000, respectively, with adaptation (Figure 2).
Comparison of Adaptation, Emissions, and Climate Modeling Uncertainty
Table 5 shows the effects of adaptation, emissions, and climate modeling uncertainties on projected impacts. It compares the largest range in impacts from all the adaptation modeling methods we investigated with a) the range in impacts from using 1 GCM run under two emissions scenarios without adaptation, and b) with the range in impacts from 5 GCMs run under one emissions scenario without adaptation. The range in impacts that arose from adaptation modeling uncertainty was greater than the range that arose because of emissions uncertainty for every city. It was also greater than the range that arose because of climate modeling uncertainty for 13 of 14 cities. These differences were considerable in some cases; for example, for Athens, Budapest, and Rome, the ranges due to adaptation uncertainty were 88, 80, and 80 deaths per 100,000, respectively, whereas for climate modeling uncertainty, they were 46, 57, and 45 deaths per 100,000 respectively.
Table 5.
Statistical ranges (maximum minus minimum values of the impact distribution) and spread (minimum to maximum values that constitute the range, in parentheses) of impacts (per 100,000) due to adaptation modeling uncertainty (calculated from the largest range in impacts from all the adaptation modeling methods investigated), climate modeling uncertainty (spread and range for 5 GCMs with no adaptation), and emissions uncertainty (spread and range for two RCPs with one GCM and with no adaptation).
| City | Range in impacts due to adaptation modeling uncertaintya | Adaptation modeling method that results in largest spread | Range in impacts due to climate modeling uncertainty | Range in impacts due to emissions uncertainty |
|---|---|---|---|---|
| Athens | 46 (46–92) | 54 (30–84) | ||
| Barcelona | 24 (18–42) | 25 (11–36) | ||
| Budapest | 57 (39–96) | 52 (27–79) | ||
| Helsinki | 27 (0–27)b | 30 (7–37)b | 21 (6–27) | |
| Ljubljana | 35 (1–36) | 23 (13–36) | 26 (10–36) | |
| London | 19 (5–24) | 15 (4–19) | ||
| Milan | 41 (31–72) | 55 (17–72) | ||
| Paris | 29 (16–45) | 25 (8–33) | ||
| Prague | 56 (0–56) | 34 (22–56) | 38 (18–56) | |
| Rome | 45 (37–82) | 51 (26–77) | ||
| Stockholm | 16 (0–16) | 16 (4–20) | 11 (5–16) | |
| Turin | 11 (0–11) | 9 (2–11) | 11 (0–11) | |
| Valencia | 79 (13–92) | Analog | 8 (7–15) | 9 (4–13) |
| Zurich | 16 (0–16) | 9 (7–16) | 12 (4–16) |
Note: The range values describe the width of each bar in Figure 2. , heat-related mortality rate attributable to climate change; GCM, Global Climate Model; RCP, Representative Concentration Pathway; Thresh, threshold.
Negative values denote that fewer deaths occur in the future with climate change than in the present-day.
The range in impacts due to adaptation modeling uncertainty is smaller than the range due to either climate modeling or emissions uncertainty.
The large ranges due to adaptation uncertainty were associated with a relative threshold shift combined with a reduction in ERF slope in all but one city (Valencia) (Table 5). Application of some of the other methods also resulted in ranges that were larger than those from climate modeling and emissions uncertainty (denoted by in Figure 2) because for 12 cities, was , with such cases usually involving the relative threshold shift method.
For all cities, the range in impacts from using an absolute threshold shift was smaller than the range from using multiple GCMs and/or RCPs (Figure 2). The ranges were larger when absolute threshold shifts were combined with reductions in ERF slope, but apart from three cities (Athens, Barcelona, and Valencia) the ranges were smaller than those from using multiple GCMs or RCPs. For all cities except Ljubljana and Valencia, the range in impacts from using analog ERFs was smaller than the range from using multiple GCMs and multiple RCPs (Figure 2).
Discussion
Application of Linear ERFs
We used city-specific ERFs that described linear relationships between daily apparent temperature and mortality in the form of a slope. They were derived from a set of nonlinear curves developed from a flexible parametric approach presented by Baccini et al. (2008) (their Figure 1). Baccini et al. (2008) summarized their nonlinear relationships by two linear terms constrained to join at a common point (the city-specific thresholds). They obtained the thresholds by the maximum likelihood approach proposed by Muggeo (2003) so that a linear slope above the threshold was used as an effect estimate for each city; these were used as the ERFs in our study. As others have noted (Kingsley et al. 2016), the summarized association between mortality and temperature per increment in temperature ( in this case) differs depending on where along the exposure–response curve one starts for nonlinear exposure–response relationships such as those defined by Baccini et al. (2008). For a highly nonlinear curve, the strength of the temperature–mortality response might be higher further along the curve where its gradient is larger (i.e., at higher temperatures) than it might be closer to the threshold where the gradient is smaller. Baccini et al. (2008) started from the threshold temperature when computing their effect estimates, so if their curves were highly nonlinear, it would be fair to assume that we under-estimated the climate change effects of temperature on heat-related mortality. However, visual inspection of the curves presented by Baccini et al. (2008) suggests that the curves are broadly linear beyond the threshold temperatures. Therefore, we did not calculate climate change impacts with nonlinear ERFs.
A goal of our study was to provide a point of reference to the sensitivity of climate change impacts to different adaptation modeling methods for researchers conducting climate change impact assessments for heat-related mortality. Considering that almost all previous assessments used linear ERFs derived from estimates of RR for an increase in temperature above a specific value (Baccini et al. 2011; Hajat et al. 2014; Peng et al. 2011; Petkova et al. 2013; Schwartz et al. 2015; Vardoulakis et al. 2014; Wu et al. 2014), we also used linear ERFs because it is likely that future studies will do so as well. Thus, our conclusions should be readily interpretable by the community. This is another reason why we did not calculate impacts with nonlinear ERFs. In addition, the application of linear ERFs makes it straightforward to apply simple changes in slope and location to represent adaptation. The potential gains of using nonlinear associations would be outweighed by the increased complexity in implementing adaptation options.
The algorithm described by Muggeo (2003) and used by Baccini et al. (2008) for the threshold temperature estimation can be unstable. This instability means that the linear relationship we used can be sensitive to the threshold. We did not investigate the sensitivity of our estimated impacts to the threshold because our goal was to demonstrate the sensitivity of impacts to adaptation methods. The drawback of this algorithm may be accounted for by using different starting points for each temperature and lag structure when running the algorithm (Rodopoulou et al. 2015).
Our projected impacts are not only a function of the projected climate but also of the baseline mortality rate, which appears in Equation 5. The sensitivity of impacts to baseline mortality values has been noted by others (Baccini et al. 2011). We controlled for this in our experimental design by holding the baseline mortality rate constant between present and future periods, in line with others (e.g., Gosling et al. 2012; Peng et al. 2011; Petkova et al. 2013; Wu et al. 2014), to isolate the effects of climate modeling, emissions, and adaptation modeling uncertainties on the impact estimates. Changing the baseline mortality rates between the future and the present would affect the projected absolute number of deaths because some future deaths would be attributable to changes in the baseline mortality rate, but it would not affect the mortality rates attributable to climate change ().
Some studies have calculated the baseline mortality rate either from daily mortality excluding deaths attributable to temperature (Hajat et al. 2014) or from mortality on nonheatwave days (Peng et al. 2011; Wu et al. 2014), meaning that the baseline mortality rate is representative of the mortality rate of the exposed population at the threshold temperature. Others have calculated the baseline mortality rate from the total number of deaths (Baccini et al. 2011; Huynen and Martens 2015; Petkova et al. 2013; Schwartz et al. 2015; Vardoulakis et al. 2014), which means that it is representative of the whole exposed population year-round (i.e., at the threshold temperature and at temperatures above the threshold). We employed the last approach simply because it is more commonly adopted, but we acknowledge that it would be useful in future work to investigate quantitatively the effect of calculating the baseline mortality rate with different methods.
Impacts Are Highly Sensitive to Adaptation Modeling Methods
Our first objective was to compare the range in projected impacts that arises from using different adaptation modeling methods. All previous assessments of the impacts of climate change on heat-related mortality have modeled adaptation with only one method (e.g., Hayhoe et al. 2004; Honda et al. 2014b; Jenkins et al. 2014; Knowlton et al. 2007; Mills et al. 2014; Zacharias et al. 2015), excluded it altogether (e.g., Baccini et al. 2011; Hajat et al. 2014; Kingsley et al. 2016; Peng et al. 2011; Vardoulakis et al. 2014; Wu et al. 2014), or, in one case, provided a comparison of impacts using only a subset of the range of modeling methods available (Huynen and Martens 2015). Here, for the first time, we have used multiple adaptation modeling methods with different assumed magnitudes of adaptation, and we have shown that the ranges in projected impacts vary significantly according to the adaptation modeling method that is employed.
This significant sensitivity is well illustrated with an example. Electing to model adaptation with a absolute threshold shift for Milan would suggest that the least effect climate change will have on heat-related mortality is an additional 44 heat-related deaths (per 100,000) each year compared with the present day (Figure 2). However, modeling adaptation with a different method (relative threshold shift with a reduction in ERF slope) suggests that there will be 2 (per 100,000) fewer deaths each year with climate change than in the present day. This magnitude of impact is only observed if this specific adaptation modeling method is applied. Such an effect does not occur with any of the other adaptation modeling methods, nor does it occur under a low-emissions (RCP2.6) scenario or when multiple GCMs are considered without adaptation, wherein the smallest effects climate change will have on heat-related mortality are an additional 17 and 31 annual heat-related deaths (per 100,000), respectively.
To this end, our results highlight that forthcoming studies need to carefully consider the methods that they use to model adaptation because we have shown that the range in projected impacts is highly sensitive to the adaptation modeling method employed.
We observed that increases in the magnitude of each adaptation modeling method (apart from analog ERF) generally had linear effects on that were similar across cities (Figure 2). This finding suggests that the sensitivity of projected heat-related mortality impacts to adaptation modeling method is likely to hold for other cities across the globe.
Comparing Uncertainty from Adaptation Uncertainty with that from Climate Modeling and Emissions
Our second objective was to compare the range in impacts arising from adaptation uncertainty to the ranges from climate modeling and emissions uncertainty. We found that adaptation modeling uncertainty results in large ranges of projected heat-related mortality impacts. In 13 of 14 cities, adaptation modeling uncertainty resulted in ranges larger than those caused by both climate modeling and emissions uncertainty. This occurred largely as a result of modeling adaptation with relative threshold shifts. When other methods were used, the ranges were still large but typically smaller than those from climate modeling and emissions uncertainty. Our results confirm those of other studies that have shown large differences in impacts between adaptation and no adaptation (e.g., Honda et al. 2014a; Jenkins et al. 2014; Petkova et al. 2016; Sheridan et al. 2012), but here, we have provided additional understanding by specifically showing that adaptation uncertainty can have a greater effect on heat-related mortality rates attributable to climate than climate modeling and emissions uncertainty.
Recommended Adaptation Modeling Methods for Future Assessments
Our third objective was to recommend one or several methods to use in future impact assessments. Our results led us to advise that future assessments should carefully consider the plausibility of the adaptation modeling methods they employ when projecting heat-related mortality.
Absolute threshold shifts are a popular method for modeling adaptation in impact studies, but they have always been shifted by between and without being informed by epidemiological evidence of observed threshold shifts (Dessai 2003; Gosling et al. 2009; Huynen and Martens 2015; Jenkins et al. 2014). However, there is growing evidence to support the magnitude of these shifts. Absolute threshold temperatures increased by 1.5–3°C between 1972 and 1994 in Tokyo (Honda et al. 2006), by between 1901 and 2009 in Stockholm (Åström et al. 2016), and by 0.7°C from 1968–1981 to 1996–2009 in France (Todd and Valleron 2015). Although observed increases in thresholds vary between studies and have occurred over different time periods, and although thresholds have decreased in a limited number of locations (Miron et al. 2007), we argue that it is reasonable in light of the epidemiological evidence to assume that ERFs might shift by between and in the future. Thus, we recommend this method for application in future impact studies. However, we also encourage further epidemiological studies that investigate the magnitude of historical shifts in absolute threshold temperatures; in addition, we recommend improved empirical assessment of the factors that drive such shifts in sensitivity and their associated costs.
Users of the relative threshold method (Honda et al. 2014a; Honda et al. 2014b; Zacharias et al. 2015) justify its application with reference to the observation that threshold temperatures can generally be estimated using the 80–85th percentile of daily maximum temperature in multiple locations in Japan (Honda et al. 2007; Honda et al. 2014b). However, relative thresholds can vary over time (Åström et al. 2016) and between countries (Gasparrini et al. 2015a), which leads to concerns about the rationale behind this method. The method has also been criticized as inappropriate for projecting climate change impacts because the relative threshold may not be a valid proxy for the absolute threshold in the future (Åström et al. 2016). In addition, referring to “100% adaptation” (Honda et al. 2014a) is somewhat misleading because we have shown that climate change still causes an increase in heat-related mortality compared with the present day under this assumption. This is because the shape and the location of the future temperature distribution change, but a relative threshold shift of 100% does not entirely account for the change in shape. In light of these limitations, the method should be applied with caution, and relative threshold shifts of 100% should be carefully considered with respect to their plausibility.
Our results confirm criticisms that impacts based on the analog ERF method may be biased if social, economic, and demographic characteristics related to mortality differ greatly between city pairs (Huang et al. 2011). Application of this method in our study did not always have the effect of reducing mortality relative to no adaptation (e.g., for Milan, Stockholm, Turin, Valencia, and Zurich). One reason for this result is that the method is sensitive to the “matching” of one city to another; some matches were better than others. Another reason is that the cities were matched based only upon their daily distributions and not on the socioeconomic characteristics that contribute to the thresholds and slopes of the city-specific ERFs (Baccini et al. 2008). The method might work well for locations that share similar socioeconomic characteristics, but not otherwise. Therefore, we recommend that future impact studies consider whether it is plausible to apply the analog ERF method when taking into account similarities and differences between the socioeconomic characteristics of the different locations under investigation.
We are aware of only one impact study that has modeled adaptation by reducing the slope of the ERF (Huynen and Martens 2015), which is surprising considering the growing body of epidemiological evidence that generally shows a decreasing sensitivity to heat over time (Barnett 2007; Bobb et al. 2014; Gasparrini et al. 2015a; Guo et al. 2012; Ha and Kim 2013; Petkova et al. 2014a; Schwartz et al. 2015; Sheridan et al. 2008). Along with others (Huang et al. 2011), we see this method as showing significant potential for application in impact studies.
Overall, we recommend that future impact studies model adaptation by absolute threshold shifts and reductions in ERF slope. This should, however, not be done arbitrarily. We suggest that researchers first check the validity of the magnitude of adaptation assumed by exploring the evidence for, and magnitude of, historical adaptation in the chosen location of investigation. This information should yield quantification of shifts in the threshold temperature and declines in slope over the historical period. The analysis should be performed using as long a time series of daily data as possible, ideally spanning because the most compelling evidence for adaptation over the historical period is from studies that have analyzed data sets of this length (Arbuthnott et al. 2016; Åström et al. 2013; Carson et al. 2006; Ha and Kim 2013; Petkova et al. 2014a). If adaptation is not observed over the historical period, if there is a lack of available data, or a combination of the two, then it should not be assumed that future adaptation is impossible. Rather, the reasons for this apparent lack of adaptation (or data) should be investigated, and adaptation modeling should be undertaken. We recommend applying a shift in absolute threshold between and in such cases because this is broadly within the range of shifts in threshold temperature observed for some locations (Åström et al. 2016; Honda et al. 2006; Todd and Valleron 2015). However, the results should be interpreted within the knowledge that historical adaptation has not occurred, that there were insufficient available data to observe it, or both. Analysis of historical trends in adaptation will indicate whether both the threshold and slope have changed over time, or whether only one has changed. This in turn should inform which method to use in the climate change impact assessment.
We assumed in our comparison that the methods employed in previous studies for particular locations could readily be transferred to different locations. Previous studies that have used these methods have also made this assumption. Apart from the analog ERF method, which we have shown may not be a plausible method for some locations, our results suggest no reason why the methods cannot be applied to locations that are different from where they have been used previously. However, as we have already noted, when using these methods for a new location, researchers should check the validity of the assumed magnitude of adaptation by exploring historical adaptation trends for that location. Although our recommendation is based upon an analysis of existing methods, we also encourage the development of new methods for modeling adaptation across large populations. These new methods might include shifts and declines in slope where the magnitudes vary seasonally or interannually to reflect the lead-in times that typify decreasing sensitivity to heat over the historical period (Arbuthnott et al. 2016; Petkova et al. 2016). It would also be worthwhile to attempt to separate the beneficial effects of autonomous adaptation from those of planned adaptation (Petkova et al. 2014b) because all of the methods we employed combine the two. In practical terms, it is likely that the two mechanisms will operate at different magnitudes, heterogeneously across locations, and at different spatial and temporal scales.
Conclusions
To the best of our knowledge, we have conducted the first climate change impact assessment for heat-related mortality that systematically compares projections using the six main methods for modeling adaptation that have been employed in previous studies.
We found that on average across all 14 cities, the range of the difference (percent) in impacts between including and excluding adaptation, independent of climate modeling and emissions uncertainty, can be as low as 28% with one method (reduction in slope of the ERF) and up to 103% with another (relative threshold shift combined with a reduction in slope of the ERF). Furthermore, we have shown that in 13 of the 14 cities, the ranges in projected impacts due to adaptation uncertainty are larger than those associated with climate modeling and emissions uncertainty.
Therefore, we strongly encourage an advancement beyond the prevailing methodological approach adopted in most impact studies, which has traditionally focused on accounting for climate modeling and/or emissions uncertainties at the expense of ignoring adaptation (e.g., Baccini et al. 2011; Hajat et al. 2014; Kingsley et al. 2016; Peng et al. 2011; Vardoulakis et al. 2014; Wu et al. 2014). This status quo has developed from an inherent assumption that the most important uncertainties to account for are climate modeling and emissions uncertainty because they have been shown to result in large ranges in impacts (e.g., Gosling et al. 2012; Hajat et al. 2014; Peng et al. 2011; Zacharias et al. 2015). Our results stand in stark contrast.
Therefore, researchers should carefully consider how to model adaptation. We call for a move towards impact assessments that explicitly report the range in impacts from using multiple GCMs, emissions scenarios, and different adaptation assumptions to provide a more comprehensive assessment of uncertainty. This will in turn provide policy- and decision makers with a more holistic picture of potential climate change impacts. Ideally, this will help decision makers adopt the appropriate scale and combination of different investments and interventions required for effective adaptation to climate change.
We treated adaptation in a purely statistical sense without consideration of the specific programs, strategies, and behavioral changes that are ultimately driving the adaptation assumptions we applied. More thorough and widespread evaluation of intervention measures will be paramount in closing this loop (Boeckmann and Rohn 2014). Therefore, in parallel to our recommendations for future research, we acknowledge that more evidence should be generated on the costs and effectiveness of the large array of adaptation mechanisms that underlie the modeling assumptions we applied here, from individual to technological to health system levels. This additional information will enable policy- and decision makers to focus on the most cost-effective interventions and will enable researchers to base their adaptation methods on more robust data.
Supplemental Material
Acknowledgments
We thank E. Gosling for her help in producing the figures. S.N.G. was funded by the European Commission Joint Research Centre (contract 154858-2015 A08-GB, “Comparative Study on Modelling Heat-related Mortality Adaptation to Climate Change”). J.L. received funding from the National Natural Science Foundation of China (41625001).
The views expressed are purely those of the authors and may not in any circumstances be regarded as stating an official position of the European Commission.
References
- Arbuthnott K, Hajat S, Heaviside C, Vardoulakis S. 2016. Changes in population susceptibility to heat and cold over time: assessing adaptation to climate change. Environ Health 15 Suppl1:S33, PMID: 26961541, 10.1186/s12940-016-0102-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Åström DO, Forsberg B, Edvinsson S, Rocklov J. 2013. Acute fatal effects of short-lasting extreme temperatures in Stockholm, Sweden: Evidence across a century of change. Epidemiology 24(6):820–829, PMID: 24051892, 10.1097/01.ede.0000434530.62353.0b. [DOI] [PubMed] [Google Scholar]
- Åström DO, Tornevi A, Ebi KL, Rocklöv J, Forsberg B. 2016. Evolution of minimum mortality temperature in Stockholm, Sweden, 1901-2009. Environ Health Perspect 124(6):740–744, PMID: 26566270, 10.1289/ehp.1509692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baccini M, Biggeri A, Accetta G, Kosatsky T, Katsouyanni K, Analitis A, et al. 2008. Heat effects on mortality in 15 European cities. Epidemiology 19(5):711–719, PMID: 18520615, 10.1097/EDE.0b013e318176bfcd. [DOI] [PubMed] [Google Scholar]
- Baccini M, Kosatsky T, Analitis A, Anderson HR, D'Ovidio M, Menne B, et al. 2011. Impact of heat on mortality in 15 European cities: attributable deaths under different weather scenarios. J Epidemiol Community Health 65(1):64–70, PMID: 19858539, 10.1136/jech.2008.085639. [DOI] [PubMed] [Google Scholar]
- Barnett AG. 2007. Temperature and cardiovascular deaths in the US elderly: changes over time. Epidemiology 18(3):369–372, PMID: 17435447, 10.1097/01.ede.0000257515.34445.a0. [DOI] [PubMed] [Google Scholar]
- Bobb JF, Peng RD, Bell ML, Dominici F. 2014. Heat-related mortality and adaptation to heat in the United States. Environ Health Perspect 122(8):811–816, PMID: 24780880, 10.1289/ehp.1307392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boeckmann M, Rohn I. 2014. Is planned adaptation to heat reducing heat-related mortality and illness? A systematic review. BMC Public Health 14:1112, PMID: 25349109, 10.1186/1471-2458-14-1112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carson C, Hajat S, Armstrong B, Wilkinson P. 2006. Declining vulnerability to temperature-related mortality in London over the 20th century. Am J Epidemiol 164(1):77–84, PMID: 16624968, 10.1093/aje/kwj147. [DOI] [PubMed] [Google Scholar]
- Davis RE, Knappenberger PC, Michaels PJ, Novicoff WM. 2003. Changing heat-related mortality in the United States. Environ Health Perspect 111(14):1712–1718, PMID: 14594620, 10.1289/ehp.6336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dessai S. 2003. Heat stress and mortality in Lisbon Part II. An assessment of the potential impacts of climate change. Int J Biometeorol 48:37–44, PMID: 12750971, 10.1007/s00484-003-0180-4. [DOI] [PubMed] [Google Scholar]
- Gasparrini A, Guo Y, Hashizume M, Kinney PL, Petkova EP, Lavigne E, et al. 2015a. Temporal variation in heat-mortality associations: a multicountry study. Environ Health Perspect 123(11):1200–1207, PMID: 25933359, 10.1289/ehp.1409070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gasparrini A, Guo Y, Hashizume M, Lavigne E, Zanobetti A, Schwartz J. 2015b. Mortality risk attributable to high and low ambient temperature: a multicountry observational study. Lancet 123(9991):1200–1207, PMID: 26003380, 10.1016/S0140-6736(14)62114-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gosling SN, McGregor GR, Lowe JA. 2009. Climate change and heat-related mortality in six cities Part 2: Climate model evaluation and projected impacts from changes in the mean and variability of temperature with climate change. Int J Biometeorol 53(1):31–51, PMID: 19052780, 10.1007/s00484-008-0189-9. [DOI] [PubMed] [Google Scholar]
- Gosling SN, McGregor GR, Lowe JA. 2012. The benefits of quantifying climate model uncertainty in climate change impacts assessment: an example with heat-related mortality change estimates. Climatic Change 112(2):217–231, 10.1007/s10584-011-0211-9. [DOI] [Google Scholar]
- Guo Y, Barnett AG, Tong S. 2012. High temperatures-related elderly mortality varied greatly from year to year: important information for heat-warning systems. Sci Rep 2:830, PMID: 23145322, 10.1038/srep00830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ha J, Kim H. 2013. Changes in the association between summer temperature and mortality in Seoul, South Korea. Int J Biometeorol 57(4):535–544, PMID: 22872184, 10.1007/s00484-012-0580-4. [DOI] [PubMed] [Google Scholar]
- Hajat S, Vardoulakis S, Heaviside C, Eggen B. 2014. Climate change effects on human health: projections of temperature-related mortality for the UK during the 2020s, 2050s and 2080s. J Epidemiol Community Health. 68(7):641–648, PMID: 24493740, 10.1136/jech-2013-202449. [DOI] [PubMed] [Google Scholar]
- Hales S, Kovats RS, Lloyd S, Campbell-Lendrum D, eds. 2014. Quantitative risk assessment of the effects of climate change on selected causes of death, 2030s and 2050s. Geneva, Switzerland:World Health Organization (WHO). [Google Scholar]
- Hayhoe K, Cayan D, Field CB, Frumhoff PC, Maurer EP, Miller NL, et al. 2004. Emissions pathways, climate change, and impacts on California. Proc Natl Acad Sci USA 101(34):12422–12427, PMID: 15314227, 10.1073/pnas.0404500101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hempel S, Frieler K, Warszawski L, Schewe J, Piontek F. 2013. A trend-preserving bias correction–the ISI-MIP approach. Earth Syst Dynam 4:219–236, 10.5194/esd-4-219-2013. [DOI] [Google Scholar]
- Honda Y, Ono M, Kabuto M. 2006. Do we adapt to a new climate as the globe warms? Epidemiology 17(6):S204, 10.1097/00001648-200611001-00519. [DOI] [Google Scholar]
- Honda Y, Kabuto M, Ono M, Uchiyama I. 2007. Determination of optimum daily maximum temperature using climate data. Environ Health Prev Med 12(5):209–216, PMID: 21432083, 10.1265/ehpm.12.209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honda Y, Kondo M, McGregor G, Kim H, Guo YL, Hales S, et al. 2014a. Heat-related mortality. In: Quantitative risk assessment of the effects of climate change on selected causes of death, 2030s and 2050s. Hales S, Kovats RS, Lloyd S, Campbell-Lendrum D, eds Geneva, Switzerland:WHO, 17–26. [Google Scholar]
- Honda Y, Kondo M, McGregor G, Kim H, Guo YL, Hijioka Y, et al. 2014b. Heat-related mortality risk model for climate change impact projection. Environ Health Prev Med 19(1):56–63, PMID: 23928946, 10.1007/s12199-013-0354-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hondula DM, Balling RC, Vanos JK, Georgescu M. 2015. Rising temperatures, human health, and the role of adaptation. Curr Clim Change Rep 1(3):144–154, 10.1007/s40641-015-0016-4. [DOI] [Google Scholar]
- Huang C, Barnett AG, Wang X, Vaneckova P, FitzGerald G, Tong S. 2011. Projecting future heat-related mortality under climate change scenarios: a systematic review. Environ Health Perspect 119(12):1681–1690, PMID: 21816703, 10.1289/ehp.1103456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huynen MM, Martens P. 2015. Climate change effects on heat- and cold-related mortality in the Netherlands: a scenario-based integrated environmental health impact assessment. IJERPH 12(10):13295–13320, 10.3390/ijerph121013295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkins K, Hall J, Glenis V, Kilsby C, McCarthy M, Goodess C, et al. 2014. Probabilistic spatial risk assessment of heat impacts and adaptations for London. Climatic Change 124(1–2):105–117, 10.1007/s10584-014-1105-4. [DOI] [Google Scholar]
- Kingsley S, Eliot M, Gold J, Vanderslice R, Wellenius G. 2016. Current and projected heat-related morbidity and mortality in Rhode Island. Environ Health Perspect 124(4):460–467, PMID: 26251954, 10.1289/ehp.1408826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kinney PL, O’Neill MS, Bell ML, Schwartz J. 2008. Approaches for estimating effects of climate change on heat-related deaths: challenges and opportunities. Environ Sci Policy 11(1):87–96, 10.1016/j.envsci.2007.08.001. [DOI] [Google Scholar]
- Knowlton K, Lynn B, Goldberg RA, Rosenzweig C, Hogrefe C, Rosenthal JK, et al. 2007. Projecting heat-related mortality impacts under a changing climate in the New York City region. Am J Public Health 97(11):2028–2034, 10.2105/AJPH.2006.102947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martens WJM. 1998. Climate change, thermal stress and mortality changes. Soc Sci Med 46(3):331–344, PMID: 9460815. [DOI] [PubMed] [Google Scholar]
- Martin SL, Cakmak S, Hebbern CA, Avramescu M-L, Tremblay N. 2012. Climate change and future temperature-related mortality in 15 Canadian cities. Int J Biometeorol 56(4):605–619, PMID: 21597936, 10.1007/s00484-011-0449-y. [DOI] [PubMed] [Google Scholar]
- Massey FJ. 1951. The Kolmogorov-Smirnov test for goodness of fit. J Am Stat Assoc 46(253):68–78, 10.2307/2280095. [DOI] [Google Scholar]
- McMichael A, Woodruff R, Hales S. 2006. Climate change and human health: present and future risks. Lancet 367:859–869, PMID: 16530580, 10.1016/S0140-6736(06)68079-3. [DOI] [PubMed] [Google Scholar]
- Mills D, Schwartz J, Lee M, Sarofim M, Jones R, Lawson M. 2014. Climate change impacts on extreme temperature mortality in select metropolitan areas in the United States. Climatic Change 131(1):83–95, 10.1007/s10584-014-1154-8. [DOI] [Google Scholar]
- Miron IJ, Criado-Alvarez JJ, Diaz J, Linares C, Mayoral S, Montero JC. 2007. Time trends in minimum mortality temperatures in Castile-La Mancha (Central Spain): 1975–2003. Int J Biometeorol 52(4):291–299, 10.1007/s00484-007-0123-6. [DOI] [PubMed] [Google Scholar]
- Muggeo VMR. 2003. Estimating regression models with unknown break-points. Stat Med 22(19):3055–3071, PMID: 12973787, 10.1002/sim.1545. [DOI] [PubMed] [Google Scholar]
- O’Neill BC, Kriegler E, Riahi K, Ebi KL, Hallegatte S, Carter TR, et al. 2014. A new scenario framework for climate change research: the concept of shared socioeconomic pathways. Climatic Change 122(3):387–400, 10.1007/s10584-013-0906-1. [DOI] [Google Scholar]
- Peng RD, Bobb JF, Tebaldi C, McDaniel L, Bell ML, Dominici F. 2011. Toward a quantitative estimate of future heat wave mortality under global climate change. Environ Health Perspect 119(5):701–706, PMID: 21193384, 10.1289/ehp.1002430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petitti DB, Hondula DM, Yang S, Harlan SL, Chowell G. 2016. Multiple trigger points for quantifying heat-health impacts: new evidence from a hot climate. Environ Health Perspect 124(2):176–183, PMID: 26219102, 10.1289/ehp.1409119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petkova EP, Horton RM, Bader DA, Kinney PL. 2013. Projected heat-related mortality in the U.S. urban northeast. Int J Environ Res Public Health 10(12):6734–6747, PMID: 24300074, 10.3390/ijerph10126734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petkova EP, Gasparrini A, Kinney P. 2014a. Heat and mortality in New York City since the beginning of the 20th century. Epidemiology 25(24):554–560, PMID: 24802366, 10.1097/EDE.0000000000000123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petkova EP, Morita H, Kinney PL. 2014b. Health impacts of heat in a changing climate: how can emerging science inform urban adaptation planning? Curr Epidemiol Rep 1(2):67–74, 10.1007/s40471-014-0009-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petkova EP, Vink JK, Horton RM, Gasparrini A, Bader DA, Francis JD, Kinney PL. 2017. Towards more comprehensive projections of urban heat-related mortality: estimates for New York City under multiple population, adaptation, and climate scenarios. Environ Health Perspect 125(1):47–55, PMID: 27337737, 10.1289/EHP166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riahi K, Rao S, Krey V, Cho C, Chirkov V, Fischer G, et al. 2011. RCP 8.5—A scenario of comparatively high greenhouse gas emissions. Climatic Change 109:33–57, 10.1007/s10584-011-0149-y. [DOI] [Google Scholar]
- Rodopoulou S, Samoli E, Analitis A, Atkinson RW, de’Donato FK, Katsouyanni K. 2015. Searching for the best modeling specification for assessing the effects of temperature and humidity on health: a time series analysis in three European cities. Int J Biometeorol 59(11):1585–1596, PMID: 25638489, 10.1007/s00484-015-0965-2. [DOI] [PubMed] [Google Scholar]
- Schwartz JD, Lee M, Kinney PL, Yang S, Mills D, Sarofim MC, et al. 2015. Projections of temperature-attributable premature deaths in 209 U.S. cities using a cluster-based Poisson approach. Environ Health 14:85, PMID: 26537962, 10.1186/s12940-015-0071-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheridan SC, Kalkstein AJ, Kalkstein LS. 2008. Trends in heat-related mortality in the United States, 1975–2004. Nat Hazards 50(1):145–160, 10.1007/s11069-008-9327-2. [DOI] [Google Scholar]
- Sheridan SC, Allen MJ, Lee CC, Kalkstein LS. 2012. Future heat vulnerability in California, Part II: projecting future heat-related mortality. Climatic Change 115(2):311–326, 10.1007/s10584-012-0437-1. [DOI] [Google Scholar]
- Smith KR, Woodward A, Campbell-Lendrum D, Chadee DD, Honda Y, Liu Q, et al. 2014. Human health: impacts, adaptation, and co-benefits. In: Climate Change 2014: Impacts, Adaptation, and Vulnerability Part A: Global and Sectoral Aspects Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Field CB, Barros VR, Dokken DJ, Mach KJ, Mastrandrea MD, Bilir TE, et al. , eds Cambridge, UK and New York, NY:Cambridge University Press, 709–754. [Google Scholar]
- Tetens O. 1930. Über einige meteorologische Begriffe. Z Geophys 6:297–309. [Google Scholar]
- Todd N, Valleron A-J. 2015. Space–time covariation of mortality with temperature: a systematic study of deaths in France, 1968–2009. Environ Health Perspect 123(7):659–664, PMID: 25803836, 10.1289/ehp.1307771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vardoulakis S, Dear K, Shakoor H, Heaviside C, Eggen B, McMichael AJ. 2014. Comparative assessment of the effects of climate change on heat- and cold-related mortality in the United Kingdom and Australia. Environ Health Perspect 122(12):1285–1292, PMID: 25222967, 10.1289/ehp.1307524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warszawski L, Frieler K, Huber V, Piontek F, Serdeczny O, Schewe J. 2014. The Inter-Sectoral Impact Model Intercomparison Project (ISI–MIP): project framework. Proc Natl Acad Sci USA 111(9):3228–3232, PMID: 24344316, 10.1073/pnas.1312330110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weedon GP, Gomes S, Viterbo P, Shuttleworth WJ, Blyth E, Österle H, et al. 2011. Creation of the WATCH forcing data and its use to assess global and regional reference crop evaporation over land during the twentieth century. J Hydrometeor 12:823–848, 10.1175/2011JHM1369.1. [DOI] [Google Scholar]
- Woodward A, Smith KR, Campbell-Lendrum D, Chadee DD, Honda Y, Liu Q, et al. Climate change and health: on the latest IPCC report. Lancet 383(9924):1185–1189, PMID: 24703554, 10.1016/S0140-6736(14)60576-6. [DOI] [PubMed] [Google Scholar]
- Wu J, Zhou Y, Gao Y, Fu JS, Johnson BA, Huang C, et al. 2014. Estimation and uncertainty analysis of impacts of future heat waves on mortality in the eastern United States. Environ Health Perspect 122(1):10–16, PMID: 24192064, 10.1289/ehp.1306670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zacharias S, Koppe C, Mücke H-G. 2015. Climate change effects on heat waves and future heat wave-associated IHD mortality in Germany. Climate 3(1):100–117, 10.3390/cli3010100. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.