A cortical–hippocampal–cortical loop of information processing during memory consolidation

Abstract

Hippocampal replay during sharp-wave ripple events (SWRs) is thought to drive memory consolidation in hippocampal and cortical circuits. Changes in neocortical activity can precede SWR events, but whether and how these changes influence the content of replay remains unknown. Here we show that during sleep there is a rapid cortical–hippocampal–cortical loop of information flow around the times of SWRs. We recorded neural activity in auditory cortex (AC) and hippocampus of rats as they learned a sound-guided task and during sleep. We found that patterned activation in AC precedes and predicts the subsequent content of hippocampal activity during SWRs, while hippocampal patterns during SWRs predict subsequent AC activity. Delivering sounds during sleep biased AC activity patterns, and sound-biased AC patterns predicted subsequent hippocampal activity. These findings suggest that activation of specific cortical representations during sleep influences the identity of the memories that are consolidated into long-term stores.

The hippocampus is critical for forming memories of daily life events, but over time memories can become independent of the hippocampus^1–3. This transition of memory representations from being strongly dependent on the hippocampus to being fully or mostly engrained in cortical networks is termed memory consolidation. According to the influential ‘two-stage model’^4,5 of consolidation, the first stage occurs during behavior, when the hippocampus rapidly encodes various aspects of the experience via changes of synaptic strengths. In the second stage, during slow-wave sleep and consummatory behaviors, the newly acquired hippocampal information is replayed repeatedly, driving plasticity in neocortex and allowing for the longer-term storage of the memory. The hippocampus has therefore been referred to as the ‘fast learner’, which teaches the cortex, the ‘slow learner’^1,6.

A number of studies have implicated hippocampal replay during SWRs as a potential mechanism of hippocampal–cortical communication underlying memory consolidation^4,7–11. SWRs originate in the hippocampus^5,12,13, and sequences of hippocampal place cell firing that occurred during wakefulness are repeatedly reactivated on an accelerated timescale during SWRs. Importantly, reactivated hippocampal representations have been suggested to engage cortical networks, as SWRs can drive excitatory responses in cortical output regions^14,15, and reactivation in some cortical regions, most notably the medial prefrontal cortex, is coordinated with hippocampal reactivation^7,16–19. Finally, studies have established a causal role for SWRs in learning: SWR rates increase in post-learning sleep²⁰, and blocking hippocampal SWRs impedes learning^8,21,22. Taken together, these findings support the idea that SWRs facilitate repeated transmission of representations of recent experiences from the hippocampus to the cortex, potentially inducing synaptic changes that would support long-term memory storage.

In the intact brain, SWRs arise at specific times relative to ongoing neocortical activity, and previous studies have established that memory consolidation involves a bidirectional interaction, or ‘dialogue’, between hippocampus and cortex^4,23,24. During sleep, SWRs occur more often after cortical down-to-up state transitions¹⁵ and around the times of cortical spindles¹⁸. Based on these findings, it has been suggested that the neocortical up-states provide feedforward excitation promoting thalamic spindles and hippocampal SWRs, resulting in coordination between SWRs, cortical up-states and spindles, and thus providing a potential mechanism of hippocampus-to-cortex information flow²³. Consistent with these findings, a previous study found that ‘activity frames’ in visual cortex precede frames in the hippocampus and demonstrated coordinated reactivation across these structures, although the direction of information flow could not be determined¹⁷. Another study showed that hippocampal reactivation during sleep can be biased by sounds, raising the possibility that this effect is mediated by a flow of sound-evoked information from the cortex to the hippocampus²⁵. Finally, selective ablation of axons from entorhinal cortex to hippocampal area CA1 after learning causes a long-term memory impairment²⁶, suggesting a role for these connections in consolidation. Taken together, these studies raise the possibility that cortical firing patterns preceding hippocampal SWRs could affect subsequent hippocampal reactivation, but the presence or absence of such a communication pattern remains to be established.

In this study, we aimed to establish the direction and nature of information flow in the hippocampal–cortical circuit around the time of SWRs. We focused on interactions between the hippocampus and the auditory cortex, as rodents have high auditory acuity and the rodent auditory cortex has been implicated in memory-related processes^27–34. Our results provide strong support for a cortical–hippocampal–cortical information-processing loop wherein cortical patterned activation precedes hippocampal SWRs and influences the content of hippocampal activity during the SWRs, while hippocampal patterns during SWRs influence subsequent cortical activity.

RESULTS

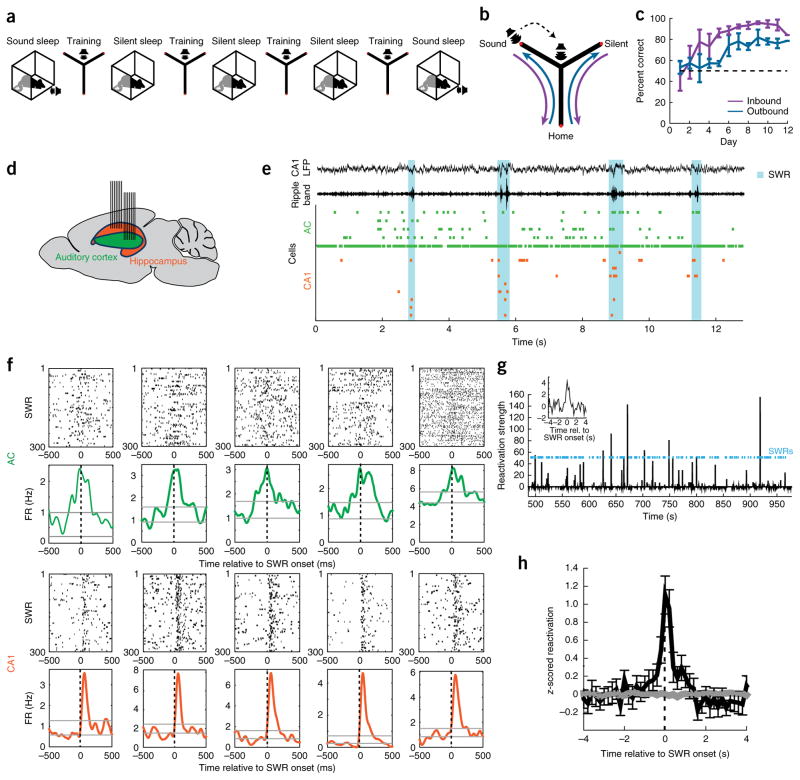
We carried out electrophysiological recordings of neuronal activity in the hippocampal CA1 region and AC in rats during learning of a sound-guided task and during interleaved sleep sessions in a rest box (Fig. 1a). Rats were trained on a Y-shaped track, where they learned to nose-poke in the home well to initiate each trial (Fig. 1b). In ~75% of trials, no sound was presented and the animal was rewarded for going to the ‘silent well’. In a pseudorandom ~25% of trials, poking in the home well was followed by presentation of a target sound, and the animal was then rewarded for visiting the ‘sound well’. Animals reached high levels of performance after ~6–8 d of training (Fig. 1c). The locations of the home, silent and sound wells were fixed across days. We recorded neuronal ensemble spiking activity across learning using tetrodes targeted to the AC and to the dorsal CA1 region of the hippocampus (Fig. 1d and Supplementary Fig. 1).

Figure 1.

Auditory cortical reactivation during hippocampal SWRs in training-interleaved sleep. (a) Daily experimental schedule. Each day included 3–4 20-min training sessions, interleaved with 20–30-min rest sessions in the rest box (silent sleep). In addition, at the beginning and end of each day, a sound protocol was presented while the animals were in the rest box (sound sleep). (b) Track and task. Rats (n = 4) initiated each trial by nose-poking in the home well and receiving a reward. In ~75% of trials the rat then had to go to the silent well for the next reward. In a pseudorandom ~25% of trials, 5 s after poking in the home well, a sound series was emitted from a speaker, indicating the rat had to go to the sound well for the next reward. The speaker was placed at the end of the sound arm in the first days of training and moved to the center junction after rats displayed consistent correct choices in more than ~70% of trials. (c) Behavioral performance on the task. Error bars indicate s.e.m. across animals. Dotted line indicates chance level of 50% correct. (d) Tetrode targeting. Seven tetrodes targeted the hippocampal CA1 region and seven tetrodes targeted primary auditory cortex in each animal. (e) Example ensemble spiking activity in auditory cortex (green) and CA1 region of the hippocampus (orange) during sleep. Each tick marks a spike from one cell. Top two traces show broadband local field potentials (LFP; 1–400 Hz) in CA1 and ripple-band filtered LFP (150–250 Hz) in CA1. Cyan shading denotes SWRs. (f) SWR-aligned rasters of example neurons and corresponding time histograms. Top examples are significantly SWR-modulated AC neurons; bottom examples are significantly SWR-modulated CA1 neurons. Gray lines mark the range (mean ± 2 s.d.) of firing rates in the preceding −1,000 to −500 ms time window. FR, firing rate. (g) Population reactivation time series of an awake pattern from an example sleep epoch. SWR events shown in cyan. Inset: SWR-triggered reactivation histogram. (h) Mean z-scored SWR-triggered reactivation histogram across all sleep epochs that showed significant reactivation (n = 69 epochs). Error bars show s.e.m. Gray trace shows result for same data when SWR timing was randomly shuffled.

Modulation of auditory cortical activity around hippocampal SWRs

We focused on spiking activity during sleep, when reactivation and consolidation processes are known to occur. CA1 reactivation of awake experience during sleep SWRs is well-established^5,9,35,36, but it is not known whether AC also shows reactivation during sleep and, if so, whether it does so in coordination with hippocampal SWRs. We examined these questions by focusing on activity during non-rapid eye movement (NREM) sleep in training-interleaved sleep sessions when no sounds were presented (‘silent sleep’; Supplementary Fig. 2). We aligned spiking activity of all cells to the onset of SWRs, derived SWR-triggered peri-SWR time histograms and used a variance-based method to detect systematic firing rate variations. Notably, the firing rates of 36% (117/322) of cells in AC were significantly modulated around the time of hippocampal SWRs (Fig. 1e,f and Supplementary Fig. 3), as were the firing rates of the majority of CA1 cells (85%, 164/192).

We then asked whether AC spiking at the time of SWRs during sleep reflected reactivation of awake experiences. We employed a previously developed principal component analysis-based method⁷ to measure the reactivation of population patterns that were observed during wakefulness. We observed significant reactivation of awake experience during silent sleep in 69/83 (83%) of rest sessions (individual session criterion of P < 0.05, shuffle test; likelihood of 69/83 significant: P < 10⁻¹⁰). The patterns of AC reactivation were similar to those reported previously for prefrontal cortex⁷, with large transient increases in reactivation amplitude (Fig. 1g and Supplementary Fig. 4). Notably, AC reactivation increased significantly around the times of hippocampal SWRs (P = 5.7 × 10⁻⁸ at lag 0, one-sided Wilcoxon signed-rank test; Fig. 1h and Supplementary Fig. 4), suggesting that reactivation could be synchronized and coordinated across these structures. In support of this possibility, and consistent with previous findings in other brain regions in rodents^15,18,37 and in humans^38,39, we found that power in the delta and spindle bands of the local field potential in AC increased around the time of hippocampal SWRs (Supplementary Fig. 5).

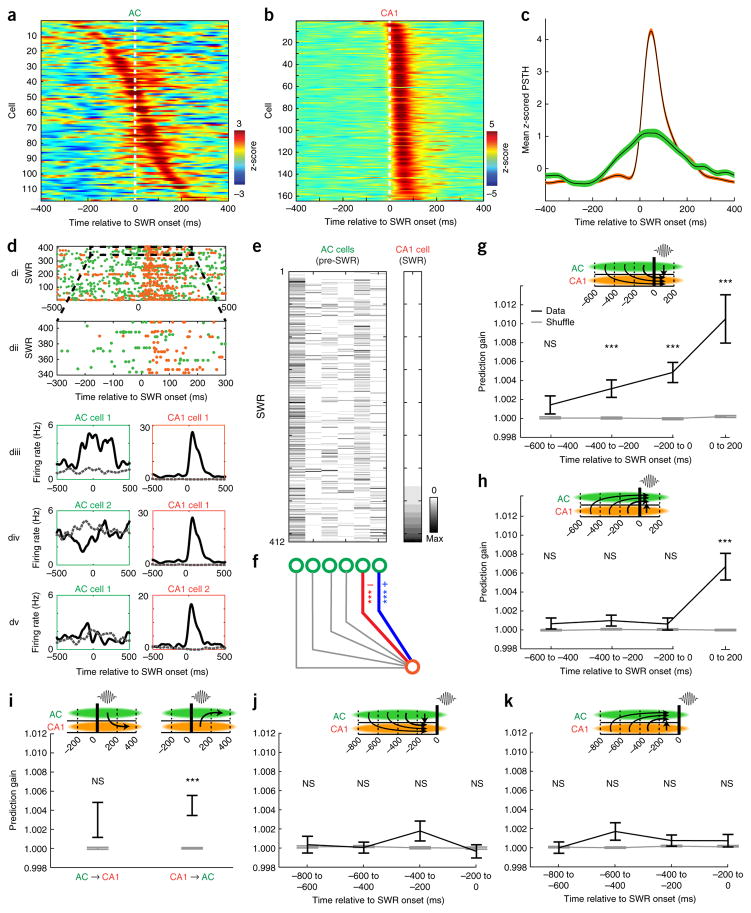
AC activity precedes and predicts CA1 spiking during SWRs

While SWRs are generated in the hippocampus, we found clear evidence for an initial flow of information from cortex to hippocampus immediately preceding SWRs. We first noted that single cells in AC often increased firing before the onset of hippocampal SWRs (Figs. 1f and 2a), while CA1 cells consistently increased firing after SWR onset (Figs. 1f and 2b). Across the population, firing rate increases could be detected in AC earlier than in CA1 (Fig. 2c and Supplementary Fig. 3). Moreover, we found that AC ensemble firing patterns could significantly predict the occurrence of hippocampal SWRs (P = 2.5 × 10⁻¹⁶ at lag 0, one-sided Wilcoxon signed-rank test; Supplementary Fig. 6).

Figure 2.

AC modulation precedes and predicts CA1 firing around SWRs. (a) z-scored SWR-triggered spiking histograms of all SWR-modulated AC neurons, sorted by timing of peak firing in −250 ms to 250 ms window. (b) Same as a for CA1 neurons. (c) Mean z-scored SWR-triggered spiking histogram across all SWR-modulated neurons for AC (green) and CA1 (orange). Shaded area indicates s.e.m. (d) Activity of an example AC–CA1 neuronal pair around SWR times. (di): overlaid SWR-triggered spike rasters of simultaneously recorded AC (green) and CA1 (orange) neurons; (dii): enlarged view of highlighted region in di; (diii): peri-SWR time histograms (PSTHs) of the AC (left) and CA1 (right) neurons from di separated by spike count of CA1 cell (≥1 spike, black; 0 spikes, dashed gray). (div): same as above, but for the same CA1 cell paired with a different AC cell. (dv): Same as above but for same AC cell as in diii but a different CA1 cell. (e) Example dataset used for generalized linear model (GLM) prediction analysis. Left matrix denotes spike counts in the pre-SWR time window (−200 to 0 ms relative to SWR onset) of 6 AC cells across SWRs. Right shows spike counts in the subsequent SWR time window (0 to 200 ms) of one CA1 cell. Spike counts of all cells are sorted by spike counts of the CA1 cell. Data corresponds to the data in d: rightmost column of the AC matrix corresponds to ‘AC cell 1’ in d, fifth column corresponds to ‘AC cell 2’ in d. Color scale denotes spikes per bin; max is 8 for AC cells and 12 for CA1 cell. (f) Prediction illustration aligned to the data in e. Blue and red edges denote individually positively and negatively predictive relationships, respectively. (g) Prediction of CA1 single-cell spiking during SWRs from ensemble spiking patterns in AC across varying time windows (n = 107 predicted CA1 cells). Black error bars indicate mean ± s.e.m. prediction gain for real data. Gray error bars indicate mean ± s.e.m. prediction gain for shuffled data. Columns represent varying time windows used as predictor data; predicted data is always the SWR time window (0–200 ms). CA1 spiking during SWRs could be predicted significantly better than shuffled data from AC ensemble spiking patterns in the −400 to −200 ms window (z = 3.45, P = 0.0006), −200 to 0 ms window (z = 4.69, P = 2.69 × 10⁻⁶) and 0 to 200 ms window (z = 6.75, P = 1.5 × 10⁻¹¹) but not from the −600 to −400 ms window (z = 0.84, P = 0.40; all tests using a two-tailed rank-sum test compared to shuffled). (h) Prediction of AC single-cell spiking during SWRs from ensemble spiking in CA1 (n = 152 predicted AC cells). AC spiking during SWRs could not be significantly predicted from pre-SWR CA1 ensemble spiking patterns but could be predicted from CA1 spiking during the SWR (−600 to −400: z = 1.02, P = 0.31; −400 to −200: z = 1.58, P = 0.115; −200 to 0: z = 0.49, P = 0.627; 0 to 200: z = 6.04, P = 1.56 × 10⁻⁹, two-tailed rank-sum test compared to shuffled). (i) Prediction of post-SWR time window from SWR spiking. AC ensemble spiking patterns during SWRs could not predict CA1 firing in post-SWR window (left; n = 108 predicted CA1 cells, z = 1.18, P = 0.237, two-tailed rank-sum test compared to shuffle), but CA1 ensemble spiking patterns during SWRs significantly predicted AC firing in post-SWR window (right; n = 150 predicted AC cells, z = 4.37, P = 1.25 × 10⁻⁵, two-tailed rank-sum test compared to shuffled). (j) CA1 spiking in the pre-SWR time window could not be significantly predicted from AC ensemble spiking patterns in any time window (n = 101 predicted CA1 cells, −800 to −600: z = 0.28, P = 0.775; −600 to −400: z = 0.28, P = 0.78; −400 to −200: z = 1.73, P = 0.083; −200 to 0: z = −0.64, P = 0.523, two-tailed rank-sum test compared to shuffle). (k) AC spiking in pre-SWR time windows could not be significantly predicted from CA1 ensemble spiking patterns in any time window (n = 152 predicted AC cells, −800 to −600: z = −0.54, P = 0.59; −600 to −400: z = 1.66, P = 0.097; −400 to −200: z = 0.34, P = 0.737; −200 to 0: z = 0.43, P = 0.668, two-tailed rank-sum test compared to shuffle). ***P < 0.001 for GLM prediction beta values.

Could specific patterns of AC spiking preceding SWRs influence subsequent hippocampal reactivation? To answer this question, we used cross-validated generalized linear models to determine whether pre-SWR ensemble activity in AC predicted the firing of single CA1 neurons during SWRs. These analyses revealed striking examples of such coordination (Fig. 2d–f), including cases in which pre-SWR firing of different AC neurons from the same recorded ensemble was either positively (Fig. 2diii), negatively (Fig. 2div) or not (Fig. 2dv) correlated with the SWR firing of individual CA1 neurons.

Across the population of CA1 cells, pre-SWR AC ensemble spiking patterns significantly predicted subsequent CA1 spiking during SWRs (n = 107 predicted CA1 cells; Fig. 2g and Supplementary Figs. 7 and 8). This prediction was highly significant for both the 200-ms window immediately preceding the SWR (−200 to 0 ms; z = 4.69, P = 2.69 × 10⁻⁶, two-tailed rank-sum test compared to shuffled) and for the preceding window (−400 to −200 ms; z = 3.45, P = 0.0006) but was not seen for a more remote window (−600 to −400 ms; z = 0.84, P = 0.40). Notably, these predictions were only significant from AC to CA1: pre-SWR CA1 ensemble spiking patterns did not predict AC activity during the SWR (n = 152 predicted AC cells, −600 to −400 ms: z = 1.02, P = 0.31; −400 to −200 ms: z = 1.58, P = 0.115; −200 to 0: z = 0.49, P = 0.627, two-tailed rank-sum test compared to shuffled; Fig. 2h). Firing-rate differences across time windows could not account for the differences in prediction (Supplementary Fig. 9). Thus, these findings provide evidence for pre-SWR AC patterns biasing CA1 firing during SWRs.

CA1 activity patterns during SWRs predict subsequent AC spiking

Our analyses also revealed that, following this initial information flow from cortex to hippocampus before SWRs, there was coordinated reactivation during SWRs and subsequent information flow in the reverse direction, from CA1 to AC. CA1 and AC activity patterns were mutually predictive of one another during the SWR (0 to 200 ms: z > 6, P < 1 × 10⁻⁸, two-tailed rank-sum tests compared to shuffled; Fig. 2g,h). In contrast, CA1 ensemble spiking patterns during the SWR significantly predicted AC spiking in the post-SWR window (200–400 ms; n = 150 predicted AC cells, z = 4.37, P = 1.25 × 10⁻⁵, two-tailed rank-sum test compared to shuffled; Fig. 2i), while AC ensemble spiking patterns during the SWR did not significantly predict CA1 activity in the post-SWR window (n = 108 predicted CA1 cells, z = 1.18, P = 0.237, two-tailed rank-sum test compared to shuffled; Fig. 2i). Significance rates of individual ensemble-cell predictions showed a similar temporal pattern between structures (Supplementary Fig. 10). These findings suggest the existence of a rapid cortical–hippocampal–cortical information-processing loop with a flow of information from AC to CA1 immediately preceding the SWR and a subsequent reverse flow of information from CA1 to AC.

Coordination is temporally specific and comparable in magnitude across structures

We then asked whether this communication loop was specific to peri-SWR times. We employed the same approach to predict activity preceding SWRs when no SWRs were detected. Activity in the pre-SWR time window in CA1 could not be predicted from ensemble spiking patterns in AC in any examined time windows (n = 101 CA1 predicted cells, −800 to −600 ms: z = 0.28, P = 0.775; −600 to −400 ms: z = 0.28, P = 0.78; −400 to −200 ms: z = 1.73, P = 0.083; −200 to 0 ms: z = −0.64, P = 0.523, two-tailed rank-sum test compared to shuffle; Fig. 2j). Similarly, activity in the pre-SWR time window in AC could not be predicted from ensemble spiking patterns in CA1 in any examined time windows (n = 152 predicted AC cells, −800 to −600: z = −0.54, P = 0.59; −600 to −400 ms: z = 1.66, P = 0.097; −400 to −200: z = 0.34, P = 0.737; −200 to 0 ms: z = 0.43, P = 0.668, two-tailed rank-sum test compared to shuffle; Fig. 2k). The absence of detectable prediction of activity in the pre-SWR window in either the AC–CA1 or CA1–AC directions indicates that coordination between these regions is strongly increased during SWRs and that this coordination cannot be explained by a slow covariance in activity across structures.

How strong is this coordination? Across all predictor-ensemble–predicted-cell combinations, the mean prediction gain of CA1 firing during the SWR from AC patterns during the SWR was 1.05%. We expected this value to be low as it was the average across all ensemble–cell combinations and was derived from relatively small ensemble sizes. To compare it to the well-established phenomenon of coordinated activity of CA1 cells during sleep SWRs, we calculated how well the spiking of single CA1 cells during the SWR could be predicted from the activity of the other CA1 cells. Specifically, we calculated prediction gains of spiking for each single CA1 cell during the SWR from the ensemble activity of the other CA1 cells during the SWR. We found that the mean prediction gain for this analysis was 2.75%. Thus, the AC-to-CA1 prediction within the SWR was ~40% of the CA1-to-CA1 prediction, while the pre-SWR AC to SWR-CA1 prediction was ~20% of the CA1-to-CA1 prediction. These relatively large values suggest substantial coordination across these structures. Finally, we also examined the relationship between AC and CA1 activity around awake SWRs. Unfortunately, the smaller number of awake SWRs and the overlap with task events like sound presentation and receipt of reward precluded us from obtaining an unambiguous result.

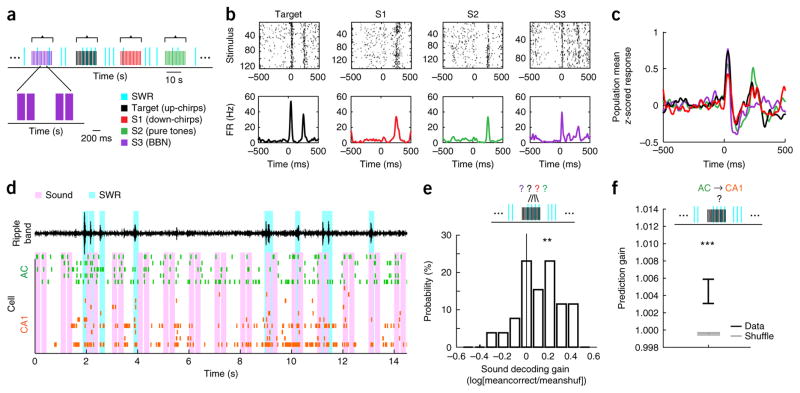
Sound-biased AC ensemble patterns predict CA1 reactivation during SWRs

These findings established patterns of prediction consistent with cortical-to-hippocampal information flow immediately before SWRs and subsequent hippocampal-to-cortical information flow during and after SWRs. As AC is a sensory region with well-characterized response properties, we hypothesized that auditory stimuli during sleep would invoke specific activity patterns in AC, which would in turn influence subsequent hippocampal SWR activity. This could account for the previously observed biasing of hippocampal reactivation by auditory stimuli²⁵. We therefore examined responses to the sounds presented during the first and final sleep epochs of each day (sound sleep; Fig. 1a), which consisted of the target sound (target) and other control sounds (S1, S2 and S3; Fig. 3a and Supplementary Fig. 11). As expected⁴⁰, AC cells showed robust and selective auditory responses during sleep (Fig. 3b,c and Supplementary Fig. 12).

Figure 3.

Sound-biased AC ensembles predict CA1 reactivation during SWRs. (a) Illustration of sound-series presentation and intermingled SWRs during sleep. Each sound series consisted of 15 pairs of sound pips of one of four sounds. Each sound pip lasted 200 ms, and pips within a pair were separated by 50 ms. Sound pip pairs within a series were presented at 1 Hz. Sound series were separated by 15–30 s. BBN, broadband noise. (b) Sound-triggered rasters (top) and corresponding PSTHs (bottom) from an example AC neuron’s responses to the four auditory stimuli. FR, firing rate. (c) Population average of z-scored PSTHs of all AC cells that were defined in both the first and last daily sound sleep epochs (n = 496 PSTHs from 248 cells) to the different sound stimuli. (d) Example ensemble spiking activity in AC (green) and CA1 (orange) during a sound series. Pink bars indicate sounds; cyan bars indicate detected SWRs. Top black trace is ripple-filtered LFP in CA1. (e) Decoding preceding sound identity from AC pre-SWR patterns within sound series. Top: decoding cartoon. Bottom: histogram of sound decoding gain across sound sleep epochs (n = 26 epochs). Decoding gain for each epoch is defined as the logarithm of the average rate of correctly decoded data (meancorrect) divided by the average rate of correctly decoded shuffled data (meanshuf). The mean of the distribution is significantly larger than 0 (t₂₅ = 3.33, P = 0.0013, cross-validated linear discriminant analysis, population test for mean larger than 0 using one-tailed t-test). (f) Using sound-biased pre-SWR AC patterns to predict CA1 firing during SWRs. CA1 SWR-firing could be significantly predicted (n = 163 predictor-ensemble–predicted-cell combinations across sound epochs, 96 unique predicted CA1 cells, z = 3.4, P = 0.00068, two-tailed rank-sum test compared to shuffled). Error bars indicate s.e.m. **P < 0.01, ***P < 0.001.

SWRs were detected both during and between sound presentations (Fig. 3a,d), and we therefore asked whether sounds biased pre-SWR AC ensemble spiking patterns (−250 to 0 ms relative to SWR onset). We found evidence for this biasing: the identity of the most recently presented sound could be decoded from pre-SWR AC ensemble patterns (n = 26 epochs, t₂₅ = 3.33, P = 0.0013, cross-validated discriminant analysis, population test for mean larger than 0 using one-tailed t-test; Fig. 3e). Notably, these sound-biased pre-SWR AC activity patterns were also predictive of subsequent CA1 spiking during the SWR. We used the generalized linear models derived from silent sleep to determine whether CA1 spiking during SWRs could be predicted from the AC pre-SWR ensemble spiking patterns during sound presentation, and we found significant predictions (n = 163 predictor-ensemble–predicted-cell combinations across sound epochs, 96 unique predicted CA1 cells; z = 3.4, P = 0.00068, two-tailed rank-sum test compared to shuffled; Fig. 3f). These findings linked sound presentations to patterns of activity in AC and to the subsequent spiking seen in CA1 during SWRs. At the same time, sound identity could not be significantly decoded from CA1 ensembles (P = 0.17; Supplementary Fig. 13), likely due to the increased cumulative variability from sounds to AC firing and from AC to CA1.

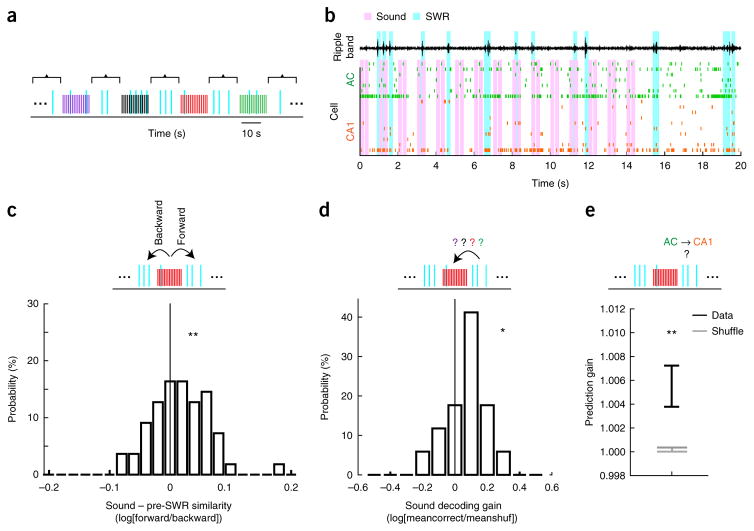
Strikingly, we also found that presentation of sounds continued to bias AC patterns well after the termination of the sound series. We analyzed SWRs that occurred between sound series (2–14 s after the onset of the last sound in each series; Fig. 4a,b) and examined the relationship between the sounds presented immediately previously, the pre-SWR AC activity and the subsequent CA1 SWR activity. The average ensemble AC pattern evoked by a sound series was more similar to pre-SWR patterns that occurred after the sound series (forward similarity) than to pre-SWR patterns that occurred before it (backward similarity; n = 55 epochs, t₅₄ = 2.49, P = 0.0079, population test for mean larger than 0 with one-tailed t-test; Fig. 4c), indicating a sustained effect of sound presentation on AC pre-SWR patterns. Moreover, the identity of the preceding sound stimulus could be significantly decoded from pre-SWR AC ensemble patterns that occurred well after the termination of the sound series (n = 17 epochs, t₁₆ = 1.84, P = 0.0418, population test for mean larger than 0 with one-tailed t-test; Fig. 4d). Finally, just as for pre-SWR patterns during the sound series, these persistent sound-biased AC patterns predicted CA1 SWR firing (n = 162 predictor-ensemble–predicted-cell combinations across sound epochs, 97 unique predicted CA1 cells, z = 2.72, P = 0.0066, two-tailed rank-sum test compared to shuffled; Fig. 4e). These data indicate that sound presentation during sleep biases pre-SWR AC patterns well after sound termination and that these patterns continued to predict CA1 reactivation.

Figure 4.

Sounds bias AC patterns for seconds after sound termination. (a) Illustration of sound series presentation and interseries SWRs during sleep; colors as in Figure 3a. (b) Example ensemble spiking activity in AC (green) and CA1 (orange) during and following a sound series. Pink bars indicate sounds; cyan bars indicate detected SWRs. Top black trace is ripple-filtered LFP in CA1. (c) Similarity between sound-evoked patterns and pre-SWR patterns. Top: similarity cartoon depicting directions for forward and backward similarity. Bottom: distribution of the logarithm of forward similarity divided by backward similarity (Online Methods). Sound patterns were more similar to pre-SWR patterns that occurred after a sound series compared to those that occurred before (n = 55 epochs, t₅₄ = 2.49, P = 0.0079, one-tailed t-test of mean vs. 0). (d) Decoding identity of preceding sound from AC pre-SWR patterns after sound series. Top: decoding cartoon. Bottom: histogram of sound decoding gain across sound sleep epochs (n = 17). Decoding gain for each epoch is defined as the logarithm of the average rate of correctly decoded data (meancorrect) divided by the average rate of correctly decoded shuffled data (meanshuf). The distribution is significantly larger than 0 (t₁₆ = 1.84, P = 0.0418, population test for mean larger than 0 with one-tailed t-test). (e) Predicting CA1 firing during SWRs from sound-biased pre-SWR AC patterns that occurred after sound series. CA1 SWR-firing (n = 162 predictor-ensemble–predicted-cell combinations across sound epochs, 97 unique predicted CA1 cells) could be significantly predicted (z = 2.72, P = 0.0066, two-tailed rank-sum test compared to shuffled). Error bars indicate s.e.m. *P < 0.05, **P < 0.01.

Learning-related and sound-specific changes in SWR density

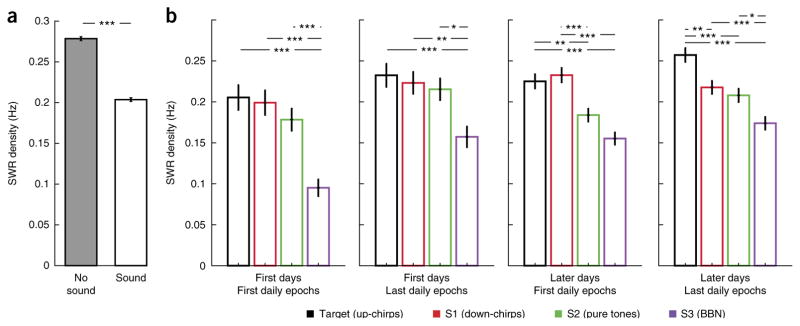
Finally, as presenting meaningful sensory stimuli during sleep can affect memory^41,42, we asked whether SWR dynamics during sound presentation in sleep changed with learning. We found that overall, sound presentation significantly reduced SWR rates as compared to periods between sound series (n = 30,782 stimuli bins and 39,899 no-stimuli bins, z = 19.85, P = 1.07 × 10⁻⁸⁷, two-tailed rank-sum test; Fig. 5a). Notably, however, we also found that SWR rates were significantly sound-specific and modulated across learning. The sounds presented during sleep included the target sound, which gained behavioral significance as the animals learned the task, as well as three other sounds that were not associated with the task. To account for potential learning effects both within and across days, we divided all sound epochs according to whether they occurred before or after the daily training (first and last daily sound epochs) and whether they occurred in the first few days (days 1–3) or later days (days 4 and after), when the rats started to show better task performance. We found that in post-learning epochs on later days of learning, higher SWR rates were observed following the learned target sound as compared to the other sounds (Fig. 5b and Supplementary Fig. 14). Thus, as the target sound became meaningful to the animals, its presentation during sleep was associated with higher SWR rates, similar to those seen outside of sound presentation.

Figure 5.

Learning-related and sound-specific changes in SWR density. (a) SWR density is lower during sound presentation as compared to during silence (n = 30,782 stimuli bins and 39,899 no-stimuli bins, z = 19.85, P = 1.07 × 10⁻⁸⁷, two-tailed rank-sum test). Error bars indicate s.e.m. (b) SWR density during presentation of the different sound series; colors as in Figure 3a. Data are separated into first (1–3) or later (≥4) d of training and denote whether it was the first or last daily sound-sleep epoch. SWR density differed significantly between stimuli in all learning phases (first days–first epochs: χ²_{3, 3,504} = 40.56, P = 8.1 × 10⁻⁹, P(Target,S1) = 0.95, P(Target,S2) = 0.4, P(Target,S3) = 8.2 × 10⁻⁸, P(S1,S2) = 0.73, P(S1,S3) = 1.1 × 10⁻⁶, P(S2,S3) = 0.0001; first days–last epochs: χ²_{3, 4,292} = 17.13, P = 6.7 × 10⁻⁴, P(Target,S1) = 0.97, P(Target,S2) = 0.84, P(Target,S3) = 0.001, P(S1,S2) = 0.98, P(S1,S3) = 0.004, P(S2,S3) = 0.015; later days–first epochs: χ²_{3, 10,948} = 54.36, P = 9.4 × 10⁻¹², P(Target,S1) = 0.98, P(Target,S2) = 0.0035, P(Target,S3) = 2 × 10⁻⁸, P(S1,S2) = 0.0007, P(S1,S3) = 4.9 × 10⁻⁹, P(S2,S3) = 0.056; later days–last epochs: χ²_{3, 12,022} = 55.87, P = 4.5 × 10⁻¹², P(Target,S1) = 0.0019, P(Target,S2) = 3.5 × 10⁻⁵, P(Target,S3) = 3.8 × 10⁻⁹, P(S1,S2) = 0.75, P(S1,S3) = 0.0005, P(S2,S3) = 0.02; Kruskal-Wallis test, stimulus-specific SWR count across stimuli: n = 823, 864, 948 and 873; 1,080, 1,156, 1,119 and 941; 2,719, 2,820, 2,720 and 2,693; and 3,142, 3,165, 2,958 and 2,761, respectively for each sound in each learning phase). Across learning, higher SWR rates occurred during presentation of target sound as compared to the control sounds. *P < 0.05, **P < 0.01, ***P < 0.001; Kruskal-Wallis test with Tukey-Kramer post hoc test. Error bars indicate s.e.m.

DISCUSSION

We found evidence for a cortical–hippocampal–cortical communication loop centered around hippocampal SWRs during sleep. Our results showed that the spiking rate of a considerable fraction of AC cells increased at the time of hippocampal SWRs and that AC ensembles showed increased reactivation of awake experience during SWRs. Fine temporal analysis revealed that pre-SWR AC activity predicted hippocampal firing during the SWR, while pre-SWR hippocampal activity was not predictive of AC firing during the SWR. Conversely, hippocampal patterns during the SWR predicted subsequent AC firing, but AC patterns during the SWR were not predictive of subsequent hippocampal firing. Furthermore, auditory stimuli could be used to influence auditory cortical activity patterns before SWRs, and these patterns were predictive of subsequent hippocampal spiking. Moreover, while sounds reduced SWR rates overall, SWR rates were higher during presentation of the target sound following learning. Thus, our findings strongly suggest that a cortical–hippocampal–cortical loop underlies memory consolidation during SWRs and that this loop can be biased using sensory stimuli.

Our results suggest that memory consolidation processes begin with patterned activity in the neocortex. This is consistent with previous observations of increases in activity in cortical areas preceding hippocampal SWRs^15,18,43. Our findings are also broadly consistent with a previous report of coordinated replay events in hippocampus and visual cortex¹⁷. That study identified and analyzed ‘frames’ of cortical and hippocampal activity, showed that cortical frames tended to occur before hippocampal frames and found that replay events in the two structures were coordinated, but they could not establish directionality of information flow during replay events. Here we extended those previous studies to show that pre-SWR increases are also seen in AC and, notably, that these increases reflect specific patterns of activity, which in turn predict subsequent hippocampal reactivation.

This result supports the notion that cortical reactivation has an instructive role in shaping hippocampus-dependent memory consolidation^44,45. As hippocampal activity preceding SWRs is not predictive of pre-SWR cortical activity, the identity of the cortical ensembles that reactivate appears to be determined by cortical dynamics rather than hippocampal inputs. Moreover, these dynamics are likely influenced by experience. Previous work has established that ensemble activity patterns in AC show similarities to sensory-evoked patterns⁴⁶. In addition, multiple lines of evidence have implicated the AC in memory-related processes on multiple time scales: responses and functional organization of auditory cortex can be substantially affected by recent^27–29 or remote^30–33 experiences. We therefore suggest that experience-driven intracortical plasticity could play an important role in determining the content of memory reactivation and thus the identity of the memories that are consolidated.

Activity from AC could influence patterns of hippocampal activity during SWRs via direct connections from AC to entorhinal⁴⁷ and perirhinal cortex⁴⁸, both of which send projections to the hippocampus. Many sensory areas project directly or disynaptically to entorhinal cortex, and it seems likely that activity in all of these areas could influence subsequent SWRs in CA1. This convergence, in addition to the sparsely sampled ensembles we recorded, is expected to yield limited predictive power when averaged across all ensemble–cell combinations. Nonetheless, the gains we measured when predicting CA1 spiking during the SWR from pre-SWR AC patterns were ~20% of the gain observed when predicting CA1 spiking from CA1 ensemble patterns within SWRs, a gain that reflects the well-established structure underlying sleep replay in CA1. Thus, our results suggest substantial influence of AC on CA1, and as information processing in these areas likely engages ensembles many orders of magnitude larger than those we measured, the prediction gains we report should be considered as a lower bound on the actual prediction gains in the system.

Significant prediction of hippocampal firing during SWRs from preceding AC activity patterns were seen both during silent sleep as well as during sleep when sounds were presented. These findings thus provide a potential mechanism for striking previous observations that sounds can bias subsequent memory^41,42 and for a study showing that sounds during sleep can bias hippocampal reactivation²⁵. In particular, we showed that sounds presented during sleep bias pre-SWR spiking patterns in AC and that these sound-biased patterns are predictive of SWR CA1 spiking. Sensory-stimulation-dependent biasing of memory during sleep may thus be a result of biasing of the cortical–hippocampal–cortical loop we describe here.

We also found that, overall, the rate of SWRs was lower during sound presentation than during quiet periods. This indicates that, while stimuli can bias the content of reactivation in cortex and hippocampus during sleep, they can simultaneously reduce the overall number of reactivation events, at least when the stimuli are relatively novel. Presenting sensory stimuli during sleep may thus lead to better-controlled but overall weaker reactivation. At the same time, SWR rates during sound presentation showed learning-dependent stimulus selectivity, with higher SWR rates observed during presentation of the target sound following learning. Based on these results, we speculate that effective sensory-stimulation-dependent memory biasing during sleep is dependent on familiarity with the biasing stimulus.

Our results also provide evidence for the reverse hippocampus to AC information flow during and after SWRs. The most obvious anatomical connections underlying this information flow are from CA1 to entorhinal cortex, which projects directly to AC (refs. 47,49). Given previous observations of activity in other brain regions during and after SWRs^7,19,37,50, it appears likely that information flow from hippocampus does not exclusively target AC, and it is likely that SWR activity from the hippocampus influences subsequent spiking across multiple cortical and subcortical structures. We note, however, that our measures of information flow are not demonstrations of causal influences between regions, and it remains possible that information flows through pathways other than those proposed here. It further remains to be determined whether the cortical–hippocampal–cortical loop described here is necessary for consolidation.

Taken together, our findings and the available literature lead us to propose that coordinated reactivation across sensory cortical regions immediately preceding SWRs facilitates a flow of reactivated sensory information into the hippocampus. This incoming information biases hippocampal reactivation, which then broadcasts an integrated representation back to the preactivated cortical networks, linking the patterns of activity across multiple cortical areas to consolidate a coherent memory representation.

ONLINE METHODS

Subjects and neural recordings

All procedures were approved by the Institutional Animal Care and Use Committee at the University of California, San Francisco and conformed to National Institutes of Health guidelines. Four Long Evans male rats aged 4–5 months and weighing 450–550 g were used in this study. Animals were housed singly under a regular 12-h light/dark cycle. All behavioral experiments were carried out in the light cycle. As previously described⁵¹, animals were first habituated to daily handling over several weeks. After habituation, animals were food deprived to 85–90% of their baseline weight and pretrained to run on an E-shaped raised track for liquid food rewards (sweetened condensed milk). After animals learned to run and collect rewards on the E-track, they were implanted with a microdrive array with 21 independently moveable tetrodes (groups of four twisted 12.5-μm nichrome wires assembled in a bundle). Seven tetrodes were targeted to the left primary AC (−4.8 mm AP, 5.5 mm ML, 25° lateral from midline) and seven tetrodes to the left dorsal CA1 region of the hippocampus (−3.6 mm AP, 2.2 mm ML). In each animal, one hippocampal tetrode was left in corpus callosum to serve as reference for the hippocampal and cortical tetrodes. The reference tetrode was itself referenced to a ground screw installed in the skull overlying the cerebellum. We also targeted left PFC (seven tetrodes, +3.0 mm AP and 1 mm ML). These data contributed to a previous manuscript¹⁶ but here were used only to assist in sleep state detection (see below). Over the course of two weeks following implantation, hippocampal tetrodes were advanced until characteristic LFP patterns and neural firing patterns indicated that the cell layer had been reached. AC tetrodes were advanced gradually and responses to sound stimuli were used to validate approach to primary AC.

Data were collected using the NSpike data acquisition system^22,52 (L.M.F. and J. MacArthur, Harvard Instrumentation Design Laboratory). We recorded continuous LFP (filtered 0.5–400 Hz and sampled at 1,500 Hz) from all tetrodes (one channel was chosen from each tetrode for LFP recording). Spike data were sampled at 30 kHz, digitally filtered between 300 Hz and 6 kHz (two-pole Bessel for high and low pass) and threshold crossing events were saved to disk (40 samples at 30 kHz). Individual units (putative single neurons) were identified by clustering spikes using peak amplitude, principal components and spike width as variables (MatClust). An infrared light emitting diode array with a large and a small cluster of diodes was attached to the preamps during recording. Behavior sessions were recorded with an overhead monochrome CCD camera (30 fps) and the animal’s position and speed were detected using the infrared diodes.

Behavioral task

After 5–7 d of recovery following microdrive implantation, animals were once again food deprived to 85–90% of their baseline weight and again pretrained for 2–3 days on the E-track with the recording cables connected. Approximately 14 d after implantation, animals were introduced to the Y-track and data gathering commenced. The Y-track (Fig. 1b) was made of 7-cm-wide metal sections with an 84-cm center arm and 64-cm side arms. Animals were trained on the Y-track for 10–12 d in 3–4 20-min training sessions per d with interleaving 20- to 30-min sleep sessions in the rest box (silent sleep). In addition, at the beginning and end of each day, a sound protocol was presented during sleep sessions in the rest box (sound sleep; Fig. 1a).

During training sessions, sweetened condensed milk rewards were automatically delivered in food wells triggered by animal’s nose-poke crossing of an IR beam. Rats initiated each trial by a nose-poke in the home well and receiving a reward. In ~75% of trials the next reward was delivered in the silent well if the rat nose-poked there. In a pseudorandom ~25% of trials (sound trials separated by 2–5 silent trials), 5 s after nose-poking in the home arm, a target sound series was emitted from a speaker, indicating that the next reward would be delivered in the sound well if the rat next nose-poked there. The speaker was placed at the end of the sound arm in the first days of training and moved to the center junction after rats displayed consistent correct choices in more than ~70% of trials. The locations of the home, silent and sound wells were fixed across days. The target sound was a pair of upward chirps, consisting of one 200-ms chirp with frequency modulated from 3 to 4 kHz, an interchirp interval of 50 ms, and a second 200-ms chirp with frequency modulated from 9 to 12 kHz (Supplementary Fig. 11). The series of target sounds was presented at 1 Hz and stopped after 12 s or once the rat made a correct or incorrect choice by a nose-poke in one of the wells. Reward amount in the sound well was double the reward amount in the home or silent well. Performance for the inbound direction was measured as the percentage of trials in which the rat correctly returned to the home well after nose-poking in one of the outer arms, and performance for the outbound direction was measured as the average of the percentage of correct visits to the sound well and the percentage of correct visits to the silent well following a departure from the home well.

Following the conclusion of the experiments, subjects were anesthetized with isoflurane and we made electrolytical lesions through tetrode tips (30 μA for 3 s) to mark the recording locations. Animals were allowed to recover overnight and were then euthanized the following day with pentobarbital and were perfused intracardially with PBS followed by 4% paraformaldehyde in PBS. The brain was postfixed in situ overnight, after which the tetrodes were retracted and the brain removed, cryoprotected (30% sucrose in PBS) and embedded in OCT compound. Coronal sections (50 μm) were taken with a cryostat and Nissl-stained with cresyl violet.

Auditory protocol in sound-sleep sessions

The auditory protocol in the sound-sleep sessions consisted of series of the target sound (target) and 3 additional sound pairs (S1, S2 and S3; Fig. 3a and Supplementary Fig. 11). S1 was a pair of down-modulated chirps (first chirp frequency modulated from 9 kHz to 6.75 kHz, second from 3 kHz to 2.3 kHz), S2 was a pair of pure tones (first tone at 5 kHz, second at 2 kHz) and S3 was a pair of amplitude-modulated broadband noise sounds (first modulated at 20 Hz, second at 4 Hz). Each sound series consisted of 15 pairs of sound pips. Like the target sound presented on the track, each sound pip lasted 200 ms, and pips within a pair were separated by 50 ms. Sound pip pairs within a series were presented at 1 Hz. Each sound series included sound pips of one of the four sounds. Sound series were separated by 15–30 s. The full protocol included a total of 10 series per sound type. Only responses that occurred during NREM sleep were analyzed. We presented additional auditory stimuli separately after the sound epochs described above, but these were not analyzed here. These stimuli included single (nonpaired) sound pips and in 2 animals, dynamic moving ripple stimuli.

Data analysis

Data analysis was performed using custom software written in Matlab (MathWorks).

Sleep detection

Hilbert amplitudes (smoothed with a Gaussian kernel, σ = 1 s) of filtered theta (6–12 Hz), delta (1–4 Hz) and spindle (8–20 Hz) band LFP were calculated for all available hippocampal and cortical tetrodes and the mean taken over tetrodes within each region. All analyses on sleep data were performed on identified NREM sleep, and all awake and REM periods were excluded. NREM sleep was identified as periods in rest epochs that met these criteria: (i) the animal was immobile (< 0.5 cm/s) for more than 10 s or spindles were detected and (ii) the animal was not in REM sleep. REM sleep was identified based on elevated ratio of hippocampal theta to cortical delta band power and elevated ratio of hippocampal theta to cortical spindle power with the requirement that a single REM bout lasted at least 10 s. Cortical spindles were identified as periods in rest epochs that met three criteria: (i) the animal was immobile (< 0.5 cm/s) for more than 5 s, (ii) the cortical spindle to delta band power ratio was >1 and (iii) the animal was not in REM sleep. We used a highly conservative speed threshold of < 0.5 cm/s to exclude periods of small head movements.

SWR detection

SWRs were detected using LFPs filtered in the 150–250 Hz range on multiple CA1 tetrodes as previously described⁵³. Increases in power in the ripple band were detected using a 3-s.d. criterion, with the condition that the SWR had to be detected on at least two tetrodes.

Unit inclusion

Only cells with more than 500 spikes in ±5-s windows around all daily sleep SWRs were included (e.g., for 500 daily SWRs this meant a minimum of 0.1 Hz around SWR times). Putative CA1 interneurons (firing rate > 7 Hz) were also excluded.

SWR modulation

To quantify the SWR modulation of AC and CA1 cells, we first created an SWR-triggered raster across SWRs that occurred in NREM sleep during all silent rest epochs in that day. To avoid contributions from other SWRs that might have occurred in close temporal proximity, we only included SWRs that were separated from other SWRs by at least 500 ms in both directions in the SWR modulation analysis, thus ensuring accurate temporal assignment of spiking activity to SWRs. We detected a daily mean ± s.e.m. of 574.9 ± 26.6 temporally well-isolated SWRs during silent NREM sleep at a rate of 0.21 SWRs per s. These relatively low SWR rates were due to our conservative procedure of analyzing only SWRs separated by at least 500ms from other SWRs to allow reliable temporal assignment of spikes to SWRs. The rate of SWRs before this procedure was 0.43 SWRs per s (Supplementary Fig. 2). We then averaged each SWR-triggered raster to yield a peri-SWR time histogram (PSTH). To quantify whether this histogram shows a significant modulation, we then created 1,000 shuffled SWR-triggered rasters by circularly jittering the spiking in each row (SWR) by a random amount. We averaged each shuffled raster to produce a shuffled PSTH. We defined a baseline PSTH as the mean of all shuffled PSTHs. We then calculated for the real and shuffled PSTHs their mean squared difference from the baseline PSTH in the −250 ms to +250 ms window relative to SWR onset.

In examining the data from single days we noted several instances where SWR modulation appeared to strengthen or weaken within the day. To ensure that we analyzed all cells that showed some degree of SWR modulation, we performed the above procedure separately for the first and second half of daily SWRs and determined that a cell was significantly SWR-modulated if in either the first or second datasets the mean squared difference of the real PSTH from the baseline PSTH was greater than 95% of mean squared differences of shuffled PSTHs from the baseline PSTH. This analysis has a false positive rate of 0.0975 (the rate of SWR modulation being not due to chance in both dataset tests is 0.95 × 0.95 = 0.9025, and therefore the false positive rate is 1 – 0.9025 = 0.0975), and the observed frequency of SWR modulation in AC cells (117/322) has a probability of occurring by chance of P < 10⁻¹⁰, given that false positive rate. Using a more stringent criterion of assessing all daily SWRs together at P < 0.05, 77/322 (24%) of AC cells and 160/192 (83%) of CA1 cells were significantly SWR modulated. The temporal profiles of the mean z-scored SWR-triggered PSTHs using this criterion showed the same pattern as using the dual condition (Supplementary Fig. 3).

Network reactivation analysis

For the network reactivation analysis we used a previously developed PCA approach^7,54. Using this method we derived ensemble patterns from activity during awake training epochs, and by using those patterns as templates on network patterns during identified NREM sleep, we quantified the similarity of the sleep ensemble activity to the awake template across time. To do so, we first binned all spiking data into 200-ms bins, only including cells that were clustered during both waking and sleep and only including ensembles with at least four AC cells. We then concatenated all included bins from the daily awake epochs, z-scored each cell’s binned firing rate and derived the correlation matrix C of all cell pairs. We calculated the first eigenvector of C (the first principal component of the data) and corresponding eigenvalue and defined the ‘projector’ as the outer product of the eigenvector with itself, multiplied by its eigenvalue and setting the diagonal to 0. Significance of principal components (PCs) were verified as in Peyrache et al.⁷ and nonsignificant PCs were excluded. The projector defines a template of pairwise correlations in the awake behaving state. To measure the similarity of this template to the ongoing network activity during NREM sleep, we first similarly binned and z-scored the network activity in NREM sleep in each silent rest epoch. For each time bin, we calculated the outer product of the network pattern (a vector of spike counts from all cells) in that time bin with itself, which describes the pairwise coactivity in that time bin. Finally, to determine how similar this coactivation pattern is to that derived from the awake template, we calculated the sum of the dot product of the projector with the outer product of the momentary network pattern.

To assess the significance of reactivation, we performed the procedure 100 times by projecting a shuffled awake pattern on the sleep ensemble activity and comparing mean reactivation strength of the real versus shuffled data. A shuffled awake pattern was constructed from independently circularly shuffling the binned spiking activity of each cell in the ensemble. The P-value of reactivation of the real data was determined as the fraction of shuffles in which the mean shuffled reactivation was larger than the mean real reactivation. Significant reactivation was determined with a P < 0.05 criterion.

To examine the temporal relationship between reactivation and SWRs, we calculated the cross-correlation between the reactivation trace and all detected SWR events in each sleep epoch (no inter-SWR minimum was applied). Each SWR-triggered reactivation profile was then z-scored before combining data across epochs.

GLM in silent sleep sessions

We constructed generalized linear models (GLMs) with a log link function to predict spike counts of single cells during SWRs in CA1 or AC from ensemble spiking patterns in AC or CA1 during specific time windows. SWRs (separated by at least 500 ms from other SWRs) detected during NREM sleep across all daily silent sleep epochs were included, and only cells that were clustered across all daily epochs were included. Spiking activity of each neuron was binned in 200-ms bins relative to SWR onset: −600 to −400 ms, −400 to −200 ms, −200 to 0 ms and 0 to 200 ms. The 0- to 200-ms bin was defined as that cell’s SWR response. An ensemble pattern in a specific bin was the vector of binned spiking responses across cells.

We used ensemble patterns in the different time bins to predict single-cell SWR responses. In a dataset for a single prediction model in a single time window, the predictor data consisted of the ensemble patterns in that time window across SWRs, and the predicted data consisted of the single-cell SWR responses across SWRs. Only cells that were active (> 0 spikes) in more than 10 SWRs were predicted. For each combination of predictor ensemble and predicted cell, we then performed five-fold cross validation (Supplementary Fig. 7). We randomly partitioned the daily SWRs into five equally sized sets, with the constraint that the number of nonzero values in the predicted vector must be approximately balanced across sets. For each fold, we used four of five folds to train the GLM model and the remaining fold to test. For the test phase, the model derived from the training phase was applied to the predictor ensemble data in the test set, yielding predictions for the predicted cell firing across SWRs.

We defined the prediction error as the mean absolute difference between the predicted spike counts and the real spike counts. For that same fold, we defined a baseline prediction error by performing 100 random shuffles of the predicted firing rates across SWRs in the test fold and taking the mean of the shuffled prediction errors. The real and shuffled prediction errors were then averaged across the five folds. Prediction gain for one predictor-ensemble–predicted-cell combination in one time window was defined as the shuffled prediction error divided by the real prediction error. Shuffled prediction gains were not different across time windows (Kruskal Wallis, P > 0.98).

For comparison, we repeated the exact same procedure described above on 100 random shuffles of the entire original dataset, where shuffling entailed random matching of activity patterns in the predictor and predicted data (e.g., taking predictor data for one SWR and using it to predict firing rate for another SWR). To assess prediction significance in a given time window, we compared the distribution of real prediction gains to the shuffled prediction gains across all ensemble/cell combinations using a two-tailed nonparametric rank-sum test.

Predictions of activity in post-SWR and pre-SWR time windows were performed using the same approach.

Analysis of sound sleep epochs

There were two sound sleep epochs per day, at the beginning and end of each day. SWRs in sound sleep sessions were identified as described for the silent sleep epochs. Only SWRs separated from other SWRs by at least 400 ms on both sides were included. We used a slightly more permissive separation window for these analyses because there was a much smaller number of SWRs and because we did not focus on timing for these analyses. Spiking data was binned into 250-ms bins, where an SWR bin was from 0–250 ms from SWR onset and the pre-SWR bin was from −250 to 0 ms. We used slightly larger bins than the 200-ms bins to capture most of the pre-SWR modulation we observed in two bins (−400 to −200 and −200 to 0) in a single bin. For the within-sound-series analyses, we included all SWRs that occurred from the onset of the first sound in each series to 2 s after the onset of the last sound (or 1.5 s after the termination of the last sound, where the sound period is defined as the sum over: first pip (200 ms), inter-pip interval (50 ms), second sound pip (200 ms) and offset response window (50 ms)). Only epochs with at least three AC cells, two CA1 cells and 30 SWRs were included.

Sound decoding from pre-SWR AC patterns

To decode sound identity from pre-SWR AC ensemble patterns, we used a cross-validated discriminant analysis classifier. For each epoch, the data consisted of AC ensemble patterns in the pre-SWR windows as predictors and the identity of the preceding sound to be predicted. The preceding sound could be any one of the four presented sounds. To have enough data for decoding, we only used epochs with at least 100 SWRs.

We used 1,000 repeats of five-fold cross validation for each dataset. For each dataset, the data was randomly partitioned into five roughly equally sized groups. For each fold, we used four of the five folds as training set while the remaining fold was used as test set. We fit a pseudoquadratic discriminant classifier on the training set and used it to predict the sound identities from ensemble patterns in the test set. Our measure of prediction quality was the rate of correctly predicted patterns averaged across folds and repeats. The same procedure was performed for a shuffled training set, in which the correspondence between ensemble patterns and sound identity were randomly shuffled. Decoding gain for an epoch was defined as the mean of correctly decoded patterns of the real data divided by the mean of correctly decoded patterns of the shuffled data. Decoding significance across epochs was quantified by determining whether the distribution of the logarithm of decoding gains was significantly larger than 0 using a one-tailed t-test.

Decoding preceding sounds from pre-SWR AC patterns that occurred after sound series termination was performed similarly but including SWRs that occurred during silent periods from 2 to 14 s after the onset of the last sound in each series.

GLM in sound sleep epochs

To determine whether sound-biased pre-SWR AC patterns were predictive of CA1 firing during the SWR, we used GLM models created from NREM sleep during silent sleep epochs and applied them to NREM sleep during sound presentation. For each combination of AC ensemble firing in the pre-SWR time window and CA1 cell firing in the SWR window, we derived the full GLM model from the silent sleep epochs. We then used this model on the sound biased AC ensemble pre-SWR data (−250 to 0 ms relative to SWR onset) to predict CA1 cell firing during the SWR (0 to 250 ms relative to SWR onset) and defined the prediction error as the mean absolute difference between predicted and real firing rates. We then defined a baseline prediction error by performing 1,000 shuffles of the predicted firing rates across SWRs and taking the mean of the shuffled prediction errors. Prediction gain was defined as the mean shuffled prediction error divided by the real prediction error. For comparison, we repeated the same procedure 100 times after shuffling the correspondence between AC ensemble firing and CA1 SWR firing across SWRs in the original silent sleep dataset. Prediction significance was estimated by comparing the distribution of real prediction gain to the distribution of the shuffled prediction gain using a two-tailed rank-sum test.

Sound–SWR similarity

We compared AC ensemble patterns evoked by a sound series to the AC ensemble patterns that occurred in pre-SWR time windows following sound-series termination (forward similarity). For this analysis we included SWRs that occurred during silent periods from 2 to 14 s after the onset of the last sound in each series. Within a sound series, we defined the response to each sound pair as the number of spikes that occurred in the 0–500 ms window from sound onset (200-ms first sound pip, 50-ms interval and 200-ms second sound pip, 50-ms offset) divided by 2 to allow direct comparison to the 250-ms pre-SWR windows. To avoid the effects of different responses to the first or last sounds within a series, we defined the sound-evoked response of one sound series as the average network pattern across all individual sounds in that series. We then measured the similarity between the sound-evoked response of a series to the ensemble patterns that occurred in the pre-SWR windows of SWRs that occurred 2–14 s after the onset of the last sound in each series. To do so, we calculated the mean Euclidean distance between the sound-response patterns and the pre-SWR patterns. For comparison and normalization we also calculated this 1,000 times while shuffling the correspondence between sound identity and pre-SWR for each cell. We defined forward similarity as the average Euclidean distance of shuffled data divided by the average Euclidean distance for the real data, and thus high values indicated higher similarity between the sound patterns and following pre-SWR patterns. We then measured the similarity of the sound-evoked patterns of sound series to pre-SWR patterns that occurred before (instead of after) the series and termed it ‘backward similarity’. For backward similarity, the sound-evoked pattern of each sound series was compared to pre-SWR patterns that occurred in the −14 to −2 s relative to onset of the first sound in the series. To determine whether sounds biased pre-SWR patterns that occurred after them we calculated for each epoch the forward similarity divided by the backward similarity and tested whether, across epochs, the logarithm of this distribution was larger than 0 with a one-tailed t-test.

SWR rate during sound series

To examine SWR rates during sound series across learning, we considered all SWRs that occurred during NREM sleep and that were separated from other SWRs by at least 400 ms on both sides. For each sound presentation, we counted the number of SWRs that occurred in a 1-s window starting from sound onset and summarized these counts by sound type and day/epoch. To calculate SWR rates during no-sound conditions (Fig. 5a), we summarized SWR counts across all 1-s time bins occurring between sound series (> 2 s after last sound). As learning occurs both within day and across days, we separated sound sleep epochs according to whether it was the first or last within a day and whether it was in the first days of training, before animals showed signs of learning the task and the meaning of the target sound (days 1–3), or later (days ≥ 4). We averaged SWR rates within each of four groups: ‘first days, first epochs’, ‘first days, last epochs’, ‘later days, first epochs’ and ‘later days, later epochs’. Difference between SWR rates across stimuli was tested using a nonparametric Kruskal-Wallis test with a Tukey-Kramer post hoc test.

Statistical methods

Mean or medians are given with s.e.m. Unless otherwise noted, all tests were two-sided and nonparametric. One-tailed t-tests were used in Figures 3e and 4c,d to test whether the distribution mean was larger than 0. The distributions in these cases did not deviate from Gaussian (Lilliefors test, P > 0.5). Multiple comparisons were corrected using Tukey-Kramer post hoc test. No statistical methods were used to predetermine sample sizes; however, sample sizes were similar to those generally employed in the field. Data collection and analysis were not performed blind to the conditions of the experiments and no randomization was used.

Data availability

The data that support the findings of this study will be made available upon reasonable request. A Supplementary methods checklist is available.

Code availability

The code used in this study will be made available upon reasonable request.