The deep history of the number words

Abstract

We have previously shown that the ‘low limit’ number words (from one to five) have exceptionally slow rates of lexical replacement when measured across the Indo-European (IE) languages. Here, we replicate this finding within the Bantu and Austronesian language families, and with new data for the IE languages. Number words can remain stable for 10 000 to over 100 000 years, or around 3.5–20 times longer than average rates of lexical replacement among the Swadesh list of ‘fundamental vocabulary’ items. Ordinal evidence suggests that number words also have slow rates of lexical replacement in the Pama–Nyungan language family of Australia. We offer three hypotheses to explain these slow rates of replacement: (i) that the abstract linguistic-symbolic processing of ‘number’ links to evolutionarily conserved brain regions associated with numerosity; (ii) that number words are unambiguous and therefore have lower ‘mutation rates’; and (iii) that the number words occupy a region of the phonetic space that is relatively full and therefore resist change because alternatives are unlikely to be as ‘good’ as the original word.

This article is part of a discussion meeting issue ‘The origins of numerical abilities’.

1. Introduction

In previous work, we introduced the formal study of rates of lexical replacement as estimated from statistical models applied to phylogenetic trees of languages [1]. By ‘lexical replacement’ we refer to the replacement over evolutionary time of a word for a given meaning by a new and non-cognate word. For example, the word hand in English is cognate to the German hand but not to the Spanish mano, which in turn derives from the Latin manus. Both the Germanic and Romance languages independently trace their ancestry back to a proto-Latin language. This suggests that the word hand is a newer and non-cognate form that probably arose somewhere along the lineage that eventually gave rise to the Germanic languages.

In our earlier study, we found that rates of lexical replacement varied around 100-fold among the 200 items in the widely used Swadesh fundamental vocabulary [2]. The Swadesh list includes words that might be expected to be found in all languages, such as common nouns, verbs, adjectives and adverbs, names of body parts, kinship terms and the number words from one to five; it avoids words specific to particular habitats or climates, as well as technical terms. We found that dirty was the most rapidly evolving word in the list, with a rate of lexical replacement of about 0.0009 per annum, or approximately one new non-cognate form every thousand years [1]. This rate of replacement yielded 47 different non-cognate forms among the 86 Indo-European (IE) languages in our sample. By comparison to words for dirty, the words with the slowest rates of lexical replacement were represented by just a single cognate form across the entire IE language tree. Among these slowly evolving forms were the number words two, three, five, and the pronouns who and I.

The rates of lexical replacement for the slowly evolving words correspond to an expectation of one change in one hundred thousand years. If this figure seems extreme, consider that the IE language family is somewhere between 7000 and 8000 years old [3]. Summing the time represented by all the branches that make up the tree of the 86 IE languages we studied yields approximately 140 000 language-years of potential evolution. Remarkably, during that time all the forms of the words for two (e.g. dos, due, deux, duo, and twee, among others) remained cognate, as did those for three, five, who and I. The words one, four, we, when and tongue round out the 10 most slowly evolving words in the IE languages.

The preponderance of number words in the list of slow evolvers raises the question of whether their slow rates of replacement are just an idiosyncrasy of IE, or represent a more general phenomenon. Some reason to think that the slow rate of change of the number words might be a general phenomenon can be found in recent work on ‘numerosity’—the ability to gauge number without a symbolic counting system—in animals. The ability to gauge number is almost certainly useful in foraging, competitive, navigation and mating situations, and studies of the brains of animals ranging from insects [4] to cephalopods [5], fish [6], amphibians [7], birds [8] and mammals [9,10] suggest the existence of dedicated populations of neurons attuned to the perception of number, especially small numbers.

Here, we extend our study of rates of lexical replacement from our previous IE sample to new data on the IEs, and to Bantu and Austronesian language datasets, with special emphasis on the relative rates of replacement of the ‘low-limit’ number words one to five.

2. Material and methods

(a). Lexical datasets

We use three published lexical datasets. The IE data comprise the words for 200 meanings in each of 103 languages [3]. The Austronesian data comprise 210 meanings and 400 languages [11], and here we use the 154 meanings with fewer than 200 cognate classes (see electronic supplementary material). The Bantu data comprise 424 languages and 102 meanings [12]. The meanings in these datasets are taken principally from the Swadesh fundamental vocabulary 200-word list [2]. The raw data for the IE and Austronesian languages are available upon request from the authors of those studies, and for the Bantu they are made available as part of the supplementary information to that paper. Alternatively, the IE data are available at IELex (ielex.mpi.nl) and the Austronesian data are made available in the Austronesian Basic Vocabulary Database (ABVD, language.psy.auckland.ns/austronesian).

(b). Phylogenetic trees

We used the Bayesian posterior samples of phylogenetic trees made available upon request by the authors of the IE and Austronesian, and for the Bantu as part of the supplementary material of the original study [3,11,12]. Each study employed Bayesian Markov Chain Monte Carlo methods [13] to estimate posterior distributions of time-calibrated trees. The trees are rooted and have node ages derived from historical calibration points and statistical inference: the IE tree is dated to approximately 7654 ± 915 years old, the Austronesian tree to 6924 ± 500 years and the Bantu tree to 6929 ± 418 years. Branch lengths on the trees are calibrated in years and so lexical replacement rates we report here are in units of expected changes per annum.

(c). Cognate classifications

The lexical datasets group the words for each meaning into between 1 and k cognate classes denoting sets of words that are derived from a common ancestral word, based on expert linguist judgements as described in the original references.

(d). Modelling rates of lexical replacement

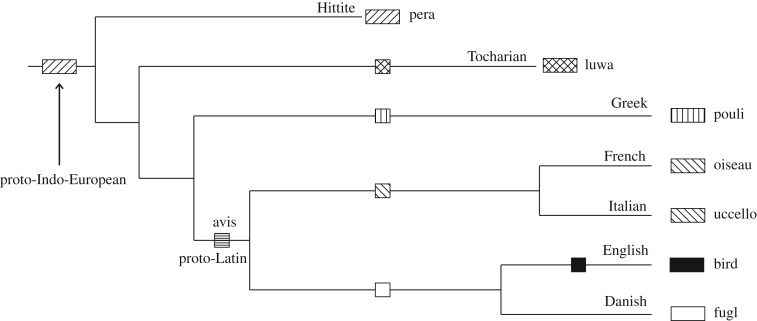
Given the lexical data for each meaning coded into k distinct cognate classes, we observe for each meaning a set of states (1 … k) at the tips of phylogenetic tree T, where the tips correspond to individual languages and the tree describes the patterns of descent of the set of languages from a common ancestor (e.g. figure 1).

Figure 1.

Partial phylogenetic tree of the IE languages showing the words that the languages use for the meaning ‘bird’, coded to identify cognate classes. Squares along the branches identify regions of the tree where new cognate classes might have arisen, although the analysis strategy integrates over all possible ancestral transitions [14] and so is not conditional upon any particular set of them.

We wish to discover the rates at which those k states arose given the assumption that they began from a common ancestral state at the root of the tree. We presume that a series of replacements has taken place throughout the tree eventually producing the k cognate sets. To capture this process, we define the instantaneous transition rates q_jk from any beginning state (cognate class) j to any end state k, for all pairs of beginning and end states jk.

The set of q_jk defines a square matrix Q of order k × k, where Q is given by

and, by convention, the main diagonal elements (q_jj) are given by .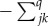

We expect k to vary considerably across meanings (e.g. compare k = 47 for dirty and k = 1 for two in our previous study), leading to the expectation of different average rates of lexical replacement among meanings. Accordingly, we re-write Q as

where r_i is now meaning i's generalized rate of transition and the term 1/c is a normalization constant that, without any loss of generality, scales the q_jk to have a mean rate of 1.0. This scaling means that the q_jk can be interpreted as deviations around the generalized rate r_i. The normalization constant is calculated as

where p_j is the probability of state j in the observed data.

With Q defined this way, the probability of a lexical change (appearance of new non-cognate word) from state j to state k over short interval of time dt, P_jk(dt) = Q_jkdt, where P and Q are matrices. To estimate the probability of transitions over longer time t, P_jk(t), Q is exponentiated to give P(t) = e^Qt, and P is the matrix of transition probabilities. This structure defines the usual continuous time Markov model (e.g. [14]).

We estimate Q using Bayesian Markov Chain Monte Carlo methods (e.g. [13]) to find

where L(D|Q,T) is the likelihood of the data (the observed cognate sets for a meaning) given Q and the phylogenetic tree T. The Monte Carlo integration is performed simultaneously over increments in Q and T and these increments are drawn from, in the case of Q, a suitable proposal mechanism for altering the values of the q_jk, and in the case of T by calculating the likelihood over the posterior sample of trees. Integrating over Q and T ensures that the estimates of the q_jk take into account uncertainty in the model of evolution and in the phylogenetic tree.

The number of elements in Q increases as the square of k, the number of cognate sets. Thus, even for a relatively small k, there can be a large number of parameters to estimate. To reduce the severity of this problem, we employ a reversible-jump Markov Chain Monte Carlo method we have previously developed [15] that automatically collapses the large number of parameters in Q into a smaller number of distinct classes within which the individual q_jk can be regarded as identical statistically.

The procedures for estimating the likelihood are implemented in the BayesTraits comparative-phylogenetic analysis package (www.evolution.reading.ac.uk). We provide a sample command file in the electronic supplementary material. The analysis yields a Bayesian posterior sample of Q and the r_i, as defined above. Our interest here is in the mean of the posterior sample of the r_i as an estimate of the generalized rate of change for meaning i.

(e). Estimation of a lexical half-life

Given a generalized rate r_i for meaning i, define the half-life of words for that meaning as the expected amount of time before there is a 50% chance that word j will have been replaced by word k [1,16]. The half-life can be written as

3. Results

(a). Rates of lexical replacement in the three language families

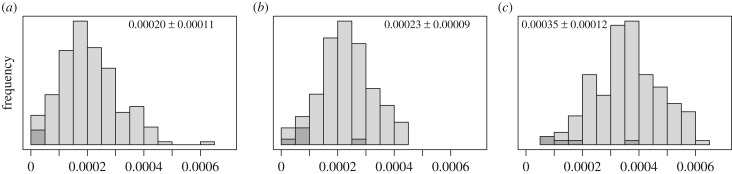
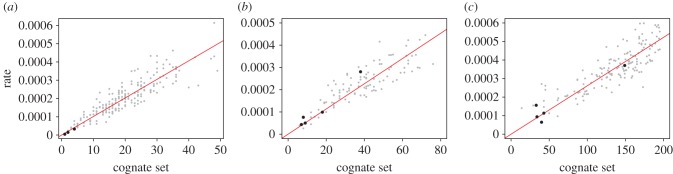
The distribution of generalized rates over the Swadesh list items takes a broadly similar uni-modal form in all three language families (figure 2a–c), and rates of lexical replacement vary within each family from 10 to over 100-fold (table 1). The rate of replacement for bird in the IE languages at 0.00017 (figure 1) falls just below the mean IE rate, and, as before, dirty has the fastest rate of replacement. The IE rates of change correlate r = 0.91 with the rates of change from our previous study [1] despite the new rates coming from a new tree that includes about 15% more languages. Rates of change correlate strongly, but not perfectly, with the number of cognate sets (a large number of cognate sets implies more replacements per unit time): r = 0.89 for IE; r = 0.86 for Bantu; r = 0.85 for Austronesian (figure 3a–c).

Figure 2.

Rates of lexical replacement per annum. (a) rates of lexical replacement in the IE languages for 200 Swadesh list meanings; (b) rates of lexical replacement in the Bantu languages for n = 102 meanings; (c) rates of lexical replacement in the Austronesian languages for n = 154 meanings. The darker shaded areas of each histogram correspond to the position of the low-limit number words (one to five). The rate for one is elevated in the Bantu and Austronesian datasets.

Table 1.

Average±standard deviations of lexical replacement rates for the fundamental vocabulary items and for the low-limit number words, and half lives for the fundamental vocabulary.

replacement rate, per annum	Indo-European (n=200 words)	Bantu (n=102 words)	Austronesian (n=154 words)
overall	0.00020 ± 0.00011	0.00023 ± 0.00009	0.00035 ± 0.00012
fastest, slowest, ratio (f/s)	0.00061, 0.0000047, 130	0.00045, 0.000026, 17	0.00065, 0.000065, 10
half-life, years: average, shortest, longest	3465, 1066, 147 000	3150, 1540, 26 659	1980, 1066, 10 582
‘low-limit’ number words (one to five)exclude one	0.00001 ± 0.00004 (p < 0.0001)	0.00011 ± 0.00009 (p < 0.003)	0.00016 ± 0.00005 (p < 0.0001)
		0.00006 ± 0.00003 (p < 0.00003)	0.00010 ± 0.0.00005 (p < 0.0001)

Figure 3.

Correlations between number of cognate sets (x-axis, NOS) and rate of lexical replacement, in (a) the IE languages for 200 Swadesh list meanings; (b) the Bantu languages for n = 102 meanings; (c) the Austronesian languages for n = 154 meanings. The darker circles correspond to the low-limit number words. The rate and number of states for one are relatively high in the Bantu and Austronesian datasets.

The lack of a perfect correlation between the number of cognate sets and rates of change illustrates the importance of the phylogenetic tree, or more generally, of history in understanding evolution. Two meanings might have an equal number of cognate sets but if the historical lexical replacements (e.g. figure 1) are distributed differently throughout the tree, the rates of replacement will also differ. This is why the scatter about the regression lines in figure 3a–c increases with the number of cognate sets—as the number of cognate sets grows there are more different ways to distribute them around the tree. For the data we report here, the phylogeny is responsible for around 21–28% of the variation in rates of change among the meanings, these figures being derived from 1 − r² of the above correlations.

The average rates of lexical replacement in the IE and Bantu languages correspond to roughly a 20% probability of lexical replacement per thousand years, remarkably close to the value Morris Swadesh proposed in the 1950s from analysing differences between pairs of ancestral and descendant languages—such as ancient and modern Greek—separated by known times [2].

The average rate of lexical replacement among the Austronesian meanings is significantly higher than for Bantu or IE. We cannot be certain whether this represents a true difference or perhaps a difference in linguistic practice in identifying cognate words, the so-called ‘lumpers’ versus ‘splitters’ problem that can also plague taxonomic practice in zoology. Alternatively, the Austronesian expansion into Oceania was a process of ‘island hopping’ as the Austronesian people pushed further and further into the unknown and uncharted Pacific [17]. It is possible then that serial founder effects have influenced the Austronesian languages[18], where idiosyncrasies among the speakers on a temporally ancestral island get magnified among the small number of speakers who move on to descendant islands. Whatever the explanation, by restricting ourselves to the 154 meanings with fewer than 200 cognate classes (see Material and methods) our average rate of lexical replacement for Austronesian could even be an underestimate.

It is difficult to know why the upper bound of the Bantu rates is lower than that for IE or Austronesian. It might reflect sampling: the 102 meanings in the Bantu list do not include the nine fastest rate items from the IE list. On the other hand, rates of lexical replacement, while significantly correlated among language families, are only modestly so: for IE and Austronesian, r = 0.47, p < 0.0001; Bantu and Austronesian, r = 0.37, p = 0.0006; IE and Bantu, r = 0.24, p = 0.0283.

Half-life figures based on the rates of lexical replacement vary widely but even among the Austronesian languages a slowly evolving word has a half-life of over 10 000 years (table 1). The IE languages seem to be extreme and this might arise, because their smaller sample size and total tree length mean some changes have been missed. The total tree length is the sum of the times over all of the branches of the phylogenetic tree. For IE this is 148 400 years, for Bantu it is 490 660 and for Austronesian it is 718 000.

(b). Rates of lexical replacement of the low-limit number words (one to five)

The low-limit number words fall at the slower (lower) end of all three distributions of rates (figure 2a–c and table 1), and dominate the list of slowly evolving words in all three language families (table 2). Their rates of replacement are 3.5–20 times slower than the average rates of replacement and 10–130 times slower than the fastest rates of replacement (table 1). Accordingly, low-limit number words account for most of the longest half-lives (table 1). Replacement rates for the number word one are higher in all three languages families than for two to five (table 2). We do not know why this is the case but speculate that it might have something to do with one being replaceable in some circumstances by ‘a’ or ‘an’. This grammaticalization by one to take over the use of articles has occurred, among other languages, in English, German, Romanian, Spanish, French and Italian. The probabilities of observing all five low-limit number words among the slowest 11 words, or four of the five as in the case of Bantu and Austronesian, are all less than 0.0004 (table 2). The extremely slow rates of lexical replacement in the IE languages for the low-limit number words might arise because 148 400 language-years is not sufficient to observe more than one change (as above).

Table 2.

Rank order of rate of lexical replacement for the 11 meanings with the slowest rates of change; rank = 1 is slowest. Words ‘one’ to ‘five’ in italics. The probability of all five low-limit number words appearing in the slowest 11 for IE is p = 0.0000002; the probability of four of the five low-limit number words appearing in the slowest 11 for Bantu is 0.00036 and 0.00007 for Austronesian.

rank	Indo-European (n = 200 words)	Bantu (n = 102 words)	Austronesian (n = 154 words)
1	two	eat	child
2	three	tooth	two
3	five	three	to pound/beat
4	who	eye	three
5	four	five	to die
6	I	hunger	eye
7	one	elephant	four
8	we	four	ten
9	when	person	five
10	tongue	child	tongue
11	name	two	eight

(c). Low-limit number words in the Pama–Nyungan family

The Pama–Nyungan language family is widely geographically distributed throughout Australia [19,20]. Its languages typically have simple low-limit number systems often not exceeding five [19]. A dated phylogenetic tree for this language family is not available, making it impossible to calculate lexical replacement rates. However, Claire Bowern (2017, personal communication) who has studied this group extensively has made available to us data for 183 vocabulary words in 190 Pama–Nyungan languages, recording the rank orders across meanings of the number of cognate sets per meaning, and classified into 17 categories, including the number words, kinship terms and words for the environment. The dataset includes three number words—one, two and three—and their mean rank order is the lowest (fewest cognate sets) of any of the seventeen categories of words.

4. Three hypotheses to explain the unusual conservation of the number words

Previously, we have shown that words used more frequently in everyday discourse tend to be among the most conserved or slowly evolving [1]. Even among the slowly evolving words, the number words are unusual in having rates of lexical replacement considerably slower than would be predicted from their frequency of use [1]. Here we speculate on three hypotheses that might explain why the number words evolve so slowly, and offer data consistent with each.

(a). Evolutionarily conserved brain regions associated with numerosity (somehow) influence the learning and use of linguistic-symbolic number words

Could the evolutionarily ancient and seemingly hard-wired nature of many animals' abilities to perceive ‘number’ independently of a symbolic language for counting [4–10] be linked to the slow replacement rate of number words? Brain regions associated with numerosity are distinct from those involved in language [10,21]. Still, brains are vast interconnected and highly parallel networks that can make available their internal representations or outputs to other brain regions. Perhaps an unambiguous brain state associated with simple judgements of different numbers of objects—so-called numerosity judgements—makes number words easier for humans to learn or strengthens the association of numerosity to the symbolic number words, thereby slowing their rates of replacement.

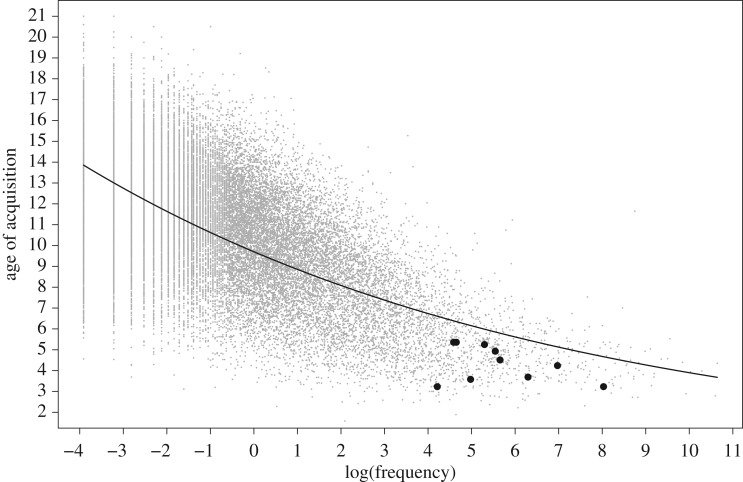
Data from a study of the age of acquisition for 30 000 English words [22] might be relevant to this idea. Children learn words earlier the more frequently those words are used in common everyday speech. But using the Kuperman et al. [22] data, we find that all 10 number words from one to ten have earlier ages of acquisition than is predicted from their frequency of use (binomial test, p < 0.002, two-tailed; figure 4).

Figure 4.

Age of acquisition of a word versus frequency of use. The numbers words from ‘one’ to ‘ten’ (heavy black dots) all fall below (have earlier ages of acquisition) than expected from their frequency of use. Regression fit r = 0.65. Raw data taken from Kuperman et al. [22].

(b). Number words are unambiguous in their meanings and therefore less likely to admit alternatives

If the number words are unambiguous in their meanings, or at least relatively so compared with other meanings, then speakers might be less likely to use alternatives for them in everyday speech. For example, shown three objects and asked to describe ‘how many’, speakers will overwhelmingly say ‘three’. But speakers describing, for example, a weather storm that includes thunder and lightning might call it a thunderstorm or thunder and lightning or perhaps a lightning storm. Each of these alternative forms is likely to be understood and thereby might be allowed to co-exist in the population of speakers.

If it is generally true that the number words admit fewer alternatives, then, from a population-genetic perspective the mutation rate (rate at which new words enter the lexicon) for number words is lower than the mutation rate for other kinds of words. The neutral theory of evolution [23] demonstrates that the rate of evolution of neutral alleles is equal to the rate of neutral mutation. If we entertain the possibility that alternative words for a meaning might be equally good—and therefore neutral—then the lower mutation rate of number words predicts their slower rate of lexical replacement.

Large-scale surveys that record the words people use in conversation [24] reveal that for some common objects and actions a variety of different words might be used, whereas for others most respondents use the same word: days of the week, months of the year and the number words fall into this latter category.

Brysbaert et al. [25] provide ratings of ‘concreteness’ for 40 000 English words. The number words for one to ten receive a mean concreteness rating (5-point scale) of 3.78 ± 0.33 (s.e.m., n = 10), significantly higher than the overall mean of 3.04 ± 0.005 (n = 39 894), although not significantly higher than nouns (3.53 ± 0.008, n = 14 592). But the Brysbaert ‘concreteness’ scale measures ‘things or actions in reality, which you can experience directly through one of the five senses’, and so is not directly relevant to the sense we are suggesting here of ‘unambiguous’, corresponding to a meaning for which, owing to the unambiguous nature of the concept, only a single word generally applies. Thus, the highest-scoring words in the Brysbaert sample included ‘spaghetti sauce’, ‘trench coat’, ‘thorn’ and ‘angelfish’, all of which received a score of five but for which one can easily imagine alternative words.

(c). Number words occupy a region of the phonetic space that is relatively full

Shorter words define a smaller space of possible words than longer ones. The exact size of the space of possible words will depend upon a language's phonotactic rules [26] governing permissible combinations of sounds. For instance, no English word begins with the velar nasal sound ng, although this combination is common in other languages and occurs at the end of many English words. If the phonotactic rules could be known precisely for a language it would be possible to generate all of the possible words of a given length for that language. But even without knowing what these rules are, the space of possible words will grow rapidly, probably something close to factorially, with a word's length.

Data from the British National Corpus [27] record the frequency of use of thousands of common words in everyday speech and writing. These data reveal that a word's length (scored conservatively here as the number of letters rather than the number of distinct sounds) declines sharply with its frequency of use (figure 5). Zipf [28] had already identified this relationship by the late 1940s when he put forward his principle of least effort to explain, among other things, why the frequently used words became shorter.

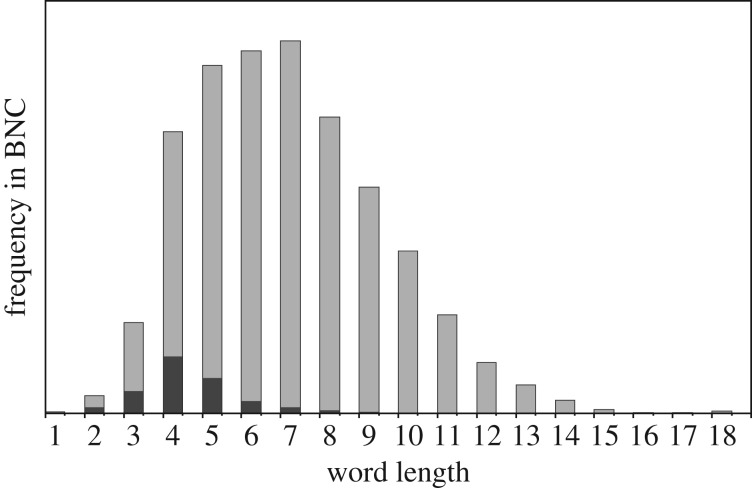
Figure 5.

Length of word (in characters) versus frequency of occurrences per million from the approximately 7700 most frequently occurring words in the rank-ordered-by-frequency list of the British National Corpus (http://ucrel.lancs.ac.uk/bncfreq/lists/1_2_all_freq.txt). Note: x-axis truncated at 5000, frequencies extend to greater than 60 000. Shaded area is region of the numbers words from ‘one’ to ‘ten’ (heavy black dots).

If we accept Zipf's principle, then words will continually evolve to become shorter, and the more so the more they are used. It might just be, then, that the pressure to become shorter means that the already smaller phonetic space of shorter words is full or nearly full compared with the space for longer words. If the space is full, then possible replacements for a word already in that small space might in general have to be longer, or more difficult to pronounce and in that sense not as ‘fit’ as the original. This lower fitness might make the word less likely to be adopted, and as a consequence would slow the rate of lexical replacement.

Anecdotally, the phonetic space for short words can seem full. Compare the words two, to, too and you in English or deux, tu and vous in French. These words, all highly used, have crowded in on each other, occupying nearly identical phonetic spaces. In the extreme this crowding produces homophones, words with the same sound but different meanings, such as pale and pail. An analogous concept in genetics is alternative splicing [29] whereby a single gene can produce more than one protein. Alternative splicing allows an organism to produce many more different proteins than would be expected from its number of genes, and can be seen as a way organisms can reduce the amount of DNA they have to carry and reproduce.

A prediction consistent with the ‘phonetic-space-full’ argument is that homophones should, in general, be shorter words than non-homophones, reflecting the pressure for words to become shorter but having a smaller phonetic space to occupy. To test this idea, we recorded the average length of 441 pairs and triples of British English homophones and then compared the average length of these homophones with the length of words in the British National Corpus (figure 6). The homophones are significantly shorter: mean homophone length = 4.56 ± 0.041 (s.e.m.), n = 441 pairs and triples or 991 words total; mean length BNC = 6.93 ± 0.029, n = 6956 (7.08 ± 0.03 excluding homophones), p < 0.0001.

Figure 6.

Frequency histogram of word length from the rank-ordered-by-frequency list of the British National Corpus (as in figure 4); shaded area is word length of homophones within the BNC sample. The BNC list includes all words down to a frequency of 10 per million, yielding n = 7726 words. Removing abbreviations, proper nouns, names and special characters leaves n = 6956 words. Mean length BNC = 6.93 ± 0.029 (s.e.m), or 7.08 ± 0.03 excluding homophones; mean length of homophones = 4.56 ± 0.041 (s.e.m.), n = 441 pairs and triples or 991 words total, p < 0.0001. Homophones taken from http://www.singularis.ltd.uk/bifroest/misc/homophones-list.html; a comparison sample of homophones is made available at http://www.teachingtreasures.com.au/teaching-tools/Basic-worksheets/worksheets-english/upper/homophones-list.htm: mean homophone length = 4.77 ± 0.045, n = 427 pairs.

There can be disagreement about whether two or more words are homophones (e.g. all and awl or close and clothes) and it might be more difficult to form homophones of longer words (although the many more possible long words might offset this), but the result in figure 6 is consistent with the idea that the vast space of possible long words makes homophones of them less necessary because there are so many more possible alternatives from which to choose. Nevertheless, a challenge for the ‘phonetic-space-full’ argument as an explanation for the number words is that it applies equally to all short words, including the pronouns and the ‘wh’ words (who, what where, why and when). These words are also among some of the most slowly evolving in the IE languages ([1]; table 2 this paper) and frequency data show that they are all highly used. But among these slowly evolving words, the rate of lexical replacement for the number words is exceptionally slow even for their frequency of use [1]. This does not necessarily invalidate the phonetic space argument, but signals that there might be some additional factor slowing replacement rates of the number words.

5. Discussion

There does seem to be something special about the number words: at least in the three language families we studied, the low-limit number words have unusually slow rates of lexical replacement, meaning that a shared form of the word can often last many thousands of years. The same also seems true of the Pama–Nyungan language family of Australia. We speculated upon three reasons why the number words have low rates of lexical replacement, and offered some evidence consistent with each. More work on each of these hypotheses would be a welcome addition to understanding the beguiling stability of the number words.

In contrast to the unusual conservation of the low-limit number words (and especially two to five), higher-level number words such as the ‘teens’ (in English 13–19) and the names of the numbers that are powers of 10 can be more variable [30]. The form these higher-level number words take—for example, sometimes adding a base number to 10, sometimes adding 10 to a base number—correlates with features of a language's grammar [30]. This greater variation and the association with grammar may indicate that the higher-level number words are relatively recent inventions, or put another way, that the low-limit number words are culturally ancestral, existing from a time when counting above small numbers was unusual or unnecessary. Indeed, some hunter-gatherer languages are claimed to lack number words altogether [31–34]. Alternatively, the combinatoric nature of the higher number words might make them inherently more prone to change.

Some words we might expect to be highly conserved are not. Names of body parts, and relational words for mother, father, husband and wife, or he and she, or perhaps words for fire or spears might all be expected to play central roles in everyday speech and especially so in ancient societies, and therefore be conserved. But with the exception of child, eye and tongue none of these words made it into the slowest-evolving set of words (table 2) for any of the language families. Indeed, in contrast to the extreme conservation of the number words, there are 43 different cognate forms of the words for husband in the IE languages, and 37 of the words for wife.

It is worth putting into a temporal context the extraordinary conservation of some of the number words. In the IE languages, the number words for two, three and five are all represented by a single cognate set. The IE language tree we used has a total tree length spanning 148 400 language-years. For a word to remain cognate among the languages of the IE tree means that every speaker of its many languages used a cognate form of that word throughout history, or at least if some other forms were tried, they never caught on. Words that can live this long should astound us, because there were no writing systems for nearly all of the history of the IE language family and the opportunities are great for an aural signal to be corrupted: when a speaker utters a word, that sound travels as a pressure wave through the air where it is transduced by a listener's ear into an electrical signal that travels to the brain and is stored in some memory state. Then, when that speaker uses the same word it must be transformed back from the stored brain state into a set of instructions to the facial muscles, lungs and abdomen of the speaker to form the pressure wave anew. That this process can be repeated millions or perhaps billions of times throughout history with such little change cries out for an understanding of how our minds achieve this prodigious feat.

Data accessibility

The rates datasets we derived for the analyses in figures 2 and 3 and tables 1 and 2 are available as electronic supplementary material to this article. The raw lexical data and the posterior samples of phylogenetic trees are available from the authors of the original articles on the IE, Austronesian and Bantu languages. The age of acquisition data are available from the authors of that study. The British National Corpus data are available online.

Authors' contributions

M.P. and A.M. both contributed to all aspects of the paper.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by Advanced Investigator Award 268744 ‘MotherTongue’ to M.P. from the European Research Council, and by BBSRC grant number BBSRC grant no. BB/L018594/1 to A.M.