Comparative cognition of number and space: the case of geometry and of the mental number line

Abstract

Evidence is discussed about the use of geometric information for spatial orientation and the association between space and numbers in non-human animals. A variety of vertebrate species can reorient using simple Euclidian geometry of the environmental surface layout, i.e. in accord with metric and sense (right/left) relationships among extended surfaces. There seems to be a primacy of geometric over non-geometric information in spatial reorientation and, possibly, innate encoding of the sense of direction. The hippocampal formation plays a key role in geometry-based reorientation in mammals, birds, amphibians and fish. Although some invertebrate species show similar behaviours, it is unclear whether the underlying mechanisms are the same as in vertebrates. As to the links between space and number representations, a disposition to associate numerical magnitudes onto a left-to-right-oriented mental number line appears to exist independently of socio-cultural factors, and can be observed in animals with very little numerical experience, such as newborn chicks and human infants. Such evidence supports a nativistic foundation of number–space association. Some speculation about the possible underlying mechanisms is provided together with consideration on the difficulties inherent to any comparison among species of different taxonomic groups.

This article is part of a discussion meeting issue ‘The origins of numerical abilities'.

1. Introduction

In the past few decades, data have emerged suggesting that several animal species of different taxonomic groups are capable of representing quantity [1,2], which allows the estimation of set sizes (for reviews of comparative literature, see [3–6]). One open issue is to what extent quantities (such as spatial distances, time durations or numbers) are encoded in the nervous systems by similar mechanisms. To be more precise: to what extent do similarities in behavioural performance correspond to similarity of mechanisms, or even to a common evolutionary origin? Although any definite answer to this question is difficult, I would like to discuss two cases in point: one is related to the encoding of some basic Euclidian geometric properties of space, such as distances and sense, the other is related to the so-called ‘mental number line’, which underscores the important fact that number and space are intimately related concepts.

2. The case of geometry

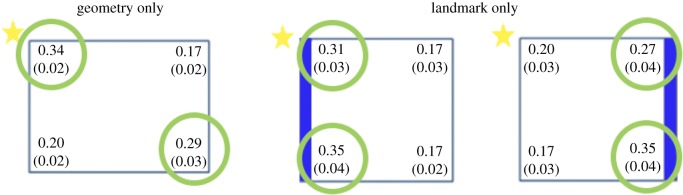
Geometry cognition has been much investigated in the past few decades using a task developed originally by Cheng & Gallistel [7–9]. Basically, in the task, animals should reorient in a rectangular environment in accord with its metrical and sense (right/left) relationship. It was noted that during initial, spontaneous reorientation (i.e. a working memory task) animals often ignore other types of cues, such as visual patterns and distinctive odours. With extended reinforcement training (i.e. in a reference memory task), animals can learn to use these other non-geometric cues, as shown by their ability to disentangle among geometrically equivalent locations; however, these non-geometric cues are merely used as local markers, or beacons, and animals do not appear to be able to learn sense relationships between them. An example is shown in figure 1, depicting some work we did with zebrafish (Danio rerio) [10]. The results show proportions of choice for the four corners of the rectangular enclosure (means on top with s.e.m. below) when only geometric cues were available (leftmost panel) and when a prominent visual cue (a blue coloured wall) was provided located either close to or far away from the correct corner. As can be seen, zebrafish chose the correct corner and its geometric equivalent in the ‘geometry only’ condition; in the ‘landmark only’ condition, by contrast, zebrafish oriented towards the visual cue provided by the blue wall but were unable to distinguish between the two blue-marked corners using sense (left–right) relationships.

Figure 1.

Zebrafish were presented with a companion visible in a corner and, after spatial disorientation in the dark, they were allowed to choose among the four corners when the companion was no longer visible. They reoriented correctly in the geometry only condition (i.e. in a rectangular enclosure in the absence of non-geometric cues). In the landmark only condition (i.e. in a square-shaped enclosure with a single blue wall), they oriented towards the blue wall but were unable to encode the relative positions of the corners using sense (left/right) information. (Online version in colour.)

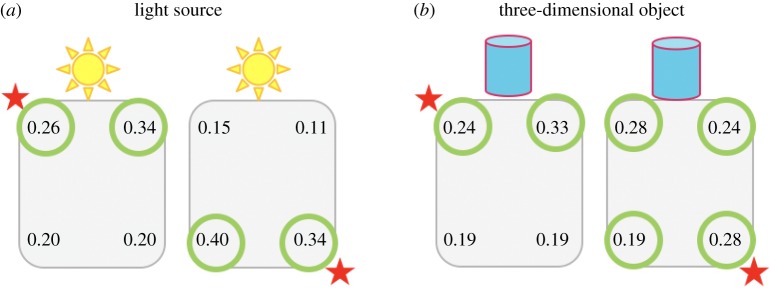
Even when using a more ecological cue (such as a light source; figure 2a) or a prominent three-dimensional object (figure 2b), fish appeared unable to discriminate the relative positions of these cues.

Figure 2.

Even when tested with a light source or a conspicuous three-dimensional object that may have provided a more ecological cue than a coloured wall (figure 2), fish appeared unable to discriminate the relative positions of the corners. (Online version in colour.)

It is thus apparent that the brain organizes spatial information into two basically different classes of environmental cues: extended boundaries and featural (non-geometric) cues (see for reviews [11,12]). The two types of cues differentially influence navigation and spatial mapping. Organisms seem to spontaneously compute relative spatial locations and directions with respect to extended boundaries such as walls (e.g. ‘the corner to the southeast of the wall’) but are more likely to use featural cues such as two-dimensional surface markings as a direct beacon to location (e.g. ‘the corner near the red wall’) rather than a relative spatial cue (e.g. ‘the corner to the east of the red wall’).

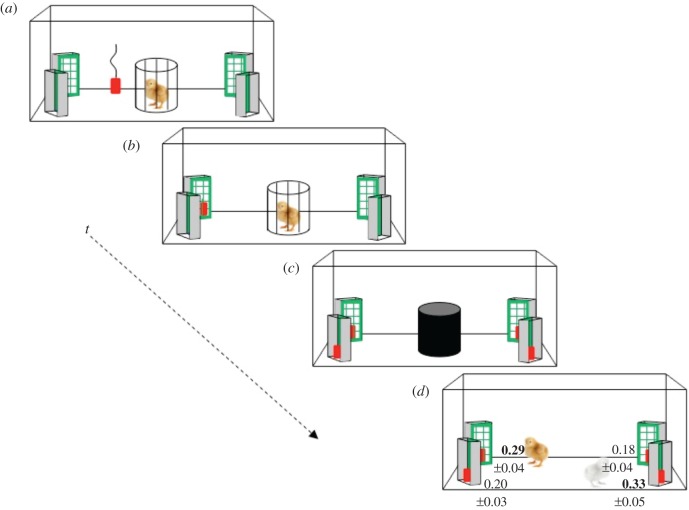
One may wonder what is the developmental origin of the ability to deal with extended boundaries. Evidence from single-cell studies in young rats [13,14] and controlled-rearing studies in newly hatched chicks [15–17] suggests that the ability to deal with geometric information is mostly predisposed in the brain, with no need for specific experience. A striking example is shown in figure 3. Here, newly hatched chicks maintained in the dark were located for the first time in a rectangular enclosure and exposed to a conspicuous object that slowly moved behind one of the four grid-panels in the corners [18].

Figure 3.

Chicks were located in a rectangular enclosure immediately after hatching in darkness, and presented (t indicates time) with an object moving (a) and hiding behind a grid placed in a corner (b). Chicks were then spatially disoriented by slowly rotating them in darkness and four identical replicas of the object were located in each corner (c) partly visible behind the grids. At test, chicks oriented by using the metric arrangement of the surfaces together with the left–right directional sense, choosing the two geometrically correct corners (yellow (dark grey in print) and grey chicks in (d) (see [18]). (Online version in colour.)

Then the chick’s vision was blocked by an opaque partition, and the chick was slowly rotated clockwise and anticlockwise to disrupt inertial orientation. The enclosure was also rotated and four identical replicas of the object were located in the corners. Finally, the chick was allowed to choose the object. As can be seen (figure 3), the animals did not return to random choice but rather searched more in the two geometrically correct corners (the correct one and its geometrical equivalent) than in the two geometrically incorrect ones.

Convergent evidence in mammals [19], birds [20], amphibians [21] and fish [22] suggests that the hippocampal formation plays a crucial role in geometry representation. There are of course also species differences. These are expected, given that the last common ancestor of all these taxonomic groups dates back some 500 Ma. For instance, in ray-finned (actinopterygian) fishes, as a result of a major divergence during early embryogenesis, the telencephalon develops by a process of eversion (bending outward of the embryonic prosencephalic plate) instead of evagination, as it does in all others vertebrate groups [23]. As a consequence, the medial-to-lateral topography of the pallial areas (which refer to the upper surface of the cerebrum) is reversed in teleost fishes compared with that of other vertebrates. Accordingly, in these species of fishes, the region considered homologous to the hippocampus is located laterally rather than medially in the telencephalon. Consistent with that, it has been found that goldfish with telencephalic lesions in the lateral pallium (but not in the medial pallium) appeared to be insensitive to geometric information [22].

Several other pieces of neurobiological evidence converge to a similar role of the hippocampal formation in different taxonomic groups. For instance, metric information seems to be encoded in the geometric task of Cheng & Gallistel in the form of distances among the walls of the enclosures, rather than in the form of lengths of the walls [24]. Chicks lesioned in the hippocampal information appear unable to find a goal using the distances between the walls of the enclosure, even though they can orient on the basis of non-geometric information [25]. Recently, Keinath et al. [26] have shown that hippocampal place cells in mice encode global shape aspects of an enclosure while being insensitive to salient non-geometric landmarks. When spatially disoriented mice reoriented in a rectangular enclosure, a given place cell could fire both when the mouse was at the place where that cell should fire and when the mouse was at the rotationally equivalent location. The cell rotational error occurred in spite of the fact that one wall was painted with white and black stripes that would have provided an unambiguous cue to distinguish between rotationally equivalent locations. These electrophysiological results match perfectly the results of (many) behavioural experiments revealing the use of purely geometric information in spatial reorientation (see also [27] for a theoretical commentary).

Thus, a strong case can be made for a common, shared and homologous mechanism in the hippocampal formation underlying spatial reorientation in vertebrates that computes distance and direction to allow an organism's heading. A challenge to this view, however, might come from research on insect orientation.

At more or less the same time as Cheng & Gallistel [7] formulated their theory of vertebrate navigation, Cartwright & Collet [28] put forward a theory of a view-based image-matching process (snapshot memories) in insects. According to this hypothesis, an animal would actively move in the environment to reduce the discrepancy between a snapshot representation of the visual scene stored in memory and the scene currently perceived. Although alternative hypotheses based on mapping-like mechanisms for insect navigation have been formulated (e.g. [29]), experiments carried out with ants and bumblebees in the specific domain of spatial reorientation suggest that these animals, like vertebrates, make rotational errors between two geometrically identically corners in the rectangular arena task [30–33]. It is of course an attractive idea that vertebrate navigation may be explained by simpler processes available also to insects. However, a major limitation of this hypothesis is that the aforementioned reorientation tests in insects were all based on a reinforcement learning paradigm. A snapshot or view-image account of reorientation may perhaps work for the cases in which it is possible for the animals to have a period of extended learning to integrate featural and geometric information (e.g. [34]), but it appears untenable for spontaneous, immediate reorientation. According to the snapshot hypothesis, the retinal salience would be the crucial factor in animals' reorientation. However, it has been shown that chicks can spontaneously reorient using geometric relationships of subtle three-dimensional terrain cues, but not by using salient two-dimensional brightness contours of surfaces or columns [35]. Direct evidence against the snapshot theory also arises from work on non-rewarded, spontaneous reorientation tasks in insects. We observed bumblebees' spatial navigation in response to the observed location of a conspecific ([36], figure 4).

Figure 4.

(a) Bumblebees were first allowed to observe the arena from a central transparent cylinder, with a conspecific visible in a small glass vial in one corner of the arena. (b) Bumblebees were then covered with an opaque cup and rotated for disorientation. (c) Bumblebees were released into an empty arena with a netted cover, and their first approaches to the four corners of the arena and their total approaches in 30 s were recorded (see for details [36]). (Online version in colour.)

When tested in a rectangular enclosure without non-geometric cues, bumblebees oriented using geometry (choosing the two geometrically correct locations over the two geometrically incorrect ones). However, when tested in a square-shaped enclosure with a coloured wall providing featural information (figure 4), bumblebees only used the feature to distinguish the corners near the feature from those distal from the feature, without discriminating the mirror-image corners from one another (figure 5). These results showed that no simple snapshot representations of corners (orange–green versus green–orange; figure 4) guided the bumblebees’ place coding; rather, the orange feature seems to have been used more like a beacon or as an associative near/far cue to location. Thus, the snapshot theory appears inadequate for both vertebrate and invertebrate navigation.

Figure 5.

(a,b) When tested in a square-shaped enclosure with an orange coloured wall (the others being uniformly green), bumblebees oriented correctly towards the orange coloured wall but were unable to discriminate between its two corners (C and S) on the basis of sense information. See [36] for details. (Online version in colour.)

3. The case of the mental number line

A natural disposition to map numbers into space has been documented since Galton's [37] classical study, in which human adults were asked to draw how they visualize numbers. People seem to represent numbers as different visuo-spatial forms, typically organized along horizontal continua oriented from left (smaller numbers) to right (larger numbers), the so-called ‘mental number line’ [37]. The phenomenon was then confirmed in a more experimental setting. Dehaene et al. [38] found that responses to relatively smaller numbers are faster for the left hand and those to relatively larger numbers are faster for the right hand (Spatial Numerical Association of Response Codes, or SNARC effect). The SNARC effect does not reverse in left-handers and in right-handers tested while they cross their hands, which suggests that the spatial correspondence between the location of the number in the mental number line and the location in which the response is executed is the crucial factor for the occurrence of a SNARC effect.

Although traditionally the left-to-right orientation of the mental number line has been accounted for in terms of reading and writing habits [39] or more generally in terms of early directional experiences (review in [40]), there is reason to believe that biological factors can also play a role. First, evidence for a left-to-right bias has been found in pre-verbal infants. When presented with increasing and decreasing left-to-right sequences of numerosities, seven-month-old infants showed a preference for the increasing left-to-right oriented sequence [41]. Moreover, eight-month-old infants tended to orient attention to the left after observing a small number, and towards the right after observing a large number [42]. Second, evidence for a privileged left-to-right direction of number–space association has been reported in non-human animals, i.e. in two species of birds (domestic chicks and Clark nutcrackers [43–45]), in monkeys [46] and in one chimpanzee [47].

Probably the most convincing evidence of a phenomenon resembling the human mental line of number has been documented in newborn domestic chicks [48]. Three-day-old chicks were first familiarized with a target number (e.g. ‘5’ in figure 6) by turning around a panel with the depicted target number to obtain a reward. When they were then presented with pairs of panels depicting different numerosities, they tended to turn preferentially to the left with a smaller number (e.g. ‘2’) and to the right with a larger number (e.g. ‘8’) [48]. It is worth noting that a same number (for instance ‘8’) was associated by chicks with the right space when the target number was, for instance, ‘5’, but it was associated with the left space when the target number was, for instance, ‘20’. Thus, chicks seem to associate relatively smaller numbers with the left space and relatively larger numbers with the right space, most as humans do (see for a discussion [50]). Preliminary results obtained with human newborns [51] and zebrafish ([52,53]) using a similar task suggest that the phenomenon can be quite general, though in the case of zebrafish, it is unclear whether they use discrete or continuous quantities (or both) for the association with space.

Figure 6.

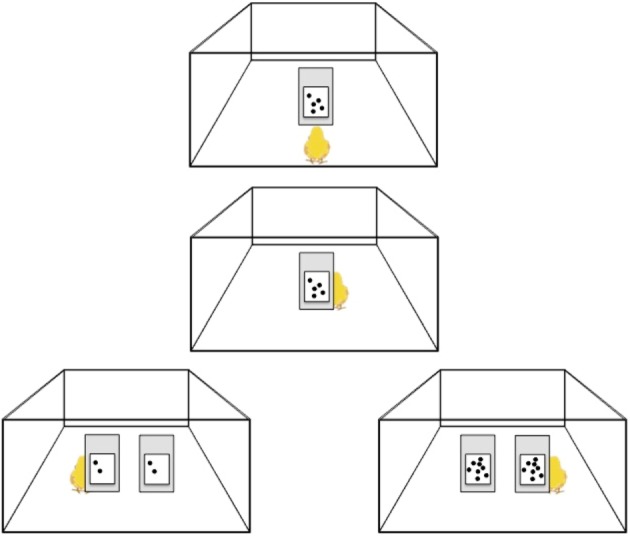
Chicks were trained to turn around a panel with five elements on it to find a food reward (upper central panels). At test, chicks were presented with two panels, one on the left and one on the right, depicting the same number of elements. When the elements were smaller than the target number (leftmost panel), chicks chose the left panel; when the elements were larger (rightmost panel), they chose the right panel (see [48] for a full description of the experiments including controls for continuous physical variables; and see also [49]). (Online version in colour.)

Clearly, the limited, if any, amount of experience available to newborn chicks and newborn humans with different numerosities before testing strongly supports an innately predisposed mechanism for the association between space and number. This would fit in well with a crucial argument that has been put forward by Gallistel [1,2] concerning the need for a common currency in the brain to represent different kinds of magnitudes (discrete as numerosities or continuous as spatial distances) in order to perform computations like ratio, which has been proved in fact to be available to both human infants [54], adult monkeys [55] and newborn chicks [56].

However, despite the behavioural resemblances, and differently from in the case of geometrical cognition, it is hard to say whether we are here facing common, homologous brain mechanisms, or evolutionary convergence, or mere resemblances reflecting completely different underlying mechanisms.

Let us start by considering current evidence for the underlying mechanisms of approximate number representation. We know that humans and other vertebrate animals share an evolutionarily old quantity representation system that allows the estimation of set sizes. There is convincing evidence that this system may be sustained by a shared homologous mechanism among mammals: single cell recording studies in monkeys [57,58] and functional magnetic resonance imaging studies in humans [59] converge in identifying a parieto-frontal cortical network in which individual neurons appear to be selectively tuned to the number of items. The physiological properties of these neurons can explain the typical signatures of numerosity judgements, such as the distance and the size effects (review in [60]). Parietal neurons represent not only discrete quantity (numerosity), but also continuous quantity (extent) and relations between quantities (proportions [61]), thus supporting the idea of a generalized magnitude system in the brain [2,62,63].

Recently, neurons have been found within the nidopallium caudolaterale, a forebrain avian structure, that selectively respond to specific numerical values. As in the monkey brain, their firing rate decreases as the numerosities shown to the animal get farther away from the preferred numerical value [64]. Although it has been proposed that the nidopallium caudolaterale could be homologous with the mammalian prefrontal cortex, a major difficulty with this view is that this structure mainly receives input from the collothalamic pathway (i.e. the collicular rather than the thalamic pathway—both routes being present and homologous in the two classes) and it seems to have no connections with the hippocampal formation (while the mammalian prefrontal cortex has). It has thus been suggested, as an alternative hypothesis, that the dorsolateral corticoid area, which is connected to the hippocampal formation, might be homologous with the mammalian prefrontal cortex [65]. If so, collopallial parietal and temporal associative cortices might be homologous with the nidopallium caudolaterale [66].

Nonetheless, even if common and shared structures could exist for birds and mammals, we know nothing about other vertebrate taxonomic groups (e.g. fish and amphibians, in spite of the evidence of their possession of an approximate number system, e.g. [67,68]). I do not discuss invertebrates here because, in my view, it is currently unclear whether they do possess an approximate number system that obeys Weber's law or if evidence for counting in animals like honeybees is limited to small numerosities (less than 3–4)—e.g. [69,70]—and would thus reflect the operating of some working memory system rather than a true quantity system (but see for a possible exception [71]).

As to the mechanisms underlying the association between number and space, things are even more complicated. One possibility is that continuous and numerical quantities are topographically represented in the brain. There is evidence for this in the human parietal cortex [72,73], at least for relatively small numerosities (less than 7) in the case of discrete quantities. Intriguingly, the topographical map of number in humans seems to be limited to the right hemisphere, for no clear topographical organization is apparent in the left hemisphere [72]. However, there is no evidence of this in other species and, more importantly, it is unclear how such topography, which maps increasing magnitudes from the medial to lateral portion of the parietal cortex, would produce the pattern of response that we observe in behaviour, with small numbers being more likely to produce a response to the left and large ones to the right. One can speculate on mirror organizations of the topography in the two hemispheres, but this seems not to be the case (in fact, there is no topographical organization at all in the left hemisphere; see above) and, besides, the functional reason for such mirror-image inversion, if existing, would be entirely mysterious.

Another possibility is that numerical and spatial cognition rely on common neural circuits [74,75], for the lateral and ventral intraparietal areas seem to play a role in both number and spatial processing in primates. Drucker & Brannon [75] argued that activation of these regions by numerical information could therefore lead to shifts in spatial attention, e.g. in left and right hemispace. However, it remains unspecified in this hypothesis why the mental line of numbers has the particular orientation it seems to have, from left to right.

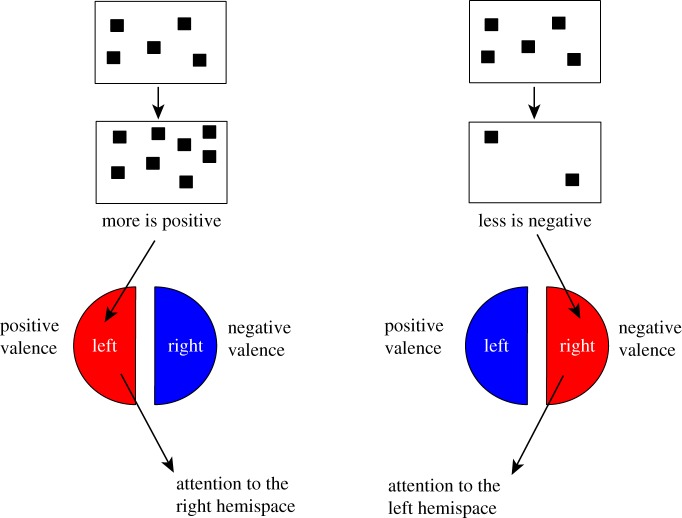
Here, I would like to propose a different hypothesis, which has the advantage of being amenable to empirical testing (figure 7). It has been argued that there exists a fundamental brain asymmetry in the control of functions related to motivation and emotion, sometimes referred to as the ‘valence hypothesis’ [76]. For example, it appears that the anterior regions of the left and right hemispheres are specialized for approach and withdrawal processes, respectively, and thus associated with positive and negative emotions. Although the valence theory was mainly developed in the context of human neuropsychology, approach and withdrawal are fundamental motivational dimensions that may be found at any level of phylogeny, and in fact there is also evidence supporting the theory in non-human species (e.g. [77]; see reviews in [78,79]). Now, let us imagine that, even if not explicitly trained for such an association, animals establish (other conditions being equal) that for appetitive stimuli, larger magnitudes are intrinsically better (and approachable) than smaller magnitudes. Then, chicks in Rugani et al.'s [48] experiments were faced with either abrupt increase or abrupt decrease in numerosities that would accordingly have evoked preferential activation of, respectively, the left hemisphere (positive emotion, approach) or the right hemisphere (negative emotion, withdrawal). This, in turn, would have promoted turning to the contralateral side of the activated hemisphere, i.e. to the left for smaller numerosities and to the right for larger numerosities (figure 7).

Figure 7.

According to the valence theories, the two hemispheres make qualitatively different contributions, e.g. negative versus positive valence or approach versus avoidance/withdrawal tendencies (review in [76]). Assuming that changes in numerosities towards larger or smaller magnitudes are associated with prevalent activation of, respectively, the left (positive valence) and right (negative valence) hemisphere, then attention to contralateral hemispace can be expected. This would nicely fit with choice for the left side with smaller magnitudes and for the right side with larger ones. (Online version in colour.)

As I said, this ‘motivational’ hypothesis is amenable to empirical investigation using, for instance, a specific association (acquired by training) between magnitudes and an aversive (rather than an appetitive) stimulus. I would predict a reduction if not an inversion of the direction of the space–number association in this case. Note also that although we found that a number–space association can be obtained for discrete numerosities when they covary with continuous physical quantities (confirming that number is salient relative to other object properties [80]), we can expect similar associations to occur for continuous physical variables as well when tested in isolation (e.g. that a change from a large-size stimulus to a small-size one would induce, via right hemispheric activation, preferential allocation of attention in the left hemispace).

Recent work in human neuropsychology by Brookshire & Casasanto [81] suggests that neural circuits for affective motivation may re-use circuits evolved for performing motor actions, and reports that individuals with strong motor asymmetries in a particular direction can actually show reversal of direction of left–right biases associated with motivation. Testing with animals artificially selected for lateralization in a particular direction may prove revealing (see, for instance, for fish [82,83]). Finally, whether this idea would also apply to the several other associations that humans seem to form between space and number and time and other quantities—the so-called ‘universal mental quantity line’ [84]—is open to empirical test.

In conclusion, coming back to the original question we asked in this paper, it is apparent in my view that the road from behaviour to the underlying mechanisms in different species is a tortuous one. We should be very cautious and attentive to the possibility of resemblances in behaviour that reflect true homologies and others that may be the outcome of homoplasic systems or that may be associated with completely different functions and underlying structures in different tasks and taxa.

Data accessibility

This article has no additional data.

Competing interests

I declare I have no competing interests.

Funding

I received no funding for this study.