All's well that ends well: why large species have short telomeres

Abstract

Among mammal species, almost all life-history traits are strongly size dependent. This size dependence even occurs at a molecular level. For example, both telomere length and telomerase expression show a size-dependent threshold. With some exceptions, species smaller than approximately 2 kg express telomerase, while species larger than that do not. Among species greater than approximately 5 kg, telomeres tend to be short—less than 25 kb—while among smaller species, some species have short and some have long telomeres. Here, we present a model to explore the role of body size-dependent trade-offs in shaping this threshold. We assume that selection favours short telomeres as a mechanism to protect against cancer. At the same time, selection favours long telomeres as a protective mechanism against DNA damage and replicative senescence. The relative importance of these two selective forces will depend on underlying intrinsic mortality and risk of cancer, both of which are size-dependent. Results from this model suggest that a cost–benefit model for the evolution of telomere length could explain phylogenetic patterns observed within the Class Mammalia. In addition, the model suggests a general conceptual framework to think about the role that body size plays in the evolution of tumour suppressor mechanisms.

This article is part of the theme issue ‘Understanding diversity in telomere dynamics'.

1. Introduction

(a). Telomeres, replicative senescence and cancer

Telomeres are repetitive DNA sequences that protect the ends of the chromosomes in eukaryote cells. As Barbara McClintock first noted more than 70 years ago [1], deficient chromosome ends stick to one another and break in mitosis, leading to gains and losses in the daughter cells. Thus, telomeres are essential for the integrity of chromosomes. However, shortening of telomeres occurs inevitably with cell replication due to the inability of DNA polymerases to copy all the way to the end of the chromosome, a phenomenon known as the end-replication problem [2]. Cells have evolved to ameliorate this problem by expressing telomerase, a ribonucleoprotein enzyme that adds telomeric repeat sequences to telomeres using an RNA template [3]. In humans, however, telomerase expression is restricted to embryonic development and a very few stem cell lineages in adult tissues (haematopoietic, colonic and gametic tissue) [4]. In the rest of somatic tissues, telomerase is repressed and, as a consequence, telomeres shorten with age.

In most animals, telomeres are composed of multiple repeats of the sequence TTAGGG, spanning several kilobases [5]. Telomeric DNA is bound by specialized proteins that form a complex called shelterin. Shelterin proteins repress multiple DNA damage signalling and repair pathways that would otherwise process the telomere as a DNA strand break [6]. Thus, the shelterin complex bound to telomeric DNA acts as an effective ‘cap’ to the chromosome ends. However, when telomeres get critically short, the complex ‘uncaps’ and the cell triggers a DNA response that results in cell senescence [7]. Cell senescence is a state of permanent growth arrest that can be triggered by different insults, including oncogene activation and excessive DNA damage [8]. To distinguish this from other triggers, senescence induced by uncapped telomeres is called ‘replicative senescence’. Replicative senescence is only operative in the absence of telomerase. When telomerase is present, telomeres are maintained and cells can proliferate indefinitely.

Telomeres also play an important regulatory role in cancer. Cancer is a multistep process of mutation, selection and clonal expansion [9], which relies on extensive cell proliferation and the progressive accumulation of mutations as cells divide. Replicative senescence is believed to have evolved as a tumour suppressor mechanism that limits cell proliferation and thus helps to prevent cancer [10]. By repressing telomerase expression, cells allow their telomeres to shorten with each cell division until they are exhausted and senescence is triggered. This acts as a very effective barrier against cancer, blocking the proliferation of cells that might have accumulated oncogenic mutations as they divide. Eventually, however, cancer cells evolve mechanisms of telomere elongation to sustain unlimited proliferation. In most cancers (approx. 85%), this mechanism consists of reactivation of telomerase, while the rest employ alternative lengthening of telomeres [4,11].

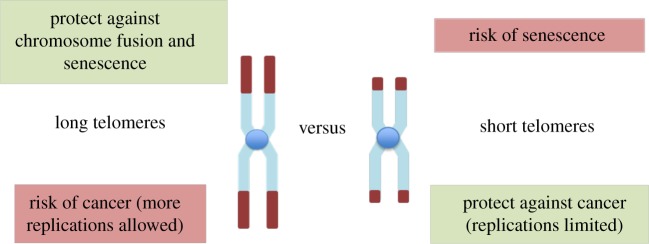
While senescence is clearly beneficial as a mechanism to arrest potential cancer cells, it also has detrimental effects for the organism because it leads to tissue degeneration and ageing phenotypes [12]. These effects are not only passively produced by arrested cells that occupy critical cellular niches, but also by their active secretion of pro-inflammatory cytokines [13]. So cellular senescence can inhibit cancer, but paradoxically, cytokines produced by senescent cells contribute to ageing-related diseases, including cancer. Thus, cell senescence constitutes an example of antagonistic pleiotropy [12], a trait that is beneficial in early life but deleterious in late life [14]. Because short telomeres trigger senescence, these trade-offs are also reflected at the individual telomere level (figure 1). While long telomeres are favoured to protect the end of chromosomes and avoid senescence, short telomeres are favoured to limit replication and protect against cancer.

Figure 1.

Opposite effects of long and short telomeres in cancer risk and senescence. (Online version in colour.)

(b). Longer telomeres or shorter telomeres: an evolutionary dilemma

Given the opposing forces acting on telomere length (TL), it is perhaps not surprising that the dynamics of telomeres have evolved to be so different among different species of mammals [15]. In species that are larger than about 2 kg, telomerase expression is turned off after embryonic development. In species smaller than that, telomerase tends to be expressed throughout life. Above about 5 kg, species tend to have short telomeres (less than 25 kb), while below that, TL is short in some species and long in others. It appears that the common ancestor of all mammals repressed telomerase as an adult, and telomerase reactivation then evolved independently multiple times [15].

As explained above, the repression of telomerase leads to replicative senescence, which acts as a tumour suppressor mechanism. This cancer-protection feature is believed to be the reason why large mammals have evolved telomerase repression and short telomeres [16]. All else being equal, the risk of cancer is expected to increase with body size because cancer originates by the random accumulation of mutations in cells. Thus, in theory, the more cells, the higher the risk. However, in nature, body size does not correlate with cancer risk, an observation known as Peto's paradox [17]. Several articles reviewed Peto's paradox in an issue of this journal in 2015 and offered excellent insights and mathematical models [18–22]. The general agreement is that Peto's paradox is explained by the evolution of tumour suppressor mechanisms. That is, species that are at higher risk of cancer because they have larger body size and/or longer lifespan have developed defences against cancer development. If this hypothesis is true, then cancer in the wild should be relatively rare across species irrespective of lifespan or body size. Although the literature on comparative oncology is scarce, this appears to be largely the case, with few exceptions [23–25].

Regarding the specific solutions for cancer suppression, in addition to replicative senescence, several other mechanisms have been described, including redundancy of tumour suppressor genes and a more efficient immune system [26]. Some of these mechanisms might be operative in some species but not in others. Of note, in an article in this issue, Tian et al. [27] report the presence of telomere-independent mechanisms of tumour suppression in small rodent species that are exceptionally long lived. Increased cancer risk in these animals is not driven by large body size, but by long lifespan. Instead of replicative senescence, these animals have evolved slow cell proliferation, which might be an optimal mechanism to prevent tumour formation in small mammals. In addition, it would be of interest to explore alternative tumour suppressor mechanisms employed by ectotherms, a topic also discussed in this issue [28]. Ectotherms do not employ replicative senescence. It has been suggested that replicative senescence evolved in homeotherms to protect from the high risk of cancer produced by the increased mutational load associated with elevated body temperatures [5]. However, ectotherms can also develop cancer and might employ additional mechanisms of tumour suppression, especially those animals that are large and/or long-lived. This deserves further investigation.

In this article, we focus on replicative senescence, because it is a well-characterized mechanism of tumour suppression, employed by virtually all mammalian species larger than 2 kg [15]. We explore the possibility that the size-specific risk of cancer might have acted as a strong selective force, especially in large mammals, leading to the evolution of replicative senescence. Specifically, we hypothesize that natural selection against cancer favours shorter telomeres, and does so in a size-dependent manner. To explore this hypothesis, we provide a numerical solution to a simple algebraic model. Our goal is to provide a quantitative framework for the debate about trade-offs between TL and life-history strategies discussed elsewhere in this issue [29,30]. Results from this model show at least one way in which selection could favour shorter telomeres in larger species.

2. Methods and results

(a). A size-dependent model of telomere length evolution

Here, we present a simple mathematical model for the evolution of TL in mammals. The specific equations that we use to describe functional relationships are presented in the appendix found in electronic supplementary material. For the most part, in this section we limit the description to graphical representation of these equations. We start with an important caveat. Mathematical models in biology necessarily make simplifying assumptions [31]. The goal of such models is to distill the problem down to the least number of necessary parameters, while being explicit about the simplifying assumptions that underlie the model. Our goal here is not to provide a comprehensive model of all demographic and evolutionary forces that shape telomere dynamics. Rather, we hope that the relatively simple model we develop will provide a useful framework with which to consider the various factors that might have influenced telomere evolution.

We are specifically interested in determining the selective costs and benefits, for a species of a given body size, of an increase or decrease in TL. We start with a set of plausible assumptions about how body size affects underlying survival rates, and how TL affects the risk of mortality due to DNA-damage-induced cell senescence and cancer. Most of these assumptions are derived from patterns found in the existing literature. The goal of this particular model is not to prove that TL evolved under the constraints that we describe here, but to present at least one plausible mechanism by which selection might have shaped TL in different species.

Our model seeks to explain a phenomenon observed in the data collected by Gomes et al. [15], who found that mammalian species larger than approximately 2 kg typically show telomerase repression and short telomeres (less than 25 kb) in adulthood. We agree with the authors' explanation that telomerase repression has evolved to enable tumour suppression by replicative senescence, and, in turn, to support larger bodies and longer lifespans. While this hypothesis has been previously formulated as a solution to Peto's paradox [19], the effect of cancer as a driving force to shorten telomeres in a size-dependent manner has not been modelled previously. Here, we combine well-established mathematical equations that explain intrinsic mortality and fitness with the Armitage–Doll model of multistep carcinogenesis, which explains size- and time-dependent cancer risk for each species. The novelty of our approach lies in the integration of TL as a tumour suppressor mechanism in the equation of multistep carcinogenesis. This allows us to ask how size could influence phylogenetic variation in TL. Importantly, to simplify the model and to adapt it to the data published by Gomes et al., we assume a single average TL value for each species. While it is well known that TL decreases with age and varies between individuals within a species, these differences did not preclude the observation by Gomes et al. [15] of clear patterns of lifespan and body size associated with TL and telomerase activity. Hence, our model does not include dynamics within populations, but rather compares mean TL between species to determine whether the risk of cancer associated with larger body sizes shaped this trait.

(i). Intrinsic mortality

We start with the assumption that intrinsic mortality rates follow the two-parameter Gompertz curve [32], with the intercept dependent on adult size,

2.1

where 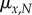is the instantaneous mortality rate at age x for a species whose adult size is determined by its number of cells N. The age/size-specific mortality curve is defined on a log-scale by size-dependent intercept 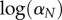and size-independent slope β. We model size either as grams or number of cells, using a simple translation of 1 g = 10⁸ cells. Figure 2a shows the log-scale mortality curves for different animal sizes assuming β =0.00833 and α = mass^−3/4, where mass is expressed in grams. Figure 2b shows the effect of size on survivorship using parameters in figure 2a and the equation 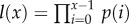, where p = e^−μ and l(0) = 1.

Figure 2.

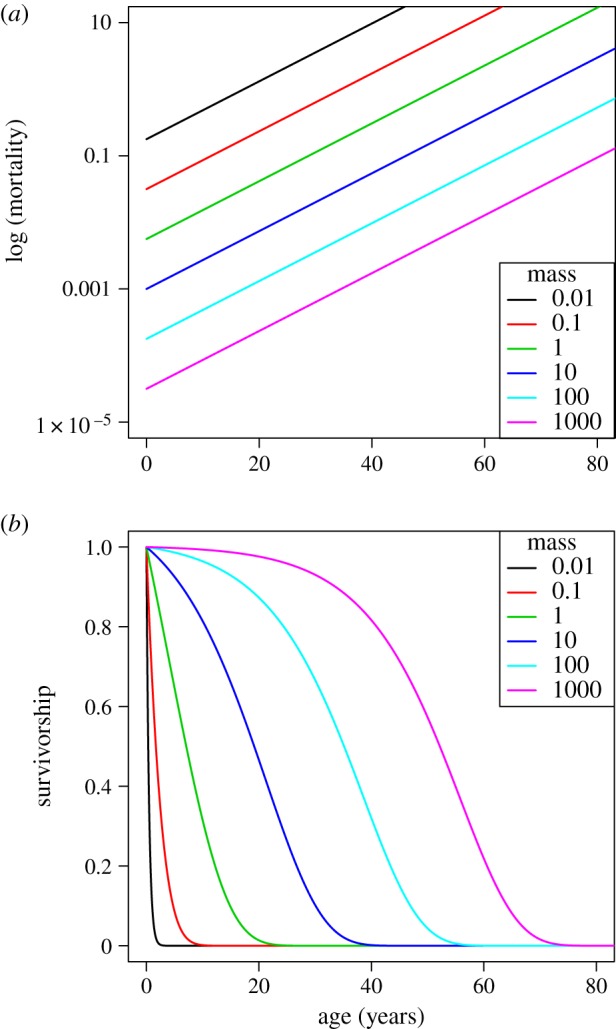
(a) Intrinsic mortality is defined by the Gompertz model, which calculates an age/size-specific mortality curve defined on a log-scale by size-dependent intercept 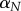and size-independent slope β (see electronic supplementary material, Equation (A 1) in the appendix). For all size classes, we assume β = 0.00833, α = mass^−3/4 where mass is given in g, and age is modelled in months. (b) Effect of size on survivorship. These values arise from the parameter values shown in figure 2a.

(ii). Size, cancer and telomere length

Armitage & Doll [33] developed the multi-stage model of cancer, where the risk of lethal metastatic cancer is directly proportional to the risk of a single cell experiencing a threshold number of oncogenic alterations. As later pointed out [34], the age-specific risk of cancer is a function of mutation rate m, threshold risk number k, age x and the number of cells in the body N (figure 3a, equation (2.2)). The threshold number k typically represents ‘hits’ or ‘events’ that lead to cancer: the higher the number of events needed, the less likely that cancer occurs. The effects of these various factors on age-dependent probability that one or more cells become cancerous are given by the following equation:

2.2

where age is given as x/12 to rescale months to years. Importantly, the threshold k takes into consideration the presence of tumour suppressor mechanisms. If tumour suppressor mechanisms are absent, then fewer events might be needed to produce cancer. For instance, telomeres that are sufficiently long to avoid replicative senescence are permissive for cancer development because they allow cell proliferation. Thus, to model the effect of TL on cancer risk, we assume that longer telomeres reduce the barrier to uncontrolled growth, lowering the threshold number of hits required by up to 1 (figure 3b, electronic supplementary material, equation (A 3) in the appendix found in the electronic supplementary material). A lower threshold implies a greater risk of a cell becoming metastatic, ceteris paribus. It is important to note, as Kokko & Hochberg [19] explore in their theoretical treatment, that all is not equal. The various factors in the model shown in equation (2.2) are likely to co-evolve, shaped in part by ecological factors that influence extrinsic risk of mortality. We will explore this further below.

Figure 3.

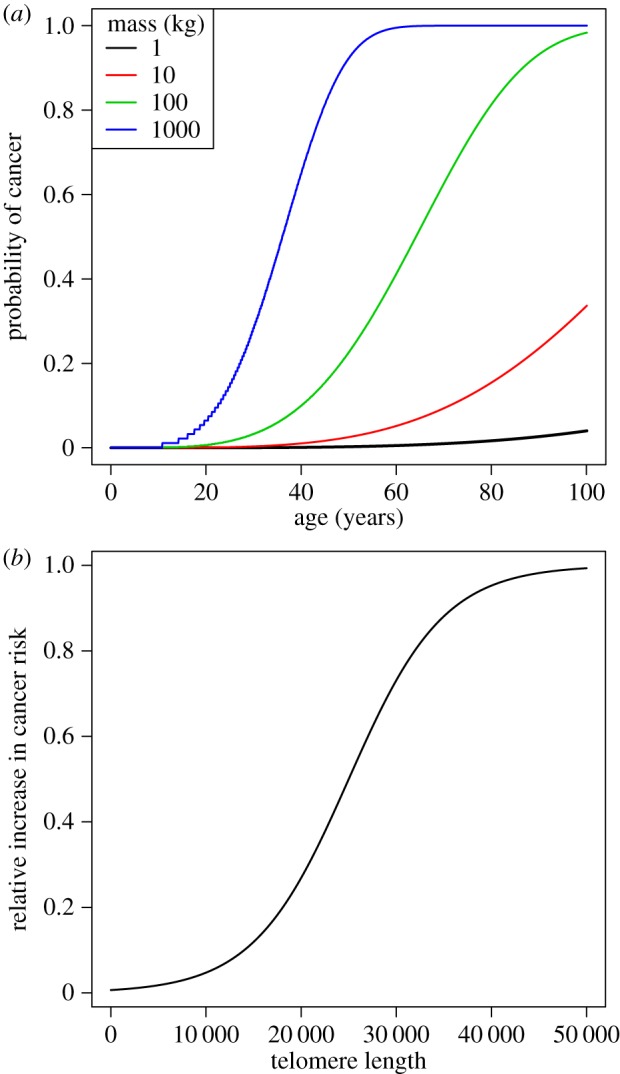
(a) Effect of body size on age-specific risk of cancer, using the Armitage–Doll model (see equation (2.2) in the text), with mutation rate m = 8 × 10⁻⁶, baseline threshold k = 4 (i.e. TL = 0). (b) We model the telomere-specific reduction in the threshold k assuming an inflection point i = 25 000 and a slope s = 0.00005.

The values for TL used in figure 3b are based on the comprehensive assessment of TL across mammal species by Gomes et al. [15]. The article reported mean TL = 15 kb (median TL = 13 kb) and mean TL = 34 kb (median TL = 37 kb) for mammal species with and without telomerase repression, respectively. Thus, we chose an intermediate value of 25 kb for the inflection point of the curve in figure 3b. We consider more than 25 kb to be ‘long’ telomeres and less than 25 kb to be ‘short’ telomeres, corresponding to the threshold observed in nature for species with and without telomerase repression. Of note, the range of TL depicted in figure 3b also corresponds to the natural range of TL in mammals, from approximately 5 to 50 kb [15].

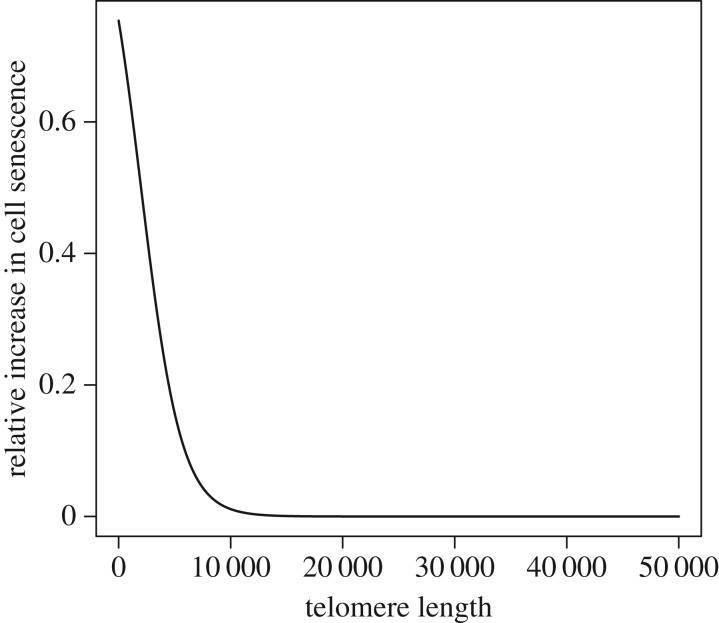
(iii). Cell senescence and telomere length

We assume that the risk of cell senescence is increased with shorter telomeres (figure 4, equation (A 7) in the appendix found in the electronic supplementary material), but that TL does not impact senescence until a certain minimal size is reached. We assume the effect of TL on the survival cost of cell senescence is size independent and we treat the cost of cell senescence as an aggregate cost across all cells within an individual (e.g. not a function of cell number). By contrast, in the case of cancer, it only takes one metastatic cell to give rise to a lethal cancer, and a larger-sized species would have more cells at risk. We assume that an increase in the risk of cell senescence increases mortality at all ages by an equivalent amount. Specifically, the age-independent parameter of the Gompertz mortality model, α (equation (2.1)) is multiplied by a factor 1 + g_TL (equation (A 7) in the appendix found in the electronic supplementary material). This factor varies from 1 (g_TL = 0, long TL with low risk of cell senescence) to 2 (g_TL = 1, short TL increasing risk of cell senescence). By multiplying α by 1 + g_TL, we make the implicit assumptions that (a) short TL has an impact on mortality at all ages and (b) there is no additional effect of yet shorter TL as individuals age. Given that mortality rates increase exponentially with age (equation (2.1)), the impact of TL-induced mortality on fitness will be minimal at early ages, when mortality is low. Thus, in effect, the impact of short TL on mortality increases with age.

Figure 4.

Effect of telomere size on relative cost of cell senescence, g_TL (i = 2000, s = 0.00014). See text for details of how we model the effect of g_TL on mortality.

(iv). Calculating size- and telomere-dependent fitness

To identify the effect of selection on telomere size, we need to measure fitness as a consequence of TL. To do this, we use the standard definition of fitness in age-structured populations. Specifically, fitness is defined as the intrinsic rate of increase, r (also known as the Malthusian parameter), which is obtained by solving the Euler–Lotka equation, 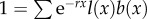(see equation (A 11) in the appendix found in the electronic supplementary material), where l(x) is the probability of surviving from age 0 to age x, and b(x) is the number of daughters produced by a female of age x. For the sake of simplicity, we assume that each population starts with TL = 25 000, fitness r = 0 and constant age-independent fecundity, such that 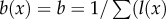. Survivorship is defined as the product of all age-specific survival rates, 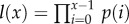. To calculate age-specific survival rate, p(x), we use the approximation p(x) = e^−μ(x), and calculate mortality μ as the sum of baseline size, age and TL-dependent intrinsic mortality (§§2(i,iii), above) and mortality due to cancer (§2(ii), above). The fecundity parameter, b, is unaffected by TL. However, by including it in the model, we scale fitness in a way that allows us to compare the consequences of changes in TL across species with very different life expectancies and fecundities.

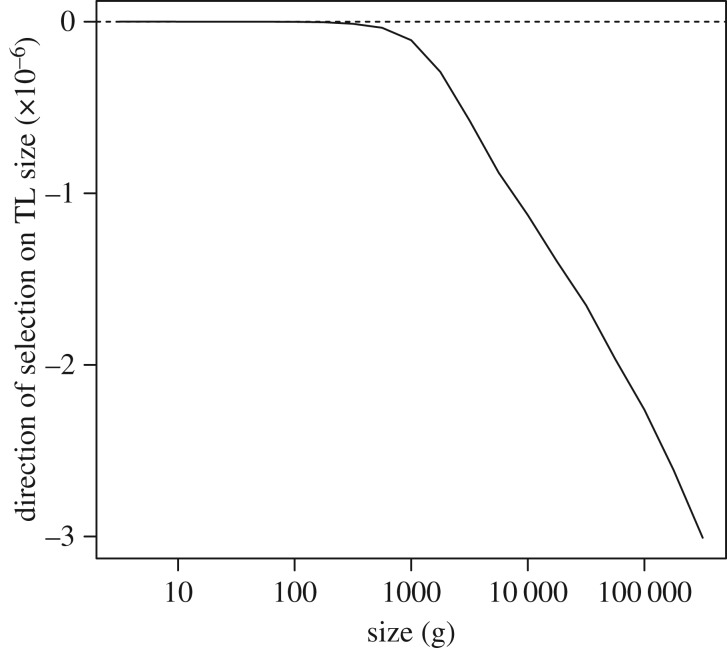
(v). Size-specific selection on telomere length

With the tools to calculate size- and TL-dependent fitness, we then ask how fitness changes in response to increases or decreases in TL for a given body size. For any size N, and initial fitness r = 0, assuming TL = 25 000, we calculate a new r for longer or shorter TL, holding fecundity constant at the initial level. We see that for species larger than approximately 1 kg, selection favours shorter TL (figures 5 and 6), while for species smaller than approximately 1 kg, there is little selection on TL, until the length of telomeres become extremely short (figure 5). We see these patterns reiterated when we look at the influence of body size on the effects of TL on lifespan (electronic supplementary material, figure S1).

Figure 5.

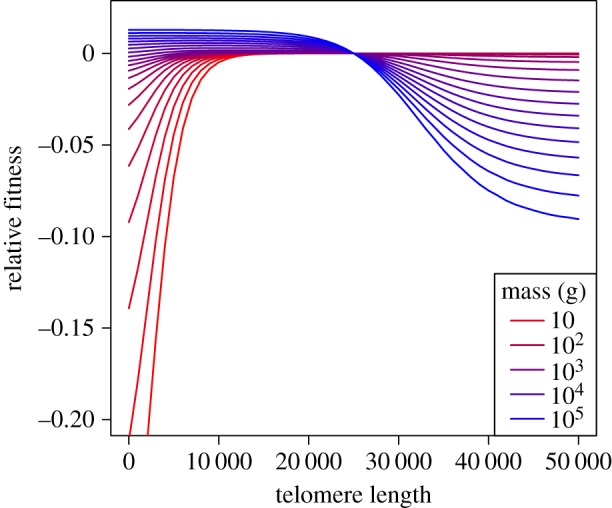
Effect of TL on relative fitness (r), by size. Lines show fitness relative to an initial TL = 25 000 and fecundity level such that r = 0. Holding fecundity constant, we then determine how fitness increases or decreases with changing TL. Note that for small species, selection would favour longer TL, while for large species, fitness would favour shorter TL.

Figure 6.

Effect of selection on TL as a function of size. Given the parameter values illustrated in figure 5, we see that selection favours longer TL below approximately 1 kg and shorter TL above approximately 1 kg.

3. Discussion

Here, we have developed a simple model to explore one possible explanation for observed phylogenetic patterns of TL [15]. As we have noted, among most mammals, large species tend to have short telomeres (less than 25 kb), while small species have either long or short telomeres. Moreover, telomerase maintains expression post-development in many small species, but only very rarely in larger species.

We are not the first to suggest that fitness trade-offs might have played a key role in shaping the evolution of telomere dynamics. For example, Stone et al. [35] noted that while short telomeres protect humans from cancer, they could account at least in part for the relatively high rate of heart disease. Also, Gorbunova et al. [16,36] have extensively studied the inverse association between telomerase activity and body mass in rodents, highlighting the fact that telomerase suppression might have evolved as a tumour suppressor mechanism in larger species. The novelty in our model rests in the formal integration of the trade-offs of TL (cancer versus senescence) into a fitness model that also takes into account the variability in mortality and cancer risk due to body size. By taking advantage of the fact that tumour suppressor mechanisms can be integrated into the Armitage–Doll equation of cancer risk, we offer a simple mathematical solution that tailors cancer risk by TL. The equations we develop here allow us to model fitness based on TL across a broad size-range of species, from a 2 g shrew to an elephant more than six orders of magnitude larger. Given this tremendous range of size across mammals, it is notable that we are able to predict the size at which shorter telomeres are favoured to within a few kilograms of the observed range.

(a). Model assumptions

By carrying out a formal mathematical model, as opposed to just providing a verbal argument, we are forced to be explicit about our assumptions [31]. This provides an important step in thinking about how plausible, and how general, this model might be. In particular, our model rests on a set of four general assumptions.

First, we assume that for reasons unrelated to telomeres or cancer, larger species of mammals live longer. The increase in lifespan in larger species is an empirical observation dating back at least to Francis Bacon in the seventeenth century [37]. While we cannot be certain that this pattern would hold even in the absence of the effects of telomeres and cancer risk, it is likely that many other mortality risks are lower in larger species, most notably predation.

Second, we assume that ceteris paribus, the risk of cancer for a given species will increase not only with lifespan, due to the longer time to accumulate oncogenic mutations, but also with size, due to the increasing number of cells at risk. These assumptions have led to the widely discussed Peto's paradox [17], which refers to the fact that large mammals like elephants and whales do not have a greater cancer incidence as expected by their large body size. In this model, we assume the most widely accepted solution to Peto's paradox, which is that species have evolved cancer suppression mechanisms as an adaptation to the selective pressure of cancer [38]. These mechanisms keep the incidence of cancer relatively low across species in the wild [25,39] and account for the lack of correlation between cancer risk and increased body mass or lifespan in mammalian species [23]. Because large body size has evolved independently multiple times in the animal kingdom, different mechanisms of tumour suppression are expected to have developed. However, cancer still arises to a certain extent in wild animals because no mechanism of tumour suppression is expected to be perfect and they might be subject to trade-offs, and because the strength of selection to counter late-age cancer is very weak [40].

Third, we assume that shorter TL is the only tumour suppressor mechanism developed by large species to decrease cancer risk, but there are others. In particular, at least in the context of the Armitage and Doll model [33], it is reasonable to assume that large species have been selected to evolve various ways to reduce the effective age-specific mutation rate (m in equation (2.2)) either through lower mutation or increased repair, and/or to increase the threshold number of mutations (k in equation (2.2)) required before a cell becomes metastatic [19]. In addition to shorter telomeres, large species appear to limit cancer risk by employing multiple copies of tumour suppressor genes [23], reducing the number of microsatellite sequences [41] and reducing the activity of endogenous retroviruses [42]. Some of these were reviewed in detail by Caulin and Maley [26] and are of obvious interest because they represent nature's own solution to suppress cancer, knowledge of which could improve current efforts to prevent cancer in humans.

Fourth, we assume that the variables explored here relate to one another as determined by a specific set of parameter values. We chose a set of values that we consider biologically plausible, and where possible, reflect known observation. For example, the effect of size on the Gompertz intercept, α, was chosen such that predicted life expectancy versus size is reasonably close to natural observation [43]. The possible range of all parameter values is effectively infinite. We hope that this modelling effort will stimulate not only additional refinements, extensions and alternatives to this model, but also attempts to ‘ground truth’ the parameter values with real-world data.

(b). Next steps

Like all models, ours necessarily leave out much biological detail. Nonetheless, it does lead to some potentially useful predictions. For example, our model suggests that among smaller species, cancer risk should be relatively independent of TL, while among larger species, longer telomeres should increase risk of cancer. This prediction is potentially testable both within and among species.

Within species, we might expect that larger individuals should have shorter telomeres to protect against an inherently higher risk of cancer (e.g. cancer incidence increases with adult height in humans [44] as well as with larger body size in breeds of domestic dogs [45]). Regarding associations with TL, increased body size is associated with reduced TL in wild house sparrows [46] and, in humans, males are larger than females and have shorter telomeres [47], even as newborns [48]. To what extent these associations are related to the cancer-protective nature of replicative senescence is unknown, but it is consistent with the model and deserves further investigation.

As we note above, our results are based on one specific set of parameter values. While a comprehensive analysis of this model is beyond the purview of this current study, future work would benefit from at least three extensions. First, it would be useful to explore a broader region of the possible parameter space in this model, to draw at least some limits on the domain of parameter values that is biological feasible and that generates the same prediction. Second, sensitivity analysis of this model would help to specify those variables that contribute most to the effect of TL on fitness. Third, it would be of interest to know the extent to which variation in TL within individuals, or among individuals within populations, might also contribute to size-dependent patterns observed among species.

Just how selection acts across the full range of TL will also require a more extensive analysis. Gomes et al. [15] found that for large species, TL tends to be quite short (less than 25 kb). For small species, there is a wide range of TL, from short to long. Some of that variation among small species could be due to variation in lifespan. For example, naked mole rats and American beaver, both among the longest-lived rodent species, have much shorter telomeres than closely related short-lived species. Alternatively, it may be that for small, short-lived species, cancer is not a strong selective force as these animals in the wild are most likely to die of causes other than cancer [38]. Thus, relatively short telomeres might have evolved due to random genetic drift, not because of their cancer protective effect. Notably, as explained above, the incidence of cancer across mammalian species, with few exceptions, is relatively low and very similar, despite orders-of-magnitude differences in body size and lifespan [23]. This suggests that the tumour suppressor mechanisms developed by each species, including the control of TL in large species, works to keep cancer at a steady low rate, at least in the wild [25]. Changes to the environment in which these mechanisms evolved, such as extended lifespans of rodents in captivity or humans in industrialized societies, are likely to push these mechanisms beyond their limits and lead to increased rates of cancer. Moreover, for larger species, the optimal range of TL to maximize fitness is likely to be much narrower than for small species. Telomeres that are too long will lead to cancer, so telomerase should be selected to be repressed in most, but not all, cells. Specifically, we see repression in all cells except germ cells, and in stem cells of tissues that need extensive life-long proliferation—most notably, haematopoietic and colonic stem cells. Enough telomerase is needed to avoid excessive telomere shortening before reproduction is accomplished. But pushing somatic cells close to this fitness cliff is ‘risky’: as telomeres shorten, more cells will enter replicative senescence and decrease organismal fitness. By fine-tuning TL throughout life, large species accomplish the task of growing big without developing cancer, at least until at or near late reproductive age.

In the past, substantial effort has gone into developing mathematical models to describe telomere dynamics within individuals [49–51]. Some have even used this approach to explore cancer-dependent trade-offs between short versus long telomeres [52]. The results presented here provide a framework for thinking about the evolution of telomere dynamics in a broader, phylogenetic framework. We hope our efforts generate interest in creating additional rigorous and comprehensive models to explain these striking evolutionary patterns.

Data accessibility

This article has no additional data.

Authors' contributions

R.A.R. and D.E.L.P. conceived the idea for the paper. Both authors jointly created the conceptual framework for the model, and D.E.L.P. then developed the equations and carried out the analysis of the model. R.A.R. and D.E.L.P. wrote and edited the paper.

Competing interests

We have no competing interests.

Funding

During the course of this work, D.E.L.P. was supported in part by NIH grant nos. AG049494 and AG044284 and R.A.R. was supported in part by NIH grant no. R01CA181308. Our initial efforts on this project were supported by a travel grant from the International Network on Telomere Biology.