Hotspot relaxation time of NbN superconducting nanowire single-photon detectors on various substrates

Abstract

Hotspot relaxation time (τ_th) is one of the essential parameter which defines the maximum count rate of superconducting nanowire single-photon detectors (SNSPDs). We studied the τ_th for NbN-based SNSPDs on various substrates using the two-photon detection method based on the pump-probe spectroscopy technique. We observed that τ_th strongly increased with increasing bias current in the two-photon detection regime. In addition, the minimum hotspot relaxation time (τ_th)_min was not significantly affected by the bath temperature; this is different from the previous observations reported for WSi SNSPDs. In addition, a strong dependency of (τ_th)_min on the substrate was found. The minimum (τ_th)_min was 11.6 ps for SNSPDs made of 5.5-nm-thick NbN on MgO (100), whereas the maximum (τ_th)_min was 34.5 ps for SNSPDs made of 7.5-nm-thick NbN on Si (100). We presented a direct correlation between the values of τ_th and degrees of disorder of NbN films grown on different substrates.

Introduction

Superconducting nanowire single-photon detector (SNSPD) is one of the most promising detectors in the near-infrared region owing to its unique combination of high speed, high detection efficiency, small timing jitter, and low dark count rate^1,2. These features make SNSPD attractive for a variety of applications, especially, quantum information processing^3,4. In recent years, many experimental and theoretical studies have investigated the detection mechanism to further enhance the count rates^5–7. The difficulty in achieving high-count-rate SNSPDs stems from their unique internal mechanism of photon detection and the external readout circuit.

A typical SNSPD comprises a meandered nanowire patterned from few-nanometer-thin superconducting films such as NbN or WSi^8,9. Absorption of a photon in a superconducting nanowire resulted in a non-equilibrium distribution of quasiparticles, with highly energetic hot electrons at a higher temperature than the Cooper pairs. The energy of the excited quasiparticles is redistributed within the electron and phonon system, which lead to an accumulation of quasiparticle excitations just above the energy gap and bring on the formation of a growing hotspot. The phonons in the nanowire dissipate the excess energy into the substrate and relax to the bath temperature; the equilibrium is restored throughout the entire superconducting sample then the hotspot disappears. The process of energy redistributed after the initial absorption of a photon is very fast (~fs) in disordered superconductors. Therefore, the energy transfer and down-conversion process following the absorption of a photon related to the formation and evolution of hotspot (hotspot relaxation process) can be characterized by a single time constant τ_th (hotspot relaxation time). The minimum time of SNSPD required for recovery to superconducting state is determined by the hotspot relaxation process. NbN-based SNSPDs have demonstrated intrinsic response times down to a few tens of ps, allowing the count rates to approach the GHz regime¹⁰. However, being limited by their large kinetic inductance (L_k) and the input impedance of the readout circuit (R_s), the devices have reset times that are several orders of magnitudes larger (~ns and larger) than their intrinsic response time. Reducing L_k and/or increasing R_s lead to a high count rate; however, the improvement in count rate is further restricted by the negative electro-thermal feedback¹¹. In addition, for superconducting materials with slow hotspot relaxation process, devices would latch into a finite voltage state instead of self-resetting to the superconducting state after detecting a photon¹². Therefore, τ_th is an important parameter that defines the maximum achievable count rate.

To quantitatively study hotspot relaxation process, several experiments have been conducted. In 2012, Heeres et al. proposed a quantum pump-probe technique based on the use of correlated photons from spontaneous parametric down-conversion (SPDC); they derived that the τ_th of an approximately 4-nm-thick NbN film grown on a sapphire substrate is ~15 ps and independent of the SPDC pump power and bias current¹³. In 2013, Zhou et al. demonstrated a novel method to measure ultrasensitive N-photon interferometric autocorrelation and determined that the τ_th of an approximately 4.3-nm-thick NbN film prepared on GaAs substrates is ~20 ps¹⁴. In 2016, Marsili et al. proposed a new technique that combined the pump-probe detection technology and Mach-Zehnder interferometer. They found that the τ_th of ~5-nm-thick WSi film on SiO₂/Si substrates varied from ~80 ps to ~800 ps with increasing bias current (I_b), bath temperature (T_B), or photon energy¹⁵.

To identify the key factors affecting the relaxation time of NbN SNSPDs, we systematically studied the τ_th of NbN SNSPDs via two-photon detection experiments based on the pump-probe spectroscopy technique. Devices with various geometric parameters (e.g., film thickness and nanowire linewidth) were fabricated on different substrates: MgO (100), MgF₂ (110), Al₂O₃ (0001), Si (100), and SiO₂/Si (100). The τ_th values of different SNSPDs were measured and compared. Besides, the temperature dependence (2.15–5 K) of τ_th was also analyzed.

Results

Determination of τ_th

SNSPD devices with different nanowire linewidth/space ratio (w/s) were fabricated from NbN films deposited on different substrates and cooled down for the characterization (see Table 1). Detailed information concerning device preparation, characterization and measurement setup can be found in the methods’ section below. The single-photon regime in SNSPD can be achieved when I_b is biased close to the switching current (I_sw). When lowering I_b, the energy of a single photon is insufficient to create a response pulse and the detector only responds to two or more photons^10,14,15. Herein, we introduced the two-photon detection method, wherein the response pulse is triggered when the two incident photons separated by the time delay (t_D) generate two hotspots that overlap spatially and temporally. According to recent research, the probability of having two absorbed photons of incident photons can be given by (ημ)²/2, where η is the two-photon detection efficiency and μ is the average number of photons per pulse^15,16. When t_D was longer than τ_th, the response probability is approximately equal to the sum of each pulse of (ημ)². When t_D was shorter than τ_th, the increased mean photon number doubled the response probability to 2 (ημ)². Consequently, the evolution of hotspot relaxation process differed from that of SNSPD recovery.

Table 1.

Substrate material, film thickness (d), nanowire linewidth (w), space (s), switching current (I_sw), switching current density (J_sw), and minimum hotspot relaxation time (τ_th)_min for the seven SNSPDs.

Sample	Substrate material	d (nm)	w (nm)	s (nm)	Isw (μA)	Jsw (MA/cm2)	(τth)min (ps)
#1	MgO (100)	5.5	90	110	33	6.7	11.6 ± 0.1
#2	MgO (100)	5.5	105	110	40	6.9	12.2 ± 0.1
#3	MgO (100)	5.5	120	110	51.5	7.8	12.6 ± 0.1
#4	MgF2 (110)	4.5	90	110	22	5.4	19.7 ± 0.1
#5	Al2O3 (0001)	7	130	70	21.5	2.4	22.5 ± 0.7
#6	SiO2/Si (100)	7	90	110	21	3.3	22.7 ± 0.1
#7	Si (100)	7.5	90	110	19	2.8	34.5 ± 0.3

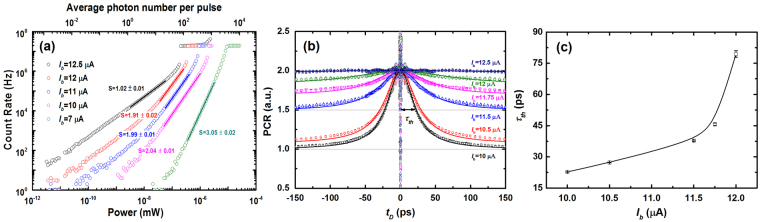
First, Sample #6 was tested (7-nm-thick NbN/SiO₂/Si (100) and 90-nm-wide nanowire with a 110-nm space) at T_B of 2.15 K. The I_sw of the device was approximately 21 μA. To distinguish the bias current range for two-photon detection, the count rates were measured as a function of the light power (average photon number per pulse) at several I_b values of 12.5 μA, 12 μA, 11 μA, 10 μA, and 7 μA. As shown in Fig. 1(a), the solid lines are fits to the measured data in the log-log scale. At I_b = 12.5 μA, and 7 μA, the fitted slope of 1.02 ± 0.01, and 3.05 ± 0.02 indicating that the detector operates in the single, and three-photon detection regime. At I_b of 12 μA, 11 μA, and 10 μA, the slopes of the fitting lines are 1.91 ± 0.02, 1.99 ± 0.01, and 2.04 ± 0.01, respectively. Therefore, the detector is dominated by two-photon detection for bias current 10 μA ≤ I_b ≤ 12 μA. We note that, there is no sharp boundary between either single or two-photon detection regime (~12 μA), and two-photon and three-photon regime (~10 μA). However, with the current lower than 10 μA, the count rate is too low to study with the fixed average photon number. With the current higher than 12.0 μA, the single-photon detection will be dominant so we cannot obtain the accurateτ_th based on Lorentz function fitting (see Fig. 1(b)). Therefore, the bias range of 10–12 μA is suitable for studying the τ_th. Figure 1(b) illustrates the photon-response count rate (PCR) as a function of t_D at different I_b values from 10 μA to 12.5 μA. The measured data were fitted with a Lorentz function and normalized to 2 at t_D = 0 ps, ignoring the optical interference in the range −2 ps ≤ t_D ≤ 2 ps. At I_b = 12.5 μA, the PCR was irrelevant to t_D as the detector was nearly working in the one-photon detection regime. When I_b was lowered to 10 μA, the normalized PCR declined from 2 to ~1, with t_D increasing from 0 ps to ~150 ps^15,17. In particular, the half width of this peak directly corresponds to τ_th. Figure 1(c) shows τ_th as a function of I_b extracted from the data in Fig. 1(b). The minimum value of the hotspot relaxation time (τ_th)_min was 22.7 ps ± 0.1 ps at I_b = 10 μA. Additionally, τ_th increased to 79.5 ps ± 1.5 ps, whereas I_b increased to 12 μA. These trends have also been reported for WSi SNSPDs and NbN waveguide-integrated SNSPDs, for which self-recombination rather than diffusive expansion explained the strong dependence of τ_th on I_b¹⁸.

Figure 1.

(a) Count rates as a function of light power (average photon number per pulse) at five different I_b values. The measured points, denoted by the open circles, were fitted with straight lines in the log–log scale. The slopes of the fitting lines are 1.02 ± 0.01, 1.91 ± 0.02, 1.99 ± 0.01, 2.04 ± 0.01, and 3.05 ± 0.02, respectively. (b) Normalized PCR as a function of t_D, which is measured when the detector operated in the two-photon detection regime at I_b values of 10, 10.5, 11.5, 11.75, and 12 μA; I_b of 12.5 μA corresponding to the one-photon detection regime is also shown for comparison. The measured data were fitted with a Lorentz function. The black arrow denotes the half width at half maximum of the curve, which directly corresponds to τ_th measured at I_b = 10 μA. (c) τ_th as a function of I_b extracted from the data in (b).

Dependence of τ_th on bath temperature

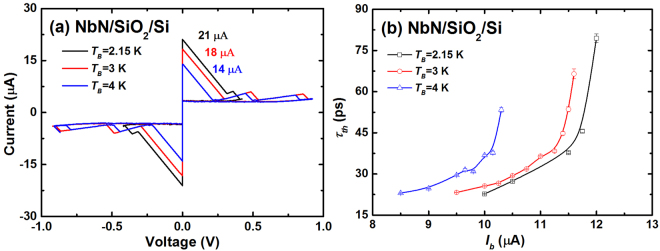
To investigate the temperature dependence of τ_th, we tuned the T_B of SNSPDs from 2.15 K to 4 K using the resistive heater. Figure 2(a) shows the current-voltage (I-V) characteristics of Sample #6 at three different temperatures (2.15 K, 3 K, and 4 K). I_sw decreased from 21 μA to 14 μA with increasing T_B. As a result, the two-photon detection ranges changed to 10 μA ≤ I_b ≤ 12 μA (2.15 K), 9.5 μA ≤ I_b ≤ 11.6 μA (3 K), and 8.5 μA ≤ I_b ≤ 10.3 μA (4 K). Then, the I_b dependence of τ_th at different T_B values were studied; τ_th gradually increased with I_b and presented a considerable change around the one-photon detection regime for all T_B values (Fig. 2(b)). However, the τ_th-I_b curve shifted to a smaller I_b with increasing T_B owing to the change of the two-photon detection range. In addition, at a fixed I_b, τ_th increased with T_B; this could be attributed to the decreased electron relaxation rate at high T_B. However, the (τ_th)_min values at T_B values of 2.15 K, 3 K, and 4 K were measured to be 22.7 ps ± 0.1 ps, 23.2 ps ± 0.1 ps, and 23.0 ps ± 0.1 ps, respectively. The results agree well with each other, and we saw a saturated trend of τ_th with decreasing the current, suggesting that the minimum hotspot relaxation time might be independent of T_B. However, it is difficult to verify it by further decreasing the current since the device no longer worked in the two-photon detection regime anymore. This is different from the results reported for WSi SNSPDs, where (τ_th)_min increased with T_B from 250 mK to 2 K¹⁵. Possibly, the smaller I_sw of WSi SNSPDs at higher temperatures restricts the ability to reach the lowest bias in the two-photon detection regime owing to the limit of the readout circuit. In other words, the (τ_th)_min of WSi SNSPDs might be smaller at high temperatures as well.

Figure 2.

(a) I-V curves and (b) τ_th as a function of I_b measured at T_B values of 2.15 K, 3 K, and 4 K, respectively, for Sample #6.

Dependence of τ_th on nanowire linewidth

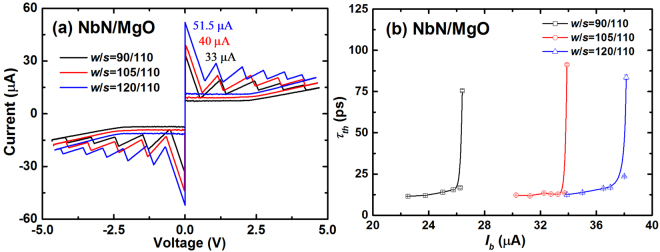
It has been well established that the w of nanowire affects not only the optical absorption but also the intrinsic detection efficiency of SNSPD^8,19. To understand the influence of w on τ_th, three different SNSPDs were fabricated on MgO substrate, wherein w was designed to be 90, 105, and 120 nm, respectively. The s value was set to 110 nm. The measured w/s is consistent with the design as the EBL and RIE processes were optimized. The other parameters are listed as Samples #1–3 in Table 1.

Figure 3(a) shows the I-V curves of the SNSPDs with three different w values (90, 105, and 120 nm) that give I_sw values of 30, 40, and 51.5 μA respectively. Similarly, we obtained the relation of τ_th as a function of I_b for the three SNSPDs, as shown in Fig. 3(b). The trend displayed in the figure is comparable to that of Sample #6, and the curve shifts to the right with increasing w while maintaining the shape similarity. The (τ_th)_min values for the three SNSPDs were determined to be 11.6 ps ± 0.1 ps, 12.2 ps ± 0.1 ps, and 12.6 ± 0.1 ps, respectively. The deviations were lesser than 1 ps. The slight increase in (τ_th)_min with increasing w is explained by the presence of less thermal relaxation channels in the center of the nanowire as opposed to at the sides of the nanowire. In addition, the values are only half of those obtained for Sample #6; this is further discussed in the next section.

Figure 3.

(a) I-V curves and (b) τ_th as a function of I_b at T_B values of 2.15 K for Sample #1–3 with different w/s.

Dependence of τ_th on the substrate

A variety of substrates, such as Si, MgO, MgF₂, and Al₂O₃, have been used to grow ultrathin NbN films for fabricating SNSPDs^20–22. To investigate the effect of substrates on τ_th, we measured and compared the τ_th of NbN SPSPDs on different substrates [Si (100), MgO (100), MgF₂ (110), Al₂O₃ (0001), and SiO₂/Si (100)].

Figure 4 shows τ_th as a function of I_b at T_B = 2.15 K for SNSPDs on various substrates. All SNSPDs showed a similar increase in τ_th with increasing I_b. The (τ_th)_min values are summarized in Table 1 and follow the simple relation (τ_th)_min(MgO) ≤ (τ_th)_min(MgF₂) ≤ (τ_th)_min(Al₂O₃) ≤ (τ_th)_min(SiO₂/Si) ≤ (τ_th)_min(Si). The maximum difference of (τ_th)_min is roughly three times. The smallest (τ_th)_min (11.6 ps ± 0.1 ps) was obtained from the MgO (100) substrate, and the largest (τ_th)_min (34.5 ps ± 0.3 ps) was obtained from the Si (100) substrate. Typically, τ_th is controlled by carrier diffusion as well as by the recombination time of the quasiparticles, which is indeed related to the degrees of disorder of the materials^15,23. In other words, a film with a lower disorder would have a smaller (τ_th)_min.

Figure 4.

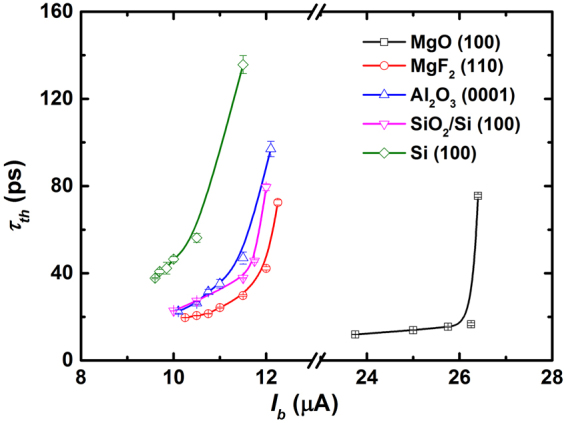
τ_th as a function of I_b at T_B values of 2.15 K for various substrates.

Role of disorder on τ_th

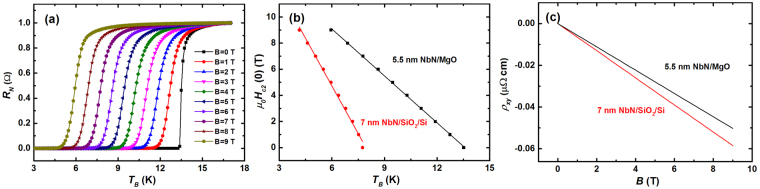
The superconducting properties of NbN films are determined by many parameters of the films. One of the key parameters is actually the film crystal structure, which is strongly influenced by not only the substrate material but many other parameters including the deposition condition. Meanwhile, NbN is a conventional s-wave superconductor and the superconducting properties of the NbN ultrathin film can be partially characterized by its degrees of disorder, which is related to not only the substrate material, but also the film thickness. The degrees of disorder of NbN films on two substrates MgO and SiO₂/Si were quantitatively analyzed. First, we measured the normalized resistance (R_N) as a function of T_B for the 5.5-nm-thick NbN/MgO and 7-nm-thick NbN/SiO₂/Si substrates under different magnetic fields via transport measurements using a physical property measurement system. To accurately determine the resistivity (ρ_n), the electrical resistance (R) was measured on a 4 μm × 40 μm microbridge using the standard four-probe method. Figure 5(a) shows the R_N-T_B relations for the 5.5-nm-thick NbN/MgO sample. The upper critical field (H_c2) values at different temperatures were then determined at the point where R_N becomes 50% of its normal value. The μ₀H_c2-T_B relations for the two samples are shown in Fig. 5(b). In the dirty limit of a superconductor film e.g., NbN, the mean electronic free path (l) is shorter than the Ginzburg–Landau coherence length (ξ_GL). Then, H_c2 (0), ξ_GL, and the electron diffusion coefficient (D) are obtained from $H_{\mathit{c}2}\left(\mathit{0}\right)=\mathit{0.69}{T}_c\left(d{H}_{\mathrm{c2}}/\mathit{dT}\right){|}_{\mathit{T}=T_c},{\xi }_{\mathit{GL}}=\sqrt{{\mathrm{\Phi }}_0/\mathit{2}\pi H_{\mathit{c}\mathit{2}}\left(\mathit{0}\right)}$, and $\mathit{D}=-\mathit{4}{k}_B/\left(\mathit{\pi }\mathit{ed}{H}_{\mathit{c}2}/\mathit{dT}\right)$, respectively, where Φ₀ is the flux quantum, k_B is the Boltzmann constant, and e is the electron charge^24,25. For NbN films epitaxially grown on the MgO substrate, the obtained D value was 0.92 cm²/s, which is approximately twice the value of the film on the SiO₂/Si substrate (0.47 cm²/s). The larger value of D suggests the presence of fewer defects and vacancies in the samples. The calculated ξ_GL values were 5.43 nm and 5.12 nm for the 5.5-nm-thick NbN/MgO and 7-nm-thick NbN/SiO₂/Si samples, respectively.

Figure 5.

(a) R_N as a function of T_B for 5.5-nm-thick NbN on MgO (100) under different magnetic fields. (b) μ₀H_c2 as a function of T_B for 5.5-nm-thick NbN on MgO (100) and 7-nm-thick NbN on SiO₂/Si (100). The solid lines are linear fits to the data. (c) ρ_xy as a function of B at 25 K for the two samples.

Next, Hall measurement was performed using a four-probe AC technique. Figure 5(c) shows the Hall resistivity (ρ_xy) as a function of B for the two samples measured at 25 K. The electron density (n) and the Ioffe–Regel parameter (k_Fl) are calculated from $\mathit{n}=1/R_{H}e,k_F={\left(3{\pi }^{2}n\right)}^{1/3}$, and $l={\rho }_{n}n{e}^2/\hslash k_F$, respectively, where $R_H={\rho }_{\mathit{xy}}/H$ is determined from the slope shown in Fig. 5(c). All the obtained values are listed in Table 2. As expected, $l<{\xi }_{\mathit{GL}}$, indicating that all NbN films are in the dirty limit irrespective of which substrate is used. However, the k_Fl values described herein range from moderately disordered (5.31) to strongly disordered (1.53), suggesting that NbN grown on the MgO (100) substrates exhibits a less disordered structure. The film superconductivity decreases with increasing disorder. The J_sw values listed in Table 1 are also confirmed the above judgments to some extent.

Table 2.

Critical temperature (T_c), normal resistivity (ρ_n), upper critical field [H_c2(0)], Ginzburg–Landau coherence length (ξ_GL), electron diffusion coefficient (D), mean electronic free path (l), and Ioffe–Regel parameter (k_Fl) for the 5.5-nm-thick NbN/MgO (100) and 7-nm-thick NbN/SiO₂/Si (100) samples.

Substrate material	d (nm)	Tc (K)	ρn (μΩ cm)	μ0Hc2 (0) (T)	ξGL (nm)	D (cm2/s)	l (Å)	k F l
MgO (100)	5.5	13.51	154	11.17	5.43	0.92	3.56	5.31
SiO2/Si (100)	7	7.71	562	12.56	5.12	0.47	1.08	1.53

Discussion

The minimum (τ_th)_min measured in our NbN SNSPDs is about only one in seven of WSi SNSPDs’, indicating a significant difference in material properties. The direct method to decrease τ_th is to decrease the degrees of disorder of the materials. However, how to decrease τ_th together with optimizing other parameters such as intrinsic detection efficiency still remains an open question, which is very interesting for not only understanding the mechanism of SNSPD but also the practical SNSPD with high performance.

In summary, the τ_th of NbN SNSPDs on various substrates were investigated with a two-photon detection measurement technique. The experimental setup was based on pump-probe spectroscopy, wherein the laser pulses were separated by time delays tuned in a wide range. To realize two-photon detection in a reasonable bias range, the typically average photon number per pulse is set as 40. The high average photon number per pulse guarantee the data collection in a reasonable time (one dot per hour) compared with the correlated photon-pair source based on SPDC.

Our results show that the bath temperature and nanowire linewidth do not significantly affects (τ_th)_min, i.e. they contribute less to the intrinsic upper limit of the count rate of SNSPD. However, (τ_th)_min is strongly affected by the substrate because the degrees of disorder of NbN films are different. Epitaxially grown 5.5-nm-thick NbN on MgO (100) has a minimum (τ_th)_min of 11.6 ps, and amorphous 7.5-nm-thick NbN on Si (100) has a maximum (τ_th)_min of 34.5 ps. As a result, it is important to choose a suitable substrate if one wants to find lower τ_th. Besides, one may further study NbN films deposited on different substrates with different deposition conditions to further identify the minimum of τ_th. It may guide the further studies in the community on not only the physics of ultrathin superconducting films, but also the practical SNSPD with high count rate. Beyond that, the results are also interesting for the study of other superconducting sensors/detectors based on hot-electron effect, for example, hot-electron mixers.

Methods

Device fabrication

Ultrathin NbN films were synthesized through reactive DC magnetron sputtering of an 8-inch Nb target in an Ar + N₂ gas mixture at room temperature. The typical background pressure was 9 × 10⁻⁶ Pa. The flow rates of Ar and N₂ were set to 30 sccm and 4 sccm, respectively, under a total pressure of 0.27 Pa. The DC magnetron power was provided by current-regulated power supply set at 2.2 A with a resulting voltage of 270 V. The deposition rate was 6 Å/s, calibrated by X-ray reflectivity. The substrates used for film growth were Si (100) with its native oxide, MgO (100), MgF₂ (110), Al₂O₃ (0001), and Si (100) with a 253-nm-thick buffering SiO₂ layer. Prior to film deposition, all the substrates were cleaned by Argon ion-beam etching in a cleaning chamber. It is worth noting that the etching process removed native oxides of the Si (100) substrate. Because the MgO (100) and MgF₂ (110) substrates allow the epitaxial growth of NbN films, NbN films on these substrates have higher critical temperature T_c than those on the Al₂O₃ (0001), SiO₂/Si (100), and Si (100) substrates. To optimize the device performance, films with different thickness (d) values, i.e., 5.5, 4.5, 7, 7, and 7.5 nm were synthesized on the MgO (100), MgF₂ (110), Al₂O₃ (0001), SiO₂/Si (100), and Si (100) substrates, respectively. The films were structured into a conventional meandered nanowire structure, which covered a 15 μm-diameter area. All nanowire structures were patterned by electron-beam-lithography (EBL) with PMMA950-A2 as the e-beam resist. Electrode structures were formed by reactive ion etching (RIE) in the CF₄ gas. Seven SNSPDs with different nanowire linewidth/space ratio (w/s) were fabricated. The detailed parameters of these SNSPDs are listed in Table 1.

Measurement setup

The experimental setup for τ_th measurement is shown in Fig. 6. The source of optical excitation is a 20-MHz mode-locked fiber laser with a 1550-nm wavelength, 500-fs pulse duration, and a typical maximum average output power of 2 mW. Laser pulses are attenuated and then divided by a 1:1 fiber beam splitter. One part of the pulse is sent to a fixed fiber, whereas the other part is sent to a motorized delay line. The time delay t_D between the two pulses can be controlled by tuning the motorized delay line with a precision of ±0.01 ps. The two pulses are combined again on a 1:1 fiber beam splitter and then coupled to the SNSPDs. The measurements for the SNSPDs are performed in a Gifford–McMahon cryocooler at 2.15–5 K. A resistive heater is placed near the sample to tune the temperature of SNSPDs.

Figure 6.

Schematic of the experimental setup for the τ_th measurements. Two fiber beam splitters (BS) and a motorized delay line were used to control the t_D between the two pulses.

Author Contributions

L.Z. and L.X.Y. designed the experiment, analyzed the data and wrote the paper. L.Z. and X.Y.Y. performed the measurements. L.Z. performed the thin film deposition and J.J.W. and W.J.Z. fabricated the SNSPD devices. C.L.L., Q.G. and H.L. provided assistance in the experiment. W.P., Z.W. and X.M.X. discussed the results. All authors reviewed the manuscript.

Competing Interests

The authors declare that they have no competing interests.