Introduction
Respondent‐driven sampling (RDS) is a network‐based method for sampling populations for whom a sampling frame is not available (Heckathorn 1997). Information about these “hard‐to‐reach” or “hidden” populations is critical for public health research with populations at high risk of acquiring HIV infection, including persons who inject drugs (PWID), men who have sex with men, and sex workers. RDS is widely used for public health surveillance of hidden populations by organizations such as the U.S. Centers for Disease Control and Prevention (CDC) (Gallagher et al. 2007), the Chinese Centers for Disease Control (Li et al. 2014), and entities funded through the President’s Emergency Plan for AIDS Relief (PEPFAR) (Hladik et al. 2012).
RDS is primarily used to estimate the prevalences of traits such as diseases and risk factors. Unbiased point and variance estimates of such prevalences from survey samples classically require calculating each participant’s probability of being sampled (“inclusion probability”). Because a sampling frame is not available, hidden population members’ inclusion probabilities cannot be calculated using standard approaches. Therefore, statistical inference from samples collected via RDS relies on models approximating the sampling process that incorporate information about the sample members’ social networks and information observed during the recruitment process.
Multiple evaluations of RDS point estimators and violations of RDS assumptions have been conducted, but significantly less work has examined RDS variance estimators (Wejnert 2009, Gile and Handcock 2010, Goel and Salganik 2010, Gile 2011, Tomas and Gile 2011, Lu et al. 2012, McCreesh et al. 2012, Merli et al. 2014, Verdery et al. 2015). Variance estimates are an essential complement to point estimates. Without good variance estimators, one cannot assess the amount of information contained in a sample and may draw invalid conclusions. In particular, statistical significance tests and confidence intervals will be misleading when the variance is under (or over) estimated. Additionally, understanding the variance of RDS point estimates in populations to which RDS is typically applied is important for calculating appropriate sample sizes for future studies.
Past research on RDS variance estimation suggested that RDS confidence intervals provide unacceptably low coverage rates and that RDS may have extremely large design effects when applied to hidden populations of public health interest (Goel and Salganik 2010, Lu et al. 2012, Verdery et al. 2015). This study is the first systematic evaluation of the different RDS variance estimators. Our results indicate that confidence interval coverage rates are often acceptable although not perfect and design effects are in the range of other complex survey designs.
Background
RDS begins with researchers choosing a small number (usually 5 to 10) of “seed” population members. The seeds are interviewed and given a small number of uniquely numbered coupons with which they can recruit population members they know into the sample (usually 3‐5). Recruited population members are interviewed and given coupons, and the process is repeated until the target sample size is reached. Participants are remunerated both for completing the survey questionnaire and for each eligible population member they recruit.
RDS survey questionnaires and associated biological tests provide data on many characteristics of interest. For the purposes of this article, without loss of generality, we will represent these variables of interest by a two‐valued trait, with values “with trait” and “without trait.” Populations sampled via RDS are connected via social network ties; we will refer to the set of persons, or “nodes,” and ties connecting them as the “population network.” We will refer to the number of ties each person has to other members of the population as that person’s “degree.”
Most RDS point estimators currently used are design‐based, including the Salganik‐Heckathorn (SH) (Salganik and Heckathorn 2004), Volz‐ Heckathorn (VH) (Volz and Heckathorn 2008), and Successive Sampling (SS) estimators (Gile 2011). The SH estimator models RDS as a Markov chain on the nodes in the population network; it is based on equating the number of network ties between population groups with different trait statuses (Salganik and Heckathorn 2004, Gile and Handcock 2010). The VH estimator uses the same Markov chain approximation to RDS, and applies a modified Hansen‐Hurwitz estimator calculated from respondent degrees and the trait statuses of sample members (Volz and Heckathorn 2008). The SS estimator models RDS as sampling population members proportional to degree without replacement; it applies an algorithm to estimate the mapping between a person’s degree and his sampling probability and applies a form of the Horvitz‐Thompson estimator (Gile 2011). More details on these estimators is available in the Supplementary Materials.
Commonly used RDS variance estimators employ a bootstrap resampling approach that approximates the RDS design (Davison and Hinkley 1997). The variance of the point estimates produced by these bootstrap resamples is computed and used to estimate the RDS variance. Two approximations that are currently used are the Salganik Bootstrap (“Sal‐BS”) (Salganik 2006) and the Successive Sampling Bootstrap (“SS‐BS”) (Gile 2011). The Sal‐BS is typically applied in conjunction with the SH or VH RDS point estimators (Salganik 2006), and the SS‐BS is applied in conjunction with the SS point estimator (Gile 2011). We refer to these point and variance estimator pairs as “SH/Sal‐BS”, “VH/Sal‐BS”, and “SS/SS‐BS”, respectively. Sal‐BS is based on ordered with‐replacement resampling draws from the sample, such that each subsequent node is selected from among the nodes whose recruiters have a trait status matching that of the previous node (Salganik 2006). SS‐BS takes a similar approach, but considers the without‐replacement structure of RDS by adjusting the set of available nodes at each resampling draw based on which nodes had been previously sampled (Gile 2011). This analysis evaluates each of these point and variance estimate pairs; for comparison, we also consider the case when the RDS data are naively treated as a simple random sample (SRS) and the sample mean point estimator is used. We refer this estimator pair as “Mean/SRS.”
The variability of estimators is typically presented as a standard error or confidence interval (CI), the latter often derived from the former. In RDS, CI’s are typically the metric of choice, as they provide an estimated range of values deemed plausible for the trait of interest. A properly‐calibrated method for computing level- α CIs produces intervals that capture the true population value for an estimand with probability at least (1 – α) (e.g., an α of .05 corresponds to a CI that includes the true population value in 95% of samples). CIs can be calculated from bootstrap variance estimates using a number of methods; the percentile and studentized bootstrap CI methods are most commonly used for RDS data (Efron and Tibshirani 1986). The lower and upper bounds of the CI under the percentile bootstrap method are the and percentiles, respectively, of the bootstrap resamples. In contrast, the studentized bootstrap CI method calculates the standard deviation (SD) of the bootstrap resample estimates and the t‐value (t) associated with the sample’s degrees of freedom; it then calculates the CI as the point estimate plus or minus t * SD for the upper and lower bounds, respectively. The percentile method can generate CIs that are asymmetric about the point estimate, whereas the studentized method always produces symmetric CIs. The SH/Sal‐BS and VH/Sal‐BS RDS estimator pairs have traditionally calculated CIs using the percentile method (Salganik 2006), while the SS/SS‐BS estimator pair has traditionally used the studentized bootstrap method (Gile 2011). The Mean/SRS estimator pair calculates a CI based on a normal approximation to the sampling distribution.
Framework for Assessing RDS
Evaluations of RDS point estimators have been conducted both with real RDS samples from non‐hidden populations and with simulated RDS samples, but the accuracy of RDS variance estimators can only be evaluated via simulation. This is because, while it is theoretically possible to know the true value of an estimand in the target population to which to compare point estimators, it is only possible to know the true variability of an estimator in a true population by conducting a large number of independent studies in the same population with the same structure, which is practically infeasible.
Evaluating RDS by simulation consists of three steps: (1) obtaining or creating a population network with certain characteristics, (2) simulating RDS on that network, and (3) applying RDS estimators to the trait of interest in the resulting samples. As these procedures are repeated many times, the resulting distribution of simulated estimates approaches the true sampling distribution of the estimators under the simulation conditions. Therefore, one is able to compare estimates of estimator uncertainty to “true” simulated levels of uncertainty.
Our primary results evaluate the performance of RDS uncertainty estimation based on the performance of the CIs calculated from different point/variance estimator pairs (e.g., SH/Sal‐BS). An estimator pair’s CI coverage is the percentage of simulations in which its CIs capture the network’s true population value, which is compared to the nominal coverage of 100 * (1 − α)% (e.g., a 95% CI should capture the true population value in 95% of simulations).
In addition to evaluating variance estimators, for comparison with previous research on RDS uncertainty estimation, we consider RDS design effects (DEs), a relative measure of the variability of an estimator calculated from a sample drawn with a complex sampling method (Goel and Salganik 2010, Verdery et al. 2015). We calculate the DE as the ratio of the variance of an estimator from a given sampling design to the hypothetical variance if the sample had been collected using SRS on the same population. Specifically, the DE is the ratio of the RDS estimate’s variance to that under an SRS design of the same sample size. A method with a DE of two would require a sample size twice as large as that required by SRS to achieve the same variability for the estimate of a given trait.
Typical DEs for many complex surveys that did not use RDS are between 1.5 and 2, but for some variables in some studies can range to 5 (Pettersson and Silva 2005, US Census Bureau 2006). Previous research on the variance of RDS estimators has suggested that RDS DEs may be significantly larger than is typical in surveys conducted using complex sampling methods other than RDS (Goel and Salganik 2010, Lu et al. 2012, Verdery et al. 2015).
While the DE of a given RDS study in the real world is unknown because it cannot be calculated from the data, we can calculate the DEs for our simulations numerically. We refer to these as the “actual DEs” below. In addition to actual RDS DEs, which previous research has also calculated based on simulations, the DEs estimated by RDS variance estimators (which can be calculated from a real RDS study’s data) are also of interest. We refer to these as “estimated DEs” below. Previous simulation studies have suggested that RDS variance estimators produce inaccurate estimated DEs when they compared the estimated and actual DEs for a given simulation (Goel and Salganik 2010, Verdery et al. 2015).
Table 1 summarizes the findings from three previous simulation studies of RDS variance estimation and design effects. The two studies that evaluated 95% CI coverage reported mean or median 95% CI coverage rates below 70%. The three studies found a wide range of design effects, with mean or median design effects greater than 5 and ranging from 5 to 30.
Table 1.
Findings from previous simulation studies of RDS variance estimation and design effects
| Study | Point Estimator | Variance Estimator | Simulation approach/CI Method | Population Network Data Used for RDS Simulations | 95% CI Coverage | DE Result |
|---|---|---|---|---|---|---|
| Goel & Salganik (Goel and Salganik 2010) | Volz-Heckathorn | Salganik | With Replacement/Percentile | 1987 attempted network census of high‐risk heterosexuals in Colorado Springs, Colorado | 52% (median) | 11 (median; multiple traits) |
| Goel & Salganik | Volz-Heckathorn | Salganik | With Replacement/Percentile | Sample of United States adolescents in 7th – 12th grades between 1994 and 1996 | 62% (median) | 5.9 (median; multiple traits) |
| Lu et al. (Lu et al. 2012) | Volz-Heckathorn | N/A | N/A | Online social network in Sweden | N/A | 5 to 13 (multiple traits) |
| Verdery et al. (Verdery et al. 2015) | Volz-Heckathorn | Salganik | With Replacement/Studentized | Sample of United States adolescents in 7th – 12th grades between 1994 and 1996 | 68% (mean) | 15 (mean; 3 traits) |
| Verdery et al. | Volz-Heckathorn | Salganik | With Replacement/Studentized | Multiple Facebook social networks of college students | 65% (mean) | 30 (mean; 2 traits) |
Methods
Evaluating RDS via simulation requires obtaining or creating a population network from which to draw samples and simulating RDS on that network. Previous studies have simulated RDS both on real and synthetic population networks. RDS is used to study hidden populations, so an RDS simulation study’s population network should be as similar to real hidden population networks as possible. Unfortunately, complete data for hidden population networks is extremely rare. Complete network data is difficult and expensive to collect in any setting (Morris 2004), and these challenges are compounded among populations whose members wish to remain hidden.
Hidden population network data are unavailable, so the real population networks in previous RDS simulation studies have come from a variety of sources (Table 1). Two of the studies used network data from a sample of United States adolescents in 7th through 12th grades (the “Add Health” study) (Harris et al. 2009, Goel and Salganik 2010, Verdery et al. 2015), and another used Facebook network data from college students when Facebook only permitted college students to use the service (Verdery et al. 2015). Notably, both of these population networks are embedded within schools. In the United States, middle schools and high schools are highly structured by grade, with students typically taking classes only with others in the same grade. Colleges are less structured by grade, but they have additional structure along academic disciplines. Students in these settings often have friends outside their grades and disciplines, but their networks are strongly shaped and constrained by those institutional structures.
Such institutional structures are not present for the vast majority of hidden population networks RDS is used to sample. RDS variance is known to be strongly positively related to homophily, the extent to which networks are assortative along characteristics of its members. These school networks demonstrate strong homophily by grade, resulting in networks that may have “bottlenecks” between population sub-groups (Goodreau et al. 2009). As noted earlier, a key element of RDS estimators is self-reported degree. In Add Health, participants were asked to name up to five boy best friends and five girl best friends (Harris et al. 2009). The degree for a given participant was the sum of the number of persons she named and the number of times she was named by participants she did not name. In contrast, RDS study participants are typically asked to state the number of persons they know in the target population who also know them (Malekinejad et al. 2008), which serves as a proxy for the number of people who might recruit them into the study. Because of the difference in how degree is elicited between Add Health and RDS studies, the degree distribution for RDS studies typically has a higher mean and higher variance than those in the Add Health school networks (Malekinejad et al. 2008, Goodreau et al. 2009). In sum, these school networks are very unlike the hidden population networks through which RDS coupons are typically passed, and some of their features make it known a priori that RDS will perform poorly in simulations.
Given the differences between the available population network data and the networks of hidden populations, we based both our simulated population networks and our simulated RDS sampling process on real RDS studies. To maximize the similarity of our simulations to RDS as it occurs in the field, our simulations are designed to reflect RDS as it was used to sample PWID by the CDC’S National HIV Behavioral Surveillance system (NHBS) in 2009 and 2012. NHBS sampled PWID in 20 U.S. cities in both 2009 and 2012 using a standard protocol, resulting in 40 RDS samples (CDC 2012, 2015). A flowchart of our simulation methods is presented in the supplemental material.
To create the simulated population networks for our study (step 1 in the 3-step process described above), we first estimated four characteristics of the PWID population in each NHBS city from each of the 40 NHBS samples: the prevalence and homophily for a two‐valued trait of public health interest; the estimated mean degree of population members; and differential activity (DA). Homophily is a measure of assortative mixing in the network defined as the proportion of ties in the network between two respondents who share a trait status relative to what would be expected by chance. DA is measure of one group’s gregariousness compared to another and is defined as the ratio of the mean degrees of population members with and without the trait. Summary statistics of these characteristics can be found in Table 2.* Using each of the 40 sets of characteristics, we then simulated 1,000 networks using exponential‐family random graph models (ERGMs) (Frank and Strauss 1986, Hunter and Handcock 2006, Hunter et al. 2008a, Hunter et al. 2008b, Handcock et al. 2014), for a total of 40,000 networks. Each simulated network had a population size of 10,000 members.
Table 2.
Summary of 40 NHBS samples used to create RDS simulations
| Characteristic | Mean | Std Dev | Median | Minimum | Maximum |
|---|---|---|---|---|---|
| Prevalence | 0.104 | 0.0653 | 0.091 | 0.018 | 0.286 |
| Mean Degree | 10.64 | 5.096 | 9.88 | 4.45 | 35.39 |
| Homophily | 1.226 | 0.2281 | 1.19 | 0.91 | 1.99 |
| Differential Activity | 0.931 | 0.2098 | 0.92 | 0.53 | 1.44 |
| Sample Size | 519.1 | 108.85 | 539.5 | 206 | 700 |
| Number of Seeds | 8 | 3.31 | 8 | 3 | 16 |
| Number of Seeds With Trait | 1.1 | 1.18 | 1 | 0 | 5 |
| Number of Seeds Without Trait | 6.8 | 3.21 | 7 | 1 | 16 |
| Number of Seeds Missing Traitˆ | 0.13 | 0.404 | 0 | 0 | 2 |
| % of Coupons Returned | 30.60% | 6.60% | 33.20% | 20.00% | 49.80% |
| Number Recruits = 0* | 33.90% | 7.01% | 35.50% | 21.40% | 48.00% |
| Number Recruits = 1* | 21.80% | 5.07% | 22.10% | 9.10% | 32.10% |
| Number Recruits = 2* | 17.70% | 3.54% | 18.20% | 10.00% | 25.10% |
| Number Recruits = 3* | 10.50% | 2.69% | 10.00% | 4.60% | 16.00% |
| Number Recruits = 4*† | 1.70% | 2.00% | 0.67% | 0% | 7.70% |
| Number Recruits = 5*† | 0.54% | 0.65% | 0.30% | 0% | 2.40% |
Assigned to be without trait for purposes of sampling simulation
Among sample members who were given coupons.
These numbers include 6 studies where a maximum of 3 coupons were distributed per subject; the counts for those studies are constrained to be 0.
We designed the RDS process (step #2 above) used in the simulations to match those observed in the NHBS samples by first measuring the following characteristics for each of the 40 NHBS samples: the sample size, the numbers of seeds with and without the trait, and the distribution of number of recruitments by sample members. Summary statistics of these characteristics can be found in Table 2.†
For each of the 1,000 networks corresponding to a given NHBS sample, we simulated one RDS sample using the RDS package in the statistical software R (step #3 above) (Handcock et al. 2015, R Core Team 2015). The simulated RDS process was implemented based on the RDS process characteristics of the NHBS sample described above; for example, a given simulated RDS sample had the same number of seeds as did its corresponding NHBS sample. Because RDS samples do not allow for repeated participation, our baseline samples were without replacement. For each simulated RDS sample, we applied each of the four point/variance estimator pairs to the trait of interest. For each of the three RDS estimator pairs, we calculated 95% CIs using both the studentized and percentile bootstrap methods.
Our analysis compares the coverage rates of the 95% CIs for the four point/variance estimator pairs and two bootstrap CI methods when sampling was with and without replacement, where the coverage rates are calculated as the proportion of the simulations in which the CI contained the true population prevalence of the trait.
We calculate the actual DEs for our simulations numerically as ratio of the variance of the distribution of point estimates across simulations to the SRS variance, where the SRS variance includes a finite population adjustment based on the proportion of the population that was sampled. We calculate the estimated DEs for our simulations as the ratio of the estimated variance to the SRS variance. Each actual DE is calculated as the variance of the 1,000 simulations for each population network. Each estimated DE is calculated from a specific estimator pair applied to a single sampling simulation. Because the actual DE varies in magnitude across population networks, we summarize the estimated DEs’ accuracy by calculating the ratio of each simulation’s estimated DE to the actual DE for that population network. We compare the actual DEs for the four point estimators and also compare the actual DEs to the DEs estimated by the RDS variance estimators.
Results
Figure 1 presents the 95% CI coverage rates for the four estimator pairs for the 40 sets of RDS simulations conducted with the baseline condition of sampling without replacement and estimating the CI via the studentized bootstrap method. The horizontal axis of the figure is the nominal 95% CI coverage rate, and the vertical axis is the 40 simulation sets ordered from top to bottom by the SS coverage rate (the red line).‡ The left panel of Figure 1 displays the full range of coverage rates on the horizontal axis. The sample mean performs poorly compared to the other estimators. Hence, the right panel omits the sample mean and displays coverage rates from 80% to 100% to allow more detailed comparison of the non‐sample mean RDS estimator pair coverages. The right panel reveals that the SH/Sal-BS and VH/Sal-BS estimates have similar performance to SS/SS-BS estimators for a majority of simulation sets, but that they have considerably worse coverage rates in at least 4 sets of simulations.
Figure 1.
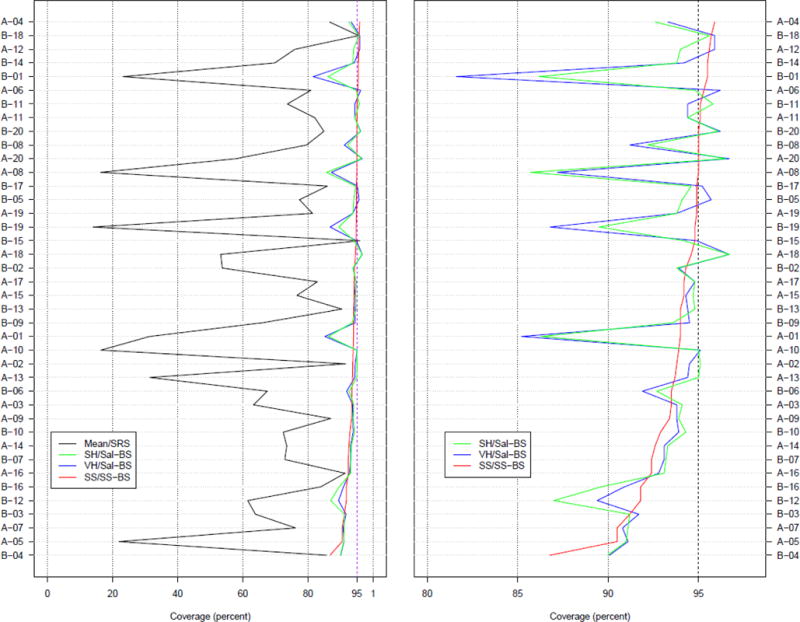
95% confidence interval (CI) coverage percentages for 40 sets of RDS simulations (sampling without replacement; studentized bootstrap CI method). The horizontal axis is the nominal 95% CI coverage percentage, and the vertical axis is the 40 simulation sets ordered from top to bottom by the SS coverage percentage (the red line). The left panel’s horizontal axis ranges from 0 to 100%; the right panel’s horizontal axis ranges from 80% to 100% for detail. The coverage percentages for the sample mean do not appear in the right panel.
The SS/SS‐BS estimator pair had overall higher coverage than the other two RDS estimator pairs: it only had one instance of coverage below 90%, whereas the SH/Sal‐BS and VH/Sal‐BS coverages were below 90% in five instances. The NHBS sample corresponding to the instance with SS/SS-BS coverage below 90% (86.8%) has trait prevalence of .034 and the smallest sample size (n=210) of all the NHBS samples.
The SH/Sal-BS and VH/Sal-BS had considerably worse coverage rates in 4 sets of simulations (Figure 1, right panel: B-01, A-08, B-19, and A-01). The NHBS samples corresponding to these extreme cases had lower differential activity and higher homophily for the trait of interest than did the other samples.
Table 3 shows summary statistics across the 40 simulation sets for these RDS estimator pair coverages along with results for the percentile bootstrap. For the SH/Sal-BS and VH/Sal-BS estimators, the studentized bootstrap performs better, with mean coverage rates 6 and 5.9 percentage points higher and median coverage rates 2 and 2.1 percentage points higher, respectively. For the SS/SS-BS the results are very similar, with the studentized mean coverage rate 0.3 and median coverage rate 0.4 percentage points lower.
Table 3.
95% confidence interval (CI) coverage percentages for four RDS point and variance estimator pairs by bootstrap CI method
| Point Estimator | Variance Estimator | Bootstrap CI Method | Mean | Standard Deviation | Median | Range | Acceptable Coverage %* |
|---|---|---|---|---|---|---|---|
| Sample mean | SRS variance | N/A | 67.4 | 23.8 | 74.9 | [14, 96] | 5 |
| Salganik- Heckathorn | Salganik | Percentile | 87 | 12.8 | 91.9 | [41, 96] | 40 |
| Salganik- Heckathorn | Salganik | Studentized bootstrap | 93 | 2.8 | 93.9 | [86, 97] | 67.5 |
| Volz-Heckathorn | Salganik | Percentile | 87 | 12.8 | 91.8 | [41, 96] | 42.5 |
| Volz-Heckathorn | Salganik | Studentized bootstrap | 92.9 | 3.2 | 93.9 | [82, 97] | 67.5 |
| Successive Sampling | Successive Sampling | Percentile | 94.1 | 1.8 | 94.6 | [87, 97] | 80 |
| Successive Sampling | Successive Sampling | Studentized bootstrap | 93.8 | 1.8 | 94.2 | [87, 96] | 75 |
Acceptable coverage percent is calculated as the percentage of confidence intervals (CIs) with coverage between 93% and 97%, inclusive, for a given estimator pair and bootstrap CI method.
Given that the conditions varied considerably across the forty simulation sets, summary statistics such as the mean may mask meaningful variation in the coverages. Therefore, we calculated a summary measure of “acceptable coverage”.§ The Mean/SRS estimator had acceptable coverage in 5% of CIs. The SH/Sal‐BS and VH/Sal‐BS with studentized bootstrap estimator pairs produced acceptable coverage for 67.5% of CIs, and the SS/SS‐BS with percentile and studentized bootstrap CI methods produced acceptable coverages for 80% and 75% of CIs, respectively.
We conducted additional simulations to investigate the higher 95% CI coverage rates for the VH/Sal-BS in our analysis (all greater than 80%; see Figure 1) than the VH/Sal-BS coverage rates reported in the seminal Goel and Salganik paper (medians of 52% and 62% coverage for the two samples analyzed) and the paper by Verdery and colleagues (means of 68% and 65% for the two samples analyzed) (Goel and Salganik 2010, Verdery et al. 2015). We hypothesized that the simulation of RDS sampling with replacement or the use of the percentile bootstrap CI method impacted the coverage findings in those papers. Figure 2 presents the coverage rates for the VH/Sal‐BS estimator pair under four conditions: sampling with replacement with percentile bootstrap CIs, sampling with replacement with studentized bootstrap CIs, sampling without replacement with percentile bootstrap CIs, and sampling without replacement with studentized bootstrap CIs. This figure shows that the estimator applied to simulations using without replacement sampling and the studentized bootstrap method (purple line and triangles) consistently outperforms simulations using with replacement sampling and the percentile bootstrap (red line and circles).
Figure 2.
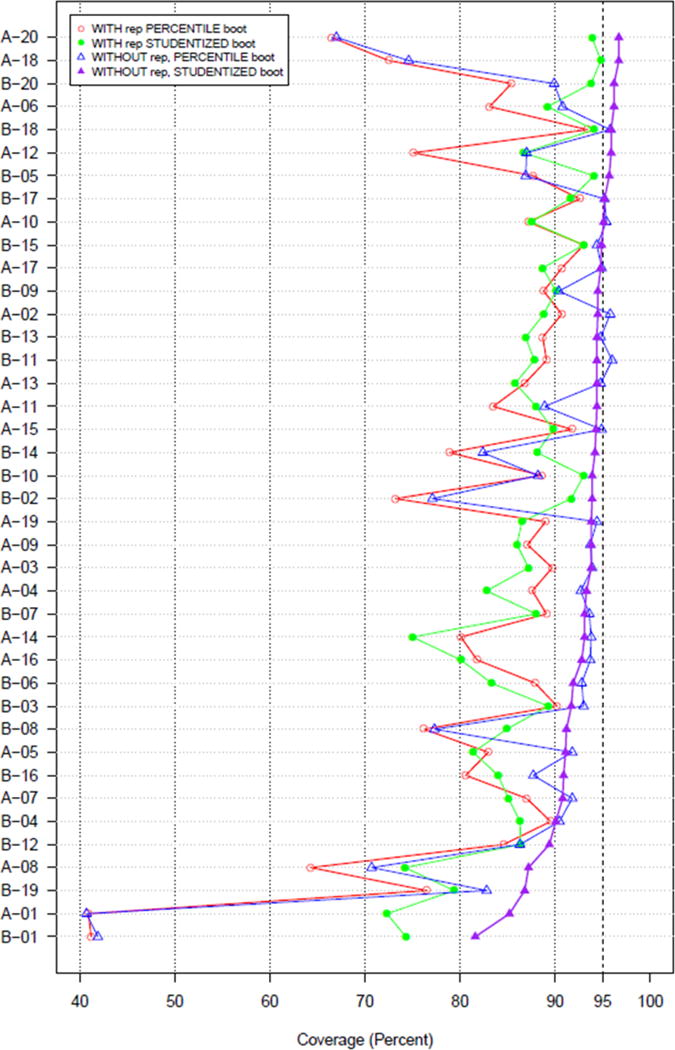
95% confidence interval (CI) coverage percentages for 40 sets of RDS simulations (VH/Sal-BS estimator pair) by bootstrap CI method and sampling with and without replacement. The horizontal axis is the nominal 95% CI coverage percentage, and the vertical axis is the 40 simulation sets ordered from top to bottom by the without replacement, studentized bootstrap condition (the purple line and triangles).
Table 4 summarizes the DEs from our RDS simulations. The first four rows of Table 4 show the actual DEs for samples drawn without replacement for the sample mean, SH, VH, and SS estimators. The median DEs for the SH, VH, and SS point estimators (table rows 2 – 4) were approximately 1.7, which is similar to the DEs observed for other complex sampling methods (Pettersson and Silva 2005, US Census Bureau 2006). For both the VH and SS estimators, the maximum DE was between 6 and 6.2; the maximum DE for SH was 95.5. In addition to its maximum DE of 95.5, the SH had 3 additional DEs that were much higher than expected. The DEs in these four scenarios were due the SH estimator failing for between 2 and 6 of the 1,000 simulation runs. Specifically, in these cases the SH produced a trait prevalence of 1 when the true prevalence was less than 0.08.¶
Table 4.
Design effects for four RDS point estimators by sampling with or without replacement
| Point Estimator (sampling method) | Range | Median | Mean | Standard Deviation |
|---|---|---|---|---|
| Sample mean (without replacement) | [0.75, 2.64] | 1.34 | 1.42 | 0.49 |
| Salganik-Heckathorn (without replacement) | [0.83, 95.51] | 1.72 | 7.47 | 19.96 |
| Volz-Heckathorn (without replacement) | [0.81, 6.19] | 1.69 | 1.91 | 0.96 |
| Successive Sampling (without replacement) | [0.83, 6.03] | 1.66 | 1.89 | 0.93 |
| Volz-Heckathorn (with replacement)* | [1.01, 7.97] | 2.34 | 2.77 | 1.48 |
Point estimator and sampling method used in Goel and Salganik 2010
The last row of Table 4 shows the DEs of the VH estimator for sampling with replacement, which was the RDS simulation process used in the papers by Goel and Salganik and Verdery and colleagues (Goel and Salganik 2010, Verdery et al. 2015). Note that for every summary statistic, the DEs are higher for the VH sampling with replacement condition than for the VH sampling without replacement condition.
Table 5 compares the estimated and actual DEs by estimator pair and sampling method. It summarizes the performance of the DEs estimated by a given estimator pair and sampling method by comparing the distribution of estimated DE to actual DE ratios across the 40,000 simulations to a benchmark. It presents three benchmarks: estimated DEs within a factor of 1.5 (i.e., 60% to 150%) of the actual DE, a factor of 2 (i.e., 50% to 200%) of the actual DE, and a factor of 3 (i.e., 33% to 300%) of the actual DE. For each benchmark, it presents the percent of estimated DEs that were within that factor and the percent of those that were within the factor that were too low. For example, 78.1% of the SH/Sal-BS without replacement estimated DEs were within a factor of 1.5 of the actual DE; of that 78.1%, 45.8% were too low.
Table 5.
Comparison of estimated and actual design effects by estimator pair and sampling method
| Point Estimator (sampling method) | Within a factor of 1.5 of the actual DEa | Within a factor of 2 of the actual DEb | Within a factor of 3 of the actual DEc | |||
|---|---|---|---|---|---|---|
| Percent | Percent of those within factor that are too low | Percent | Percent of those within factor that are too low | Percent | Percent of those within factor that are too low | |
| SH/Sal-BS (without replacement) | 78.1 | 45.8 | 83.7 | 46.2 | 88.3 | 47.0 |
| VH/Sal-BS (without replacement) | 83.5 | 46.6 | 91.8 | 47.3 | 97.5 | 48.0 |
| SS/SS-BS (without replacement) | 92.9 | 51.3 | 98.6 | 51.0 | 99.8 | 51.0 |
| VH/Sal-BS (with replacement)* | 56.9 | 79.4 | 79.9 | 82.8 | 93.5 | 84.5 |
Between 66% and 150% of the actual DE
Between 50% and 200% of the actual DE
Between 33% and 300% of the actual DE
Point estimator and sampling method used in Goel and Salganik 2010
Table 5 shows that for without replacement sampling, the pattern of estimated DE performance for the estimators is consistent for all three benchmarks: the SS/SS-BS estimator pair had the highest percentage within the factor, the VH/Sal-BS had the second-highest percentage, and the SH/Sal-BS had the lowest percentage. This ordering was the same for the percentage of estimates within the benchmark that were too low, with the SS/SS-BS pair having the most even distribution (percentages closest to 50%). This pattern reflects the SH/Sal-BS and VH/Sal-BS pairs having less accurate estimated DEs that are biased upward, and the SS/SS-BS pair having more accurate estimated DEs that are approximately unbiased.
For with replacement sampling the VH/Sal-BS estimator pair shows much lower accuracy than all three without replacement estimators for the most stringent benchmark factor. It also has a high proportion of estimated DEs that are too low, with more than 79% of estimated DEs lower than the actual DE.
Discussion
Our simulations suggest that the coverage of 95% CIs for RDS samples is usually above 90% (with no coverage rates above 97%). This is better than past work has suggested, demonstrating that reasonably accurate RDS variance estimation is feasible and that conclusions drawn from past analyses of RDS data that applied one of these estimators may well be reasonable in scenarios where RDS assumptions are met.
While the RDS estimators performed better than expected, the SRS variance estimator significantly underestimates the variability of RDS samples and provides very low coverage. Because of the complexity of RDS, it may be tempting to dispense with complicated inferential approaches and use the sample mean and SRS variance approximation. Our results show that this approach is likely to cause significant under-estimation of uncertainty and lead to misleading conclusions.
We found that the SS/SS‐BS estimator pair had overall higher coverage than the other two estimator pairs. The SS/SS-BS exhibited its lowest coverage when applied to a sample with lower prevalence and a smaller sample size than the other samples. In contrast, the SH/Sal‐BS and VH/Sal‐BS had lower coverage for samples with levels of differential activity much lower than those of the other samples in combination with higher levels of homophily than those of the other samples.
Note that the difference between the SS and VH estimators is a finite population adjustment that requires knowing the true size of the population, which is typically unavailable. The impact of error in the population size specified for the SS estimator in a given sample is a function of the true size of the population. The impact is relative, so the impact of a given absolute error in the specified population size will be larger for smaller population sizes (e.g., an error of 500 in the specified population size will have more impact when the true population size is 1,000 than when it is 10,000). For large population sizes the SS estimator approaches the VH estimator because the finite population adjustment has little impact, so using the SS estimator with a too-large population size specification will pull it toward the VH estimate. Therefore, the SS will perform at least as well as the VH unless the population size is dramatically underestimated.
The complexity of the relationship between a population’s characteristics and RDS CI coverage is high, so the specific relationships between prevalence, sample size, and homophily and the performance of RDS estimator pairs require further investigation. More generally, the number of such population characteristics that must be systematically varied in a simulation (the “parameter space”) to disentangle the combinations of factors that influence RDS CI coverage is very large. A systematic study of that parameter space is needed to provide evidence about RDS CI coverage in the large variety of settings in which RDS is applied.
While other work has suggested RDS variance estimators perform poorly, our analysis suggests those results can, at least partially, be attributed to the choice of bootstrap method and unrealistic use of with-replacement sampling in prior studies. For the SH and VH estimators, we found that using the studentized bootstrap, as compared to the percentile bootstrap, significantly increased the percentage of CIs with good coverage from 40 to 67.5 and 42.5 to 67.5, respectively (Table 2). Goel and Salganik’s findings of low CI coverage were likely at least partially due to their use of with‐replacement sampling and the percentile bootstrap CI method (see Figure 2). Other work, such as that by Chernick and LaBudde, has studied the relative performance of studentized and percentile bootstrap CI estimates and found that in most scenarios the studentized approach is more accurate (Chernick and LaBudde 2014).
We also found significantly smaller DEs than Goel and Salganik, with evidence that sampling with replacement increases the DE. For example, for without replacement sampling, both SS/SS and VH/Sal-BS produced actual DEs less than 3 in 92.5% of our conditions (37/40) and 62.5% less than 2, whereas for with replacement sampling the VH/Sal-BS estimator pair DE was less than 3 in only 67.5% of our conditions with only 30% less than 2. This echoes findings by Lu and colleagues and Gile and Handcock that sampling without replacement may reduce the DEs for RDS (Gile and Handcock 2010, Lu et al. 2012).
Furthermore, the estimated DEs were more accurate for sampling without replacement than for sampling with replacement. For example, for the VH/Sal-BS estimator pair sampling without replacement produced estimated DEs within a factor of 2 of the actual DEs 91.8% of the time, with slightly less than half (47.3%) being lower than the actual DE (the anti-conservative direction). In contrast, for with replacement sampling the estimated DEs were within a factor of 2 of the actual DEs only 79.9% of the time, with a significant majority (82.8%) being lower than the actual DE. Overall, the estimated DEs for the SS/SS estimator pair were the most accurate: 92.9% within a factor of 1.5, with fewer large outliers (see the Technical Supplement for more detail).
The RDS sampling process is highly complex and only partially observed in real RDS studies, so many choices about simulation design and specification must be made without reference to empirical data. Because the ultimate goal of RDS simulation studies is to understand how RDS performs in the real world, we recommend conducting RDS simulations without replacement and with parameters informed by real RDS samples to the extent possible.
This study’s simulations find that RDS DEs are in the range suggested in other methodological work that did not use simulation studies (Wejnert et al. 2012). We found that simulated RDS DEs in cases chosen to approximate the NHBS are usually between 1 and 3, in contrast with suggestions in past simulation work that DEs may often be greater than 10 (Goel and Salganik 2010, Verdery et al. 2015). This means that, in instances where RDS assumptions are met, RDS provides samples with statistical precision similar to that of other complex sampling methods (although with significantly less precision than simple random samples of the same populations).
We used data from a large number of real RDS studies to parameterize our simulated networks and RDS sampling process. These RDS samples were of PWID in large US urban areas, so the results are likely most applicable to RDS samples drawn from large cities. Most of the largest RDS studies in the world occur in such places, such as studies conducted in China and Brazil (Szwarcwald et al. 2011, Li et al. 2014). However, many RDS samples are drawn from smaller populations in less urban areas, which may have population networks with significantly different structures than those in NHBS cities (Malekinejad et al. 2008). Sampling fractions may be substantial in studies of small populations, making it important to use RDS estimators that accommodate RDS sampling without-replacement (which the SH and VH estimators do not). McCreesh and colleagues conducted an RDS methodological study in Uganda that is more similar to such small populations than are NHBS samples (McCreesh et al. 2012). They found that some sub-populations under-represented in the sample (relative to the population) did not have correspondingly lower mean degree, which led the RDS estimators to perform poorly. However, the poor performance of RDS estimators was also partially due to some recruiters’ misunderstanding of which population members were eligible for the study (and should be considered for recruitment) due to differences between the researchers’ and the local population’s interpretation of the language used to communicate the eligibility criteria (McCreesh et al. 2012). This misunderstanding led to systematically biased recruitment by some sample participants. With all sampling methods, but especially in peer-driven methods such as RDS, it is critical that researchers understand and account for the cultural norms and context of the communities they are sampling. These differences in population structure, RDS execution, and RDS estimation highlight the importance of context in understanding the applicability of RDS methodological study findings.
Our results are subject to a number of limitations. First, although the networks created for our simulations were designed with some structural characteristics similar to those of PWID networks in NHBS cities, the true structure and complexity of hidden population networks is unknown. Almost all social networks contain structure that is not observed in RDS data. For example, an outcome might vary across a city’s neighborhoods, and the PWID networks in some neighborhoods may have few connections to those in other neighborhoods. The ERGM used to create our simulated networks did not directly specify such complex network structure, as it is unclear what the correct levels of such structure should be. Note that for such network structure to strongly influence RDS estimation, it must be strongly related to the outcome (e.g., quite different prevalences of the trait across the weakly connected subgroups).
Second, the characteristics we used to create the networks for our simulations were estimated from NHBS samples using RDS estimators. Therefore, the simulations are not replicates of the 40 samples collected by NHBS but are, instead, examples of networks and RDS processes similar to those observed in the NHBS samples. The results may be sensitive to our use of large networks and small sampling fractions as in the NHBS samples. The stability of NHBS samples of PWID over time suggests that our findings are applicable to future NHBS studies of PWID.
Third, our simulations implemented RDS with only a few statistical assumptions not met. Both the SH and VH point estimators assume that recruitment trees do not branch (i.e., each sample member makes exactly one recruitment) and that sampling is with-replacement, neither of which was true in our simulations. Other RDS statistical assumptions such as participants recruiting randomly from their set of contacts and, for the SS estimator, that the population size is known, were met. It is known that violations of RDS point estimator assumptions decrease the accuracy of RDS point estimates (Gile and Handcock 2010, Tomas and Gile 2011, Lu et al. 2012). This is likely true for RDS variance estimators as well. Future work will examine the effects of violations of assumptions on the performance of RDS variance estimators.
Fourth, our analysis did not evaluate all RDS variance estimators. Some work has proposed new point estimators that were accompanied by minor modifications to an existing variance estimator to incorporate the new point estimator (Lu 2013, Lu et al. 2013). Gile and Handcock introduced an estimator that simulates RDS on a synthetic network created from characteristics of the sample data (Gile and Handcock 2015). Yamanis and colleagues proposed a modification to the Salganik bootstrap that reflects the branching structure of RDS samples (Yamanis et al. 2013). Baraff and colleagues recently proposed a tree bootstrap in which each resample replicates recruitment trees’ structures by sampling with replacement from each recruiter’s set of recruits (Baraff et al. 2016). We look forward to evaluating these variance estimators and understanding how their differences impact estimate coverage.
Conclusion
Sampling hidden populations is critical for public health surveillance and planning around the world. RDS is effective at reaching members of hidden populations that other sampling methods cannot and is inexpensive enough to be used in low‐resource settings. These strengths have led to its wide use around the world for many different applications.
Past research on RDS variance estimation suggested that RDS variance estimator CIs provide very low coverage rates and that RDS has higher DEs than has been assumed in the public health literature (Goel and Salganik 2010, Verdery et al. 2015). Our results indicate instead that both CI coverage rates and DEs are often acceptable but not perfect. However, researchers should evaluate whether a given study has characteristics similar to those found in our simulations that produced good (or poor) coverage. Additionally, deviations from the assumed RDS sampling process or population network structures not examined in this paper may impact the CI coverage rates and DE magnitudes for a given study.
RDS is used around the world to sample hidden populations that suffer from high rates of infection by HIV and other diseases. It is critical that researchers draw correct conclusions from RDS data by applying appropriate statistical techniques. We look forward to an improved understanding of RDS estimation that will better inform the policies critical to preventing and reducing the burden of disease borne by hidden populations worldwide.
Supplementary Material
Footnotes
Disclaimer: The findings and conclusions in this paper are those of the authors and do not necessarily represent the official position of the Centers for Disease Control and Prevention.
De-identified characteristics for each sample may be found in the supplementary materials.
De-identified characteristics for each sample may be found in the supplementary materials.
Samples numbers are prefixed with “A” for samples from 2009 and “B” for samples from 2012. Sample numbers were randomly assigned to cities and are consistent across the two survey years (e.g., A-01 is the same city as B-01).
Acceptable coverage percent is calculated as the percentage of confidence intervals (CIs) with coverage between 93% and 97%, inclusive, for a given estimator pair and bootstrap CI method.
We have also observed this pattern of SH estimator behavior in its implementation in the Respondent-Driven Sampling Analysis Tool v7.1 software (Volz et al. 2012). It typically, but not always, occurs when ‘0’ cells are present in the recruitment matrix (e.g., when two population sub-groups do not recruit one another).
References
- Baraff AJ, McCormick TH, Raftery AE. Estimating Uncertainty in Respondent-Driven Sampling Using a Tree Bootstrap Method. Proceedings of the National Academy of Sciences. 2016 doi: 10.1073/pnas.1617258113. 201617258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- CDC. Hiv Infection and Hiv-Associated Behaviors among Injecting Drug Users—20 Cities, United States, 2009. MMWR. 2012;61:133–138. [PubMed] [Google Scholar]
- CDC. Hiv Infection and Hiv-Associated Behaviors among Persons Who Inject Drugs — 20 Cities, United States, 2012. MMWR. 2015 [PMC free article] [PubMed] [Google Scholar]
- Chernick MR, LaBudde RA. An Introduction to Bootstrap Methods with Applications to R. John Wiley & Sons; 2014. [Google Scholar]
- Davison AC, Hinkley DV. Bootstrap Methods and Their Applications. Cambridge: Cambridge University Press; 1997. [Google Scholar]
- Efron B, Tibshirani R. Bootstrap Methods for Standard Errors, Confidence Intervals, and Other Measures of Statistical Accuracy. Statistical science. 1986:54–75. [Google Scholar]
- Frank O, Strauss D. Markov Graphs. Journal of the American Statistical Association. 1986;81:832–842. [Google Scholar]
- Gallagher KM, Sullivan P, Lansky A, Onorato IM. Behavioral Surveillance among People at Risk for Hiv Infection in the U.S.: The National Hiv Behavioral Surveillance System. Public Health Reports. 2007;122(Suppl 1):32–38. doi: 10.1177/00333549071220S106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gile KJ. Improved Inference for Respondent-Driven Sampling Data with Application to Hiv Prevalence Estimation. Journal of the American Statistical Association. 2011;106:135–146. [Google Scholar]
- Gile KJ, Handcock MS. Respondent-Driven Sampling: An Assessment of Current Methodology. Sociol Methodol. 2010;40:285–327. doi: 10.1111/j.1467-9531.2010.01223.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gile KJ, Handcock MS. Network Model‐Assisted Inference from Respondent‐Driven Sampling Data. Journal of the Royal Statistical Society: Series A (Statistics in Society) 2015;178:619–639. doi: 10.1111/rssa.12091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goel S, Salganik MJ. Assessing Respondent-Driven Sampling. Proceedings of the National Academy of Sciences. 2010;107:6743–6747. doi: 10.1073/pnas.1000261107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodreau SM, Kitts JA, Morris M. Birds of a Feather, or Friend of a Friend? Using Exponential Random Graph Models to Investigate Adolescent Social Networks. Demography. 2009;46:103–125. doi: 10.1353/dem.0.0045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Handcock MS, Fellows IE, Gile KJ. Rds: Respondent-Driven Sampling 2015 [Google Scholar]
- Handcock MS, Hunter DR, Butts CT, Goodreau SM, Krivitsky PN, Morris M. Ergm: Fit, Simulate and Diagnose Exponential-Family Models for Networks. 2014 doi: 10.18637/jss.v024.i03. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris KM, Halpern CT, Whitsel E, Hussey J, Tabor J, Entzel P, Udry JR. The National Longitudinal Study of Adolescent Health: Research Design [Www Document] 2009 [Google Scholar]
- Heckathorn DD. Respondent-Driven Sampling: A New Approach to the Study of Hidden Populations. Social Problems. 1997;44:174–199. [Google Scholar]
- Hladik W, Barker J, Ssenkusu JM, Opio A, Tappero JW, Hakim A, Serwadda D, for the Crane Survey Group Hiv Infection among Men Who Have Sex with Men in Kampala, Uganda–a Respondent Driven Sampling Survey. PLoS ONE. 2012;7:e38143. doi: 10.1371/journal.pone.0038143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hunter DR, Goodreau SM, Handcock MS. Goodness of Fit of Social Network Models. Journal of the American Statistical Association. 2008a;103 [Google Scholar]
- Hunter DR, Handcock MS. Inference in Curved Exponential Family Models for Networks. Journal of Computational and Graphical Statistics. 2006;15 [Google Scholar]
- Hunter DR, Handcock MS, Butts CT, Goodreau SM, Morris M. Ergm: A Package to Fit, Simulate and Diagnose Exponential-Family Models for Networks. Journal of Statistical Software. 2008b;24:1–29. doi: 10.18637/jss.v024.i03. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X, Lu H, Cox C, Zhao Y, Xia D, Sun Y, He X, Xiao Y, Ruan Y, Jia Y, Shao Y. Changing the Landscape of the Hiv Epidemic among Msm in China: Results from Three Consecutive Respondent-Driven Sampling Surveys from 2009 to 2011. BioMed Research International. 2014;2014:10. doi: 10.1155/2014/563517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu X. Linked Ego Networks: Improving Estimate Reliability and Validity with Respondent-Driven Sampling. Social Networks. 2013;35:669–685. [Google Scholar]
- Lu X, Bengtsson L, Britton T, Camitz M, Kim BJ, Thorson A, Liljeros F. The Sensitivity of Respondent-Driven Sampling. Journal of the Royal Statistical Society: Series A (Statistics in Society) 2012;175:191–216. [Google Scholar]
- Lu X, Malmros J, Liljeros F, Britton T. Respondent-Driven Sampling on Directed Networks. Electronic Journal of Statistics. 2013;7:292–322. [Google Scholar]
- Malekinejad M, Johnston LG, Kendall C, Kerr LR, Rifkin MR, Rutherford GW. Using Respondent-Driven Sampling Methodology for Hiv Biological and Behavioral Surveillance in International Settings: A Systematic Review. AIDS Behav. 2008;12:S105–130. doi: 10.1007/s10461-008-9421-1. [DOI] [PubMed] [Google Scholar]
- McCreesh N, Frost SD, Seeley J, Katongole J, Tarsh MN, Ndunguse R, Jichi F, Lunel NL, Maher D, Johnston LG, Sonnenberg P, Copas AJ, Hayes RJ, White RG. Evaluation of Respondent-Driven Sampling. Epidemiology. 2012;23:138–147. doi: 10.1097/EDE.0b013e31823ac17c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merli MG, Moody J, Smith J, Li J, Weir S, Chen X. Challenges to Recruiting Population Representative Samples of Female Sex Workers in China Using Respondent Driven Sampling. Social Science & Medicine. 2014 doi: 10.1016/j.socscimed.2014.04.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris M. Network Epidemiology: A Handbook for Survey Design and Data Collection. Oxford University Press; 2004. [Google Scholar]
- Pettersson H, Silva PL. Household Sample Surveys in Developing and Transition Countries. New York, NY: United Nations Department of Economic and Social Affairs Statistics Division; 2005. Analysis of Design Effects for Surveys in Developing Countries. [Google Scholar]
- Core Team R. R: A Language and Environment for Statistical Computing 2015 [Google Scholar]
- Salganik MJ. Variance Estimation, Design Effects, and Sample Size Calculations for Respondent-Driven Sampling. Journal of Urban Health. 2006;83:i98–112. doi: 10.1007/s11524-006-9106-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salganik MJ, Heckathorn DD. Sampling and Estimation in Hidden Populations Using Respondent-Driven Sampling. Sociol Methodol. 2004;34:193–239. [Google Scholar]
- Szwarcwald CL, de Souza Junior PR, Damacena GN, Junior AB, Kendall C. Analysis of Data Collected by Rds among Sex Workers in 10 Brazilian Cities, 2009: Estimation of the Prevalence of Hiv, Variance, and Design Effect. Journal of Acquired Immune Deficiency Syndromes. 2011;57(Suppl 3):S129–135. doi: 10.1097/QAI.0b013e31821e9a36. [DOI] [PubMed] [Google Scholar]
- Tomas A, Gile KJ. The Effect of Differential Recruitment, Non-Response and Non-Recruitment on Estimators for Respondent-Driven Sampling. Electronic Journal of Statistics. 2011;5:899–934. [Google Scholar]
- Census Bureau US. Current Population Survey Design and Methodology Technical Paper 66 2006 [Google Scholar]
- Verdery AM, Mouw T, Bauldry S, Mucha PJ. Network Structure and Biased Variance Estimation in Respondent Driven Sampling. PLoS ONE. 2015;10:e0145296. doi: 10.1371/journal.pone.0145296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volz E, Heckathorn DD. Probability Based Estimation Theory for Respondent Driven Sampling. Journal of Official Statistics. 2008;24:79. [Google Scholar]
- Volz E, Wejnert C, Cameron C, Spiller MW, Barash V, Degani I, Heckathorn DD. Respondent-Driven Sampling Analysis Tool (Rdsat) Version 7.1 2012 [Google Scholar]
- Wejnert C. An Empirical Test of Respondent-Driven Sampling: Point Estimates, Variance, Degree Measures, and out-of-Equilibrium Data. Sociol Methodol. 2009;39:73–116. doi: 10.1111/j.1467-9531.2009.01216.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wejnert C, Pham H, Krishna N, Le B, DiNenno E. Estimating Design Effect and Calculating Sample Size for Respondent-Driven Sampling Studies of Injection Drug Users in the United States. AIDS Behav. 2012;16:797–806. doi: 10.1007/s10461-012-0147-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamanis TJ, Merli MG, Neely WW, Tian FF, Moody J, Tu X, Gao E. An Empirical Analysis of the Impact of Recruitment Patterns on Rds Estimates among a Socially Ordered Population of Female Sex Workers in China. Sociological methods & research. 2013;42:392–425. doi: 10.1177/0049124113494576. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


