Why lipostatic set point systems are unlikely to evolve

Abstract

Objectives

Body fatness is widely assumed to be regulated by a lipostatic set-point system, which has evolved in response to trade-offs in the risks of mortality. Increasing fatness makes the risk of starvation lower but increases the risk of predation. Yet other models are available. The aim of this work is to evaluate using mathematical modeling whether set-point systems are more likely to evolve than the alternatives.

Methods

I modeled the trade-off in mortality risks using a simple mathematical model, which generates an optimum level of fatness that is presumed to be the driver for the evolution of a set-point. I then mimicked the likely errors in this optimum level, that derive from the variation in the component parameters of the mortality curves using Markov Chain Monte Carlo (MCMC) simulation by Bayesian inference Using Gibbs Sampling (BUGS).

Results

The error propagation generated by the simulations showed that even very small errors in the model parameters were magnified enormously in the location of the optimum fatness level. If the model parameters had coefficients of variation of just 1% then the coefficient of variation in the optimum level of fatness was between 20 and 90%. In that situation, a set-point centered at the mathematical optimum from the component curves would be at the correct level of fatness that minimizes mortality, and hence maximizes fitness, on less than 8% of occasions.

Conclusions

Set-point regulation of body fatness is hence highly unlikely to evolve where there is any realistic level of variation in the parameters that define mortality risks. Using further MCMC modeling, I show that a dual-intervention point system is more likely to evolve. This mathematical simulation work has important implications for how we interpret molecular work concerning regulation of adiposity.

Highlights

• •Most molecular studies of obesity are implicitly or explicitly interpreted under the lipostatic feedback framework.
• •The lipostatic model however is unproven.
• •Lipostatic regulation is presumed to evolve due to contrasting consequences of fat storage for starvation and predation.
• •I show such systems are unlikely to evolve and that dual-intervention point models are more probable.
• •Interpretations of data under the dual-intervention point model may enhance our understanding and remove some anomalies.

1. Introduction

It is widely assumed that body fatness is regulated by a lipostatic regulatory system, as originally proposed by Kennedy [1]. By this model a signal from the body reflecting the level of stored fat is compared to a set-point in the brain, and deviations of the body fat from the set-point result in compensatory responses in both energy intake and expenditure [2], [3], [4], [5], [6], [7], [8]. The discovery of leptin [9] provided a potential molecular reality for the signal reflecting the level of stored fat. The molecular basis of the lipostatic set-point to which it is hypothetically compared, however, has never been discovered. Set-point models are not the only possible theoretical way in which body fatness can be regulated, and various other models are available: including settling point and dual intervention point models [10]. Moreover, mathematical models of body fatness changes have called into question whether animal responses to metabolic perturbations actually behave as expected from a lipostatic set-point regulation system [11].

How the supposed set point system for body fatness evolved has been a no less active but largely independent area of enquiry from studies aiming to elucidate the molecular basis of the system. It has been suggested that the lipostatic set-point evolves because of two contrasting evolutionary pressures relating to mortality consequences of fat storage [12], [13], [14]. One of these pressures favors storage of more fat. This is generally presumed to be the risk of starvation (but see [15] for an argument that it is more likely to be disease risk). The starvation argument is that under conditions of complete failure in the food supply those individuals storing more fat will survive longer. Hence, storing more fat reduces the risk of starvation-induced mortality. However, there is a counteracting pressure which favors storage of less fat. This has widely been assumed to be the risk of predation. Individuals storing more fat may be less maneuverable and slower to evade predators and hence storing more fat increases predation mortality [13], [14].

The tension between these opposing forces then generates an optimal level of fat storage that minimizes mortality. This situation can be modeled by a juxtaposition of negative and positive exponential relationships between mortality and fat storage [15]. If the mortality due to starvation (M_s) follows a negative exponential relationship M_s = ae^−bx, where x is fat storage, and mortality due to predation rises as a positive exponential M_p = ce^gx. Then overall mortality at any given level of fat storage M_tot = M_s + M_p and the optimal fat storage level that minimizes mortality turn out to be analytically defined as

F_A = log(ab/cg) / (b + g) (1)

This fitness landscape is presumed to provide the selective environment in which a lipostatic set-point system can evolve, centered around the point F_A. That is, individuals regulating body fatness at levels that do not coincide with the optimal level F_A would suffer greater mortality; hence, the genes defining these deviant levels of fatness regulation would be purged from the population. What would then evolve is a lipostatic set-point regulating fatness at F_A. It is my contention here that such an evolutionary scenario is untenable and that such set-point regulatory systems for body fatness are unlikely to evolve (at least by this proposed mechanism).

The problem with such mathematical models is that they assume that the curves defining the risks of mortality are stable in space and time. That is, the constants defining the mortality curves (a, b, c and g) are truly constant. This is extremely unlikely. The curve relating level of fatness to mortality risk from predation, for example, will likely depend on the local population of predators and the populations and sizes of other potential prey. Such variation may make the position of the optimal fatness unstable and hence make it difficult for a lipostatic set-point system to evolve. The key question is how much this likely variation in these parameters would affect the value of F_A. If, for example, changing the parameters up or down by 5% has only minimal impacts on F_A then the optimal solution will be robust to the parameter estimates and a lipostatic set-point system could still evolve. However, if F_A turns out to be highly variable dependent on the component parameter variation then this would make evolution of a lipostatic set-point system unlikely.

2. Methods

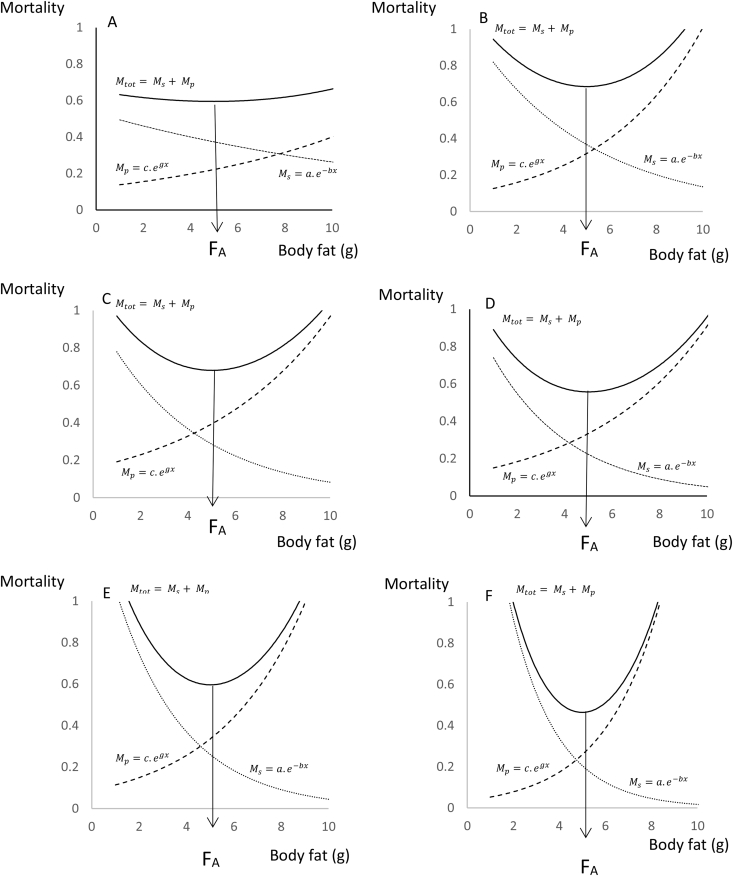
To investigate this question, I used Markov Chain Monte Carlo (MCMC) simulation by Bayesian inference using Gibbs Sampling (BUGS) (using the winBUGS software; [16]). I used the mortality trade-off model from [15], briefly outlined above, as the basis of the simulation. I selected the values of the model parameters a, b, c, g so as to generate an optimal body fatness (F_A) of 5 units. I will refer to this from now on as 5 g as if we were modeling fat storage in a typical small mammal, but the units are arbitrary and the model can be applied to any size of animal. If you are more familiar with human fat storage then you may prefer to think about the units as kg rather than grams. I then selected six combinations of the four parameters that reflected different potential mortality landscapes. These combinations are detailed in Table 1, and the mortality patterns they generate are illustrated in Figure 1. The scenarios are identified as A to F and involve an escalating dependence of the mortality curves on body fatness. This is reflected in the fold change in mortality risk from both sources as fatness increases from 1 to 10 g (Table 1). Hence, in scenario A, the least sensitive situation, this 10-fold increase in fatness increases mortality due to predation by a factor of 2.7 but decreases the mortality from starvation by a factor of 1.9. In contrast, for scenario F, the most sensitive situation, the 10-fold increase in fatness from 1 to 10 g resulted in a 36-fold increase in mortality due to predation and a 90-fold reduction in mortality due to starvation.

Table 1.

Six different scenarios that were used to model evolution of set-points. The scenarios are labeled A to F and are ordered by the increasing sensitivity of mortality to changes in body fatness. Sensitivity is expressed as the fold change in mortality due to starvation (M_s) and predation (M_p) that accompanies a 10 fold change in the level of stored fat. The model involves contrasting positive and negative exponentials and generates an optimal fatness (F_A). Parameters of the model (a, b, c, g) for each scenario are shown.

Scenario	A	B	C	D	E	F
Sensitivity to
Ms	1.9	6.04	9.48	14.9	23.3	90.0
Mp	2.7	7.99	5.03	6.0	11.1	36.6
Mean	2.3	7.02	7.26	10.4	17.2	63.3
Parameters
a	0.53	1.0	1.0	1.0	1.5	2.5
b	0.07	0.2	0.25	0.3	0.35	0.5
c	0.123	0.1	0.16	0.123	0.087	0.035
g	0.117	0.231	0.18	0.2	0.27	0.4

Figure 1.

Patterns of change in total mortality (solid line) and component mortalities due to starvation (M_s) and predation (M_p) (dotted lines) in relation to body fatness. Six different scenarios are modeled in which the dependence of mortality on fatness is progressively greater from A to F. Parameters of the equations under different scenarios are in Table 1. F_A is the optimum fatness that minimizes mortality and is solved analytically for the different functions. In all these scenarios the model parameters were selected so that F_A = 5.

I then assumed that variation in the four parameters followed a normal distribution, with the means defined as in Table 1 and that the standard deviation of each distribution was defined by a given coefficient of variation. The winBUGS model specification text is available on request. The six levels of the coefficients of variation studied included 0.0001%, 0.001%, 0.01%, 0.1%, 1%, and 2%. I applied these equally to all 4 parameters. That is, I didn't model the situation where the coefficients of variation themselves varied between parameters. The program was allowed to generate initial values based on the distributions. In each condition, I ran 10,000 iterations of the program, drawing random samples from the respective parameter distributions. These were then combined in Eq. (1) to generate a sample of the output variable F_A. This resulted in 36 separate output distributions (6 scenarios multiplied by 6 different levels of parameter variation). The output distributions of F_A were then characterized by their means and standard deviations.

In a second set of simulations, I used the same scenarios to generate the profile of mortality (M_tot) at different levels of fatness. For this model, the mortality was simulated by drawing random samples from the same distributions of the four parameters that define the mortality curves, but this time instead of calculating F_A the program calculated total mortality (M_tot) as a result of both predation and starvation. I set the CV of the defining parameters at 1%, and allowed the program to generate initial values from the starting distributions. The model was then iterated for 10,000 samples at each of 31 values of body fatness between 2 and 8 g (at 0.2 g intervals) for all 6 mortality scenarios. The mean and Monte Carlo standard error for mortality at each fat level were recorded.

3. Results

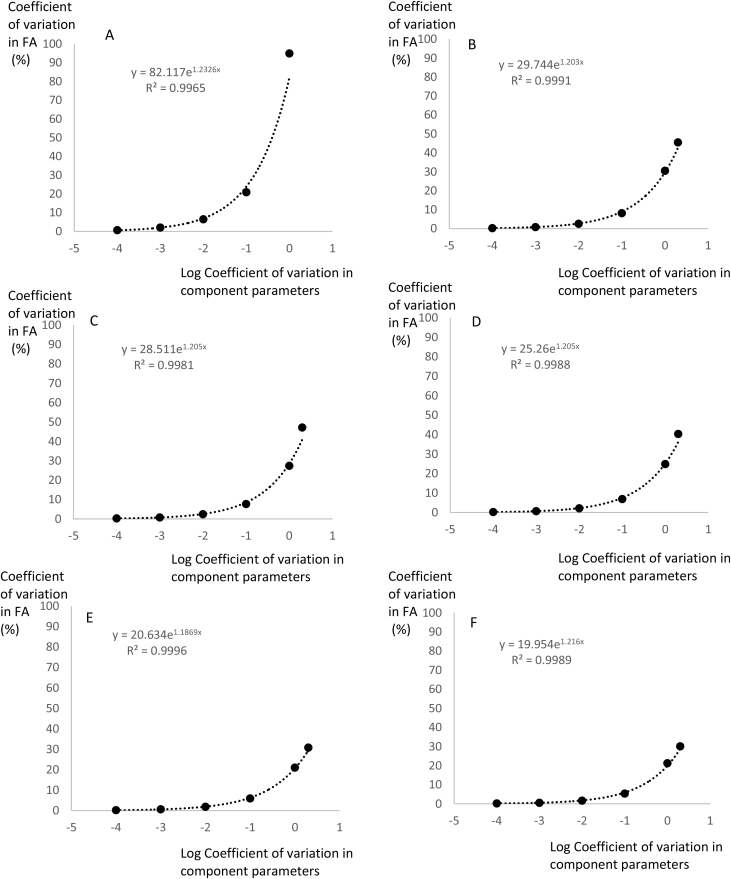
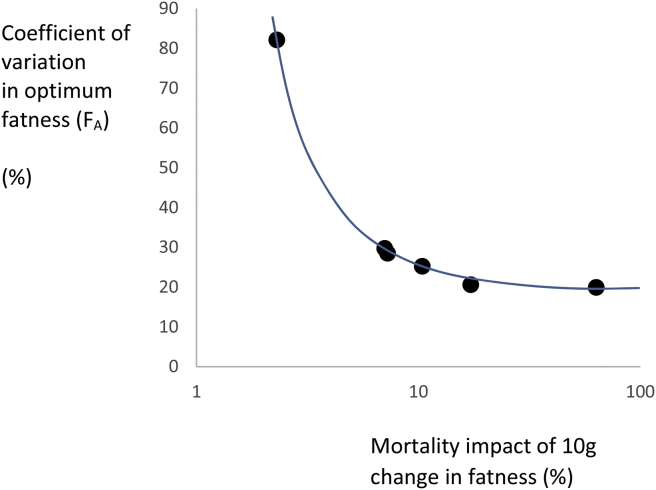
As expected, given the assumed normal distributions for the component parameter values, the resultant distribution of F_A was also roughly normal. I therefore characterized the distributions based on their coefficients of variation and plotted these against the modeled coefficient of variation in the component parameters (Figure 2). This showed that when the component parameters had only very low levels of variation (CV = 0.0001 and 0.001%), the coefficient of variation in the output F_A was between 0.16 and 2.0% depending on the mortality consequences of the fat storage. Hence, there was a dramatic impact of even minute levels of variation in the components on the position of the optimum fatness. When the variation in the components was higher (1%), the coefficient of variation in the optimum F_A varied between 20 and 90%. The gradients of exponential fits to these relationships all had exponents around 1.2. The intercepts (equal to the coefficients at component variances of 1%) were strongly linked to the average of the mortality impacts of the initial relationships (Figure 3). In other words, when the scenario was strongly sensitive to mortality effects the optimum was less variable. Nevertheless, even when the average mortality effect was 60-fold (Scenario F), 1% coefficients of variation in the 4 component parameters led to a 20% coefficient of variation in F_A.

Figure 2.

Variation in the optimum fatness F_A (Coefficient of variation %) in relation to the logged variation in the component parameters of the equation also expressed as coefficients of variation of the parameters a, b, c, g. These six plots directly refer to the six different scenarios shown in Figure 1. Fitted exponential equations are shown with the r². The CV of FA was derived from Markov Chain Monte Carlo simulation using the winBUGS software.

Figure 3.

Variation in the optimum fatness F_A (Coefficient of variation %) when the component parameters of the equation from which F_A is calculated all vary with CV's of 1%, plotted against the mortality sensitivity of the given scenario. Mortality sensitivity is the fold change impact on both predation and starvation mortality resulting from a change in fatness from 1 g to 10 g.

To model the consequences of this variation in the optimum body fatness for the evolution of set points, I considered the following situation. Imagine an animal has a set point system which is centered on a value of 5 g (the mathematical optimal solution for the models defined without error). Assume this value has a tolerance of 0.1 g. That is, the animal's physiological system cannot distinguish values within the range from 4.9 to 5.1 g (4% of the mean). This sort of percentage variation is typical for other set-point systems that we are aware of such as the regulation of body temperature or blood glucose levels. If the optimum fatness F_A falls within this range, then the animal is regulating fatness at the optimum level within the limits of its own physiology. Given this lipostatic set-point system, what percentage of the optimum fatness values fall within this range under each scenario? I calculated this using z-scores of the resultant MCMC derived distributions of F_A (Table 2). Hence, for example, with Model 2, in the situation in which the component parameters have a CV of 0.0001%, the distribution of F_A has a mean of 5 and sd of 0.013 g. Therefore, the described lipostat with a range of 4.9–5.1 g would include values up to 7.7 standard deviations from the mean, and hence the lipostatic set-point system effectively always includes the optimum fatness value (p > 0.9999). In contrast, in the same scenario but with the component parameters, at a CV of 1%, the resultant sd was 1.525 g; hence, a lipostatic set point system as described would only cover 0.065 standard deviations each side of the mean, or 5.2% of the optimum fatness values. These data show that whatever the mortality sensitivity scenario, if the component variables had CVs of only 1%, the lipostatic set point system with 4% tolerance would cover only between 1.6 and 7.8% of the optimal fatness values. For a lipostatic set point system to evolve, there would need to be less than 0.01% variation in the parameters defining the model.

Table 2.

Calculated variation (CV%) in the optimal level of fatness (F_A) resulting from variation in the component parameters for each scenario detailed in Table 1. The values to the left labeled ‘CV parameters’ are the assumed CV in the component parameters of the model. Using an assumed set-point at the analytical solution to the scenarios (F_A = 5) with a tolerance of 4%, the proportion of situations where the set-point system would be regulating at the optimum level of fatness is also shown labeled as P(correct).

Scenario	A	B	C	D	E	F
CV parameters = 0.0001%
CV% FA	0.64	0.254	0.246	0.22	0.184	0.164
P(correct)	0.9974	0.9999	0.9999	0.9999	0.9999	0.9999
CV parameters = 0.001%
CV% FA	2.05	0.806	0.76	0.68	0.518	0.568
P(correct)	0.6666	0.9864	0.9914	0.9968	0.9998	0.998
CV parameters = 0.01%
CV% FA	6.51	2.54	2.40	2.16	1.86	1.64
P(correct)	0.2434	0.5646	0.5934	0.646	0.718	0.7776
CV parameters = 0.1%
CV% FA	20.11	8.16	7.69	6.88	5.94	5.33
P(correct)	0.0796	0.1934	0.2052	0.2282	0.2598	0.293
CV parameters = 1.0%
CV% FA	94.92	30.50	27.38	24.84	21.88	21.22
P(correct)	0.016	0.0518	0.058	0.0638	0.0718	0.076
CV parameters = 2.0%
CV% FA		45.50	47.12	40.32	33.02	31.10
P(correct)		0.034	0.032	0.0398	0.0478	0.044

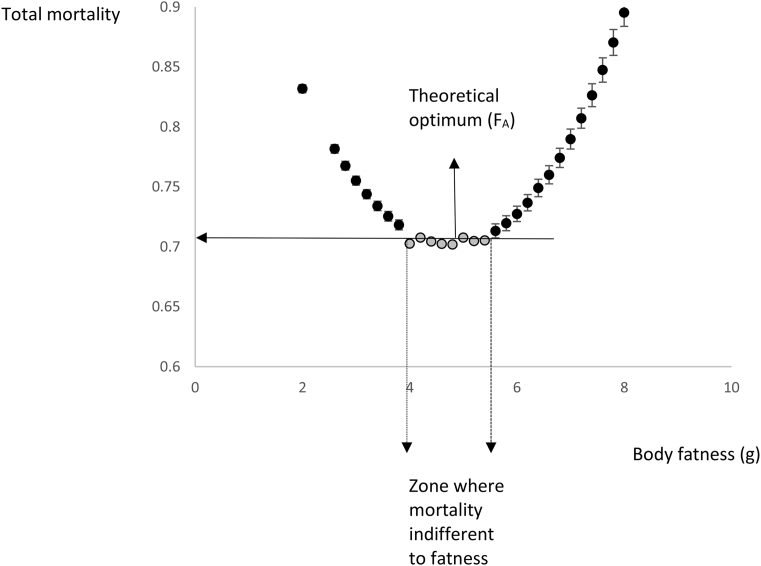
Figure 4 shows the total mortality pattern (mean values with MC error) at intervals of 0.2 g in fatness between 2 and 8 g for scenario B, which was derived from the second set of modeling. The plot shows a curve with a flat bottom; as fatness increases, the reduction in mortality risk due to starvation is offset almost exactly by increases in mortality due to predation. The grey data points define the values where the mortality differed by less than 1% from that at the lowest point. The range that includes data which differed by less than 1% in mortality from the lowest value was from 4 to 5.4 g. This range depends on the mortality impact in the scenario. For scenario A, in which the mortality impact was low, the range was 2.8–6.2 g. For mortality scenario F, with the highest mortality sensitivity, the range was 4.6–5.2 g.

Figure 4.

Total mortality estimates (M_tot) derived from Markov Chain Monte Carlo simulations at various levels of body fatness. Points are the means of 10,000 iterated calculations drawing values of the fixed parameters in the equation for M_tot from simulated distributions. Error bars show the MC standard error, which, in some cases, was smaller than the dimensions of the points. The mortality shows a curve with a flat bottom (grey points) where the mortality differs by less than 1% from the mortality observed at the fitted optimum. This defines a zone where mortality is independent to fatness.

4. Discussion

Given the reality of what these mortality curves represent (effects of fatness on the risk of mortality from starvation and predation), it seems highly unlikely that the defining parameters for the curves would have a variation (CV) lower than 1%; it is likely, however that they would be considerably higher. The simulations above show that in this situation (CV = 1% in all four component parameters), if an animal had a lipostatic set-point system that regulated fatness with a tolerance of 4% (i.e. 5 g plus or minus 0.1 g), it would only be regulating at the level of fatness that maximizes fitness on 1.6–7% of occasions. That is, over 90% of the time, the lipostatic system would be regulating at a set-point that was sub-optimal in terms of maximizing fitness. A system generating the wrong fitness solution more than 90% of the time is unlikely to evolve by the process of natural selection. Set point regulation of body fatness, therefore, is unlikely to evolve, at least if the underlying driver of the system is the contrasting mortality patterns in relation to stored fat due to starvation and predation, as is generally assumed.

One might argue that the result is an artifact of the nature of the curves (a negative and positive exponential) that were selected to represent the contrasting mortality effects. There are limited alternative options, however, for these relationships. If the curves are made linear rather than exponential, the solution is that when the gradient for the starvation effect exceeds that of the predation effect, the animal should always store as much fat as possible. Conversely, when the gradient of the predation effect exceeds the gradient of the starvation effect, the animal should store no fat at all. When the gradients are equal, the mortality is independent of fat storage. Hence, with linear relationships, there is no optimum fat level which minimizes mortality to result in selection for a lipostatic set-point. If the curves are made convex rather than concave, then the mortality reaches a maximum at intermediate levels of fatness rather than a minimum. Again, this would not result in selection for a lipostatic set-point that minimizes mortality. So, the most credible formulation that leads to a minimum mortality potentially capable of generating a body fatness set point is to combine a negative and a positive exponential.

If the modeling suggests that a lipostatic set point system is unlikely to evolve, then what is the most likely alternative? This question was addressed by the second set of modeling. This simulation showed that there is always a zone where increasing fatness leads to decreased risk of mortality from starvation that is almost exactly balanced by increased risk of mortality from predation (Figure 4). In this range, it would not matter what the animals body fatness is because the mortality implications are negligible. Natural selection would be unable to favor a given regulation set point in this range, when other options in the same range have equal mortality and hence fitness. However, selection would be able to distinguish the points where this zone starts and ends: that is natural selection would be able to distinguish a difference of 3% much more readily than a difference of less than 1%. A more likely system to evolve then would be a system locating these upper and lower edges of the constant mortality zone. The less sensitive fatness levels are to mortality effects the wider this zone will be. This is familiar as the ‘dual intervention point’ model [10], [17], [18], [19].

A different critique might be that the initial choice of tolerance for fatness in the lipostatic set-point model at 4% was too narrow. As noted in the methods, this stringency was chosen on the basis of the level of tolerance observed in other known set-point systems – such as body temperature and blood glucose levels. If we were to relax this by a factor of ten so that the tolerance was 40% (i.e. from 5 ± 0.1 g to 5 ± 1.0 g), this changes the level of variation in the mortality curves that still produces a level of $F_A$ that is compatible with the ‘set-point’ (i.e. inside the tolerance zone). Hence, instead of the mortality curves needing to have a variance less than 0.01%, this would be relaxed to around 1%, particularly if the mortality impact was large (scenario F). Nevertheless, 1% variation in the component mortality curves is still extremely low. Moreover, a set-point with a tolerance of ±20% would not normally be regarded as a set-point at all. For example, we would consider that something was seriously awry in the set-point regulation of body temperature if it varied at random by ±20% before any counter-regulation occurred. In fact, because the upper and lower limits of the tolerance zone are so far apart, a set-point with such low tolerance actually behaves as a dual intervention point system. Hence, while changing the set-point tolerance changes the precise outcome of the modeling, it converges on the same ultimate conclusion that dual-intervention point systems can more easily evolve than set-point systems.

This mathematical simulation exercise has some important implications for our interpretation of studies into the molecular biology of the regulation of body fatness. If the conditions for a lipostatic set-point system to evolve almost never exist, then this may explain why the molecular nature of the reference point of such a system has never been found. Clearly, further searching for it may end up a ‘holy grail’ type endeavor. Much previous work has interpreted the role of leptin as the signal from the body that signals the level of body fatness to the supposed lipostatic set point system. If this was the case, then levels of leptin falling below the set-point would be expected to generate compensatory responses to increase intake and reduce expenditure. Such actions of leptin are often observed [20]. Similarly if leptin levels increase above the set-point compensations to reduce intake and elevate expenditure should also be observed. Such responses are largely absent, which led to the notion of leptin resistance to explain the absence of response [21], [22]. However, we only expect these responses because we start from the assumption that there is a lipostatic set-point regulation system controlling things. From an evolutionary standpoint, a set-point system regulating fatness with leptin resistance poses enormous challenges to understanding how that situation might arise. We have seen here that lipostatic set-point systems are only likely to occur where there are large impacts of fatness on mortality (Scenario F). Hence, an animal showing leptin resistance on top of a lipostatic system would be exposing itself to the elevated mortality associated with body fatness above the set point for adiposity. Such individuals would likely be purged from the population. So, it is unclear how ‘leptin resistance’ might evolve.

Consider, in contrast, if the evolved system we study is actually a dual intervention point system for body fatness (as suggested here), and our observations largely concern what is happening at the lower intervention point. Such a model would predict the same responses to falling leptin. That is if leptin signaled that fatness had fallen below the lower intervention point the individual would be predicted to show compensatory responses to increase intake and decrease expenditure to bring fatness back up above the intervention point. If leptin rises above this point, however, it would signal only that fatness had risen into the zone of indifference (Figure 4). Hence, we would predict no response to such rising levels. And this is indeed what is observed – an asymmetry in response [23]. I suggest this asymmetry is not a lipostat with leptin resistance but observations around the lower intervention point of a dual-intervention point system for body fatness. Leptin resistance is a construct to try to explain data that do not fit the lipostatic set point model. A more likely scenario suggested here is that lipostatic set point system doesn't exist in the first place.

If we assume that a dual intervention point system is a more likely system to evolve, as indicated here, then a major outstanding question is what happens at the upper intervention point? Is fatness at this position also indicated by leptin? Such a role has been recently questioned [24], [25], [26]. If it does not, identifying what does, and the molecular nature of the upper intervention point, should be key future aims. One might argue that an upper intervention point is superfluous and searching for the nature of this upper intervention point is no different than searching for the ‘adiposity set-point’. Why can the system not just be an asymmetric set point that strongly regulates on the downside, but only weakly on the upside? The first objection to this interpretation is that given our current ideas about factors influencing mortality in relation to fatness, it is entirely unclear how such a system could evolve. The second problem is that this model ignores the wealth of data indicating mortality impacts of elevated fatness due to predation which was likely a major force during our evolutionary history [15], [19], which would drive evolution of an upper-regulatory point. Finally, it ignores the evidence that many people, despite living in an ‘obesogenic environment,’ do curb their increase in adiposity, pointing to a regulatory upper boundary that is variable between individuals. I have elaborated elsewhere where such individual variability might emerge from [27].

Conflict of interest

None declared.