Abstract
In this review we describe recent advances in transition metal oxyhydride chemistry obtained by topochemical routes, such as low temperature reduction with metal hydrides, or high-pressure solid-state reactions. Besides the crystal chemistry, magnetic and transport properties of the bulk powder and epitaxial thin film samples, the remarkable lability of the hydride anion is particularly highlighted as a new strategy to discover unprecedented mixed anion materials.
Keywords: Oxyhydride, hydride, mixed anions, solid-state chemistry
Classification: 60 New topics / Others, 107 Glass and ceramic materials, 201 Electronics / Semiconductor / TCOs, 203 Magnetics / Spintronics / Superconductors
1. Introduction
In the early 1990s, the chemistry of metal oxyhydrides had been the subject of very scarce studies, mostly implicating electropositive p-group elements (eventually combined with transition metals to form an alloy) or more seldom intermetallic compounds containing non-metallic elements. Despite their very similar ionic radii (ca. 1.4 Å), the coexistence of hard oxide anions and soft, polarizable, hydride anions with a lower charge in a crystalline solid was usually considered as thermodynamically unlikely except under very reducing conditions able to stabilize the hydride anion [1].
The discovery of the very first mixed oxyhydride solid is considered as dating from 1982 with the solid-state synthesis at 900 °C under pure hydrogen of the ternary compound LaHO [2]. Subsequent X-ray and neutron powder diffraction experiments [3] pointed out that this material crystallizes in a fluorite superstructure featuring an ordered cubic anionic environment for lanthanum characterized by hitherto unseen oxygen–hydrogen contact distances of 2.85 Å. Such distances are specific of negatively charged hydrogen species, as they are much longer than the O2––H+ interatomic distance encountered in OH– groups ranging from 1.32 to 1.37 Å. It is worth pointing out that LaHO turned out to be readily hydrolysable under ambient moisture, thereby releasing hydrogen. Later on, only few other stable materials containing both oxide and significant amount of hydride anions were reported, such as oxygen-stabilized η-carbides Zr3V3ODx (x max = 4.93; D– within Zr and V-tetrahedral interstices) [4] or Zr5Al3O1–x, an oxygen-stabilized Nowotny phase able to uptake up to 4.8 interstitial hydride per formula unit [5]. One can also cite the inverse perovskite-type Ba3AlO4H [6] or the hydrogen-stabilized Zintl phase of barium Ba21T2O5Hx (T = Ge, Si, Ga, In, Tl; x max = 24) [7] synthesized under drastically reducing conditions (1100 °C under a H2 pressure of ~1 bar). In both latter compounds, isolated hydride occupies interstices inside distorted barium polyhedra.
Regarding more specifically transition metal oxyhydrides and anion substitution, thermodynamics suggest that only oxides with a strong formation enthalpy are prone to survive under reducing conditions and hence form oxyhydrides. Second, it should be recalled that the hydride itself is a very reducing chemical species, able to reduce the transition metal cation to the metal. Nonetheless, using a soft chemistry method (‘chimie douce’), Rosseinsky et al. reported in 2002 the low temperature CaH2 solid-state synthesis of LaSrCoO3H0.7 [8]. Contrary to the aforementioned examples of electropositive main group metal oxyhydrides, the chemical route at play here is of topochemical type—keeping intact the architecture of the layered perovskite reactants—and moreover in LaSrCoO3H0.7 cobalt–anion–cobalt pathways for magnetic exchange interactions are present. Interestingly, those pathways exhibit different strengths depending on whether an oxide or a hydride is locally present, allowing control of the electronic or magnetic properties. This new layered perovskite cobalt oxyhydride and its successors LnSrCoO3+aHb with Ln = Pr, Nd [9] and Sr3Co2O4.33H0.84 [10] exhibit a rather low formal oxidation state for cobalt +1.7 and +1.75, respectively, that was considered as a stabilization condition for hydride-oxide systems [11]. The discovery in 2012 by Kobayashi et al. of an unanticipated Ti3+/4+ barium oxyhydride, exhibiting hydride exchange and electronic conductivity [12], has renewed the chemistry of transition metal oxyhydrides. Here, the oxidation state of the B-site cation is not unusual, as many other Ti3+ compounds exist. Ever since, this family of materials has steadily grown, based on not only the topochemical route but also with the use of high-pressure solid-state reactions, extending the compositions to the Sc [13], V [14,15], Cr [16] or Mn [17] elements on top of the initial Co or Ti oxyhydrides.
The aim of this review is to present this new family of transition metal oxyhydrides, obtained by low temperature reduction with metal hydrides, or under high pressure and high temperature. Additionally, the synthesis, crystal chemistry, physical properties of the bulk powder and epitaxial thin film samples, and the remarkable lability of the hydride anion as a new strategy to discover unprecedented mixed anion materials will be presented.
2. Synthesis of oxyhydrides
The synthesis of oxyhydrides requires special care, given the unusual properties of the hydride anion. Preparation typically requires strongly reducing conditions, so excessive reduction of 3d cations to the metallic state may occur. Additionally, at high temperatures, many known hydride compounds decompose via H2 release, so this is a potential issue in any oxyhydride compound. Treating oxides with H2 typically only reduces the oxide to the metallic state at most; so far no syntheses of transition metal oxyhydrides from H2 gas have been reported yet. Hence, the use of a hydride itself as a starting material is necessary; potential examples are the use metal hydrides such as CaH2, NaH, and TiH2, which may be commercially obtained or prepared in the lab by treating metals with H2 gas at moderate temperatures. These starting materials are naturally useful in the synthesis of various Ca, Na, and Ti-containing transition metal oxyhydrides, but one is not bound to these compositions. For example, CaH2 can be reacted with another oxide, and the resulting CaO can be removed from the reaction mixture by washing. These typically involve topochemical reactions. Hence, there are two main approaches to preparing oxyhydrides: the first involves the topochemical reduction of a parent oxide followed by removal of unwanted byproducts; the second involves a more direct synthesis from a mixture of hydride and oxide precursors, with no removal of intended byproducts. Recently, the latter has often been conducted under high pressure.
2.1. Topochemical synthesis
In solid-state chemistry, a topochemical synthesis is a synthesis based on the conversion of a parent compound converting to a product based on a very limited rearrangement of atoms, where the only bonds broken/formed are those which are necessary for the transformation. Topotactic reactions, a related but not necessarily exclusive term, signify that the overall symmetry of the structure before and after reaction are closely related. One simple example is ion exchange, whereby select atoms are exchanged while the other atoms do not diffuse and rather preserve the original crystal structure. Thus, unlike most high-temperature solid-state reactions, the structures of the starting materials and products of topochemical synthesis resemble each other quite closely. As low temperatures are involved and only ‘minimal’ changes to the structure are made, metastable products may also result. In terms of removing O2– (for subsequent replacement with H–) from oxides, the early work of Rosseinsky and Hayward [18–21], Kageyama [22–26], and Greenblatt [27] provides a starting point. For example, the three-dimensional (3D) perovskite LaNiO3 can be treated with NaH at relatively low temperatures (200–300 °C) to yield the layered LaNiO2 structure and NaOH/Na2O, which is washed away [18]. The resulting LaNiO2 structure resembles the original perovskite lattice, only in that selected ‘apical’ oxide anions have been removed. Similar novel oxygen-deficient structures have been reported for Mn [20,28], Fe [22–24] and Co [19,21]. Of course, these are not oxyhydrides, but the procedure for preparing oxyhydrides remains essentially the same.
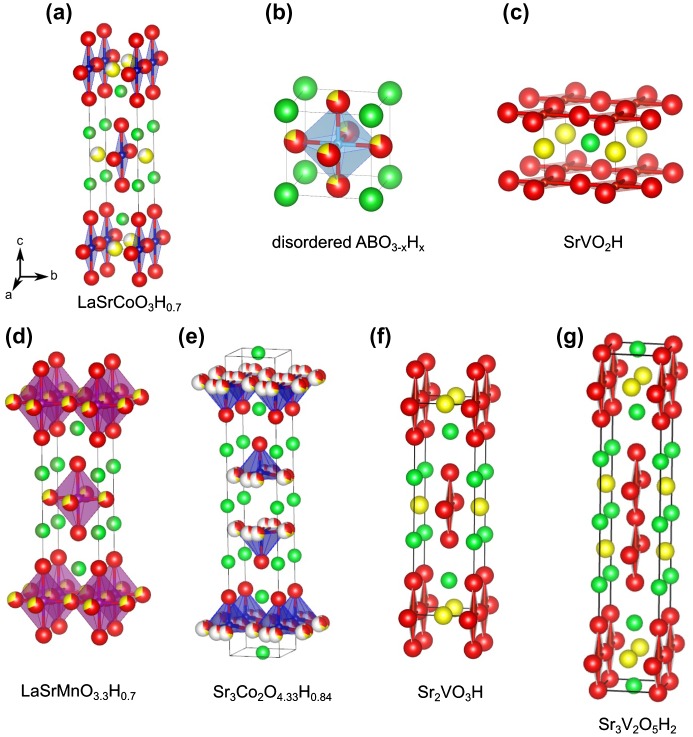
The first transition metal oxyhydride, LaSrCoO3H0.7 (see Figure 1(a)) was prepared by the topochemical reduction of LaSrCoO4 [8]. Other subsequent oxyhydrides which have been reported are titanates, such as (Ba, Sr, Ca, Eu)TiO3–xHx [12,29,30] (structure shown in Figure 1(b)), and vanadates, such as SrVO2H [15] (Figure 1(c)). All of these examples involve grinding the parent oxide with CaH2 and pelletizing within a glovebox, followed by sealing in an evacuated glass ampoule. Heating to 300–600 °C results in the oxyhydride product and CaO by-product, the latter of which is washed away in a methanol solution of weak acid (ammonium chloride). This method has also been applied to the preparation of oxyhydrides in thin form. Typically the parent oxide (SrTiO3, LaSrCoO4, etc.) is deposited on a suitable substrate via vacuum techniques such as pulsed-laser deposition. The film/substrate is then treated in the same way as powder, by immersion in loose CaH2 powder and sealing in a Pyrex tube under vacuum. Consequent heat treatments can be conducted at slightly lower temperatures. In this way, films of (Ba, Ca,Sr)TiO3–xHx [31,32] and LaSrCoO4−xHx [33] have been prepared.
Figure 1.
Structures of various oxyhydride compounds. For all structures, unit cells are oriented in the same a, b, c direction, as indicated in (a). Hydride is shown by yellow spheres, and oxide by red spheres. For the layered structures, interlayer La and Sr cations are shown by shades of green. For disordered ABO3–xHx in (b), the primitive cubic cell seen with BaScO2H, SrCrO2H, SrTiO3–xHx, and BaTiO3–xHx is shown; octahedral tilting is observed for certain Ca-Sr solid solutions (Ca,Sr)TiO3–xHx, resulting in larger unit cells (not shown).
While not being a transition metal oxyhydride, we note that the interesting calcium aluminate oxyhydride C12A7:H– is also formed from its parent oxide (C12A7 for mayenite 12CaO ⋅ 7Al2O3) either by reaction at 1300 °C with 20% H2/80% N2 [34] or alternatively using a CaH2 reduction process at 800 °C leading typically to a higher hydride content than the high-temperature solid–gas route [35]. For the titanate cases, the amount of hydride can be varied within x = 0–0.6 for a BaTiO3–xHx formula by adjusting the temperature and CaH2 amount. However, increasingly strenuous conditions eventually lead to decomposition of the original oxide framework, observed in terms of reduced crystallinity and increasing amounts of TiH2 [12]. We further note that it is not yet possible to predict whether an oxygen-deficient product or oxyhydride product will result; for example, an anatase TiO2 film simply gives a dark-colored TiO2–x phase when treated with CaH2 [36], whereas BaTiO3 gives the oxyhydride. La2Ti2O7 contains only minute amounts of hydride [37].
Most hydride reductions to date have used CaH2, with fewer examples with NaH and LiH. We can see that the surrounding thermodynamics differ when using these various hydrides [38]. For example, in the absence of any oxide to reduce, NaH and CaH2 will decompose at high temperatures:
| (1) |
| (2) |
As Ca2+ is a divalent cation, the lattice enthalpy of CaH2 is considerably higher than that of NaH. Thus, while at 210 °C a H2 pressure of 10 Torr may result, the equilibrium constant for eq. 2 is predicted to be only 10−8 even at 400 °C (assuming ΔH° and ΔS° values are independent of temperature). Hence, CaH2 is probably suitable at a higher temperature rather than NaH, otherwise, the experiment simply becomes a reduction using pure Na or Ca metal. Obviously, a suitable reduction temperature also depends on how easily the target oxide can be reduced (e.g. Fe vs. Ti), but the trend above still holds.
In comparing these hydride reducing agents, it is also necessary to compare the thermodynamics of the by-products. For example, a reduction with NaH could possibly yield either Na2O or NaOH; similarly, CaH2 could yield either Ca(OH)2 or CaO. The question in essence here is whether a one-electron or two-electron reduction is involved [38], that is,
| (3) |
| (4) |
In reality, NaOH is quite stable compared to Na2O, as demonstrated for example by the extreme difficulty of dehydrating NaOH to Na2O. Hence, reductions with NaH probably result in the two-electron reduction, yielding NaOH rather than Na2O. Another further point to consider is the side reaction between any hydroxide by-product and remaining hydride:
| (5) |
| (6) |
For NaH, the small K eq of Equation (5), combined with the dominance of Equation (3) over Equation (4) imply that any hydrogen pressure during the experiment is the result of a thermal decomposition (Equation (1)), rather than reduction of the parent oxide. This should be taken into account during synthesis, as the experiment may be more sensitive to reaction temperature and ampoule volume.
In the case of CaH2, only a small amount of H2 will be released from thermal decomposition. Rather, H2 will be released from either one-electron reduction of the oxide (Equation (4)), or any Ca(OH)2 impurities with the CaH2. Depending on the reactant quantities, this pressure can be substantial (up to 20 atm), leading to minor explosions. The effect of H2 pressure on the oxyhydride formation has been briefly discussed previously [9], and should be taken into account when standardizing experimental procedures. Gas-phase contributions toward the formation of oxygen-deficient oxides using CaH2 and NaH have been demonstrated in the past [18,38].
The benefits of these topochemical hydride synthesis are the relative ease (compared with the next method) in terms of equipment. Additionally, synthetic explorations are simple to plan, where one may choose any (in theory) oxide where one believes that there is O2– which may be removed/exchanged, and the products typically do not yield multiple phases or drastically different crystal structures, making structural analysis straightforward. The drawback, however, lies in the inherent reduction nature of the process itself; that is, for the reaction to occur, the transition metal must undergo a reduction. For example, BaTiO3 (Ti4+) is reduced to BaTiO2.5H0.5 (Ti3.5+). Zr, however, is considerably more difficult to reduce, and the synthesis of BaZrO2.5H0.5, or other irreducible elements such as Sc or Al is difficult to conceive. Hence, while there are still no Nb, Ta, or W oxyhydrides reported so far, for example, the explorative space is eventually limited by the repertoire of parent oxide. Additionally, over-reduction can also occur; our attempts to prepare iron-based oxyhydrides almost always result in the formation of Fe metal.
2.2. Direct synthesis via high pressure
A direct synthesis of transition metal oxyhydrides without any redox processes eliminates the problems encountered above for topochemical reductions. Hypothetically, BaTiO2H could be synthesized by reacting stoichiometric amounts of BaH2, BaO, and Ti2O3. The method can be used to achieve compositions based on irreducible elements, such as SrAlO2H. However, BaH2 and other simple hydrides often decompose to release H2 gas at the elevated temperatures necessary to achieve these solid-state reactions. The use of solid-state high-pressure techniques eliminates this problem by enclosing the reaction mixture in a solid container with virtually no head space; heating under these conditions prevents the loss of hydrogen, making oxyhydride synthesis possible. A sample cell is shown in Figure 2. To form a gas-tight seal, care must be taken in choosing the cell materials. In our own research, we have found that Au and Pt components seem to react with alkali/alkali earth reagents. NaCl sleeves work well, as they are soft enough to fuse into gas-tight seals under pressure, unlike other materials such as BN or Pt foil. NaCl has the additional advantage in that it may be removed by washing. Supplementary sources of H2 can be included within the cell, as with a mixture of NaBH4/Ca(OH)2 [14]. The high-pressure technique has been quite successful in forming the oxyhydride compounds; to date Sr2VO3H [14], SrCrO2H [16], LaSrMnO3.3H0.7 [17], and BaScO2H [13] have been reported (see Figure 1).
Figure 2.
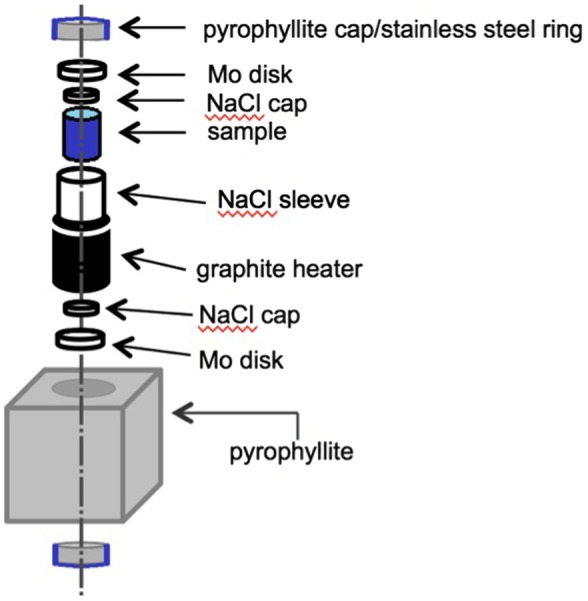
Schematic of a sample cell for high-pressure of oxyhydrides. The pyrophyllite cube is approximately 1.5 cm × 1.5 cm × 1.5 cm. Tungsten carbide blocks (anvils) apply pressure to the pyrophyllite cube from all six faces. Heating is achieved by electric current, via electrical contacts running through the tungsten carbide anvil, steel ring, and Mo disk to the graphite heater.
3. Specificity of oxyhydride characterization
Generally speaking, hydride as a negatively charged hydrogen atom should be characterized as any hydrogen species in a solid. The difficulty to chemically and structurally characterize transition metal oxyhydrides depends obviously on the level of hydride content in the investigated material. For oxyhydrides prepared by direct synthesis, an initial estimation of the hydride content can be made based on the reaction stoichiometry, but for topochemical reactions the amount of hydride will depend on the temperature and duration of the CaH2 reduction step. Furthermore, at the crystal-averaged atomistic level, the location of hydride anions in the unit cell may be difficult to identify owing to the ordered or disordered character of the anionic sublattice. In the latter case, the presence of H– on an anionic site also statistically occupied by an oxide anion is not so straightforward to ascertain and it is quite easy to miss. In fact these three species, hydride, oxide and vacancies, can in principle be present in the material and thus can coexist on the same crystallographic site, constituting a complex situation. Moreover, the simultaneous presence of hydroxide molecules coexisting with hydride anions is also possible in metal oxides or calcium phosphates as brought up recently by Hayashi et al. by nuclear magnetic resonance (NMR) [39] or based on maximum entropy method (MEM) analysis of neutron diffraction data by Masuda et al. [40]. The combined use of different characterization techniques is therefore highly required. The sought chemical composition is actually dependent on several assumptions, for instance, the correctness of the mass fractions refined by Rietveld analysis in case of coexisting phases and the oxygen stoichiometry of the eventually remaining starting pure oxide. These highlight the difficulty to get an unambiguous chemical and structural description of highly disordered oxyhydrides. We summarize below most of the techniques used so far for characterizing oxyhydrides, underlining their respective advantages and disadvantages.
Diffraction techniques, namely laboratory or synchrotron X-ray powder diffraction (XRD) as well as neutron powder diffraction (NPD), are widely used to investigate the structure and composition of obtained products. Clearly NPD, although not always accessible within a reasonable period of time, is required for a correct structural analysis of oxyhydrides as XRD is not able to detect hydrogen in the presence of heavy elements (e.g. Sr, Ba, La, Pr, Nd etc.). For Eu [30,41], or other highly absorbing elements (e.g. Sm, Gd, Dy) NPD should be nonetheless avoided, though not impossible with a special cell arrangement [41]. High-resolution time-of-flight (TOF) NPD instruments are often more suited than constant-wavelength diffractometers to determine subtle structural features, for instance coexistence of O2– and H– on the same site, as shown in LnSrCo3+αHβ oxyhydrides (Ln = Pr, Nd) [9]. A combined Rietveld refinement of XRD and NPD data collected at the same temperature allows a structural model more robust and less prone to least-squares correlations between occupancy and atomic displacement parameters, as they help in benefitting from very different atomic scattering factors of each chemical species with X-rays and neutrons. Such an approach is particularly useful to demonstrate the hydride location and the chemical occupancies of each site [8,12]. The eventual presence of impurity phases plus small amount of starting material may make the multi-phase Rietveld refinement challenging. It is worth noticing it is not always possible to exclude by diffraction the possible presence of a low amount of oxide anions on a hydride site. If resulting metal-O bond length is rather short (e.g. 1.80 Å vs. 2.18 and 1.94 Å for the pure oxide O1-apical and O2-equatorial sites in LaSrCoO3H0.7 [8]) this assumption can be reasonably discarded, by relying also on chemical analysis results.
In the course of the structural determination of LaSrCoO3H0.7 [8], a pure oxide, without hydride anion, was first proposed from synchrotron XRD data according to an Immm Sr2CuO3-type model consisting of chains of corner-sharing CoO4 squares. Intuitively, it would correspond to a reductive topotactic transformation from LaSrCo+IIIO4 (octahedral cobalt) into the LaSrCo+IO3 structure (square planar cobalt) during which the oxide anions which connect the octahedra in the b axis within the equatorial plane were removed in an ordered manner (see Figure 1(a)). While NPD gave a satisfactory fit for magnetic reflections, the nuclear peaks remained still poorly modeled by the Immm LaSrCoO3 structural model. A difference Fourier map showed the presence of a substantial hole of negative nuclear density at these sites. As hydrogen is one of five natural elements to exhibit a negative coherent scattering length (together with Li, V, Ti and Mn), it was successfully incorporated in the model at this position, yielding in a greatly improved refinement.
In a similar manner, for BaTiO3–xHy [12] it was the significant discrepancy between the oxygen content refined from the synchrotron XRD data and from the NPD data on the other hand that led to suspect the presence of hydride. Initially, after reduction of BaTiO3, a refined stoichiometry of BaTiO2.59(6) was obtained from synchrotron XRD data. An independent refinement of the NPD data led to a much lower oxygen content (BaTiO1.91(3)), corresponding to an unrealistic Ti valence of +1.82. Such discrepancy in terms of oxygen content derived from NPD and XRD diffraction experiments could be explained only by the presence of negative-scattering hydrogen randomly disordered with oxide on the single anionic site, decreasing the apparent nuclear density of this site with respect to the initially calculated density. If only oxygen is considered by NPD Rietveld (ignoring hydrogen) its content is then underestimated, while by XRD—insensitive to the presence of hydrogen—the oxygen content is correctly determined, although intrinsically less accurate as oxygen is a light element for X-rays in presence of heavy elements. Introducing hydrogen on the anionic site and refining again the NPD data alone increased the oxygen content to BaTiO2.33(2), a value much closer to the one obtained by synchrotron XRD. A combined Rietveld refinement of XRD and NPD data was conducted to obtain the final refined formula, BaTiO2.38(1)H0.62. NPD allowed additionally to discard the presence of hydroxide molecules in the solid as Fourier difference maps did not show any significant negative holes at around 1 Å from the anionic site. Based on the agreement of X-ray and neutron refinement data with a model consisting of only hydride and oxide at the anionic site, the combination of these two data-sets also revealed the total or almost total absence of vacancies.
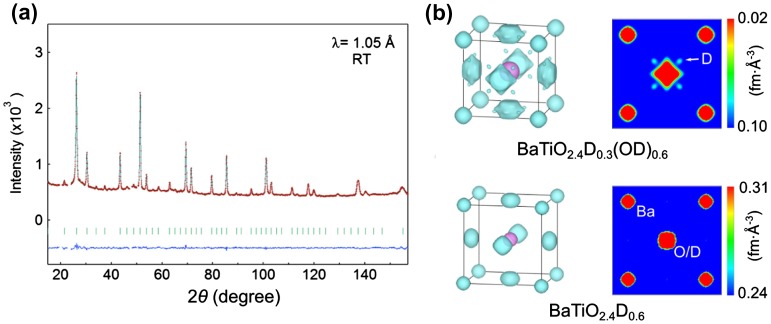
The MEM applied to powder neutron diffraction data [42]) is in principle more accurate than conventional Fourier difference maps, leading to less biased nuclear density maps with less background. Figure 3(a) shows a neutron diffraction pattern of a BaTi(O2–, D–, OD–), and a nuclear density map based on MEM analysis in Figure 3(b). Small spots of nuclear density are observed approximately 1 Å from the oxygen centers, signifying the presence of hydroxide (in deuterium form). In contrast, MEM analysis of BaTiO2.4D0.6 does not exhibit any such lobes (Figure 3(c)). Thus, this method was able to suggest the stable coexistence of H+ and H– at ambient conditions in BaTiO2.4(D–)0.3(OD–)0.3 [40], and a subsequent combined Rietveld refinement of neutron and X-ray diffraction data was used to obtain the precise anionic stoichiometry.
Figure 3.
Neutron diffraction pattern (a) and nuclear density maps from MEM analysis (b) to differentiate anionic species.
Other techniques than diffraction are used to qualitatively and quantitatively determine the hydride content in oxyhydrides. For example, mass spectrometry (as typically encountered in a TG-MS setup) can be used. The presence of hydride in LaSrCoO3H0.7 [8] was chemically confirmed by quantitative mass spectrometric monitoring of the H2O evolved simultaneously with oxidation of the oxyhydride material under flowing O2(g) at 272 °C, yielding 0.4 H– per formula unit, a value almost half of the hydride stoichiometry determined by diffraction. Of course, heating hydroxides also yields H2O, so the release of H2 when heating under inert atmospheres such as Ar or He can be taken as an indication of hydride within the lattice [12]. Quantification of hydride is not trivial, but may be accomplished with rigorous use of internal standards within the gas stream and standard hydride samples. Another approach to quantification has been acid digestion of the sample, and volumetric/mass spectrometric analysis of the evolved gases. For example Yoshizumi et al. and Kobayashi et al. dissolved their C12A7:H– [43] and BaTiO3–xHx samples [12] in DCl/D2O or D2SO4, and collected the evolved gases to prove and quantify the existence of lattice hydride.
As a related technique to heating the sample under inert atmospheres and measuring the released H2 gas, thermal desorption spectroscopy [44] has also been used as a characterization tool. This typically requires a dedicated instrument, composed of a high vacuum chamber, in-line mass spectrometer, and IR heating stage. Quantification is possible with careful calibration, and was used by Bouilly et al. [33] and Bang et al. [14] for their thin film and powder samples.
Thermogravimetry analysis (TGA) can be used under oxidative atmosphere to confirm the suspected stoichiometry via weight change. Any oxyhydride obtained by topochemical reduction can be reoxidized to the original parent oxide, undergoing a weight change reflecting the original hydride content, assuming there are no anion vacancies. For BaTiO3–xHy [12] the refined formula from Rietveld analysis, BaTiO2.38(1)H0.62, compares nicely well with the one deduced from TGA in air, BaTiO2.38H0.62. Reductive TGA may also be performed; for Sr3Co2O7–yHy [10] the observed relative mass loss by reductive TGA under 5%H2 in N2 was used (in combination with other results) to confirm a Sr3Co2O4.33H0.84 formula.
TGA experiments revealed in LnSrCo3+αHβ oxyhydrides (Ln = Pr, Nd) an oxygen stoichiometry substantially higher than 3.0 (up to 3.33) [9], contrary to LaSrCoO3H0.70. Based on this additional information, extra oxide anions were introduced in the crystallographic model on or very close to the hydride site bridging the cations in the ab plane. This implied that the substitution of oxide for hydride within the CoOH1–x sheet was incomplete in those Pr- and Nd-containing cobalt oxyhydrides; the additional substitutional disorder in the transition metal layer induced local variations in the Co environment such as displacements of the pure oxide O2 equatorial site handled by a ‘split-atom’ model.
Simple, routine elemental analysis using commercial CHN analyzers can play an important role to quantitatively confirm the results from NPD/synchrotron XRD combined Rietveld refinement. Regarding LaSrCoO3H0.7 [8] a more accurate global hydrogen content was obtained by elemental analysis, revealing 0.26(2)% H by mass, very close to the 0.21% mass from the combined Rietveld refinement, definitely confirming the absence of oxide anion on the hydride site, which is statistically occupied by only hydrides and vacancies. 1H magic angle spinning nuclear magnetic resonance spectroscopy (MAS NMR) qualitatively confirmed the presence of hydride in the Sr3Co2O7 majority phase by comparison with a CaH2 spectrum [10]. 1H MAS NMR measurements otherwise confirmed the same chemical state and environment for hydrogen species in BaTiO3–xHy [12]. As mentioned above, H–/OH– are not so simple to differentiate by NMR (see the recent study by Hayashi et al. [39]). But this spectroscopic technique remains one of the few tools for exclusively seeing hydrogen and its position, though not so usable if one deals with magnetic or conducting samples.
Use of H/D isotopes can help when dealing with neutron diffraction or mass spectrometry. The H– and D– exchange within BaTiO3–xHy was shown to occur in D2(g) atmosphere at 400 °C monitored in situ by MS, confirmed by NPD experiments before and after deuteration [12].
The valence of the transition metal can be checked by Curie–Weiss fitting against magnetic susceptibility data, on the other hand X-ray absorption spectroscopy (XAS) is also used to confirm the formula. The average oxidation state of Co calculated from the refined anionic content in LaSrCoO3H0.7 [8] was shown to be consistent with an X-ray absorption Co K-edge position very close to that of the Co(II) standard (LaSrCoO3.5). In BaTiO3–xHy magnetic susceptibility data showed a +3.4 oxidation state for Ti strengthening more the refined formula [12].
Muon spin rotation (μSR) experiments confirmed LaSrCoO3H0.7 was magnetically ordered [8] and quasi-elastic neutron scattering experiments [45] were carried out to probe dynamics of the same material within the –0.4 and 0.4 meV energy transfer window with an instrumental resolution of 17.5 meV in FWHM. This corresponds to a timescale of 1–75 ps. The onset of hydride mobility along the a axis within the perovskite layer was revealed above 402 °C, associated with an ionic conductivity of ca. 3–5 S cm−1 around 427 °C, significantly higher than in protonic conductors.
Besides the different relevant techniques mentioned hereinabove (XRD, NPD, TGA, MS, magnetic susceptibility, NMR, XAS, chemical analyses etc.), hydrogen forward scattering (HFS) [46] can also be cited as another experimental method used so far for the analysis of TM oxyhydrides [30], quantification requiring curve fitting.
As far as they are concerned, epitaxial thin films of ATiO3–xHx (A = Ba, Sr, Ca) [31] were characterized by XRD and by secondary ion mass spectroscopy (SIMS). Low temperature CaH2 reduction and subsequent hydride insertion was shown to induce small change in unit cell parameters relative to the as-grown oxide film. SIMS, that is an expensive technique and requires standards for quantification but compulsory for thin films, gave hydrogen density (that turned out to be large, e.g. SrTiO2.75H0.25) and its depth dependence, pointing out a uniform distribution in the film.
4. Chemical reactivity of oxyhydrides: lability and exchange
The chemical reactivity of hydride is unlike that of any other anion. The redox potential of H– between H2 and H– is highly negative (–2.23 V). Thus, H– can be readily oxidized to H2 gas. The oxidant may be an external species, or one of the metal cations within the compound itself; the latter is more conveniently described as a reductive elimination of hydride. This property is illustrated in the release of H2 from TiH2 when heated at approximately 400 °C, for example [47,48].
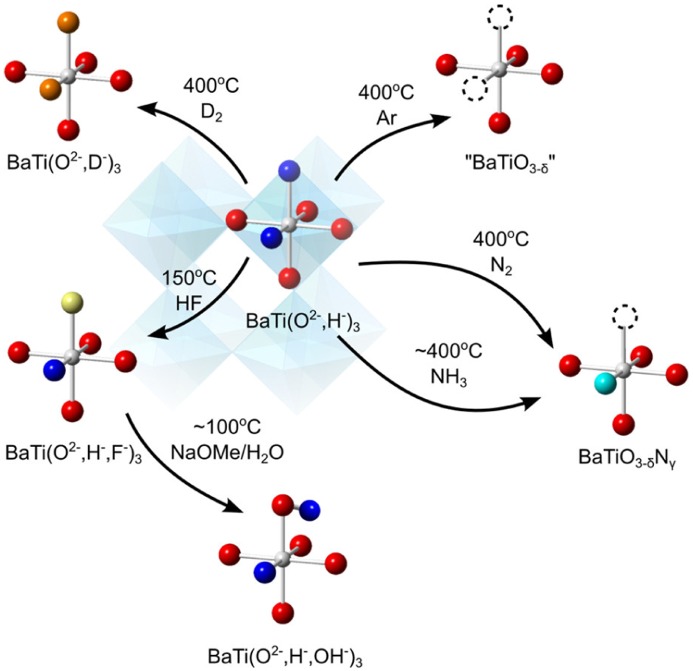
This release of H2 can also be seen in certain oxyhydrides, and in reversible manner. Using a TG-MS apparatus under flowing Ar, Kobayashi et al. observed the release of H2 from BaTiO2.4H0.6 at approximately 400 °C during a linear temperature ramp from room temperature to 600 °C (and presumably yielding a BaTiO3–δ product, see Figure 4). Repeating the experiment under D2 gas led to the detection of HD gas, also peaking at 400 °C. The oxyhydride product was found to be almost fully deuterated (based on neutron diffraction), indicating that hydride exchange with gaseous hydrogen is possible at 400 °C, the same temperature as the release temperature.
Figure 4.
Different anion exchange routes starting from an oxyhydride.
This demonstrated thermolability of hydride is quite interesting as it makes anion exchange possible. In solution chemistry, the broad range of various inorganic complexes rests upon the fact that various (precursor) ligands are labile, that is, they do not bind too strongly neither too weakly, making consequent ligand exchange possible. Hydride in oxyhydrides appears to be of similar use. Other than the thermal lability described above, we note that H–, as a base, would also be prone to acid-base reactions with acids, also permitting it to leave as H2 gas under moderate conditions.
The thermal lability for synthetic purposes has been demonstrated by Yajima et al. [49] and Masuda et al. [40] recently by their synthesis of oxynitride BaTiO3–xNy. Typically, the preparation of oxynitrides has required the use of NH3 at high temperatures of 800–1300 °C. In the case of preparing the oxynitride version of BaTiO3, the highest nitrogen content has been BaTiO2.85–δN0.1 which was prepared with flowing NH3 at 950 °C. In contrast, by the use of a BaTiO2.4H0.6 precursor, treatment with NH3 at temperatures of 375–550 °C led to considerably higher nitrogen contents of BaTiO2.4H0.3N0.1 – BaTiO2.4N0.4. Furthermore, Masuda et al. [40] have reported that even N2 can yield oxynitride BaTiO2.5N0.2 at 500 °C. Presumably, once the labile hydride anion leaves, the Ti cation becomes coordinatively unsaturated, and thus becomes active enough to react with N2 gas despite its triple N–N bond.
Apart from the thermal lability, an acid-base reaction involving hydride has also been invoked to yield new mixed-anion compounds. Masuda et al. reacted BaTiO2.5H0.5 with controlled amounts HF, to yield the mixed oxide-hydride-fluoride compound BaTiO2.5H0.25F0.25 [40]. The closely related compound BaTiO2.9F0.1 has so far been reported only by the use of high temperature and pressure (3 GPa, 1300 °C) [50]. Further F–/OH– exchange is possible from here, as demonstrated by the preparation and characterization of BaTiO2.4D0.3(OD)0.3 from BaTiO2.4D0.3F0.3. This compound is an unusual case involving the co-existence of H– and H+ (or in actuality, D– and D+) within the same lattice, and has been made possible by the anion-exchange techniques starting from the labile oxyhydride precursor.
The two aforementioned reactions involve the direct exchange of H– with other anions. However, even at higher temperatures where the hydride has already left, the remaining anion-deficient structure can be useful for further anion-exchange reactions. This has been demonstrated by the formation of EuTiO2N by Mikita et al. [41]. Here, EuTiO2.82H0.18 was first prepared. Treating with NH3 at 400 °C resulted in direct N3–/H– exchange, to yield EuTiO2.82N0.1▢0.06. Further treatment at 800 °C resulted in the further oxygen to be removed, despite no hydride being present, to yield EuTiO2N. This contrasts with the reactivity of EuTiO3, which shows no reactivity with NH3 even at 600 °C. Treatment of EuTiO3 at 800 °C result in EuTiO2.25N0.75, but the composition EuTiO2N is not attained, unlike in the case when the oxyhydride was used as the starting material. This implies that the presence of the anionic vacancy during the reaction (2% in EuTiO2.82N0.1▢0.06) has a significant impact on the anion-exchange reaction.
5. Physical properties in oxyhydrides: transport and magnetism
5.1. Titanate oxyhydride perovskites
The alkali earth titanate oxyhydrides exhibit semiconducting to metallic character, depending on the hydride doping amount. Loosely pressed pellets of powder BaTiO3–xHx (100 nm) exhibit semiconducting temperature dependences with a room temperature conductivity of 4 × 10−4 S/cm. This is probably not the inherent behavior, though, as single crystal films deposited by pulsed laser deposition on substrates yielded comprehensive results, showing metallic behavior at high doping levels.
Yajima et al. and Bouilly et al. have examined the conductivity of various titanate perovskite oxyhydride films [31,32]. SrTiO2.75H0.25, BaTiO2.36H0.64, and CaTiO2.32H0.69 films on (LaAlO3)0.3(SrAl0.5Ta0.5O3)0.7 (LSAT) substrates showed high conductivities at room temperature, ranging from 102 to ~104 S/cm, and detailed temperature-dependent studies showed metallic behavior. The SrTiO2.75H0.25 films are somewhat analogous to previously reported Sr(Ti0.8Nb0.2)O3 films [51], in terms of doping level, carrier concentration, and conductivity, with both systems essentially being heavily n-doped systems. For the barium titanate system, one may compare the BaTiO2.36H0.34 films to reduced BaTiO3. A key difference is that it is difficult to introduce a large number of oxygen vacancies in the perovskite structure due to structural instability, but extremely high doping levels can be achieved with hydride, as the anionic sites are always filled. The reduced BaTiO3 films, with very small carrier concentrations, were metallic, with several ferroelectric transitions resulting in anomalies on ρ–T curves [52]. However, the BaTiO2.36H0.34 samples exhibited no such anomalies. The dependence of electrical properties on hydride content for SrTiO3–xHx and BaTiO3–xHx films has also been examined. While the Sr films always exhibit metallicity the Ba films are semiconducting at low hydride amounts. The reason for this may be the same as for Nb-doped (Ba, Sr)TiO3–δ, where incoherent displacement of Ti from the octahedral center led to increased electron scattering [53].
Another titanate oxyhydride, EuTiO2.7H0.3 has been synthesized [30]. Thin film studies also show metallic conductivity for this sample due to 3d electrons of Ti, induced from the hydride reduction. The A-site europium is in the +2 oxidation state, and has ferromagnetic order (T c = 12 K) from spins on Eu 4f orbitals being mediated by itinerant Ti 3d electrons, in contrast to EuTiO3 which is an antiferromagnetic insulator. The ferromagnetism based on the RKKY mechanism is also found in Eu1–xLnxTiO3 and EuTi1–xCrxO3, but here T c is somewhat lower, implying the superiority of aliovalent hydride substitution at the anionic site in comparison with the cationic counterpart.
5.2. Vanadate oxyhydride perovskites and derivatives: SrVO2H, Sr2VO3H, Sr3V2O5H2
The electronic and magnetic structures of SrVO2H, and its related layered analogues, Sr2VO3H, and Sr3V2O5H2, (Figure 1(c), (f), and (g)) have been examined in detail [14,54,55]. These stoichiometric systems possess anion ordering, making them suitable for systematic studies. As shown in Figure 1(c), in the SrVO2H case, hydride occupies ‘apical’ sites (or trans octahedral VO4H2), whereas in the layered cases (Figure 1(f) and (g)), equatorial sites are occupied by hydride. Experimentally, neutron diffraction and muon spin relaxation shows that all three compounds have antiferromagnetic states. The Néel temperatures (T N) are 170 and 240 K for Sr2VO3H and Sr3V2O5H2 [15]. Surprisingly, the Néel temperature of SrVO2H is well above room temperature despite the two-dimensional structure. Sr2VO3H and Sr3V2O5H2 are regarded, respectively, as quasi one- and two-dimensional magnets. The nearly temperature-independent susceptibility and the absence of anomalies near at the ordering temperatures may reflect the low-dimensional feature of these compounds, with short-ranged magnetic correlations being developed well above T N [15].
The bonding and electronic structure in this system has been summarized by Romero et al. [15], Bang et al. [14] and Wei et al. [54], among others. A simple point is shown for SrVO2H in Figure 1(c). Here, H– occupies the ‘apical’ site. For oxides such as SrVO3, the t 2g orbitals would remain triply degenerate and each form π bonds with O 2p orbitals (Figure 5). Additionally, H– cannot form π bonds since it consists of only s orbitals. Hence, given the hydride in the ‘apical’ position, the d xz and d yz orbitals experience less repulsion and decrease in energy, splitting the t 2g state into a doubly degenerate d xz and d yz bands with a d xy band above. The two d electrons partially fill the lower d xz and d yz bands; calculations predict the bands to have narrow dispersion, inducing a Mott transition to an insulator. This contrasts with the metallic SrVO3, with band valence photoelectron spectroscopy on thin film samples confirming this difference [55]. The experimentally observed antiferromagnetic ordering has also been predicted by spin-polarized band structure calculations [54].
Figure 5.
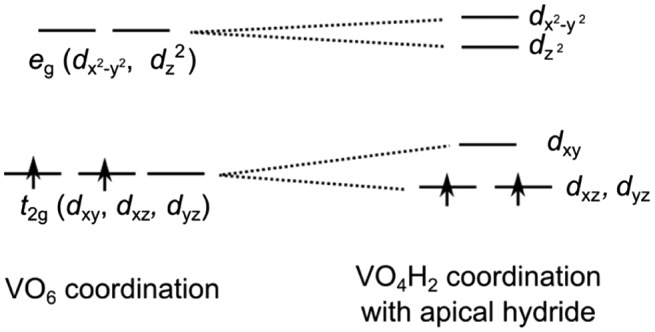
Molecular orbital diagram for SrVO2H.
Recently, there has been much work concerning electronic doping VO2 using various species. Doping VO2 results in metal-insulator transitions, and so far oxide vacancies [56] and protons (H+/e–, via H2 reduction) [57] have been introduced for n-doping to achieve alternate electronic states. Proton doping (via H2 reduction) has the advantage of not inducing disorder, but hydride is unique given its s character, and should therefore be a valuable addition to the various tools available for the modulation of electronic states, which have recently been garnering attention [58,59].
5.3. Cobalt oxyhydride perovskite derivatives: LaSrCoO3H0.7, Sr3Co2O4.33H0.84
While the non-stoichiometric nature of the cobalt oxyhydrides has limited electronic structural calculations and thus close examination of electronic structure, the cobaltates, starting with LaSrCoO3H0.7, were the first reported transition metal oxyhydrides [8]. As shown in Figure 1(a), the structure of LaSrCoO3H0.7 is based a Ruddlesden–Popper layered perovskite, but with hydride anions and vacancies preferentially occupying select equatorial sites to form an orthorhombic lattice. As in the case of the previously mentioned vanadates, antiferromagnetic order is observed at room temperature, signifying that strong covalent interactions through the Co-H-Co chains, together with the larger magnetic moments, contribute to the enhanced T N. Sr3Co2O4.33H0.84 (Figure 1(e)) is based on the n = 2 member of the Ruddlesden–Popper series [10]. While hydride has been incorporated, at this point oxygen removal is extensive, resulting in a mixture of tetrahedra and square pyramids. This extensive anion disorder and amount of vacancies is probably the reason for the lack of any observed magnetic order [10].
5.4. SrCrO2H
The transition metal oxyhydride family was further expanded to chromates using high-pressure and high-temperature synthesis. SrCrO2H was prepared by heating powders of SrO, SrH2 and Cr2O3 at 5 GPa and 1000 °C [16]. The successful synthesis of this material probably benefits from the high stability of the Cr3+ cation. Trivalent chromium oxides do not reduce even under harsh reducing conditions, allowing the high-pressure/high-temperature and hydride-rich environment sustainable for this species. The structure is cubic and its stoichiometry could be determined using a combination of X-ray and neutron diffraction, as previously used for LaSrCoO3H0.7. The oxide and hydride anions do not order in this structure, thus explaining the cubic structure. The magnetic properties of SrCrO2H were studied by variable-temperature NPD, revealing a G-type antiferromagnetic order with a Néel temperature as high as 380 K. The T N observed in this system is much higher than those of isovalent RECrIIIO3 (RE = rare earth) structures with the highest previously known value for LaCrO3 at T N = 290 K. At a first glance, this behavior is strange as the octahedral environment in Cr3+ (t 2g 3) only allows π-type superexchange interactions (with the neighboring ligand) that cannot occur with the 1s orbital of the H– anion. However, an hypothesis for this behavior is that the high symmetry of the SrCrO2H with a large Sr2+ cation (144 pm) gives a tolerance factor near 1; the cubic structure leads to ideal 180° Cr–O–Cr bond angles that allow strong superexchange antiferromagnetic interactions. In the case of oxide perovskites with smaller trivalent cations at the A site, distortions exist with tilting of the octahedra that leads to smaller T N. As shown in Figure 6, the Néel temperature of Cr3+ perovskites increase linearly with the tolerance factor but SrCrO2H has a slightly lower than expected Néel temperature.
Figure 6.
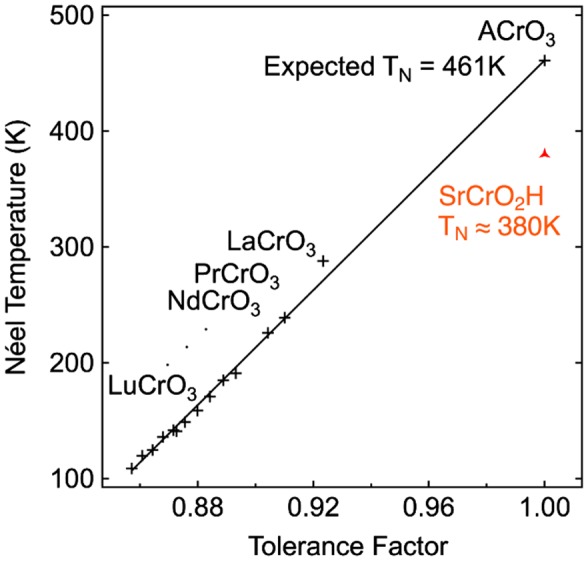
Change of Néel temperatures of various RECrO3 (RE = rare earth) phases with the tolerance factor.
Liu and coworkers investigated the electronic and magnetic properties of SrCrO2H using DFT calculations on a hypothetical ordered trans-coordinated model isostructural with the reported SrVO2H [60]. In their study, the authors speculated a possible secondary effect where the hydride’s lower electronegativity was partially responsible for the high T N. The lower electronegativity of hydride should lead to delocalized orbitals along the Cr–H bonds, which in turn reinforces Cr–O bonds and strengthens the superexchange interactions along Cr–O–Cr paths.
5.5. LaSrMnO3.3H0.7
The synthesis of LaSrMnO3H0.7 was achieved via high pressure and high temperature at 5 GPa and 1000 °C on using powders of La2O3, MnO, Mn2O3, SrH2 [17]. LaSrMnO3.3H0.7 crystallizes in the tetragonal I4/mmm space group with disorder of the oxide and hydride anions mainly in the equatorial plane (Figure 1(d)). This configuration confirms the trend observed also in cobaltate LaSrCoO3H0.7 and vanadates Sr2VO3H and Sr3V2O5H2. An important difference, however, lies in the lack of ordering of the two anions and therefore the observation of tetragonal symmetry rather than the orthorhombic symmetry found in the ordered Co and V systems. The anionic non-stoichiometry, determined by synchrotron X-ray and neutron diffraction, leads to a mixed valence Mn2+ and Mn3+ system with an average valence of Mn2.3+. While magnetic susceptibility measurements confirm this valence, they also exhibit magnetic behavior suggesting a spin glass transition at T SG = 22 K. The absence of magnetic Bragg reflections in the low temperature neutron diffraction is consistent with this spin glass picture. The negatively large value of a Curie–Weiss temperature θ = –149 K suggests the strong magnetic interactions. A fairly large frustration factor of f ~ 6 (|θ|/T SG) was discussed in terms of competing magnetic interactions between neighboring Mn cations, i.e. ferromagnetic Mn2+–O–Mn3+ and antiferromagnetic Mn3+–O–Mn3+ and Mn2+–O–Mn2+.
6. Crystallographic site selectivity of hydride in layered systems
Total or partial anion ordering has been the topic of many studies for a long time in various mixed anion transition metal materials isolated so far, including oxyhalides and oxynitrides. Besides DFT first-principles calculations, energy calculations (the Madelung part of the lattice energy) and the bond valence sum method, basics Pauling’s electronegativity arguments have been evoked, whereby the more electronegative anion would be preferentially coordinated to the more electropositive cation, but without a total success in oxyfluorides, oxynitrides, or oxychlorides [61]. Another simple and general method for predicting the anion distribution not requiring the exact knowledge of the crystal structure has been proposed by Fuertes [62] according to the historic Pauling’s Second Crystal Rule (PSCR) published in 1929 [63] as one of the principles governing the structure of complex ionic crystals. It is obviously assumed each cation is coordinated to anions at the corner of a polyhedron and vice versa. Those principles have been deduced from empirical knowledge of known crystal structure at that time, as well as from stability considerations in terms of crystal energy. Their application scope was limited by Pauling himself [63] as follows: small cations with relatively large electric charges (+3 or +4 typically) and crystal radii lower than about 0.8 Å; large univalent or divalent anions (over 1.35 Å) not too highly deformable such as oxygen or fluorine anions. Furthermore the chemical bonds in the crystal should not be of the ‘extreme non-polar or shared electron pair type’, thus excluding copper compounds and ‘many other eighteen-shell atoms’. The PSCR or electrostatic valence principle [63] is based on the so-called strength s of the electrostatic valence bond (between one given cation and each adjacent anion) defined as where z is the formal charge of the cation and ν its coordination number (in anions). In a stable coordination structure, the formal charge –ζ of each anion (coordinated to C cations) approximately satisfies the following equation:
In materials (with anions of different charge) exhibiting chemically inequivalent anionic sites, for instance in lower than cubic symmetry layered perovskite structures, one can calculate according to the PSCR the charge –ζ of each anionic site that should be rather close to the charge of the anion actually occupying this site, allowing to predict the distribution of anions. Fuertes et al. [61,62] have shown this predictive method works well for many layered oxynitrides, oxyfluorides and oxychlorides (with the noteworthy exception of Nd2AlO3N [64], for which the difference between ζ equatorial and ζ apical calculated according to the PSCR, around 0.15, is very fine): the more charged anion would preferentially occupy the site showing the larger PSCR charge and conversely. Moreover for oxynitrides, oxyfluorides and one oxybromide of other structural types (e.g. antifluorite, baddeleyite, Th3P4, wurtzite …), PSCR appears as generally fulfilled though to a less extent for oxychlorides.
The discovery of LaSrMnO3.3H0.7 [17] by Tassel et al. has been naturally a motivation to confront this PSCR method with layered oxyhydride systems (including the previously published LaSrCoO3H0.7 [8], NdSrCoO4–xHy [9], PrSrCoO4–xHy [9] cobaltates or Sr2VO4–xHx vanadates [14,15] in order to check its applicability range over this new series of mixed anion systems. The PSCR calculated anion formal charge at the equatorial site appears as systematically higher than at the apical site (see Table 1), leading to a predicted apical site preference for H– while in all the K2NiF4 transition metal oxyhydrides hydride anions are located only on the equatorial site, except to be complete the case of Sr2VO3.62H0.38 and Sr2VO2.99H1.01 [14] though extremely low chemical occupancy of respectively 4 and 1.5% for H– are suggested on the apical site (vs. 15 and 93%/5% on the equatorial site(s)). Hence it turns out the PSCR is not able to predict the anion ordering in transition metal oxyhydrides. However it should be stressed that the difference between PSCR ζ equatorial and ζ apical remains small for all the highlighted examples of Table 1, reaching at best 0.28.
Table 1. Formal charge of the apical and equatorial anionic site in known K2NiF4 transition metal oxyhydrides calculated according to the Pauling’s Second Crystal Rule (PSCR).
| Oxyhydride | ζapical | ζequatorial |
|---|---|---|
| LaSrMnO3.3H0.7 | –1.61 | –1.89 |
| LaSrCoO3H0.7 | –1.67 | –1.68 |
| NdSrCoO4−xHy | –1.67 | –1.68 |
| PrSrCoO4−xHy | –1.67 | –1.68 |
| Sr2VO4−xHx | –1.77 | –1.88 |
One singularity of hydride anion that could also explain the violation of the PSCR in oxyhydrides is its small Pauling’s electronegativity (2.1), as low as astatine, 2.2, the rare heaviest halogen, that may be too small for an electrostatic-based principle. It is worth noticing the lowest electronegative anion used by Fuertes et al. [61,62] to support the PSCR is bromine (χ = 2.96). Also hydride is highly polarizable and shows in crystals an ill-defined size ranging from 1.35 to 1.53 Å depending on the covalent to ionic bond character with a metal [65], property that strongly contradicts PSCR’s prerequisites underlined above in terms of non-deformability of anions.
Ordering/disordering of hydride within the equatorial plane of layered oxyhydrides has been controlled by Bouilly et al. [33] in epitaxial thin films through the use of different orientations of the LSAO (LaSrAlO4) substrate leading to two orientations (perpendicular or parallel) of the layer c-axis of the oxyhydride with respect to the substrate. CaH2-topochemical conversion of the c-axis and b-axis oriented LaSrCoO4 films (deposited by pulsed laser deposition on LSAO (0 0 1) and LSAO (1 0 0) substrates, respectively) leads to LaSrCoO3H0.7 oxyhydride films with tetragonal and orthorhombic symmetry, respectively. The latter and former cases correspond respectively to a crystallographically ordered and disordered hydride/oxide arrangement within the equatorial plane (see Figure 1(a) of [33]). In other words, the anionic order observed in bulk LaSrCoO3H0.7 [34] is recovered when the precursor oxide is deposited on the LSAO with c-axis within the film surface, while remarkably an original hydride/oxide disorder is created within the equatorial plane when the precursor oxide is deposited with a c-axis perpendicular to the film surface. These results demonstrate that strain engineering can lead to new materials with designed anion arrangement in mixed anion materials.
7. Summary and outlook
As discussed in this review, oxyhydrides have gone through rapid development over the past 10 years. We have summarized the various compounds and their characteristics in Table 2. Among the 3d transition metals, only Fe, Cu, and Zn oxyhydrides remain to be discovered. In terms of properties, hydride has certain characteristics unlike any other mixed anions. The 1s character gives it unusual bonding and hence magnetic/electronic implications, and may be useful in controlling the electronic properties of various materials with applications in devices. In terms of ionic conductivity, recently, reports on pure hydride ion conductivity for layered non-transition metal hydride perovskites have been reported [66], opening the doorway to hydride-based ionics. One can even imagine high-potential electrochemical cells based on the H–/H+ redox couple; such applications would not be possible without a wide range of hydride-based materials to choose from. We have also discussed the chemical lability of hydride, and this may serve as a useful approach to new hydrogenation catalysts based on (oxy-) hydrides. With these potential applications in devices, ionics, and catalysis, together with their fundamental scientific impact, it is evident that transition metal oxyhydrides will continue to gain prominence in the future.
Table 2. Summary of transition metal oxyhydride compounds.
| Compound | Preparation* | Properties* | Anion arrangement* | Reference |
|---|---|---|---|---|
| LaSrCoO3H0.7 | CaH2 | I; AFM (TN > RT); H– diffusion | Partial order, eq. | [8,33,45] |
| NdSrCoO3.1H0.80, NdSrCoO3.21H0.58 | CaH2 | AFM (TN = 410 K) | Partial order, eq. | [9] |
| AFM (TN = 375 K) | ||||
| PrSrCoO3.16H0.68 | CaH2 | AFM (TN = 445 K) | Partial order, eq. | [9] |
| Sr3Co2O4.33H0.84 | CaH2 | PM | Partial order, eq. | [10] |
| (Ca, Ba, Sr)TiO3–xHx | CaH2 | MS; PM | Random | [29,31,32] |
| EuTiO3–xHx | CaH2 | M; FM from Eu moments | Random | [30] |
| (Tc = 12 K) | ||||
| Ln2Ti2O7−xHx | CaH2 | Electrocatalysis | Unknown (trace) | [37] |
| SrVO2H | CaH2 | I; AFM (TN > RT) | Ordered, apical | [15,55] |
| Sr2VO3H | CaH2 | I; AFM (TN = 170 K) | Ordered, equatorial | [15] |
| Sr2VO3–xHx | HP | Partial order, eq. | [14] | |
| Sr3V2O5H2 | CaH2 | I; AFM (TN = 240 K) | Ordered, equatorial | [15] |
| SrCrO2H | HP | I; AFM (TN = 380 K) | Random | [16] |
| LaSrMnO3.3H0.7 | HP | I; SG (TSG = 22 K) | Partially ordered | [17] |
| BaScO2H | HP | I; local order (1H NMR, DFT) | Random | [13] |
CaH2 = reduction with CaH2, HP = high pressure, AFM = antiferromagnetism, FM = ferromagnetism, PM = paramagnetism, SG = spin glass, eq. = equatorial, I = insulating, M = metallic, S = semiconducting.
Disclosure statement
No potential conflict of interest was reported by the authors.
Funding
This work was supported by the CREST [No. JPMJCR1421] program from the Japan Science and Technology Agency (JST); and Grant-in-Aid for Scientific Research on Innovative Areas ‘Mixed anion’ [JP16H06439] from MEXT.
Acknowledgements
A significant portion of this work was assisted by the Japan–France Bilateral Joint Research Project from the Japan Society for the Promotion of Science (JSPS), and the Centre National de la Recherche Scientifique, (CNRS), [PRC No. 0684 2013-2014].
References
- [1]. Norby T, Widerøe M, Glöckner R, et al. Hydrogen in oxides. Dalton Trans. 25;2004:3012–3018 10.1039/B403011G [DOI] [PubMed] [Google Scholar]
- [2]. Brice JF, Moreau A. Synthèse et conductivité anionique des hydruro-oxydes de lanthane de formule LaHO, LaH1+2xO1-x et LaH1+yO1-x (y < 2x). Ann Chim Fr. 1982;7:623–634. [Google Scholar]
- [3]. Malaman B, Brice JF. Étude structurale de l’hydruro-oxyde LaHO par diffraction des rayons X et par diffraction des neutrons. J Solid State Chem. 1984;53:44–54. 10.1016/0022-4596(84)90226-3 [DOI] [Google Scholar]
- [4]. Rotella FJ, Flotow HE, Gruen DM, et al. Deuterium site occupation in the oxygen‐stabilized η‐carbides Zr3V3ODx. I. Preparation and neutron powder diffraction. J Chem Phys. 1983;79:4522–4531. 10.1063/1.446339 [DOI] [Google Scholar]
- [5]. Clark NJ, Wu E. Hydrogen absorption by M5X3 phase Zr-Al compounds. J Less Common Metals. 1988;142:145–154. 10.1016/0022-5088(88)90171-3 [DOI] [Google Scholar]
- [6]. Huang B, Corbett JD. Ba3AlO4H: synthesis and structure of a new hydrogen-stabilized phase. J Solid State Chem. 1998;141:570–575. 10.1006/jssc.1998.8022 [DOI] [Google Scholar]
- [7]. Huang B, Corbett JD. Ba21Ge2O5H24 and related phases. A corrected structure type and composition for a Zintl phase stabilized by hydrogen. Inorg Chem. 1998;37:1892–1899. [Google Scholar]
- [8]. Hayward MA, Cussen EJ, Claridge JB, et al. The hydride anion in an extended transition metal oxide array: LaSrCoO3H0.7 . Science. 2002;295:1882–1884. 10.1126/science.1068321 [DOI] [PubMed] [Google Scholar]
- [9]. Bowman A, Claridge JB, Rosseinsky MJ. Anion composition control and magnetic short- and long-range order in transition metal oxide hydrides. Chem Mater. 2006;18:3046–3056. [Google Scholar]
- [10]. Helps RM, Rees NH, Hayward MA. Sr3Co2O4.33H0.84: an extended transition metal oxide-hydride. Inorg Chem. 2010;49:11062–11068. [DOI] [PubMed] [Google Scholar]
- [11]. Poulsen FW. Speculations on the existence of hydride ions in proton conducting oxides. Solid State Ionics. 2001;145:387–397. 10.1016/S0167-2738(01)00935-3 [DOI] [Google Scholar]
- [12]. Kobayashi Y, Hernandez OJ, Sakaguchi T, et al. An oxyhydride of BaTiO3 exhibiting hydride exchange and electronic conductivity. Nat Mater. 2012;11:507–511. [DOI] [PubMed] [Google Scholar]
- [13]. Goto Y, Tassel C, Noda Y, et al. Pressure-stabilized cubic perovskite oxyhydride BaScO2H. Inorg Chem. 2017;56:4840–4846. [DOI] [PubMed] [Google Scholar]
- [14]. Bang J, Matsuishi S, Hiraka H, et al. Hydrogen ordering and new polymorph of layered perovskite oxyhydrides: Sr₂VO4−xHx . J Am Chem Soc. 2014;136:7221–7224. 10.1021/ja502277r [DOI] [PubMed] [Google Scholar]
- [15]. Romero DF, Leach A, Möller JS, et al. Strontium vanadium oxide-hydrides: “square-planar” two-electron phases. Angew Chem Int Ed Engl. 2014;53:7556–7559. 10.1002/anie.201403536 [DOI] [PubMed] [Google Scholar]
- [16]. Tassel C, Goto Y, Kuno Y, et al. Direct synthesis of chromium perovskite oxyhydride with a high magnetic-transition temperature. Angew Chem Int Ed. 2014;53:10377–10380. 10.1002/anie.201405453 [DOI] [PubMed] [Google Scholar]
- [17]. Tassel C, Goto Y, Watabe D, et al. High-pressure synthesis of manganese oxyhydride with partial anion order. Angew Chem Int Ed Engl. 2016;128:9819–9822. 10.1002/ange.201605123 [DOI] [PubMed] [Google Scholar]
- [18]. Hayward MA, Green MA, Rosseinsky MJ, et al. Sodium hydride as a powerful reducing agent for topotactic oxide deintercalation: synthesis and characterization of the nickel(I) oxide LaNiO2 . J Am Chem Soc. 1999;121:8843–8854. 10.1021/ja991573i [DOI] [Google Scholar]
- [19]. Seddon J, Suard E, Hayward MA. Topotactic reduction of YBaCo2O5 and LaBaCo2O5: square-planar Co(I) in an extended oxide. J Am Chem Soc. 2010;132:2802–2810. 10.1021/ja910103d [DOI] [PubMed] [Google Scholar]
- [20]. Dixon E, Hadermann J, Ramos S, et al. Mn(I) in an extended oxide: the synthesis and characterization of La1−xCaxMnO2+δ (0.6 ≤ x ≤ 1). J Am Chem Soc. 2011;133:18397–18405. 10.1021/ja207616c [DOI] [PubMed] [Google Scholar]
- [21]. Romero FD, Coyle L, Hayward MA. Structure and magnetism of Sr3Co2O4Cl2 an electronically driven lattice distortion in an oxychloride containing square planar CoII centers. J Am Chem Soc. 2012;134:15946–15952. 10.1021/ja306683y [DOI] [PubMed] [Google Scholar]
- [22]. Tsujimoto Y, Tassel C, Hayashi N, et al. Infinite-layer iron oxide with a square-planar coordination. Nature. 2007;450:1062–1065. 10.1038/nature06382 [DOI] [PubMed] [Google Scholar]
- [23]. Tassel C, Pruneda JM, Hayashi N, et al. CaFeO2: a new type of layered structure with iron in a distorted square planar coordination. J Am Chem Soc. 2009;131:221–229. 10.1021/ja8072269 [DOI] [PubMed] [Google Scholar]
- [24]. Tassel C, Watanabe T, Tsujimoto Y, et al. Stability of the infinite layer structure with iron square planar coordination. J Am Chem Soc. 2008;130:3764–3765. 10.1021/ja800415d [DOI] [PubMed] [Google Scholar]
- [25]. Yamamoto T, Li Z, Tassel C, et al. Synthesis and thermal stability of the solid solution AFeO2 (A = Ba, Sr, Ca). Inorg Chem. 2010;49:5957–5962. [DOI] [PubMed] [Google Scholar]
- [26]. Seinberg L, Yamamoto T, Tassel C, et al. Fe-site substitution effect on the structural and magnetic properties in SrFeO2 . Inorg Chem. 2011;50:3988–3995. [DOI] [PubMed] [Google Scholar]
- [27]. Poltavets VV, Lokshin KA, Dikmen S, et al. La3Ni2O6: a new double T’-type nickelate with infinite Ni1+/2+O2 layers. J Am Chem Soc. 2006;128:9050–9051. 10.1021/ja063031o [DOI] [PubMed] [Google Scholar]
- [28]. Hadermann J, Abakumov AM, Adkin JJ, et al. Topotactic reduction as a route to new close-packed anion deficient perovskites: structure and magnetism of 4H-BaMnO2+x . J Am Chem Soc. 2009;131:10598–10604. 10.1021/ja903216d [DOI] [PubMed] [Google Scholar]
- [29]. Sakaguchi T, Kobayashi Y, Yajima T, et al. Oxyhydrides of (Ca, Sr, Ba)TiO3 perovskite solid solutions. Inorg Chem. 2012;51:11371–11376. [DOI] [PubMed] [Google Scholar]
- [30]. Yamamoto T, Yoshii R, Bouilly G, et al. An antiferro-to-ferromagnetic transition in EuTiO3–xHx induced by hydride substitution. Inorg Chem. 2015;54:1501–1507. [DOI] [PubMed] [Google Scholar]
- [31]. Yajima T, Kitada A, Kobayashi Y, et al. Epitaxial thin films of ATiO3–xHx (A = Ba, Sr, Ca) with metallic conductivity. J Am Chem Soc. 2012;134:8782–8785. 10.1021/ja302465c [DOI] [PubMed] [Google Scholar]
- [32]. Bouilly G, Yajima T, Terashima T, et al. Electrical properties of epitaxial thin films of oxyhydrides ATiO3–xHx (A= Ba and Sr). Chem Mater. 2015;27:6354–6359. 10.1021/acs.chemmater.5b02374 [DOI] [Google Scholar]
- [33]. Bouilly G, Yajima T, Terashima T, et al. Substrate-induced anion rearrangement in epitaxial thin films of LaSrCoO4−xHx . CrystEngComm. 2014;16:9669–9674. 10.1039/C4CE01268B [DOI] [Google Scholar]
- [34]. Hayashi K, Matsuishi S, Kamiya T, et al. Light-induced conversion of an insulating refractory oxide into a persistent electronic conductor. Nature. 2002;419:462–465. 10.1038/nature01053 [DOI] [PubMed] [Google Scholar]
- [35]. Hayashi K. Heavy doping of H– ion in 12CaO 7Al2O3 . J Solid State Chem. 2011;184:1428–1432. 10.1016/j.jssc.2011.04.008 [DOI] [Google Scholar]
- [36]. Kitada A, Kasahara S, Terashima T, et al. Highly reduced anatase TiO2−δ thin films obtained via low-temperature reduction. Appl Phys. Express. 2011;4:035801. 10.1143/APEX.4.035801 [DOI] [Google Scholar]
- [37]. Pussacq T, Kabbour H, Colis S, et al. Reduction of Ln2Ti2O7 layered perovskites: a survey of the anionic lattice, electronic features, and potentials. Chem Mater. 2017;29:1047–1057. [Google Scholar]
- [38]. Kobayashi Y, Li Z, Hirai K, et al. Gas phase contributions to topochemical hydride reduction reactions. J Solid State Chem. 2013;207:190–193. 10.1016/j.jssc.2013.09.006 [DOI] [Google Scholar]
- [39]. Hayashi K, Sushko PV, Hashimoto Y, et al. Hydride ions in oxide hosts hidden by hydroxide ions. Nat Commun. 2014;5:1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40]. Masuda N, Kobayashi Y, Hernandez O. Hydride in BaTiO2.5H0.5: a labile ligand in solid state chemistry. J Am Chem Soc. 2015;137:15315–15321. 10.1021/jacs.5b10255 [DOI] [PubMed] [Google Scholar]
- [41]. Mikita R, Aharen T, Yamamoto T, et al. Topochemical nitridation with anion vacancy-assisted N3–-/O2–-exchange. J Am Chem Soc. 2016;138:3211–3217. 10.1021/jacs.6b00088 [DOI] [PubMed] [Google Scholar]
- [42]. Izumi F, Momma K. 2011. Three-dimensional visualization of electron-and nuclear-density distributions in inorganic materials by MEM-based technology. In: IOP Conference Series: Materials Science and Engineering. Vol. 18 IOP Publishing; p. 022001 10.1088/1757-899X/18/2/022001 [DOI] [Google Scholar]
- [43]. Yoshizumi T, Kobayashi Y, Kageyama H, et al. Simultaneous quantification of hydride ions and electrons incorporated in 12CaO 7Al2O3 cages by deuterium-labeled volumetric analysis. J Phys Chem C. 2012;116:8747–8752. 10.1021/jp2106742 [DOI] [Google Scholar]
- [44]. Castro FJ, Meyer G. Thermal desorption spectroscopy (TDS) method for hydrogen desorption characterization (I): theoretical aspects. J Alloys Compd. 2002;330–332:59–63. 10.1016/S0925-8388(01)01625-5 [DOI] [Google Scholar]
- [45]. Bridges CA, Fernandez-Alonso F, Goff JP, et al. Observation of hydride mobility in the transition-metal oxide hydride LaSrCoO3H0.7 . Adv Mater. 2006;18:3304–3308. [Google Scholar]
- [46]. Lu X, Cheung NW, Strathman MD, et al. Hydrogen induced silicon surface layer cleavage. Appl Phys Lett. 1997;71:1804–1806. [Google Scholar]
- [47]. Sandim HRZ, Morante BV, Suzuki PA. Kinetics of thermal decomposition of titanium hydride powder using in situ high-temperature X-ray diffraction (HTXRD). Mater Res. 2005;8:293–297. [Google Scholar]
- [48]. Liu H, He P, Feng JC, et al. Kinetic study on nonisothermal dehydrogenation of TiH2 powders. Int J Hydrogen Energy. 2009;34:3018–3025. 10.1016/j.ijhydene.2009.01.095 [DOI] [Google Scholar]
- [49]. Yajima T, Takeiri F, Aidzu K, et al. A labile hydride strategy for the synthesis of heavily nitridized BaTiO3 . Nat Chem. 2015;7:1017–1023. [DOI] [PubMed] [Google Scholar]
- [50]. Endo T, Kobayashi T, Sato T, et al. High pressure synthesis and electrical properties of BaTiO3–xFx . J Mater Sci. 1990;25:619–623. 10.1007/BF00714085 [DOI] [Google Scholar]
- [51]. Ohta H, Sugiura K, Koumoto K. Recent progress in oxide thermoelectric materials: p-type Ca3Co4O9 and n-type SrTiO3 . Inorg Chem. 2008;47:8429–8436. [DOI] [PubMed] [Google Scholar]
- [52]. Kolodiazhnyi T. Insulator-metal transition and anomalous sign reversal of the dominant charge carriers in perovskite BaTiO3 − δ . Phys Rev B: Condens Matter Mater Phys. 2008;78:045107. 10.1103/PhysRevB.78.045107 [DOI] [Google Scholar]
- [53]. Page K, Kolodiazhnyi T, Proffen T, et al. Local structural origins of the distinct electronic properties of Nb-substituted SrTiO3 and BaTiO3 . Phys Rev Lett. 2008;101:205502. 10.1103/PhysRevLett.101.205502 [DOI] [PubMed] [Google Scholar]
- [54]. Wei Y, Gui H, Li X, et al. The effect of hydrogen ordering on the electronic and magnetic properties of the strontium vanadium oxyhydride. J Phys Condens Matter. 2015;27:206001. 10.1088/0953-8984/27/20/206001 [DOI] [PubMed] [Google Scholar]
- [55]. Katayama T, Chikamatsu A, Yamada K, et al. Epitaxial growth and electronic structure of oxyhydride SrVO2H thin films. J Appl Phys. 2016;120:085305. 10.1063/1.4961446 [DOI] [Google Scholar]
- [56]. Zhang Z, Zuo F, Wan C, et al. Evolution of metallicity in vanadium dioxide by creation of oxygen vacancies. Phys Rev Appl. 2017;7:034008. [Google Scholar]
- [57]. Yoon H, Choi M, Lim T-W, et al. Reversible phase modulation and hydrogen storage in multivalent VO2 epitaxial thin films. Nat Mater. 2016;15:1113–1119. [DOI] [PubMed] [Google Scholar]
- [58]. Shi J, Zhou Y, Ramanathan S. Colossal resistance switching and band gap modulation in a perovskite nickelate by electron doping. Nat Commun. 2014;5:1–9. [DOI] [PubMed] [Google Scholar]
- [59]. Lu N, Zhang P, Zhang Q, et al. Electric-field control of tri-state phase transformation with a selective dual-ion switch. Nature. 2017;546:124–128. 10.1038/nature22389 [DOI] [PubMed] [Google Scholar]
- [60]. Liu K, Hou Y, Gong X, et al. Orbital delocalization and enhancement of magnetic interactions in perovskite oxyhydrides. Sci Rep. 2016;6:1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61]. Tobías G, Beltrán-Porter D, Lebedev OI, et al. Anion ordering and defect structure in Ruddlesden-Popper strontium niobium oxynitrides. Inorg Chem. 2004;43:8010–8017. [DOI] [PubMed] [Google Scholar]
- [62]. Fuertes A. Prediction of anion distributions using Pauling’s second rule. Inorg Chem. 2006;45:9640–9642. [DOI] [PubMed] [Google Scholar]
- [63]. Pauling L. The principles determining the structure of complex ionic crystals. J Am Chem Soc. 1929;51:1010–1026. 10.1021/ja01379a006 [DOI] [Google Scholar]
- [64]. Marchand R, Pastuszak R, Laurent Y. Structure cristalline de Nd2AlO3N. Détermination de L’ordre oxygène-azote par diffraction de neutrons. Rev Chim. 1982;19:684–689. [Google Scholar]
- [65]. Morris DFC, Reed GL. Pauling L.Crystal radius of the hydride ion. J Inorg Nucl Chem. 1965;27:1715–1717. 10.1016/0022-1902(65)80037-9 [DOI] [Google Scholar]
- [66]. Kobayashi G, Hinuma Y, Matsuoka S, et al. Pure H– conduction in oxyhydrides. Science. 2016;351:1314–1317. 10.1126/science.aac9185 [DOI] [PubMed] [Google Scholar]