Systems Pharmacology Model of Gastrointestinal Damage Predicts Species Differences and Optimizes Clinical Dosing Schedules

Abstract

Gastrointestinal (GI) adverse events (AEs) are frequently dose limiting for oncology agents, requiring extensive clinical testing of alternative schedules to identify optimal dosing regimens. Here, we develop a translational mathematical model to predict these clinical AEs starting from preclinical GI toxicity data. The model structure incorporates known biology and includes stem cells, daughter cells, and enterocytes. Published data, including cellular numbers and division times, informed the system parameters for humans and rats. The drug‐specific parameters were informed with preclinical histopathology data from rats treated with irinotecan. The model fit the rodent irinotecan‐induced pathology changes well. The predicted time course of enterocyte loss in patients treated with weekly doses matched observed AE profiles. The model also correctly predicts a lower level of AEs for every 3 weeks (Q3W), as compared to the weekly schedule.

Study Highlights.

WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

☑ Preclinical models can be informative when studying GI toxicants; however, they often have different clinical presentation and time courses, diminishing relevance for clinical development of oncology agents.

WHAT QUESTION DID THIS STUDY ADDRESS?

☑ This study uses irinotecan as an exemplar to address whether a translational modeling approach could be used to predict clinical GI AEs and optimize dosing schedules to minimize clinical toxicity.

WHAT THIS STUDY ADDS TO OUR KNOWLEDGE

☑ Differences between time course and severity of preclinical and clinical chemotherapeutic AEs can be predicted based on differences in physiology between species. Optimal dosing schedules in the clinic can then be accurately predicted based on this understanding.

HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?

☑ The present study can be useful in the development of novel oncology agents with GI activity. Because the model separates between system‐specific parameters governing GI physiology and drug‐specific parameters governing the drug toxicity, the model and approach presented here could be extended to optimize novel therapies under development.

Both cytotoxics and targeted oncology therapeutics induce a range of on‐target toxicities, including hematological and gastrointestinal (GI) adverse events (AEs) that limit their clinical utility.1, 2, 3, 4 The rapid turnover of the intestinal epithelium from a pool of actively dividing cells may predispose the GI tract in particular to damage from a variety of antineoplastics, including DNA damage agents, antimitotics, and targeted agents that affect protein homeostasis, epigenetic regulation, and developmental pathways.2, 5

The incidence of severe GI toxicity often necessitates dosing schedules that use dosing holidays in order to achieve efficacious exposures while maintaining tolerability.2, 6 Many of these schedules were identified empirically in the clinic, through direct head‐to‐head comparison of efficacy and safety. Recent work has demonstrated the utility of quantitative pharmacology approaches to optimize dose and schedule with the potential to minimize lengthy and costly phase I/II trials.7, 8, 9 Mathematical models exist for other on‐target oncology toxicities, such as neutropenia, and they allow prediction of neutrophil counts in individual patients.10 These models have been used to predict the drug effect across species11 and optimize dosing schedules in the clinic.12

The GI tract is an ideal system for mechanistic modeling, as cell types and underlying biological processes are readily observed and measured. Cell position along the crypt‐villus axis correlates with cell type and function (Figure 1 a), allowing detailed studies into the cell types and dynamics.13 Mathematical models of GI cell dynamics have been developed and applied to understand cellular differentiation, colorectal cancer development, and irradiation damage and recovery.14, 15, 16, 17, 18 However, none of these efforts addresses the quantitative translation of preclinical toxicity of oncology agents to the clinical scenario.

Figure 1.

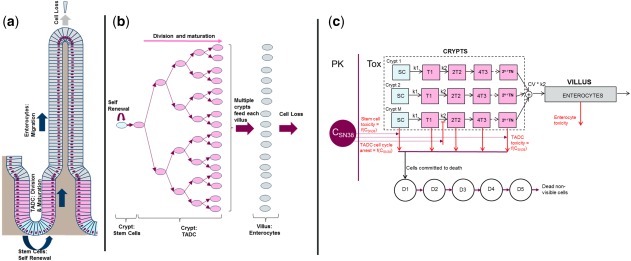
Schematic description of the renewal of the intestinal epithelium and of the mathematical model for drug‐induced GI (gastrointestinal) toxicity (TOX). (a) Schematic description of homeostasis in the intestinal epithelium wherein stem cells (blue) at the base of the crypt divide asymmetrically to give rise to transit amplifying daughter cells (TADCs, pink). TADCs undergo successive rounds of cell division and differentiate into enterocytes (gray). The proliferating cells (stem cells and TADCs) and the differentiated enterocytes, respectively, occupy the crypts and the villi. (b) The process of cell division and differentiation creates a steady flux of cells from the base of the crypts to the tips of villi from which mature enterocytes are shed. The organization of the intestinal epithelium is such that between 5 and 7 crypts reside at the base of each villus and together contribute to the enterocytes in the villus. (c) Schematic of the mathematical model. There are M crypts with stem cells (SCs) that divide with rate constant k1 and daughter cells (T1,T2) that divide with rate constant k2. There are multiple rounds of TADC division leading to multiple generations of daughter cells, with the final generation differentiating into enterocytes. The finite time taken for the migration of an enterocyte from the base of the crypt to the tip of the villus is captured via the transit of enterocytes through five hypothetical transit compartments (not shown here). In the model, drug‐induced GI toxicity is captured via the effect of the plasma concentration on cell death and proliferation (red lines). The finite time taken from the initiation of cell death to actual cell loss is captured by using the transit compartments D1‐D5. PK, pharmacokinetic; SN38, the active metabolite of irinotecan.

To address this gap, we developed a systems pharmacology model to describe the pathophysiology of GI damage induced by oncology agents. The model contains compound‐independent “system parameters” that enable us to capture the differences in GI homeostasis between rodents and humans. Specifically, we approach the problem of predicting GI damage by modeling irinotecan‐induced GI toxicity. Irinotecan is known to induce GI‐related AEs in the clinic19, 20 and induces apoptosis of cells resulting in villous atrophy in preclinical models.21 Here, we model the time course of crypt and villous atrophy in rats treated with irinotecan to gain insight into the mechanism of damage and to determine the potency of the compound. We then combine the compound parameters with the human GI system parameters to predict the effect of different clinical doses and schedules. We compare model predictions with clinical GI toxicity data to validate the approach. We then simulate a range of clinical schedules, many of which have not been tested extensively until this date, and rank schedules based on propensity to lower the extent of GI toxicity.

METHODS

Rat in vivo experiments

To assess the GI pathology time course following administration of irinotecan, groups of rats (CRL:Han Wistar) were treated with i.p. doses of irinotecan from 12.5–100 mg/kg. Toxicokinetic data was collected as part of a satellite study at various time points up to 24 hours postdose and analyzed for irinotecan and SN38 (the active metabolite of irinotecan) level (Supplementary Figure S1b). In the toxicity study, rats were euthanized at specific time points postdose and tissue was processed for pathology assessment. Crypts and villi in various sections of the small intestine were scored on a numbered categorical scale based on the severity of observed pathology findings described in Supplementary Table S1 and illustrated in Supplementary Figure S2. The data presented here are for pathology severity scores in the jejunum, which was the most sensitive in terms of the severity of the lesions. Similar observations and dose responses were observed for other regions of the small intestine (duodenum and ileum as well). Jejunal pathology scores were modeled as described in the following sections to quantify the potency of SN38 and to understand the mechanism underlying GI toxicity.

Description of the mathematical model

Cytotoxics, such as irinotecan and 5‐fluorouracil, can induce GI damage by acting on the rapidly proliferating cells in the intestinal crypts21, 22, 23 leading eventually to a reduction of the enterocytes in the villus. This villus atrophy is an important driver of chemotherapy‐induced diarrhea.2, 24 Here, we built a parsimonious mathematical model that would allow us to capture the key aspects of intestinal cell dynamics (Figure 1 a,b), fit rat data on crypt and villus atrophy, and translate the results into quantitative predictions of enterocyte loss and recovery kinetics in man. In the model (Figure 1 c; see Supplementary Methods for details), cell division in the crypts leads to a steady flux of cells out of the crypts and into the enterocytes. At steady state, the flux of cells into the base of each villus is driven by cell differentiation in the crypts, and is balanced with the rate of cell loss from the tip of the villus (Figure 1 c) leading to a constant number of crypt and villus cells. This parsimonious structure allows us to specify the steady‐state behavior of the system and the recovery following injury using a small set of system parameters (Table 1). Drug effects are incorporated via concentration‐dependent cell death or reduction in cell proliferation. Transit compartments are used to account for potential delays between initiation of cell death and visible crypt cell loss. Model simulations are started with steady state numbers for stem cells, transit amplifying daughter cells (TADCs) and enterocytes (Supplementary Table), and the model predicts the change in cell numbers as the function of time following dosing. The key assumptions in the mathematical model are summarized in Supplementary Table S4.

Table 1.

Model parametersa

Parameter	Rodent parameter		Human parameter
	Value	Source	Value	Source
No. of stem cells per crypt (system parameter)	10	Ref. 13	10	Ref. 13
Stem cell doubling rateb (system parameter)	1.5/day	Ref. 25	0.333/day	Ref. 13
TADC doubling rate (system parameter)	2/day	Ref. 25	0.75/day	Ref. 26
Number of TADC generationsc (system parameter)	4	Ref. 13	5	Ref. 13
Enterocyte shedding rated (system parameter)	0.45/day	Ref. 13, 27	0.25/day	Ref. 13, 27
Number of crypts feeding each villus (system parameter)	7	Ref. 13	7	Ref. 13
SN38 TADC kill parameterse: kdeath = Emax CH/(EC50H + CH)	Emax = 4.41/day EC50 = 3.1 µM H = 0.5	Rat data fit	Emax = 4.41/day EC50 = 7.8 µM H = 0.5	Rat fits & EC50man = EC50rat*furat/fuman
SN38 TADC arrest parametersf kprol = kprol0 * [1 ‐C/(EC50 + C)]	EC50 = 0.03 µM	Rat data fit	EC50 = 0.075 µM	Rat fits & EC50man = EC50rat*furat/fuman

EC₅₀, half‐maximal effective concentration; E_max, maximum effect; TADC, transit amplifying daughter cell.

^aSystem parameters and SN38 drug effect parameters needed to predict intestinal cell loss and recovery dynamics are shown. Additional parameters necessary for fitting rat pathology data are in Supplementary Table S2. ^bThe human value stem cell doubling time is reported to be on the order of 4–8 days in ref. 13. The value chosen here is based on the requirement of a shedding flux of ∼1,600 cells/villus/day reported in refs. 13 and 28. ^cThe higher value in man was necessary to match the villus shedding rate and the numbers of enterocytes and TADCs that have been reported.13 ^dThe shedding rates were set based on the reported differences in villus turnover in rodents and man, and the shedding fluxes and cell numbers noted in ref. 13. ^eThe death rate of TADCs is expressed as a hill function of the SN38 concentration, C; fu_rat = 9.4% based on internal data generated at AstraZeneca and fu_man = 4% based on ref. 29. ^fThe decrease in the TADC proliferation rate from the basal value kprol0 is a function of SN38 concentration C.

Parameter estimation for irinotecan‐induced GI toxicity in the rat

We applied the model to irinotecan‐induced GI toxicity data from rats to quantify GI toxicity potency of SN38 (the active metabolite of irinotecan). We first fit rat pharmacokinetic (PK) data for irinotecan and SN38 using a published rat PK model (Supplementary Figure S1). Here, we assume that the plasma concentrations of SN38 are a reasonable surrogate for drug exposure at the crypt and drive the cell toxicity using this quantity. It may also be possible that luminal concentrations of SN38 play a role as well. For instance, there is literature suggesting that the SN38 glucuronidation state in the GI lumen has a bearing on toxicity levels in preclinical models.30, 31 However, these data do not rule out increased lumen concentrations of SN38 through enterohepatic recirculation that leads to increases in plasma SN38 that then contributes to toxicity. It is likely that both lumen and plasma exposure of SN38 contribute to the intracellular exposure and total observed GI toxicity. Further, studies in rats show similar SN38 exposures in plasma and the GI tract32 and any differences that did exist between cellular and plasma concentration would be absorbed in the EC50 parameter. Given this ambiguity and the fact that we cannot directly measure the luminal concentrations of SN38, we use the plasma exposure to drive the toxicity.

We then tested various possibilities for the effect of SN38 on the different cell types. For each scenario, we used the model to predict the numbers of various cell types as a function of time following drug administration. Because the experimental readout for the extent of damage was categorical in nature (pathology scores), we linked the model outputs for the fractional loss of crypt cells and the fractional loss of enterocytes as a function of time to the observed crypt and villus pathology scores, respectively, via ordinal logistic regression (Supplementary Material). We then fit data on the incidence of various pathology grades as functions of dose and time to estimate the potency of SN38 for inducing cell death and cell cycle arrest. Final estimates for the compound‐specific parameters of SN38 are presented in Table 1 with confidence intervals determined using the profile likelihood method presented in Supplementary Figure S3 and Supplementary Table S2.

Simulations of time course of enterocyte loss in man

To generate predictions of enterocyte loss in humans, we applied the mathematical model with the human values for the system parameters and the SN38 compound potencies for cell death and cell cycle arrest (Table 1). These IC50 values were corrected for the 2.5‐fold higher levels of plasma protein binding in humans relative to that in rats (Table 1). Concentration profiles were generated using the human PK model and parameters for irinotecan and SN38 published in the literature.33 These concentrations were then combined with the human GI parameter values in Table 1 to generate predictions of fractional enterocyte loss for any given schedule. These predictions were then compared with the time courses of incidence of diarrhea in the clinic, as described in the Results section. A local sensitivity analysis was performed to determine the effect of various parameters on predictions of enterocyte loss (Supplementary Figure S4).

RESULTS

Modeling rat GI pathology data

The system‐specific parameters in the model were informed first, and based on data from rodent GI physiology from the literature. To inform the drug‐specific parameters in the GI model (Figure 1) we assessed the kinetics of GI pathology in rats exposed to various doses of irinotecan. We observed a clear temporal progression in the nature of intestinal findings with crypt apoptosis observed within 3 hours of dosing (Supplementary Figure S5). Crypt atrophy peaked at 2 days postdose and resolved by 4 days postdose, whereas villus atrophy peaked at 4 days postdose and resolved by 6 days postdose. This progression indicated that: (i) the findings are a result of compound‐induced changes in the crypt, which then lead to the loss of enterocytes in the villus; and (ii) the loss of crypt cells occurs in a delayed fashion following the exposure. We accounted for this in the model through a delay between the commitment to cell death and the actual loss of crypt cells (Methods section). We then tested various hypotheses for the effect of SN38, the active metabolite of irinotecan, on cells in the crypt.

Our observation was that apoptosis was concentrated in the upper crypt, and we, therefore, tested models in which SN38 induced death and arrest of the TADCs alone. Our results indicated that both TADC death and a cell cycle arrest were necessary to fit the data (Table 1). As seen in Figure 2, model predictions for crypt and villus atrophy following a 100 mg/kg dose (Figure 2 c,d) were in good agreement with the observed pathology time course (Figure 2 a,b). Further, the model was able to describe the pathology onset and recovery kinetics extremely well over the entire dose range tested (Figure 2 e,f), and model parameters could be estimated with good confidence (Supplementary Table S2 and Supplementary Figure S3).

Figure 2.

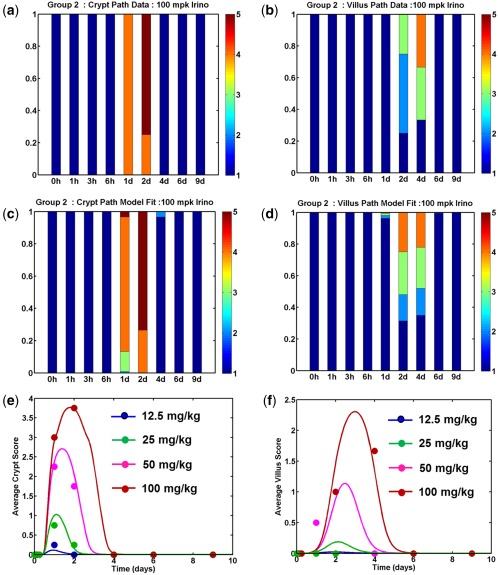
Model fits to rat histopathology data. Rats were given single intraperitoneal doses of irinotecan from 12.5–100 mg/kg and groups were terminated at various times following dosing to assess intestinal pathology. Data on the severity of crypt and villus pathology was fit using a mathematical model to determine the parameters for SN38‐induced toxicity. Observations (a,b) and model predictions (c,d) for the distribution of severity scores for crypt atrophy (a,c) and villus mucosal atrophy (b,d) for an irinotecan dose of 100 mg/kg. Each bar presents pathology severity scores (1 = NAD, 2 = minimal, 3 = mild, 4 = moderate, and 5 = marked) from 4–6 rats collected at that time point. Average severity scores for crypt atrophy (e) and villus atrophy (f) are plotted as a function of time for various doses. In each panel, markers represent the observed data, and the lines are model predictions.

Human predictions on a weekly dose schedule

We next replaced the rat system parameters with human parameters, corrected the compound potencies for protein binding differences (Table 1), and generated predictions of enterocyte loss for man. As a check of the model predictions, we compared the enterocyte loss predicted in man to clinical data on villus shortening following chemotherapy and found reasonable agreement in magnitude of loss and timing of recovery (Supplementary Figure S6). We then predicted the enterocyte loss time course for a dose of 125 mg/m² administered on a 4 week on 2 week off schedule (Figure 3 a), commonly referred to as the weekly schedule, which is the most common schedule that is used in the United States. On this schedule, the model predicts a peak level of enterocyte loss of ∼40% with a sustained level of loss observed for weeks 2–4 of dosing on both the first and second cycles. The predicted time course of enterocyte loss is in good agreement with the time course of diarrhea incidence (Figure 3 a, blue vs. brown lines). To better examine the relationship between enterocyte loss and diarrhea, we plotted the incidence of high‐grade diarrhea vs. the model‐predicted enterocyte loss on each day of dosing over 2 cycles (Figure 3 b). The data in Figure 3 b illustrate a steep relationship between the extent of enterocyte loss and the incidence of diarrhea, whereby grades 3 and 4 AEs increase rapidly beyond an enterocyte loss level of ∼30% (i.e., below a normalized enterocyte level of 0.7).

Figure 3.

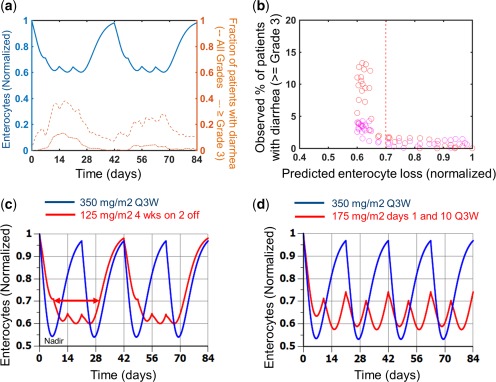
Model predictions of enterocyte loss for clinical schedules. (a) Model predictions of enterocyte loss for 125 mg/m² irinotecan given as a weekly 90‐minute infusion on a 4‐week on, 2‐week off schedule for a total of 12 weeks (2 cycles; solid blue line) are compared with the incidence of all grades of diarrhea (dashed brown line) and severe diarrhea (grade ≥3; dash‐dot brown line). (b) The percentage of patients with severe (grades 3 and 4) diarrhea on each study day of the trial is plotted against model predictions of enterocyte loss for that day. (c) Comparison of enterocyte loss predictions for a 350 mg/m² once every 3 weeks (Q3W; 1‐on/2‐off) schedule (blue line) with a 125 mg/m² 4‐on/2‐off schedule (red line). The doses used in these simulations were 325 mg/m² and 95 mg/m², respectively, for the blue and red lines, to account for the actual delivered dose in the clinical study. (d) Comparison of enterocyte loss predictions for a 350 mg/m² once every 3 weeks schedule (blue line) with 175 mg/m² delivered on days 1 and 10 on an every 3 week cycle (red line). The doses used in these simulations were 315 mg/m² and 168 mg/m², respectively, for the blue and red lines to account for the actual delivered dose in the clinical study. The nadir (point of maximal enterocyte loss) and the duration of time for which the enterocyte loss exceeds 30% are indicated on panel a for illustration. The blue regimens in panels c and d with less frequent dosing had lower incidence of late onset diarrhea than the red regimens.

Comparison of model to clinical irinotecan dosing schedules

A key question is whether the model is able to distinguish between the levels of toxicity observed with alternate clinical schedules of irinotecan. To address this, we generated predictions of enterocyte loss for schedules that have been tested in a head‐to‐head manner in clinical trials. In Figure 4 a we compare predictions for the weekly schedule that is currently used in the United States with a 350 mg/m² “once in 3 week” schedule that is used in Europe. These two schedules have similar dose intensities averaging between 80 and 120 mg/mg²/week but differ in the number of consecutive doses delivered in a given cycle. A large phase III trial has shown that the European trial has a lower incidence of late onset diarrhea than the weekly schedule.20

Figure 4.

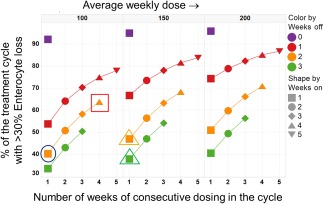
Simulations of enterocyte loss for various irinotecan schedules. The percentage of the treatment duration with >30% enterocyte loss is plotted for various schedules. Results are shown for 3 different average weekly dose levels of 100 mg/m², 150 mg/m², and 200 mg/m². The x‐axis denotes the total number of consecutive weeks of dosing in a cycle, whereas the markers and lines within each panel are color‐coded based on the number of weeks of dose holiday within the cycle (purple = continuous, red = 1 off, orange = 2 off, and green = 3 off). As an illustration, the points encircled by a blue circle and a red square in the panels for the 100 mg/m²/week average dose, represent results for a 300 mg/m² 1 week on 2 weeks off and 150 mg/m² 4 weeks on 2 weeks off schedules. These are roughly in line with the schedules that are currently applied in Europe and the United States, respectively. The orange and green triangles in the 150 mg/m²/week panel represents results for a 450 mg/m² 1‐on/2‐off schedule and a 600 mg/m² 1‐on/3‐off schedule, respectively. The results shown here were generated by simulating the model for a duration of 12–15 weeks, as appropriate to ensure that at least 2 to 3 cycles were simulated for each schedule.

Predictions indicate that the once in 3 week schedule would have a slightly lower nadir (maximal level of enterocyte loss) and almost identical average enterocyte loss over the treatment duration. However, simulation suggests that the European schedule would result in significantly lower time with >30% enterocyte loss (Figure 4 a, Supplementary Table S5). This metric (duration with >30% enterocyte loss) was evaluated due to our weekly schedule analysis (Figure 3), in which there was significant increase in all‐grade clinical observations when enterocyte loss was predicted to be >30%. Our comparison of the European and weekly schedules (Figure 4 a) also suggests that more sustained levels of enterocyte loss would translate to a greater number of patients with GI AEs during the course of the treatment, and that the maximal level of enterocyte loss (the nadir) is less important in this regard.

We additionally generated simulations to better understand the results reported in ref. 34, in which they tested the European schedule against an atypical schedule of 175 mg/m² delivered on days 1 and 10 every 21 days. The model prediction indicated a more sustained level of enterocyte loss for this schedule with a greater duration spent at level >30% loss over the treatment as well as a higher average level of enterocyte loss for this schedule (Figure 4 b, Supplementary Table S5). Together, these results suggest that schedules with more sustained enterocyte loss would translate to a greater AE occurrence in the population.

Simulations to identify optimal schedules

Next, we used the model to examine a range of different irinotecan schedules, including ones that have not been extensively tested in the clinic. For the comparisons in Figure 4, we fixed the average weekly dose delivered (dose density) and simulated a range of dose‐fractionated schedules to see if any would be expected to be optimal. By varying the number of consecutive weeks of dosing (weeks on, x axis) and the duration of the dose holiday (weeks off, colored markers) between cycles, we generated schedules in which the same average weekly dose of say 100 mg/m²/week was delivered as a sharp burst (400 mg/m² 1‐on/3‐off) or in a more spread out dosing paradigm (150 mg/m² 4‐on/2‐off). Predictions for the duration of the treatment with >30% enterocyte loss are shown in this figure. In Figure 4, results representative of the United States and European schedules are highlighted with the red square and the blue circle, respectively. The model predicts a more sustained level of enterocyte loss for schedules in which the dose is more evenly spread out across the cycle. Focusing in on an average weekly dose of 100 mg/m² (left panel) the model predicts a lower level of toxicity for a 400 mg/m² 1‐on/3‐off schedule compared to the European schedule of 300 mg/m² given 1‐on/2‐off. Importantly, the predictions indicate that a 150 mg/m²/week intensity – a higher dose intensity than what is currently used – may be delivered with a level of toxicity comparable to existing regimens if administered on a 1‐on/2‐off (450 mg/m² 1‐on/2‐off) or a 1‐on/3‐off (600 mg/m² 1‐on/3‐off) schedule. In this regard, we note that although a dose of 350 mg/m² 1‐on/2‐off was deemed to be the maximum tolerated dose in the European studies,35 higher doses have been effectively administered in other settings with careful management.36, 37 There have been no reported studies with a 1‐on/3‐off schedule, and evaluation of this option from both a safety and efficacy perspective may be warranted.

DISCUSSION

Gastrointestinal toxicity remains a major obstacle for oncology drug development, frequently limiting the dose for both cytotoxic compounds and targeted therapies. Historically, these toxicities have been mitigated through palliative treatments,2 or through modifications to dose and schedule, with the latter being optimized in the clinic by testing of alternative schedules in phase I or phase II cohorts. Preclinical models of GI toxicity have not frequently been utilized, as there are differences in the manifestation of GI findings, as well as differences in the timescale of damage and recovery.

In the present work, we present a quantitative pharmacology approach to model the GI toxicity of irinotecan. Rather than using a black‐box PK/pharmacodynamic (PD) approach, we developed a mechanistic model that accounts for the underlying biology.38 The model was fit to preclinical measurements of irinotecan effects in rats and was able to translate these findings into human GI toxicity kinetics. Most notably, the model was correctly able to predict both the time course of chemotherapy‐induced villous shortening as well as the time course of irinotecan‐induced diarrhea based purely on known mechanistic differences between the species. Further, based on the relationship between enterocyte loss and diarrhea score, the model was also able to suggest a correct ordering between various schedules that had been tested head‐to‐head in the clinic. Finally, the model was used to explore alternate schedules in addition to those tested clinically, with a finding that dosing holidays predict for greater total density, as measured by dose per month.

Although any decision about an optimal dosing schedule to be utilized in the clinic needs to consider and balance both efficacy and safety, the analysis done in this manuscript suggests that the increase in dose holidays may lead to increased tolerability. This is in contrast with the data on efficacy, which suggests that while the United States and European schedules have different tolerability profiles, the similar total dose density led to similar levels of efficacy.20

In constructing the model of GI toxicity, we find that differences between time scales of GI toxicity in man and rats can be explained through mechanistic differences in time scales of GI turnover and cell counts. These differences are evident when comparing predictions in which human PK is combined with rodent system parameters (a traditional PK/PD approach; see Supplementary Figure S7) rather than using human system parameters, as in Figure 3. Importantly, the translation between species is still possible even though the clinical observations are different between the rat and man because the model is based on the underlying effects on crypt and villous pathology, an effect shared by both species.

In fitting the model, we identified that neither cell death nor cell arrest alone would explain the results and that a combination of both effects was needed to reproduce the time course of GI damage observed in vivo. This is not entirely unexpected, as double stranded breaks in DNA, like those elicited by treatment with SN38, can lead to both transient cell cycle arrest followed by apoptosis. A sensitivity analysis of the clinical predictions (Supplementary Figure S4) revealed that the cell death parameters played a more important role in dictating the predicted extent of enterocyte loss.

In contrast to the translational approach for neutropenia from rat to man, which incorporates differences between species obtained from in vitro potency data, we find that for irinotecan these were not necessary. As other compounds are modeled and new in vitro GI toxicity assays become available, these data could be incorporated. It may eventually be possible to incorporate in vitro GI toxicity parameters directly in the model structure presented here, allowing for direct in vitro to in vivo extrapolation, bypassing species differences between the rat and man.

Although the present work is focused on irinotecan‐induced GI toxicity, the underlying model structure is built on data derived from normal gastrointestinal physiology. In this way, it provides a natural separation between parameters relating to the biology and parameters relating to drug effects on crypt cells. Similar work has shown that such systems pharmacology approaches can be expanded to include multiple compounds with the same model structure to capture the underlying physiology.10, 39 Because of this, the model presented here may be applicable to prediction of GI toxicities for a wider variety of oncology compounds that have an effect on cell cycle or survival. We should note that a very different set of model assumptions and structure would likely be needed to capture other types of GI toxicity, such as secretory diarrhea. Future work may be able to go beyond making translational predictions for other antineoplastic agents, and could also extend this model so that it can be applied directly to clinical data as is common practice with hematopoietic toxicities.10 In addition, we have focused on modeling a median typical human GI response and implicitly considered population variability by examining the relationship between enterocyte loss and the likelihood of an AE. Extension of the model from a typical response to a population response may be enabled through more detailed individual patient measurements with additional compounds.

Although the model applied in this manuscript was developed on a preclinical toxicological species, future work may enable in vitro data collected in GI organoids or 3D models to be translated directly to AEs. We hope that a model, such as the one presented here, would provide a solid foundation for scaling the cell number, turnover, and sensitivity observed in vitro into clinical effects following a similar paradigm as that presented for preclinical to clinical translation.

Conflict of Interest

The authors are employed by AstraZeneca and RES Group, as disclosed in the affiliations.

AUthor Contributions

J.T.M. and H.S. wrote the manuscript. J.T.M., H.S., and A.C. designed the research. J.T.M., H.S., A.C., J.B., P.S., J.T., and P.J. performed the research. H.S., J.T., and P.J. analyzed the data.

Supporting information

Supplmentary Material Contents

Supporting Information