Using Full Matching to Estimate Causal Effects in Nonexperimental Studies: Examining the Relationship Between Adolescent Marijuana Use and Adult Outcomes

Abstract

Matching methods such as nearest neighbor propensity score matching are increasingly popular techniques for controlling confounding in nonexperimental studies. However, simple k:1 matching methods, which select k well-matched comparison individuals for each treated individual, are sometimes criticized for being overly restrictive and discarding data (the unmatched comparison individuals). The authors illustrate the use of a more flexible method called full matching. Full matching makes use of all individuals in the data by forming a series of matched sets in which each set has either 1 treated individual and multiple comparison individuals or 1 comparison individual and multiple treated individuals. Full matching has been shown to be particularly effective at reducing bias due to observed confounding variables. The authors illustrate this approach using data from the Woodlawn Study, examining the relationship between adolescent marijuana use and adult outcomes.

In nonexperimental studies, researchers are often interested in examining the effect of some event or treatment (e.g., substance use) on an outcome (e.g., educational attainment). This is done by comparing individuals who experienced that event or treatment (e.g., substance users) to individuals who did not (e.g., nonusers). In experimental studies with random assignment, treatment and control groups are similar on all background characteristics—observed and unobserved—as a consequence of the randomization, allowing for straightforward comparison of outcomes. In contrast, in nonexperimental studies, the treatment and comparison individuals may differ significantly on background characteristics—some that are observed and others that may be unknown. For example, substance users and nonusers are likely to be different on characteristics such as family history of drug use as well as on individual behaviors such as aggression. Thus, any difference in outcomes between the two groups may be due to these background covariates or to the treatment itself (i.e., substance use). The question then is how best to compare substance users with nonusers to clearly separate the effects of substance use from any of these other differences in background characteristics.

Matching methods, such as nearest neighbor propensity score matching, are increasingly popular techniques for controlling for observed confounding variables when estimating causal effects in nonexperimental studies. The goal of matching methods is to ensure that the distributions of observed covariates in the treatment and comparison groups are similar, replicating what would have occurred had the treatment been randomly assigned, at least with respect to the observed covariates. Although regression has often been used to adjust for background differences and estimate causal effects in nonexperimental studies, it relies heavily on modeling assumptions (e.g., linearity) that may not be valid and can be especially problematic if the treatment and comparison groups are very different on background covariates.

Propensity score matching, followed by regression adjustment on the matched sample, can often be a stronger approach for estimating causal effects than is regression on an unmatched sample. Specifically, the benefits of propensity score matching include (a) reduced bias in the estimation of causal effects using nonexperimental data, partly through reduced reliance on the outcome model itself (e.g., violations of the assumption of a normal distribution or linearity); (b) intuitive and easy explanation to nontechnical audiences; and (c) diagnostics that are easy to understand and implement.

Randomized experiments offer a clear advantage over nonrandomized studies when estimating a treatment effect in that randomization is designed to ensure similarity of treated and control individuals on all covariates—observed and unobserved. In non-experimental studies, researchers must assume that there are no unobserved differences between the treatment group and a comparison group after conditioning on the observed covariates. This assumption is known in various fields as unconfounded treatment assignment, no hidden bias, or no unobserved confounding and is made in nearly all nonexperimental studies that estimate causal effects. The aim in this article, and with propensity score matching methods in general, is to control for the observed covariates as well as possible and assume that there are no additional differences between the groups on unobserved covariates. In addition, matching on the observed covariates also matches on the unobserved covariates, in so much as they are correlated with those that are observed. Analyses can also be done to assess the sensitivity of the results to the existence of an unobserved confounder related to both treatment assignment and the outcome (e.g., Rosenbaum & Rubin, 1983a).

Propensity Score Matching

The propensity score, defined as the conditional probability of receiving the treatment, given the observed background covariates, was initially defined by Rosenbaum and Rubin (1983b). Since then, propensity scores have been used in a variety of fields, including psychology (Foster, 2003; Harder, Morral, & Arkes, 2006; Hill, Waldfogel, Brooks-Gunn, & Han, 2005), education (Barnard, Frangakis, Hill, & Rubin, 2003; Behrman, Cheng, & Todd, 2004; Rosenbaum, 1986), sociology (DiPrete & Gangl, 2004; Morgan & Harding, 2006; H. Smith, 1997), economics (Dehejia, 2005; Imbens, 2004; J. Smith & Todd, 2005), and health care (Christakis & Iwashyna, 2003; Perkins, Tu, Underhill, Zhou, & Murray, 2000; Rubin, 2004; Weitzen, Lapane, Toledano, Hume, & Mor, 2004).

The motivation behind propensity scores can be understood by considering an idealized situation in which the treatment and comparison groups are similar on all background characteristics (as is attained in a randomized experiment).¹ In nonexperimental studies, researchers might aim to find for each treated individual a comparison individual who looks exactly the same as the treated individual on all observed pretreatment covariates.² Thus, assuming no hidden bias, as discussed above, any difference in outcomes within these pairs could be attributed to the treatment and not to any other differences between the treated and comparison individuals. However, in applied situations, this exact pair matching is generally infeasible because there are usually too few potential comparison individuals and too many covariates to find an exact match.

Propensity scores facilitate this matching by collapsing the set of observed background covariates into a single summary measure (the propensity score), representing an estimate of the probability of receiving the treatment. Then, instead of trying to find treated and comparison individuals with the same values of all covariates, one can match each treated individual to a comparison individual with a similar value of the propensity score. Rosenbaum and Rubin (1983b) showed that, if treatment assignment is independent of the potential outcomes given the full set of covariates (treatment assignment is unconfounded), then it is also independent of the potential outcomes given the propensity score. This implies that the benefits of matching on all covariates individually are also attained when matching on the propensity score. In other words, within a set of treated and comparison individuals with similar propensity scores, the treatment and comparison groups will also have similar distributions of all the covariates that went into the propensity score. The success of the matching procedure is then examined by comparing the distributions of the covariates in the resulting matched treatment and comparison groups.

Rosenbaum and Rubin (1983b) discussed three primary ways of using the propensity score: (a) for matching, such as by selecting k comparison individuals for each treated individual (often, k = 1); (b) for subclassification, in which groups of individuals with similar propensity scores are formed; and (c) as a predictor variable in regression adjustment.³ In fact, propensity scores work best when approaches (a) or (b) are combined with regression adjustment on the matched samples (Ho, Imai, King, & Stuart, 2007; Rubin, 1973; Rubin & Thomas, 2000), which is the approach we take here.

In their simplest forms, each of these three approaches has a drawback. With respect to simple k:1 nearest neighbor matching (Approach a), many potential comparison individuals may be discarded and not used in the analysis. Whether or not this bias/variance trade-off (i.e., reduced bias due to the selection of the most comparable individuals but increased variance because relatively few individuals are used) is worth it will depend on particular research problems (H. Smith, 1997).⁴ Treated individuals may also not be matched sometimes, which can lead to bias in estimating and difficulties in interpreting the effect, as it may no longer reflect the effect for all treated individuals (Rosenbaum & Rubin, 1985).

With respect to simple subclassification (Approach b), for example, creating five or six subclasses on the basis of the propensity score (Rosenbaum & Rubin, 1984), there are often still some differences in the observed characteristics of the treated and comparison individuals within each subclass, which can lead to substantial bias. In addition, it is sometimes difficult to determine how many subclasses to form, without clear guidance on that matter (Du, 1998). The standard advice is five or six subclasses (Rosenbaum & Rubin, 1984), but with larger sample sizes, more subclasses may work better. The number of subclasses can be selected by optimizing the resulting covariate balance, but the process of comparing the balance on each covariate across different numbers of subclasses can be time consuming. In addition, it is not always clear which number of subclasses leads to the best balance overall because of trade-offs in balance across different covariates. If the goal is to reduce differences in the propensity score itself, full matching (described below) will automatically determine the optimal number of subclasses.

Finally, with respect to regression adjustment (Approach c), simply including the propensity score in a regression model of the outcome without discarding or down-weighting individuals who are dissimilar on background characteristics (as is frequently done in the medical literature; see Weitzen et al., 2004) is the least ideal use of propensity scores. This is because the resulting inferences still rely on the regression model assumptions, such as linearity, which may not be valid, and the method does not make use of the propensity score’s ability to create well-matched samples (Rubin, 2004).⁵ In other words, if there are large covariate differences between the treated and comparison groups, then there will also be large differences in the propensity score distribution, leading to extrapolation and reliance on the regression model. In this case, the propensity score has not helped to ensure that similar individuals are compared. In fact, simply replacing all of the individual covariates by the propensity score in the outcome regression model may be worse than including the individual covariates in the model and not using the propensity score at all, as propensity scores are not designed for reducing dimensions in that way. Finally, as Rubin (2004) discussed, propensity scores are ideal for setting up the “design” of a nonexperimental study; moving straight to regression modeling of the outcome with the propensity score as a predictor does not incorporate the idea of the careful design of a nonexperimental study.

Full Matching

The method illustrated in this article, full matching, overcomes these disadvantages. It can be thought of as a compromise between the k:1 matching and subclassification approaches. Full matching, first developed by Rosenbaum (1991) and illustrated by Hansen (2004), uses all available individuals in the data by grouping the individuals into a series of matched sets (subclasses), with each matched set containing at least 1 treated individual (who received the treatment of interest) and at least 1 comparison individual (who did not). Full matching forms these matched sets in an optimal way, such that treated individuals who have many comparison individuals who are similar (on the basis of the propensity score) will be grouped with many comparison individuals, whereas treated individuals with few similar comparison individuals will be grouped with relatively fewer comparison individuals. The method is thus more flexible than traditional k:1 matching, in which each treated individual is required to be matched with the same number of comparison individuals (k), regardless of whether each individual actually has k good matches (Ming & Rosenbaum, 2000).

We first illustrate the use of full matching with a very simple example, shown in Table 1. In this example there are 4 treated individuals to be matched to 5 comparison individuals on the basis of their family’s annual income (in the $10,000s). We defined the distance between 2 individuals to be the absolute value of the difference in their incomes; individuals with a small distance between them are considered to be good matches. A “greedy” 1:1 nearest neighbor matching algorithm would simply look at each treated individual one at a time (starting with “A”) and pick the best match for each, yielding the following matched sets (pairs, in this case): {Ab}, {Bd}, {Ce}, and {Dc}. Defining the total or global distance as the sum of the distances of all pairs of treated and comparison individuals within each matched set, across all matched sets, yields a global distance of 17 (0 + 1 + 1 + 15). An “optimal” 1:1 nearest neighbor matching algorithm finds the best pair matches to minimize that global distance measure. In that case, the matched pairs would be {Ab}, {Bc}, {Cd}, and {De}, for a global distance of 13 (0 + 2 + 10 + 1). Both of these algorithms lead to 1 comparison individual not being matched. In contrast, by not restricting each matched set to have 1 treated and 1 comparison individual, full matching uses all individuals and leads to better matched samples. Full matching would lead to the following matched sets: {Aab}, {Bcd}, and {CDe}. All nine units are placed into a matched set, and the global distance is just 7 (2 + 0 + 2 + 1 + 1 + 1). We thus see that full matching enables the creation of well-matched sets that also use all available individuals.

Table 1.

Hypothetical Data to Illustrate Matching Methods

Treated individuals		Comparison individuals
Individual	Income (in $10,000)	Individual	Income (in $10,000)
A	42	a	44
B	35	b	42
C	24	c	37
D	22	d	34
		e	23

Next, we provide details of full matching by applying this approach to a study estimating the effect of adolescent marijuana use on adult outcomes. Because marijuana use cannot be experimentally assigned and there is much speculation over whether associated consequences are a result of the marijuana use or of differences in background characteristics, this provides an ideal application of a propensity score method.

In this example, we extended the analyses of Green and Ensminger (2006) to examine the continued effects of heavy adolescent marijuana use on outcomes in middle adulthood. Green and Ensminger (2006), analyzing longitudinal data collected from the Woodlawn Study, used 1:1 nearest neighbor matching to estimate the effect of heavy adolescent marijuana use on outcomes in young adulthood, including high school dropout status, employment status, marital status, parenting status, and drug use in adulthood, separately for men and women. In this example, we focused on middle adulthood socioeconomic attainment, as this is one area in which there may be long-term effects. Numerous studies have shown adolescent marijuana use to be associated with more immediate education effects (see Lynskey & Hall, 2000, for a review). These education effects may then go on to impair employment status and other indicators of socioeconomic attainment much later in life. Others have found an association of early marijuana use with low occupational expectations, unemployment, and job mobility in early adulthood, although it is unclear whether these effects are causal (Brook, Adams, Balka, & Johnson, 2002; Brook, Ritcher, Whiteman, & Cohen, 1999; Fergusson & Horwood, 1997; Green & Ensminger, 2006; Kandel, Davies, Karus, & Yamaguchi, 1986; Kandel & Yamaguchi, 1987). We also examined drug use in middle adulthood, as such use may be one explanation if there are effects on the socioeconomic status indicators. Again, we conducted analyses separately for men and women. We matched 78 male heavy marijuana users and 44 female heavy marijuana users to male and female participants who were not heavy marijuana users, respectively, matching on background characteristics collected in first grade: family history of substance use, maternal education, childhood family income and poverty, and first-grade teachers’ ratings of aggression, shyness, underachievement, immaturity, and inattention.

Method

The Woodlawn Study

Data were from the Woodlawn Study, a prospective, longitudinal study of African Americans. All first graders in the Woodlawn neighborhood of Chicago were assessed in 1965–1966 (N = 1,242; 13 families declined participation). When this study began, Wood-lawn was a socially disadvantaged, inner-city community in Chicago. First-grade teachers and mothers provided data. Follow-ups with those who remained in the Chicago area were conducted in adolescence (when participants were 16–17 years of age; N = 705), young adulthood (when participants were 32 years of age; N = 952), and middle adulthood (when participants were 42 years of age; N = 833). (For additional details on the Woodlawn Study population, see Crum et al., 2006; Ensminger, 1990; Ensminger, Kellam, & Rubin, 1983; Kellam, Branch, Agrawal, & Ensminger, 1977; and Kellam, Brown, Rubin, & Ensminger, 1983.)

The sample size for the analysis was 481: 265 female participants and 216 male participants. This represented 39% of the original sample. The reduction in sample size was mainly due to the targeting of only a subset for the adolescent assessment. Mortality, inability to locate sample members, and refusals added to the attrition. Attrition analyses revealed that those missing the adolescent assessment did not differ on gender, mother’s education, poverty, family income, or family type during first grade or on having an official criminal record or adult alcohol or drug dependence. For those missing the assessment during middle adulthood, missingness was not related to maternal education, poverty status, adolescent marijuana use, or educational attainment in young adulthood.

Measures

Table 2 presents the means, standard deviations, and coding for all study variables. We show these statistics for the total sample and separately for male and female participants.

Table 2.

Means and Standard Deviations for Study Variables

Variable	Female participants (N = 265)		Male participants (N = 216)		Total (N = 481)
	M	SD	M	SD	M	SD
Independent/treatment variable
Heavy adolescent marijuana use (0 = used fewer than 20 times or have not used, 1 = used 20 times or more)	0.17	.37	0.36	.48	0.25	.44
Matching variables
Maternal history of substance use (0 = no, 1 = yes)	0.09	.29	0.13	.33	0.11	.31
Mothers’ years of schooling (0 = no formal schooling, 18 = over 18 years of schooling)	10.55	2.40	10.46	2.47	10.51	2.43
Family income for 1965–1966 (1 = under $2,000, 10 = $10,000+)	4.95	2.76	4.78	2.83	4.88	2.79
Poverty status (0 = no, 1 = yes)	0.49	.50	0.55	.50	0.52	.50
First-grade classroom adaptation (0 = adapting, 3 = severely maladapting)
Teacher rating of underachievement	0.55	.92	0.67	.92	0.61	.93
Teacher rating of aggression	0.34	.73	0.67	1.02	0.49	.89
Teacher rating of shyness	0.37	.72	0.51	.88	0.43	.80
Teacher rating of immaturity	0.53	.91	0.69	1.01	0.60	.96
Teacher rating of inattention	0.41	.84	0.70	1.05	0.54	.95
Outcome variables
Educational attainment (1 = dropout, 2 = GED, 3 = high school graduate, 4 = some college/associate’s degree, 5 = college graduate)	3.39	1.21	3.04	1.23	3.23	1.23
Household income (1 = less than $1,000, 18 = $100,000+)	10.10	4.74	10.22	4.97	10.15	4.84
Poverty status (0 = no, 1 = yes)	0.28	.45	0.21	.41	0.25	.43
Employed at 42 years of age (0 = unemployed, 1 = employed)	0.74	.44	0.75	.43	0.75	.43
Had an unemployment bout (0 = no, 1 = yes)	0.59	.49	0.59	.49	0.59	.49
Marijuana use (0 = no, 1 = yes)	0.25	.43	0.34	.48	0.29	.46
Cocaine use (0 = no, 1 = yes)	0.14	.35	0.23	.42	0.18	.39
Heroin use (0 = no, 1 = yes)	0.04	.20	0.08	.27	0.06	.23
Drug abuse (0 = no, 1 = yes)	0.10	.10	0.15	.36	0.12	.33

Independent/treatment variable

Marijuana use of 20 times or more during adolescence (heavy use) was the independent or treatment variable (see Green & Ensminger, 2006).

Matching variables

Maternal lifetime history of drug or alcohol use was self-reported by mothers in 1975–1976. Mothers who reported any use of marijuana, cocaine, heroin, hallucinogens, inhalants, stimulants, amphetamines, sedatives, or tranquilizers or regular use of alcohol were coded as having a history of drug or alcohol use. For maternal education, mothers reported the number of years of schooling they had completed. For income, mothers reported their total household income before taxes for the previous year. We determined poverty status using U.S. Census Bureau estimates for the poverty threshold for 1966 on the basis of household income and size reported by mothers during the first assessment. First-grade teachers rated each child on their social adaptational status on a 4-point scale in five areas: underachievement, aggression, shyness, immaturity, and inattention using the Teacher’s Observation of Classroom Adaptation (TOCA; see Kellam et al., 1977, for reliability and validity establishment).

Outcome variables

All outcome measures were collected at the time of the interview during middle adulthood (when participants were 42 years of age). Education level was determined by asking a series of questions about the last time participants had formal schooling and any degrees obtained. Total household income for the previous year was self-reported. Poverty level was assessed on the basis of the federal government definition for 2002, and we took into account total household income and size. Current employment status was determined by asking respondents a single question about their work status the previous week. We coded those responses reporting temporary absences from employment (e.g., vacation, illness) as employed. Unemployment in middle adulthood was assessed by asking respondents whether they had had any period of unemployment during the past 10 years.

Drug use during middle adulthood was assessed by asking respondents whether they had used marijuana, cocaine, or heroin, among other substances, during the past 10 years. Those who reported any illicit drug use during the past 10 years were asked about drug abuse symptoms. Drug abuse was assessed using a module modeled after the one developed at the University of Michigan for the National Comorbidity Survey from the Composite International Diagnostic Interview (CIDI; Kessler & Üstün, 2004), which was developed to assess disorders in an interview format.

Details of Full Matching

The first step in implementing full matching was to generate propensity scores using the observed pretreatment background characteristics. This was done using logistic regression with heavy marijuana use as the outcome and the observed characteristics as predictors. For each individual, all the covariates were then summarized by a single number: the propensity score, which was the predicted probability of being treated (a heavy user in our example) generated from the logistic regression. Next, we used these propensity scores to “match” individuals. To do this, we first needed to define how we would determine whether a given treated individual (a heavy user; i) and a given comparison individual (nonheavy user; j) were similar. To measure this similarity, we used the difference in the logit transformations of their propensity scores as a measure of the distance between them:

$${\mathrm{\delta }}_{ij}\equiv \mid \text{logit}(\widehat{e}(X_i)-\text{logit}(\widehat{e}(X_j))\mid ,$$

where ê(X_k)was the estimated propensity score for individual k. This is similar to the distance measure used in the example in Table 1. The difference here is that, because there were many covariates, we used the difference in propensity score values (as a summary of all of the covariates) instead of the difference in just one covariate (income, in that example).⁶ Small values of δ_ij indicate good matches (individuals with similar propensity scores); large values indicate individuals who should not be matched to each other.⁷

Full matching divides the full sample of all treated and all comparison individuals into a series of matched sets (S), such that each set will contain either 1 treated individual and multiple comparison individuals or 1 comparison individual and multiple treated individuals. The ratio of treated:comparison individuals in each matched set will depend on the relative number of treated and comparison individuals with similar propensity scores. Full matching minimizes the sum of the distances between all pairs of treated and comparison individuals within each matched set, across all matched sets, written mathematically as follows:

$$\sum _{i\in T,S(i)>0}\sum _{j\in C,S(i)=S(j)}{\mathrm{\delta }}_{ij}.$$

This is similar to the global distance measure described for the example in Table 1. The details of how full matching minimizes this global distance were given by Rosenbaum (1991) and Hansen (2004); the methods are related to network flow theory.

One problem with full matching is that it sometimes leads to matched sets with widely varying ratios of treated to comparison individuals, which can lead to large variance of the resulting effect estimates. This is similar to survey sampling, in which having unequal selection probabilities leads to greater variance in comparison with all individuals having the same probability of selection and to the problem sometimes encountered when one uses propensity scores as inverse probability weights, in which a few individuals may get extremely large weights (Schafer & Kang, 2006). In an example in Hansen’s (2004) work, the matched sets ranged from 6 treated and 1 comparison individual to 1 treated and 161 comparison individuals! We thus used (and demonstrated the advantages of) a constrained full matching procedure described by Hansen (2004) that limits the ratio of treated to comparison individuals in each matched set. In particular, we limited the ratio of treated:comparison individuals to be no less than half and no more than double what it was in the original data set. So, for example, for female participants, for whom for every treated individual there were approximately 5 comparison individuals, we allowed the matched sets generated by constrained full matching to have treated:comparison ratios ranging from 2:5 to 1:10. Another way to avoid large discrepancies in the ratio of treated:comparison individuals in each subclass is to discard individuals who are outside the range of the propensity scores of the other group. In other words, discard comparison individuals with propensity scores lower than the lowest propensity score in the treatment group (and/or discard treatment individuals with propensity scores higher than the highest propensity score in the comparison group). More complicated approaches can also identify areas within the overall propensity score distribution without overlap, termed common support (Heckman, Ichimura, & Todd, 1997, 1998). These methods can be particularly helpful when there are many comparison individuals with propensity scores very different from those in the treated group, as reported by Dehejia and Wahba (1999).

Measures of Effectiveness of Matching Procedures

The primary goal in any matching procedure is to reduce bias in the estimated treatment effect. Thus, the primary way by which researchers examine the performance of each procedure is by the resulting covariate balance in the matched treatment and comparison groups. A high degree of similarity between the treatment and comparison groups on covariates should lead to small bias in the estimated treatment effect. A secondary goal is to obtain a precise estimate of that treatment effect—given two methods with similar bias, researchers would select the one with lower variance (and thus lower mean square error). Thus, there are two primary diagnostics researchers use to judge the adequacy of full matching and compare it to other matching procedures: (a) measures of covariate balance after matching and (b) a measure of the relative precision of the resulting impact estimates obtained after matching.

In terms of measures of balance, researchers primarily use the standardized bias to examine how similar the matched treatment and comparison groups are. The standardized bias for a particular covariate is defined as the weighted difference in means, divided by the standard deviation in the original full comparison group (Rubin, 2001). The weights used depend on the matching method and are defined below. Standardized biases of less than 0.25 imply the groups are well matched (Ho et al., 2007). T tests, Mantel-Haensel tests, and Kolmogorov-Smirnov tests are also commonly used as measures of balance. In addition, we also examined graphical displays of the propensity score and quantile-quantile plots of the covariates. See Ho, Imai, King, and Stuart (2006, 2007) for more information on diagnostics for matching methods.

To compare the relative precision of impact estimates calculated after two different matching methods (Method 1 and Method 2), we used a formula from Hansen (2004) that computed the ratio of the standard deviations of impact estimates obtained using the two matched samples. A ratio equal to 1 implies that the estimates have the same precision; a ratio of less than 1 implies the precision from Method 1 is greater than that from Method 2; a ratio greater than 1 implies the precision resulting from Method 1 is less than that from Method 2.

Analysis of Data After Full Matching

There are two primary ways to estimate treatment effects (e.g., the effects of heavy marijuana use) after doing full matching: fixed-effects regression and weighting. The fixed-effects regression explicitly estimates an effect for each matched set, and then these effects are averaged to obtain an overall effect. The matched set-specific effects are obtained by fitting a regression model with terms that allow both the treatment and comparison group means to vary across matched sets. In technical terms, this is done by fitting a regression with a fixed effect for each matched set and an interaction term between treatment and each matched set. This can be written as follows: Y_i = τ_S(i) + Δ_S(i) + ε_i, where E(ε) = 0, Cov(ε) = σ²I, σ² < ∞ (Hansen, 2004). The Δ_s(i) are the matched set fixed effects (i.e., the matched set-specific comparison group means), and the τ_S(i) are the treatment comparison differences in each matched set (i.e., the matched set-specific treatment effects). An overall effect is calculated by averaging the matched set-specific effects (τ_S(i)), weighted by the number of treated individuals in each matched set. See Hansen (2004) for more details. This approach will be particularly useful if there is interest in examining the heterogeneity of treatment effects across the matched sets, as an effect is calculated for each matched set.

In our application, with approximately 78 matched sets for male participants and 44 for female participants and relatively few individuals in each (see below), we instead used a weighting approach. Treated individuals received a weight of 1. Comparison individual i in matched set S(i) received a weight proportional to the number of treated individuals in set S(i) divided by the number of comparison individuals in set S(i). The sum of the comparison individuals’ weights was scaled to equal the total number of matched comparison individuals. For example, in a matched set with 1 treated individual and 2 comparison individuals, the 2 comparison individuals will each get a weight proportional to one half. In a matched set with 5 treated and 2 comparison individuals, the 2 comparison individuals each get a weight proportional to five halves. (See the documentation of the MatchIt [Version 2.2–11] software package [Ho et al., 2006] for more details.) These weights are then used in the calculation of balance measures and in the regression models of the outcome variables. With a linear model, the overall impact estimates are the same as those obtained from the fixed-effects regression model described above. In our example, we exported the data to Stata 9 (Release 9; StataCorp, 2005) so that we could provide marginal effects for ease of interpreting coefficients. We used weighted logistic regression for the binary outcomes of employment, unemployment, and poverty status and the four adult drug outcomes. We used weighted linear regression for income and education. All regression models include the matching variables as predictors in order to further adjust for small differences remaining in the matched samples after matching (Ho et al., 2007).

Results

Success of Full Matching Method

Because of potential sex interactions, all analyses were done separately for male and female participants, and so we discuss each in turn. For each group (male and female participants), we first estimated the propensity score using a logistic regression predicting treatment status (heavy marijuana user; nonheavy marijuana user) given the set of matching variables. In particular, the predictors used in our initial propensity score models for male and female participants were maternal history of substance use, maternal education, family income, poverty status, and five first-grade teacher ratings: aggression, shyness, inattention, immaturity, and underachievement. We then performed a series of diagnostic checks (similar to those described by Dehejia, 2005) to assess this simple model. These checks involved examining the balance of the square of each covariate, as well as all two-way interactions of covariates within each of six propensity score subclasses. We then included any squared terms or interactions that were imbalanced in multiple subclasses in a subsequent propensity score model. If the subsequent model improved balance overall, this more complex model was used. If it did not improve overall balance, the simpler propensity score model was used instead. For female participants, the simple propensity score model with no interactions led to the best balance. For male participants, the best propensity score model also included each of the teacher rating measures squared.

Next, we implemented a series of matching procedures to demonstrate and compare the performance of various matching approaches in terms of the resulting balance and precision from each. As discussed by Rubin (2001), because the outcome variable was not used in the matching process or the diagnostics of that process, we were able to try a variety of matching methods and to select the approach that led to the best balance in the resulting matched samples. The five matching methods examined were as follows:

1. Optimal nearest neighbor matching (1:1). For each heavy marijuana user, this method selected the nonheavy marijuana user with the closest propensity score while minimizing the global distance across all pairs. Thus, 44 female heavy users were matched with 44 female nonheavy users, and 78 male heavy users were matched with 78 male nonheavy users. This can be thought of as forming 44 matched sets for female participants (and 78 for male participants), in which each matched set consists of one heavy user and one nonheavy user.

2. Optimal nearest neighbor matching (2:1). This method is the same as Method 1, except that two matches were selected for each heavy marijuana user. Hence, the 44 female heavy users were matched with 88 female nonheavy users, forming 44 matched sets, with 1 heavy user and 2 nonheavy users in each set. This kind of 2:1 matching was not possible for the 78 male heavy users, as there were not 156 male participants who were nonheavy users.

3. Simple subclassification. Six matched sets (or subclasses) were formed using quantiles of the heavy marijuana users’ propensity score distribution. In this method, each matched set had approximately the same number of heavy marijuana users (between 7 and 8 for female participants; 13 for male participants) but varying numbers of nonheavy users (between 18 and 66 for female participants; between 9 and 45 for male participants).

4. Full matching. We used the original full matching procedure described above. For female participants, this created 43 matched sets, with between 1 and 2 heavy users and between 1 and 23 nonheavy users in each set. For male participants, this created 59 matched sets, each with between 1 and 3 heavy users and between 1 and 7 nonheavy users.

5. Constrained full matching. This is the same as Method 4, except that the ratio of marijuana users to nonheavy users in each matched set was restricted to be no less than half and no more than double what it was in the full data set. Thus, for female participants, constrained full matching created 44 matched sets, with 1 heavy user and between 1 and 10 nonheavy users in each set. For male participants, constrained full matching resulted in 78 matched sets, with 1 heavy user and between 1 and 4 nonheavy users in each set.

Methods 3 through 5 all resulted in matched samples that contained all available individuals (all male participants or all female participants); the difference between the methods was in how individuals were placed in the matched sets, and thus the implicit weights that the individuals received. All matching methods were implemented using the R package MatchIt (Ho et al., 2006; See Appendix A in the supplemental materials for details). Tables 3 and 4 summarize the results of these five matching procedures as applied to the data for female and male participants, respectively. The summary statistics include, for the full data set and for each method, the standardized bias for the propensity score and for each matching variable and the precision compared to a 1:1 match and a 2:1 match. (The comparison with a 2:1 match could not be done for male participants, as there were not enough male nonheavy users).

Table 3.

Comparison of Standardized Biases After Matching: Female Participants

Variable	All female participants	Method 1	Method 2	Method 3	Method 4	Method 5
Propensity score	0.38	0.02	0.03	0.06	0.02	0.06
Maternal substance use history	−0.11	0.09	0.00	0.10	0.02	−0.03
Maternal years of schooling	0.07	0.10	0.08	0.07	0.08	0.03
Family income	−0.03	0.06	0.00	0.18	0.01	0.02
Below poverty threshold	0.12	0.05	0.02	0.18	0.00	0.02
Teacher rating of underachievement	0.02	0.10	0.02	0.15	−0.09	0.00
Teacher rating of aggression	0.23	0.00	0.00	0.13	−0.03	0.04
Teacher rating of shyness	0.14	0.06	0.06	0.10	−0.10	0.00
Teacher rating of immaturity	0.18	0.04	0.03	0.10	−0.02	−0.01
Teacher rating of inattention	0.17	0.12	0.04	0.13	−0.04	0.03
Precision relative to a 1:1 match		1.00	0.82	0.80	0.86	0.81
Precision relative to a 2:1 match		1.22	1.00	0.92	0.99	0.93
N	265	88	132	265	265	265

Note. Standardized bias is defined as the weighted difference in means divided by the standard deviation in the full group of participants who were not heavy marijuana users. Numbers in bold indicate standardized biases that decreased in comparison with the original sample. Methods are as follows: 1 = 1:1 optimal nearest neighbor matching; 2 = 2:1 optimal nearest neighbor matching; 3 = six subclasses; 4 = full matching; and 5 = constrained full matching.

Table 4.

Comparison of Standardized Biases After Matching: Male Participants

Variable	All male participants	Method 1	Method 2	Method 3	Method 4	Method 5
Propensity score	0.44	0.08		0.06	−0.01	0.08
Maternal substance use history	−0.12	0.08		0.12	−0.01	−0.02
Maternal years of schooling	−0.05	−0.01		0.16	0.04	0.06
Family income	−0.18	−0.11		0.20	−0.12	−0.04
Below poverty threshold	0.14	0.16		0.14	0.15	0.05
Teacher rating of underachievement	−0.03	−0.06		0.14	−0.16	−0.10
Teacher rating of aggression	0.24	0.00		0.13	−0.04	−0.02
Teacher rating of shyness	−0.09	0.01		0.08	−0.03	−0.02
Teacher rating of immaturity	0.07	0.05		0.10	−0.01	0.03
Teacher rating of inattention	0.13	0.00		0.13	−0.06	−0.04
Precision relative to a 1:1 match		1.00		0.95	1.15	0.95
N	216	156		216	216	216

Note. Standardized bias is defined as the weighted difference in means divided by the standard deviation in the full group of participants who were not heavy marijuana users. Numbers in bold indicate standardized biases that decreased in comparison with the original sample. Methods are as follows: 1 = 1:1 optimal nearest neighbor matching; 2 = 2:1 optimal nearest neighbor matching (could not be done for male participants because there were not twice as many male participants who were not heavy marijuana users as there were male participants who were heavy users); 3 = six subclasses; 4 = full matching; 5 = constrained full matching.

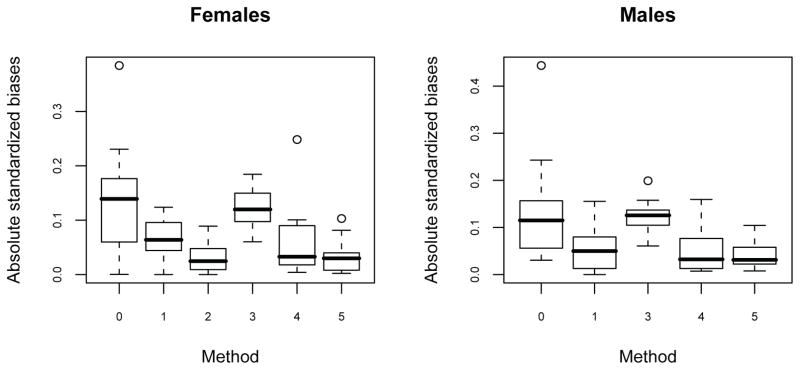
For female participants, all matching methods resulted in large reductions in standardized bias (Table 3). However, 2:1 matching and constrained full matching appeared to produce the most closely matched samples, with consistently small standardized biases across all of the observed covariates. This can also be seen in Figure 1, with the constrained full matching having absolute standardized biases closest to zero. Constrained full matching was the only method that led to a reduction in absolute standardized bias for every variable considered. Constrained full matching has the additional benefit of using all individuals in the original data set, and thus has slightly higher precision relative to 2:1 matching, as shown by the relative precision value of less than 1.

Figure 1.

Boxplots of absolute standardized biases for covariates shown in Tables 3 and 4 before and after matching. Absolute standardized bias on each variable was defined as the absolute value of the weighted difference in the means of matched samples divided by the standard deviation in the full group of participants who were not heavy marijuana users. Constrained full matching led to the smallest absolute standardized biases. Methods are as follows: 0 = no matching—original data; 1 = 1:1 optimal nearest neighbor matching; 2 = 2:1 optimal nearest neighbor matching (could not be done for male participants because there were not twice as many male nonheavy marijuana users as there were male heavy users); 3 = six subclasses; 4 = full matching; and 5 = constrained full matching.

A similar result was seen for male participants, as shown in Table 4 and the right side of Figure 1, in that most methods do a good job at reducing standardized biases, although the smaller number of available male nonheavy users meant that the overall reductions were not as large as they were for the female participants. Again, we see that the constrained full matching led to the most reductions in standardized bias, reducing the absolute bias in all but one of the covariates.

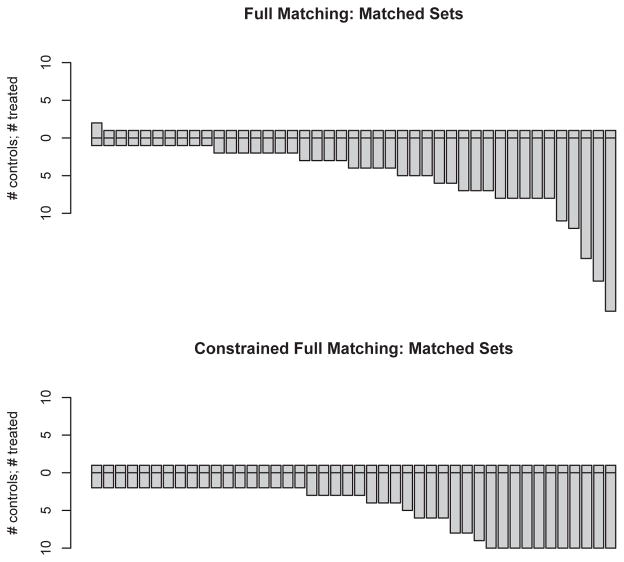
Figure 2 shows, for female participants, the number of treated and comparison individuals in the matched sets created by full matching and by constrained full matching. This figure illustrates an advantage of full matching or constrained full matching in comparison with simple 1:1 or 2:1 matching. In Figure 2, each pair of bars (above and below the zero line) represents one matched set for female participants. Bars that go up (positive numbers) show the number of heavy marijuana users in the matched set; bars that go down (negative numbers) show the number of nonheavy marijuana users in the matched set. With either full matching method, each treated individual was essentially their own matched set, with varying numbers of comparison matches.⁸ In contrast, with 1:1 or 2:1 matching, every treated individual was given a fixed number of matches, regardless of how many good matches each treated individual actually had. Full matching and constrained full matching selected the best treated individuals to get more than one match on the basis of how many similar comparison individuals there were.

Figure 2.

Number of treated and comparison individuals in matched sets created by full matching and constrained full matching (female participants).

However, as shown in Figure 2, there was also an advantage of constrained full matching over standard full matching. The ratio of treated:comparison individuals (heavy users:nonheavy users) in each matched set was much more variable for full matching than it was for constrained full matching. The higher variability in these ratios was also reflected by the fact that the precision was higher for constrained full matching than for standard full matching (Table 3). Thus, both methods led to similar bias reduction (in terms of standardized biases), but constrained full matching yielded more precise estimates. The plot for male participants was similar (not shown).

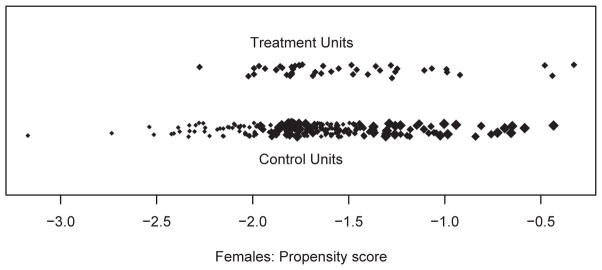
The assigned weights for the constrained full matching are illustrated in Figure 3. Figure 3 shows, for female participants, a jitter plot of the propensity scores for the heavy marijuana users and the nonheavy users: each point represents one individual, and the size of the point reflects that individual’s weight in the matched sample. All treated individuals received a weight of 1. For comparison individuals, the weight depended on how many treated and comparison individuals had similar propensity scores, and thus how many treated and comparison individuals were in that individual’s matched set. For example, comparison individuals with small propensity scores got small weight because there were no treated individuals with propensity scores that low (i.e., there were very few treated units in the matched sets in that region). This jitter plot can also be used to examine the general overlap of the propensity scores in the two groups; in this case there was substantial overlap, which is a good setting for estimating causal effects (the jitter plot for male participants, not shown, looks similar). We would be concerned if there were many treated individuals with propensity scores outside the range of the comparison individuals’ propensity scores, or vice versa; some of the common support methods might be helpful if that were the case.

Figure 3.

Jitter plot of propensity scores for female participants. The size of each point reflects the weight given to that individual as a result of constrained full matching; larger points reflect more weight. Propensity score is given on a linear scale.

Results of Analyses After Matching

Table 5 presents the marginal effects found when regression analyses for the long-term socioeconomic and drug consequences of adolescent marijuana use were run using the weights generated by constrained full matching. As shown, after matching, heavy marijuana use during adolescence increased the risk for poor educational attainment for both male and female participants. Female participants who were heavy adolescent marijuana users also were at greater risk of having an unemployment bout in the past 10 years (between the ages of 32 and 42 years), having lower household income, living below the poverty line, and using marijuana in midlife (between the ages of 32 and 42 years). Male participants who were heavy adolescent marijuana users were at greater risk for using marijuana (marginally significant, p = .080), cocaine, and heroin between the ages of 32 and 42 years and of meeting criteria for drug abuse.

Table 5.

Effects of Heavy Adolescent Marijuana Use on Middle Adulthood Outcomes After Constrained Full Matching

Outcome	Male participants			Female participants
	Marginal effect	95% CI	p	Marginal effect	95% CI	p
Educational attainment	−0.446	−0.763, −0.129	.006	−0.589	−0.941, −0.238	.001
Being currently employed	0.097	−0.025, 0.219	.120	−0.059	−0.205, 0.087	.431
Unemployment bout in past 10 years	−0.050	−0.190, 0.090	.483	0.204	0.058, 0.350	.006
Household income	−0.293	−1.571, 0.985	.653	−1.929	−3.348, −0.509	.008
Poverty status	−0.020	−0.138, 0.098	.741	0.220	0.053, 0.387	.010
Marijuana use in past 10 years	0.122	−0.014, 0.259	.080	0.317	0.158, 0.476	≤.001
Cocaine use in past 10 years	0.238	0.115, 0.361	<.001	0.128	−0.003, 0.259	.055
Heroin use in past 10 years	0.073	0.004, 0.141	.039a	0.017	−0.023, 0.057	.395
Drug abuse	0.125	0.020, 0.229	.020	0.091	−0.010, 0.193	.078

Note. All analyses match on and adjust for all matching variables. CI = confidence interval.

^aTeacher rating of shyness was dropped from the predictors because it perfectly predicted heroin use for female participants (i.e., no heroin users were rated as shy).

Discussion

Using Full Matching

Many questions of substantive interest in developmental psychology cannot be addressed using experiments, and researchers are left to deal with the complexities of nonexperimental data. Propensity score matching methods in general provide a way to adjust for observed confounders in nonexperimental studies, ensuring that comparisons are done on individuals as similar as possible on all observed characteristics except the treatment of interest. However, simple matching methods may not always yield the best matched samples and do not always make use of all of the available data. This example illustrates the potential usefulness of a relatively new method, full matching, which may overcome those limitations in some examples, such as the one given here. In practice, we recommend that researchers follow the model presented here of considering a variety of matching methods and selecting the one that yields the most closely matched samples. Full matching has the potential to produce matched samples with very good balance and thus may often be a good choice, particularly if there is desire to use data on all individuals available. However, although full matching is designed to produce the best balance on the propensity score, it is important to also examine the resulting balance on individual covariates. Although we found that full matching did lead to the best matched samples, this may not always be the case.

This work also leads to suggestions for further methodological advances that would make it easier for researchers to determine which matching method is likely to yield the best matched samples in any particular study. First, work should be done to identify the scenarios in which particular matching methods (e.g., full matching, simple subclassification, or 1:1 matching) are likely to work the best. This could help researchers narrow down the large selection of matching methods to a smaller set likely to yield the greatest reduction in bias. Second, the comparison of the results of matching methods would be facilitated by better diagnostics of matching methods. Measures that collapse all of the multidimensional covariates into meaningful and relevant summary statistics are crucial. We showed simple standardized biases and diagnostic plots in this article; however, a variety of diagnostics exist, and there is ongoing debate regarding the best choices (Imai, King, & Stuart, in press). Thus, although matching methods in general, and full matching in particular, have the potential to reduce observed confounding in nonexperimental studies, more work is needed to fully understand the best ways of using these methods.

Impacts on Adult Outcomes

The results from our application suggest that heavy marijuana use during adolescence does continue to have effects in middle adulthood, 25 years later. Having used propensity scores and full matching to control for a wide range of pretreatment background characteristics found in the literature to be associated with adolescent drug use (Hawkins, Catalano, & Miller, 1992), we are able to minimize the concern that the association was spurious or due to a common cause. However, although we were able to capture much of the confounding, it is important to keep in mind that we may not have captured all possible confounding, as we were limited to the variables collected by the study over 35 years ago and the precision of their measurement. To make causal statements, we must assume that there are no differences between heavy marijuana users and nonheavy users on unobserved characteristics, given the characteristics that we do observe. An extension of this work could examine the sensitivity of the results to some unobserved difference between the heavy users and nonheavy users that may explain some of the impact on adult outcomes (Rosenbaum & Rubin, 1983a).

As expected, we found participants who were heavy marijuana users when they were adolescents had lower educational attainment than participants who were light users or who did not use marijuana when they were adolescents. (Note that only 8% of individuals furthered their education between young adulthood and middle adulthood, making this less of a distal effect.) For female participants, we also found effects on socioeconomic indicators, including an increased risk of being in poverty, having a lower household income at the age of 42 years, and having an unemployment bout between the ages 32 and 42 years. For male participants, we did not find heavy adolescent marijuana use to be related to any of the socioeconomic indicators in midlife. These results suggest that socioeconomic effects of early marijuana use do continue into adulthood for women. These gender differences may be because of the greater stigma experienced by women who use drugs than by men who use drugs (Copeland, 1997) or perhaps because of the fewer opportunities for unskilled women than for men.

For both male and female participants, we found an increased risk of drug use (marijuana for female participants and cocaine and heroin for male participants) and abuse (male participants only) in middle adulthood among heavy adolescent marijuana users. This seems particularly problematic due to the seriousness of the drug, its problematic use, or the timing of the use (occurring at an age when drug use has typically ended). Further, this finding may explain adult consequences in other areas. For example, this increased risk of adult marijuana use for women should be explored as a potential explanatory mechanism for adult socioeconomic effects.

In summary, full matching using propensity scores is a useful tool for estimating causal effects of a wide range of factors that are not experimentally controlled, such as substance use, voluntary social programs, a particular diet, or parenting practices. This work should prompt further use of this method, as well as the development of other methods for controlling observed confounding in nonexperimental studies.