Robust estimation of encouragement-design intervention effects transported across sites

Abstract

We develop robust targeted maximum likelihood estimators (TMLE) for transporting intervention effects from one population to another. Specifically, we develop TMLE estimators for three transported estimands: intent-to-treat average treatment effect (ATE) and complier ATE, which are relevant for encouragement-design interventions and instrumental variable analyses, and the ATE of the exposure on the outcome, which is applicable to any randomized or observational study. We demonstrate finite sample performance of these TMLE estimators using simulation, including in the presence of practical violations of the positivity assumption. We then apply these methods to the Moving to Opportunity trial, a multi-site, encouragement-design intervention in which families in public housing were randomized to receive housing vouchers and logistical support to move to low-poverty neighborhoods. This application sheds light on whether effect differences across sites can be explained by differences in population composition.

1 Introduction

Multi-site interventions are common in public health, public policy, and economics. Do we expect an intervention effect in one site to be the same as the intervention effect in another site? In many cases, we would answer “no” for one of two reasons. First, there could be differences in site-level variables related to intervention design/implementation or contextual variables, like the economy, that would modify intervention effectiveness. Such variables suggest that the intervention either is not the same or does not work the same in the two sites. Second, there could be differences in person-level variables—population composition—across sites that also modify intervention effectiveness. This could cause intervention effects to differ across sites even if the interventions are structured and implemented in an identical fashion.

That intervention effects may differ for sites with different population composition motivates previous work on transportability (Pearl and Bareinboim, 2011). Transportability (which has been discussed as generalizability (Cole and Stuart, 2010) and external validity (Rothwell, 2005)) is the idea of applying the results of an experiment in one setting/population to a target setting/population based on the observed characteristics of that target population. Pearl and Bareinboim have formalized this goal by developing transport formulas and enumerating the necessary assumptions associated with each transport formula (Pearl and Bareinboim, 2011).

These transport formulas can be applied to predict the effect of an intervention in a target population based on the observed composition of that population and intervention results from the original population. This prediction can be useful for researchers wanting to estimate the potential long-term effects of an intervention in a new site based on long-term follow-up results in an original site. An example of this would be predicting effects from the expansion of home-visiting programs for low-income pregnant women under the Affordable Care Act based on long-term follow-up results from the Nurse Family Partnership trials (Eckenrode et al., 2010).

Transported predictions may also be useful in determining the extent to which differences in intervention effects across sites can be explained by differences in population composition. An example of this, which we use to motivate this work, is from the Moving to Opportunity (MTO) trial (Kling et al., 2007). MTO is a five-site, encouragement-design intervention in which families in public housing were randomized to receive housing vouchers and logistical support to move to low-poverty neighborhoods. To date, there has been no quantitative examination of the underlying reasons for differences in MTO’s effects across sites (Orr et al., 2003).

We are not aware of any literature on the development of estimators incorporating transport formulas. However, there is a related literature on generalizing results from randomized controlled trials. The simplest of these methods is post-stratification or nonparametric direct standardization (Miettinen, 1972), but this method breaks down when there are many population characteristics to control for or if those characteristics are continuous. Previous model-based approaches have involved Horvitz-Thompson weighting, propensity score matching, and principal stratification (Stuart et al., 2011; Cole and Stuart, 2010; Frangakis, 2009). These are important contributions but may be limited by their reliance on correct model specification. In addition, with the exception of principal stratification, we know of no extensions of these methods to encouragement-design interventions. Model-based approaches for such an intervention design would involve models relating 1) site (or population) to covariates, 2) instrument to exposure conditional on covariates and relevant effect modifiers, and 3) exposure to outcome conditional on covariates and relevant effect modifiers.

We address this research gap by first extending Pearl and Bareinboim’s transport formulas to the case of an encouragement design intervention such as MTO. Next we develop and evaluate targeted maximum likelihood estimators (TMLEs) for transporting three estimands: the intent-to-treat average treatment effect (ITTATE), the average causal effect of the exposure on the outcome, ignoring the instrument (henceforth referred to as the EACE), and the complier average causal effect (CACE) (Imbens and Rubin, 1997). This estimation approach has several advantages. First, it is robust to multiple model misspecification scenarios. Second, TMLE is efficient. Third, we target marginal population quantities, which are most relevant to policy and program leaders, while allowing for potential effect modification across a high-dimensional vector of covariates. Fourth, these estimators can easily incorporate machine learning algorithms, thereby reducing bias due to model misspecification.

The paper is organized as follows. In Section 2, we introduce notation and define the structural causal model. In Sections 3–5, we develop a TMLE for each of the three estimands of interest. The ITTATE is discussed in Section 3, the EACE is discussed in Section 4, and the CACE is discussed in Section 5. A reader who is interested in one of the three estimands can skip the other two sections without compromising understanding. For each estimand, we present the identification result, robustness properties, influence function-based inference, and steps for computing the TMLE. In Section 6, we present results from a simulation study in which we demonstrate consistency, efficiency and robustness of each TMLE estimate under different model specification scenarios and degrees of practical positivity violations. In Section 7, we apply these methods to the MTO example. Section 8 concludes.

2 Notation and Structural Causal Model

We observe the following vector of data for each of n participants: O = (S, W, A, Z, S × Y). S is an indicator of the site; S = 1 for the site for which we have long-term follow-up data and S = 0 for the site for which we do not have follow-up data. W is a vector of covariates, the distribution of which depends on S. A is a binary instrument, which is randomized. Z is the binary exposure of interest. Y is the outcome of interest, which we only observe for those in the site with long-term outcome data (S = 1).

We assume that each participant’s data vector O is an independent, random draw from the unknown true data distribution P₀ on O. We use a subscript 0 to denote values under P₀. In contrast, P is any probability distribution in the statistical model, $ℳ$, where $ℳ$ is the collection of probability distributions under which an estimand is identifiable and is defined for each of the estimands that follow. Values under a particular P are given without a subscript for brevity. Estimates are denoted with subscript n.

The objective is to develop a TMLE to estimate each of three target parameters: the ITTATE = ψ₁, the EACE = ψ₂, and the CACE = ψ₃. TMLE is a semiparametric estimation approach that has been described previously (van der Laan and Rubin, 2006). It results in a substitution estimator for a particular parameter of interest. TMLEs can be implemented as regular asymptotically linear semiparametric estimators that are locally efficient in their class. This often results in double or multiple robustness, meaning that the estimator is still consistent under certain types of model misspecification. Its consistency and efficiency properties derive from the fact that it solves the efficient influence curve estimating equation. Thus, to develop a TMLE, we first need to identify the parameter of interest and derive that parameter’s efficient influence curve. We go through each step in Sections 3–5 that follow.

3 ITTATE

The intent-to-treat average effect of the instrument on the outcome for participants in the site without follow-up data (S = 0) is defined as ψ₁ = E(Y¹ − Y⁰|S = 0), where for each a ∈ {0, 1}, Y^a denotes the counterfactual outcome that would be observed if instrument A = a were assigned and if Y were observed for participants with S = 0.

3.0.1 Identification

Under the assumptions given below, the causal effect, ψ₁ equals the statistical estimand, Ψ₁(P). Ψ₁(P), given in Equation 1 below, is defined as a mapping ${\mathrm{\Psi }}_1(P):ℳ\to R$ that takes a probability distribution P in statistical model $ℳ$_, and maps it to a real number. The true value is obtained by applying Ψ₁ to the true distribution, P₀. The statistical model, $ℳ$, is the collection of probability distributions of O that satisfy assumption 3 (below) and possibly put restrictions on P(A = a|W, S = 0). The other two assumptions do not put restrictions on the data, so they do not affect the statistical model.

$$\begin{array}{l}{\mathrm{\Psi }}_1(P)\equiv E([E\{E(Y\mathrm{|}S=1,W,A=1,Z)\mathrm{|}S=0,W,A=1\}\\ -E\{E(Y\mathrm{|}S=1,W,A=0,Z)\mathrm{|}S=0,W,A=0\}]\mathrm{|}S=0)\end{array}$$ (1)

The assumptions needed to identify ψ₁ from the statistical target parameter Ψ₁ are:

1. E₀(Y | S = 0, W, A, Z) = E₀(Y | S = 1, W, A, Z). This means that there is a common outcome model across the two sites. In other words, it assumes that the expectation of the outcome conditional on its parents—the instrument, exposure, and covariates (including those needed to guarantee exchangeability of A)—must be equal between the two sites. Relating this to Pearl and Bareinboim’s transport causal diagrams (Pearl and Bareinboim, 2011), this assumption means that there is no S node that points into the Y node.

2. A is independent of (Z^a, Y^a), given W, S = 0. This is an exchangeability assumption and means that A is independent of the potential outcomes Z^a and Y^a conditional on W and S = 0.

3. $P_0(S=1,A=a\mathrm{|}W,Z)>0P_{0,W,Z\mathrm{|}A=a,S=0}-\mathrm{a}.\mathrm{e}.$This is the positivity assumption and means that every P(S = 1, A = a|W, Z) that one could draw from the true joint distribution of W, Z given A = a and S = 0 must be greater than 0. In other words, it means that selection into a site and instrument category are nondeterministic given W and Z—that there is a nonzero, positive probability of every site-instrument combination given any W, Z.

The proof of this identifiability result is in the supplementary Web Appendix.

3.0.2 Efficient influence curve and robustness properties

Let ${\mathrm{\Psi }}_1(P)\equiv {\mathrm{\Psi }}_1^1(P)-{\mathrm{\Psi }}_1^0(P)$, where Ψ₁(P) is defined in Equation 1 and for each a ∈{0, 1}, ${\mathrm{\Psi }}_1^a(P)$ denotes the counterfactual mean outcome one would observe if instrument A = a were assigned and if Y were observed for participants with S = 0. In addition, let $\overline{Q}(1,W,A,Z)=E(Y\mathrm{|}S=1,W,A,Z)$, let g_A(A = a | s, W) = P(A = a | S = s, W), and let g_Z(Z = z | a, s, W) = P(Z = z | A = a, S = s, W).

Result 1

The efficient influence curve of $P\to {\mathrm{\Psi }}_1^a(P)$ on the model $ℳ$ that makes at most assumptions about P(A = a | W, S = 0) and positivity is given by:

$$D_{{\mathrm{\Psi }}_1}^a(P)=D_Y^a(P)+D_Z^a(P)+D_W^a(P),$$

where

$$\begin{array}{l}{D}_W^a(P)=\frac{I(S=0)}{P(S=0)}[E\{\overline{Q}(1,W,a,Z)\mathrm{|}S=0,W,A=a\}\\ -E[E\{\overline{Q}(1,W,a,Z)\mathrm{|}S=0,W,A=a\}\mathrm{|}S=0]]\\ D_Z^a(P)=\frac{I(A=a,S=0)}{g_A(A=a\mathrm{|}W,S=0)P(S=0)}\\ \times [\overline{Q}(1,W,a,Z)-E\{\overline{Q}(1,W,a,Z)\mathrm{|}S=0,W,A=a\}]\\ D_Y^a(p)=\frac{I(S=1,A=a)}{g_A(A=a\mathrm{|}W,S=1)P(S=1)}\frac{gz(Z=z\mathrm{|}a,W,S=0)P(W\mathrm{|}S=0)}{gz(Z=z\mathrm{|}a,W,S=1)P(W\mathrm{|}S=1)}\\ \times \{Y-\overline{Q}(1,W,a,Z)\}.\end{array}$$

We note that

$$\frac{P(W\mathrm{|}S=0)}{P(W\mathrm{|}S=1)}=\frac{P(S=0\mathrm{|}W)P(S=1)}{P(S=1\mathrm{|}W)P(S=0)}.$$ (2)

There are three scenarios under which an estimator that solves the efficient influence equation will be consistent (robustness result). First, the Y model may be misspecified if all other models are correct. Second, the S and A models may be misspecified if the Y and Z models are correct. Third, the S and Z models may be misspecified if the Y and A models are correct.

We provide the derivation for the robustness properties in the supplementary Web Appendix.

3.0.3 Targeted maximum likelihood estimator

There are two TMLEs that can be computed to estimate the transported ITTATE. In this section, we describe how to compute one of them and describe how to compute the other in the supplementary Web Appendix. The TMLE described in this section can be computed in one-step and is particularly suitable when Z is high dimensional.

Let ${\overline{Q}}_n^0$ be an initial estimate of $\overline{Q}$, and let g_Z,n, g_S,n, and g_A,n be estimators of g_Z(Z = z | a, s, W), g_S(S = s | W), and g_A(A = a | s, W), respectively. Consider submodel $\text{Logit}{\overline{Q}}_n^0(\epsilon )=\text{Logit}{\overline{Q}}_n^0+\epsilon C_Y(g_{Z,n},g_{S,n})$, where

$$C_Y(g_Z,g_S,g_A)=\frac{I(S=1,A=a)}{g_A(A=a\mathrm{|}W,S=1)P(S=1)}\frac{g_Z(Z=z\mathrm{|}a,W,S=0)P(W\mathrm{|}S=0)}{g_Z(Z=z\mathrm{|}a,W,S=1)P(W\mathrm{|}S=1)},$$

noting again Equation 2.

The above estimators can be calculated as follows. The predicted values of Y from a regression of Y on A, Z, W among participants with S_i = 1 can estimate ${\overline{Q}}_n^0$. Alternatively, one could use a machine learning approach, but we will use regression terminology for simplicity. Similarly, g_A,n(A = a | W, S = 1) can be estimated by the predicted probabilities from a logistic regression model of A = a on W among participants with S_i = 1, and g_S,n(S = s|W) can be estimated by the predicted probabilities from a logistic regression model of S = s on W. For binary Z, g_Z,n(Z = z|a, s, W) can be estimated by the predicted probabilities setting A = a from a logistic regression model of Z = z on A and W among strata of observations with S_i = s.

Let ${\epsilon }_n^0$ be the fitted coefficient for C_Y in the univariate logistic regression model of Y on C_Y using $\text{Logit}{\overline{Q}}_n^0$ as an offset, using the binary log-likelihood loss function multiplied by I(S = 1, A = a) (i.e., only using the observations with S_i = 1, A_i = a). If Y is not on the [0, 1] scale, it can be bounded as previously recommended (Gruber and van der Laan, 2010). The updated estimator is denoted with ${\overline{Q}}_n^1={\overline{Q}}_n^0({\epsilon }_n^0)$.

Next, run a regression of $E\{{\overline{Q}}_n^1(1,W,a,Z)\mathrm{|}S=0,W,A=a\}$ by regressing the predicted values ${\overline{Q}}_n^1(1,W,a,Z)$ on W among strata of observations with A_i = a, S_i = 0. Denote this estimator of ${\overline{Q}}_Z=E\{\overline{Q}(1,W,a,Z)\mathrm{|}S=0,W,A=a\}$ with ${\overline{Q}}_{Z,n}^0$. Consider the submodel

$$\text{Logit}{\overline{Q}}_{Z,n}^0(\epsilon )=\text{Logit}{\overline{Q}}_{Z,n}^0+\epsilon C_Z(g_{A,n}),$$

where,

$$C_Z(g_A)=\frac{I(A=a,S=0)}{g_A(A=a\mathrm{|}W,S=0)P(S=0)}.$$

Let ε_1,n be the fitted coefficient for this univariate logistic regression model that uses the binary log-likelihood loss function treating ${\overline{Q}}_n^1(1,W,a,Z)$ as the outcome and $\text{Logit}{\overline{Q}}_{Z,n}^0$ as an offset, restricted to the observations with S_i = 0, A_i = a. Denote this update with ${\overline{Q}}_{Z,n}^1={\overline{Q}}_{Z,n}^0\left({\epsilon }_{1,n}\right)$.

The TMLE of ${\psi }_1^a$ is given by $Q_{W,n\mathrm{|}S=0}{\overline{Q}}_{Z,n}^{1,a}$. This is the empirical mean of ${\overline{Q}}_{Z,n}^{1,a}$ among the observations with S_i = 0 and setting A = a. Q_W,n|S=0 is the empirical distribution of W among those with S_i = 0 — a function of the participant’s covariates. So, our final estimator of ${\psi }_1={\psi }_1^1-{\psi }_1^0$ is $Q_{W,n\mathrm{|}S=0}({\overline{Q}}_{Z,n}^{1,a=1}-{\overline{Q}}_{Z,n}^{1,a=0})$. This is the empirical mean of the difference in ${\overline{Q}}_{Z,n}^1$ setting a = 1 versus a = 0 among observations with S_i = 0. This TMLE solves the efficient influence function $P_n{D}_{{\mathrm{\Psi }}_1}^a(g_{Z,n},g_{S,n},g_{A,n},{\overline{Q}}_n^{1,a},{\overline{Q}}_{Z,n}^1,Q_{W,n\mathrm{|}S=0})=0$, where $P_{n}f=1/n{\displaystyle {\sum }_{i}f(O_i)}$ (the empirical mean of function f(O)).

We can estimate the variance of the TMLE with ${\sigma }_n^2=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\{D_{{\mathrm{\Psi }}_1,n}^1(O_i)-D_{{\mathrm{\Psi }}_1,n}^0(O_i)\}}^2}$, which is the sample variance of the efficient influence curve, which was given in Result 1.

4 EACE

The average effect of the exposure on the outcome for participants in the site without long-term follow-up data (S = 0) is defined as ψ₂ = E₀(Y¹ − Y⁰ | S = 0), where for each z ∈ {0, 1}, Y^z denotes the counterfactual outcome that would be observed if exposure Z = z were assigned and if Y were observed for participants with S = 0.

4.0.4 Identification

Under the assumptions given below, the causal effect ψ₂ can be identified from the statistical estimand Ψ₂(P). Ψ₂(P), given in Equation 3 below, is defined as a mapping ${\mathrm{\Psi }}_2:ℳ\to R$. The statistical model, $ℳ$, is the collection of probability distributions of O that satisfy assumption 3 (below). The other two assumptions do not put restrictions on the data, so they do not affect the statistical model.

$${\mathrm{\Psi }}_2(P)\equiv E[\{E(Y\mathrm{|}S=1,W,Z=1)-E(Y\mathrm{|}S=1,W,Z=0)\}\mathrm{|}S=0],$$ (3)

The assumptions needed to identify ψ₂ from Ψ₂ are:

1. E₀(Y|S = 0, W, Z) = E₀(Y|S = 1, W, Z). As in Section 3.0.1, this means that there is a common outcome model across the two sites. In other words, it assumes that the expectation of the outcome conditional on the exposure and covariates (including those needed to guarantee exchangeability of Z) must be equal between the two sites. Relating this to Pearl and Bareinboim’s transport causal diagrams (Pearl and Bareinboim, 2011), this assumption means that there is no S node that points into the Y node.

2. Z is independent of Y^a given W. This exchangeability assumption means that Z is independent of the potential outcome Y^a conditional on W.

3. $P_0(Z=z\mathrm{|}W,S=1)>0P_{0W\mathrm{|}S=0^{-a.e.}}$ This is the positivity assumption and means that every P(Z = z W, S = 1) that one could draw from the true distribution of W given S = 0 must be greater than 0. In other words, it means exposure is nondeterministic given W —that there is a nonzero, positive probability of every exposure given any W for those in the site where Y is observed.

The proof of this identifiability result is trivial and known from the average treatment effect literature.

4.0.5 Efficient influence curve

Let ${\mathrm{\Psi }}_2(P)\equiv {\mathrm{\Psi }}_2^1(P)-{\mathrm{\Psi }}_2^0(P)$, where Ψ₂(P) is defined in Equation 3 and for each z ∈ {0, 1}, ${\mathrm{\Psi }}_2^z(P)$ denotes the counterfactual mean outcome one would observe if exposure Z = z were assigned and if Y were observed for participants with S = 0. Unless otherwise specified, we use the same notation as in Section 3.

Result 2

The efficient influence curve of $P\to {\mathrm{\Psi }}_2^z(P)$ on the model $ℳ$ that at most makes assumptions about P(Z = z|W, S = 0) and positivity is given by

$$\begin{array}{l}{D}_{{\mathrm{\Psi }}_2}^z(P)(O)=\frac{I(S=1,Z=z)}{P(S=1,Z=z\mathrm{|}W)}\frac{P(S=0\mathrm{|}W)}{P(S=0)}\{Y-\overline{Q}(1,W,z)\}\\ +\frac{I(S=0)}{P(S=0)}[\overline{Q}(1,W,z)-E\{\overline{Q}(1,W,z)\mathrm{|}S=0\}].\end{array}$$

We have two scenarios under which an estimator that solves the efficient influence curve will be consistent (robustness result). First, the S and Z models may be misspecified if the Y model is correct. Second, the Y model may be misspecified if the S and Z models are correct. We provide the derivation of the robustness properties in the supplementary Web Appendix.

4.0.6 Targeted maximum likelihood estimator

Consider the submodel $\text{Logit}{\overline{Q}}_n^0\left(\epsilon \right)=\text{Logit}{\overline{Q}}_n^0+\epsilon C_Y(g_{Z,n},g_{S,n})$, where

$$\begin{array}{l}{C}_y(g_Z,g_S)\equiv \frac{I(S=1,Z=z)}{P(S=1,Z=z\mathrm{|}W)}\frac{P(S=0\mathrm{|}W)}{P(S=0)}\\ =\frac{I(S=1,Z=z)}{P(Z=z\mathrm{|}S=1,W)P(S=1\mathrm{|}W)}\frac{P(S=0\mathrm{|}W)}{P(S=0)}.\end{array}$$

The components of C_Y can be calculated as described in Section 3. Let ${\epsilon }_n^0$ be the fitted coefficient for this clever covariate C_Y in the univariate logistic regression model of Y on C_Y using $\text{Logit}{\overline{Q}}_n^0$ as an offset, using the binary log-likelihood loss function multiplied by I(S = 1, Z = z) (i.e., only using the observations with S_i = 1, Z_i = z). Again, if Y is not on the [0, 1] scale, it can be bounded as recommended previously (Gruber and van der Laan, 2010). The updated estimator is denoted with ${\overline{Q}}_n^1={\overline{Q}}_n^0\left({\epsilon }_n^0\right)$.

The TMLE of ${\psi }_2^z$ is given by $Q_{W,n\mathrm{|}S=0}{\overline{Q}}_n^{1,z}$, which is the empirical mean of ${\overline{Q}}_n^1$ among the observations with S_i = 0 setting Z = z. So, our final estimator of ${\psi }_2={\psi }_2^1-{\psi }_2^0$ is $Q_{W,n\mathrm{|}S=0}({\overline{Q}}_n^{1,z=1}-{\overline{Q}}_n^{1,z=0})$, which is the empirical mean of the difference in ${\overline{Q}}_n^1$ setting z = 1 versus z = 0 among the observations with S_i = 0. This TMLE solves the efficient influence function $P_n{D}_{{\mathrm{\Psi }}_2}^2(g_{Z,n},g_{S,n},{\overline{Q}}_n^{1,z})=0$.

Again, we can estimate the variance of the TMLE with ${\sigma }_n^2=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\{D_{{\mathrm{\Psi }}_{2,n}}^1(O_i)-D_{{\mathrm{\Psi }}_{2,n}}^0(O_i)\}}^2}$, which is the sample variance of the efficient influence curve, which was given in Result 2.

5 CACE

The complier average effect of the exposure on the outcome in the site without long-term follow-up data is defined as ψ₃ = E(Y¹ − Y⁰|Z¹ − Z⁰ = 1, S = 0), where for each a ∈ {0, 1}, Y^a denotes the counterfactual outcome that would be observed if instrument A = a were assigned and if Y were observed for participants with S = 0, and Z^a denotes the counterfactual exposure that would be observed if instrument A = a were assigned. The CACE is also called the instrumental variables (IV) estimand and the local average instrument effect (LATE), even in the case of a binary instrument and binary exposure (Angrist et al., 1996).

5.0.7 Identification

Under the assumptions given below, the causal effect, ψ₃, equals the statistical estimand, Ψ₃(P). Ψ₃(P), given in Equation 4 below, is defined as a mapping ${\mathrm{\Psi }}_3:ℳ\to R$. The statistical model, $ℳ$, is the collection of probability distributions of O that satisfy assumption 5. Ψ₃(P) is a ratio of two statistical estimands:

$${\mathrm{\Psi }}_3(P)\equiv \frac{{\mathrm{\Psi }}_1(P)}{\tilde{\mathrm{\Psi }}(P)},$$ (4)

where Ψ₁(P) is defined in Equation 1, and $\tilde{\mathrm{\Psi }}(P)$ is the statistical estimand of the non-transported average effect of the instrument on the exposure for participants with S=0:

$$\tilde{\mathrm{\Psi }}(P)\equiv E\{E(Z\mathrm{|}S=0,W,A=1)-E(Z\mathrm{|}S=0,W,A=0)\mathrm{|}S=0\}.$$

The assumptions needed to identify ψ₃ from Ψ₃ are:

1. E₀(Y | S = 0, W, A, Z) = E₀(Y | S = 1, W, A, Z). As in Sections 3.0.1 and 4.0.4, this means that there is a common outcome model across the two sites. In other words, it assumes that the expectation of the outcome conditional on its parents—the instrument, exposure, and covariates (including those needed to guarantee exchangeability of A)—must be equal between the two sites. Relating this to Pearl and Bareinboim’s transport causal diagrams (Pearl and Bareinboim, 2011), this assumption means that there is no S node that points into the Y node.

2. A = f_A(U_A) is independent of (Z^a, Y^a), given W, S = 0. This is an exchangeability assumption and means that A is independent of the potential outcomes Z^a and Y ^a conditional on W and S = 0.

3. Y^az = Y^z, which is the exclusion restriction assumption, stating that the instrument A only affects the outcome Y through the exposure Z. In other words, it assumes that there is no direct effect of A on Y – only its indirect effect through Z.

4. Z¹ − Z⁰ ≥ 0, which is the monotonicity assumption, meaning that the instrument A cannot decrease exposure.

5. $P_0(S=1,A=a\mathrm{|}W,Z)>0P_{0,W,Z\mathrm{|}A=a,S=0}-\mathrm{a}.\mathrm{e}.$ and E₀(Z¹ − Z⁰|S = 0, W) ≠ 0. This first part means that every P(S = 1, A = a|W, Z) that one could draw from the true joint distribution of W, Z given A = a and S = 0 must be greater than 0. In other words, it means that selection into a site and instrument category are nondeterministic given W and Z—that there is a nonzero, positive probability of every site-instrument combination given any W, Z. The second part means that the nontransported average effect of the instrument on the exposure of participants with S = 0 does not equal 0.

These assumptions have analogs in Angrist and Fernandez-Val’s work extrapolating LATE (Angrist and Fernandez—Val, 2013). Specifically, assumptions 2–5 correspond to Angrist and Fernandez-Val’s Assumption 2, ‘Conditional LATE’. Our assumption 1 is similar to their Assumption 3, ‘Conditional Effect Ignorability’, except we assume that heterogeneity in predicted outcomes values (instead of causal effects) across sites (instead of across instruments) is entirely due to differences in measured variables.

5.0.8 Efficient Influence Curve

For the efficient influence curve of Ψ₃, we first need to give the efficient influence curve of $\tilde{\mathrm{\Psi }}(P)$. Recall from above that $\tilde{\mathrm{\Psi }}(P)$ is the statistical estimand of the ATE of the effect of A on Z among those with S = 0. The TMLE estimate of an ATE has been given previously in van der Laan and Rubin (2006). For each a ∈ {0, 1}, ${\tilde{\mathrm{\Psi }}}^a(P)$ denotes the counterfactual mean exposure one would observe if instrument A = a were assigned for participants with S = 0. The efficient influence curve of $P\to {\tilde{\mathrm{\Psi }}}^a(P)$ on the model $ℳ$ that at most makes assumptions about P(A = a|W, S = 0) and positivity is given by $D_{\tilde{\mathrm{\Psi }}}^a(P)(O)=\frac{I(S=0,A=a)}{P(S=0,A=a\mathrm{|}W)}\{Z-g_Z(Z=z\mathrm{|}a,W,S=0)\}+\frac{I(S=0)}{P(S=0\mathrm{|}W)}[g_Z(Z=z\mathrm{|}a,W,S=0)-E\{g_Z(Z=z\mathrm{|}a,W,S=0)\}]$.

Let ${\mathrm{\Psi }}_3(P)\equiv {\mathrm{\Psi }}_3^1(P)-{\mathrm{\Psi }}_3^0(P)$, where Ψ₃(P) is defined in Equation 4 and for each a ∈ {0, 1}, ${\mathrm{\Psi }}_3^a(P)$ denotes the counterfactual mean outcome one would observe if instrument A = a were assigned and if Y were observed for participants with S = 0. Unless otherwise specified, we use the same notation as in Section 3.

Result 3

The efficient influence curve of $P\to {\mathrm{\Psi }}_3^a(P)$ on the model $ℳ$ that at most makes assumptions about P(A = a|W, S = 0), P(Z = z|a, W, S = 0), and positivity is given by

$$D_{{\mathrm{\Psi }}_1,\tilde{\mathrm{\Psi }}}^a(P)=\frac{1}{\tilde{\mathrm{\Psi }}(p)}{D}_{{\mathrm{\Psi }}_1}^a(P)-\frac{{\mathrm{\Psi }}_1(P)}{\tilde{\mathrm{\Psi }}{(P)}^2}{D}_{\tilde{\mathrm{\Psi }}}^a(P).$$

An estimator that solves the above efficient influence curve will be consistent (robustness result) if both the numerator and denominator from Equation 4 are correct. So, applying the robustness results from Ψ₁ and $\tilde{\mathrm{\Psi }}$ (see van der Laan and Rubin (2006) for $\tilde{\mathrm{\Psi }}$ robustness results), there are three scenarios under which this will happen. These scenarios are the same as those for Ψ₁. First, the Y model may be misspecified if the S, Z, and A models are correct. Second, the S and A models may be misspecified if the Y and Z models are correct. Third, the S and Z models may be misspecified if the Y and A models are correct. We provide the derivation for the efficient influence curve in the supplementary Appendix.

5.0.9 Targeted maximum likelihood estimator

This TMLE is estimated as the ratio of two TMLEs: the TMLE detailed in Section 3.0.3 over the TMLE for the average effect of A on Z as detailed previously (van der Laan and Rubin, 2006). A limitation of this estimator is that it does not constrain the ratio to be between −1 and 1 when Y is binary. An area for future work is to develop a TMLE directly targeting this ratio, which would constrain the estimate to lie within the parameter space.

We refer to Section 3.0.3 for the steps to estimate the TMLE in numerator. The TMLE in the denominator can be estimated as follows (van der Laan and Rubin, 2006).

Consider the submodel $\text{Logit}{g}_{Z,n}^0\left(\epsilon \right)=\text{Logit}{g}_{Z,n}^0+\epsilon C_Z(g_{A,n})$, where

$$C_Z(g_A)\equiv \frac{I(S=0,A=a)}{P(S=0,A=a\mathrm{|}W)}$$

The components of C_Z can be calculated as described in Section 3.

For binary Z, let ${\epsilon }_n^0$ be the fitted coefficient for this clever covariate C_Z in the univariate logistic regression model of Z = z on C_Z using $\text{Logit}{g}_{Z,n}^0$ as an offset, using the binary log-likelihood loss function multiplied by I(S = 0, A = a) (i.e., only using the observations with S_i = 0, A_i = a). The updated estimator is denoted with $g_{Z,n}^1=g_{Z,n}^0({\epsilon }_n^0)$.

The TMLE in the denominator is $Q_{W,n\mathrm{|}S=0}(g_{Z,n}^{1,a=1}-g_{Z,n}^{1,a=0})$, which is the empirical mean of the difference in $g_{Z,n}^1$ setting a = 1 versus a = 0 among the observations with S_i = 0.

The CACE TMLE solves the efficient influence function $P_n{D}_{{\mathrm{\Psi }}_1,\tilde{\mathrm{\Psi }}}^a=0$. We can estimate the variance of the CACE TMLE with the sample variance of its efficient influence curve, which was given in Result 3. Alternatively, the variance can be estimated using the multivariate delta method, which we show in the supplementary Web Appendix.

6 Simulation Study

6.1 Overview and set-up

We conduct a simulation study to examine finite sample performance of the TMLE estimators for ψ₁, ψ₂, and ψ₃. We consider two data-generating mechanisms (DGMs) from the same structural causal model, shown in Table 1. The magnitude of several coefficients increases in the second DGM compared to the first, which results in practical positivity violations. Practical positivity violations are a potential issue for each estimator—specifically, in the estimation of g_Z,n and g_S,n. Because of the transport component, this is even the case for the ITTATE estimator with an instrument A as the intervention of interest—seen in the clever covariate in Table 2. Comparing performance between the two DGMs allows us to examine sensitivity to the positivity assumption.

Table 1.

Simulation DGMs.

DGM 1: no positivity violations generated	DGM 2: positivity violations generated
S ~ Ber(0.5)	S~ Ber(0.5)
W1 ~ Ber(0.4 + 0.2S)	W1 ~ Ber(0.3 + 0.5S)
W2 ~ N(0.1S, 1)	W2 ~ N(0.5S, 1)
W3 ~ N(1 + 0.2S, 1)	W3 ~ N(1 + S, 2)
A ~ Ber(0.5)	A ~ Ber(0.5)
Z ~ Ber(−log(1.6) + log(4)A − log(11)W2 − log(1.3)W3)	Z ~ Ber(−log(1.6)+log(4)A − log(2)W2 + log(2)W3)
Y ~ Ber(log(1.6) + log(1.9)Z − log(1.3)W3 − log(1.2)W1 + log(1.2)AW1)	Y ~ Ber(log(1.6) + log(1.9)Z − log(1.3)W3 − log(1.2)W1 + log(1.2)AW1)

Table 2.

Characteristics of the clever covariate from the first simulation iteration for DGMs 1 and 2 and from the application to MTO.

	CY (A = 1)				CY (A = 0)
	Mean (SD)		Min	Max	Mean (SD)	Min	Max
ITTATE
DGM 1	0.55 (0.26)		0.14	2.12	0.60 (0.28)	0.15	2.13
DGM 2	1.16 (1.58)		0.84×10−2	21.35	1.25 (1.64)	1.06×10−2	22.82
Application	1.09 (1.54)		0.83×10−2	8.77	2.69 (3.89)	1.73×10−2	21.77
EACE
DGM 1	0.49 (0.38)	0.05		2.46	0.55 (0.31)	0.14	1.75
DGM 2	1.07 (1.62)	0.15×10−2		26.26	1.33 (2.26)	0.04×10−2	41.49
Application	2.05 (2.76)	4.54 10×−2		13.11	1.13 (1.82)	1.01×10−2	10.69

For each of the ITTATE, EACE, and CACE we show TMLE estimator performance in terms of mean percent bias, closeness to the efficiency bound (mean estimator standard error (SE, estimated from the sample variance of the EIC) × the square root of the number of observations), 95% confidence interval coverage, and mean squared error (MSE) across 10,000 simulations for a sample size of N=5,000. We evaluate performance under correct model specification and various model misspecifications where misspecification of the S and Z models involved specifying a null model and misspecification of the Y included a term for Z only.

6.2 Results

As seen in Table 3, the TMLE estimators are consistent under the robustness properties derived for each estimand. Specifically, the TMLE estimators have less than 1% bias for all model specifications except when all of the models (site, exposure, and outcome models) are misspecified. The 95% CI for the TMLE estimator results in coverage of about 95% for unbiased estimates. Table 3 gives results for N=5,000; results for N=500 are in Table 1 in the supplementary Web Appendix.

Table 3.

Simulation results from DGM 1 without positivity violations. N=5,000. 10,000 simulations. The estimator standard error $\times \sqrt{n}$ should be compared to the efficiency bound, which is 1.49 for the ITTATE, 4.50 for the CACE, and 1.60 for the EACE.

Specification	%Bias	SE× $\sqrt{n}$	95%CI Cov	MSE
ITTATE
All models correct	−0.67	1.50	95.01	0.0004
S model misspecified	−0.49	1.37	95.34	0.0004
Z model misspecified	−0.67	1.49	95.00	0.0004
Y model misspecified	−0.71	1.52	95.36	0.0005
S,Z models misspecified	−0.49	1.37	95.29	0.0004
S,Z,Y models misspecified	6.05	1.38	94.84	0.0004
EACE
All models correct	−0.31	1.60	94.94	0.0005
S model misspecified	−0.38	1.46	93.68	0.0005
Z model misspecified	−0.31	1.48	93.01	0.0005
Y model misspecified	−0.29	1.62	95.09	0.0005
S,Z models misspecified	−0.43	1.36	92.95	0.0004
S,Z,Y models misspecified	14.46	1.37	76.27	0.0009
CACE
All models correct	−0.13	4.54	95.17	0.0041
S model misspecified	0.04	4.15	95.50	0.0034
Z model misspecified	−0.13	4.53	95.20	0.0041
Y model misspecified	−0.17	4.54	95.00	0.0042
S,Z models misspecified	0.05	4.14	95.37	0.0034
S,Z,Y models misspecified	6.60	4.18	94.76	0.0036

Performance of these estimators in the presence of practical positivity violations is of interest for several reasons. First, the sites involved may have very different covariate distributions, which could contribute to such violations. Second, the sites may differ in how the instrument, A, is related to the exposure of interest, Z, which could also contribute to the violations. Third, predicted probabilities from these two models are multiplied together in the clever covariate, which may compound positivity violations from the first two sources. When there are practical violations of the positivity assumption, theory no longer guarantees consistency of the estimators (Petersen et al., 2010).

As compared to the results in Table 3 without positivity violations, Table 4 shows that in the presence of such violations even the estimators using correctly specified models are slightly biased. Table 4 gives results for N=5,000; results for N=500 are in Table 2 in the supplementary Web Appendix. MSE is particularly compromised due to increased variability across the simulations. This variation is likely due to a combination of the positivity issues and increased variance of the baseline covariates (which were increased to add positivity violations when estimating g_S). Coverage for the TMLE EACE is also compromised because of this variability. The standardized TMLE EACE estimates are slightly skewed with heavier tails. Calculating the 95% CI coverage using the percentile method from bootstrapping corrects this under-coverage (results not shown but available upon request).

Table 4.

Simulation results from DGM 2 with positivity violations. N=5,000. 10,000 simulations. The estimator standard error $\times \sqrt{n}$ should be compared to the efficiency bound, which is 2.68 for the ITTATE, 11.33 for the CACE, and 4.09 for the EACE.

Specification	%Bias	SE× $\sqrt{n}$	95%CI Cov	MSE
ITTATE
All models correct	−0.88	2.68	94.85	0.0015
S model misspecified	0.32	1.38	95.19	0.0004
Z model misspecified	−0.88	2.77	95.61	0.0015
Y model misspecified	−0.41	2.85	95.81	0.0015
S,Z models misspecified	0.34	1.39	95.28	0.0004
S,Z,Y models misspecified	18.34	1.42	94.06	0.0004
EASE
All models correct	0.18	3.60	91.36	0.0029
S model misspecified	1.98	1.96	86.33	0.0012
Z model misspecified	0.18	2.67	82.93	0.0029
Y model misspecified	2.09	4.17	96.05	0.0027
S,Z models misspecified	2.18	1.38	79.27	0.0009
S,Z,Y models misspecified	−52.11	1.41	2.49	0.0065
CACE
All models correct	2.57	11.42	94.96	0.0265
S model misspecified	3.73	5.84	95.42	0.0068
Z model misspecified	2.57	11.85	95.86	0.0265
Y model misspecified	3.06	11.42	94.85	0.0270
S,Z models misspecified	3.98	5.93	95.60	0.0069
S,Z,Y models misspecified	23.00	6.12	94.23	0.0085

The presence of these positivity violations exacerbates sensitivity to model misspecification of the TMLE estimator. This is largely due to increased variability in the estimates across the simulations and non-normally distributed standardized estimates—the consequences of which are seen in the lower coverage and greater MSE.

Weight truncation is a common and easy-to-implement strategy that may lessen sensitivity to practical positivity violations. Although truncation has the potential to improve both bias and variance due to positivity violations, it may also increase bias due to misspecification (Petersen et al., 2010; Cole and Hernán, 2008; Bembom and van der Laan, 2008). We repeated the simulations under DGM 2 truncating the clever covariate at several different lower bound/upper bound truncation levels: 0.01/100, 0.05/20, and 0.1/10. We compare the untruncated results to the truncated results in Table 3 in the supplementary Web Appendix. Truncation resulted in the expected improvements in terms of reduced variance and MSE but compromised confidence interval coverage for all estimands. Truncation also resulted in increased bias for the EACE.

7 Application

7.1 Overview and set-up

We now apply the transport estimators to an example from the Moving to Opportunity trial (MTO). MTO is a large-scale social policy experiment that has been described in the Introduction and previously (Kling et al., 2007). In discussing potential differences in effects across sites, MTO researchers concluded:

…if it had been possible to attribute differences in impacts across sites to differences in site characteristics, that would have been very valuable information. Unfortunately, that was not possible…to disentangle the underlying factors that cause impacts to vary across sites. (Orr et al., 2003, p.B11)

We ask whether our transport estimators can shed light on this previously intractable problem. Taking two MTO sites, Boston and Los Angeles (LA), we test the null hypothesis that the predicted effect of the intervention on school dropout for LA equals the true effect for LA, where the predicted effect borrows the conditional outcome model from Boston and makes use of differing distributions of population characteristics between the sites through transport formulas. If we fail to reject the null hypothesis that the predicted effect equals the true effect, this suggests that the intervention may be transportable based on the covariates included in the transport formula. If we reject the null, it suggests that the intervention is not transportable given our measured covariates.

We use the same school dropout outcome as reported previously for adolescents 15–19 years (completed less than 12 years of school, did not receive high school diploma or GED, and is not enrolled in school) (Sanbonmatsu et al., 2011). We define a binary instrument as has been done previously: randomized receipt of a voucher to move versus no voucher (Osypuk et al., 2012). The exposure of interest is defined as moving to a low-poverty neighborhood during follow-up. Neighborhoods were defined based on participant addresses geocoded to Census tracts. Neighborhood poverty was calculated as the percent of residents living at or below the federal poverty line based on the 2000 Census. A low-poverty neighborhood was defined as less than 25% of residents living below poverty based on theory and breakpoints in the site-specific distributions. Population composition characteristics included an extensive set of baseline characteristics spanning several domains: sociodemographic characteristics of the adolescent and adult family member, behavior and learning characteristics of the adolescent, neighborhood characteristics, and reasons for participation. A full list of the characteristics included is in the supplementary Web Appendix. We consider two sites for simplicity. For the purpose of this illustration, we ignore MTO study weights and only consider participants with non-missing data (n=260 in Boston; n=270 in LA). A more in-depth analysis of this and other MTO effects is the topic of a future paper.

Because we do not know the true models relating instrument to exposure, exposure to outcome, and covariates to site, we use nonparametric methods instead of the standard parametric regression models. Specifically, we use the nonparametric, ensemble machine learning method, Superlearner (van der Laan et al., 2007), to generate the predicted probabilities needed for the TMLE transport estimators. Briefly, Superlearner weights multiple machine learning algorithms to minimize the cross-validated mean squared prediction error. We conducted a simulation showing that incorporating Superlearner into the TMLE transport estimators did not change estimator performance relative to using parametric regression models (results not shown but available upon request). The clever covariate for the ITTATE TMLE estimator ranges from 0.83 × 10⁻² to 21.77 (Table 2). This suggests that practical positivity violations may be a minor problem.

7.2 Results

Figure 1 shows the ITTATE, EACE, and CACE estimates. We see that the true site-specific ITTATE and CACE estimates for Boston and LA differ. For Boston, the ITTATE estimate is statistically significant, which suggests that the MTO intervention was successful in reducing high school dropout. We see no effect of the intervention on high school dropout for the LA site.

Figure 1.

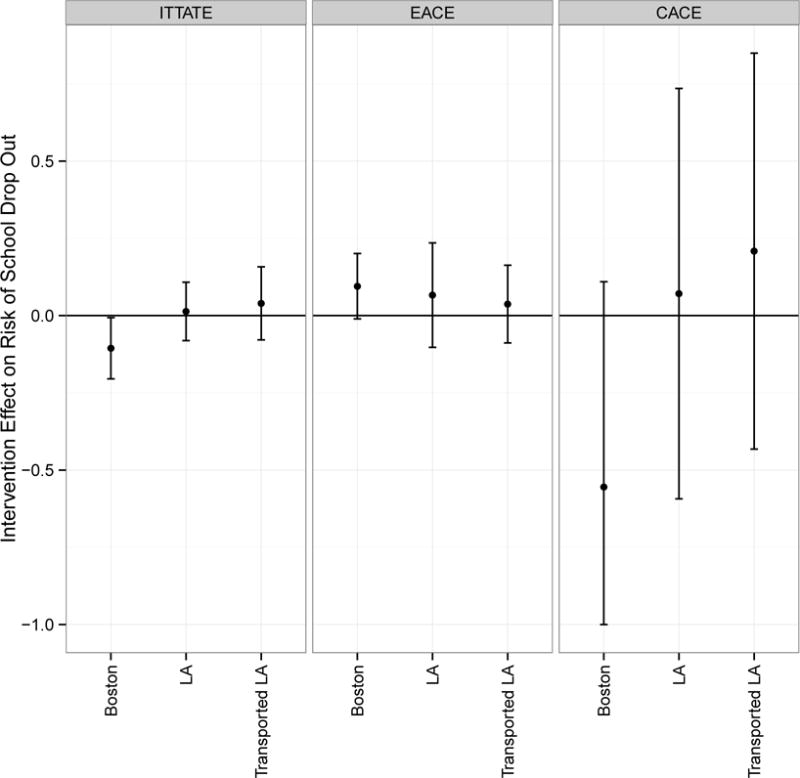
Effect estimates and 95% confidence intervals using data from the Moving to Opportunity Interim Follow-up. The ITTATE is interpreted as the effect of being randomized to one of the voucher groups on risk of dropping out of high school. The EACE is interpreted as the effect of moving to a low-poverty neighborhood on the risk of dropping out of high school. The CACE is interpreted as the effect of moving to a low-poverty neighborhood on the risk of dropping out of high school among compliers.

Our goal is to determine if the differences in the ITTATE and CACE estimates between sites can be explained by population characteristics. Specifically, we transport the effects estimated for Boston to LA using the population characteristics in LA but no outcome data. Figure 1 compares the TMLE transported ITTATE, EACE, and CACE estimates to the site-specific estimates. We see that the transported estimates for LA are similar to true LA estimates for each of the 3 estimands. This means that the difference in ITTATE and CACE estimates between Boston and LA could be largely explained by population composition if the identifying assumptions hold. The strongest of these assumptions is that the outcome model is the same for Boston and LA.

8 Conclusion

In this paper, we developed robust TMLE estimators for transporting average treatment effects from a study population to a target population. This complements graphical work on the subject of transportability and fills the key gap in estimation strategies in this area (Pearl and Bareinboim, 2011). These transport estimators are applicable for encouragement design interventions as well as randomized experiments and observational studies.

Development of new estimators is useful insofar as they are practical and easy to implement. To facilitate the use of these estimators, we provide step-by-step instructions for implementing each transport TMLE in the article. In the supplementary Web Appendix, we provide R code for each estimator as well as sample code for application.

A limitation of these estimators is their sensitivity to practical violations of the positivity assumption. This limitation is not unique to these estimators, but applies to broad classes of estimators that rely on weights either exclusively or partially outside the $\overline{Q}$ model, e.g., TMLE estimators, inverse probability of treatment weighted (IPTW) estimators, and augmented IPTW (A-IPTW) estimators (Robins et al., 2007). Truncation of the clever covariate, which is related to the general strategy of weight truncation, is a common strategy to deal with this limitation (Petersen et al., 2010; Cole and Hernán, 2008; Bembom and van der Laan, 2008), but we found that it did not appreciably improve performance in our simulations. Although it slightly improved MSE, the trade-off was increased bias and reduced CI coverage. An area for future work is to optimize estimator performance in the presence of such practical positivity violations. We are currently pursuing two strategies. The first is to reduce instances of practical positivity violations by drawing on the screening and pruning strategies employed in collaborative TMLE (van der Laan and Gruber, 2010). The second is reduce the influence of practical positivity violations by moving part of the clever covariate into the $\overline{Q}$ model (Stitelman et al., 2012). This is a middle ground between TMLE and weighted G-computation, the latter of which has been shown to be robust to practical positivity assumptions (Kang and Schafer, 2007; Robins et al., 2007; Rudolph et al., 2014).

Another limitation is that the first identifiability assumption for each of the estimators—of a common outcome model across sites—is a strong assumption that may not hold in some cases. A nonparametric omnibus test has recently been developed that can test such an assumption if outcome data are available (Luedtke et al., 2015). However, this paper is written for the more general scenario—and more likely real-world scenario—where we only observe outcome data for one site (e.g., E(Y|W, A, Z, S = 0) cannot be modeled). In this scenario, the assumption is not testable. Strategies to relax this assumption are desirable and an area for future work. In addition, the assumption of a common outcome model may be sensitive to the variables included in W. Variable selection for W is based on assumptions about the structural causal model. In the illustrative example, we selected variables included in W that theory and previous research suggest act as confounders of the relationship between neighborhood poverty and adolescent risk behavior. We then applied Superlearner (van der Laan et al., 2007) using this full set. Algorithms included in the SuperLearner library removed some variables through pruning and added others through interactions and higher order polynomials.

In an era of shrinking budgets, it is important to recognize that what works in one population may not work for another so that resources can be targeted optimally. Applying these TMLE estimators to examine site differences in multi-site epidemiologic studies and large-scale policy or program interventions contribute to achieving that goal.