Energy-labeling and –read-out of reactive intermediates in solution enabled by energy-dependent reaction selectivity

Abstract

Any long-lived chemical structure in solution is subject to statistical energy equilibration, so the history of any specific structure does not affect its subsequent reactions. This is not true for very short-lived intermediates, since energy equilibration takes time. Here, this idea is applied to achieve the energy labeling of a reactive intermediate. The selectivity of the ring-opening α-cleavage reaction of 1-methylcyclobutoxy radical is found here to vary broadly depending on how the radical was formed. Reactions that provide little excess energy to the intermediate lead to high selectivity in the subsequent cleavage (measured as a kinetic isotope effect) while reactions that provide more excess energy to the intermediate exhibit lower selectivity. Allowing for the expected excess energy allows the prediction of the observed product ratios, and in turn the product ratios can be used to obtain a read-out of the energy present in a intermediate.

A fundamental implicit assumption in chemistry is that the structure of a compound fully determines its chemical properties. It is then unnecessary to know the origin of a reactant or intermediate to understand its reactivity. This principle is used in diverse ways. For example, the identity of a putative intermediate may be affirmed, or denied, by the observation of identical versus differing reactivity when the intermediate is generated by an independent process. The exceptions prove the rule. That is, when expectantly identical structures react differently, such “memory effects” are attributable to subtle actual differences in the structures, such as differing conformations, ion pairing, supramolecularity, or electronic excited states.^1,2,3,4,5

On a sufficiently short time scale, however, molecules always differ depending on their origin. This is because the products of any reaction involving an energy barrier are initially invested with excess vibrational energy, energy that is also not statistically distributed. This excess energy is subject to flow within the molecule (intermolecular vibrational energy redistribution, IVR)⁶ and interchange with the environment (intermolecular energy transfer, IET). Both take time, often tens of ps for simple molecules in solution, and IVR is usually faster that IET.^7,8,9 The effects of the excess energy in intermediates are a routine consideration in gas phase kinetics because of the long times required for IET. The nonstatistical energy distribution after a transition state can also steer the products derived from short-lived intermediates to provide memory effects, either through the selective activation of a part of a molecule¹⁰ or by the process of dynamic matching.^11, We have previously shown how the consideration of the amount of excess energy and its distribution is required to understand the reactions of intermediates in solution.^12,13

We hypothesized that this short-lived excess energy in newly-formed molecules could effect the energy labeling of reactive intermediates in solution. That is, when an intermediate can be generated in diverse ways, then it can be formed with varied amounts of energy. If the intermediate is subject to a rapid reaction that occurs before energy equilibration, then the amount of excess energy can be read from the rate or selectivity of its reactions. In turn, the energy displayed by an intermediate can provide information about the mechanism of its formation. We demonstrate here the realization of these ideas.

Results and Discussion

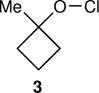
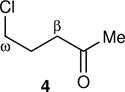
Energy labeling required an intermediate that was A. short lived, so that the initial energy would still be present in its reactions, B. open to multiple reaction pathways, allowing a read-out of the energy from the selectivity, and C. accessible in diverse ways, allowing the initial energy to be varied. Our recent study of energy partitioning effects in alkoxy radicals¹² suggested that the methylcyclobutoxy radical 1 might meet these requirements (Fig. 1). Radical 1 reacts by an α-cleavage reaction to afford the ring-opened radical 2. Two equivalent ring carbon-carbon bonds may be broken in this cleavage. When a ¹³C is present in the β-position of 1, the two cleavage processes, affording 2 or 2′, may be distinguished by the location of the ¹³C in the β versus ω position of products derived from 2/2′. The 2 : 2′ selectivity reflects an intramolecular kinetic isotope effect (KIE) on the ring opening. The potential energy barrier for the α-cleavage of 1 is only 3.0 kcal/mol, making the ring opening very rapid. When 1 was formed from the free-radical chain decomposition of 1-methylcyclobutyl hypochlorite (3) in solution, the product ratio did not fit with predictions from transition state theory but did match expectations from RRKM theory.¹² This suggested that 1 reacted while it still contained excess energy from its formation, and much more rapidly than thermal equilibration, making 1 well suited for energy labeling.

Figure 1.

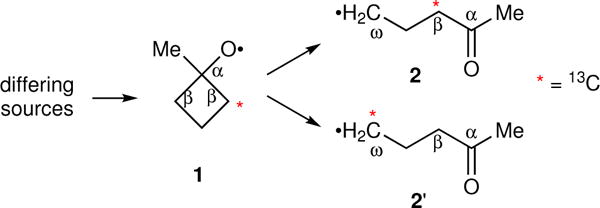
The observable selectivity in the ring opening of reactive intermediate 1.

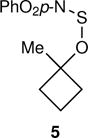
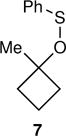
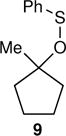
The arene sulfenic esters 5 and 7 provide a series of alternative sources of 1 with varied initial energies (Table 1). On absorption of a photon, sulfenic esters uniformly react by S-O bond cleavage,¹⁴ providing a direct entry into alkoxy radical/thiyl radical geminate pairs containing excess energy from the photochemical process. Irradiations of the 4-nitrophenylsulfenate 5 and the unsubstituted sulfenate 7 then afford 6 and 8, respectively, after the ring opening of 1 to 2 and geminate radical recombination. Chain mechanisms were blocked by the addition of a radical scavenger, and for 8 the non-chain nature of the product was verified using a crossover experiment (see below). Alternatively, it was expected that alkoxy radicals with lower excess energy could be generated from thermal free-radical chain reactions of sulfenic esters, taking advantage of the relatively weak S-O bond.¹⁵ This was accomplished for the conversion of 7 to 8 using triethylborane with the slow addition of O₂ at 20 °C. This combination generates ethyl radicals¹⁶ that initiate a chain by abstracting the phenylthio group to produce ethyl phenyl sulfide and 1. As a control reaction, we also examined the photochemical conversion of the less-strained 9 to 10. Because the barrier for ring opening of the cyclopentyl analog of 1 is high (10.8 kcal/mol), the reaction of 9 should involve a thermally equilibrated alkoxy radical.¹²

Table 1.

History-dependent selectivity in the reaction of 1.

source of 1	conditions	product	KIEa (13Cβ/13Cω)	CVT/SCTKIE	predicted Evibb [read-out Evib]	RRKMpredictionc
	42 °C		1.044(1)d	1.060d	4.8d [4.6 ± 0.3]	1.043d
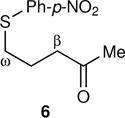
	hν, 350 nm 30 °C hν, 450 nm 25 °C		1.051(2) 1.051(2)	1.062 1.063	2.9 [3.4 ± 0.5] 2.9 [3.4 ± 0.5]	1.053 1.053
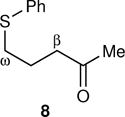
	Et3B, O2 20 °C hν, 350 nm 35 °C hν, 450 nm25 °C		1.058(1) 1.027(2) 1.032(1)	1.064 1.061 1.063	1.0 [1.7 ± 0.3] 10.5 [14.6 ± 2.7] 6.3 [8.9 ± 0.8]	1.060 1.030 1.037
	hν, 350 nm 30 °C		1.067(2)	1.066

^aThe experimental KIEs have the 95% confidence range for the last digit listed in parentheses.

^bThe predicted excess vibrational energy present in 1 on formation by the method specified, in kcal/mol.

^cThe RRKM predictions include a small approximate tunneling correction, as described in Supplementary Section II.H.

^dResult taken from reference¹².

For each reaction, the KIE for the ring-opening was measured by the analysis of the ¹³C content in the β versus ω positions of the products at natural abundance by NMR methodology.^17,18,19 For comparison, the expected KIEs if the intermediate alkoxy radicals were thermally equilibrated were calculated. These calculations employed canonical variational transition state theory (CVT) including small-curvature tunneling (SCT), using the GAUSSRATE/POLYRATE set of programs.^20,21 The results along with those previously reported for 3 are summarized in Table 1.

The conversion of 9 to 10 exhibited a KIE that matched that predicted from CVT/SCT calculations within the experimental error of the measurement. This fits with the anticipated involvement of a thermally equilibrated intermediate. In contrast, the varied reactions of 3, 5, and 7 all exhibited KIEs that are substantially lower than the CVT/SCT predictions. This is consistent with reactions in which an intermediate 1 underwent ring opening faster than the loss of energy to its surroundings in solution.

The most striking observation was that the KIE varied broadly depending on the source of 1. The thermal chain reaction of 7 mediated by Et₃B/O₂ exhibited a high KIE, only modestly below CVT/SCT expectations. In contrast, the photochemical reactions of 7 exhibited low KIEs that notably depended on the wavelength of the light employed in the photolysis. Quite different results were seen with the 4-nitrophenylsulfenate 5, as the KIE was high and now did not depend on the wavelength employed. The thermal chain decomposition of 3 exhibited a KIE in a middle range. All of these results have been reproduced with independent reactions and KIE measurements.

Ordinarily, the diverse KIEs would demand the conclusion that the various reactions involved different intermediates. We will consider instead whether the results can be rationalized by the involvement of a single intermediate, 1, imbued with varying amounts of energy. We first examine each of the reactions in turn to gauge how much excess energy they provide to 1. In this analysis, we treat the reactions within a gas-phase model that partitions the energy evolved into vibrational (E_vib), rotational (E_rot), and translational (E_trans) components. Our analysis makes the approximation that only the E_vib in 1 is available to promote the ring opening, as would be true in the gas phase. See Supplementary Section VI for a discussion of this issue.

For the reaction of 7 mediated by Et₃B/O₂, the formation of 1 would be expected to occur through abstraction of the phenylthio group by an alkyl radical (Fig. 2a). The radical-chain nature of the formation of 8 in this reaction was supported by a crossover experiment (see Supplementary Section I.C and below). The E_vib provided to 1 by the abstraction reaction was assessed by Hase’s classical single-trajectory approximation.²² Trajectories were started from the abstraction TS 11^‡, providing no energy other than a Boltzmann-random energy in the transition vector. The trajectories were then propagated forward in time and the vibrational, rotational, and translational energies were evaluated as the products separated. Of the 19 kcal/mol of excess energy in 11^‡ relative to the two products, only 1.0 kcal/mol was partitioned to E_vib in 1.

Figure 2. Partitioning of energy to 1 provided by differing mechanistic origins.

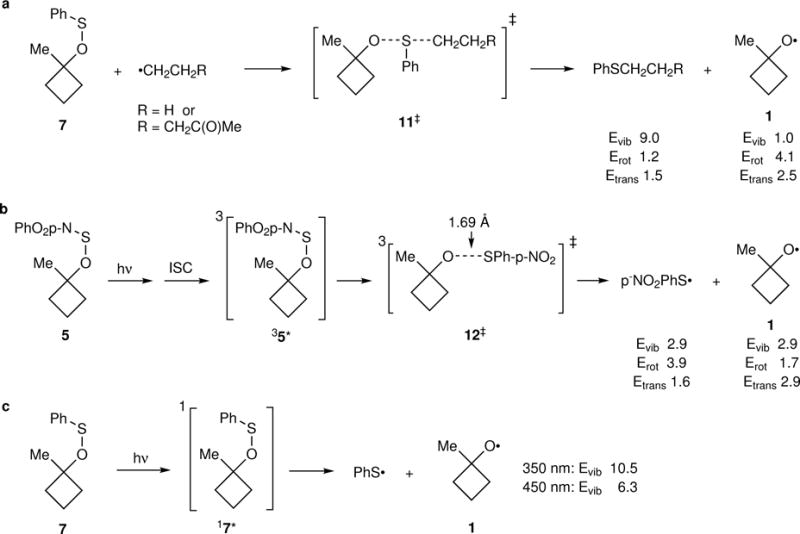
a, The thermal free-radical chain formation of 1 from 7 provides relatively little E_vib. b, The photochemical cleavage of the triplet state of 5 provides more energy to 1. c, The direct cleavage of singlet excited 7 affords 1 with a large wavelength-dependent energy.

Pasto has previously presented evidence that photochemical reactions of alkyl 4-nitrophenylsulfenates proceed through the triplet state after excitation of a π → π* transition.²³ Such indirect photochemical cleavage reactions occurring after intersystem crossing involve relatively long-lived excited states with lifetimes easily sufficient for thermal equilibration. As a result, the subsequent chemistry should not depend on the excitation energy. The energy in 1 would then depend on the relative energy of the triplet transition state for cleavage, 12^‡, versus the separate radicals 1 and 4-NO₂PhS•, and the partitioning of that energy between the two molecules and between vibrational, rotational, and translational forms (Fig. 2b). This was assessed by the single-trajectory method on the triplet M11/6-31+G** surface. Of the 15.9 kcal/mol available, 2.9 kcal/mol becomes E_vib in 1.

Unlike 5, 7 has no low-lying π → π* transition. Instead, the lowest-energy UV absorbance of phenyl sulfenic esters is an n → σ* excitation with a λ_max of ~300 nm. Time-dependent DFT calculations predict that the excitation of this band would directly break the S–O bond (Fig. 2c). In adiabatic quasiclassical trajectory calculations on the excited-state surface, the O–S bond cleavage to >2.5 Å takes <50 fs, too short for significant energy loss to solvent. The energy available for partitioning into 1 and PhS• would then depend on the excitation energy. To calculate the average wavelength of the photons absorbed, the radiant output spectrum of the light sources employed was weighted by the fraction of light absorbed at each wavelength, allowing for the UV-vis spectrum of 7, its concentration, and the path length. For the 350-nm and 450-nm (blue LED) light sources employed, the average absorption wavelengths were 352 and 412 nm, respectively. These absorptions provide 29.2 and 17.4 kcal/mol of excess energy, respectively, above the 52 kcal/mol dissociation energy of the S–O bond in 7. The amount of this energy that is partitioned into vibrational energy in 1 could not be calculated by the single-trajectory method, owing to discontinuities in the time-dependent DFT energy surface. Instead, an impulsive model²⁴ was applied to the excited state of 7, assuming that all of its excess energy is supplied to an impulse that breaks the S–O bond (see Supplementary Section II.E). This model leads to predicted E_vib values in 1 of 10.5 and 6.3 kcal/mol for the nominal 350 nm and 450 nm light sources, respectively.

The above analysis of the excess energy provided to 1 by the varying reactions provides both a qualitative and a quantitative explanation of the experimental results. Qualitatively, the six reactions can be ordered from lowest E_vib (the Et₃B/O₂ reaction of 7) to highest (the photochemical reaction of 7 at 350 nm), and this order fits exactly with the order of the KIE values from highest to lowest. This is strong evidence that the differing KIEs arise from the varying amount of energy supplied to 1. For a quantitative comparison, the E_vib values for 1 in the series of reactions were used to predict the KIEs from RRKM theory. These calculations make the approximations, to be considered below, that IVR is rapid, so that E_vib is statistically distributed within 1, and that IET is negligible. The resulting. KIEs in Table 1 closely match the experimental KIEs. It should be understood that the RRKM-predicted KIEs are sensitive to the small errors in the calculated E_vib, and the limitations in the calculations make small errors unavoidable. Given this, the agreement of the calculated KIEs with experiment is outstanding.

A critical question is whether the experimental observations can be explained in alternative ways that are unrelated to E_vib. In this regard, it should be recognized that the various transition states leading to 1 are will be conformationally unsymmetrical with respect to the two competitively broken C_α-C_β bonds, as in 13 versus 13′ (Fig. 3). As a result, the initial impulse on the oxygen atom that puts energy into 1 will itself be unsymmetrical. Due to the short 0.3 to 2 ps lifetime of 1, the molecular environment surrounding 1 will remain unsymmetrical as a C_α-C_β bond breaks, as in 14 versus 14′. If either asymmetry were to strongly influence which C_α-C_β bond is broken,²⁵ this would decrease or quench the observed KIE since the bond broken would be determined by whether the bond was proximal or distal to the breaking O-X bond, not the location of the isotope. To explore this issue, a series of quasiclassical direct-dynamics trajectories were carried out starting from each of 11^‡, 12^‡, and the transition state for the formation of 1 from 3.¹² (See Supplementary Section V for details.) For these three series, the ratios of proximal to distal C_α-C_β bond breakage were 33:29, 22:18, and 85:89, respectively. The asymmetry of the transition state did not significantly dictate which C_α-C_β bond is broken. Next, the influence of nearby p-NO₂PhS• and PhSEt molecules was explored by fixing these groups at their minimum-energy distance and orientation in the products from 11^‡ and 12^‡ (with C_β - aromatic carbon distances < 4 Å), then determining the barrier for breaking the proximal versus distal C_α-C_β bonds. In each case the barriers differed by less than 0.1 kcal/mol. These results suggest that the asymmetry of 13 and 14 should not have a strong effect on the KIEs. Unfortunately, comparable studies could not be carried out for the photochemical reactions of 7 due to discontinuities in the calculated energy surface, as noted above. However, asymmetry in the diradical derived from 7 provides no explanation for the wavelength dependence of the KIE. Finally, it is not clear how the asymmetric positioning of a ClCH₂R molecule derived from the reaction of 3 could affect the proximal/distal selectivity for C_α-C_β bond breaking in the midst of CH₂Cl₂ solvent. Overall, none of the experimental or computational observations support a significant role for environmental asymmetry in the variation in the KIEs.

Figure 3.

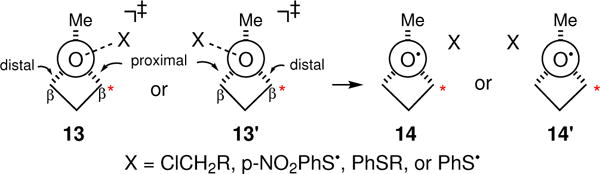
Asymmetry in the transition states forming 1 and its molecular environment

The energy-labeling reasoning can be reversed to read the amount of energy in 1 based on the observed KIE. The match of experimental and predicted KIEs observed with 9 as well as previous related reactions¹² suggests that statistical rate theories can predict the KIEs in these systems with great accuracy if the excess energy is known accurately and statistically distributed. We will assume the latter for now but come back to this issue. It may then be asked what amount of excess energy would give rise to an observed KIE. Table 1 shows the results of this calculation of the read-out E_vib for the various reactions. The uncertainty in the experimental KIEs leads to the shown uncertainty in the read-out E_vib values. For example, the relatively large uncertainty in the KIE for 350-nm irradiation of 7, 1.027 ± 0.002 (95% confidence), leads to a relatively large uncertainty in the read-out E_vib.

The RRKM-predicted KIEs and the read-out E_vib values are subject to a number of potential sources of error, including of course ordinary error in the calculated energy surfaces used for the RRKM predictions. One expected error arises from the approximation that IET is negligible, since some portion of the excess energy imbued in 1 would surely be lost to solution. The calculated CVT/SCT lifetime for 1, that is with no excess energy, is ~2 ps, and the RRKM lifetime with 10.5 kcal/mol of E_vib is ~300 fs. However, energy loss would tend to make the experimental KIEs higher than those predicted by the RRKM calculations here, since they do not allow for any IET. In actuality, Table 1 exhibits the opposite trend: the experimental KIEs tend to be smaller than the RRKM-predicted values. This trend suggests that the energy lost from the intermediate 1 before reaction is small. A more interesting potential source of error is that the ring opening of 1 may be subject to non-statistical dynamics.^{10,11,12,13,26} That is, the short lifetime of 1 may not allow sufficient time for statistical IVR. This would violate a central assumption inherent in the RRKM predictions. The low KIE seen in the 350-nm irradiation of 7 for example might not reflect a very high initial energy in 1, but rather could be the result of lower energy in 1 with a non-statistical localization of the energy in modes that aid the ring-opening reaction. This possibility is difficult to assess. Known times for IVR tend to be longer than the expected lifetime for 1, casting doubt on a statistical energy distribution, but the experimental literature is focused on IVR from specific high-energy modes.^7–9 The impulse forming 1 would provide energy to a series of low-energy modes, and in a classical simulation this energy is distributed among most of the low-energy modes in 1 within about 300 fs (see Supplementary Section VII). Fully statistical IVR likely takes much longer, but RRKM theory can often make good predictions without full statisticality.^6,27 Overall, a role for non-statistical dynamics cannot be excluded, but the success of the RRKM predictions suggests that the approximation of statistical energy distribution is sufficient to account for the experimental observations in the reactions of 1.

The energy read-out can aid in the assignment of an unknown mechanism. The irradiation of 7 at 450 nm in the absence of a radical scavenger afforded 8 with a KIE of 1.053(2) (Fig. 4a). The isotope effect by itself would not be directly interpretable mechanistically, but the energy read-out, 2.9 kcal/mol, is far lower than that available if 1 were formed by a direct photochemical cleavage. It is also higher than would be expected for any likely free-radical chain mechanism under these conditions. Instead, it was hypothesized that the reaction was taking place by a mixture of mechanisms, predominantly a radical chain but with some contribution from direct photochemical cleavage. To evaluate this possibility, a crossover experiment was carried out using a 1:1 mixture of 7 and 7-d₈ (Fig. 4b). This afforded a 1.00 : 0.96 : 0.88 : 1.17 mixture of 8-d₀, 8-d₃, 8-d₅, and 8-d₈ isotopologs by mass spectrometric analysis. If a free-radical chain mechanism predominated then the ratio of the four isotopologs would be approximately 1 : 1 : 1 : 1, while a purely intramolecular mechanism would provide no crossover. The observed ratio suggests that a chain mechanism is dominant but that a small amount of the product is formed intramolecularly. The isotope effect by itself might have suggested this, given that the observed KIE is in between that observed for the Et₃B/O₂ reaction and the photochemical cleavage in the presence of radical scavenger, but parsimony favors the interpretation of a lone observation in terms of a single mechanism. The read-out E_vib then allowed a clearer interpretation of the observation.

Figure 4. Energy read-out in the assignment of an unknown mechanism.

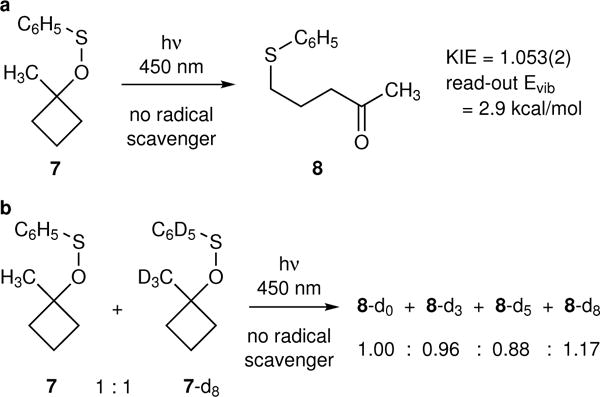
a, The photochemical cleavage of 7 in the absence of a radical scavenger leads to an increased selectivity, implying a lowered E_vib. b, A crossover experiment suggests that a chain mechanism is dominant though not exclusive.

Conclusions

The results here demonstrate that a single reactive intermediate can react with differing selectivities depending on how much energy is provided to the intermediate in its formation. This expands the meaning of structure in solution chemistry, since one must define both the molecular geometry and the molecular energy to predict reactivity. This idea has a series of implications. The first is that care must be taken when judging the identity of an intermediate based on comparison with observations in independent syntheses. Sufficiently short-lived intermediates in solution need not react identically when generated differently. The second is that it is possible under some circumstances to control the behavior of reactive intermediates through the choice of their synthesis. This was already clear from Carpenter’s work on dynamic matching,¹¹ but the current work greatly expands the possibilities since there is no required involvement of nonstatistical dynamics. A third implication is that the interpretation of experimental observations such as isotope effects or other selectivity from short-lived reactive intermediates may need to consider the history of the intermediate. The idea that all molecules are born with excess energy is implicit in the understanding of gas-phase chemistry, and differing product ratios depending on how an intermediate alkoxy radical was formed has been previously observed in the gas phase.²⁸ The results here show that the amount of excess energy can be important in the understanding of solution reactions.

Finally, the energy read-out provides an added dimension in mechanistic analysis. In complex mechanisms, experimental studies are often limited to probing just the rate-limiting steps or selectivity-determining steps, leaving many steps uncharacterized. A selectivity observation ordinarily only provides information about the specific transition state(s) involved in exerting the selectivity. The energy read-out, however, provides information about the transition state prior to the selectivity. In this way an experimental study can provide information about mechanistic steps that are inaccessible to ordinary probes.