The Volume–Outcome Relationship Revisited: Practice Indeed Makes Perfect

Abstract

Objective

To examine the causal effect of a hospital's experience with treating hip fractures (volume) on patient treatment outcomes.

Data Sources

We use a full sample of administrative data from German hospitals for 2007. The data provide detailed information on patients and hospitals. We also reference the hospitals’ addresses and the zip codes of patients’ place of residence.

Study Design

We apply an instrumental variable approach to address endogeneity concerns due to reverse causality and unobserved patient heterogeneity. As instruments for case volume, we use the number of potential patients and number of other hospitals in the region surrounding each hospital.

Principal Findings

Our results indicate that after applying an instrumental variables (IV) regression of volume on outcome, volume significantly increases quality.

Conclusions

We provide evidence for the practice‐makes‐perfect hypothesis by showing that volume is a driving factor for quality.

Quality of (hospital) care is the result of interaction between many factors. It reflects, for example, the care provided by physicians, nurses, and other hospital staff. At the same time, it reflects the implementation of and adherence to treatment standards. It can also indicate the effective and efficient usage of specialist technical equipment (Mainz 2003). The case volume of a hospital is often used as a proxy for the mentioned structure and processes of care with the assumption of a positive correlation (Halm, Lee, and Chassin 2002). Hence, it is an indirect measure of quality and related to the interaction of several factors.

Luft, Bunker, and Enthoven (1979) showed in their seminal paper that there is a correlation between volume and outcome quality in 10 of 12 procedures; that is, a higher case volume is associated with better outcomes. This correlation has been referred to as the volume–outcome relationship. The studies that followed have predominantly confirmed this correlation (Halm, Lee, and Chassin 2002; Gandjour, Bannenberg, and Lauterbach 2003). However, these studies inherently assume that volume is the driving factor for outcome. A hospital's accumulated case volume is supposed to reduce adverse event rates through the improvement of skills, greater standardization, and better organization. Later, when the learning process is completed, high‐volume hospitals can maintain their high level of learning by performing procedures more regularly (Gandjour and Lauterbach 2003). In the volume–outcome literature, this is called the practice‐makes‐perfect hypothesis, which inherently not only includes the process of obtaining practice but also the process of maintaining practice and routines (Gandjour and Lauterbach 2003). Here, the causal direction goes from case volume to quality; that is, higher volume leads to better quality.

Another plausible hypothesis states that the correlation between volume and outcome may only exist because high‐quality providers are able to attract more patients (selective‐referral hypothesis); that is, higher volume follows from better quality (e.g., Luft, Hunt, and Maerki 1987). Here, high‐quality hospitals lead primary physicians to refer their patients there because of the increased probability of good outcomes. This is a process of development. Initially, primary physicians may choose the hospitals at random, but if complications occur, they change their referral strategies and choose hospitals with better outcomes. This leads to high‐quality hospitals ending up with higher volumes and low‐quality hospitals with lower volumes (Luft et al. 1990). The selective‐referral hypothesis has received little attention in the empirical literature so far, even though volume may be endogenous due to the reversed causality of the selective‐referral hypothesis. Furthermore, estimates of the size of the effect of volume on outcome may also be biased by unobserved characteristics; patients may choose hospitals based on their current state of health (Tay 1999).

It is therefore essential in any empirical strategy to consider both hypotheses and control for unobserved patient heterogeneity due to the policy impact of the volume–outcome relationship: The volume–outcome effect is the foundation for minimum‐volume standards. For example, minimum‐volume standards were introduced in Germany for five interventions in 2004.1 As a consequence, hospitals that do not achieve a certain number of cases within a specific diagnosis are no longer allowed to treat patients with that diagnosis. This regulation was introduced based on international evidence that largely confirmed a positive correlation between volume and outcome; that is, minimum‐volume standards are implicitly based on the practice‐makes‐perfect hypothesis. The same is true for recommendations by the Leapfrog Group in the USA, which also sees volume as a driving factor for quality (Leapfrog Group, 2016). However, it is not possible to achieve quality improvement as intended by the law or other recommendations if selective referral is mainly responsible for the relationship between volume and outcome. In this case, quality can even deteriorate or at least will not improve; that is, a higher provider volume may not lead to a better outcome. To ensure that the minimum‐volume policy has a real effect on quality, causality must be determined.

The recent literature is fairly sparse when it comes to determining the causal effect of the volume–outcome relationship. Only a few studies use instrumental variables (IV) regression or simultaneous equation models to overcome endogeneity. Common instruments are the number of hospital beds (Luft, Hunt, and Maerki 1987; Farley and Ozminkowski 1992; Norton et al. 1998; Allareddy et al. 2012) and geographical factors (Seider, Gaynor, and Vogt 2004; Tsai et al. 2006; Barker, Rosenthal, and Cram 2011). However, the number of hospital beds, and hence the size of a hospital, has been shown to influence quality directly (Keeler et al. 1992); that is, larger hospitals tend to be of better quality. Therefore, this instrument may be invalid. Avdic, Lundborg, and Vikström (2014) use Swedish register data and take hospital closures as an instrument for volume. The authors provide evidence for the practice‐makes‐perfect hypothesis for cancer surgery. Hamilton and Hamilton (1997) use a duration model with hospital fixed effects. After controlling for fixed differences between hospitals, volume became insignificant, which supports the selective‐referral hypothesis. Overall, the evidence for the direction of the volume–outcome relationship is mixed and could also be condition‐specific.

This study examines the causal relationship between volume and outcome for hip fracture patients.2 Hip fractures are a common reason for hospital admission among the elderly, and the mortality rate is comparatively high. Therefore, it is important to detect factors that drive treatment quality. We extend the analysis of Hentschker and Mennicken (2015), who identify a correlation between volume and outcome for hip fracture patients. We use an instrument similar to Seider, Gaynor, and Vogt (2004) and Gaynor, Seider, and Vogt (2005). The instruments are the number of potential patients and the number of other hospitals in the region surrounding each hospital. A hospital's case volume should increase if more potential hip fracture patients live in the area around the hospital and decrease if other hospitals in the same area also treat hip fractures. Using administrative data from all inpatients in Germany for 2007, we find that after applying IV regression, volume has a significant positive effect on outcome; that is, higher volumes lead to lower mortality rates.

Our analysis contributes to the literature in two ways. First, to our knowledge this is the first study to provide empirical evidence of a causal volume–outcome relationship in Germany. This is of particular importance because minimum‐volume standards have already been introduced in Germany without consideration of a causal relationship. Second, the majority of the causal volume–outcome literature focuses only on bias through reversed causality (Farley and Ozminkowski 1992; Gaynor, Seider, and Vogt 2005; Barker, Rosenthal, and Cram 2011). We also consider the bias created by unobserved patient heterogeneity in detail and explain the different directions of the distortions caused by reversed causality and unobserved patient heterogeneity. Even though IV regression automatically considers both biases, it is important to have explanations for the direction of the distortion.

The remainder of this study is organized as follows: The section entitled  Empirical Strategy explains the endogeneity concerns when investigating the volume–outcome relationship and presents the empirical strategy. The section entitled  Data describes the data and variables used in the analysis. The section entitled  Results shows the estimation results. Finally, the section entitled  Conclusion summarizes the main findings and concludes.

Empirical Strategy

We specify our dependent variable y _ih as a binary variable that indicates whether patient i died in hospital h after being treated for a hip fracture. We estimate the following probit model via maximum‐likelihood estimation (MLE):

$$\begin{array}{cc}\hfill y_{ih}^{\ast }& ={\mathit{\alpha }}_0+{\mathit{\beta }}_1\text{ln}{(\text{vol})}_h+{\mathit{x}}_{ih}^{\prime }{\mathit{\beta }}_{\mathbf{2}}+{\mathit{k}}_h^{\prime }{\mathit{\beta }}_{\mathbf{3}}+{\mathit{\epsilon }}_{ih}\hfill \\ \hfill y_{ih}& =1\text{if}{y}_{ih}^{\ast }\ge 0\hfill \end{array}$$ (1)

where ln (vol)_h is the logarithm of case volume, x _ih are patient characteristics, k _h are hospital characteristics, and ε _ih is a random error term. The coefficient β ₁ is of primary interest: It measures how case volume affects a hospital's outcomes.

Regression model (1) neglects possible endogeneity threats. Volume can be endogenous for two reasons: reverse causality and unobserved patient heterogeneity:

First, reverse causality may occur if higher quality results in higher volume rather than a higher volume resulting in better quality. The practice‐makes‐perfect hypothesis states that higher case volume leads to better quality because of learning effects and economies of scale (Luft, Hunt, and Maerki 1987; Seider, Gaynor, and Vogt 2004). Hospitals that treat more patients with a specific condition reduce mistakes, optimize processes, and develop better routines. Hence, volume is the leading cause of good practice. By contrast, the selective‐referral hypothesis assumes that good‐quality hospitals have a higher case volume. This is the result of the reputation of the hospital: Referring physicians know which hospitals are of good quality and refer patients to a specific hospital (Luft, Hunt, and Maerki 1987). Another reason for this could be that patients inform themselves via quality reports and choose hospitals with the lowest mortality rates. Based on these arguments, quality is the leading cause of high case volume. Both hypotheses are possible, resulting in probit estimates of β ₁ being biased downwards.

Second, the volume–outcome relationship may also be biased as a result of an omitted variable bias due to unobserved patient heterogeneity. Patients may choose hospitals based on their current state of health (Tay 1999). Patient characteristics are usually unequally distributed across hospitals. University hospitals, for example, often treat patients whose conditions are more severe in terms of age and comorbidities. If patient health status is not fully observed, unobserved patient characteristics captured in the error term may be correlated with both the volume variable and the outcome variable (Iezzoni 2003). Therefore, it is essential to control for information on patient characteristics in order to identify the volume–outcome relationship adequately.

Most studies analyzing the volume–outcome relationship use administrative data (Halm, Lee, and Chassin 2002). While these datasets often contain very detailed information, clinical parameters such as laboratory values, functional status or symptoms, and detailed socioeconomic characteristics of the patients are often missing. If patients who are unobservably sicker were treated more often in high‐volume hospitals, this would result in a decline in the measured quality for these institutions as these patients have a higher mortality risk independent of the hospital quality. Unobserved characteristics would then lead to an upward bias of the effect of volume in a regression of volume on outcome.

We use an IV approach to correct for both endogeneity problems. To implement this strategy, we require an instrument Z _h that is strongly correlated with volume (cov(ln(vol)_h , Z _h) ≠ 0) but uncorrelated with the error term (cov(Z _h , ε _ih) = 0). We use two instruments similar to Seider, Gaynor, and Vogt (2004): the number of potential patients p _h and the number of other hospitals h _h in the area surrounding that hospital (see Data ). Apart from that, we use an alternative instrument specification and use a combination of both instruments to build the ratio between the number of potential patients and the number of hospitals in the area. In general, patients choose hospitals that are closer to their residence. Consequently, the case volume of a hospital should increase if more patients with a specific condition live near that hospital and decrease when more nearby hospitals treat the same condition.

The number of potential patients and the distance of each patient from a hospital should have no direct influence on the quality of treatment. Patient residence can be considered as exogenous to hospital quality, because it is unlikely that patients choose where to live on the basis of the quality of care of a nearby hospital. There may be other unobserved factors that are correlated with patient residence and hospital outcomes, such as income. These differences are captured by nine settlement structure indicators. The indicators distinguish regions by population density and by urban and rural status. Additionally, we add socioeconomic characteristics (purchasing power per inhabitant and unemployment rate) at the patient zip code level. Population and hospital density show substantial variation throughout Germany. These differences are also taken into account through our settlement structure indicators.

With these instruments, we specify the following first‐stage equation (2), where the logarithm of case volume is regressed on all covariates of equation (1) and the instruments $p_h$ and h _h.3 In the second‐stage equation (3), the fitted values of ln(vol)_ih from equation (2) are used to model the causal effect of volume on outcome.

$$\text{ln}{(\text{vol})}_{ih}={\mathit{\alpha }}_0+{\mathit{x}}_{ih}^{\prime }{\mathit{\pi }}_{\mathbf{1}}+{\mathit{k}}_h^{\prime }{\mathit{\pi }}_{\mathbf{2}}+{\mathit{p}}_h^{\prime }{\mathit{\gamma }}_{\mathbf{1}}+{\mathit{h}}_h^{\prime }{\mathit{\gamma }}_{\mathbf{2}}+u_{ih}$$ (2)

$$\begin{array}{cc}\hfill y_{ih}^{\ast }& ={\mathit{\alpha }}_0+{\mathit{\beta }}_1\text{ln}{(\widehat{\text{vol}})}_{\mathit{\iota }h}+{\mathit{x}}_{ih}^{\prime }{\mathit{\beta }}_{\mathbf{2}}+{\mathit{k}}_h^{\prime }{\mathit{\beta }}_{\mathbf{3}}+{\mathit{\nu }}_{ih}\hfill \\ \hfill y_{ih}& =1\text{if}{y}_{ih}^{\ast }\ge 0\hfill \end{array}$$ (3)

Note that the IV approach in equation (3) identifies only a local average treatment effect (LATE); that is, we only measure the effect for hospitals that are influenced by the number of potential patients and other hospitals in the area (compliers).

Data

We use administrative data from all German hospitals for 2007. The data contain the total inpatient population in Germany, excluding psychiatric cases. They provide detailed patient information, including age, gender, main and secondary diagnoses, procedure codes, admission and discharge reasons, and residential zip codes. We also have access to data on hospital characteristics, such as ownership type, teaching status, and bed capacity, as well as full addresses. We geocoded the hospital addresses and the centroids of all German zip codes, meaning that we are able to calculate each patient's distance from the hospital and the distances between hospitals (Ozimek and Miles 2011).

In the empirical analysis, we concentrate on patients with hip fractures. We use the diagnosis and procedure codes based on the definition of the Federal Office for Quality Assurance (BQS, 2008). We only include patients with the main diagnosis hip fracture and a matching procedure code. The main diagnosis is defined as the main reason for the hospital stay. We also only include patients who received a surgical intervention in the form of either an open or closed reposition or the implantation of an endoprosthesis.

We exclude 21 patients with missing patient characteristics and 821 patients who have no valid zip code. For the last group, the distances needed to construct the instruments are not computable. We exclude 133 patients who are under the age of 20 at the time of treatment; these patients may have needed specialist treatment compared to older patients. We also exclude patients whose recorded discharge reason is “transfer to another hospital” (N = 9,210). For these patients, we are not able to determine the treatment outcome. Our final sample consists of 89,541 patients treated in 1,262 hospitals. The exact identification algorithm can be found in the Figure A1 in Appendix SA2.

Generally, our data allow us to identify each hospital using a unique identifier. Using data from other sources, we are able to identify further hospital locations under the same identifier for 99 hospitals; that is, patients were treated in 157 hospital locations, but the original dataset can only distinguish 96 hospitals. For these hospitals, we are not able to identify the actual location where the patient was treated. In these cases, we randomly assigned patients to possible hospital locations based on the share of hip fracture patients documented in the quality reports. This results in the total of 1,262 hospitals mentioned above. We estimate all models without dividing the sample. The results remained essentially the same and are available upon request.

We use in‐hospital mortality as our outcome measure. Mortality is the most frequently used outcome measure in volume–outcome studies for two reasons. First, mortality is a clearly defined outcome. This is important because each hospital records its own data and coding differences may exist between hospitals; however, such differences are impossible for mortality. Second, for hip fracture patients, mortality is an approved indicator by the Agency for Healthcare Research and Quality (AHRQ). This indicator can be used to determine quality differences between hospitals (AHRQ, 2007). Unfortunately, the available data meant that we are unable to track patients after discharge, meaning that we cannot consider out‐of‐hospital mortality.

Our main explanatory variable is the case volume of each hospital, which varies from 1 to 387 hip patients treated per hospital per year. In our model, we use the logarithm of volume (Farley and Ozminkowski 1992; Hamilton and Hamilton 1997).

As we have the total inpatient population for Germany, we are able to determine the number of other hospitals and total number of patients in the areas around each hospital. These variables serve as our instruments (see Empirical Strategy ) and are similar to Seider, Gaynor, and Vogt (2004). For the specification of the instruments, we choose different radii around each hospital referring to the time usually needed to reach a hospital by car; this was calculated based on Google Maps. For the number of potential patients, we specify three variables; that is, we choose three radii (0–10, 10–20, and 20–30 minutes) and add up all hip fracture patients that reside within these radii for each hospital, irrespective of whether they are treated in that particular hospital. For the number of hospitals, we specify only two variables and choose two radii (0–15 and 15–30 minutes), reflecting the smaller number of hospitals, and add up all hospitals treating hip fractures within the radii of each hospital. The thresholds for the radii are somewhat arbitrary. We estimated models with different thresholds and distances in kilometers as well as Euclidean distance; however, the results essentially do not change. Additionally, we use a modification of our instrument and build a ratio with the number of potential patients within a radius of 15 minutes in the numerator and the number of hospitals within 15 minutes (including the considered hospital) in the denominator.

The outcome of a hospital treatment depends not only on the hospital's case volume but also on patient risk factors. We use age, gender, admission reason (scheduled, emergency, transfer), and the Elixhauser comorbidities as control variables. We expect that older patients and those with more comorbidities would have a higher mortality risk independent of hospital quality. The Elixhauser comorbidities are frequently used to conduct risk adjustments with administrative data (Elixhauser et al. 1998).4 They consist of 30 diagnoses that are not directly related to the main diagnosis but potentially increase the probability of a worse outcome compared to a patient without such a diagnosis, for example, diabetes, congestive heart failure, and hypertension (Elixhauser et al. 1998). We specify each diagnosis as a binary variable that is 1 if the patient has the illness and 0 otherwise. For this purpose, we use diagnosis codes developed by Quan et al. (2005), who mapped the original codes from the International Classification of Diseases (ICD)‐9 system to the ICD‐10 system used in Germany. We add dummy variables for admission during winter, which is 1 if admission was in the months of November to February and 0 otherwise, as well as for admissions during weekends and public holidays. The first variable captures possible seasonal patterns during winter, when there is more chance of people falling on icy ground. The latter captures weekend and public holiday effects due to lower staffing levels in comparison with weekdays (Bell and Redelmeier 2001; Kuntz, Mennicken, and Scholtes 2014). We also include a binary variable that differentiates patients with a femoral neck fracture and a pertrochanteric fracture. There are no individual socioeconomic characteristics available which also can correlate with the health status. For this reason, we control for purchasing power per inhabitant and unemployment rate at the patient zip code level (Budde and Eilers 2014; Microm Consumer Marketing 2014; Microm Micromarketing‐Systeme und Consult GmbH 2015a, b, c).

It has been shown that besides case volume, other hospital characteristics, such as ownership (Milcent 2005), teaching status (Ayanian and Weissman 2002), and hospital size (Keeler et al. 1992), can influence the quality of a hospital. Hence, we include indicator variables for ownership type, teaching hospital, university hospital, intensive care unit (ICU), and number of beds. Teaching hospitals are defined as nonuniversity hospitals where part of the medical training can take place.

We use nine settlement structure indicators to differentiate between hospitals located in areas with different population densities as well as urban and rural areas. The indicators range from metropolitan areas with more than 100,000 inhabitants per county to rural counties with fewer than 100 inhabitants per square kilometer. An overview of the indicators can be found in Schmid and Ulrich (2013).

Table 1 shows descriptive statistics for the patient and hospital characteristics. The descriptive statistics for the distribution of the Elixhauser comorbidities are shown in the Table A1 in Appendix SA2. Overall, 6.3 percent of patients die in hospital. Most of the hip fracture patients are female (75 percent), and the average age is 80. A third of patients are admitted in winter and 28 percent are admitted on a weekend. Most hospitals treating hip fractures are public hospitals (44 percent) or teaching hospitals (43 percent), while 3 percent are university hospitals. On average, 80 hip fracture patients live within a 10‐minute radius of a hospital and two additional hospitals are within a 15‐minute radius of each hospital.

Table 1.

Descriptive Statistics for Hip Fracture Patients

	Mean	SD	Min	Max
Patient level (N = 89,541)
Death	0.063	0.243	0	1
Age	79.546	11.299	20	108
Male	0.251	0.434	0	1
Emergency	0.761	0.427	0	1
Transfer	0.020	0.141	0	1
Femoral neck fracture	0.537	0.499	0	1
Winter	0.331	0.471	0	1
Weekend	0.284	0.451	0	1
Purchasing power per inhabitant (patient zip code level)	18.640	4.277	5.3	56.5
Unemployment rate (patient zip code level)	8.039	4.464	0.0	25.7
Hospital level (N = 1,262)
Case volume	70.952	47.913	1	387
Ownership: private not‐for‐profit	0.418	0.493	0	1
Private for‐profit	0.158	0.365	0	1
University hospital	0.031	0.173	0	1
Teaching hospital	0.395	0.489	0	1
Beds: 201–499	0.449	0.498	0	1
>500	0.169	0.375	0	1
ICU	0.350	0.477	0	1
Potential patients within: 0–10 minutes	80.830	91.380	0	570
10–20 minutes	292.506	367.124	0	1,978
20–30 minutes	562.810	648.183	0	3,372
Further hospitals within: 0–15 minutes	2.431	3.839	0	21
15–30 minutes	10.585	13.200	0	69
Pot. patients per hospital between 0 and 15 minutes	54.338	32.332	0	293

Results

Table 2 shows the coefficients of ln case volume. Models (1) to (4) show the results of a probit model. In the first model, we just estimate a bivariate specification of outcome on case volume. We add patient characteristics and hospital characteristics in models (2) and (3) separately and both in model (4). In model (5) we also control for socioeconomic and settlement structure indicators. We find a strong negative effect of case volume on outcome (p < .01). Patients who are treated in hospitals with higher case volume have a lower probability of death. The coefficient increases in absolute terms if patient characteristics and hospital characteristics are added to the model. In the case of patient characteristics compared to the bivariate specification, the case volume coefficient increases in absolute terms from 0.0086 to 0.0104. This is an increase of 21 percent, which emphasizes the importance of patient characteristics. This is also true for hospital characteristics: We observe an increase of the case volume coefficient from 0.0086 to 0.0115 (34 percent). Hence, both patient and hospital characteristics are correlated with case volume and outcome. Our further control variables show the expected signs. The complete regression results for the full models are shown in the Table A2 in Appendix SA2.

Table 2.

Marginal Effects of Probit and IV‐Probit Estimates

(a) Probit Estimation
	(1)	(2)	(3)	(4)	(5)
ln case volume	−0.0086***	−0.0104***	−0.0115***	−0.0142***	−0.0123***
	(0.0015)	(0.0015)	(0.0020)	(0.0021)	(0.0022)
Patient characteristics	No	Yes	No	Yes	Yes
Hospital charcteristics	No	No	Yes	Yes	Yes
Socioeconomic indicators	No	No	No	No	Yes
Settlement structure indicators	No	No	No	No	Yes
Observations	89,541	89,541	89,541	89,541	89,541
Number of hospitals	1,262	1,262	1,262	1,262	1,262

(b) IV‐Probit; Instrument: Number of Potential Patients and Further Hospitals in the Regional Area
	(6)	(7)	(8)	(9)	(10)
Ln case volume	−0.0191***	−0.0247***	−0.0289***	−0.0355***	−0.0334***
	(0.0037)	(0.0039)	(0.0055)	(0.0058)	(0.0061)
Patient characteristics	No	Yes	No	Yes	Yes
Hospital charcteristics	No	No	Yes	Yes	Yes
Socioeconomic indicators	No	No	No	No	Yes
Settlement structure indicators	No	No	No	No	Yes
First‐stage F‐statistic	78.1848	80.0255	47.8049	48.2419	42.3054
Test for endogeneity (p‐value)	0.0005	0.0000	0.0002	0.0000	0.0001
Overidentification test (p‐value)	0.0043	0.0006	0.0936	0.039	0.0999
Observations	89,541	89,541	89,541	89,541	89,541
Number of hospitals	1,262	1,262	1,262	1,262	1,262

(c) IV‐Probit; Instrument: Number of Potential Patients per Hospital in the Regional Area
	(11)	(12)	(13)	(14)	(15)
Ln case volume	−0.0138***	−0.0176***	−0.0217***	−0.0280***	−0.0259***
	(0.0037)	(0.0041)	(0.0060)	(0.0066)	(0.0071)
Patient characteristics	No	Yes	No	Yes	Yes
Hospital charcteristics	No	No	Yes	Yes	Yes
Socioeconomic indicators	No	No	No	No	Yes
Settlement structure indicators	No	No	No	No	Yes
First‐stage F‐statistic	186.7512	189.1469	130.9806	130.7457	119.6255
Test for endogeneity (p‐value)	0.0930	0.0372	0.0557	0.0175	0.0299
Observations	89,541	89,541	89,541	89,541	89,541
Number of hospitals	1,262	1,262	1,262	1,262	1,262

Clustered standard errors (at the hospital level) in parentheses. *p < .10, **p < .05, ***p < .01.

The probit coefficients show only an association between volume and outcome rather than a causal effect. Therefore, we consider the IV estimation results. The first‐stage regressions for the full models of the two different instrument specifications (Table A3 in Appendix SA2) show that the instruments are separately statistically significant (p < .01) and have the expected sign: the more hip fracture patients in the area around hospital i, the higher the case volume of hospital i, and the more other hospitals in the area of hospital i, the lower the case volume of hospital i. The coefficients decrease with increasing radii. Also for the single instrument we find the expected sign: the higher the number of potential patients per hospital in a regional area, the higher the case volume of hospital i. The instruments are also jointly significant with an F‐test of 42 for the full model, which is above the generally accepted value of 10, or 15 in the case of five instruments (Stock, Wright, and Yogo 2002). This is also true for the single instrument with an F‐test of 120. As such, it seems that we do not have problems with weak instruments in our case. Using the exogeneity test, we have to reject the null hypothesis that case volume is exogenous at the 5 percent level and therefore use IV regression. We also apply an overidentification test to the validity of overidentifying instruments. We cannot reject the null hypothesis (p > .05) that the instruments are valid for the last model—our preferred specification.

The IV coefficients (Table 2, models (6)–(15)) reflect the causal effect of volume on outcome. Both instruments lead to qualitatively the same results but in case with the single instrument case volume coefficients are smaller. We want to stick to the more conservative estimate and go further in explanations with the single instrument.

Our preferred specification is model (15), with a ln case volume coefficient of −0.026, indicating that an increase of 1 percent in case volume reduces the probability of death by 0.026 percentage points (pp).5 Based on these estimated relationships, a patient who is treated in a hospital with 60 cases has a probability of death of 4.56 percent. An increase of 10 cases reduces the probability of death by 0.36 pp to 4.20 percent. We calculated the probability changes for an “average” patient, that is, set all variables of the model except case volume at their means.

As the functional form, we chose the logarithm of volume with the assumption that the effect of case volume decreases with increasing case volume. However, because there are no clear theoretical recommendations about the functional form (Luft et al. 1990), we also estimated our model with a linear function of volume and a square root function of volume. The coefficients are not directly comparable but all show a significant negative effect of volume on mortality. Hence, we measure the effect of case volume for each specification, taking the “average” patient once again. We show the probability of death for each functional form with increasing case volume in Figure 1. It is clear that the functional forms differ only for low volumes, while with increasing volume, the effects of the different functional forms converge.

Figure 1.

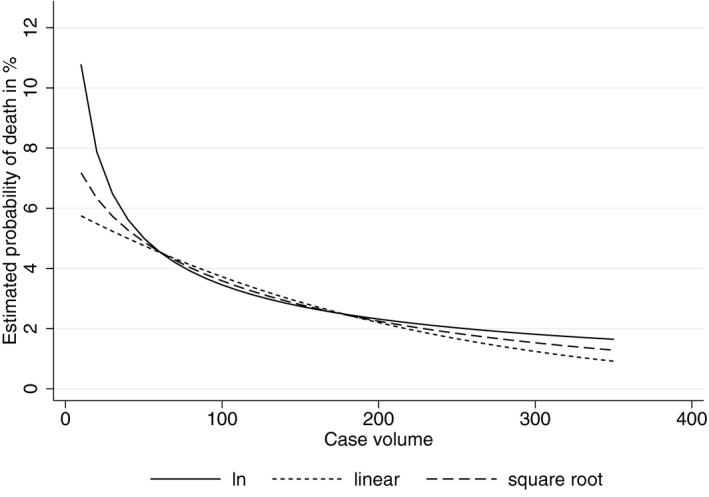
Estimated Probability of Death for Different Volume Functions

As shown in Figure 1, the three curves exhibit a similar shape from a case volume of 60 onward. In total, 20,446 patients are treated in hospitals with 60 patients or fewer. Using a case volume of 60 and our “average” patient, we derive an estimated probability for an in‐hospital mortality rate of 4.6 percent, based on our IV‐Probit model. This means that 941 of the 20,446 patients treated in these hospitals would die. Note that this is an optimistic estimate of in‐hospital mortality for this patient population as the actual case volume for these hospitals varies between 1 and 60 and for patients treated in hospitals with much fewer than 60 cases, the actual in‐hospital mortality would be higher.

For patients treated in hospitals with more than 60 cases (N = 69,095), the “median patient” is treated in a hospital with 110 cases with an estimated average mortality rate of 3.3 percent, which is again based on our IV‐Probit model. If 20,446 patients treated in hospitals with 60 patients or fewer are in fact treated in the same way as this “median patient,” the number of deaths in this subsample could be reduced from 941 to 675. This means that 266 deaths (95% confidence interval, 204–327 deaths) could have been avoided if patients were treated in a hospital with an average of 110 cases. If hip fracture surgeries were no longer done in hospitals with volumes below 60, then within a travel time of 20 minutes, 52 percent of the patients cared for in those facilities could have reached one treating over 60 cases, and in that same time frame, 31 percent of the cases seen at low‐volume sites could have been seen at centers with volumes exceeding 110 cases. If the target travel time is 30 minutes, the comparable figures are 79 and 53 percent.

Conclusion

In this paper, we examine the causal relationship of volume on outcome for hip fracture patients. We use a full sample of all inpatients in Germany from 2007. To overcome endogeneity concerns, we apply an IV approach, which allows us to assess the plain effect of volume on outcome by excluding any effects of selective referral or unobserved patient heterogeneity. We find evidence of a causal relationship of volume on outcome. Our results indicate that increasing the number of cases treated by a hospital from 60 to 70 decreases the probability of death by 0.36 pp. For an estimate of the number of potentially avoidable deaths, we calculated the number of deaths among patients treated in hospitals with 60 cases or fewer using the estimated in‐hospital mortality rates for hospitals with 110 cases. If these patients had been treated in a higher volume facility, 266 deaths could have been avoided.

With this study, we are the first who provide evidence for the practice‐makes‐perfect hypothesis using German data. Analyzing the causal relationship of the volume–outcome effect is essential as policies could otherwise be focused in the wrong direction. We contribute to the debate on minimum‐volume regulations in Germany by showing that volume is a driving factor for quality and, as such, minimum‐volume regulations could be beneficial by driving very‐low‐volume providers out of the market. However, before such policies are introduced, or rather, before policy changes are made, more analyses are needed when it comes to deriving adequate minimum‐volume standards, that is, to determine the thresholds at which significant quality differences are observable. We refrain from deriving specific thresholds owing to several study limitations. First, using administrative data we have only been able to use in‐hospital mortality as the quality outcome. Before recommending thresholds, other outcomes, such as walking distance at discharge or postoperative infection rate, should also be considered (AQUA 2015). Second, at low volumes our sensitivity analyses regarding the functional form of volume show substantial variations. Given that we cannot provide conclusive evidence for the superiority of a specific functional form, any recommendation for a minimum‐volume standard would be premature. Third, we had to delete all patients who had “transfer” as a discharge reason due to the fact the outcome is undetermined for these patients. We observe patients with discharge reason transfer in every volume category with the similar shares and we notice that it is highly unlikely that they all are transferred to die in another hospital. However, we do not know the actual outcome of these patients, and we believe that we cannot make any concluding remarks about this sample of transferred patients. Further research should link patients with the admitting institution to track the outcomes. Fourth, even though we can control for many confounders in our dataset, that is, patient and hospital characteristics, we cannot preclude whether there are still any unobserved instrument‐outcome confounders, which influence the results.

However, with the introduction of minimum volumes, there are further important factors that need to be considered to guarantee sufficient care provision. The preclusion of treatment in specific conditions for hospitals that do not achieve the minimum‐volume means that access to care is deteriorating. However, recent evidence suggests that access to health care is not at risk in Germany (Mennicken et al. 2014; Hentschker and Mennicken 2015), meaning that maintaining access cannot be used as an excuse for lower standards in the German context: There are only a few regions in the country where it may be necessary for sole providers to remain open even if they are under the minimum‐volume threshold in order to guarantee sufficient access to care (Gale and Coburn 2003).

What remains unclear are the possible consequences for quality from a higher concentration of providers in the market. Economic theory states that with decreasing competition quality declines. The empirical literature confirms this theory (e.g., Kessler and McClellan 2000; Gaynor, Moreno‐Serra, and Propper 2013). Some studies come to different conclusions (e.g., Mukamel, Zwanziger, and Tomaszewski 2001; Gowrisankaran and Town 2003). To date, however, most of the studies show a negative effect of concentration on outcomes (Gaynor and Town 2012). The trade‐off between better quality through high volume and lower quality through fewer providers still must be solved. One solution may be to start with lower minimum‐volume standards. This would mean that only hospitals with the lowest volumes drop out of the market, with negligible consequences for market concentration.

Supporting information

Appendix SA1: Author Matrix.

Appendix SA2:

Figure A1. Inclusion and Exclusion Criteria for Hip Fracture Patients.

Table A1. Descriptive Statistics for Hip Fracture Patients – Elixhauser Comorbidities.

Table A2. Marginal Effects of Probit and IV‐Probit Estimates (Full Models).

Table A3. First‐Stage Regression Explaining In Case Volume.